Rhombic Coulomb diamonds in a single-electron transistor based on an Au nanoparticle chemically anchored at both ends

Abstract

Rhombic Coulomb diamonds are clearly observed in a chemically anchored Au nanoparticle single-electron transistor. The stability diagrams show stable Coulomb blockade phenomena and agree with the theoretical curve calculated using the orthodox model. The resistances and capacitances of the double-barrier tunneling junctions between the source electrode and the Au core (R₁ and C₁, respectively), and those between the Au core and the drain electrode (R₂ and C₂, respectively), are evaluated as 4.5 MΩ, 1.4 aF, 4.8 MΩ, and 1.3 aF, respectively. This is determined by fitting the theoretical curve against the experimental Coulomb staircases. Two-methylene-group short octanedithiols (C8S2) in a C8S2/hexanethiol (C6S) mixed self-assembled monolayer is concluded to chemically anchor the core of the Au nanoparticle at both ends between the electroless-Au-plated nanogap electrodes even when the Au nanoparticle is protected by decanethiol (C10S). This is because the R₁ value is identical to that of R₂ and corresponds to the tunneling resistances of the octanedithiol chemically bonded with the Au core and the Au electrodes. The dependence of the Coulomb diamond shapes on the tunneling resistance ratio (R₁/R₂) is also discussed, especially in the case of the rhombic Coulomb diamonds. Rhombic Coulomb diamonds result from chemical anchoring of the core of the Au nanoparticle at both ends between the electroless-Au-plated nanogap electrodes.

---

1. Introduction

Formation of a functional structure of a desired texture on the subnanometer scale is a primary concern in the design of nanodevices such as single-electron and molecular devices.^1–4 A molecule-based chemical assembly technique is one of the candidate methods for realizing subnanometer-scale formation, as molecules have unique structures and can be used as building blocks.^4,5 Despite their simple structures, alkanethiols and alkanedithiols consisting of alkyl chains and thiols groups have been extensively studied in both electronics and photonics fields.^6–8 It is well known that the thiol groups in these molecules can be chemically bonded onto the surfaces of metal electrodes. Further, their tunneling resistance depends on the chain lengths of the alkyl units; therefore, they are strong candidates for use as building blocks in nanodevices.^4,9–11

Single-electron transistors (SETs) have been studied extensively as prospective nanodevices because of their potential for low power consumption and high charge sensitivity.^12–18 In SETs, a quantum dot is electrically connected to the two reservoirs of the source (S) and drain (D) electrodes as a Coulomb island, to form double-barrier tunneling junctions (DBTJs). The gate electrode is located near the Coulomb island to control the offset charge of the quantum dot using the gate voltage V_G. The drain current (I_D) flows between the S and D electrodes by way of the Coulomb island. The drain current–drain voltage (I_D–V_D) characteristics of the SETs involve the Coulomb blockade region, where the current flow is restricted even under the application of V_D, and exhibit a Coulomb staircase profile. These characteristics are described by the orthodox model, that is governed by tunneling rates and master equations for DBTJs.^10,14,19 The I_D–V_D characteristics can be calculated by considering the following five parameters: the capacitance between the source and the Coulomb island (C₁) and that between the Coulomb island and the drain (C₂), the tunneling resistance between the S electrode and the Coulomb island (R₁), and that between the Coulomb island and the D electrode (R₂), and the offset charge (Q₀).^10,19–21 These five parameters can be evaluated by fitting the theoretical curves obtained from the orthodox model to the experimental I_D–V_D characteristics.^10,19 Over the past two decades, many SET structures have been realized, based on top-down silicon techniques and two-dimensional electron gases of GaAs-based materials, for example.^22–29 SETs have also been fabricated by combining top-down and bottom-up technologies.^30–39

Recently, we have demonstrated the fabrication processes for chemically assembled SETs consisting of electroless-Au-plated nanogap electrodes^40–42 covered by alkanethiol- and alkanedithiol-mixed self-assembled monolayers (SAMs),^8,10,43,44 with chemically anchored Au nanoparticles^20,45–47 positioned between the nanogap electrodes. Chemically assembled SETs exhibit ideal and reproducible Coulomb diamonds,^48–50 uniform and controllable charging energy E_C,^48,51–53 discrete Au nanoparticle energy levels,⁵⁴ adoption of SiNx passivation,⁵⁵ and all the two-input logic operations.⁵⁶ The robustness of the chemically assembled SETs is extremely high, for instance, the gate voltage of ±12 V is available.⁴⁸ The structures of these SETs have been discussed in terms of the values of the five parameters determined from the experimental Coulomb diamonds. In particular, C₁ and C₂ have been found to be dependent on the diameter of the Coulomb island and to agree with a concentric sphere model.⁵¹

On the other hand, R₁ and R₂ have been analyzed in a step-by-step manner as follows: in the case of a physisorbed Au nanoparticle on an Au electrode surface, the tunneling resistance between the Au core and the Au electrodes was found to be identical to that of a chemically bonded alkanethiol protecting molecule on an Au core surface using scanning tunneling spectroscopy (STS) measurements. These tunneling resistances were evaluated as 460 MΩ and 7.6 GΩ on hexanethiol (C6S) and octanethiol (C8S), respectively. This indicates an increase of one order of magnitude in the tunneling resistance with increasing alkyl chain length in a two-methylene group.^{4,8,10,20,57,58} In the case of our SETs consisting of a decanethiol (C10S)-protected Au nanoparticle and electroless-Au-plated nanogap electrodes, the C10S-protected Au nanoparticles were chemisorbed by the use of the decanedithiol (C10S2) anchor molecule in a C10S2/S8S mixed SAM on the surfaces of electroless-Au-plated nanogap electrodes. In the case of an Au nanoparticle single-side chemisorbed by a C10S2 anchor molecule, the typical resistance of the chemisorbed nanoparticles between the Au core and the Au(111) substrate was measured at 1.2 GΩ.⁴⁸ As reduction in the tunneling resistance is key to improving the SET signal-to-noise, it is important to attempt to shorten the chain length of the anchor molecule.

In this study, we demonstrate rhombic Coulomb diamonds on a chemically assembled SET consisting of a C10S-protected Au nanoparticle anchored by octanedithiol (C8S2) between the electroless-Au-plated nanogap electrodes. The adsorption of the Au nanoparticle is discussed in terms of the values of resistances and capacitances of the DBTJs between the Au core and the S/D electrodes. The tunneling resistance ratio (R₁/R₂) dependence of the Coulomb diamond shapes is also discussed.

2. Results and discussion

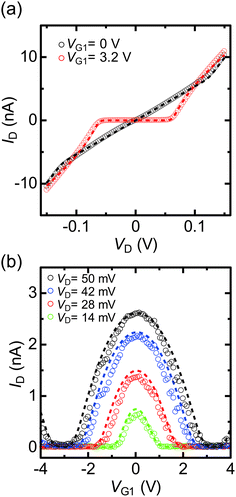
Fig. 1(a) shows the equivalent circuit of a fabricated SET with two side-gate (G1 and G2) electrodes, while Fig. 1(b) is a scanning electron microscopy (SEM) image of the SET. A single bright spot can be confirmed between the S and D electrodes in the SEM image. Fig. 1(c) shows the candidate schematic diagram of the SET with the top view perspective. Chemical anchoring of the core of the Au nanoparticle between the electroless-Au-plated nanogap electrodes is discussed as follows. Fig. 2(a) shows the experimental I_D–V_D characteristics under the application of G1 voltage (V_G1) = 0 and 3.2 V, which correspond to the on and off states (Q₀ = 0.5e and 0) of the SET, respectively. The experimental I_D–V_D characteristics were fitted against theoretical curves,^10,19 and agree with the theoretical curve obtained for the parameters R₁ = 4.5 MΩ, R₂ = 4.8 MΩ, C₁ = 1.4 aF, and C₂ = 1.3 aF. Note that R₁ and R₂, and C₁ and C₂, were almost equivalent.

Fig. 1 (a) Equivalent circuit of chemically assembled SET with G1 and G2. (b) SEM image of fabricated SET. (c) Schematic diagram of the magnified SET with the top-view perspective. Two-methylene-group short C8S2s in a C8S2/C6S mixed self-assembled monolayer chemically anchor the core of the Au nanoparticle at both ends between the electroless-Au-plated nanogap electrodes while the Au nanoparticle is protected by C10S.

Fig. 2 (a) Experimental I_D–V_D characteristics under applied V_G1 = 0 and 3.2 V at T = 9 K. Theoretical I_D–V_D characteristics (dashed lines) are also shown. Here, Q₀ = 0.5e for V_G1 = 0 and Q₀ = 0 for V_G1 = 3.2 V. (b) Experimental I_D − V_G1 characteristics under applied V_D = 14, 28, 42, and 50 mV. The theoretical characteristics calculated for Q₀ = 0.5e are also shown. In (a) and (b), the common parameters for the theoretical calculation are: R₁ = 4.5 MΩ, R₂ = 4.8 MΩ, C₁ = 1.4 aF, C₂ = 1.3 aF, and T = 9 K.

Fig. 2(b) shows the experimental I_D–V_G1 characteristics under the application of V_D = 14, 28, 42 and 50 mV. Clear and stable Coulomb oscillations were observed. Theoretical curves were calculated using the same R₁, R₂, C₁, and C₂ parameters as above, with the G1 capacitance (C_G1) being 0.025 aF. The theoretical curves in Fig. 2(a) (dashed lines) also agree with the experimental results. In Fig. 2(b), the experimental I_D–V_G1 characteristics were symmetric at the axis of V_G1 = 0. These symmetric Coulomb oscillations originated from the same R₁ and R₂.²⁴

Next, we consider the Coulomb oscillation dependence on R₁/R₂. Fig. 3(a) shows the R₁/R₂ ratio dependence of the theoretical I_D–V_G1 curves under the application of V_D = 28 mV, which was almost half the Coulomb-diamond peak voltage. The value of R₂ was adjusted to yield R₁/R₂ ratios within the 0.001–1000 range, with R₁ = 4.5 MΩ, C₁ = 1.4 aF, C₂ = 1.3 aF, and C_G1 = 0.025 aF. I_D was normalized by the maximum current I_peak. At R₁/R₂ = 1, the symmetric Coulomb oscillation at the V_G1 = 0 axis was observed. In contrast, the I_D/I_peak peak voltages negatively and positively shifted under R₁ < R₂ and R₁ > R₂ conditions, respectively, however, the current rising and falling V_G1 voltages did not change, as the Coulomb blockade break voltages are defined by C₁ and C₂.^10,19Fig. 3(b) shows the V_G1 peak shift (ΔV_G, illustrated in Fig. 3(a)) dependence on the R₁/R₂ ratio under various V_D. From this calculation, the large difference between R₁ and R₂ as well as the large V_D resulted in large ΔV_G. The difference between R₁ and R₂ means that the adsorption condition of the Au nanoparticle between the S and D electrodes was asymmetric. Therefore, chemical anchoring of Au nanoparticles onto both the S and D electrodes resulted in symmetric I_D–V_G1 characteristics.

Fig. 3 (a) I_D–V_G1 calculated for varying R₁/R₂ ratios under applied V_D = 28 mV. Here, I_D is normalized by I_peak, and V_G1 is normalized by the Coulomb oscillation period (e). The following parameters are used: C₁ = 1.4 aF, C₂ = 1.3 aF, C_G1 = 0.025 aF, R₁ = 4.5 MΩ, and T = 9 K. (b) ΔV_G dependence on the R₁/R₂ ratio under various V_D.

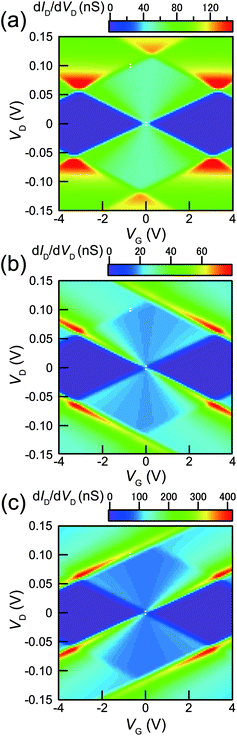
Fig. 4(a) and (b) show the experimental stability diagrams obtained by plotting the color maps of dI_D/dV_D for the SET as functions of V_D and V_G1 and V_D and V_G2, respectively. In both the stability diagrams, clear and reproducible Coulomb diamonds can be observed. As indicated above, C₁, C₂, and C_G can be evaluated from the shape of the Coulomb diamonds.¹² From the boundary slopes of the diamonds and the gate voltage difference between neighboring diamonds, C₁, C₂, C_G1, and C_G2 were evaluated as 1.4, 1.3, 0.025 and 0.015 aF, respectively. The C₁ and C₂ values obtained from Fig. 4(a) and (b) agree with the values obtained from the theoretical fitting shown in Fig. 2(a). Note that the Coulomb diamond shapes are primarily determined by C₁, C₂, C_G1, and C_G2, as reported in a previous study.¹² For the majority of the experimentally reported Coulomb diamonds, including those in our previous reports, the diamonds were parallelograms rather than rhombuses, because of differences between C₁ and C₂.^{48,49,54–56} In contrast, comparable C₁ and C₂ result in the almost rhombic diamond shapes apparent in Fig. 4(a) and (b).

Fig. 4 Experimental stability diagrams obtained by plotting color maps of dI_D/V_D for the fabricated SET as functions of (a) V_D and V_G1 and (b) V_D and V_G2. Both measurements are carried out at T = 9 K.

Compared with the diamond shapes, the external regions of the Coulomb diamonds are also noteworthy. In our previous reports, the conductance peak lines along the edges of the Coulomb diamonds were extrapolated outside the diamonds.^48,51,54,56 In contrast, the experimental Coulomb diamonds in Fig. 4(a) and (b) did not exhibit such extrapolated conductance peak lines. Besides the conductance peak lines, higher conduction regions were observed near the Coulomb diamond vertexes, such as V_D = 0.07 V and V_G1 = 3.2 V in Fig. 4(a). This difference cannot be explained by consideration of the capacitance values.

Previously, we have measured the Coulomb staircases in DBTJs consisting of a scanning-probe/vacuum-gap/alkanethiol-protected Au nanoparticle/Au(111) electrode as a function of the set point current using scanning tunneling spectroscopy,¹⁰ demonstrating that the Coulomb staircase profiles depend on R₁/R₂. This result indicates that not only the Coulomb staircase profiles, but also those of the stability diagrams depend on the R₁/R₂ ratio. Fig. 5(a) shows the stability diagrams (dI_D/dV_D plots) calculated for R₁ = 4.5 MΩ, R₂ = 4.8 MΩ, C₁ = 1.4 aF, C₂ = 1.3 aF, C_G1 = 0.025 aF, and Q₀ = 0.5e at a temperature (T) of 9 K. The theoretical stability diagram agrees with the experimental stability diagram shown in Fig. 4(a). Fig. 5(b) shows the stability diagram calculated using the same parameters in Fig. 5(a), except R₂ = 5R₁ (= 22.5 MΩ). Under this condition, higher conduction regions were not observed near the Coulomb diamond vertexes, but downward conductance peak lines were extrapolated along the Coulomb diamond edges. Fig. 5(c) shows the theoretical stability diagram calculated for the same parameters of Fig. 5(a), except R₂ = 0.2R₁ (= 0.90 MΩ). Under this condition, conductance peak lines extrapolated upward along the Coulomb diamond edges were observed. Consequently, the shapes of the SET stability diagrams are strongly dependent on R₁/R₂.

Fig. 5 Theoretical stability diagrams calculated under different R₂ of: (a) 4.8 MΩ (R₂ ≃ R₁), (b) 22.5 MΩ (R₂ = 5R₁), and (c) 0.90 MΩ (R₂ = ⅕R₁). The other parameters: R₁ = 4.5 MΩ, C₁ = 1.4 aF, C₂ = 1.3 aF, C_G = 0.025 aF, Q₀ = 0.5e and T = 9 K, are identical for (a)–(c).

In general, the tunneling resistances of R₁ and R₂ are exponentially proportional to the tunneling distance between the Au core and the S/D electrodes, in contrast, the capacitances C₁ and C₂ are approximately inversely proportional to the distance between the Au core and the S/D electrodes. When R₁ becomes comparable to R₂ as shown in Fig. 2(a), the distance between the Au core and the surface of the source electrode is equal to that between the Au core and the surface of the drain electrode. Due to these two different dependences against the distance, the comparable R₁ and R₂ results in comparable C₁ and C₂, since the shape of the Au nanoparticle is spherical. It is also noted that the comparable C₁ and C₂ does not always result in the comparable R₁ and R₂. Consequently, rhombic Coulomb diamonds result from chemical anchoring of the Au core by octanedithiols at the both ends between the electroless-Au-plated nanogap electrodes.

In our previous chemically assembled SETs,^{48–52,54–56} a C10S2/C8S mixed SAM was used to anchor a C10S-protected Au nanoparticle and different R₁ and R₂ pair values were observed. In contrast, here we used a C8S2/C6S mixed SAM to anchor a C10S-protected Au nanoparticle to reduce the tunneling resistances. As a result, equal and smaller R₁ and R₂ of 4.5 and 4.8 MΩ, respectively were obtained. Fig. 6 shows the SEM images of C10S-protected Au nanoparticles on a C8S2/C6S mixed SAM/Au substrate. The C8S2/C6S mixed SAM/Au substrate fabrication method and the Au nanoparticle solution immersion time were identical to those of the SETs. In this case, the Au nanoparticle density was 88 per 100 × 100 nm². We have previously reported the anchoring of a C10S-protected Au nanoparticle by a C10S2 molecule within C10S2/C8S SAMs using STM and STS measurements, with a density of 22 per 100 × 100 nm².⁸ It should be noted that the density of the C8S2-anchored C10S-protected Au nanoparticles is of the same order of magnitude as the C10S2-anchored C10-protected Au nanoparticles, even if the alkyl chain length of the anchor molecule is shorter than that of the protecting molecule. The values of the tunneling resistances (4.5 MΩ) are comparable to that of the resistance of C8S2 on Au electrodes, as measured using an Au-coated atomic force microscopy tip.⁹ Due to the two thiol groups in C8S2, the molecular length of C8S2 as the anchor molecule becomes almost the same as that of C10S as the protecting group of the Au nanoparticle. Consequently, as shown in the top view schematic diagram of Fig. 1(c), two-methylene-group short C8S2 in a C8S2/C6S mixed self-assembled monolayer is concluded to chemically anchor the core of the Au nanoparticle at both ends between the electroless-Au-plated nanogap electrodes even when the Au nanoparticle is protected by C10S. Moreover, the tunneling resistance decreased through use of the C8S2 anchor molecule, with the value being more than one order of magnitude less than in the case involving C10S2 anchoring. Because of this improved fabrication process, rhombic Coulomb diamonds were demonstrated. The availability of the two-methylene-group shorter anchoring molecule is significant for the applications of chemically assembled SETs, as lower and more stable tunneling resistance can be obtained.

Fig. 6 SEM images of Au nanoparticles anchored by C8S2 on the C8S2/C6S mixed SAM/Au substrate. The Au nanoparticle solution immersion time was 12 h and the Au nanoparticle density was 88 per 100 × 100 nm².

3. Experimental

We used electron beam lithography and a lift-off process to fabricate the initial Ti (2 nm)/Au (10 nm) electrode patterns, comprising S, D, G1 and G2 electrodes on a SiO₂ (50 nm)/Si substrate. Prior to the electroless Au plating, the initial Au electrodes were cleaned using O₂ plasma treatment. Probing electrodes of 150 × 150 μm² area were then added via photolithography, and electroless plating in an Au iodine solution reduced the nanogap sizes via a self-termination reaction.^40–42 The nanogap electrodes were immersed in a 1 mM hexanethiol [CH₃(CH₂)₅SH, C6S] solution in ethanol for 12 h to allow the formation of the C6S self-assembled monolayers (SAMs); the electrodes were then rinsed with ethanol twice. Subsequently, the sample was immersed in a 1 mM octanedithiol [HS(CH₂)₈SH, C8S2] solution in ethanol for 12 h to yield C8S2/C6S mixed SAMs. It was then rinsed with ethanol twice.⁸ After the substitution, the sample was immersed in a solution of decanethiol [CH₃(CH₂)₉SH, C10S]-protected Au nanoparticles with a core diameter of 6.2 ± 0.8 nm in toluene for 12 h. It was then rinsed with toluene twice. The electrical measurements were conducted using a semiconductor parameter analyzer (Agilent B1500, USA) in a vacuum (∼10⁻⁵ Pa) at 9 K (in a helium refrigerator, Nagase GRAIL10-LOGOS01S, Japan). The experimental differential conductances dI_D/dV_D were numerically calculated based on the experimental I_D–V_D characteristics.

4. Conclusions

We have demonstrated rhombic Coulomb diamonds in a chemically anchored Au-nanoparticle SET consisting of a C10S-protected Au nanoparticle anchored by C8S2 molecules at both ends of an electroless-Au-plated nanogap. The I_D–V_D characteristics showed Coulomb blockade phenomena and agree with the theoretical fitting curve calculated using the orthodox model. The evaluated R₁ and R₂ were almost identical, at 4.5 and 4.8 MΩ, respectively, and are attributed to the tunneling resistance of the chemisorbed octanedithiol at both ends. The experimental stability diagram agreed with the theoretical calculation with R₁, R₂, C₁, and C₂ being evaluated from the I_D–V_D characteristics. The changes in the stability diagrams for R₁ ≃ R₂ (double-anchored Au nanoparticle), R₁ > R₂, and R₁ > R₂ (single-anchored Au nanoparticle) were discussed. In the stability diagrams, identical R₁ and R₂ did not yield extrapolated conductance peak lines. In contrast, different R₁ and R₂ corresponded to asymmetric adsorption, as indicated by the extrapolated conductance peak lines. The realization of a symmetric chemically anchored Au nanoparticle between S and D electrodes is significant, as it yields rhombic Coulomb diamonds.

Acknowledgements

We thank Ms M. Miyakawa for technical support regarding SEM. This study was partially supported by the MEXT Elements Strategy Initiative to Form Core Research Center of the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan; JSPS KAKENHI (15K17483) (Y. A.), the Collaborative Research Project of the Materials and Structures Laboratory, Tokyo Institute of Technology; the Collaborative Research Project of the Institute of Chemical Research, Kyoto University (Grant 2015-72); and the BK Plus program, the Ministry of Education of Korea through the Basic Research Science Program (NRF-2014R1A6A1030419).

References

1. M. Ratner, Nat. Nanotechnol., 2013, 8, 378–381.
2. J. Park, H. Park, A. K. L. Lim, E. H. Anderson, A. P. Alivisatos and P. L. McEuen, Nature, 2000, 407, 57–60.
3. S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J.-L. Brédas, P. Stuhr-Hansen, N. Hedegård and T. Bjø rnholm, Nature, 2005, 425, 698–701.
4. Y. Yasutake, Z. Shi, T. Okazaki, H. Shinohara and Y. Majima, Nano Lett., 2005, 5, 1057–1060.
5. K. Ariga and H. S. Nalwa, Bottom-up Nanofabrication, Volume 3 Self-Assemblies-I, American Scientific Publishers, California, 2009.
6. P. E. Laibinis, G. M. Whitesides, D. L. Allara, Y.-T. Tao, A. N. Parikh and R. G. Nuzzo, J. Am. Chem. Soc., 1991, 113, 7152–7167.
7. R. Yamada and K. Uosaki, Langmuir, 1997, 13, 5218–5221.
8. X. Li, Y. Yasutake, K. Kono, M. Kanehara, T. Teranishi and Y. Majima, Jpn. J. Appl. Phys., 2009, 48, 04C180.
9. V. B. Engelkes, J. M. Beebe and D. Frisbie, J. Am. Chem. Soc., 2004, 126, 14287–14296.
10. H. Zhang, Y. Yasutake, Y. Shichibu, T. Teranishi and Y. Majima, Phys. Rev. B: Condens. Matter, 2005, 72, 205441.
11. W. Wang, T. Lee and M. A. Reed, Phys. Rev. B: Condens. Matter, 2003, 68, 035416.
12. Z. A. K. Durrani, Single-Electron Devices and Circuits in Silicon, Imperial College London, London, 2009.
13. K. Nakazato, R. J. Blaikie and H. Ahmed, J. Appl. Phys., 1994, 75, 5123–5134.
14. K. K. Likharev, Proc. IEEE, 1999, 87, 606–632.
15. K. Yano, T. Sano, T. Mine, F. Murai, T. Hashimoto, T. Kobayashi, T. Kure and K. Seki, Single-electron memory for giga-to-tera bit storage, Proc. IEEE, 1999, 87, 633–651.
16. Y. Ono, A. Y. Fujisawa, K. Nishiguchi, H. Inokawa and Y. Takahashi, J. Appl. Phys., 2005, 97, 031101.
17. K. Ishibashi, S. Moriyama, D. Tsuya, T. Fuse and M. Suzuki, J. Vac. Sci. Technol. A, 2006, 24, 1349–1355.
18. R. J. Schoelkopf, P. Wahlgren, A. A. Kozhevnikov, P. Delsing and D. E. Prober, Science, 1998, 280, 1238–1242.
19. A. E. Hanna and M. Tinkham, Phys. Rev. B: Condens. Matter, 1991, 44, 5919–5922.
20. S. Kano, T. Tada and Y. Majima, Chem. Soc. Rev., 2015, 44, 970–987.
21. S. Kano, K. Maeda, D. Tanaka, M. Sakamoto, T. Teranishi and Y. Majima, J. Appl. Phys., 2015, 118, 134304.
22. Y. Takahashi, H. Namatsu, K. Kurihara, K. Iwadate, M. Nagase and K. Murase, IEEE Trans. Electron Devices, 1996, 43, 1213–1217.
23. U. F. Keyser, H. W. Schumacher, U. Zeitler, R. J. Haug and K. Eberl, Fabrication of a single-electron transistor by current-controlled local oxidation of a two-dimensional electron system, Appl. Phys. Lett., 2010, 76, 457–459.
24. C. Wasshuber, Computational Single-Electronics, Springer-Verlag, Wien, 2001.
25. Y. S. Yu, S. W. Hwang and D. Ahn, IEEE Trans. Electron Devices, 1999, 46, 1667–1671.
26. K. Uchida, K. Matsuzawa, J. Koga, R. Ohba, A. Takagi and S. ans Toriumi, Jpn. J. Appl. Phys., 2000, 39, 2321–2324.
27. X. Wang and W. Porod, Superlattices Microstruct., 2000, 28, 345–349.
28. S.-H. Lee, D. H. Kim, K. R. Kim, J. D. Lee, B.-G. Park, Y.-J. Gu, G.-Y. Yang and J.-T. Kong, IEEE Trans. Nanotechnol., 2002, 1, 226–232.
29. G. Lientschnig, I. Weymann and P. Hadley, Jpn. J. Appl. Phys., 2003, 42, 6467–6472.
30. D. L. Feldheim and C. D. Keating, Chem. Soc. Rev., 1998, 27, 1–12.
31. D. I. Gittins, D. Bethell, D. J. Schiffrin and R. J. Nichols, Nature, 2000, 408, 67–69.
32. Y. Cui and C. M. Lieber, Science, 2001, 291, 851–853.
33. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
34. C. S. Wu, C. D. Chen, S. M. Shih and W. F. Su, Appl. Phys. Lett., 2002, 81, 4595–4597.
35. S.-W. Chung, D. S. Ginger, M. W. Morales, Z. Zhang, V. Chandrasekhar, M. A. Ratner and C. A. Mirkin, Small, 2005, 1, 64–69.
36. W. Lu and C. M. Lieber, Nat. Mater., 2007, 6, 841–850.
37. K. Ariga, J. P. Hill and Q. Ji, Phys. Chem. Chem. Phys., 2007, 9, 2319–2340.
38. L. Zhi and K. Müllen, J. Mater. Chem., 2008, 18, 1472–1484.
39. Y. Noguchi, M. Yamamoto, H. Ishii, R. Ueda, T. Terui, K. Imazu, K. Tamada, T. Sakano and K. Matsuda, Jpn. J. Appl. Phys., 2013, 52, 110102.
40. Y. Yasutake, K. Kono, M. Kanehara, T. Teranishi, M. R. Buitelaar, C. G. Smith and Y. Majima, Appl. Phys. Lett., 2007, 91, 203107.
41. V. V. M. Serdio, Y. Azuma, S. Takeshita, T. Muraki, T. Teranishi and Y. Majima, Nanoscale, 2012, 4, 7161–7167.
42. V. V. M. Serdio, T. Muraki, S. Takeshita, S. D. E. Hurtado, S. Kano, T. Teranishi and Y. Majima, RSC Adv., 2015, 5, 22160–22167.
43. S. Kano, Y. Azuma, M. Kanehara, T. Teranishi and Y. Majima, Appl. Phys. Express, 2010, 3, 105003.
44. H. Koo, S. Kano, D. Tanaka, M. Sakamoto, T. Teranishi and Y. Majima, Appl. Phys. Lett., 2012, 101, 083115.
45. T. Teranishi, S. Hasegawa, T. Shimizu and M. Miyake, Adv. Mater., 2001, 13, 1699–1701.
46. T. Shimizu, T. Teranishi, S. Hasegawa and M. Miyake, J. Phys. Chem. B, 2003, 107, 2719–2724.
47. M. Kanehara, J. Sakurai, H. Sugimura and T. Teranishi, J. Am. Chem. Soc., 2009, 131, 1630–1631.
48. N. Okabayashi, K. Maeda, T. Muraki, D. Tanaka, M. Sakamoto, T. Teranishi and Y. Majima, Appl. Phys. Lett., 2012, 100, 033101.
49. Y. Azuma, Y. Yasutake, K. Kono, M. Kanehara, T. Teranishi and Y. Majima, Jpn. J. Appl. Phys., 2010, 49, 090206.
50. Y. Azuma, S. Suzuki, K. Maeda, N. Okabayashi, D. Tanaka, M. Sakamoto, T. Teranishi, M. R. Buitelaar, C. G. Smith and Y. Majima, Appl. Phys. Lett., 2011, 99, 073109.
51. S. Kano, D. Tanaka, M. Sakamoto, T. Teranishi and Y. Majima, Nanotechnology, 2015, 26, 045702.
52. S. Kano, Y. Azuma, D. Tanaka, M. Sakamoto, T. Teranishi, L. W. Smith, C. G. Smith and Y. Majima, J. Appl. Phys., 2013, 114, 223717.
53. J. C. Frake, S. Kano, C. Ciccarelli, J. Griffiths, M. Sakamoto, T. Teranishi, Y. Majima, C. G. Smith and M. R. Buitellar, Sci. Rep., 2015, 56, 10858.
54. S. Kano, Y. Azuma, K. Maeda, D. Tanaka, M. Sakamoto, T. Teranishi, L. W. Smith, C. G. Smith and Y. Majima, ACS Nano, 2012, 6, 9972–9977.
55. G. Hackenberger, Y. Azuma, S. Kano, D. Tanaka, M. Sakamoto, T. Teranishi, Y. Ohno, K. Maehashi, K. Matsumoto and Y. Majima, Jpn. J. Appl. Phys., 2013, 52, 110101.
56. K. Maeda, N. Okabayashi, S. Kano, S. Takeshita, D. Tanaka, M. Sakamoto, T. Teranishi and Y. Majima, ACS Nano, 2012, 6, 2798–2803.
57. Y. Azuma, M. Kanehara, T. Teranishi and Y. Majima, Phys. Rev. Lett., 2006, 96, 016108.
58. Y. Majima, D. Ogawa, M. Iwamoto, Y. Azuma, E. Tsurumaki and A. Osuka, J. Am. Chem. Soc., 2013, 135, 14159–14166.

---