An ab initio study of the nickel-catalyzed transformation of amorphous carbon into graphene in rapid thermal processing

Abstract

Ab initio molecular dynamics (AIMD) simulations are employed to investigate the chemical mechanism underlying the Ni-catalyzed transformation of amorphous carbon (a-C) into graphene in the rapid thermal processing (RTP) experiment to directly grow graphene on various dielectric surfaces via the evaporation of surplus Ni and C at 1100 °C (below the melting point of bulk Ni). It is found that the a-C-to-graphene transformation entails the metal-induced crystallization and layer exchange mechanism, rather than the conventional dissolution/precipitation mechanism typically involved in Ni-catalyzed chemical vapor deposition (CVD) growth of graphene. The multi-layer graphene can be tuned by changing the relative thicknesses of deposited a-C and Ni thin films. Our AIMD simulations suggest that the easy evaporation of surplus Ni with excess C is likely attributed to the formation of a viscous-liquid-like Ni–C solution within the temperature range of 900–1800 K and to the faster diffusion of C atoms than that of Ni atoms above 600 K. Even at room temperature, sp³-C atoms in a-C are quickly converted to sp²-C atoms in the course of the simulation, and the graphitic C formation can occur at low temperature. When the temperature is as high as 1200 K, the grown graphitic structures reversely dissolve into Ni. Because the rate of temperature increase is considerably faster in the AIMD simulations than in realistic experiments, defects in the grown graphitic structures are kinetically trapped. In this kinetic growth stage, the carbon structures grown from sp³-carbon or from sp²-carbon exhibit marked differences.

---

1. Introduction

Graphene is a highly desired two-dimensional (2D) material due to its exceptional electronic, optical, and mechanical properties.^1–3 For industrial applications, however, large-area and high-quality graphene is demanded at low cost. To date, many experimental approaches have been developed to produce graphene, including mechanical exfoliation,⁴ liquid-phase exfoliation,⁵ chemical exfoliation via graphene oxide,^6,7 epitaxial growth on silicon carbide,^8,9 and metal-catalyzed chemical vapor deposition (CVD).^10–12 Among these approaches, metal-catalyzed CVD has been widely used to fabricate large-area and high-quality graphene.^13–15 Correspondingly, previous theoretical investigations on graphene growth have mainly focused on CVD growth. It is known that the CVD growth of graphene is substrate-, carbon-feedstock-, and growth-condition-dependent. To optimize the experimental CVD parameters, an in-depth understanding of the CVD growth mechanism at the atomic level is desired. Two common metal catalysts for CVD growth are Ni and Cu. Accordingly, two widely accepted but different CVD growth mechanisms are the carbon segregation/precipitation process in Ni with high carbon solubility and the surface adsorption process on Cu with negligible bulk solubility.¹⁶ Due to the huge time- and length-scale differences between realistic experiments and molecular simulation studies to describe the graphene growth mechanism, simulations typically focus on a specific aspect of the CVD growth.

Previous theoretical studies of the CVD growth of graphene mostly employed three computational methods: ab initio computation, molecular dynamics (MD) and Monte Carlo (MC) simulations, and multi-scale hybridized methods. Ab initio computation can predict quantitative reaction barriers in certain chemical processes that are involved in the graphene growth, especially for the dehydrogenation of gaseous carbon feedstock on metal surfaces.^17–19 It can also assess the relative energies of well-designed models, targeted to some specific problems such as suppression of grain boundaries by a Cu–Mn alloy²⁰ and graphene edge stabilization by Au atoms on a Ni(111) step.²¹ Ding and coworkers used density functional theory (DFT) calculations to study the thermodynamic and kinetic aspects associated with special processes in the graphene growth, such as preference of graphene nucleation near the Ni(111) step edge,²² the C₂₁ precursor in the CVD growth of graphene,²³ metal-surface-passivation-induced graphene edge reconstruction,²⁴ preferential growth of zigzag edge of graphene on Cu surfaces,²⁵ vacancy formation and healing,²⁶ and the effect of H₂ pressure on the formation of single-layer or multi-layer graphene.²⁷ To reproduce dynamic growth processes in the CVD growth of graphene, classical MD simulations combined with the reactive force-field (ReaxFF)^28–30 and the kinetic MC simulations (parameters derived from ab initio calculations)³¹ were also used by a few groups. The non-equilibrium MD simulations with the second generation of Brenner potential, REBO2, was utilized to investigate the reconstruction of divacancy in graphene under electron irradiation.³² Ding and coworkers also ran long-time MD simulations based on their developed REBO2 potential to investigate graphene growth on Ni(111) surfaces.³³ Moreover, hybrid reactive MD/MC simulations were used to study graphene formation through a combined deposition–segregation mechanism at different substrate temperatures and under the far-from-equilibrium high precursor flux conditions.³⁴ The more accurate quantum mechanical MD simulations in the framework of the self-consistent-charge density-functional tight-binding (SCC-DFTB) method have been employed by Morokuma's group to investigate the dynamics of CVD growth of graphene, such as the pentagon-first mechanism and the promotion of hexagonal ring formation in the presence of a coronene-like C₂₄ template in the initial nucleation stage on the Ni surface,³⁵ formation of graphene precursors underneath the Ni(111) surface,³⁶ comparison of catalysis of Fe(111), Ni(111), and Cu(111) surfaces,³⁷ graphene nucleation from different nickel carbides,³⁸ malleable Ni(111) step edges,³⁹ and defect healing on surface-molten copper.⁴⁰

Thus far, only a few ab initio MD (AIMD) studies have been reported for the mechanistic study of graphene growth, largely due to the very high computational cost and relatively short time scale (of the order of ∼10² ps) in AIMD.^40–42 In an early AIMD simulation based on the spin-polarized Perdew–Burke–Ernzerhof (PBE) functional with van der Waals (vdW) correction (PBE-D2) and projector augmented-wave (PAW) potentials, Ongun Özçelik et al. studied epitaxial growth of graphene without a substrate or on a boron-nitride substrate by adding C monomers or dimers to the edge of a graphene platelet.⁴¹ Shibuta et al. performed 5-ps AIMD simulations to study CH₄ decomposition on a Ni(111) surface at the initial stage of CVD growth.⁴² They found that newly formed C monomers can be buried under the subsurface region to exhibit dissolution of C in Ni.⁴² In this paper, we performed comprehensive AIMD simulations using the PBE-D3 functional with the Gaussian plane-wave (GPW) basis, implemented in the CP2K software package, to investigate the atomic-scale mechanism of metal-catalyzed transformation of amorphous carbon (a-C) to graphene in rapid thermal processing (RTP). The PBE-D3 method is shown to be quite accurate to describe the metal–metal, metal–carbon, and carbon–carbon interactions in the metal–carbon solution, on the basis of the computed formation energies of Ni–Ni, Ni–C, and C–C as a function of interatomic distance (see ESI Fig. S1†).

Our computational study was motivated by recent experimental studies of the metal-catalyzed transformation of a-C into graphene.^43–47 In particular, based on the single-step RTP, Xiong et al. successfully fabricated wafer-scale and high-quality graphene on various dielectric surfaces by direct evaporation of surplus Ni (typically ∼65 nm thin film) and excess a-C (typically 5 nm thin film) at an elevated temperature (1100 °C).⁴⁷ The RTP approach can eliminate the post-growth treatment, the removal of metal substrate and graphene transfer, and limit the wrinkle formation in graphene.⁴⁷ To our knowledge, this is the first atomic-level simulation study of the growth mechanism underlying the metal-catalyzed transformation of a-C into graphene in RTP. We are aware of one previous QM/MD study, using the non-consistent charge DFTB method, of the catalyst-free transformation of a-C into graphene.⁴⁸ Here, the more accurate and computationally more demanding AIMD simulations are performed to study the mechanism underlying the RTP growth of graphene from a-C. We found that the Ni-catalyzed transformation of a-C follows the metal-induced crystallization and layer exchange mechanism proposed from a previous experimental study,⁴⁴ rather than the known dissolution/precipitation mechanism. We also found that when the temperature is higher than 600 K, C atoms diffuse faster than Ni atoms in the Ni–C solution. The easy evaporation of surplus Ni and C may be attributed to the formation of a viscous-liquid-like Ni–C solution at 1100 °C.

2. Computational details

2.1 a-C/Ni₃C slab model setup

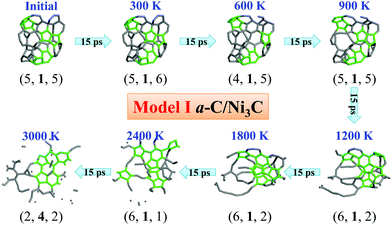
The Ni-catalyzed transformation of a-C into graphene by thermal annealing and cooling has been thoroughly investigated via experiments.^43–46 Note, however, that these experiments^43–46 differ from the RTP growth of graphene⁴⁷ in which the Ni thin film is directly evaporated at an elevated temperature (although the temperature is still below the melting point of bulk Ni) to fabricate the graphene on different dielectric surfaces. Regardless of whether the a-C layer is deposited prior to the deposition of the Ni layer⁴³ or after it,⁴⁵ the newly formed graphene is always on the top of the Ni layer. In a previous experimental study, Saenger et al. indicated that the a-C layer could be dissolved into the Ni layer during heating and expelled from the solution upon cooling below the solid solubility limit, if the graphene growth from a-C followed the CVD dissolution/precipitation mechanism.⁴⁴ In fact, the graphitic C formation starts at temperatures of 640–730 °C at which the C solubility in Ni is very low, suggesting that the graphitization is through a metal-induced crystallization and layer exchange mechanism, rather than the dissolution/precipitation mechanism.⁴⁴ For metal-induced crystallization, Saenger et al. proposed that C in Ni has a low concentration and a high transport rate even at low temperature and that the formation of crystalline C (more stable than a-C) on top of the Ni layer can further induce continued dissolution of the bottom a-C layer.⁴⁴ The in situ electron microscopy study gives the same conclusion that the saturation of the metal with C and the self-diffusion of C in the metal precede the nucleation and growth of graphene, and the transformation of a-C into the thermodynamically more favorable graphene occurs above 600 °C, still at the heating stage.⁴⁶

The growth of graphene in RTP⁴⁷ appears to follow a similar mechanism. Moreover, a new and important piece of experimental evidence is the emergence of an intermediate Ni₃C phase in the temperature range of 200–800 °C, which offers a new insight into the RTP-growth of graphene.⁴⁹ To understand the role of Ni₃C formation and the associated mechanism of graphene growth, we set up six slab models (Models I–VI) in Fig. 1a–f, viewed along the surface y axis. For each model, the slab dimensions are set at 12.8 Å × 14.8 Å × 40 Å, where the x–y dimensions are the same as those of a graphene supercell containing 72 carbon atoms, and the vacuum layer along the z direction was cut to highlight reactive solid layers (the whole model system with a vacuum layer (>20 Å) of Model I is depicted in ESI Fig. S2a†).

Fig. 1 Initial (a–f) and final configurations of (a′–f′) of Model I a-C/Ni₃C, Model II sp²-C/Ni₃C, Model III a-C with 12 Ni, Model IV sp²-C with 12 Ni, Model V a-C, and Model VI sp²-C based on the stepwise temperature increase from 300 K, 600 K, 900 K, 1200 K to 1800 K every 15 ps in AIMD simulations. The Ni and C atoms are shown in blue and grey, respectively. The number of C atoms or Ni atoms in each model is also highlighted in insets. All the slab models are viewed along the surface y axis, and the vacuum layer along the z axis for each model is cut to highlight reactive solid layers.

In Model I or II (Fig. 1a and b), 72 a-C atoms with 3/8 of them being sp³-C atoms or all of them being sp²-C atoms are directly deposited on a Ni₃C layer with 96 atoms. The optimal thicknesses of a-C and Ni layers of 5 and 65 nm, respectively, are suggested by the RTP experiment to achieve high-quality graphene monolayers.⁴⁷ Both thicknesses are not feasible in our AIMD simulations. However, 72 C atoms and the Ni₃C layer with 96 atoms in Models I and II yield the thickness of the solid layer to be about 17 Å while the ratio of the thicknesses of the Ni₃C layer to the C layer is about 3.5. Both models are built to provide some insights into the growth mechanism at the nanoscale, mimicking the model system of a four-layer Ni(111) slab built by Xu et al. to investigate the graphene growth, including carbon dissolution, precipitation, and continuous growth.³³ Since there would be carbon dissolution into the Ni-C solution and the formation of graphitic C from the Ni–C solution in our models, here we do not fix any layer within the reactive solid layers. Models I and II are also designed to understand the importance of the formation of the Ni₃C phase in the RTP growth, considering the limited time scale for the AIMD simulations as it is impractical to simulate the whole series of dissolution of a-C into Ni, saturation of Ni with C, and diffusion of C into Ni, prior to the formation of nucleation sites on the top surface. It is expected that the carbon cluster C_n species can be formed in the Ni–C solution before precipitation.³⁶ Thus, the precipitated C_n clusters can be sp²/sp³-mixed-C clusters or pure sp²-C clusters as shown in Fig. 1a and b. To further demonstrate the influence of Ni₃C formation on easy Ni evaporation and graphene formation in the RTP experiment, four new models (VIII to XI), including 72 a-C and pure sp²-C deposited on NiC [48 atoms, created based on a Ni(111) surface, replaced half the number of atoms by C atoms] and pure Ni layers [72 atoms, created based on a 3-layer Ni(111) surface], with decreased C content of supporting and catalyst layers, are built to make comparisons with Models I and II (see ESI Fig. S3–S5 and Table S1†).

Models III and IV (Fig. 1c and d) are designed to illustrate the catalysis effect of the Ni atoms and to further compare with Models I and II that contain Ni₃C. We notice that a recent study showed that the conversion of a-C to graphene can occur without the Ni catalyst by annealing.⁴⁸ Models V and VI (Fig. 1e and f) are to draw a comparison among all the models shown in Fig. 1. In addition, for the Ni-catalyzed transformation of a-C into graphene experiments, the formation of single-layer or multi-layer graphene can be controlled by changing the relative thicknesses of deposited a-C and Ni thin films.^43,45,47 To further reproduce the dynamic growth process of the second graphene layer, we also built a model (Model VII graphene/a-C/Ni₃C) with one more fixed graphene layer (72 C atoms) deposited on the a-C/Ni₃C layers to study the formation of the second graphene layer (see Fig. 8).

2.2 AIMD simulations

To mimic the thermal heating process in the RTP experiment, eleven independent AIMD simulations are performed with eleven model systems (Model I–VI in Fig. 1, Model VII in Fig. 8, and Model VIII–XI in ESI Fig. S3†) in the NVT ensemble with the increase of temperature (T) from 300 K, 600 K, 900 K, 1200 K to the final 1800 K (15 ps for each given temperature). Note that this rate of temperature increase is exceedingly faster than in real experiments. As a result, the kinetics of growth becomes much more dominant than the thermodynamics.⁵⁰ Since the ultrafast growth rate in numerical simulations would induce kinetically trapped defects in the graphitic C structures,⁵¹ computational high-temperature annealing can be employed to accelerate the continuous graphene growth and at the same time reduce the number of defects within the graphene layer.^51,52 The temperature range of 1200 K to 1800 K covers the experiment temperature (1100 °C) in RTP.⁴⁷ We also examined the effect of increasing the growth temperature directly from 1200 K to 1800 K to accelerate the graphene growth, which did not notably perturb our studied systems. Note also that in the previous QM/MD simulations of the catalyst-free transformation of a-C into graphene, the simulation temperature was increased from 600 K, 1200 K to 1800 K, while the energy change of the system still remained continuous.⁴⁸

In addition, for Model I, the AIMD simulation is further carried out with the increase of temperature up to 2400 K and then to 3000 K (15 ps for each given temperature) to examine post-annealing of the grown graphitic C structures. As a benchmark, four additional model systems are built (Fig. 3), including Ni bulk with 48 atoms, a graphene monolayer with 72 atoms, a Ni₃C slab, and a Ni(111) surface doped with C atoms (with 144 Ni atoms and 48 C atoms). For these four models, 15-ps, 25-ps, 50-ps, and 50-ps AIMD simulations are performed, respectively, all at 1200 K, to validate specific solid–liquid properties of nanoscale Ni–C solution by computing the mean square displacement (MSD)–time curves and comparing with those of Ni bulk and perfect graphene.

All the AIMD simulations are performed within the framework of the Kohn–Sham formulation of DFT by using the GPW method in the QUICKSTEP program of the CP2K software package. The PBE-D3 functional is employed with a cutoff radius of 20 Å for all dispersion calculations. A polarized double-ξ quality Gaussian basis in conjunction with the norm-conserving Goedecker–Teter–Hutter (GTH) pseudopotential is used. The auxiliary plane-wave basis set is defined by an energy cutoff of 330 Ry, accompanied by a relative cutoff of 33 Ry for Gaussian basis set collocation. The self-consistent field (SCF) convergence is set at 10⁻⁶ a.u. The time step in AIMD simulations is set at 1 fs. The temperature is controlled by a Nosé–Hoover chain thermostat.

3. Results and discussion

After 75-ps AIMD simulations with stepwise temperature increase, the final configurations of Models I–VI and Models VIII–XI are presented in Fig. 1a′–f′ and S3c′–f′,† respectively. As shown in Fig. 1a′ and b′, the graphitic layer and the Ni₃C layer tend to separate from each other. A few a-C atoms can enter the Ni₃C layer, while some surface Ni atoms stabilize the dangling C atoms in the graphitic layer. In addition, a two-layer graphitic structure is formed from a-C with 3/8 sp³-C atoms on the Ni₃C layer, while a relatively flat graphitic structure with a localized dome-like patch is formed from pure sp²-C. Interestingly, the graphitic structure grown from the pure sp²-C atoms is much flatter than that grown from the a-C. Without the support of the Ni₃C layer, a carbon roll (Fig. 1c′) and a carbon shell (Fig. 1e′) are formed from a-C, respectively, whereas a relatively flat graphitic structure is formed from pure sp²-C (see Fig. 1d′ and f′). The C structure in Fig. 1d′ exhibits higher (concave) curvature compared to that in Fig. 1f′. Fig. 1c′ and d′ show that the catalysis effect of Ni atoms is important to the stabilization of the dangling C atoms by forming the σ-bonds besides dissolution of C atoms or supporting the newly-formed graphene. Moreover, after the formation of graphitic C structures, the Ni atoms tend to gather together, which can be attributed to the strongest C–C interaction among Ni–Ni, Ni–C, and C–C interactions in the Ni–C solution.³⁶ This result is also in line with the estimated formation energies of Ni–Ni, Ni–C, and C–C bonds given in ESI Fig. S1.† For Model VIII a-C/NiC and Model IX sp²-C/NiC (ESI Fig. S3c′ and d′†), the final structures are quite similar to graphitic C structures shown in Fig. 1c′ and d′ because the number of Ni atoms in the NiC layer is small, just twice that of Models III and IV, resulting in decomposition of the NiC layer in the end. Moreover, Ni atoms still prefer aggregation (see ESI Fig. S3c′ and d′†). For Model X a-C/Ni and Model XI sp²-C/Ni (ESI Fig. S3e′ and f′†), the graphitic C structures can be found to grow on Ni layers. The Ni layers still provide catalytic support to the grown C structures, the same as Ni₃C layers in Models I and II. Remarkably, quite a few C atoms dissolve into the Ni layers in their final configurations.

3.1 Viscous-liquid-like Ni–C solution and faster diffusion of C atoms: easy evaporation of Ni in RTP growth of graphene

Based on computed MSDs of Ni and C atoms in the Ni₃C layer of Model I at different temperatures, the role of Ni₃C formation in the easy Ni evaporation can be analyzed. According to the Auger electron spectroscopy (AES) results in a recent RTP experiment,⁴⁹ the Ni₃C intermediate forms in the temperature range of room temperature to 400 °C. In addition, accompanied by the vanishing of Ni₃C, the C atoms diffuse to the top surface at 800 °C, and the bulk-to-surface diffusion of C atoms within Ni can be observed above 400 °C.⁴⁹ Although the explicit a-C diffusion to the top layer is not observed in our 75-ps AIMD simulations (separation between the graphitic layer and the Ni₃C layer in Fig. 1a′), the self-diffusion coefficient (D) of Ni or C atoms in the Ni₃C layer offers a guide to understand the specific phase behavior of nanoscale Ni–C solution. As shown in Fig. 2a, the MSD curves for Ni and C atoms in the Ni₃C layer at 300 K and 600 K are nearly flat, indicating solid-like behavior of the Ni₃C layer at both temperatures. At 600 K, the C and Ni atoms exhibit similar diffusion rates. From 900 K to 3000 K, the C atoms diffuse faster than the Ni atoms (see Fig. 2a–c). The self-diffusion coefficients of Ni and C atoms in the Ni₃C layer (Table 1) are computed from the linear fitting of the MSD–time curves in Fig. 2. When the temperature is increased from 900 K to 1800 K, the diffusion coefficients are in the range of 10⁻⁷–10⁻⁶ cm² s⁻¹, consistent with the previous experimental estimation of volume diffusion of C in Ni at 1100 °C (D = D₀ exp(−E/k_BT) where D₀ ≈ 0.1 cm² s⁻¹, E ≈ 1.5 eV, and k_B is the Boltzmann constant.),⁵³ which indicates that the Ni–C solution behaves like a viscous liquid in this temperature range (900–1800 K). The Ni–C solution behaves like a liquid when the temperature is higher than 2400 K (because the diffusion coefficients are higher than 10⁻⁵ cm² s⁻¹).

Fig. 2 Variations of mean square displacement (MSD) with time of Ni (solid lines) and C (dashed lines) atoms in the Ni₃C layer of Model I at (a) 300 K, 600 K, and 900 K, (b) 1200 K and 1800 K, and (c) 2400 K and 3000 K based on the AIMD simulations. The corresponding linear fitting of the MSD–time curves is in violet.

Table 1 Computed self-diffusion coefficients, D (unit: cm² s⁻¹), of Ni and C atoms in the Ni₃C layer of Model I at different temperatures (stepwise increase every 15 ps), and in the Ni₃C crystal and C-doped Ni(111) in Fig. 3c and d at 1200 K (50 ps) through linear fitting of the MSD–time curves shown in Fig. 2 and Fig. 4c and d, respectively, on the basis of AIMD simulations

	900 K	1200 K	1800 K	2400 K	3000 K
Ni 3 C layer of Model I
Ni	3.3 × 10^−7	6.4 × 10^−7	3.7 × 10^−6	1.8 × 10^−5	3.9 × 10^−5
C	4.8 × 10^−7	1.6 × 10^−6	8.6 × 10^−6	3.9 × 10^−5	7.9 × 10^−5
Ni 3 C bulk crystal
Ni			4.7 × 10^−7
C			1.5 × 10^−6
C-doped Ni(111)
Ni			6.0 × 10^−7
C			1.6 × 10^−6

---

To further confirm the phase behavior of the Ni₃C layer, four more model systems are built (see Fig. 3). Note that the surplus Ni with excess C atoms appears to evaporate at 1100 °C in the experimental RTP growth of graphene.⁴⁷ The Ni bulk (Fig. 3a) and the graphene monolayer (Fig. 3b) are taken as benchmark systems to confirm that both behave like a solid at 1200 K (which is slightly below the evaporation temperature 1100 °C in the RTP experiment⁴⁷), as indicated by MSD–time curves (Fig. 4a and b) from our AIMD simulations. For the Ni₃C slab model (carved from the bulk crystal, Fig. 3c) and the Ni(111) doped with C atoms (Fig. 3d), the diffusivity is investigated via 50-ps AIMD simulations at 1200 K. The system of Ni(111) doped with C atoms is generated from the Ni(111) thin film with some Ni atoms evenly replaced by C atoms so that the ratio of Ni to C is 3 : 1. Note that both model systems have more atoms than the Ni₃C layer in Model I. As shown in Fig. 3c and d, the tendency for C atoms to diffuse onto the surface is still difficult to observe even after 50-ps AIMD simulations. The MSD–time curves are plotted every 10 ps after the initial 10-ps AIMD run (Fig. 4c and d). The computed diffusion coefficients shown in Table 1 (averaged over four MSD–time curves) are very close to the diffusion coefficients of the Ni₃C layer in Model I at 1200 K and suggest that the Ni–C solution at 1200 K behaves like a viscous liquid.

Fig. 3 Four model systems: (a) Ni bulk, (b) graphene monolayer, (c) Ni₃C slab (144 Ni and 48 C atoms), and (d) C-doped Ni(111) surface, used in the AIMD simulations at 1200 K. The 50-ps snapshots of Ni₃C slab and C-doped Ni(111) are highlighted in the right panel in (c) and (d). The Ni and C atoms are shown in blue and grey, respectively.

Fig. 4 Variations of mean square displacement (MSD) with time of the Ni atoms of (a) Ni bulk, C atoms of (b) graphene monolayer, and Ni and C atoms of (c) Ni₃C slab and (d) C-doped Ni(111) surface at 1200 K based on the AIMD simulations. The corresponding linear fitting of the MSD–time curves is in violet. For Ni bulk, the non-spin-polarized and spin-polarized AIMD simulations are performed at 1200 K for comparison.

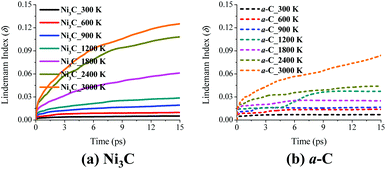
Furthermore, the phase behavior of Ni₃C and graphene in Model I can be analyzed by the estimation of Lindemann index (δ). A commonly used value that characterizes the solid/liquid phase transition is δ = 0.1.⁴⁰ As shown in Fig. 5, the a-C layer behaves like a solid in the whole temperature range of 300–3000 K, due to δ < 0.09. When the temperature is higher than 2400 K, δ of the Ni₃C layer would be greater than 0.1 if the simulation time is long enough due to the transition to the liquid phase.

Fig. 5 Lindemann index (δ) of the (a) Ni₃C layer and (b) a-C layer in Model I, estimated from the 15-ps AIMD simulations with the increase of temperature from 300 K, 600 K, 900 K, 1200 K, 1800 K, 2400 K to 3000 K.

At the nanoscale, the Ni–C solution and the pure Ni thin film exhibit a different phase behavior compared to the bulk Ni and graphene C. As mentioned above, pure bulk Ni and graphene C behave like a solid at 1200 K. When C atoms are dissolved into Ni to form a Ni₃C solution at 1200 K, the solution becomes viscous-liquid like. This viscous-liquid-like phase behavior can also be found in the Ni–C solution with the ratio of Ni to C being 1 : 1, and the pure Ni layer at 1200 K, as shown in ESI Fig. S4 and Table S1.† For Model VIII a-C/NiC and Model X a-C/Ni (ESI Fig. S4†), the NiC and pure Ni layers behave like a solid at 300 K and 600 K, but is viscous-liquid-like when the temperature is in the range of 900–1800 K, similar to the Ni₃C layer in Model I. Notably, C atoms in the NiC layer (Model VIII) diffuse slightly faster than Ni atoms at all temperatures considered, except 600 K. At 600 K, C atoms in the NiC layer diffuse much faster than Ni atoms. As shown in ESI Table S1,† diffusion coefficients of Ni or C atoms in the NiC layer (Model VIII) and in the Ni layer (Model X) have nearly the same order of magnitude as those in the Ni₃C layer (Model I). Importantly, these diffusion coefficients of Ni or C atoms in the NiC and pure Ni layers are all slightly higher than those in the Ni₃C layer, indicating that the viscous-liquid-like Ni₃C at 900–1800 K may be more stable than either the NiC phase or the Ni thin film. This also supports the existence of Ni₃C phase in a wide temperature range (from room temperature to 800 °C) based on the AES measurement, and its existence even at 1100 °C based on the glancing-angle X-ray diffraction (GAXRD) measurement of the RTP growth.⁴⁹ Lindemann-index results for NiC, Ni, or a-C layers in Model VIII a-C/NiC and Model X a-C/Ni (ESI Fig. S5†) are similar to those of Model I a-C/Ni₃C (Fig. 5).

Different from previous studies of Ni-catalyzed transformation of a-C to graphene,^43–46 the RTP growth entails a quite fast heating rate to induce direct Ni evaporation at an elevated temperature.^47,49 In reality, because of the rapid heating rate, a metastable Ni₃C intermediate is found in the RTP experiment.^47,49 Based on our AIMD simulations, the viscous-liquid-like behavior of nanoscale Ni₃C gives a possible explanation for the easy Ni evaporation at 1100 °C in the RTP experiment, even though the Ni evaporation is not directly observed in the AIMD simulations due to the limited time scale. In the realistic system,⁴⁹ the fast diffusion of C atoms (also observed by our AIMD simulations) can be attributed to the formation of the Ni₃C layer as the temperature increases, and also contributes to the formation of the Ni–C viscous liquid at an elevated temperature.

3.2 Kinetically trapped graphitic structures in AIMD simulations

The simulations discussed above suggest that the graphene formation in the RTP growth follows the metal-induced crystallization and layer exchange mechanism proposed by Saenger et al.⁴⁴ The direct deposition of a-C and sp²-C layers on the Ni₃C layer (Models I and II) can be used to show the evolvement of graphitic structures in the RTP experiment after precipitation as the temperature increases. The transformation of a-C and sp²-C into graphitic structures is summarized in Fig. 6. The Ni₃C layer or Ni atoms are omitted in Fig. 6 to illustrate only the temperature-dependent C structure evolvement of a-C and sp²-C in Models I–VI, where the temperature increase is from 300 K to 1800 K. In addition, C atoms in the five, six, and seven-membered rings within the sp²-C-network are highlighted in green (others in grey). The integers in parentheses below the C structures represent the numbers of five, six, and seven-membered rings within the sp²-C network. Since the rate of temperature increase in the AIMD simulations is exceedingly faster than that in real experiments, the condition of graphene growth is far from the equilibrium, and the kinetics of growth becomes much more dominant than the thermodynamics.⁵⁰ The ultrafast growth rate in numerical simulations would lead to kinetically trapped defects in the sp²-C structures.⁵¹ As shown in Fig. 6, the graphitic structures grown at 1800 K contain many non-hexagonal rings (polygonal defects). In this kinetic growth stage, the grown graphitic structures are C-source dependent as the structures evolved from a-C with 3/8 sp³-C or from pure sp²-C are markedly different.

Fig. 6 Temperature-dependent C structure evolvement of (a) Model I a-C/Ni₃C, (b) Model II sp²-C/Ni₃C, (c) Model III a-C with 12 Ni, (d) Model IV sp²-C with 12 Ni, (e) Model V a-C, and (f) Model VI sp²-C based on AIMD simulations with the increase of temperature every 15 ps from 300 K, 600 K, 900 K, 1200 K to 1800 K. C atoms of the sp²-C-network-related five, six, and seven-membered rings are highlighted in green (the rest in grey). The numbers in brackets below the C structures indicate the numbers of five, six, and seven-membered rings within the sp²-C network. The Ni₃C layers are omitted in Models I and II and the Ni atoms are omitted in Models III and IV to highlight the evolvement of C structures.

Although the a-C layer in Models I, III, and V has a high fraction of sp³-C atoms in the initial structures, these sp³-C atoms are quickly converted to sp²-C atoms after structure optimization and AIMD simulations even at room temperature (300 K). After 15-ps AIMD simulations at 300 K, the constituents of 5, 6, and 7-membered rings are nearly unchanged, compared with the initial structures (Fig. 6a, c, and e), indicating that the energetically favorable 5, 6, and 7-membered rings stem from fused 5, 6, and 7-membered rings in the initial C clusters. These polygonal rings are kinetically trapped in the AIMD simulations. Upon the increase of temperature every 15 ps up to 1800 K, the constituents of the sp²-C networks change a little, but the sp²-C networks gradually extend. In the a-C layer of Models I, III, and V (Fig. 6a, c, and e), the number of 5-membered rings gradually increases, while the number of 6-membered rings changes a bit, and the number of 7-membered rings fluctuates as the temperature increases to 1200 K. From 1200 to 1800 K, the C structures exhibit notably more changes. In Model III (Fig. 6c), the numbers of 6- and 7-membered rings increase. In Model V (Fig. 6e), the numbers of 5- and 7-membered rings decrease while the number of 6-membered rings increases. Although the numbers of 5, 6, and 7-membered rings exhibit little change in Model I (Fig. 6a) at 1200 K and 1800 K, the sp²-C networks contain C strings which would not arise in the C structures for T < 1200 K, supporting the experimental observation of the reverse dissolution of graphitic C for T > 950 °C.⁴⁴ Compared to the grown C structures in Models III and V (Fig. 6c and e) which contain a smaller number of C strings at 1200 K and 1800 K, one can conclude that the Ni₃C layer can stabilize newly formed C strings while re-dissolving the graphitic structures at high temperatures.

In the pure sp²-C layer of Models II, IV, and VI (Fig. 6b, d, and f), the grown C structures are all restively flat at different temperatures, unlike the structures of carbon rolls or shells out of the a-C layer in the case of Models I, III, and V. The fused 6-membered rings also originate from the initial pure sp²-C. From 1200 K to 1800 K, the C structures of the sp²-C layer also undergo slightly more changes like those in the case of the a-C layer. The numbers of fused 6-membered rings decrease while the numbers of 5 and 7-membered rings increase. These results are consistent with the experimental observation that the grown graphitic C would reversibly dissolve for T > 950 °C.⁴⁴

As shown in Fig. 7, we have performed additional AIMD simulations on the structure of Model I with the increase of temperature from 1800 K to 2400 K and then to 3000 K, each for 15 ps to visualize possible defect healing in real experiments. At 2400 K, isolated C atoms start to appear and the sp²-C network exhibits some changes. At 3000 K, isolated C atoms spring up, indicating further reverse dissolution of graphitic structures in Ni. However, the sp²-C core exhibits an increasing number of 6-membered rings. Apparently, the ultrahigh temperature can remove the defects in the sp²-C network, consistent with the results from a previous tight-binding MC simulation of isolated graphene.⁵¹ However, the high temperature can also induce the reverse dissolution of graphitic C when the catalyst metal coexists.

Fig. 7 Temperature-dependent C structure evolvement of Model I a-C/Ni₃C based on AIMD simulations with the increase of temperature every 15 ps from 300 K, 600 K, 900 K, 1200 K, 1800 K, 2400 K to 3000 K. C atoms of the sp²-C-network-related five, six, and seven-membered rings are highlighted in green (the rest in grey). The numbers in brackets below the C structures indicate the numbers of five, six, and seven-membered rings within the sp²-C network. The Ni₃C layer is omitted here to highlight the evolvement of C structures.

3.3 Formation of the orderly carbon core in the second graphene layer

In the metal-catalyzed transformation of a-C to graphene experiments, the formation of a number of graphene layers can be tuned by altering the thicknesses of deposited a-C and Ni thin films.^43,45,47 In the Ni-catalyzed transformation of a-C to graphene experiments, the formation of single-layer or multi-layer graphene can be controlled by altering the thicknesses of deposited a-C and Ni thin films.⁵⁴ When the quantity of a-C is abundant, the mechanism of Ni-catalyzed transformation of a-C to graphene differs from the self-limiting one. The graphene growth in the RTP experiment appears to follow the metal-induced crystallization and layer exchange mechanism. The grown graphene on the surface of Ni–C solution can further promote continued dissolution of the a-C layer.⁴⁴ Even after the surface of Ni–C solution is entirely covered by a graphene layer, the replenished C clusters by continued dissolution of abundant a-C can give rise to new nucleation sites to further grow the second layer of graphene. To support this view, we build a new model (Model VII graphene/a-C/Ni₃C) with one more graphene layer deposited on the a-C/Ni₃C layers to study the formation of the second graphene layer (see Fig. 8). Here, the first perfect graphene layer is fixed in the AIMD simulations. As shown in Fig. 8a, a dome-like graphitic C structure forms between the graphene layer and the Ni₃C layer. This newly formed sp²-C network in Fig. 8 appears to be more orderly than that without the first graphene layer coating, as compared to the grown C structure from Model I (Fig. 1a′ and 6a). As shown in Fig. 8b, the numbers of 5, 6, and 7-membered rings in the second sp²-C network of Model VII are more than those in the C structure of Model I (Fig. 6a). It seems that the first graphene layer could accelerate the formation of the orderly C core in the second graphitic layer.

Fig. 8 (a) Initial and final configurations, viewed along the y axis, and (b) temperature-dependent C structure evolvement of Model VII graphene/a-C/Ni₃C based on AIMD simulations with the increase of temperature every 15 ps from 300 K, 600 K, 900 K, 1200 K to 1800 K. For (a), the Ni and C atoms are shown in blue and grey, respectively. The perfect first graphene layers are also highlighted with the purple vdW surface. The vacuum layer along the z axis is cut to highlight reactive solid layers (the whole supercell is depicted in ESI Fig. S2b†). For (b), the Ni₃C layer is omitted to highlight the evolvement of C structures. C atoms of the sp²-C-network-related five, six, and seven-membered rings are highlighted in green (the rest in grey). The numbers in brackets below the C structures indicate the numbers of five, six, and seven-membered rings within the sp²-C network.

4. Conclusions

We have performed comprehensive AIMD simulations to investigate the atomic-scale mechanism of Ni evaporation and graphene formation in the RTP growth of graphene. Our simulations suggest that the easy evaporation of Ni at 1100 °C in the RTP experiment is likely due to the formation of a viscous-liquid-like Ni–C solution (even at 900 K), a phase behavior specific to the nano-scale Ni–C system. The graphitization in the RTP growth follows the Ni-induced crystallization and layer exchange mechanism. C atoms in Ni have a low concentration and a relatively high diffusion rate. When the temperature is higher than 600 K, C atoms diffuse faster than Ni atoms in the Ni–C solution. The graphitic C formation can start at low temperature. Even at 300 K, the sp³-C atoms no longer exist. The main sp²-C-network-related structures, i.e., 5, 6, and 7-membered rings, as nucleation sites, stem from fused 5, 6, and 7-membered rings of initial C clusters precipitated from the Ni–C solution. In the kinetic growth stage of the RTP experiment, the grown C structures depend on the C sources (either sp³-C or sp²-C). Since the rate of temperature increase in the AIMD simulations is exceedingly faster than in the real experiments, the grown graphitic structures in the simulations contain many kinetically “trapped” defects. The grown graphitic structures from a-C with sp³-C atoms tend to form carbon rolls or carbon shells, while the grown graphitic structures from pure sp²-C tend to form flat haeckelites. In the presence of the first graphene layer, new nucleation sites for growing the second graphene layer can quickly form from the Ni–C solution. In the RTP experiment, the Ni catalyst can stabilize the dangling C atoms, dissolve C atoms, and support the newly-grown flat graphene. When the temperature is as high as 1200 K, the grown graphitic structures can reversely dissolve. In the AIMD simulations, the kinetically trapped defects in the graphitic structure can be healed at ultrahigh temperature. However, with the metal catalyst, the ultrahigh temperature can reversely dissolve the grown graphitic structure.

Acknowledgements

This work was supported by a grant from the Nebraska Center for Energy Sciences Research in the University of Nebraska-Lincoln and by the University of Nebraska Holland Computing Center.

Notes and references

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. A. K. Geim, Science, 2009, 324, 1530–1534.
3. K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200.
4. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
5. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568.
6. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217–224.
7. D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240.
8. C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196.
9. K. V. Emtsev, A. Bostwick, K. Horn, J. Jobst, G. L. Kellogg, L. Ley, J. L. McChesney, T. Ohta, S. A. Reshanov, J. Rohrl, E. Rotenberg, A. K. Schmid, D. Waldmann, H. B. Weber and T. Seyller, Nat. Mater., 2009, 8, 203–207.
10. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
11. A. Reina, X. Jia, J. Ho, D. Nezich, H. Son, V. Bulovic, M. S. Dresselhaus and J. Kong, Nano Lett., 2009, 9, 30–35.
12. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
13. R. S. Edwards and K. S. Coleman, Acc. Chem. Res., 2013, 46, 23–30.
14. K. Yan, L. Fu, H. Peng and Z. Liu, Acc. Chem. Res., 2013, 46, 2263–2274.
15. Y. Zhang, L. Zhang and C. Zhou, Acc. Chem. Res., 2013, 46, 2329–2339.
16. X. Li, W. Cai, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4268–4272.
17. W. Zhang, P. Wu, Z. Li and J. Yang, J. Phys. Chem. C, 2011, 115, 17782–17787.
18. G. Gajewski and C.-W. Pao, J. Chem. Phys., 2011, 135, 064707.
19. K. Li, C. He, M. Jiao, Y. Wang and Z. Wu, Carbon, 2014, 74, 255–265.
20. W. Chen, H. Chen, H. Lan, P. Cui, T. P. Schulze, W. Zhu and Z. Zhang, Phys. Rev. Lett., 2012, 109, 265507.
21. Y. Huang, J. Du, T. Zhou, C. Ling, S. Wang and B. Geng, ACS Catal., 2014, 4, 892–902.
22. J. Gao, J. Yip, J. Zhao, B. I. Yakobson and F. Ding, J. Am. Chem. Soc., 2011, 133, 5009–5015.
23. Q. Yuan, J. Gao, H. Shu, J. Zhao, X. Chen and F. Ding, J. Am. Chem. Soc., 2012, 134, 2970–2975.
24. J. Gao, J. Zhao and F. Ding, J. Am. Chem. Soc., 2012, 134, 6204–6209.
25. H. Shu, X. Chen, X. Tao and F. Ding, ACS Nano, 2012, 6, 3243–3250.
26. L. Wang, X. Zhang, H. L. W. Chan, F. Yan and F. Ding, J. Am. Chem. Soc., 2013, 135, 4476–4482.
27. X. Zhang, L. Wang, J. Xin, B. I. Yakobson and F. Ding, J. Am. Chem. Soc., 2014, 136, 3040–3047.
28. L. Meng, Q. Sun, J. Wang and F. Ding, J. Phys. Chem. C, 2012, 116, 6097–6102.
29. L. Meng, J. Jiang, J. Wang and F. Ding, J. Phys. Chem. C, 2014, 118, 720–724.
30. Y. Lu and X. Yang, Carbon, 2015, 81, 564–573.
31. P. Wu, H. Jiang, W. Zhang, Z. Li, Z. Hou and J. Yang, J. Am. Chem. Soc., 2012, 134, 6045–6051.
32. Z. Liang, Z. Xu, T. Yan and F. Ding, Nanoscale, 2014, 6, 2082–2086.
33. Z. Xu, T. Yan, G. Liu, G. Qiao and F. Ding, Nanoscale, 2016, 8, 921–929.
34. E. C. Neyts, A. C. T. v. Duin and A. Bogaerts, Nanoscale, 2013, 5, 7250–7255.
35. Y. Wang, A. J. Page, Y. Nishimoto, H.-J. Qian, K. Morokuma and S. Irle, J. Am. Chem. Soc., 2011, 133, 18837–18842.
36. H.-B. Li, A. J. Page, Y. Wang, S. Irle and K. Morokuma, Chem. Commun., 2012, 48, 7937–7939.
37. A. J. Page, Y. Wang, H.-B. Li, S. Irle and K. Morokuma, J. Phys. Chem. C, 2013, 117, 14858–14864.
38. M. Jiao, H. Qian, A. Page, K. Li, Y. Wang, Z. Wu, S. Irle and K. Morokuma, J. Phys. Chem. C, 2014, 118, 11078–11084.
39. Y. Wang, A. J. Page, H.-B. Li, H.-J. Qian, M.-g. Jiao, Z.-J. Wu, K. Morokuma and S. Irle, Nanoscale, 2014, 6, 140–144.
40. H.-B. Li, A. J. Page, C. Hettich, B. a. Aradi, C. Köhler, T. Frauenheim, S. Irle and K. Morokuma, Chem. Sci., 2014, 5, 3493–3500.
41. V. O. Özçelik, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter, 2012, 85, 235456.
42. Y. Shibuta, R. Arifin, K. Shimamura, T. O. F. Shimojo and S. Yamaguchi, Chem. Phys. Lett., 2013, 565, 92–97.
43. M. Zheng, K. Takei, B. Hsia, H. Fang, X. Zhang, N. Ferralis, H. Ko, Y.-L. Chueh, Y. Zhang, R. Maboudian and A. Javey, Appl. Phys. Lett., 2010, 96, 063110.
44. K. L. Saenger, J. C. Tsang, A. A. Bol, J. O. Chu, A. Grill and C. Lavoie, Appl. Phys. Lett., 2010, 96, 153105.
45. C. M. Orofeo, H. Ago, B. Hu and M. Tsuji, Nano Res., 2011, 4, 531–540.
46. J. A. Rodríguez-Manzo, C. Pham-Huu and F. Banhart, ACS Nano, 2011, 5, 1529–1534.
47. W. Xiong, Y. S. Zhou, L. J. Jiang, A. Sarkar, M. Mahjouri-Samani, Z. Q. Xie, Y. Gao, N. J. Ianno, L. Jiang and Y. F. Lu, Adv. Mater., 2013, 25, 630–634.
48. A. Barreiro, F. Börrnert, S. M. Avdoshenko, B. Rellinghaus, G. Cuniberti, M. H. Rümmeli and L. M. K. Vandersypen, Sci. Rep., 2013, 3, 1115.
49. W. Xiong, Y. S. Zhou, W. J. Hou, T. Guillemet, J.-F. Silvain, Y. Gao, M. Lahaye, E. Lebraud, S. Xu, X. W. Wang, D. A. Cullen, K. L. More, L. Jiang and Y. F. Lu, RSC Adv., 2015, 5, 99037–99043.
50. X. Zhang, H. Li and F. Ding, Adv. Mater., 2014, 26, 5488–5495.
51. S. Karoui, H. Amara, C. Bichara and F. Ducastelle, ACS Nano, 2010, 4, 6114–6120.
52. M. Jiao, W. Song, H.-J. Qian, Y. Wang, Z. Wu, S. Irle and K. Morokuma, Nanoscale, 2016, 8, 3067–3074.
53. E. V. Rut'kov and N. R. Gall, Equilibrium Nucleation, Growth, and Thermal Stability of Graphene on Solids, in Physics and Applications of Graphene – Experiments, ed. S. Mikhailov, InTech, 2011, pp. 209–292, ISBN: 978-953-307-217-3.
54. R. S. Weatherup, H. Amara, R. Blume, B. Dlubak, B. C. Bayer, M. Diarra, M. Bahri, A. Cabrero-Vilatela, S. Caneva, P. R. Kidambi, M.-B. Martin, C. Deranlot, P. Seneor, R. Schloegl, F. Ducastelle, C. Bichara and S. Hofmann, J. Am. Chem. Soc., 2014, 136, 13698–13708.

---

Footnote

† Electronic supplementary information (ESI) available: Formation energies of Ni–Ni, Ni–C, and C–C atoms as a function of intermolecular distance in Fig. S1, the whole supercells with the vacuum layer of Models I and VII in Fig. S2, and the initial and final configurations (Fig. S3), MSD–time curves (Fig. S4), diffusion coefficients (Table S1), and Lindemann index (Fig. S5) of four new models (VIII–XI). See DOI: 10.1039/c5nr08614k

---