Experimental verification of nanofluid shear-wave reconversion in ultrasonic fields

Abstract

Here we present the verification of shear-mediated contributions to multiple scattering of ultrasound in suspensions. Acoustic spectroscopy was carried out with suspensions of silica of differing particle sizes and concentrations in water to find the attenuation at a broad range of frequencies. As the particle sizes approach the nanoscale, commonly used multiple scattering models fail to match experimental results. We develop a new model, taking into account shear mediated contributions, and find excellent agreement with the attenuation spectra obtained using two types of spectrometer. The results determine that shear-wave phenomena must be considered in ultrasound characterisation of nanofluids at even relatively low concentrations of scatterers that are smaller than one micrometre in diameter.

---

1. Introduction

Silica in water suspensions have been used for many years as typical nanofluids for ultrasonics research on account of the monodispersity, size-uniformity, and ease of dispersion attainable. Silica itself is fundamental to life and amongst biominerals is second in abundance only to calcium carbonate.¹ In plants silica-mineralisation is thought to be coupled to transpiration, with the tissues in the vascular system, epidermal cells, and stomata having the highest concentrations, for the provision of structural strength and defence against insects, bacteria, and disease.² Soil composition can include high levels of silica and plants such as Oryza sativa (Asian rice) can contain up to 17% silica as dry matter, with a correlation between high concentration and high transpiration rates.³ In some forms of biosilica, highly polyanionic phosphoproteins have been shown to regulate biomolecules responsible for silica formation, with the ratio of native silaffin controlling the structural characteristics and giving rise to spheres (100–1000 nm) or porous structures with the addition of silicic acid.⁴ Thus, it may be possible to use unique amino acid and protein combinations with silica to produce specialised self-assembled structures artificially.^5,6 The structures themselves can contain, for example, periodic lattice structures of silica spheres.⁷

However, determination of the bulk physical properties of assembling structures is not possible using conventional methods on account of the concentration levels rendering the systems optically opaque. Light scattering techniques cannot penetrate the systems and can also change the energy levels of the nanoparticles and their interactions. An alternative solution is to use low-power ultrasound waves that can penetrate into the bulk, allowing a more representative particle size characterisation in concentrated systems, whilst also allowing information to be obtained about the volume fraction and density.⁸

With use of bio-mimicry, nano-restructuring of tissue is possible, with regenerative medical practices offering new techniques of scaffolding and repair.^9,10 Indeed long-chain polyamines have been used to generate hexagonally arranged structures composed of silica in vitro.¹¹ In most cases of bio-structuring spherical silica can emerge in the polymerisation processes at different concentrations and stages. In nanomedicine silica is desirable due to its bio-compatibility and versatility. With the understanding gleaned from bio-systems for the production and use of silica, more efficient methods for controlled chemical synthesis of silica are emerging. This has also led to new methods for coating silica particles with functional cargo molecules.¹² As the particles become smaller the surface to volume ratio increases and the relatively large surface area makes them potentially more reactive. The control of the particle sizes, agglomeration and flocculation, and concentration are important properties to enable accurate characterisation of new nano-drugs and understanding of nanoparticles present in biology. For these reasons, new techniques of identifying the physical properties of the system are required, with use of electromagnetic fields or ultrasonics. Ultrasound, being non-invasive,¹³ has greater potential for accurate particle size distribution, density, and concentration investigations. For the interpretation of data obtained by scattering of ultrasound through colloidal suspensions, a complementary theory of multiple scattering is required to unlock this potential. This study addresses the use of ultrasound as a nanofluid characterisation tool and in particular the development of a suitable scattering model for interpreting data obtained in such systems.

When concentrations of silica become high and the particle radii approach the nanoscale, the ultrasonic compressional wave scatters with the addition of two other wave modes. These are the thermal wave (which is most significant in fluid materials) and the shear wave (which dominates in suspensions of solid particles). These two wave modes decay over a short distance from the particle surface and because of this the long-standing multiple scattering models (e.g. that of Lloyd and Berry¹⁴) neglected their effect on neighbouring particles. The energy dissipated in these two modes contributes to the net attenuation of the compressional ultrasound wave. However, when particles are close together, at high concentrations, or high number density, the thermal and shear modes scattered by one particle may have significant amplitude when they reach the surface of a neighbouring particle.^15–17 They can then be re-scattered by that particle, and contribute to the scattered compressional wave. This kind of mode-conversion is also generated partially as a result of the difference in acoustic impedance between the scatterer and the surrounding medium. As we find in our work, an aqueous medium, hydrogel, or biofluid (ρ ≈ 1 g cm⁻³) supports the propagation of shear-waves when there are concentrated levels of nanoparticles (e.g. SiO₂, with density ≈2 g cm⁻³), making it important to understand these extra modes, particularly when trying to replicate biological processes for silica (or even pure silicon) production and structuring.

Throughout this work we are concerned with developing the theory of ultrasound propagation against experimental observation for systems of stable nanoparticles, without flocs or aggregates in order to progress understanding in ultrasonic characterisation of nanoparticles. The electrostatic repulsion between colloidal silica nanoparticles is weak below pH 7 and sufficient to produce a stable solution at pH 7 and above.^12,18 The high negative surface charge of silica at the nanoscale allows preparation of stable suspensions at neutral pH and allows the investigation of a pure silica/water suspension enabling testing of ultrasonic theoretical models. In the following, we will briefly discuss the multiple scattering theory, then outline the characteristics of the systems, the acoustic spectroscopy performed and the preparation of the silica suspensions investigated experimentally. The results of experimental and simulated (with and without shear-effects) attenuation at a broad-range of frequencies, particle sizes (primarily 100–1000 nm), and concentrations are then compared. Here, the inclusion of shear-mode effects into the multiple scattering model provides an almost exact reproduction of the attenuation observed experimentally.

2. Theory of ultrasonic wave propagation in colloids with shear-effects

The development of ultrasonic theory for the analysis of nanoparticles in solution is of the utmost importance for particle size determination because ultrasonic characterisation can be used without alteration of the mixture's state.¹⁹ The first step in particle characterisation is to use ultrasonic spectroscopy to determine the attenuation and then use an algorithm, based upon a theoretical model, to find the particle size.^20,21 The theoretical foundations for ultrasonics lie with formulating wave equations that describe particle/wave interaction.^20,22,23 These models can be highly complex and sometimes numerically unstable. Due to this, simplifications are sought in the analytical and numerical solvers that can encapsulate the physics but also match experimental observations. We take this perspective and develop a multiple scattering theory, inclusive of the visco-inertial effect, that maintains accuracy and enables particle-sizing, whilst also allowing efficient computation. Herein, we consider frequencies that allow characterisation of the particles within the “long-wavelength limit”, whereby the silica particles are much smaller than the wavelength of the ultrasonic field.²⁴

Scattering theory of light and ultrasonics has shared an evolution starting from the time of Rayleigh.¹⁹ Single particle analyses of particle/field interactions were predominant in the beginning, with an evolution towards understanding larger group effects. The works of Epstein & Carhart,²² and Allegra & Hawley²³ are the most successful single particle models. The combination of the two form the basis of the ECAH model which was initially derived to investigate the fine particles in fog. Multiple scattering formulations have until the present day been based upon the work of Foldy,²⁵ Lax,²⁶ Waterman & Truell,²⁷ and Fikioris & Waterman.²⁸ A corrected form of the Waterman Truell model was given by Lloyd & Berry (LB)¹⁴ in 1967 and later re-derived classically by Linton & Martin²⁹ in 2006. A new model was formulated in 2012 by Luppé, Conoir, & Norris (LCN) that enables a multiple scattering approach inclusive of thermal and viscous effects.^30,31 Other approaches to ultrasonics modelling are the Hipp, Storti & Morbidelli core–shell model³² (similar to that of Anson & Chivers³³) that was also used to investigate silica of various sizes and concentrations in water. It has the disadvantage, however, of being computationally expensive and can be numerically unstable.¹⁷ It is from the LB, ECAH, and LCN models that we formulate tractability through analytical and numerical simulations that are inclusive of shear-mode conversion effects. For nanoparticles in solution these extra shear-effect terms have significant contributions to the attenuation and phase velocity. The LCN model was applied to compressional waves, extracting first order coefficients, and assuming negligible thermal-effects (see ref. 15 for a similar approach for emulsions, where thermal effects dominate). Shear-mode scattering coefficients were found by taking the first term in a series expansion in k_Cr using the boundary equations of the ECAH model,^22,23 where k_C is the compressional wavenumber and r is the radius of a silica nano/micro-sphere. These scattering coefficients are driven by a dependency upon the ratio of the densities of the dispersed silica (ρ′) and a continuous phase (ρ) such as water: [small rho, Greek, circumflex] = ρ′/ρ. This can be seen in the following equations where the compressional–compressional (T^CC₁), compressional-shear (T^CS₁), shear-compressional (T^SC₁) and shear–shear (T^SS₁) coefficients are defined for partial wave order one:

with F(k_S) = h₂(k_Sr)j₀(k_Sr) − h₀(k_Sr)j₂(k_Sr) and D(k_Sr) = 3h₂(k_Sr) − 2([small rho, Greek, circumflex] − 1)h₀(k_Sr). Here h_0,2 and j_0,2 are spherical Hankel and Bessel functions, and k_S is the shear-mode wavenumber. The effective wavenumber becomes a sum of that found through the LB model and two extra-terms due to the shear-mode conversion (second and third order terms, respectively):with

X = Y₀ + 2Y₂ (8)

and

Y_n = k_Cbj′_n(k_Cb)h_n(k_Sb) − k_Sbj_n(k_Cb)h′_n(k_Sb) (9)

where ϕ is the volume fraction, and b = 2r is the radius of the excluded volume around a particle that is inaccessible to other particles. Using the above formulations, the attenuation and speed of sound through a sample can be found from the effective wavenumber, K_eff.¹⁹ These equations are used to calculate the predicted attenuation and then compared with experiment. In both second and third order mode-conversion terms, only the dominant contributions have been retained. At second order, compressional–thermal conversions are neglected here, and at third order only terms relating to shear-shear and shear-compressional conversion are retained. The dominance of these terms was confirmed numerically. In addition, terms in Y₂ were neglected in the third order contributions since Y₂/Y₀ is O(k_Cr) which is neglected in our expansion. Particles were assumed to be randomly distributed apart from the excluded volume.

3. Experiments

3.1. Sample preparation and properties

In order to show the progressive influence of shear-waves as the diameter of the silica particles approaches the nanoscale, four sample sizes were used in the experiments: 100 nm, 214 nm, 430 nm, and 1000 nm. The 100 nm silica (Snowtex-ZL) was supplied by Nissan Chemical Industries, whereas the other sizes were purchased from Fiber Optics Center (Angstromspheres of nominal sizes 250 nm, 500 nm, 1000 nm). Particle size distributions were determined using photon correlation spectroscopy (Beckman Coulter Delsa Nano), high resolution field emission gun scanning electron microscopy (Carl Zeiss 1530 VP), light scattering and Brownian motion (Malvern Nanosight LM10). In Fig. 1 scanning electron microscopy images of the silica powders with nominal sizes 250 nm and 500 nm are shown ((a) and (b), respectively). In Fig. 1(b) an electron backscattering diffraction system incorporated into the SEM system allowed analysis of the sample surface and in (d) energy dispersive X-ray spectroscopy produced a chemical analysis, both of which demonstrate the purity of the silica (with only a minute trace of sodium also present).

Fig. 1 Field emission gun scanning electron microscopy analysis of silica powder of nominal sizes (a) 250 nm, and (b)–(d) 500 nm with additional crystallography of the sample surface (b) and X-ray chemical analysis (d). In (a) and (c) localised magnification of the silica powders deposited on carbon substrates are shown, along with calculated diameters. In (b) colour maps of the elements present in the samples are shown, with some trace of carbon from the substrate and a minute level of sodium. The weight percent of each element is plotted in (d). A thin film of gold covered each sample to allow electron imagery.

To determine the densities of each silica sample, a helium pycnometer was used (Micromeritics Multivolume Pycnometer 1305, with absolute density accuracy: ±0.1 to 0.2%). The 100 nm powder was found to have a density of 2.280 g cm⁻³. The powder was obtained by first centrifuging some Nissan-ZL solution at 3500 rpm for 90 min before pipetting off most of the clear water and heating in a vacuum oven at 45 °C for 24 hours to completely dry out the sample. The other silica samples were originally in powder form, and the Angstromsphere 250 nm was found to have ρ = 1.980 g cm⁻³, whilst the 500 nm had a similar value of ρ = 1.986 g cm⁻³. The Angstromsphere 1000 nm had a larger density of 2.041 g cm⁻³. It was important to determine the density of the silica in order to accurately calculate the concentration of silica in water and because of the sensitivity of ultrasonic modelling. Other physical properties of silica were taken from Challis et al. as standard values given for silica.¹⁹ The physical properties used in the modelling are in Table 1.

Table 1 Physical properties of silica, of nominal sizes a 100 nm, b 250 nm, c 500 nm, d 1000 nm, and water

	Silica	Water
Density (kg m^−3)	a: 2280 b: 1980; c: 1986; d: 2041	997
Speed of sound (m s^−1)	5968	1497
Shear modulus (GPa)	30.9	—
Shear viscosity (Pa s)	—	0.00089
α (Np m^−1 MHz^−2)	2.6 × 10^−10	0.023

---

The Angstromsphere silica powders were each dispersed into deionised water (Millipore-Q); silica was added gradually and mixed into the water. A magnetic stirrer was then used to further disperse the silica before using pulses of high intensity ultrasound (Branson Digital Sonifier) to fully disperse the samples. The samples were analysed using the Delsa Nano analyser to find the particle size distributions. Once dispersed the suspensions were continuously stirred using magnetic stirring. After conclusion of the acoustic experiments, gravimetric analyses were conducted once again to verify the volume fractions of each sample. About 25 ml of each sample was separated by centrifugation. The supernatant liquid was then removed with a pipette and the silica pellet was dried in a Technico Vacuum Dryer overnight. The masses of the samples before and after this process were measured allowing determination of the actual concentrations (all concentrations throughout are stated by volume and calculations assume D₅₀ monodispersity).

3.2. Ultrasonic spectroscopy

Two systems were used to find the attenuation properties of the silica suspensions. The first was a Digusonic DSX pseudo-random binary sequence spectrometer linked to a computer via a high-speed serial data link and to pairs of Olympus Panametrics transducers (V309/5 MHz, V311/10 MHz, V319/15 MHz types with 0.5 inch diameter) through BNC terminated coaxial cables. The DSX system uses digital waveforms to generate ultrasonic responses and cross-correlation to extract ultrasonic attenuation. The ultrasonic transducers were inserted into a cell machined from acrylic with a central reservoir for the solutions that has a capacity of 50 ml. The reservoir also has space for a small magnetic stir-bar that enables one to maintain fluid flow. The cell was mounted atop a small magnetic stirrer. Prior to testing the suspensions the DSX was calibrated using deionised water as a reference sample with each set of transducers.^34–36

The second system used was a Malvern Instruments Ultrasizer MSV spectrometer, based at Leeds University, in the School of Food Science and Nutrition. For this system sample volumes of 500 ml had to be prepared. An agitator with variable rotational speed was also used to maintain the homogeneity of the sample during a measurement. The sample temperature was maintained at 25 ± 0.2 °C. Calibration checks were performed using deionised water. The same sample batches at 250–1000 nm were used for experiments in the DSX and the Ultrasizer systems. The pre-suspended 100 nm silica was taken as supplied from the manufacturer and diluted to desired concentrations (from 22.6% v/v). The Ultrasizer has the capability to analyse a broad range of frequencies with a calibrated switching between two pairs of transducers. Here we are interested in and analyse the regime up to 20 MHz because until now multiple scattering models have broken down at relatively low concentrations, sizes approaching the nanoscale, and at low frequencies.^17,32 The silica was homogeneously dispersed and any discrepancies between the two spectrometer systems results occur as a consequence of the optimum dynamic range in each and choice of measurement strategy. For example, in the Ultrasizer the transducers are moved mechanically to obtain the best possible signal to noise ratio and accuracy, whereas the DSX set-up was configured to operate with the transducers positioned at a fixed path length. The spectral quality of the Ultrasizer has to be kept ≤5 to produce accurate results,³⁷ and in all the cases reported here was <2.5. In the DSX system a sequence length has to be chosen to define the dynamic range and resolution.³⁸ We operated with a sequence length of 262 144 (measurement time is a function of the sequence length and this value was optimal for our experiments).

4. Results

In the following, comparison is made between simulations conducted with and without shear-mediated multiple scattering effects included (using eqn (5) with and without the extra terms defined by eqn (6) and (7)). Further comparison is made between the experimental data from the ultrasonic spectroscopy experiments using the two kinds of spectrometer described above. We will begin with relatively large particles and move towards the nanoscale, in our discussion of the results. Attenuation (in Np m⁻¹ – 1Np is equivalent to 8.686 dB) is demonstrated at each particle size as a function of frequency and volume fraction.

The DSX and Ultrasizer experiments were repeated 30 and 5 times, respectively, for each concentration and particle size (except for the 100 nm samples used with the DSX where 10 repeat measurements were made for each concentration). Standard deviation was very small in all cases, with the coefficient of variation at each frequency less than 1%, giving confidence in the accurate repeatability of the experiments.

4.1. Silica of 1000 nm diameter

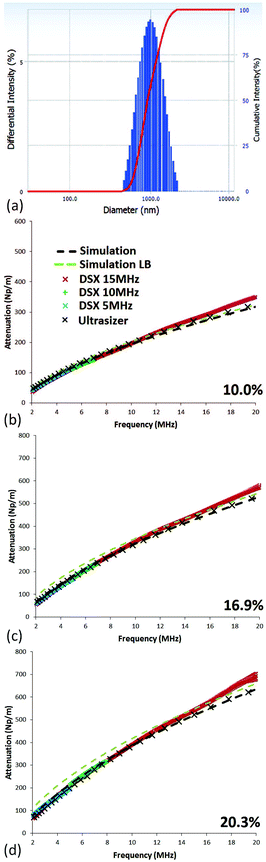
Multiple scattering theory has been found to be most successful in describing relatively dilute suspensions and those composed of microparticles in the past. As the size of the particles becomes smaller than several micrometres, shear-effects begin to take hold. In Fig. 2, the attenuations for suspensions of 1000 nm diameter silica are simulated using the Lloyd–Berry formalism alone (light-green dashed lines) and inclusive of shear-mode effects (black dashed lines). Also, shown are the experimental results using the Digusonic DSX spectrometer (blue, green, and red crosses) and the Ultrasizer (black crosses). The particle size distribution can be seen in Fig. 2(a), as obtained by photon correlation spectroscopy, and the D₅₀ value of the monodisperse samples used in the simulations. The acoustic spectrometer results at 10% concentration, Fig. 2(b), agree with the light scattering particle sizing as evidenced by the very close match between LB and shear-mode (SM) modelling with experimental data. In this case, at 10%, one can determine that there is little or no contribution from shear-effects because LB and SM models agree. There are, however some significant observations to be made as the concentration increases. For example, in Fig. 2(c), the two models attenuations diverge slightly, with the higher attenuation of the LB simulations becoming clearer as concentration further increases, as can be seen by comparison to (d) at 20.3%.

Fig. 2 Simulated and experimental results for 1000 nm silica particles in water. (a) Particle size distribution determined through photon correlation spectroscopy. The attenuation as a function of frequency at volume percentages (b) 10.0%, (c) 16.9%, and (d) 20.3%.

4.2. Silica of 430 nm diameter

The attenuation is now investigated for 430 nm sized particles in a water continuous phase (Fig. 3). For concentration 6.7% the data obtained from the two spectrometers agree, with the results of simulations from the two models also very closely aligned. This is shown in Fig. 3(a), and although the LB model gives slightly higher attenuation values than the SM model, the difference is relatively small. Thus, shear-mode effects are minimal at this concentration. At 13.4%, Fig. 3(b), the experimental results from the 5 MHz and 10 MHz transducers used with the DSX and the Ultrasizer data agree. There is a departure of agreement at the higher frequencies obtained using the 15 MHz transducers on this occasion. Up until 10 MHz the simulations inclusive of shear-effects agree with the experimental results of both spectrometers. The LB method consistently over-states the attenuation except against the higher frequency results of the DSX, at which point they align. However, at this concentration, weak indications that the shear-effects are in operation emerge in the form of experimentally lower attenuation than found using the LB method. This trend continues when the concentration is further increased to 16.2% and 19.4%, Fig. 3(c) and (d), respectively. The shear-mode modelling matched the curvature of the experimental attenuation very well, particularly at 19.4%; whereas neglecting these shear-conversion phenomena results in a large departure from experimentally observed attenuation. It is now clear that decreases in the sizes of the suspended phases and elevated concentration levels lead to conditions for strong hydrodynamical effects attributable to visco-elastic phenomena.

Fig. 3 Simulated and experimental results for 430 nm silica particles in water. The attenuation as a function of frequency at volume percentages (a) 6.7%, (b) 13.4%, (c) 16.2%, and (c) 19.4%.

4.3. Silica of 214 nm diameter

Next the particle sizes are reduced again, to 214 nm, in order to gauge the significance of the shear-wave contributions as they approach nano-dimensions. In Fig. 4, results at higher concentration (16% and 19%) clearly show that the shear-mode contribution to the multiple scattering gives a strong agreement against the spectrometer data, whereas without it (LB) there are large differences of ≈100%. Thus, we have established that the phenomena associated with shear-effects are size and concentration dependent. In addition, the largest effects due to particle size at specific concentrations lie not at the smallest diameters but at some intermediate scale. To illustrate this point, in Fig. 5 the attenuation is plotted as a function of particle diameter, starting at 20 nm and ending at 2000 nm, at three different concentrations (6.45%, 19.4%, and 20.3%) for different frequencies. Here the simulated attenuation curves show that at a particle diameter of 20 nm there are no discernible shear-effects (i.e. the two models are not significantly different). Also shown are the experimental attenuations obtained from use of the DSX for particle sizes of 214 nm and 430 nm, which demonstrate agreement with the SM model, (orange (6.2 and 19%) and red dots (6.7 and 19.4%), respectively). Fig. 5 clearly shows that the largest effects are to be found between particle diameters of ≈20–750 nm at around 6% and ≈20–1000 nm in the frequency regimes examined herein. For example, after 1000 nm at 6.45% (first three plots of Fig. 5) the two models largely agree and shear-mode effects are deemed to be very small. As the concentration increases to, for example 19.4% (next five plots of Fig. 5), this is not the case and one can see that in contrast to the lower concentration at 6.45%, at frequencies up to 15 MHz there are still shear-effects in evidence through differences between the models. It is also shown that at the lower end of the frequencies we examine, at high concentration and small particle size, traditional methods of analysis (LB) cannot accurately reflect the attenuation properties unless particles become much larger, frequency increases, or concentration is drastically reduced. In the production of silica, as expansion of particles occurs through, for example Oswald ripening, any attempt to simulate the growth of particles from the nanoscale upwards is impossible using conventional modelling, and only with shear effects included can this be monitored. The final plot of Fig. 5 is for the case of 1 μm diameter silica, that has a density of 2041 kg m⁻³. The ultrasonic fields are applied at 6 MHz and 10 MHz. The green dots are from experimental data found from use of the DSX spectrometer. There is a clear match of the experimental and simulated data, confirming the maxima of the attenuation for specific particle sizes as demonstrated throughout Fig. 5.

Fig. 4 Simulated and experimental results for 214 nm silica particles in water. The attenuation as a function of frequency at volume percentages (a) 16.0% and (b) 19.0%.

Fig. 5 Attenuation at specific frequencies (for 6.45%: 6, 8, 10 MHz and for 19.4%: 3, 5, 9, 11, and 15 MHz) for particle sizes from 20 nm up to 2000 nm with silica of density 1.980 g cm⁻³ (except in the last plot where a density of 2.041 g cm⁻³ is used to compare simulated results inclusive of shear-wave effects with experimental values for 1000 nm diameter particles at 6 MHz and 10 MHz – green circles). Simulation results, in the first eight plots, inclusive of shear-effects and without (crosses and triangles, respectively) are plotted alongside experimental results obtained using a Digusonic DSX spectrometer (orange circles, 214 nm diameter silica, and red circles, 430 nm). The experimental values of the density of the 214 nm and 430 nm silica was 1.980 g cm⁻³ and 1.986 g cm⁻³, respectively. In the last plot the concentration is 20.3%.

4.4. Silica of 100 nm diameter

It is now necessary to investigate the transition to the true nanoscale. Typically this is defined as ≤100 nm, and given the preceding arguments and evidence, one should expect that shear-mode effects dominate at this particle size over a wide concentration range. This does indeed occur, and in Fig. 6, even at relatively low concentrations, the accurate comparison to experimental data can be seen using SM modelling with large departures from the real system results using LB (to an even greater level than the previous cases). At concentrations 6% to 20.6% the ultrasonic spectrometry of the DSX is compared to the simulation results with very clear correlation. The inset of Fig. 6 shows a snapshot of the 100 nm silica in a very dilute sample imaged with a Malvern Nanosight system, showing dispersion and no aggregation. The policy employed here to use two spectrometer systems, now for 100 nm silica in water, allows one to conclude that the DSX, Ultrasizer and simulation results (SM) all largely agree. Three examples of comparison to the Ultrasizer data are given in Fig. 7, at 6.9%, 12.7%, and 16.3%. This size of silica attenuates much less than the larger particles examined for similar concentrations, with little difference between that measured at 13.9% and 20.6% in Fig. 6. This is reflected in the SM modelling which remained accurate, but with the LB a rapidly increasing attenuation/frequency gradient occurs that deviates significantly from the real system.

Fig. 6 The attenuation (Np m⁻¹) at 4–18 MHz for 100 nm silica particles in water at different volume percentages. The simulations inclusive of shear-effects (black dashed lines) are compared against experimental values obtained using a Digusonic DSX spectrometer with three pairs of transducers of nominal centre frequencies 5 MHz (blue crosses), 10 MHz (dark green crosses), and 15 MHz (red crosses). The simulation results of multiple scattering without shear-effects (Lloyd–Berry (LB) method) are also plotted (light green dashed lines).

Fig. 7 Comparison of theoretical results with and without shear-wave effects (black and light-green dashed lines, respectively) against experimental results using Digusonic DSX (nominal centre frequencies of transducers: 15 MHz (red), 10 MHz (dark-green), and 5 MHz (blue)) and Malvern Ultrasizer spectrometers. Top: volume percentage of 100 nm silica in water, 6.9%; middle: 12.7%; bottom: 16.3%.

5. Discussion and conclusions

Indicative of shear-mode effects, the results throughout demonstrate that ultrasonics can be used as a successful modality for particle size distribution analyses. Moreover, because ultrasound can even penetrate the most opaque of samples and consider them in their entirety (without dilution as in light scattering techniques), it can be argued that ultrasonics technology and methods of analysis are reaching a level to compare and exceed more commonly used optical techniques. Once again, approaching the nanoscale the behaviour of particles is different to that of macroscopic systems composed of essentially the same materials. Here we have shown that when the shear-effects are accounted for a significant decrease in attenuation ensues – matching experimentally observed behaviour. This allows one to characterise the properties of common suspensions such as those composed of silica. Whether self-assembling in a biochemical process, or being introduced into a plant or mammal artificially, the concentration effects of silica need to be monitored in order to better understand the transport and bio-processes involved, for ecological and medical reasons. We have shown that there emerge fundamentally different phenomena at the nanoscale than larger systems when ultrasonic fields are applied to suspensions of nano-scatterers. The shear-mode effects become pronounced as the size of the silica decreases from a few micrometres and becomes very clear when the concentration increases concomitantly. We saw that the effects occur over a large dimensional scale ending at the lower limit of 20 nm for the concentrations investigated. It remains to be seen whether the shear-effects become strong once again at higher concentrations than explored herein. We can surmise that they will, but currently the modelling is successful up to a volume percent of 25%. We have investigated silica in aqueous continuous phases to experimentally verify the phenomenon. Work is under-way to extend the range of the modelling to higher concentrations and with inclusion of correlation function methods³⁹ it is thought that new terms in the expansion of the effective wavenumber may become strong enough at elevated concentrations to allow a match with the experimental results. The range of frequencies herein, 1–20 MHz, are commonly used in medical ultrasound and the simulations have been demonstrated to accurately reflect experimental results. It is of note that at these frequencies, some gels have similar or the same physical properties as water. In these hydro-gels matrices of silica or other nanoparticles can accumulate in varying concentrations too. Thus, use of the modelling herein can be incorporated into particle, density and concentration testing of an effective medium such as a gel structure or scaffold loaded with nanoparticles. As well as investigative and medical processes in mammals, understanding of plant transpiration may also ensue and limitations on the uptake of nanoparticles examined in slurries introduced to plants such as rice may have benefits for food production or even understanding the functions of silica production in vivo. When the silica has a reasonably small particle size distribution, stability is easily achieved when the attractive van der Waals force is weak in comparison to steric or electrostatic repulsion. Consequently, build up of a lattice structure of silica is possible by increasing the transportation of nanoparticles and increasing the volume fraction.⁷ In order to determine the quality of internal structuring in a liquid or gel medium ultrasonic characterisation is perhaps the only technique that can give true particle sizing and knowledge of flocculation because it is impervious to a sample's opacity.

Acknowledgements

The authors thank Professor Malcolm Povey and Dr Melvin Holmes for use of the Ultrasizer spectrometer system at University of Leeds, in the School of Food Science and Nutrition. Thanks are also extended to Nissan Chemical Industries for supplying Snowtex-ZL, with particular gratitude to Takashi Sonoda. The authors acknowledge funding from the EPSRC, grant number EP/L018780/1. The data reported here is held in the Loughborough University repository with DOI: 10.17028/rd.lboro.2056149.

References

1. H. A. Lowenstam and S. Weiner, On Biomineralization, Oxford University Press, USA, 1st edn, 1989.
2. E. Trembath-Reichert, J. P. Wilson, S. E. McGlynn and W. W. Fischer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5449–5454.
3. K. W. Euliss, B. L. Dorsey, K. Benke, M. K. Banks and A. P. Schwab, Ecol. Eng., 2005, 25, 343–348.
4. N. Poulsen, M. Sumper and N. Kröger, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12075–12080.
5. J. Yun, W. Wang, S. M. Kim, T.-S. Bae, S. Lee, D. Kim, G.-H. Lee, H.-S. Lee and M. Song, Energy Environ. Sci., 2015, 8, 932–940.
6. D. M. Forrester, Med. Hypotheses, 2015, 85, 10–16.
7. S.-H. Kim, S. Y. Lee, S.-M. Yang and G.-R. Yi, NPG Asia Mater., 2011, 3, 25–33.
8. A. K. Hipp, B. Walker, M. Mazzotti and M. Morbidelli, Ind. Eng. Chem. Res., 2000, 39, 783–789.
9. D. Fan, G. R. Akkaraju, E. F. Couch, L. T. Canhamc and J. L. Coffer, Nanoscale, 2011, 3, 354–361.
10. G. Poologasundarampillai, B. Yu, O. Tsigkou, E. Valliant, S. Yue, P. D. Lee, R. W. Hamilton, M. M. Stevens, T. Kasugad and J. R. Jones, Soft Matter, 2012, 8, 4822–4832.
11. M. Sumper, Angew. Chem., Int. Ed., 2004, 43, 2251–2254.
12. C. C. Lechner and C. F. W. Becker, Mar. Drugs, 2015, 13, 5297–5333.
13. D. J. McClements, Ultrasonic measurements in particle size analysis, in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley and Sons, Chichester, England, 2000, pp. 5581–5588.
14. P. Lloyd and M. V. Berry, Proc. Phys. Soc., 1967, 91, 678–688.
15. V. J. Pinfield, J. Acoust. Soc. Am., 2014, 136, 3008–3017.
16. V. J. Pinfield, Food Hydrocolloids, 2014, 42, 48–55.
17. R. E. Challis and V. J. Pinfield, Ultrasonics, 2014, 54, 1737–1744.
18. K.-M. Kim, H. M. Kim, W.-J. Lee, C.-W. Lee, T. Kim, J.-K. Lee, J. Jeong, S.-M. Paek and J.-M. Oh, Int. J. Nanomed., 2014, 9, 29–40.
19. R. E. Challis, M. J. W. Povey, M. L. Mather and A. K. Holmes, Rep. Prog. Phys., 2005, 68, 1541–1637.
20. F. Alba, G. M. Crawley, J. Fatkin, D. M. J. Higgs and P. G. Kippax, Colloids Surf., A, 1999, 153, 495–502.
21. A. S. Dukhin and P. J. Goetz, Adv. Colloid Interface Sci., 2001, 92, 73–132.
22. P. S. Epstein and R. R. Carhart, J. Acoust. Soc. Am., 1953, 25, 553–565.
23. J. R. Allegra and S. A. Hawley, J. Acoust. Soc. Am., 1972, 51, 1545–1564.
24. M. J. W. Povey, Ultrasonic Techniques for Fluids Characterization, Academic Press Ltd, California, USA, 1st edn, 1997.
25. L. L. Foldy, Phys. Rev., 1945, 67, 107.
26. M. Lax, Rev. Modern Phys., 1951, 23, 287–310.
27. P. C. Waterman and R. Truell, J. Math. Phys., 1961, 2, 512–537.
28. J. G. Fikioris and P. C. Waterman, J. Math. Phys., 1964, 5, 1413–1420.
29. C. M. Linton and P. A. Martin, SIAM J. Appl. Math., 2006, 65, 1649–1668.
30. F. Luppé, J. M. Conoir and A. N. Norris, J. Acoust. Soc. Am., 2012, 131, 1113–1120.
31. V. Pinfield and D. M. Forrester, J. Acoust. Soc. Am., 2015, 137, 2293.
32. A. K. Hipp, G. Storti and M. Morbidelli, Langmuir, 2002, 18, 405–412.
33. L. W. Anson and R. C. Chivers, J. Acoust. Soc. Am., 1993, 93, 1687–1699.
34. N. Bilaniuk and G. S. K. Wong, J. Acoust. Soc. Am., 1993, 93, 1609–1612.
35. N. Bilaniuk and G. S. K. Wong, J. Acoust. Soc. Am., 1996, 99, 3257.
36. V. A. Del Grosso and C. W. Mader, J. Acoust. Soc. Am., 1972, 52, 1442–1446.
37. M. Asif Inama and C. Frances, Powder Technol., 2010, 201, 21–26.
38. R. E. Challis and V. G. Ivchenko, Meas. Sci. Technol., 2011, 22, 025902.
39. H. D. Ursell, Math. Proc. Cambridge Philos. Soc., 1927, 23, 685–697.

---