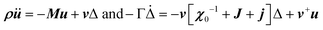Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular disorder and translation/rotation coupling in the plastic crystal phase of hybrid perovskites
J.
Even
 *a,
M.
Carignano
b and
C.
Katan
*a,
M.
Carignano
b and
C.
Katan
 c
c
aFonctions Optiques pour les Technologies de l'Information, FOTON UMR 6082, CNRS, INSA de Rennes, 35708 Rennes, France. E-mail: Jacky.Even@insa-rennes.fr
bQatar Environment and Energy Research Institute, Hamad Bin Khalifa University, Doha, Qatar
cInstitut des Sciences Chimiques de Rennes, ISCR UMR 6226, CNRS, Université de Rennes 1, 35042 Rennes, France
First published on 26th November 2015
Abstract
The complexity of hybrid organic perovskites calls for an innovative theoretical view that combines usually disconnected concepts in order to achieve a comprehensive picture: (i) the intended applications of this class of materials are currently in the realm of conventional semiconductors, which reveal the key desired properties for the design of efficient devices. (ii) The reorientational dynamics of the organic component resembles that observed in plastic crystals, therefore requiring a stochastic treatment that can be done in terms of pseudospins and rotator functions. (iii) The overall structural similarity with all inorganic perovskites suggests the use of the high temperature pseudo cubic phase as the reference platform on which further refinements can be built. In this paper we combine the existing knowledge on these three fields to define a general scenario based on which we can continue the quest towards a fundamental understanding of hybrid organic perovskites. With the introduction of group theory as the main tool to rationalize the different ideas and with the help of molecular dynamics simulations, several experimentally observed properties are naturally explained with possible suggestions for future work.
1. Introduction
Having demonstrated the first truly low-cost photovoltaic devices with more than 20% conversion efficiency, hybrid organic perovskites (HOP) are currently a phenomenal scientific and technological revolution for the entire sector.1–7 Being brought back to the forefront among the current hot topics, they have also revealed undeniable assets for light emitters8 and water splitting applications9 along with potential outcomes in spintronics.10 Meanwhile and despite a tremendous effort of the DFT community, there is still need for further theoretical work in connection with both fundamental and applied issues. In this context, there is hope for a theoretical framework and generic tools to streamline the analysis of recent but also older experimental and computational data on HOP. To achieve these goals, we believe that HOP must be placed in context and viewed along with other classes of materials (Fig. 1). This had made it possible to exploit the concept and tools developed over decades for conventional semiconductors11 and to identify key differences such as reverse band edge electronic state ordering.12 This line of comparison also points out that the performance of devices depends heavily on the quality of the material, for instance the degree of crystallinity in silicon-based solar cells. Given the inherent complexity of HOP as compared to silicon, it also raises the question of a bulk crystal structure, related phase transitions and their impact on the physical properties.13 In this regard, a comparison with all inorganic perovskites (AIP) has already yielded interesting results, among which is the proposal to consider their cubic high temperature phase as the reference phase for HOP.14 This prompts the question: to what extent the hybrid character is important for the intended applications? In other words, how it affects materials growth and properties and how it can be accounted for in theoretical approaches or numerical modeling. Regarding the latter, given the symmetry of possible organic cations that fit in the cuboctahedral cage of the 3D inorganic framework, the high temperature reference phase must be thought as pseudo-cubic with static or dynamical orientational disorder of the organic moieties. From early investigations on methylammonium (CH3NH3+, hereinafter referred to as MA) lead-based perovskites, we know that the organic cation is tumbling between various orientations with a typical timescale of picoseconds. This led to the suggestion that, in HOP, excitons may undergo a dielectric screening due to the rotational degrees of freedom of the MA molecule, which has recently been confirmed experimentally.14–16 From the device point of view, this promotes improved transport properties based on free carriers.17,18 | ||
| Fig. 1 Room temperature properties of hybrid perovskites viewed as a merging of properties of all-inorganic perovskites, conventional semiconductors and plastic crystals. | ||
Such an orientational degree of freedom is also reminiscent of plastic crystals.14,19,20 Indeed, liquid and plastic crystal phases are possible intermediate stages between ordered crystal and liquid phases. Liquid phases exhibit both translational and orientational/conformational disorder, whereas in a plastic crystal phase atoms and the molecular centers of mass (CM) are located at well-defined positions within the periodic lattice. If the disorder is mainly related to molecular rotations rather than molecular conformations, the phase is frequently referred to as a “rotor phase”. In that sense, there is clear experimental evidence of the rotational motion of the organic cations in the high temperature pseudo-cubic phase of HOP, namely from NMR, dielectric measurements, millimeter wave spectroscopy and neutron diffraction.21–24 Although a couple of scenarios for the orientation of the molecular cation are considered, based on the early work by Onoda et al.,22 there is yet no theoretical framework that provides an in-depth uniform analyses.
In this paper, after a brief introduction to AIP and HOP, we will first revisit the available experimental data related to phonons in AIP and put them into perspective with HOP for which similar data is still lacking. Next, we will subsequently develop two approaches that allow taking the stochastic molecular degrees of freedom into account. The first simplified approach is based on the concept of pseudospins (PS), recently introduced by one of us,19 which offers a discrete representation of possible random orientations of the molecular cation accounting for both its elastic and electric multipoles. We then examined how rotator functions, which provide continuous variables, can contribute to rationalize the properties of HOP. To complement the available experimental data, we performed molecular dynamics (MD) simulations at several temperatures and for several super-cells. This work presents for the first time MD simulations25–28 combined with group theory analysis19 applied to HOP. All these different approaches, when implemented with the support of the group theory, are shown to help streamline the couplings between stochastic molecular excitations and lattice vibrations, the structural phase transitions and possible orientational glassy behavior of perovskite structures.
2. Computational method
First principles molecular dynamics simulations were performed using the CP2K package, which implements a hybrid methodology combining Gaussian basis functions and plane waves.29–31 All simulations were performed under NVT ensemble using periodic boundary conditions with the temperature being controlled by using a Nosé–Hoover thermostat with three chains and a time constant of 50 fs.32,33 The electronic structure properties were calculated using the PBE functional with the addition of the Grimme D3 scheme to correct the dispersion interactions.34,35 The Kohn–Sham orbitals were expanded in Gaussian basis sets (DZVP-MOLOPT for Pb, I, C, N and H)36 and the norm-conservative GTH pseudopotentials were employed.37,38 The auxiliary plane-wave basis set was defined by an energy cutoff of 300 Ry. The time-step for the integration of the dynamic equation was set to 1 fs.The preparation of the systems was made using the available crystallographic data, obtained at 400 K for the cubic phase of MAPbI3. Different systems were prepared by the replication of the unit cell for a larger quasi-cubic simulation box. System-222 (96 atoms) contains 2 unit cells in each Cartesian direction. Analogously, larger systems having up to 5 unit cells per direction were prepared. The largest case, System-555, contains 1500 atoms. All the systems were tempered by a succession of NVE simulations to introduce a representative thermal disorder before starting the NVT simulations, which were integrated for at least 40 ps in each case.
3. Results and discussion
3.1. The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/h3_char_0033_0304.gif) m crystal structure as a reference phase
m crystal structure as a reference phase
The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase of CsPbX3 compounds (Z = 1) is chosen as the reference for the high temperature phase of 3D AIP and HOP with a general formula, AMX3.39–46 The metal (M), the 3 halogens (X) atoms and the cation (A) are located at sites (0,0,0) (M, 1a), (1/2,0,0) (X, 3d) and (1/2,1/2,1/2) (A, 1b), respectively (Fig. 2a). Structural data is available for 3D AIP with A = Cs+ or Rb+. In 3D HOP, the orientations of the organic cations are dynamically averaged in the Pm
m cubic phase of CsPbX3 compounds (Z = 1) is chosen as the reference for the high temperature phase of 3D AIP and HOP with a general formula, AMX3.39–46 The metal (M), the 3 halogens (X) atoms and the cation (A) are located at sites (0,0,0) (M, 1a), (1/2,0,0) (X, 3d) and (1/2,1/2,1/2) (A, 1b), respectively (Fig. 2a). Structural data is available for 3D AIP with A = Cs+ or Rb+. In 3D HOP, the orientations of the organic cations are dynamically averaged in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase. The molecular CM is located at the site (A, 1b) of the cubic cell (Fig. 2a). Most of the photovoltaic devices made of perovskites have been developed with the MA cation, to a lesser extent with formamidinium (FA: [HC(NH2)2]+), but guanidinium (GA: [C(NH2)3]+), dimethylammonium (DMA), trimethylammonium (TMA) and tetramethylammonium (TeTMA) are also possible.47–50
m cubic phase. The molecular CM is located at the site (A, 1b) of the cubic cell (Fig. 2a). Most of the photovoltaic devices made of perovskites have been developed with the MA cation, to a lesser extent with formamidinium (FA: [HC(NH2)2]+), but guanidinium (GA: [C(NH2)3]+), dimethylammonium (DMA), trimethylammonium (TMA) and tetramethylammonium (TeTMA) are also possible.47–50
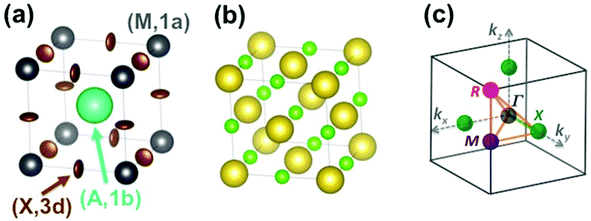 | ||
| Fig. 2 (a) Simple cubic structure of CH3NH3PbBr3 at high temperature.45 The center of mass (CM) of the CH3NH3 (MA) cation is represented by the large green sphere, and lead atoms by grey spheres. Bromide atoms exhibit anisotropically disordered motions as indicated by the brown ellipsoids. Site labels are also indicated. (b) NaCl-type structure of NaCN at high temperature. The sodium cations are represented by large yellow spheres, the CM of cyanides by small light green spheres. (c) Reciprocal space 3D view of the brillouin zone (BZ) with conventional labels for points of high symmetry (Γ, R, M, X). | ||
Here we will mainly discuss MA-based 3D HOP, but the methodology can be applied for other organic cations having a different geometry, symmetry or polarity. Noteworthily, the replacement of the molecular CM by a simple cation (Na+ or Cs+) mimics the influence of ionic interactions on the electronic band diagrams close to the band gap.12–14 However, it is necessary to go beyond this simple model in order to describe the crystal packing and structural instabilities, as well as the complex coupling between the disordered orientational dynamics and lattice vibrations. The first step of our approach consists of decoupling translational and rotational degrees of freedom of the cation A. These degrees of freedom can be analyzed separately yielding, for the translational part, a common vibrational analysis for both AIP and HOP bulk solids. The rotational part must be treated carefully to account for the possible disorder effect and will be investigated in a second step. Then rotation–translation coupling allowed by symmetry in the cubic phase will be considered in a third step. Our analysis strongly relies on the use of group theory39,40 (see for example the pedestrian guide in ref. 19) and reciprocal space.11,43 The labels of the main high symmetry points related to the first Brillouin Zone (BZ) of the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group are shown in Fig. 2c. For the irreducible representation (IR), we will mainly use Miller and Love notations.19,40
m space group are shown in Fig. 2c. For the irreducible representation (IR), we will mainly use Miller and Love notations.19,40
In order to analyze the symmetry properties of lattice vibrations (phonons) belonging to a Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure, 5 atoms (among which 1 is a pseudo atom for the molecular CM in HOP) must be considered.11,19,42 The three acoustic modes belong to the Γ4− IR whereas the twelve optical phonons correspond to the 3Γ4− + Γ5− IR (Table 1). At the R and M points of the BZ, the optical mode IR decompositions yield R1+ + R3+ + R4+ + 2R5+ + R4− and M1+ + M2+ + M3+ + M4+ + M5+ + M2− + 2M3− + 3M5−, respectively. Noteworthily, neither the metal nor the A atom/CM is involved in the M3+ and R4+ degenerate phonon modes, but only the X atoms. These modes related to antiferro-distortive instabilities correspond to the rotations of the metal halide octahedra. The IR decomposition at Γ are useful to analyze electron to optical phonon coupling. For electron to acoustic phonon coupling, the symmetry properties of the strain tensor components are relevant. The volumetric strain (qa = ε1 + ε2 + ε3), tetragonal strains (qoz = ε1 − ε2 and qtz = 2ε3 − ε1 − ε2) and shear strains (ε4, ε5, ε6) are described by the Γ1+, Γ3+ and Γ5+ IRs, respectively (Table 1).
m structure, 5 atoms (among which 1 is a pseudo atom for the molecular CM in HOP) must be considered.11,19,42 The three acoustic modes belong to the Γ4− IR whereas the twelve optical phonons correspond to the 3Γ4− + Γ5− IR (Table 1). At the R and M points of the BZ, the optical mode IR decompositions yield R1+ + R3+ + R4+ + 2R5+ + R4− and M1+ + M2+ + M3+ + M4+ + M5+ + M2− + 2M3− + 3M5−, respectively. Noteworthily, neither the metal nor the A atom/CM is involved in the M3+ and R4+ degenerate phonon modes, but only the X atoms. These modes related to antiferro-distortive instabilities correspond to the rotations of the metal halide octahedra. The IR decomposition at Γ are useful to analyze electron to optical phonon coupling. For electron to acoustic phonon coupling, the symmetry properties of the strain tensor components are relevant. The volumetric strain (qa = ε1 + ε2 + ε3), tetragonal strains (qoz = ε1 − ε2 and qtz = 2ε3 − ε1 − ε2) and shear strains (ε4, ε5, ε6) are described by the Γ1+, Γ3+ and Γ5+ IRs, respectively (Table 1).
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m BZ. The contributions from each site (1a, 1b, 3d) are indicated. The symmetric (+) and antisymmetric (−) PS IR correspond to elastic and electric multipoles, respectively
m BZ. The contributions from each site (1a, 1b, 3d) are indicated. The symmetric (+) and antisymmetric (−) PS IR correspond to elastic and electric multipoles, respectively
| Γ | R | M | |
|---|---|---|---|
| Volumetric strain | Γ 1 + | — | — |
| Tetragonal strain | Γ 3 + | — | — |
| Shear strain | Γ 5 + | — | — |
| Phonons (1a) | Γ 4 − | R 4 − | M 3 − + M5− |
| Phonons (1b) | Γ 4 − | R 5 + | M 2 − + M5− |
| Phonons (3d) | 2Γ4− + Γ5− | R 1 + + R3+ + R4+ + R5+ | M 1 + + M2+ + M3+ + M4+ + M5+ + M3− + M5− |
| PS (A, 1b) | Γ 1 + + Γ3+ | R 5 + | M 3 + + 2M4+ |
| Γ 4 − | R 2 − + R3− | M 2 − + M5− | |
| PS (B, 1b) | Γ 1 + + Γ3+ + Γ5+ | R 4 + + R5+ | M 1 + + M3+ + 2M4+ + M5+ |
| Γ 4 − + Γ5− | R 2 − + R3− + R4− | M 2 − + M3− + 2M5− | |
| PS (C, 1b) | Γ 1 + + Γ5+ | R 1 + + R5+ | M 1 + + M4+ + M5+ |
| Γ 2 − + Γ4− | R 2 − + R4− | M 2 − + M3− + M5− | |
| PS (D, 1b) | Γ 1 + + Γ2+ + 2Γ3+ + Γ4+ + Γ5+ | 2R4+ + 2R5+ | M 1 + + M2+ + 3M3+ + 3M4+ + 2M5+ |
| 2Γ 4 − + 2Γ5− | R 1 − + R2− + 2R3− + R4− + R5− | 2M1− + 2M2− + 4M5− |
3.2. Phonon dynamics in AIP
Phonon dynamics has already been thoroughly investigated only in the CsPbCl3 AIP, especially in its cubic phase that is the most relevant to this work. For instance, an empirical force constant model is in good agreement with the available spectroscopic data and phonon dispersion curves.51,52 Neutron scattering measurements clearly indicate that the energy of the whole acoustic phonon density of states is remarkably low at 80 °C, as compared to other perovskite crystals such as SrTiO3 or KMnF3. According to the direct measurements from Γ to R, M and X points show that the transverse acoustic (TA) branches are limited to about 2 meV over the entire BZ.51 The optical soft phonon branches, which lie in the same energy range (<2 meV) and are related to the structural instabilities close to the R and M points, are heavily overdamped over half the BZ. It was suggested that anharmonicity plays an important role in the phonon dynamics, as also revealed by the unusually large Debye–Waller factors. Similar observations were reported for the high temperature cubic phase of CsPbI3, which exhibits significant anisotropy of the halogen thermal ellipsoids similarly to that of CsPbCl3 (Fig. 2a).41,53 The halogen thermal motion is consistent with a small bulging of its distribution that is related to thermal anharmonicity. The central peak observed by Raman scattering in the cubic phase of CsPbCl3 was originally attributed to order–disorder long-range correlations in the high temperature phases and fitted by a Debye-type relaxor function: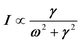 , where γ = 1/τ is the relaxation rate and τ the relaxation time.54 However, it corresponds to the signature of the strongly overdamped phonon observed by neutron scattering at M and R.51 In fact, the scattering cross-section for a phonon is given by
, where γ = 1/τ is the relaxation rate and τ the relaxation time.54 However, it corresponds to the signature of the strongly overdamped phonon observed by neutron scattering at M and R.51 In fact, the scattering cross-section for a phonon is given by 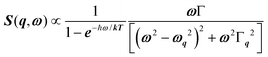 , where (ωq,Γq) are the phonon frequency and damping.55,56 For an overdamped phonon, Γq ≫ ωq, the neutron scattering cross section exhibits a signature similar to that of a relaxor,
, where (ωq,Γq) are the phonon frequency and damping.55,56 For an overdamped phonon, Γq ≫ ωq, the neutron scattering cross section exhibits a signature similar to that of a relaxor, 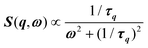 , with 1/τq = ωq2Γq. At high temperature, a phonon signature and a central peak with a true relaxor dynamics may be simultaneously observed by neutron scattering in many materials.55–58 The simultaneous observation of the two signatures corresponds to a more complex dynamical susceptibility:
, with 1/τq = ωq2Γq. At high temperature, a phonon signature and a central peak with a true relaxor dynamics may be simultaneously observed by neutron scattering in many materials.55–58 The simultaneous observation of the two signatures corresponds to a more complex dynamical susceptibility: 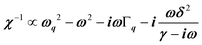 , where the phonon (ωq,Γq) is linearly coupled to a true relaxor through the coupling constant δ. When the two signatures lie in different frequency ranges, the neutron scattering cross-section is the sum of two contributions whose intensities are related:
, where the phonon (ωq,Γq) is linearly coupled to a true relaxor through the coupling constant δ. When the two signatures lie in different frequency ranges, the neutron scattering cross-section is the sum of two contributions whose intensities are related: 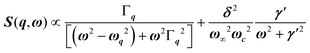 , with renormalized relaxor
, with renormalized relaxor 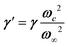 and optical phonon ω∞2 = ωq2 + δ2. Such a refinement was not necessary for CsPbCl3, as it was for KMnF3 or SrTiO3, and the neutron scattering data were only described with an overdamped phonon model by the same authors.51,58 All the phonon peaks are strongly broadened in the high temperature cubic phase. In fact, the high frequency optical phonons (>5 meV) are not observable in CsPbCl3 by neutron scattering due to broadening. Thus, from the inspection of the available literature on 3D AIP, we may conclude that the phonon spectrum in the pseudocubic phase is split in two parts: (i) heavily damped optical phonons, which are overdamped very close to the M, R and X edges of the BZ, and (ii) acoustic phonons at very low energy (<2 meV). The former contribution corresponds to pretransitional thermal fluctuations. The large damping of phonons observed in 3D AIP can be explained by a strong anharmonicity, which particularly shows off for the thermal vibrational motions of halogen atoms and leads to a relaxor-like signature close to the M and R points of the BZ. However, there is no experimental evidence of an additional quasi-elastic central peak like in KMnF3 or SrTiO3 perovskites.
and optical phonon ω∞2 = ωq2 + δ2. Such a refinement was not necessary for CsPbCl3, as it was for KMnF3 or SrTiO3, and the neutron scattering data were only described with an overdamped phonon model by the same authors.51,58 All the phonon peaks are strongly broadened in the high temperature cubic phase. In fact, the high frequency optical phonons (>5 meV) are not observable in CsPbCl3 by neutron scattering due to broadening. Thus, from the inspection of the available literature on 3D AIP, we may conclude that the phonon spectrum in the pseudocubic phase is split in two parts: (i) heavily damped optical phonons, which are overdamped very close to the M, R and X edges of the BZ, and (ii) acoustic phonons at very low energy (<2 meV). The former contribution corresponds to pretransitional thermal fluctuations. The large damping of phonons observed in 3D AIP can be explained by a strong anharmonicity, which particularly shows off for the thermal vibrational motions of halogen atoms and leads to a relaxor-like signature close to the M and R points of the BZ. However, there is no experimental evidence of an additional quasi-elastic central peak like in KMnF3 or SrTiO3 perovskites.
Unfortunately, similar detailed phonon spectroscopic data and vibrational models are still lacking for 3D HOP. From the available experimental reports on AIP and HOP, we may only infer that the spectra of optical modes lie in the same energy ranges.59 Diffraction studies on HOP crystals also report on strongly anisotropic thermal ellipsoids for halide atoms in HOP (Fig. 2a), which can be assigned to a strong anharmonicity.45,46 The MA cation reorientations21,23,24 have been investigated recently by inelastic incoherent neutron scattering in MAPbI3,60,61 exhibiting two quasi-elastic responses based on the same technique as used for phonons in AIP. The last neutron scattering investigation61 (which appeared while this manuscript was at the revision stage) contains a symmetry analysis of the tetragonal phase related to the approach developed in the present work (vide infra). The MA tumbling dynamics is described by discrete jumps between the four equivalent positions in the tetragonal phase, and a fast dynamics around the C–N axis, which is still present in the low temperature orthorhombic phase.61 A recent neutron scattering study of MAPbBr3 shows that the low-temperature harmonic (phonon) fluctuations cross over to fast overdamped relaxational dynamics and coupling to molecular dynamics at higher temperatures.62 The random reorientations at high temperature thus deserve a specific theoretical framework, which is discussed in the next section.
3.3. Taking into account molecular degrees of freedom
When plastic crystals are cooled, the rotational motion freezes and an orientational order appears at a certain temperature. Plastic crystals may exhibit two different behaviors at low temperature. In the first case, the rotational motion freezes under careful cooling, keeping quasistatic random molecular orientations. These orientational glasses exhibit most of the properties related to conventional glasses such as specific heat anomalies, ageing and distributions of relaxation times. Prototypes of orientational glasses are cyclohexanol64 and cyanoadamantane.66 In the second case, the plastic crystal may undergo a structural transition at low temperature to a partially or completely ordered crystalline phase, if spatial correlations or interactions between the molecular orientations are strong enough. Noteworthily, these interactions can be direct or indirect (vide infra). Prototypes of plastic crystals exhibiting structural phase transitions are the NaCN and KCN compounds.20 The structural transitions are usually associated to a structural symmetry breaking related to a collective molecular freezing and to an order–disorder character. Displacive and order–disorder dynamical processes are the two limiting cases for the microscopic mechanism driving a continuous structural phase transition. The order parameter dynamics is critical at the transition temperature and for a specific wavevector. For a soft phonon mode and a second order phase transition, the frequency goes to zero at Tc,67 whereas for a critical order–disorder relaxation, a similar behavior is observed for the relaxation rate.67,68 The high temperature relaxation mechanism in a plastic crystal is not necessarily critical at the structural phase transition corresponding to the molecular freezing. The order parameter of the structural phase transition can be related to a soft phonon mode of the surrounding lattice. The variable (PS or rotator function) describing the stochastic orientational motion is a secondary order-parameter, linearly coupled to the main displacive order parameter, which leads to a long range ordering of the frozen orientations at low temperature. Long-range correlations may be destroyed in alloys such as (NaCN)1−x(KCN)x, inducing an orientational glass transition at low temperature instead of a structural phase transition.69
HOP compounds undergo structural transitions to low temperature phases, where the molecular orientations are fixed. The existence of stochastic orientational degrees of freedom at high temperature can be assessed from the experimental results reported in the literature. Onoda and coworkers first demonstrated that the specific heat anomalies and entropy contributions at the structural phase transition temperatures are characteristic of order–disorder processes.22 Kawamura and coworkers showed that the cubic to tetragonal transition, in MAPbI3, is associated to a partial and collective molecular freezing, together with a displacive-like antiferrodistortive rotation of the metal halide octahedra.70 Moreover, Debye-type functions, which are characteristic of relaxational motions, were used to interpret nicely, both dielectric and millimeter-wave spectroscopy results in the three MAPbX3 compounds.21,23 In the prototype MAPbI3 HOP, the quasi-elastic neutron scattering signatures60,61 are also consistent with the simultaneous fast rotations of the methyl and ammonium groups around the C–N axes24 and the slower tumbling of the C–N axis between the symmetry equivalent positions.21,23 This is described in detail in ref. 61 with a C4 × C3 symmetry-based jump model designed for the tetragonal phase. The same model is used for the cubic phase, although as quoted by the authors, a O × C3 model expected to be more correct, yields essentially the same result.61 A reasonable description of the experimental results is also afforded by an isotropic orientational distribution.61 Both molecular motions are related to entropy contributions at the transition temperatures,22 but this work focuses on the tumbling of the molecular axis, namely the C–N axis in MA-based HOP, to discuss PS or rotator functions. The existence of a stochastic reorientational motion, leading to a collective freezing at low temperature, and thus a plastic crystal behavior, seems to be consistent with all available experimental data on MAPbX3 compounds. However the nature of the critical mechanism (displacive or order–disorder) is still not clear from the inspection of the literature. This point will be discussed further in section 3.4.4.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phases of MAPbX3.21,23 Unfortunately, the available experimental data are insufficient to definitely conclude about the prevailing scenario. The {1,0,0} direction (scenario A) appears among the preferred MA orientations: MA cations are considered to be mainly oriented toward the faces of the cube where no atoms are located, but probably also partly toward the halogen anions at the cell edges or the lead atoms in the corner, that is scenario B.45
m cubic phases of MAPbX3.21,23 Unfortunately, the available experimental data are insufficient to definitely conclude about the prevailing scenario. The {1,0,0} direction (scenario A) appears among the preferred MA orientations: MA cations are considered to be mainly oriented toward the faces of the cube where no atoms are located, but probably also partly toward the halogen anions at the cell edges or the lead atoms in the corner, that is scenario B.45
The concept of PS is also useful to rationalize properties of other crystals. Table 2 gathers a few examples of plastic crystals showing orientational disorder that can be described by PS in a high temperature cubic phase.20 NH4Br and MAPbX3 are two examples for a Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice, whereas NaCN corresponds to a face-centered Fm
m lattice, whereas NaCN corresponds to a face-centered Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic lattice. NaCN crystallizes in a NaCl-type structure (Fig. 2b), where the CN− disordered anion occupies the (1/2,1/2,1/2) (A, 1b) site in the cubic cell. The first, second and third nearest neighbors of CN− are Na+, CN− and Na+, respectively. For this reason preferred CN− orientations correspond to {1,0,0} and, to a less extent, {1,1,1} directions. In addition a CN− head to tail disorder is usually assumed, approximating the molecule to a symmetric dumbell.20 Finally, in the NH4Br crystal, the tetrahedral molecule in the center has eight nearest neighbor Br anions in the corners. The protons point toward the corners of the cube, which define only two preferred orientations. The NH4Br example further shows that besides the site symmetry, the molecular symmetry is also important.
m cubic lattice. NaCN crystallizes in a NaCl-type structure (Fig. 2b), where the CN− disordered anion occupies the (1/2,1/2,1/2) (A, 1b) site in the cubic cell. The first, second and third nearest neighbors of CN− are Na+, CN− and Na+, respectively. For this reason preferred CN− orientations correspond to {1,0,0} and, to a less extent, {1,1,1} directions. In addition a CN− head to tail disorder is usually assumed, approximating the molecule to a symmetric dumbell.20 Finally, in the NH4Br crystal, the tetrahedral molecule in the center has eight nearest neighbor Br anions in the corners. The protons point toward the corners of the cube, which define only two preferred orientations. The NH4Br example further shows that besides the site symmetry, the molecular symmetry is also important.
| Substance | Cubic space group |
|---|---|
| NaCN |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (FCC) m (FCC) |
| CH3NH3PbI3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SC) m (SC) |
| NH4Br |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SC) m (SC) |
In the PS simplified picture, a discrete variable ξi is defined for each possible molecular orientation i. ξi is equal to 1 or 0, whether orientation i is occupied or not. Symmetry-adapted combinations of ξi can be computed for a single crystal cell: 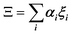 . Let's consider scenario A in detail with i = 1–6 for, (1,0,0), (0,1,0), (0,0,1), (−1,0,0), (0,−1,0) and (0,0,−1) orientations respectively. The symmetry-adapted combinations decompose as Γ1+ + Γ3+ + Γ4− (Table 1):
. Let's consider scenario A in detail with i = 1–6 for, (1,0,0), (0,1,0), (0,0,1), (−1,0,0), (0,−1,0) and (0,0,−1) orientations respectively. The symmetry-adapted combinations decompose as Γ1+ + Γ3+ + Γ4− (Table 1):
| Γ1+: ΞΓ1+ = ξ1 + ξ2 + ξ3 + ξ4 + ξ5 + ξ6 |
| Γ3+: ΞΓ3+ = ξ1 − ξ2 + ξ4 − ξ5 and ΞΓ3+2 = −ξ1 − ξ2 + 2ξ3 − ξ4− ξ5 + 2ξ6 |
| Γ4−: ΞΓ4− = ξ1 − ξ4, ΞΓ4−2 = ξ2 − ξ5 and ΞΓ4−3 = ξ3 − ξ6 |
The totally symmetric combination ΞΓ1+ is always equal to 1, whatever the value taken by ξi. In order to better understand the significance of these symmetrized combinations, we may consider the average values of the ξi in relation to the orientation occupation numbers.19,71 If one considers a thermally activated disorder of the molecular orientations, the dynamically averaged value, compatible with lattice symmetry, is <ξi> = 1/6. It yields 〈ΞΓ1+〉 = 1, and 0 for the other symmetry-adapted combinations. This can be considered as the ground state of the system in scenario A. The Γ3+ and Γ4− IR are relevant to describe dynamically excited configurations corresponding to thermally activated population fluctuations <ξi> = 1/6 + δξi with 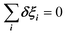 . For instance, the
. For instance, the  symmetrized combination corresponds to δξ1 = −δξ4 and δξ2 = δξ3 = δξ5 = δξ6 = 0, that is, to a net electric dipole along the x axis. In turn, all the other symmetrized excited combinations yield 0.
symmetrized combination corresponds to δξ1 = −δξ4 and δξ2 = δξ3 = δξ5 = δξ6 = 0, that is, to a net electric dipole along the x axis. In turn, all the other symmetrized excited combinations yield 0.
The PS concept is able to account for both dynamic and static orientational disorders. Indeed, a molecule with a frozen (static) random orientation and pointing toward a face (ξ1 = 1 for example) corresponds to a superposition of ΞΓ1+,  , ΞΓ3+2 and
, ΞΓ3+2 and 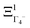 . Static configurations automatically exhibit strong deviations from the dynamically averaged values <ξi>, which are the only ones fully compatible with lattice symmetries.
. Static configurations automatically exhibit strong deviations from the dynamically averaged values <ξi>, which are the only ones fully compatible with lattice symmetries.
Nonpolar even configurations, like Γ1+ + Γ3+, correspond to elastic multipoles whereas, polar and odd configurations like Γ4− correspond to electric multipoles (Table 1). A qualitative understanding about the various relaxation modes for the molecular tumbling can be obtained by adapting the relaxation model by Poglitsch et al.21 originally designed for scenario C {1,1,1} having 8 possible orientations of the dipole. This model is based on a single relaxation rate γ between adjacent neighboring orientations in a given cubic cell. Noteworthily, it neglects the correlations between neighboring cells. In an extended microscopic description,20 the potential energy of the crystal can be developed in the harmonic approximation as a function of translation and rotation variables (PS or rotator functions):
| V = VR + VTT + VTR + VRR+⋯ |
For scenario A, each dipole has 4 neighbors. Adapting Poglitsch's model, the system of 6 rate equations for the occupation numbers reads: 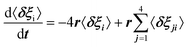 , where i = 1–6 stands for the 6 possible orientations, and j = 1–4 for the 4 nearest neighbors. Then, the eigenvalues of the relaxation matrix are:
, where i = 1–6 stands for the 6 possible orientations, and j = 1–4 for the 4 nearest neighbors. Then, the eigenvalues of the relaxation matrix are:
- γ0 = 0 for the trivial solution δξ1 = δξ2 = δξ3 = δξ4 = δξ5 = δξ6 (= 0) corresponding to the Γ1+ IR
- γ1 = 4γ for the triply degenerate solution corresponding to the polar relaxation (Γ4− IR)
- γ2 = 6γ for the twice degenerate solution corresponding to the non-polar relaxation (Γ3+ IR).
The relaxation rate γ1 can be measured by experimental techniques related to electric dipoles such as dielectric measurements,21,23 whereas γ2 can be probed by experimental techniques relevant to elastic multipoles, like Raman scattering.72 Both types of relaxation are expected to yield an experimental signature by incoherent neutron scattering (vide infra),60,61 the best technique being triple axis neutron scattering, but large monocrystals are necessary.55,56
Noteworthily, more realistic modelling of the interactions between neighboring cells (vide infra section 3.4.2) may change the γ2/γ1 ratio equal to 1.5 in this simplified model. Correlations between the tumbling of cations in neighboring cells also lead to dispersions of relaxation rates. In that case, it is useful to define collective PS variables accounting for the space group symmetry: 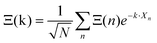 where k is a wave vector in the BZ, n is for a given molecule at the position Xn and N is the total number of molecules. The symmetrized decompositions for these collective variables are given in Table 1 as Γ, R and M for scenarios A–D. Finally, we may consider that the orientational disorder in the Pm
where k is a wave vector in the BZ, n is for a given molecule at the position Xn and N is the total number of molecules. The symmetrized decompositions for these collective variables are given in Table 1 as Γ, R and M for scenarios A–D. Finally, we may consider that the orientational disorder in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phases of MAPbX3 is a superposition of the three scenarios A, B and C. Then, the total number of cells is
m cubic phases of MAPbX3 is a superposition of the three scenarios A, B and C. Then, the total number of cells is 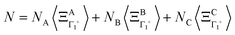 , where NA, NB, and NC are the number of cells undergoing, respectively, A, B, and C type disorder, respectively. But, as it turns out, such a mixing is better described by rotator functions that will be considered in the next section.
, where NA, NB, and NC are the number of cells undergoing, respectively, A, B, and C type disorder, respectively. But, as it turns out, such a mixing is better described by rotator functions that will be considered in the next section.
In the cubic phase of MAPbI3 at T = 370 K, the experimental analysis of the tumbling motion is difficult.61 A fully isotropic random rotation model compatible with the lattice symmetry was used. This continuous model further assumes no correlation between the rotations of the neighbouring molecules. It yields a relaxation rate equal to 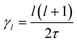 for the rotation with an angular momentum l (τ = 1.62 ps at T = 370 K). According to this model γ2/γ1 is thus equal to 3. By comparison γ2/γ1 is equal to 1.5 and 2, respectively, in the Poglitsch discrete jump models for scenarios A (Γ3+/Γ4−, see the above derivation) and C (Γ5+/Γ4−, Table 1). For scenario B, two IR (Γ3+ and Γ5+ see Table 1) correspond to an angular momentum l = 2, while only Γ4− is relevant for l = 1. γ2/γ1 is equal to 2 and 3 in a Poglitsch discrete jump model, respectively, for Γ3+/Γ4− and Γ5+/Γ4−.
for the rotation with an angular momentum l (τ = 1.62 ps at T = 370 K). According to this model γ2/γ1 is thus equal to 3. By comparison γ2/γ1 is equal to 1.5 and 2, respectively, in the Poglitsch discrete jump models for scenarios A (Γ3+/Γ4−, see the above derivation) and C (Γ5+/Γ4−, Table 1). For scenario B, two IR (Γ3+ and Γ5+ see Table 1) correspond to an angular momentum l = 2, while only Γ4− is relevant for l = 1. γ2/γ1 is equal to 2 and 3 in a Poglitsch discrete jump model, respectively, for Γ3+/Γ4− and Γ5+/Γ4−.
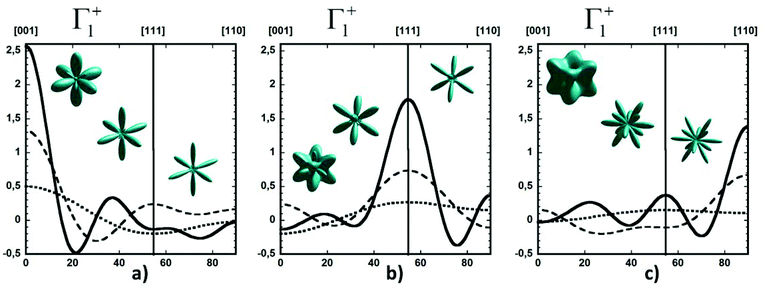
Considering a Oh molecular site-symmetry,19 the probability distribution of the C–N axis orientation as a function of the two polar angles (ϑ,φ), i.e. the unit vector u = (cos(φ)sin(ϑ), sin(φ)sin(ϑ), cos(ϑ)) is given by: 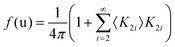 where the 〈K2i〉 coefficients are the ensemble average of the cubic harmonics. A cubic harmonic K2i is a specific combination of spherical harmonics of order 2i.73 The expansion is usually limited to a few terms and may be used to refine diffraction data. Particular combinations of 〈K2i〉 coefficients are useful to describe a preferred scenario. Noteworthily, pure [001], [110] and [111] orderings are described by infinite series of coefficients and correspond to the limit of PS discrete probability distributions.
where the 〈K2i〉 coefficients are the ensemble average of the cubic harmonics. A cubic harmonic K2i is a specific combination of spherical harmonics of order 2i.73 The expansion is usually limited to a few terms and may be used to refine diffraction data. Particular combinations of 〈K2i〉 coefficients are useful to describe a preferred scenario. Noteworthily, pure [001], [110] and [111] orderings are described by infinite series of coefficients and correspond to the limit of PS discrete probability distributions.
By limiting the expansion to the K4 term (Table 3, Fig. 3), pure [001] (Fig. 3a) or [111] (Fig. 3b) ordering are qualitatively well described but not the pure [110] one (Fig. 3c), given that the dotted line in Fig. 3c presents a maximum for the [111] direction instead of [110]. It is thus necessary to extend the expansion for pure [110] at least up to K6 (Table 3, Fig. 3b). Inclusion of terms up to K12 affords a description very close to delta like angular functions for the pure [001], [111] and [110] orientations (see 3D schematic representations shown as inset in Fig. 3). In real systems, fewer terms are usually needed for cubic harmonics expansions. Fig. 4 reports on the experimental results analyzed in the past for NaCN and KCN with an expansion up to K6 (Table 3).74 For both these materials the [1,1,0] orientation corresponds to an absolute minimum of the probability distribution. NaCN has a preferred orientation along the [001] direction, but significantly different from pure [001] ordering. Indeed, the dashed line in Fig. 4 has a smaller deviation from the horizontal line (corresponding to the isotropic case) than the dashed line in Fig. 3b and the distribution of CN− orientations presents a clear secondary maximum along the [111] direction. The MD simulations performed at 400 and 450 K for MAPbI3 are analyzed using the same formalism (Table 3, Fig. 4). The molecular axis exhibits a preferred orientation along [001] but the deviation from the isotropic distribution is less important than in cyanide compounds. This may explain why a reasonable fit of neutron scattering experimental data was obtained in the cubic phase with a purely isotropic rotational model.61 Moreover, the [111] direction corresponds to a minimum distribution. This analysis shows that the molecular orientations in MAPbI3 correspond to a mixing of A, B and C scenarios, with a preference for scenario A and to a lesser extent for B. In cyanide solids, the [001] and [111] directions correspond to attractive interactions between the CN− and Na+ ions (Fig. 2b), whereas a repulsive interaction between MA+ and Pb2+ is expected along [111] in MAPbX3 crystals (Fig. 2a).
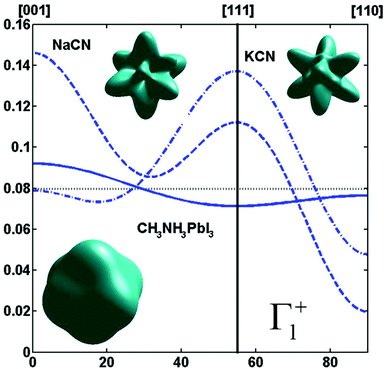 | ||
Fig. 4 Angular dependence (φ = 45° and θ = [0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90°]) of the probability distribution functions relevant for Γ1+ for molecular orientation in NaCN (dashed line) and KCN (dashed-dotted line) limiting the cubic harmonic expansion to K4 and K6 contributions,74 and for MAPbI3 (solid line) obtained from MD simulation at 450 K (best fit for K6 = 0, Table 3). 3D representations of the corresponding rotator functions are also inserted. 90°]) of the probability distribution functions relevant for Γ1+ for molecular orientation in NaCN (dashed line) and KCN (dashed-dotted line) limiting the cubic harmonic expansion to K4 and K6 contributions,74 and for MAPbI3 (solid line) obtained from MD simulation at 450 K (best fit for K6 = 0, Table 3). 3D representations of the corresponding rotator functions are also inserted. | ||
By analogy to symmetry-adapted combinations that are able to describe PS excited states, it is also possible to design symmetry-adapted rotator functions for rotational excited states. These expansions from spherical harmonics are available for all the IR of the Oh group.73 They are connected to the symmetry-adapted polynomial expansions provided that the unit vector is expressed as u = (x, y, z). The Γ4− vectorial (l = 1) IR appears in the expansion of the PS for A, B and C scenarios. The lowest-order symmetry-adapted polynomials with Γ4− symmetry appearing as a possible term for a Γ4− rotator function are thus (x, y, z). They correspond to the orientation of the CN axis of MA+. The average time dependence of the autocorrelation function of this vector extracted from MD simulation at 400 K is plotted in Fig. 5 for various cubic supercell sizes.
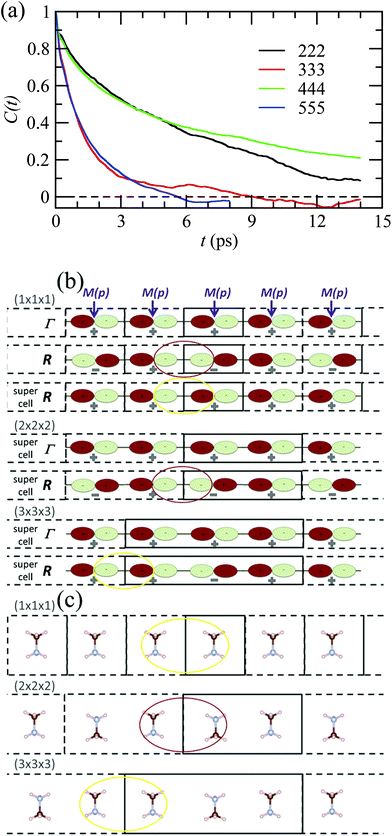 | ||
| Fig. 5 (a) Time dependence of the average autocorrelation function of the CN axis orientation in MAPbI3 extracted from MD simulation at 400 K for various supercell sizes having an odd or an even number of cubic cells along each direction. (b) Linear chain of p-atomic orbitals of the metal (M(p)) for even and odd numbers of unit cells in the supercell, illustrating, respectively, proper (red oval) and improper (yellow oval) account of the wave function phase factor at the BZ center (Γ) and BZ boundary (R).43 (c) Linear chain of MA molecules highlighting the presence of unphysical ferroelectric dipole–dipole interaction (yellow oval) when the supercell is made of an odd number of unit cells. | ||
Interestingly, the relaxation time depends much on the parity of the number of cells along one direction of the supercell. The CN axis orientation is more stabilized for an even number of cubic cells. The reasons are at least twofold. First, given that the MD simulations are limited to a Γ point sampling of the BZ, hybridization of atomic orbitals related to BZ-folding cannot be adequately addressed with an odd number of cells in one direction. This major effect is exemplified by considering a linear chain in Fig. 5b.43 Next, the stabilization of the CN axis obtained with an even number most probably results from enhanced anti-ferroelectric interactions between the molecular dipoles, whereas frustrated interactions are expected with an odd number of cells (Fig. 5c). In the latter case parallel dipole orientations between neighboring supercells may result in unphysical ferroelectric dipole–dipole interactions that are not present in the real bulk crystal. In fact, even though some hybrid perovskites may exhibit phase transitions with a ferroelectric character (vide infra), MAPbI3 essentially undergoes antiferro-distortive collective phase transitions at low temperatures, where long-range antiparallel arrangements of the molecular dipoles have been evidenced by diffraction experiments. This highlights the need for appropriate design of supercells in MD simulations, which should not break by construction of the overall symmetry, nor such long-range correlations.
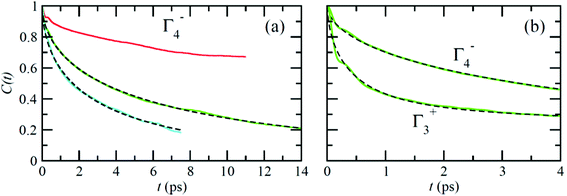
Fig. 6 reports on the temperature dependence of the average autocorrelation function for Γ4− deduced from simulations at three different temperatures. In each case, the relaxation time corresponds to the relaxation rate γ1 derived within the PS picture for the tumbling of dipoles. As expected, lowering the temperature induces a slowing down of the molecular tumbling. But, the time dependence is strongly non-exponential and can be nicely fitted using stretched exponentials (Fig. 6): C(t) = e−(t/τ)β. Due to issues related to affordable time scales, it can hardly be extracted at 300 K. For the other temperatures, 400 and 450 K, the stretching parameter β can be reasonably estimated to 0.56. The relaxation time deduced for the electric dipole (l = 1) dynamics (Γ4−), from the simulation at T = 400 K (Fig. 6a), amounts to 10.5 ps. At high temperature, the available experimental data are not consistent: the dynamics is either described by a single relaxation time with a large value of 12.7 ps at T = 370 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 or, a superposition of relaxation dynamics, whose vectorial (l = 1) component has a relaxation time equal to 1.62 ps at the same temperature.61
60 or, a superposition of relaxation dynamics, whose vectorial (l = 1) component has a relaxation time equal to 1.62 ps at the same temperature.61
The Γ3+ quadrupolar (l = 2) IR also appears in the expansion of the PS scenarios A and B (Table 1). The lowest-order symmetry-adapted polynomial with Γ3+ symmetry appearing as a possible term for an elastic quadrupole is Y02 ∝ (3z2 − 1). The relaxation time for the autocorrelation function of this rotator extracted from MD simulation at 400 K is equal to 6.6 ps. It corresponds to the γ2 coefficient of the simple PS analysis reported in section 3.3.2. The actual ratio γ2/γ1 is equal to 1.6, which is closer to PS scenario A than to scenarios B and C (section 3.3.2). This is also consistent with the maximum observed along the [001] direction for the probability distribution function (Fig. 4). The computed relaxation time is smaller than the experimental one (0.54 ps) deduced from a fully isotropic model for the angular momentum l = 2.61
The analyses of neutron scattering data60,61 do not consider lateral coupling between the rotational motions of molecules. Individual molecular random reorientations are also described by simple PS relaxation models in section 3.3.2. A similar picture emerges from the MD study presented in section 3.3.3, provided that spurious spatial correlations are removed with supercells containing only an even number of cubic cells (Fig. 5). A random isotropic molecular tumbling is described by a single relaxation time in ref. 60, whereas a more elaborate isotropic model leads to the definition of a relaxation time for each angular momentum in ref. 61. The PS and rotator models presented in this work explicitly take into account both the symmetry of the cubic cage and the vectorial symmetry related to the C–N axis. This idea is close to the jump model proposed in ref. 61, where the molecular tumbling is described by a C4 symmetry in the tetragonal phase, neglecting inversion and mirror reflections. The same symmetry was used in the cubic phase, although a more correct approach should require the O point group as quoted by the authors. The two models of sections 3.3.2 and 3.3.3 correspond to the Oh point group, essentially adding the inversion symmetry (Oh = O × Ci) to the description of ref. 61. This is necessary to account for both electric and elastic multipolar effects, as well as to be able to discuss the possibility of ferroelectric phase transitions. Further analyses of neutron scattering data using symmetry adapted Oh rotators should provide a better description of the rotational molecular disorder in HOP.
3.4. Linear coupling between collective pseudospins/rotators and lattice vibrations
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cell distortions relevant to HOP, leading to possible collective ferroelectric phase transitions illustrated in Fig. 7.10
m cell distortions relevant to HOP, leading to possible collective ferroelectric phase transitions illustrated in Fig. 7.10
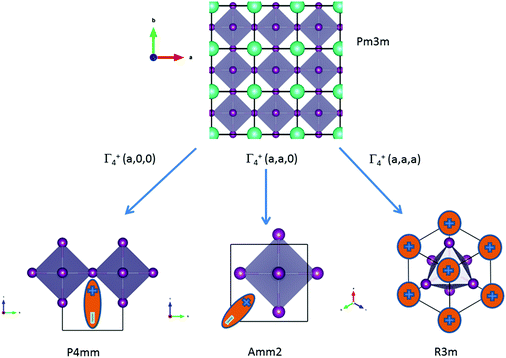 | ||
Fig. 7 Schematic representation of possible ferroelectric phase transitions in HOP from the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase (Table 4). These transitions involve various components of the Γ4− degenerate IR. MA cations are schematically represented by electric dipoles. m cubic phase (Table 4). These transitions involve various components of the Γ4− degenerate IR. MA cations are schematically represented by electric dipoles. | ||
| Order parameters | Γ 4 − | Z | Example | ||
|---|---|---|---|---|---|
| q1 | q2 | q3 | |||
| P4mm | 0 | 0 | a | 1 | MAPbI3 |
| Amm2 | a | a | 0 | 2 | FASnI3 |
| R3m | a | a | a | 3 | MAGeCl3 |
For MAPbI3, the P4mm polar group is a possible alternative to the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group for structural refinement of the high temperature diffraction data.44 Our MD simulations however suggest that local polar symmetry breaking may only occur in relation to frozen configurations of the cations, and not collective fluctuations. The Amm2 appears in the crystallographic analysis of the room temperature phase of FASnI3.44 The R3m space group is relevant for germanium compounds, MAGeX3.43,76 As shown by a systematic study on germanium iodide compounds, CsGeI3, MAGeI3 and FAGeI3,76 the appearance of a ferroelectric trigonal R3m space group and thus a large SHG response was attributed to the high density of states in the valence band due to sp-hybridization of the Ge and I orbitals. It shows that ferroelectricity for this class of HOP and AIP is essentially related to the instability of the Pm
m space group for structural refinement of the high temperature diffraction data.44 Our MD simulations however suggest that local polar symmetry breaking may only occur in relation to frozen configurations of the cations, and not collective fluctuations. The Amm2 appears in the crystallographic analysis of the room temperature phase of FASnI3.44 The R3m space group is relevant for germanium compounds, MAGeX3.43,76 As shown by a systematic study on germanium iodide compounds, CsGeI3, MAGeI3 and FAGeI3,76 the appearance of a ferroelectric trigonal R3m space group and thus a large SHG response was attributed to the high density of states in the valence band due to sp-hybridization of the Ge and I orbitals. It shows that ferroelectricity for this class of HOP and AIP is essentially related to the instability of the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic structure against a phonon mode related to the inorganic lattice, rather than collective reorientational motions of the cations. However, for larger organic cations like GA, DMA or TMA, the influence of the lattice instability is reduced and the size and shape of the cations may induce a variety of crystallographic structures, some of them being non-polar like P21/c for GAGeI3.76
m cubic structure against a phonon mode related to the inorganic lattice, rather than collective reorientational motions of the cations. However, for larger organic cations like GA, DMA or TMA, the influence of the lattice instability is reduced and the size and shape of the cations may induce a variety of crystallographic structures, some of them being non-polar like P21/c for GAGeI3.76
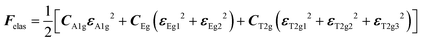 with the symmetry-adapted elastic constants given by CA1g = C11 + 2C12,
with the symmetry-adapted elastic constants given by CA1g = C11 + 2C12, 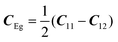 , CT2g = C44 and strain tensor components εA1g = (ε1 + ε2 + ε3)/√3 (proportional to the volumetric strain), εEg1 = (2ε3 − ε1 − ε2)/2√3 and εEg2 = (ε1 − ε2)/2 (tetragonal strains) and εT2g1 = ε4, εT2g2 = ε5, εT2g3 = ε6 (shear strains).20 In order to predict the effect of linear coupling between strain and the random orientational degrees of freedom, the total free energy is written as a function of the phonon displacement variables u and the orientational variables
, CT2g = C44 and strain tensor components εA1g = (ε1 + ε2 + ε3)/√3 (proportional to the volumetric strain), εEg1 = (2ε3 − ε1 − ε2)/2√3 and εEg2 = (ε1 − ε2)/2 (tetragonal strains) and εT2g1 = ε4, εT2g2 = ε5, εT2g3 = ε6 (shear strains).20 In order to predict the effect of linear coupling between strain and the random orientational degrees of freedom, the total free energy is written as a function of the phonon displacement variables u and the orientational variables 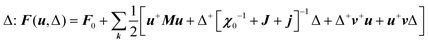 where M is the bare k dependent dynamical matrix related to VTT, the single particle susceptibility matrix χ0 and the bare k dependent coupling matrix J are related to VRR and v the translation–rotation linear coupling matrix to VRT.j is the onsite lattice self-energy connected to the indirect interaction between the molecule orientations and is related to both VRT and VTT. Separating the two degrees of freedom leads to renormalized (or dressed) coupling J′ = J − v+M−1v and dynamical M′ = M − v[χ0−1 + J + j]−1v+ matrices.20 These renormalizations may lead to ferroelastic structural instabilities77 that, to the best of our knowledge, are not observed in hybrid perovskites. In more standard cases, the linear coupling leads to renormalized elastic constants and additional temperature dependences related to
where M is the bare k dependent dynamical matrix related to VTT, the single particle susceptibility matrix χ0 and the bare k dependent coupling matrix J are related to VRR and v the translation–rotation linear coupling matrix to VRT.j is the onsite lattice self-energy connected to the indirect interaction between the molecule orientations and is related to both VRT and VTT. Separating the two degrees of freedom leads to renormalized (or dressed) coupling J′ = J − v+M−1v and dynamical M′ = M − v[χ0−1 + J + j]−1v+ matrices.20 These renormalizations may lead to ferroelastic structural instabilities77 that, to the best of our knowledge, are not observed in hybrid perovskites. In more standard cases, the linear coupling leads to renormalized elastic constants and additional temperature dependences related to 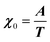 :20
:20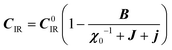 where C0IR is the elastic constant for a given IR and B is the corresponding constant of the coupling matrix. The additional term may induce an unusual increase of the elastic constant with temperature,78 which could be tested experimentally in hybrid perovskites to gauge the importance of translation/rotation coupling.
where C0IR is the elastic constant for a given IR and B is the corresponding constant of the coupling matrix. The additional term may induce an unusual increase of the elastic constant with temperature,78 which could be tested experimentally in hybrid perovskites to gauge the importance of translation/rotation coupling.
Another possible outcome of linear translation–rotation couplings, even more characteristic of the stochastic molecular dynamics, is an additional acoustic damping related to the tumbling relaxational dynamics.20 When combining a Lagrangian, which includes the total free energy plus an additional kinetic energy term depending on the density ρ, with a dissipative part accounting for frictional forces, it is possible to predict the relaxation dynamics of the tumbling as well as its effect on acoustic wave propagation.20,79 Keeping only a damping matrix Γ for the relaxational motion, the set of linearly coupled dynamical equations reads:
For a single orientational degree of freedom, the relaxation rate without translation–rotation coupling is: γ = 1/τ = [χ0−1 + J + j]/Γ. Separating the two degrees of freedom leads to a dressed dynamical matrix 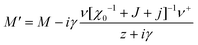 , where the Laplace transform variable is z = ω + iε+ in the limit of vanishing bare phonon damping. This result is similar to the one discussed above (section 3.2) for the coupling between a relaxor and optical modes in KMnF3 or SrTiO3, but the impact of damping renormalization is expected to be very important and close to the Γ point. The coupling will thus lead to two separate signatures, one from relaxor and another from the acoustic phonon, as long as the acoustic phonon energy is much larger than the relaxation energy. However, due to acoustic phonon dispersion, a strong damping affects the whole acoustic phonon branch when k is close to the BZ center. Such a strong damping may affect a large part of the acoustic phonon spectrum in hybrid perovskites, especially the transverse acoustic phonon branches that are limited to about 2 meV over the entire BZ (section 3.2), given that the typical relaxation time of 5 ps (Fig. 6) corresponds to 0.12 meV. Thus, a careful investigation of the temperature dependence of the acoustic phonon spectrum would yield fruitful information about the influence of the stochastic dynamics on the translation–rotation coupling.
, where the Laplace transform variable is z = ω + iε+ in the limit of vanishing bare phonon damping. This result is similar to the one discussed above (section 3.2) for the coupling between a relaxor and optical modes in KMnF3 or SrTiO3, but the impact of damping renormalization is expected to be very important and close to the Γ point. The coupling will thus lead to two separate signatures, one from relaxor and another from the acoustic phonon, as long as the acoustic phonon energy is much larger than the relaxation energy. However, due to acoustic phonon dispersion, a strong damping affects the whole acoustic phonon branch when k is close to the BZ center. Such a strong damping may affect a large part of the acoustic phonon spectrum in hybrid perovskites, especially the transverse acoustic phonon branches that are limited to about 2 meV over the entire BZ (section 3.2), given that the typical relaxation time of 5 ps (Fig. 6) corresponds to 0.12 meV. Thus, a careful investigation of the temperature dependence of the acoustic phonon spectrum would yield fruitful information about the influence of the stochastic dynamics on the translation–rotation coupling.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Here, we adapt this model to the case of AIP and HOP, with contributions from the disordered organic part in the latter.
m space group. Here, we adapt this model to the case of AIP and HOP, with contributions from the disordered organic part in the latter.
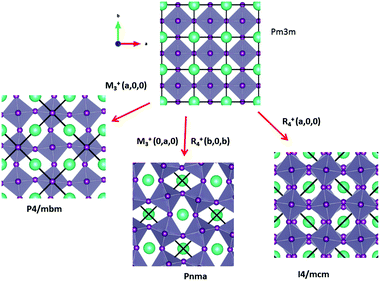
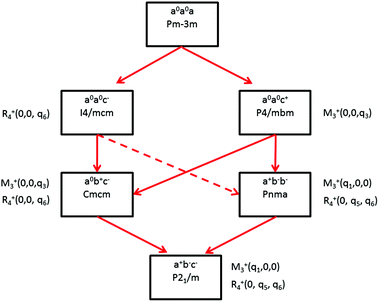
Some of the related antiferro-distortive space group changes associated with order parameters for AIP (P4/mbm) and HOP (I4/mcm and Pnma) are summarized in Table 5 and illustrated in Fig. 8 and 9. M3+ and R4+ define octahedra tilting, whereas Γ3+, M2+, and R3+ correspond to the secondary order parameters.
| Order parameters | M 3 + | R 4 + | ||||
|---|---|---|---|---|---|---|
| q1 | q2 | q3 | q4 | q5 | q6 | |
| I4/mcm | 0 | 0 | 0 | a | 0 | 0 |
| Pnma | 0 | a | 0 | b | 0 | b |
| P4/mbm | a | 0 | 0 | 0 | 0 | 0 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to I4/mcm phase transition shows that the order parameter is related to one of the components of the triply degenerate R4+ IR. In SrTiO3 or CaTiO3, this phase transition is attributed to the condensation of one of the triply degenerate octahedra rotations of R4+ symmetry (Table 1). Symmetry analysis confirms that such a vibrational mode, mainly related to the inorganic lattice, exists in the high temperature phase of HOP. As condensation of a vibrational mode is usually related to a displacive mechanism, a phonon mode softening should be observed in HOP: (i) at the BZ boundary (R point) by neutron scattering in the high temperature phase, (ii) at the BZ zone center both by neutron and Raman scattering in the low temperature phase.62 Symmetry analysis further shows that the phase transition can also be associated to a mode involving the collective tumbling of molecular cations. This is true for the PS scenario B, namely for the C–N axis pointing toward iodine atoms, or the mixed A/B or D scenario, where the C–N axis is pointing toward an intermediate direction between a face and an edge. It shows that an additional order parameter having the same lattice symmetry as the octahedra rotations (R4+) is associated to molecular tumbling. From the Landau theory point of view, these order parameters undergo a linear coupling. But, the mechanism associated to these additional order parameters has an order–disorder nature. In other words, even though a linear coupling is predicted between these order parameters in the Pm
m to I4/mcm phase transition shows that the order parameter is related to one of the components of the triply degenerate R4+ IR. In SrTiO3 or CaTiO3, this phase transition is attributed to the condensation of one of the triply degenerate octahedra rotations of R4+ symmetry (Table 1). Symmetry analysis confirms that such a vibrational mode, mainly related to the inorganic lattice, exists in the high temperature phase of HOP. As condensation of a vibrational mode is usually related to a displacive mechanism, a phonon mode softening should be observed in HOP: (i) at the BZ boundary (R point) by neutron scattering in the high temperature phase, (ii) at the BZ zone center both by neutron and Raman scattering in the low temperature phase.62 Symmetry analysis further shows that the phase transition can also be associated to a mode involving the collective tumbling of molecular cations. This is true for the PS scenario B, namely for the C–N axis pointing toward iodine atoms, or the mixed A/B or D scenario, where the C–N axis is pointing toward an intermediate direction between a face and an edge. It shows that an additional order parameter having the same lattice symmetry as the octahedra rotations (R4+) is associated to molecular tumbling. From the Landau theory point of view, these order parameters undergo a linear coupling. But, the mechanism associated to these additional order parameters has an order–disorder nature. In other words, even though a linear coupling is predicted between these order parameters in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase, the characteristic dynamics appear in different frequency ranges. Detailed derivations of the possible Landau free energy expansions are known.80 A linear–quadratic coupling is also predicted between the two linearly coupled R4+ order parameters and two components of the strain tensor, ε1 + ε2 + ε3 and 2ε3 − ε1 − ε2 that correspond to the Γ1+ and Γ3+ IR, respectively. The cubic to tetragonal phase transition presents an improper ferroelastic character. Such a linear–quadratic coupling is in agreement with the available diffraction data recorded on MAPbI3.70 Below the critical temperature Tc, antiferro-distortive octahedra rotation was found to vary as (Tc − T)0.25 and the tetragonal strain as (Tc − T)0.42.70 The anomalies of elastic constants are predicted as a function of the order-parameter. These anomalies could be tested experimentally in order to quantify the linear–quadratic coupling with strains.
m phase, the characteristic dynamics appear in different frequency ranges. Detailed derivations of the possible Landau free energy expansions are known.80 A linear–quadratic coupling is also predicted between the two linearly coupled R4+ order parameters and two components of the strain tensor, ε1 + ε2 + ε3 and 2ε3 − ε1 − ε2 that correspond to the Γ1+ and Γ3+ IR, respectively. The cubic to tetragonal phase transition presents an improper ferroelastic character. Such a linear–quadratic coupling is in agreement with the available diffraction data recorded on MAPbI3.70 Below the critical temperature Tc, antiferro-distortive octahedra rotation was found to vary as (Tc − T)0.25 and the tetragonal strain as (Tc − T)0.42.70 The anomalies of elastic constants are predicted as a function of the order-parameter. These anomalies could be tested experimentally in order to quantify the linear–quadratic coupling with strains.
In oxide perovskites, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to Pnma and Pm
m to Pnma and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to I4/mcm instabilities compete in the same way as in MAPbI3 and MAPbBr3. The Pm
m to I4/mcm instabilities compete in the same way as in MAPbI3 and MAPbBr3. The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to Pnma instability is related to the simultaneous condensation of R4+ and M3+ rotational modes of the octahedra. Our symmetry analysis confirms that an M3+ rotational mode, mainly related to the inorganic lattice, exists in the high temperature phase of HOP (Table 1). The Pm
m to Pnma instability is related to the simultaneous condensation of R4+ and M3+ rotational modes of the octahedra. Our symmetry analysis confirms that an M3+ rotational mode, mainly related to the inorganic lattice, exists in the high temperature phase of HOP (Table 1). The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to Pnma structural instability is indeed directly observed in the [536–602 K] temperature interval for CsPbI3, leading to a Pnma phase at room temperature without the intermediate I4/mcm phase.41 In MAPbX3, additional PS order parameters with the M3+ symmetry exist for disordered collective molecular tumbling in scenarios A and B, as well as in the mixed scenario D (Table 1). They are expected to present an order–disorder character and to be linearly coupled with the displacive order parameter.
m to Pnma structural instability is indeed directly observed in the [536–602 K] temperature interval for CsPbI3, leading to a Pnma phase at room temperature without the intermediate I4/mcm phase.41 In MAPbX3, additional PS order parameters with the M3+ symmetry exist for disordered collective molecular tumbling in scenarios A and B, as well as in the mixed scenario D (Table 1). They are expected to present an order–disorder character and to be linearly coupled with the displacive order parameter.
Finally, it appears that the Pm3m to P4/mbm instability is only observed in some AIP, namely CsPbCl3.51 This instability is triggered by a heavily over-damped M3+ rotational displacive mode of the lead halide octahedra in AIP. This result suggests that the potential anharmonicity associated to this normal vibrational mode is large in the cubic phase, and that the phase transition has an intermediate character between displacive and order–disorder. The Pm3m to P4/mbm phase transition is followed by P4/mbm to Cmcm and Cmcm to P21/m phase transitions (Fig. 9).51
3.5. Translational symmetry-breaking and orientational glass behavior
Neutron scattering data have revealed that only a minor fraction of the MA cations is involved in both the rotational motions at high temperature.60 This is consistent with MD simulations that will be described in this section. Moreover, some authors claim that structural refinements are not easy in pure HOP, even at low temperatures, due to the remaining lattice disorder.44 It often leads to neglecting a large number of weak Bragg peaks in the structural refinement of diffraction data. This might be indicative of the remaining disorder in the orientations of the cations, thus leading to an incomplete long range freezing of cation orientations. The time dependence of the average autocorrelation function for molecular reorientation in the MD is strongly non-exponential and can be nicely fitted using stretched exponentials (Fig. 6). A detailed inspection of the dynamics of the CH3NH3+ cations at T = 400 K (Fig. 10b) reveals that it is related to a wide dispersion of reorientation dynamics of individual molecules. A significant part of the cations (roughly 30%, represented in white in Fig. 10a) remain almost frozen with respect to a tumbling motion on the time scale of our MD trajectory. These results are qualitatively consistent with the recent neutron scattering data, which indicate that 60%–77% of the cations have residence times exceeding 200 ps.60 In pure cyanide compounds, the CN− tumbling motion exhibits long-range correlations, because it is associated to a single orientational degree of freedom. Frustrated interactions and behavior typical of orientational glass are thus observed in mixed cyanide crystals by either anion (KBrxCN1−x) or cation (NaxK1−xCN) alloying.69,81 We may infer that frustrated cation orientations are more likely in MAPbX3 compounds for two reasons: the probability distribution functions of molecular orientation exhibits a lower contrast (Fig. 4) and additional disordered rotational degrees of freedom are associated to the rotation of methyl and ammonium groups around the C–N axis. As shown by NMR and neutron scattering, this reorientational motion occurs on a time-scale comparable to the C–N tumbling.24,60,61 The absence of long range spatial correlations between the individual reorientations could be better assessed from MD simulations using even larger supercells, although it appears to be consistent with the analyses of neutron scattering data (section 3.3.3).60,61 However, from Fig. 5 we know that one should focus on even numbers of cells, namely 4 × 4 × 4 in the present work. Unfortunately, a 6 × 6 × 6 supercell is already too large, given the available computational resources. Therefore, it is difficult to explore more in detail the long-range critical correlations appearing at the continuous cubic to tetragonal phase transition within a first-principles approach.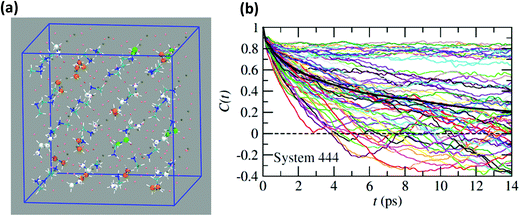 | ||
| Fig. 10 (a) Atomistic representation at T = 400 K of the 444 supercell restricted to the CH3NH3+ cations. (Orange) cations having a very short relaxation time (τ < 1 ps), (green) cations with average relaxation time, (white) cations almost frozen on the time scale of the simulation (τ > 14 ps). (b) Time dependence of the autocorrelation function for all molecules within the 444 supercell extracted from MD simulation at T = 400 K. The average time dependence (Fig. 5 and 6) is plotted in bold dark for comparison. | ||
4. Conclusion
The main aim of this work was to show that room temperature properties of hybrid perovskites can be viewed as a merging of properties of all-inorganic perovskites, conventional semiconductors and plastic crystals. Both the stochastic molecular orientational dynamics and the frozen static configurations can be explored rigorously on the basis of simplified and symmetry-based discrete PS as well as using continuous rotator functions. For instance, it has been shown how molecular orientational degrees of freedom can couple with the order parameters, both for ferroelectric and antiferro-distortive phases. Theoretical predictions and experimental guidelines are provided to explore the linear couplings between the various stochastic degrees of freedom and acoustic or optical phonon modes. Thorough Brillouin, Raman and neutron scattering experiments should help gauging the importance of linear translation/rotation coupling in these materials. Finally, as indicated by molecular dynamics simulation, an orientational glass behavior may result from the frustrated molecular interactions and degrees of freedom.Acknowledgements
The work was supported by Cellule Energie du CNRS (SOLHYBTRANS Project) and the University of Rennes 1 (Action Incitative, Défis Scientifiques Emergents 2015). J. E.'s work is supported by the Fondation d'entreprises banque Populaire de l'Ouest under Grant PEROPHOT 2015.References
- N. G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429 CrossRef CAS.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- H. S. Kim, S. H. Im and N. G. Park, J. Phys. Chem. C, 2014, 118, 5615–5625 CAS.
- P. Gao, M. Graëtzel and M. K. Nazeeruddin, Energy Environ. Sci., 2014, 7, 2448–2463 CAS.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- V. Gonzalez-Pedro, E. J. Juarez-Perez, W. S. Arsyad, E. M. Barea, F. Fabregat-Santiago, I. Mora-Sero and J. Bisquert, Nano Lett., 2014, 14, 888–893 CrossRef CAS PubMed.
- W. Nie, H. Tsai, R. Asadpour, J.-C. Blancon, A. Neukirch, G. Gupta, J. J. Crochet, M. Chhowalla, S. Tretiak, M. A. Alam, H.-L. Wang and A. Mohite, Science, 2015, 347, 522–525 CrossRef CAS PubMed.
- F. Deschler, M. Price, S. Pathak, L. E. Klintberg, D.-D. Jarausch, R. Higler, S. Hüttner, T. Leijtens, S. D. Stranks, H. J. Snaith, M. Atatüre, R. T. Phillips and R. H. Friend, J. Phys. Chem. Lett., 2014, 5, 1421–1426 CrossRef CAS PubMed.
- J. Luo, J.-H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N.-G. Park, S. D. Tilley, H. J. Fan and M. Grätzel, Science, 2014, 345, 1593–1596 CrossRef CAS PubMed.
- M. Kepenekian, R. Robles, C. Katan, D. Sapori, L. Pedesseau and J. Even, ACS Nano, 2015 DOI:10.1021/acsnano.5b04409.
- J. Even, L. Pedesseau, C. Katan, M. Kepenekian, J.-S. Lauret, D. Sapori and E. Deleporte, J. Phys. Chem. C, 2015, 119, 10161–10177 CAS.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, Phys. Status Solidi RRL, 2014, 8, 31–35 CrossRef CAS.
- J. Even, L. Pedesseau and C. Katan, J. Phys. Chem. C, 2014, 118, 11566–11572 CAS.
- H.-H. Fang, R. Raissa, M. Abdu-Aguye, S. Adjokatse, G. R. Blake, J. Even and M. A. Loi, Adv. Funct. Mater., 2015, 25, 2378–2385 CrossRef CAS.
- A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T. S. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582–587 CrossRef CAS.
- S. D. Stranks, V. M. Burlakov, T. Leijtens, J. M. Ball, A. Goriely and H. J. Snaith, Phys. Rev. Appl., 2014, 2, 034007 CrossRef.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- J. Even, J. Phys. Chem. Lett., 2015, 6, 2238–2242 CrossRef CAS PubMed.
- R. M. Lynden Bell and K. H. Michel, Rev. Mod. Phys., 1994, 66, 721–762 CrossRef CAS.
- A. Poglitsch and D. J. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1392 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 935–939 CrossRef CAS.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- E. Mosconi, C. Quarti, T. Ivanovska, G. Ruani and F. De Angelis, Phys. Chem. Chem. Phys., 2014, 16, 16137–16144 RSC.
- R. Lindblad, D. Bi, B.-W. Park, J. Oscarsson, M. Gorgoi, H. Siegbahn, M. Odelius, E. M. J. Johansson and H. Rensmo, J. Phys. Chem. Lett., 2014, 5, 648–653 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler and A. Walsh, APL Materials, 2014, 2, 081506 CrossRef.
- M. A. Carignano, A. Kachmar and J. Hutter, J. Phys. Chem. C, 2015, 119, 8991–8997 CAS.
- G. Lippert, M. Parrinello and J. Hutter, Mol. Phys., 1997, 92, 477–488 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1986, 34, 2499–2500 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter, 1996, 54, 1703–1710 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 CrossRef CAS.
- S. L. Altmann and P. Herzig, Point-Group Theory Tables, Clarendon, Oxford, 1994 Search PubMed.
- S. C. Miller and W. F. Love, Tables of Irreducible Representations of Space Groups and Co-Representations of Magnetic Space Groups, Preutt, Boulder, 1967 Search PubMed.
- D. M. Trots and S. V. Myagkota, J. Phys. Chem. Solids, 2008, 69, 2520–2526 CrossRef CAS.
- G. L. Hua, J. Phys.: Condens. Matter, 1991, 3, 1371–1388 CrossRef CAS.
- C. Katan, L. Pedesseau, M. Kepenekian, A. Rolland and J. Even, J. Mater. Chem. A, 2015, 3, 9232–9240 CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- T. Baikie, N. S. Barrow, Y. Fang, P. J. Keenan, P. R. Slater, R. O. Piltz, M. Gutmann, S. G. Mhaisalkar and T. J. White, J. Mater. Chem. A, 2015, 3, 9298–9307 CAS.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- G. Giorgi, J.-I. Fujisawa, H. Segawa and K. Yamashita, J. Phys. Chem. C, 2015, 119, 4694–4701 CAS.
- G. Thiele and B. R. Serr, Zeitschrift für Kristallographie, 1996, 211, 47 CAS.
- A. Möller and J. Felsche, J. Appl. Crystallogr., 1982, 15, 247–248 CrossRef.
- A. Möller and J. Felsche, J. Appl. Crystallogr., 1979, 12, 617–618 CrossRef.
- Y. Fujii, S. Hoshino, Y. Yamada and G. Shirane, Phys. Rev. B: Solid State, 1974, 9, 4549–4559 CrossRef CAS.
- M. M. Sinha and K. Wakamura, Solid State Ionics, 2000, 136, 1345–1350 CrossRef.
- J. Hutton, R. J. Nelmes, G. M. Meyer and V. R. Eiriksson, J. Phys. C: Solid State Phys., 1979, 12, 5393–5410 CrossRef CAS.
- C. Carabatos-Nédelec, M. Oussaïd and K. Nitsch, J. Raman Spectrosc., 2003, 34, 388–393 CrossRef.
- J. Even, M. Bertault, B. Toudic, H. Cailleau, J. L. Fave, F. Moussa and R. Currat, Phys. Rev. B: Condens. Matter, 1994, 49, 11602–11612 CrossRef CAS.
- J. Even, B. Toudic, M. Bertault, H. Cailleau and F. Moussa, Phys. Rev. B: Condens. Matter, 1995, 52, 7142–7150 CrossRef CAS.
- F. Schwabl, Phys. Rev. Lett., 1972, 28, 500–503 CrossRef CAS.
- S. M. Shapiro, J. D. Axe, G. Shirane and T. Riste, Phys. Rev. B: Solid State, 1972, 6, 4332–4341 CrossRef CAS.
- A. Maalej, Y. Abid, A. Kallel, A. Daoud, A. Lautié and F. Romain, Solid State Commun., 1997, 103, 279–284 CrossRef CAS.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. H. Law, X. Li, F. Foglia, A. Walsh, B. C. O'Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S. Lee, Phys. Chem. Chem. Phys., 2015, 14, 31278–31286 RSC.
- I. P. Swainson, C. Stock, S. F. Parker, L. Van Eijck, M. Russina and J. W. Taylor, Phys. Rev. B: Condens. Matter, 2015, 92, 100303(R) CrossRef.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS.
- K. Adachi, H. Suga and S. Seki, Bull. Chem. Soc. Jpn., 1968, 41, 1073–1087 CrossRef CAS.
- J.-I. Koga and T. Odagaki, J. Phys. Chem. B, 2000, 104, 3808–3811 CrossRef CAS.
- O. Delcourt, M. Descamps, J. Even, M. Bertault and J. F. Willart, Chem. Phys., 1997, 215, 51–57 CrossRef CAS.
- R. A. Cowley, Adv. Phys., 1980, 29, 1–110 CrossRef CAS.
- M. T. Dove, Am. Min., 1997, 82, 213–244 CAS.
- A. Loidl, T. Schräder, R. Bohmer, K. Knorr, J. K. Kjems and R. Born, Phys. Rev. B: Condens. Matter, 1986, 34, 1238–1249 CrossRef CAS.
- Y. Kawamura, H. Mashiyama and K. Hasebe, J. Phys. Soc. Jpn., 2002, 71, 1694–1697 CrossRef CAS.
- B. Tadic, R. Pirc, R. Blinc, J. Petersson and W. Wiotte, Phys. Rev. B: Condens. Matter, 1994, 50, 9824 CrossRef CAS.
- D. Fontaine and R. M. Pick, J. de Physique, 1979, 40, 1105–1121 CrossRef CAS.
- S. L. Altmann and A. P. Cracknell, Rev. Mod. Phys., 1965, 37, 19–32 CrossRef.
- J. M. Rowe, D. G. Hincks, D. L. Price, S. Susman and J. J. Rush, J. Chem. Phys., 1973, 58, 2039–2042 CrossRef CAS.
- K. H. Michel and J. M. Rowe, Phys. Rev. B: Condens. Matter, 1985, 32, 5818–5826 CrossRef CAS.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed.
- W. Rehwald, J. R. Sandercock and M. Rossinelli, Phys. Status Solidi A, 1977, 42, 699–705 CrossRef CAS.
- K. H. Michel and J. Naudts, J. Chem. Phys., 1977, 67, 547–558 CrossRef CAS.
- E. Courtens, J. de Physique, Lettres, 1976, 37, L21–L24 CrossRef.
- M. A. Carpenter, Am. Min., 2007, 92, 309–327 CrossRef CAS.
- S. Bhattacharya, S. R. Nagel, L. Fleishman and S. Susman, Phys. Rev. Lett., 1982, 48, 1267–1270 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |