Soft self-assembled nanoparticles with temperature-dependent properties

Abstract

The fabrication of versatile building blocks that reliably self-assemble into desired ordered and disordered phases is amongst the hottest topics in contemporary materials science. To this end, microscopic units of varying complexity, aimed at assembling the target phases, have been thought, designed, investigated and built. Such a path usually requires laborious fabrication techniques, especially when specific functionalisation of the building blocks is required. Telechelic star polymers, i.e., star polymers made of a number of f di-block copolymers consisting of solvophobic and solvophilic monomers grafted on a central anchoring point, spontaneously self-assemble into soft patchy particles featuring attractive spots (patches) on the surface. Here we show that the tunability of such a system can be widely extended by controlling the physical and chemical parameters of the solution. Indeed, under fixed external conditions the self-assembly behaviour depends only on the number of arms and on the ratio of solvophobic to solvophilic monomers. However, changes in temperature and/or solvent quality make it possible to reliably change the number and size of the attractive patches. This allows the steering of the mesoscopic self-assembly behaviour without modifying the microscopic constituents. Interestingly, we also demonstrate that diverse combinations of the parameters can generate stars with the same number of patches but different radial and angular stiffness. This mechanism could provide a neat way of further fine-tuning the elastic properties of the supramolecular network without changing its topology.

---

1. Introduction

Designing novel materials on the nanometer scale requires a careful choice of the microscopic building blocks.¹ In the last decade, theoretical and numerical research has demonstrated that adding anisotropy to selected building blocks greatly enlarges the realm of possibility.² Indeed, photonic materials, lightweight gels, self-healing plastics and devices for medical imaging and drug delivery have all been realised in silico³ and, to a lesser extent, in experiments.^4,5 Many interesting effects arising in these systems can be rationalised in terms of a reduced valence: the anisotropic nature of the interaction limits the number of reversible bonds that each nanoparticle can establish, effectively stabilising open, i.e. low-density, ordered and disordered structures.⁶ A simple yet very successful toy model with a built-in limited valence is provided by the so-called patchy particles, e.g., colloids decorated with attractive spots (patches) on their surface.^6–9 The richness of their phase behaviour, ranging from low-density reversible gels¹⁰ to open crystals^4,11,12 and cluster phases,^13,14 spurred the development of new methods for their synthesis.^15–17 However, the fabrication of bulk quantities of monodisperse patchy colloids with tunable interactions has not been achieved yet. Recently, the idea of using polymer-based systems to synthesise anisotropically-interacting particles has been proposed.^18,19 In particular, a very promising idea revolves around telechelic star polymers (TSPs), which can be readily synthesised, for example by using polybutadiene stars functionalised with zwitterionic end groups.^20–22 TPSs are macromolecules made of a number of f diblock copolymers grafted on a central anchoring point.^19,23–26 Each of the f diblock-co-polymeric arms is made of a ratio of α solvophobic and (1 − α) solvophilic monomers; the dual nature of their arms makes TSPs particularly sensitive to variations of the external conditions, such as temperature or ionic strength in the case of zwitterionic telechelics, and allows each particle to self-assemble into a soft particle with attractive patches on the surface. As a result, TSPs undergo a hierarchical self-assembly: on the single-scale particles can be tuned to self-assemble into building blocks with predetermined properties; on a larger scale, particles can then self-assemble into meso- and macroscopic structures^19,27 which can be exploited in materials science and for medical applications.^28,29

Polymeric molecular building blocks present several advantages. In terms of synthesis, no cumbersome preparation techniques are required.^30,31 From a theoretical point of view, the self-assembling nature of the particles makes them inherently soft and floppy, providing additional control over the target structure and its properties.^32,33 However, such a subtle dependence of the bulk properties on the single-star conformation calls for a precise determination of the latter. In this work, we carry out extensive simulations of single, large telechelic star polymers for a wide range of parameters, characterising the self-assembly process and the resulting conformation as functionality, diblock copolymer length and solvent quality vary. We show that by tuning the chemical and physical parameters in solution, it is possible to influence and control the number and size of the attractive patches that each particle forms. Interestingly, we also demonstrate that different combinations of the parameters can generate stars with the same number of patches but different radial and angular stiffness. This mechanism could provide a neat way of tuning the elastic properties of the supramolecular network without changing its topology.

2. Models and methods

We simulate TSPs made of f diblock copolymer chains, anchored to a central point through their athermal parts. Each chain is made of N_A monomers of type A (solvophilic) and N_B monomers of type B (solvophobic). We define the fraction of monomers of type B as α = N_B/(N_A + N_B). We fix the minimum number of A and B monomers per chain to N^min_A = 40 and N^min_B = 80, respectively. The resulting stars are thus comparable with experimental systems.^20,21,34 Bonded neighbours, i.e. particles which share a backbone link, are kept close together by a FENE potential of the form:where r_F is the allowed maximum distance between monomers. We set r_F = 1.5σ. ε is the interaction strength. In what follows, we set σ = 1, ε = 1 and also k_B = 1 (Boltzmann's constant) and we express all dimensional quantities (length, density and temperature) in these units.

All the repulsive interactions acting between both bonded and non-bonded A–A and A–B pairs are modelled through a generalised Lennard–Jones (LJ) potential,

with r^c_rep = 2^1/24σ ≈ 1.03. Finally, the attraction between the terminal solvophobic monomers is provided by the attractive tail of the same generalised LJ potential as in eqn (2), rescaled by a parameter λ:

Therefore, the λ parameter plays the role of an inverse temperature for the B–B interaction. The value of λ at which purely solvophobic chains have a Gaussian statistics, equivalent to the so-called θ-temperature, is λ_θ ≈ 0.92. For performance reasons we truncate and shift this potential at r_c = 1.5.

We run Brownian dynamics simulations at fixed temperature kT/ε = 0.5.³⁵ Single TSPs with functionality f ranging between 3 and 18 and values of α ranging between 0.3 and 0.8 are investigated. In this work we characterise how chemical and physical parameters can influence single star properties, self-assembling behaviour, localisation and flexibility of the patches, both angular and radial, focussing on monomer-resolved stars so as to access a broad temperature range and investigate a large number of (f, α) combinations.

Recent studies³³ showed that soft patchy particles assemble into different gel-like structures depending on the softness of both angular and radial positions of the patches with respect to the equilibrium position; at the same time, studies on coarse-grained telechelic star polymers²⁷ showed that the single star self-aggregating scenario is preserved upon increasing density in solution, for stars with various different (f, α) combinations. It hence becomes important to completely characterise, on the full monomer scale, how a change of chemical (solvent quality e.g. λ⁻¹ – temperature effect), and physical parameters (such as (f, α) combinations) can lead to the formation of particles with a given number of patches, and how the radial and angular flexibility of those functionalised domains can be tuned and controlled by parameters external to the macromolecules. We hence carry out extensive characterisation of the stars and of their self-assembling behaviour as a function of λ, f and α.

The first parameter that we use to classify the stars is the number of patches N_p that the macromolecules self-assemble, defined as the number of clusters formed by multiple arms. If the interaction energy between at least two monomers of different arms is negative, i.e., if they experience a net attraction, then the two arms belong to the same cluster, and hence to the same patch. According to this definition, N_p ≈ 0 in the good solvent limit (λ → 0), since the attractive nature of the entropic-solvophilic monomers does not play any significant role in the self-aggregating behaviour that is instead driven by the enthalpic-solvophobic part of the molecule.

We start off by making a characterisation of the stars based on the number of self-assembled functionalised regions. We then move deeper into the description of the soft molecular building blocks by quantifying how the patch population s_p, defined as the number of arms that form a patch, is influenced by the choice of the parameters. Stars with different compositions can assemble into soft-patchy nano building blocks decorated by the same number of functionalised regions. Their radial and angular flexibility will crucially depend on the number of arms that are participating in the formation of a patch and on the size of the patch itself. Hence we perform a radial–angular flexibility analysis by characterising the geometry of the assembled TSP. We compute the average distance between the centre of mass of a patch and the position of the anchoring point, r_p, and the average angle between two patches, θ_p, defined as the angle between two vectors pointing towards each pair of patches, starting from the anchoring point. The quantities r_p and θ_p are two very important parameters to consider when looking to hierarchically self-assemble specific structures. For example, particles with an excess of radial and angular flexibility might lose the capability to crystallise.³⁶

The overall conformation and shape of the stars is another key characteristic, and we will elucidate its dependence on f, α and λ. The latter analysis is done by computing the shape anisotropy δ, the prolateness S and the acylindricity c.^37–39 These quantities are derived from the gyration tensor:

where N is the total number of monomers, r_i^m is the m-th component of the position of the i-th monomer and r_cm^m is the m-th component of the position of the star centre of mass. Diagonalising the tensor G yields three eigenvalues λ_i, i = 1, 2, 3, which are ordered as λ₁ ≥ λ₂ ≥ λ₃. We use these values to compute the aforementioned shape parameters, which are defined as follows:where I₁ = λ₁ + λ₂ + λ₃ and I₂ = λ₁λ₂ + λ₂λ₃ + λ₃λ₁ and the angular brackets have the meaning of ensemble averages. The first parameter, δ, is positive definite and quantifies the asphericity, S, which takes values between −0.25 and 2, measures prolateness (S > 0) or oblateness (S < 0). We notice that, in the system under investigation, δ and S turn out to follow the exact same trends. Therefore, for the sake of clarity and conciseness we decided to only show the latter quantity. The last parameter, c, is always equal to or larger than 0 and quantifies the cylindrical symmetry of the star, taking the value 0 only for perfectly cylindrical conformations. It is defined taking into account the fact that, as demonstrated in section 2, all investigated conformations are always prolate, i.e. S > 0.

Finally, here and in what follows we use the expression soft particle to refer to building blocks that are partially or completely interpenetrable and exhibit an intrinsic floppiness, in contrast to the usual “hard” colloids. An overview of wide classes of soft particles can be found in ref. 40.

3. Results

Due to their intrinsic nature, telechelic star polymers exhibit a self-assembling behaviour arising from the competition between the entropic self-avoiding repulsion of the inner part and the enthalpic attractions amongst the solvophobic tails of the f arms that constitute the macromolecules. It hence appears evident how a change in solvent quality (chemical perturbation to the system that can be performed by a change in temperature), modifies the enthalpic contribution, therefore affecting the whole single-macromolecule self-assembling process. For small values of the coupling constant λ, stars with a small percentage of attractive monomers do not have enough enthalpic contribution to assemble into a patchy structure. However, as soon as a minimum amount of attractive monomers is reached (a number that depends on the solvent quality and it is thus linked to the λ parameter), patchy structures arise.

Fig. 1 shows representative snapshots of a star with f = 15 and α = 0.5 for different values of the attraction coupling constant λ. The picture sketches the self-assembly process that takes place as λ increases for a fixed (f, α) combination. When the B-monomers, coloured in green, are in a good solvent (i.e. for small values of λ), the star is open and the inter-chain attraction is negligible. In this regime stars resemble the usual athermal star polymers.⁴¹ Upon worsening the solvent-quality, the solvophobic monomers start to collapse on themselves forming patches. A further increase of the attraction leads to a coarsening of the patches, which decrease in number but grow in size, as shown in the rightmost snapshot of Fig. 1. Similar figures are used in the plots throughout the paper to increase readability and to show how stars with different parameters look like.

Fig. 1 A TSP with f = 15 and α = 0.5 for, from left to right, λ = 0.80, 1.00 and 1.10.

We note that the functionalities investigated here yield small numbers of patches, ranging from one to four. We will put particular emphasis on stars that exhibit one to three patches since these can be used to generate low-density disordered (gel) phases.^10,14,42 However, other combinations of (f, α) can be used to select higher-valency particles that can be used to assemble denser, and possibly ordered, phases.^19,27 Additional control could be provided by confining the system, effectively reducing its dimensionality to generate two-dimensional or quasi two-dimensional phases with distinct symmetries and properties.^43,44

3.1. Characterisation of the patches

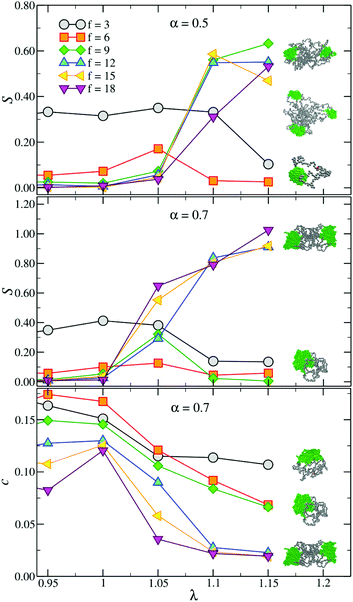
Extensive studies of toy models of rigid hard patchy particles have shown that the single most important parameter in determining the overall phase behaviour of the system is the number of patches.^45,46 These models usually employ particles with fixed numbers of patches, even though it is possible to enforce a temperature-dependent valence by using particles decorated with dissimilar patches.^14,42 By contrast, soft self-assembling systems as soft patchy particles or molecular telechelic star polymers present a variable number of patches that depends on external parameters such as solvent quality or temperature, a role which is here played by λ. Therefore, understanding how a change in λ affects the average number of patches N_p for stars with fixed combinations of f and α will allow a change in the functionalisation of the molecular building blocks, and hence their hierarchical self-assembling process, without the need to change the molecules in solution.

Fig. 2 shows N_p as a function of λ for all investigated f and α = 0.3, 0.5 and 0.7. For the lowest values of λ investigated here, all the curves are increasing functions of the coupling constant, signalling the onset of the self-assembly process. A comparison between different α suggests that this onset occurs at lower values of λ as α increases. For the lowest value of α considered here, all the curves except for f = 18 are monotonic with both λ and f. However, for high values of α and λ the curves exhibit a clear non-monotonicity. Indeed, when the attraction between solvophobic monomers exceeds a certain threshold, the arms start feeling a strong mutual attraction, collapsing on themselves and forming fewer, although larger, patches. Upon further increasing λ (λ > 1.15) these high-α systems fall off equilibrium and N_p eventually plateaus. A visual inspection of the configurations shows that monomers in the largest patches eventually crystallise.

Fig. 2 Number of patches N_p as a function of λ for (top) α = 0.3, (middle) α = 0.5 and (bottom) α = 0.7.

Depending on the number and size of the patches, these low-valence TSPs will assemble into different large-scale structures. A single patch can yield micelles or interconnected (wormlike) micelles, depending on the patch size.²⁵ As the number of patches increases so does the connectivity, meaning that the inter-star bonds become more common, eventually leading to network formation. The overall properties of this network will depend not only on the number and size of the patches, as it is the case for patchy colloids,⁶ but also on the radial and angular stiffness of the stars themselves.³³

We now move on to the average patch population s_p, which is defined as the average number of arms per patch. Fig. 3 shows s_p for α = 0.3 and 0.5. At low λ-values all curves approach 2, which is the minimum value according to our definition of a patch. For all the investigated state points s_p is, within the statistical error, monotonic with λ. The observed growth of N_p at intermediate values of λ is thus accompanied by an increase of s_p, which then plateaus as the systems undergo a dynamical arrest for λ > 1.15. At this stage all the arms are involved in a patch, thereby s_p → f/N_p.

Fig. 3 Patch population s_p as a function of λ for (top) α = 0.5 and (bottom) α = 0.7.

The formation of specific macroscopic phases with the desired properties and symmetry often requires building blocks with a well-defined valence and patch size.^10,47 We thus have to be sure that all the relevant quantities yield not only the right average values but also small fluctuations. We estimate the conformation fluctuations by looking at the patch population distribution P(s_p), shown in Fig. 4. At small λ all the distributions are peaked at s_p = 2. As λ increases P(s_p) starts developing longer and longer tails, making the distribution very wide and almost flat. For even stronger attractions, P(s_p) becomes non-monotonic and more and more peaked; this non-monotonicity is characteristic of systems forming aggregates with a preferential size. Indeed, systems undergoing self-assembly processes, such as micelle-formation, have cluster-size distributions which exhibit similar behaviour.⁴⁸ The particular value λ_c at which the self-assembly of the patches occurs, i.e. at which most of the arms are part of a patch, depends on α but not, or very weakly, on f, and it roughly coincides with the λ-value at which the number of patches and the average s_p reach the first plateau as shown in Fig. 2 and 3. Indeed, λ_c decreases from ≈1.15 for α = 0.3 to ≈1.00 for α = 0.7, while its dependence on f is negligible.

Fig. 4 Patch population distribution P(s_p) for a TSP with (top) f = 9, α = 0.5, (middle) f = 9, α = 0.7 and (bottom) f = 15, α = 0.7. The snapshots show configurations of systems with typical values of the patch population.

The results obtained with toy models have shown that the phase behaviour of patchy systems, and in particular the symmetry of the ordered or partially ordered phases, is determined not only by the number of patches, but also by their size and geometrical arrangement.^49,50 In addition, internal flexibility has been proven to play a fundamental role in the thermodynamics of these systems.³⁶ It is thus very important to characterise the patch arrangement. We start off by introducing a vector r_pⁱ that connects the centre of mass of the i-th patch to the star centre. We then define for each pair of patches i and j an angle θ_p = arccos(r_pⁱ·r_p^j). Fig. 5 shows the distribution of the cosine of this angle, P(cos θ_p), for different values of α, f and λ. All the curves are clearly peaked around values that directly reflect the number of patches of the nanoparticle: for two and three patches the arrangement is planar and hence the average angle is slightly smaller than π and 2π/3, respectively. For f = 12, α = 0.5 we also observe a coexistence between the two conformations: the number of patches of the nanoparticle continuously changes between two and three, giving rise, for intermediate values of λ, to a double-peaked P(cos θ_p). For higher values of α or f this transition happens in a narrower range of λ-values and we do not observe any double-peaked distribution for the investigated parameters. The effect of the functionality on the distribution of the angle is also interesting: as f increases the distributions become more and more peaked, due to the higher local density of monomers close to the anchoring point.

Fig. 5 Distribution of the angle between patches, P(cos θ_p), for a TSP with (top) f = 12 and (bottom) f = 18 for high values of λ and for (left) α = 0.5 and (right) α = 0.7. The snapshots show configurations of systems with typical average angles.

The functionality f plays a similar role in determining the distribution of the radial patch–anchor distance r_p, P(r_p), which is linked to the stiffness of the particle. Fig. 6 shows P(r_p) for fixed α = 0.7, λ = 1.10 and three different functionalities, f = 12, 15 and 18, chosen so as to yield the same number of patches, N_p = 2. As f increases we observe a monotonic growth of the average patch–anchor distance and a narrowing of the distribution. The net effect of f is thus to stiffen and elongate the nanoparticle.

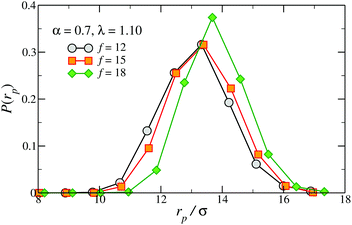Fig. 6 Distribution of the distance between a patch and the TSP centre, P(r_p), for f = 12, 15 and 18, λ = 1.10 and α = 0.7.

As a consequence of the above single-particle properties, two networks built with stars with different functionalities but the same number of patches would differ in the spacing between neighbours and in the overall stiffness. Indeed, both are increasing functions of f, due to the narrowing of the angle and radial distributions. On the contrary, the topology, being primarily determined by the number and arrangement of the patches, would be less affected by f. We thus provide an additional degree of control on these hierarchically self-assembled materials: the mechanical and elastic properties of bulk materials can be tuned to a certain degree without varying their topology. In other words, stars with different functionalities can be exploited to obtain phases which are similar from the structural point of view but behave differently, e.g. under shear.

3.2. Characterisation of the shape

All the results above have been obtained by employing our specific definition of a patch given in section 2. Even though the results themselves, as well as visual inspections of the conformations, confirm that the definition we use is self-consistent, there is always an intrinsic ambiguity when dealing with threshold-based cluster algorithms. Therefore, it is important to also characterise the star conformation in a way that does not depend upon our specific definition of a patch. We do this by computing the gyration tensor and the resulting shape parameters, as defined in eqn (5)–(7).

Fig. 7 shows the dependence of the shape parameters on f, α and λ. We start off by considering the prolateness parameter S which, as noted in section 2, has the same qualitative behaviour as the asphericity δ, which is thus not shown here. S is always positive, indicating that the stars are always prolate, regardless of f, α and λ, as also observed for chain- and ring-polymers.⁵¹ Comparing Fig. 7 with Fig. 3 shows that the steep increase of S at high values of f and λ is associated with the presence of two patches which, as also shown in Fig. 1, result in dumbbell-like, very prolate conformations. By contrast, stars with smaller functionalities end up in almost spherical single-patch states having S ≈ 0. As a consequence, at high values of λ there is a clustering of the curves with different f, depending solely on the number of patches and not on the functionality. We note that the f = 18, α = 0.7 case, which form 4 patches at intermediate λ-values (see Fig. 2), exhibits a very small prolateness, demonstrating that S is sensibly different from 0 only for N_p ≤ 3. We deduce that the number of patches controls the overall shape of the star, while f affects size, stiffness and deformability of the assembled nanoparticles, as shown in the previous section.

Fig. 7 Prolateness parameter S for (top) α = 0.5 and (middle) α = 0.7 and (bottom) acylindricity parameter c for α = 0.7 for all the investigated functionalities. The snapshots on the right show typical configurations of high-λ systems.

The last investigated parameter, the acylindricity c, is always small and decreases for large values of λ. This demonstrates that stars are mostly symmetrical around the main axis. In agreement with the trends observed for the other shape parameters, this tendency is enhanced when stars assemble into dumbbells due to the presence of two large patches. Indeed, at high f and λ, c ≈ 0.

4. Conclusions

Understanding how to manufacture self-assembling building blocks with specific softness, functionalisation, shape and flexibility by tuning a few microscopical details has an extremely important impact on the materials science community for a two-fold reason: first of all, it allows one to drive a bottom up self-assembly scheme to engineer new materials starting from the microscopic symmetries and properties. Secondly, it makes it possible to add external chemical/physical parameters that allow one to tune even more the properties of such new materials, without the need to re-formulate their molecular structure.

Here we showed that the self-assembly of a very promising class of polymeric building blocks, namely telechelic star polymers, can be controlled with great precision by changing the functionality or the solvophobic-to-solvophilic ratio, as well as by a careful tuning of the temperature. We have studied how the number and size of attractive spots on the surface, herein referred to as patches, vary under changing conditions, showing that, at low temperature, these quantities exhibit single-peaked, narrow distributions, thereby providing a robust route for the generation of microscopic building blocks with specific, well-defined properties. We have also studied the flexibility and stiffness of the stars, demonstrating that those depend not only on the number of patches, but also on the functionality. This opens up the possibility of selecting the elastic properties of the resulting macroscopic phases without changing their topology and average structure.

Reliable thermosensitive flexible patch formation and tunable dependence on the number of patches on temperature for a given molecular unit is a key ingredient that allows one to obtain different mesoscopic self-assembling behaviours from the same molecular species. As a consequence, different, possibly ordered, structures, as well as diverse viscoelastic properties can be obtained with the same microscopic constituents.²⁷ The results reported here should be considered together with the notion that the conformation of single stars is preserved in low-density bulk phases.²⁷ Indeed, in this case a direct link between the conformation of the building blocks and the final structure and phase behaviour of the resulting macroscopic material can be established, for example by means of coarser-grained models,³³ or theoretical treatments.⁵² The investigation of such hierarchical self-assembly processes will provide an excellent testing ground for the development of new multiscale methods and also guidance for experiments for the synthesis of smart materials of the next generation.

Acknowledgements

LR acknowledges support from the Austrian Research Fund (FWF) through the Lise-Meitner Fellowship M 1650-N27. BC acknowledges support from the ÖAW through the APART Fellowship 11723. Computer time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.

References

1. D. Fennell Evans and H. Wennerström, The colloidal domain, Wiley-Vch, 1999.
2. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
3. F. Smallenburg, L. Leibler and F. Sciortino, Phys. Rev. Lett., 2013, 111, 188002.
4. Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384.
5. S. Biffi, R. Cerbino, F. Bomboi, E. M. Paraboschi, R. Asselta, F. Sciortino and T. Bellini, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15633–15637.
6. E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397–6410.
7. V. N. Manoharan, M. T. Elsesser and D. J. Pine, Science, 2003, 301, 483–487.
8. G. Zhang, D. Wang and H. Möhwald, Nano Lett., 2005, 5, 143.
9. Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413.
10. E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301–168304.
11. E. G. Noya, C. Vega, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2010, 132, 234511.
12. F. Romano and F. Sciortino, Nat. Commun., 2012, 3, 975.
13. F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801.
14. L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Rev. Lett., 2013, 111, 168302.
15. A. B. Pawar and I. Kretzschmar, Langmuir, 2008, 24, 355.
16. Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55.
17. G.-R. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101.
18. G. Srinivas and J. W. Pitera, Nano Lett., 2008, 8, 611–618.
19. B. Capone, I. Coluzza, F. Lo Verso, C. N. Likos and R. Blaak, Phys. Rev. Lett., 2012, 109, 238301.
20. M. Pitsikalis, N. Hadjichristidis and J. W. Mays, Macromolecules, 1996, 29, 179–184.
21. D. Vlassopoulos, T. Pakula, G. Fytas, M. Pitsikalis and N. Hadjichristidis, J. Chem. Phys., 1999, 111, 1760–1764.
22. D. Vlassopoulos, M. Pitsikalis and N. Hadjichristidis, Macromolecules, 2000, 33, 9740–9746.
23. F. Lo Verso, C. N. Likos, C. Mayer and H. Löwen, Phys. Rev. Lett., 2006, 96, 187802.
24. F. Lo Verso, C. N. Likos and H. Löwen, J. Phys. Chem. C, 2007, 111, 15803.
25. F. Lo Verso, A. Z. Panagiotopoulos and C. N. Likos, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2009, 79, 10401.
26. C. Koch, A. Z. Panagiotopoulos, F. Lo Verso and C. N. Likos, Soft Matter, 2013, 9, 7424.
27. B. Capone, I. Coluzza, R. Blaak, F. Lo Verso and C. N. Likos, New J. Phys., 2013, 15, 95002.
28. B. Helms and E. W. Meijer, Science, 2006, 313, 929–930.
29. K. Sakai-Kato, N. Nishiyama, M. Kozaki, T. Nakanishi, Y. Matsuda, M. Hirano, H. Hanada, S. Hisada, H. Onodera, H. Harashima, Y. Matsumura, K. Kataoka, Y. Goda, H. Okuda and T. Kawanishi, J. Controlled Release, 2015, 210, 76–83.
30. D. B. Alward, D. J. Kinning, E. L. Thomas and L. J. Fetters, Macromolecules, 1986, 19, 215.
31. E. L. Thomas, D. B. Alward, D. J. Kinning, D. C. Martin, D. L. Handling and L. J. Fetters, Macromolecules, 1986, 19, 2197.
32. L. Rovigatti, F. Smallenburg, F. Romano and F. Sciortino, ACS Nano, 2014, 8, 3567–3574.
33. E. Bianchi, B. Capone, G. Kahl and C. N. Likos, Faraday Discuss., 2015, 181, 123–138.
34. M. Gauthier and A. Munam, Macromolecules, 2010, 43, 3672–3681.
35. J. Russo, P. Tartaglia and F. Sciortino, J. Chem. Phys., 2009, 131, 14504.
36. F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558.
37. D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478.
38. M. O. Steinhauser, J. Chem. Phys., 2005, 122, 094901.
39. G. Zifferer and W. Preusser, Macromol. Theory Simul., 2001, 10, 397–407.
40. C. N. Likos, Soft Matter, 2006, 2, 478–498.
41. G. S. Grest, K. Kremer and T. A. Witten, Macromolecules, 1987, 20, 1376–1383.
42. J. Russo, J. M. Tavares, P. I. C. Teixeira, M. M. Telo da Gama and F. Sciortino, Phys. Rev. Lett., 2011, 106, 085703.
43. A. Halperin and S. Alexander, Macromolecules, 1987, 20, 1146–1152.
44. S. van Teeffelen, A. J. Moreno and C. N. Likos, Soft Matter, 2009, 5, 1024–1038.
45. E. Bianchi, P. Tartaglia, E. Zaccarelli and F. Sciortino, J. Chem. Phys., 2008, 128, 144504.
46. G. Foffi and F. Sciortino, J. Phys. Chem. B, 2007, 111, 9702.
47. F. Romano, E. Sanz and F. Sciortino, J. Chem. Phys., 2011, 134, 174502.
48. M. A. Floriano, E. Caponetti and A. Z. Panagiotopoulos, Langmuir, 1999, 15, 3143–3151.
49. F. Romano, E. Sanz and F. Sciortino, J. Phys. Chem. B, 2009, 113, 15133.
50. G. Doppelbauer, E. G. Noya, E. Bianchi and G. Kahl, Soft Matter, 2012, 8, 7768–7772.
51. A. Narros, A. J. Moreno and C. N. Likos, Macromolecules, 2013, 46, 3654–3668.
52. L. Rovigatti, F. Bomboi and F. Sciortino, J. Chem. Phys., 2014, 140, 154903.

---