The mechanism of Claisen rearrangement of allyl phenyl ether from the perspective of topological analysis of the ELF

Abstract

The Claisen rearrangement of allyl phenyl ether to 6-(prop-2-en-1-yl) cyclohexa-2,4-dien-1-one has been studied by means of Bonding Evolution Theory (BET), which combines the topological analysis of the electron localization function (ELF) and catastrophe theory. The reaction can be presented as consisting of 10 main steps separated by fold and cusp catastrophes. The description of the mechanism of C–O bond breaking is complicated and depends on the DFT method used. It proceeds through a heterolytic cleavage (B3LYP, M052x) with the formation of the V₃(O) non-bonding basin in step II (M052x) or with electron density resonating between oxygen and carbon atoms in step II (B3LYP). The C–C bond between the allyl group and the phenol ring is formed after the TS in step VIII. The reaction is terminated by the formation of two localized C=C bonds in the phenyl ring in steps IX and X. The localization of V_i=1,2(C,C) basins – typical of localized double bonds – in the phenyl ring proves the process of dearomatisation. The electronic structure of the transition structure distinguishes the non-bonding electron density concentrated in the vicinity of the C2 atom, represented by the V(C2) basin, with a population of 0.28e. This basin is a “bridgehead” for the “construction” of the C–C bond between the phenyl ring and the allyl group.

---

1. Introduction

The Claisen rearrangement is a powerful synthetic tool in organic synthesis¹ and is sometimes described as an oxy-variant of the Cope reaction. In 1912 for the first time the [3,3] – sigmatropic rearrangement of an allyl aryl ether and an allyl vinyl ether was reported by Claisen.² The mechanism of the Claisen rearrangement of an allyl phenyl ether (APhE) consists of breaking of the carbon–oxygen bond and formation of a new carbon–carbon bond. Furthermore, this process is associated with migration of a double C=C bond, formation of a double C=O bond and dearomatisation of an aromatic ring (see Scheme 1).

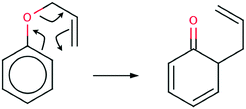Scheme 1 The Lewis formula for the Claisen rearrangement of allyl phenyl ether to the ketonic form of o-allylphenol.

The product of the reaction is the ketonic form of o-allylphenol (KAPh). Finally, a molecule of o-allylphenol is formed.

The mechanism of the Claisen rearrangement of an allyl phenyl ether is usually represented by the Lewis formula with curly arrows showing movements of (formal) electron pairs. However, such a mechanism seems to be oversimplified because a few rather fundamental questions may be raised: (1) why does the electron density from the delocalised C⋯C bond of a phenyl ring flow only to the C–O bond (it will be transformed into a double C=O bond) and not to both C–O and C⋯C regions? (2) Is the mechanism of the Claisen rearrangement of an allyl phenyl ether concerted and synchronous i.e. C=O and C–C bonds are formed simultaneously with a breaking of the C–O bond? (3) In which moment of the reaction are two localized C=C bonds of the phenyl ring formed from previously delocalized C⋯C bonds? Those and other questions may be answered by using topological analysis of the Electron Localization Function (ELF)^3–8 and elements of catastrophe theory.⁹ Mechanisms of different organic reactions have been explained using both methods^10–13 and their combined use is known in the scientific literature as Bonding Evolution Theory (BET)¹⁴ and was elaborated by Krokidis et al.^15–17

In the past, many theoretical efforts have been made to elucidate the nature and geometry of the transition structure (TS), which is important for understanding Claisen rearrangements and is believed to be concerted and chairlike.¹⁸ From the point of view of organic reactivity, the TS may be considered in terms of the early structure versus its late character and the 1,4-diyl versus aromatic transformation versus bis-allyl character.^19–22 The geometrical structures of the TS have been analyzed by using AM1, MP2/6-31G(d), RHF/6-31G(d), Becke3LYP/6-31G(d), 6-311+G(d,p) and CASSCF/6-31G(d) computational methods.²³

In this study, the mechanism of the Claisen rearrangement of allyl phenyl ethers is studied by means of BET. Our goal is to show the mechanism of the reaction as a sequence of bond breaking and bond formation steps that are precisely located on the reaction path by means of catastrophe theory. Furthermore, we want to answer the questions raised above and compare the typical scheme of the flow of electron density with that obtained on the basis of an ELF-topological study. Though the Claisen rearrangement of APhE is terminated by the formation of an o-allylphenol, we have constrained our study to the first reaction where the ketonic form of the o-allylphenol is formed.

2. Computational details

Optimizations of geometrical structures and calculation of the internal reaction coordinate (IRC) path were performed using Gaussian 03,²⁴ the B3LYP^25–28 hybrid electron density functional, and the 6-31G(d) basis set^29–40 as referenced in the G03 program and the M052x global hybrid functional⁴¹ from the family of Minnesota functionals as referenced in the Gaussian 09 program.⁴² The probing of the IRC path using different DFT functionals encountered many problems therefore standard B3LYP and M052x functionals have been chosen. The DFT (M052x) method with the 6-311G(d)⁴³ basis set has been used only to study the reaction path from the TS to APhE.

All stationary points were characterized to have the correct type of vibrational eigenvalues, and the transition structure was verified to connect to the correct minima by using the IRC method.^44,45 The zero-point vibrational energy of the TS has been calculated by ignoring one imaginary frequency.

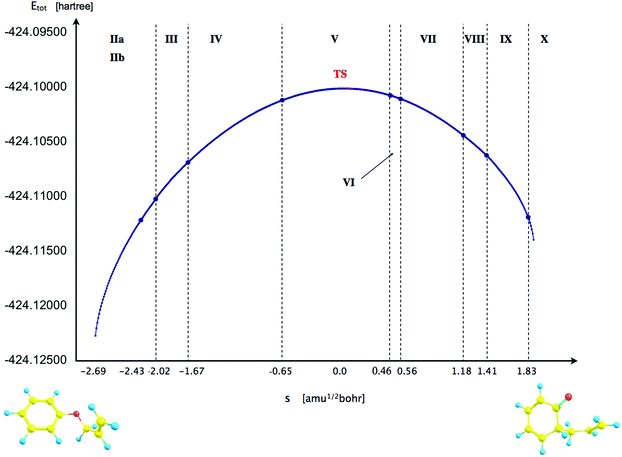
For the BET analysis a reaction path was taken from an IRC calculation in mass-weighted Cartesian coordinates with the step length of 0.01 (amu)^1/2 Bohr. The points on the IRC were not interpolated by any specific equation and the line in Fig. 3 is presented to emphasize a trend.

The ELF topological analysis was performed by using the TopMod⁴⁶ program with a rectangular parallelepiped grid and a step size of 0.05 Bohr. Visualization of molecular structures was done using ChemCraft.⁴⁷

The analysis of the evolution of the critical points (CPs) is constrained only to attractors localized in the field of the ELF.

The discussion of the points on the IRC path and the corresponding interatomic distances, where the process of A–B bond formation begins and ends is based on the catastrophes of the ELF field. The catastrophe that causes the creation of a non-bonding V(A) or V(B) attractor shows the beginning of bond formation and the catastrophe that causes the appearance of the V(A,B) bonding attractor shows the end of bond formation. Those catastrophes have been described for the first time by Krokidis et al.^14,15 for C–C and N–B bond breaking in C₂H₆ and NH₃BH₃ molecules.

3. Results and discussion

3a. Electronic structure of isolated molecules and transition state

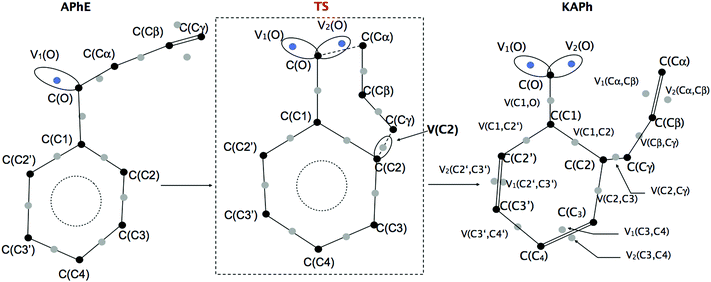
The geometrical structure of the allyl phenyl ether, the ketonic form of the o-allylphenol, and the transition state (TS) of the Claisen rearrangement (see Fig. 1) have been optimized at the B3LYP/6-31G(d) computational level.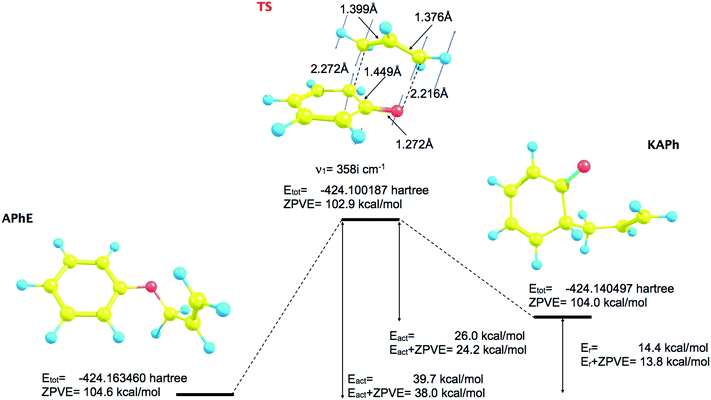

Fig. 1 The optimized geometrical structures of minima and transition structure (TS) for the Claisen rearrangement of allyl phenyl ether (APhE).

The predicted activation barrier is 39.7 kcal mol⁻¹ (36.5 kcal mol⁻¹ in ref. 48) and 38.0 kcal mol⁻¹ including the zero-point vibrational energy (ZPVE).

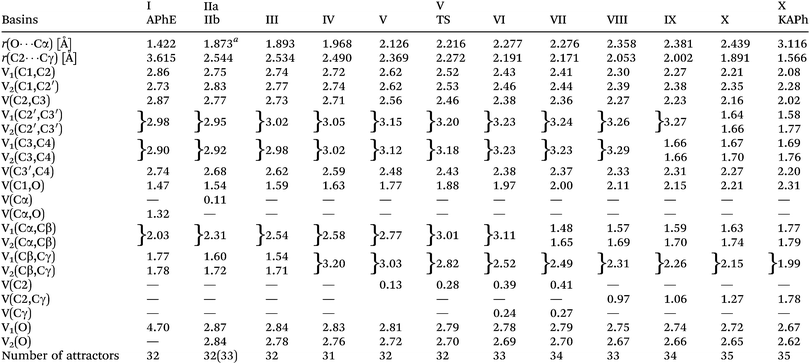
The reaction begins from the APhE molecule therefore its electronic structure will be analyzed first. The electron densities associated with core regions, covalent bonds and lone pairs are characterized by the local maxima of the ELF field (attractors). All attractors localized in APhE are presented in Fig. 2.

Fig. 2 Valence (monosynaptic, disynaptic) and core (monosynaptic) attractors of the ELF field localized for the minima (APhE, KAPh) and transition structure (TS) for the Claisen rearrangement of allyl phenyl ether. The protonated attractors have been omitted for clarity.

The protonated attractors corresponding to H atoms are omitted for clarity. The values of the mean electron population (N̄) calculated for each basin of the attractor are collected in Table 1.

Table 1 Population (in e) of the ELF-localization basins for different steps in the Claisen rearrangement of allyl phenyl ether (APhE). The first point (after catastrophe) in each domain of structural stability (step of the reaction) is presented

a The distance when the V(Cα) is observed for the first time.

---

The aromatic ring in APhE is characterized by six valence bonding disynaptic attractors V(C1,C2), V(C2,C3), V(C3,C4), V(C3′,C4), V(C2′,C3′) and V(C1,C2′). There are no observed pairs of the V_i=1,2(Ci,Cj) attractors that are usually found for localized double C=C bonds.⁴⁹ The values of the basin population (N̄) are in the range from 2.73e for V(C1,C2′) to 2.98e for V(C2′,C3′) yielding the value of the ELF-topological bond order for the C–C bonds in the ring between 1.37 and 1.49. Those values are close to the formal value of 1.5 expected for benzene. Thus, a delocalized character of valence electron density in the ring has been confirmed. A similar conclusion may be reached on the basis of the values of relative fluctuation, the quantum-mechanical measure of delocalization of electron density^49–51 that is equal to 0.47 (λ) for each localization basin representing the C–C bond in the ring (0.46 – benzene⁵²).

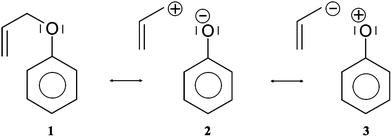
The formally single bond Cα–Cβ in the side chain –O–Cα–Cβ=Cγ is characterized by the single bonding attractor V(Cα,Cβ) and formally the double bond Cβ=Cγ by pair of the V_i=1,2(Cβ,Cγ) bonding attractors. Those attractors support the Lewis representation assuming that one attractor corresponds to one bond in the Lewis representation. The double bond Cβ=Cγ “contains” 3.59e (1.77e + 1.78e), and that value is slightly (0.41e) smaller than the formal value of 4e. The character of the single bond Cα–Cβ is confirmed by the population of 2.03e. The C1–O and Cα–O bonds with 1.47 and 1.32e, may be described respectively as electron depleted single bonds, and the “missing” electron density (in respect to a formal value of 2e) is mainly localized in the nonbonding V₁(O) basin. This result suggests a largely polarized character of the carbon–oxygen interaction and its nature may be described by a resonance of three hybrids with the covalent bond, C–O, and the ionic bonds, C⁺O⁻, C⁻O⁺ (see Scheme 2).

Scheme 2 Three resonance hybrids that describe delocalisation of electron density in the C–O bond in APhE and during the process of dissociation in steps I and II. The Lewis structures have been drawn on the basis of the results of ELF analysis.

The values of (λ) for the V(C1,O) and V(Cα,O) basins are 0.62 and 0.64, respectively, thus the electron density in those basins are delocalized to a greater degree than for the carbon–carbon bonds in the phenyl ring (0.47). The non-bonding electron density of oxygen is characterized by a single valence nonbonding monosynaptic basin V₁(O) with 4.70e. The large value of N̄ proves that this basin corresponds to two lone pairs in the Lewis formula.

The product of the reaction, that is, the ketonic form of the o-allylphenol, is formed after migration of the allyl group to the ortho position of the phenyl ring. All attractors localized in KAPh are presented in Fig. 2.

The C2–Cγ bond between the phenyl ring and the allyl group is reflected in the ELF-topology by the the V(C2,Cγ) bonding basin. The basin population of V(C2,Cγ) is 1.78e. The Cα–Cβ bond, which is characterized by the single bonding basin V(Cα,Cβ) in APhE is transformed into the double bond Cα=Cβ. The total value of the N̄ for the two basins V₁(Cα,Cβ) and V₂(Cα,Cβ) is equal to 3.56e (1.77e + 1.79e). That value is smaller than the formal population of 4e expected for the C=C bond and the “missing” electron density (in respect to a formal value of 4e) is localised in other valence basins. The ketonic form of the o-allylphenol exhibits an essential dearomatisation because for two bonds C2′=C3′ and C3=C4 in the phenyl ring two pairs of disynaptic bonding attractors are found, V_i=1,2(C2′,C3′) and V_i=1,2(C3,C4) with the values of the basin population: 1.58, 1.77e and 1.69e, 1.76e, respectively. The total values of N̄ of 3.35e and 3.48e, respectively, are about 0.4e larger than the corresponding basins in APhE with the aromatic ring. It is worth emphasizing that the V_i=1,2(C2′,C3′) and V_i=1,2(C3,C4) basins are not observed in APhE before Claisen rearrangement. Since the Cα–O bond is broken about 0.6e is moved to the region of the non-bonding electron density of oxygen where two non-bonding basins are localized V₁(O) and V₂(O) with 2.67e and 2.62e, respectively. The formally double bond C1=O is described by only a single V(C1,O) basin with 2.31e, thus similarly to the C1–O and Cα–O bonds in APhE the resonance hybrids with ionic bonds C⁺O⁻ and C⁻O⁺ have to be considered in the description of their electronic structure. It is worth noting that the population of the V(C1,O) basin in KAPh is 0.84e larger than that in APhE thus this difference shows that the C1–O bond is saturated with the electron density which may be deduced from comparison of the Lewis formulas (see Scheme 1).

3b. Analysis of the reaction mechanism using the DFT (B3LYP) method

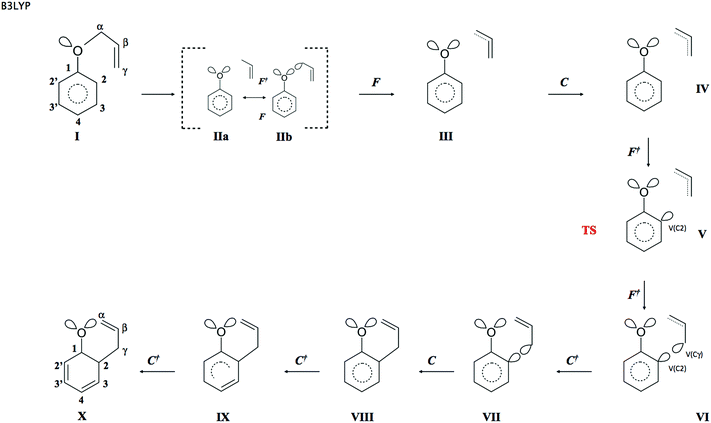
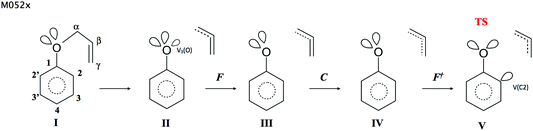
The reaction has been followed by performing topological analysis of the ELF for 475 nuclear configurations selected along the IRC path (see Fig. 3).

Fig. 3 The IRC path calculated for the Claisen rearrangement of the allyl phenyl ether to the ketonic form of o-allylphenol with marked domains of structural stability (steps of the reaction) separated by the catastrophes of the ELF field.

The values of N̄ for the localisation basins observed for each domain of structural stability – separated by fold and cusp catastrophes of ELF – are shown in Table 1. The Lewis-like structures, representing the evolution of chemical bonds, lone pairs and non-bonding regions during the reaction course, are presented in Fig. 4.

Fig. 4 The Lewis-like structures representing the chemical bonds, lone pairs and regions with non-bonding electron density for each step of the Claisen rearrangement of allyl phenyl ether. The results obtained at the DFT(B3LYP)/6-31G(d) computational level. The fold and cusp catastrophes that cause the increase and decrease of the total number of attractors are denoted respectively as F^†, C^† and F, C.

In the first step of the reaction the topology of the ELF of the reacting molecule is the same as it has been described for APhE with the geometrical structure optimised to an energy minimum. The number of core and valence attractors is equal to 32. Among three resonance hybrids shown in Scheme 2 the dominant is hybrid 1.

As a result of the increase of the Cα⋯O separation, the electronic structure of APhE changes and the weight of hybrids 2 and 3 increases. The electron density from the Cα–O bond is localised on the Cα or/and O atom. What is interesting, the electronic structure implied by both resonance hybrids is visible in the topological analysis of the ELF field. The localisation of the electron density on the O atom is represented by the second V₂(O) basin localised in the vicinity of the C(O) core basin, while localisation of electron density on the Cα atom is represented by the monosynaptic non-bonding basin V(Cα) localised in the vicinity of the C(Cα) core basin (see modified Lewis structures IIa and IIb in Fig. 4). It is worth noting that the V₂(O) attractor is found in the position where a monosynaptic basin of the second lone electron pair of oxygen is expected and not in the bonding region. Thus a typical monosynaptic valence attractor, being the remains of the Cα–O bond breaking, which should appear between the C(O) and C(C) core attractors, as shown by Krokidis¹⁴ for the C–C bond in a process of covalent bond breaking, has not been observed. The synaptic type⁵³ of the V(Cα) basin is not clear because it may also be disynaptic V(Cα,O). All points on the IRC path up to s = −2.43 (amu)^1/2 Bohr exhibit mainly ELF-topology with the second V₂(O) basin in the valence shell of oxygen (modified Lewis structures IIa). It shows that the local electronic structure of the carbon–oxygen bond in a process of its cleavage is dominated by resonance hybrid 2. The total number of attractors in the molecule does not change with respect to APhE with the geometrical structure optimised to an energy minimum and is equal to 32. For larger values of the Cα⋯O separation the weight of resonance hybrid 3 increases and some part of the electron density from the Cα–O bond is also localised in the vicinity of the C(Cα) core. In addition to the V₂(O) basin the analysis of the ELF-topology shows the monosynaptic non-bonding basin V(Cα). The total number of attractors increases to 33 (see modified Lewis structure IIb). We comply with an interpretation that breaking of the Cα–O bond has a complicated mechanism and at an early stage of its dissociation the electron density fluctuates between Cα and O atoms.

The change of the topology of the ELF between steps I and II is complicated, because it is the result of two processes: a flow of the electron density from the V(Cα,O) basin to a region of the V₁(O) basin and redistribution of the electron density to the vicinity of the C(Cα) core basin. Both processes are observed in step I. At least three fold catastrophes of the ELF field between steps I and II may be observed. The new valence attractor V₂(O) in the vicinity of the oxygen core C(O) appears in the fold (F⁺). The increase of the electron density in the non-bonding region of the O atom results in the qualitative change of electron localisation and the isolation of the second local maximum of the ELF, V₂(O) that corresponds to the second lone pair in the formal Lewis representation of the oxygen atom. The V₂(O) attractor corresponds to the lone pair of oxygen (see Fig. 4) thus some electron density has been transferred from the bonding to the nonbonding region of oxygen. The decrease of the electron density in the Cα–O bond and the change of electron localisation may be associated with another fold catastrophe (F) that would describe annihilation of the bonding attractor. The third fold catastrophe (F⁺) results in the appearance of the V(Cα) attractor (or the V(Cα,O) attractor). Unfortunately, a comprehensive description of the Cα–O bond rupture with the verification of the synaptic type of V(Cα) and full characterisation of catastrophes requires a detailed study of all critical points of the ELF field, as presented by Krokidis et al.¹⁴ for the dissociation of the H₃N–BH₃ molecule. Owing to the complexity of the ELF field in APhE such analysis cannot be performed presently. In Table 1 the basin formed in the vicinity of the C(Cα) core is denoted as V(Cα) which will be used in the text.

From the chemical point of view the covalent-polarized Cα–O bond in step II is partially broken. The basin population of V₂(O) is equal to 2.84e and is very similar to the one computed for the V₁(O) lone pair with 2.87e. The basin population of V(Cα) ranges between 0.11 and 0.13e. It is worth noting that a very small value of N̄ for V(Cα) may be explained by the small weight of resonance hybrid 3 where the negative charge is localised on the carbon atom. Further lengthening of the Cα⋯O separation results in redistribution of the electron density mainly from the V(Cα) basin to the Cα–Cβ bond. Because of the fluctuating electron density between the Cα and O atoms in step II it is not possible to discuss precisely the bond lengths associated with the catastrophes.

The third step (III) of the reaction starts for s = −2.019 (amu)^1/2 Bohr with the fold catastrophe (F). The monosynaptic non-bonding attractor V(Cα) and the CP of index 1 are annihilated and a wandering point i.e. a point at which the gradient of the ELF is not equal to 0 is created. The valence non-bonding basin V(Cα) disappears as a consequence of electron flow to neighbouring V_i=1,2(Cα,Cβ) basins and a change of electron localization in the vicinity of the Cα core. The basin population of V_i=1,2(Cα,Cβ) increases from 2.31e (II) to 2.54e (III). From the beginning of the reaction (step II) the population of both lone pairs V₁(O) and V₂(O) gradually decreases because the electron density flows to the V(C1,O) basin (the double C1=O bond in KAPh). Bearing in mind that the V(Cα) basin in step II was the remains of the Cα–O bond the annihilation of V(Cα) in step III proves (from ELF-topological point of view) that the Cα–O bond in step III is entirely destroyed.

Step IV of the reaction starts with the cusp catastrophe (C) observed in the region of the Cβ=Cγ bond of the allyl group. Two attractors V_i=1,2(Cβ,Cγ) and the CP of index 1 are annihilated and a new single attractor V(Cβ,Cγ) appears. Two bonding disynaptic basins V_i=1,2(Cβ,Cγ) are joined into a single basin V(Cβ,Cγ). Because two attractors V_i=1,2(Cβ,Cγ) are typical of a localized double C=C bond the observed change of the ELF field may be interpreted as “reduction” of the double Cβ=Cγ bond to the single Cβ–Cγ bond. The change of the ELF-topology is a consequence of transfer of the electron density mainly from valence basins in the allyl group to a region where the C2–Cγ bond will be formed and from the Cβ=Cγ bond to the Cα–Cβ bond. The mean electron population of the V(Cβ,Cγ) basin is equal to 3.20e. The catastrophe is found for s = −1.669 (amu)^1/2 Bohr and r(O⋯Cα) and r(C2⋯Cγ) distances of 1.968 Å and 2.490 Å, respectively. In this step all chemical bonds are topologically described by single valence bonding attractors.

The topology of the ELF in step V is determined by the next fold catastrophe (F⁺) observed for s = −0.649 (amu)^1/2 Bohr and r(O⋯Cα) and r(C2⋯Cγ) distances: 2.126 Å and 2.369 Å, respectively. From the point of view of interpretation of the mechanism of Claisen rearrangement this step is very important because it characterizes the transition state (TS). Valence and core attractors are presented in Fig. 2. It is worth emphasizing that a new bond C2–Cγ is not yet formed in the TS, however the progress of the reaction is reflected by the formation of a new monosynaptic valence basin V(C2) in the vicinity of the C2 core. The V(C2) basin will be transformed into the C2–Cγ bond in step VIII. The catastrophe “separating” step IV from step V is fold. The basin population of V(C2) is equal to 0.28e in the TS and during step V increases from 0.13 to about 0.39e in step VI (see Table 1). All chemical bonds are characterized by single basins with the largest values of N̄ calculated for V_1∪2(C2′,C3′), V_1∪2(C3,C4) and V(Cα,Cβ) with 3.20, 3.18 and 3.01e, respectively. Those basins will be transformed into double bonds.

The sixth step is very short (about 11 points on the IRC path) and begins with the fold (F⁺) catastrophe (s = 0.464 (amu)^1/2 Bohr). The non-bonding valence attractor V(Cγ) and the CP of index 1 are created in the valence shell of the terminal carbon atom Cγ of the –Cα–Cβ=Cγ allyl group. The total number of attractors increases to 33. The topology of the ELF between the C2 and Cγ atoms is characterized by the V(C2) and V(Cγ) non-bonding attractors. We can say – applying the language of engineering – that the “construction” of the C2–Cγ bond is a very advanced step (see Fig. 4). The mean electron population of the V(C2) and V(Cγ) basins is equal to 0.39 and 0.24e, respectively. The formation of the V(Cγ) basin causes a large decrease of the population of the V(Cβ,Cγ) basin from 2.82e (TS) to 2.52e (step VI). The values of the r(O⋯Cα) and r(C2⋯Cγ) distances for the first point in this step are 2.277 Å and 2.191 Å, respectively.

The seventh step is associated with a change of electron localization in the allyl group where the cusp catastrophe (C⁺), identified for s ≈ 0.564 (amu)^1/2 Bohr, leads to the creation of the critical point of index 1 and two new disynaptic attractors V₁(Cα,Cβ) and V₂(Cα,Cβ) from the single disynaptic attractor V(Cα,Cβ). The total number of attractors increases to 34. The cusp occurs for the r(O⋯Cα) and r(C2⋯Cγ) distances of 2.276 Å and 2.171 Å. From a chemical point of view, the single-type Cα–Cβ bond is transformed into the double Cα=Cβ bond, assuming that the localization of two bonding disynaptic attractors V_i=1,2(Cα,Cβ) is a typical feature of localized double carbon–carbon bonds. The formation of the Cα=Cβ bond is expected on the basis of the general mechanism of the Claisen rearrangement of APhE. It is worth emphasizing that the emergence of the typical feature of the C=C bond occurs before the formation of the new C2–Cγ bond that binds the phenyl ring and the allyl group. After the catastrophe the values of the basin population of V₁(Cα,Cβ) and V₂(Cα,Cβ) are 1.48e and 1.65e, respectively. The process of their saturation, through steps VIII–X, continues until maximum values of 1.77e and 1.79e are obtained for the KAPh molecule (see Table 1).

The formation of the C2–Cγ bond, between the phenyl and allyl groups, is observed in step VIII for the r(O⋯Cα) and r(C2⋯Cγ) distances of 2.358 Å and 2.053 Å, respectively and reaction coordinates s = 1.182 (amu)^1/2 Bohr. In the cusp catastrophe (C) two valence attractors associated with monosynaptic basins V(C2), V(Cγ) and a single CP of index 1 are annihilated yielding a new attractor V(C2,Cγ). The number of attractors decreases to 33. From the chemical point of view, the observed rearrangement of the ELF-basins is very important – it is evident that a covalent bond between the C2 and Cγ atoms has been formed. Thus, the allyl group and the phenyl ring have been “put together”. After the cusp the basin population of V(C2,Cγ) is equal to 0.97e and increases to 1.06e and 1.27e in steps IX and X, respectively, with a maximum of 1.78e for KAPh with the geometrical structure optimized to the energy minimum.

Two last steps, IX and X, characterize the formation of two double bonds C3=C4, C2′=C3′ in an initially fully aromatic phenyl ring. It is worth noting that the signs of dearomatisation of the phenyl ring – visible in topology of ELF – are observed just at the end of the Claisen rearrangement. The electron density delocalized in the phenyl ring is concentrated in the C3=C4 and C2′=C3′ bonds and this process is associated with a local change of electron localization and finally with the change of the ELF-topology. Two catastrophes of the cusp type (C⁺) are observed for s = 1.409 (IX) and 1.827 (X) (amu)^1/2 Bohr, which correspond to the r(O⋯Cα) and r(C2⋯Cγ) distances of 2.381, 2.002 Å and 2.439, 1.891 Å, respectively. The double bond C3=C4 exhibits the topology of the ELF with two bonding basins V_i=1,2(C3,C4) for 1.361 Å and the C2′=C3′ bond with two V_i=1,2(C2′,C3′) basins for 1.359 Å, thus both bond lengths are very similar. It is also worth noting that first in step IX the V_i=1,2(C3,C4) basins are formed for the bond that is separated by only one single C2–C3 bond from the allyl group. The C2′=C3′ bond is formed in the last step X and that bond is separated from the allyl group by two single bonds C1–C2 and C1–C2′. Dearomatisation of the ring results from the electron density redistribution which proceeds (see Scheme 3) mainly from the C1–C2′, C3′–C4 and C2–C3 bonds. The value of the basin population for the newly created C3=C4 bond is 1.66e (both basins) and for C2′=C3′ is 1.64e (V₁(C2′,C3′)) and 1.66e (V₂(C2′,C3′)).

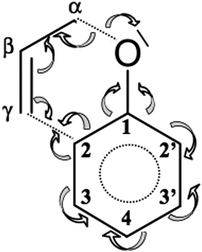Scheme 3 Redistribution of electron density during Claisen rearrangement of allyl phenyl ether obtained from topological analysis of the ELF.

From the perspective of ELF-analysis the formation of the product of the Claisen reaction of APhE, that is, the ketonic form of the o-allylphenol, has been terminated in step X. The Lewis-like formula for the KAPh, obtained on the basis of the topology of the ELF (see Fig. 4), is very similar to the Lewis structure drawn on the basis of the assumption that carbon and oxygen atoms achieve a valence shell electron configuration with a full octet of electrons and hydrogen with a doublet of electrons. The difference is found for the carbon–oxygen bond that is formally represented by the double C=O bond, meanwhile the topological analysis of the ELF exhibits only one V(C1,O) attractor and basin. Thus, the carbon–oxygen bond is much polar than suggested by the Lewis structure and at least three resonance hybrids should be used: C–O, C⁺O⁻ and C⁻O⁺. In effect the C–O bond in step X (see Fig. 4) is represented only by a single line. In the valence space of the oxygen atom two non-bonding basins of oxygen, V₁(O) and V₂(O), are observed with a total basin population of 5.29e.

3c. Analysis of the reaction mechanism using the DFT (M052x) method

The changing location of the V₂(O) and V(Cα) attractors, observed for the points on the IRC path in step II, may be related to the electron density functional and the basis set used in the calculations. Therefore, an analysis has been repeated using the DFT (M052x) method and the 6-311G(d) basis set. 459 points on the IRC path, from the TS towards the substrate (APhE), have been analyzed with a step of 0.01 (amu)^1/2 Bohr. The analysis of the ELF for the isolated APhE molecule shows different topology than obtained using the DFT (B3LYP) method. In the region of non-bonding electron density of oxygen two monosynaptic non-bonding basins V_i=1,2(O) have been localised with a population of 2.35 and 2.50e. Two non-bonding basins and two bonding basins, V(C1,O) and V(Cα,O), associated with the oxygen atom correspond to the sp³ hybridisation of atomic orbitals and support the Lewis structure of APhE. The electronic structure of the TS is very similar to that obtained using the B3LYP functional with a characteristic non-bonding attractor V(C2) with a basin population of 0.25e.

The picture of the Cα–O bond dissociation is less complicated than that obtained using the DFT (B3LYP) method. The topological analysis of the ELF, performed for the points on the IRC path, shows five domains of structural stability (see Fig. 5). Structures IIa and IIb, which reflect delocalisation of the bonding pair between the Cα and O atoms (B3LYP), have not been observed. The heterolytic cleavage of the Cα–O bond is characterised in step I by annihilation of the disynaptic V(Cα,O) attractor and the appearance of a new monosynaptic attractor V₃(O). Unfortunately, the change of the topology of the ELF associated with bond lengthening is complicated hence the exact position and type of catastrophe on the IRC path could not be obtained. It is worth noting that the V₃(O) basin is localised between the C(Cα) and C(O) core basins, and not in the position of the V₂(O) attractor, as it was shown by analysis using the B3LYP functional. This issue suggests that both computational methods exhibit different details of evolution of the electronic structure of the Cα–O bond. The V₃(O) attractor is annihilated in step III for the Cα⋯O distance of 1.816 Å. The non-bonding attractor V(C2) that reflects the beginning of the formation of the C2–Cγ bond, is observed for the TS for the C2⋯Cγ distance of 2.159 Å. The analysis of the DFT (M052x) data supports and complements the description of the mechanism of the C–O bond breaking obtained using the DFT (B3LYP) method. However, it should be considered that the number and synaptic type as well as localisation in space of valence basins associated with the C–O bond breaking may depend on the used DFT functional.

Fig. 5 The Lewis-like structures representing the chemical bonds, lone pairs and regions with non-bonding electron density for five steps of the Claisen rearrangement of allyl phenyl ether. The results obtained at the DFT(M052x)/6-311G(d) computational level.

4. Conclusions

The application of Bonding Evolution Theory for the DFT (B3LYP) and DFT (M052x) data allowed us to explain precisely the mechanism of the Claisen rearrangement of allyl phenyl ethers in real space without using the concept of molecular orbitals in Hilbert space. The process of bond breaking and bond formation during transformation of APhE to KAPh has been clearly characterized.

The reaction consists of 10 main steps (B3LYP) and each step may be characterized as follows: at first the chemical bond Cα–O is broken (step IIa, IIb), the remains of the Cα–O bond, that is, the non-bonding V(Cα) basin, is annihilated as a result of the transfer of the electron density to the Cα–Cβ bond (step III), the double bond Cβ=Cγ in the allyl group is “reduced” to the single bond Cβ–Cγ as a result of the transfer of electron density to the Cα–Cβ and C2⋯Cγ regions (step IV), starts the “construction” of the C2–Cγ bond between the allyl group and the phenyl ring through the formation of the V(C2) basin (step V), the “construction” of the C2–Cγ bond continues through the formation of the second V(Cγ) basin (step VI), the double bond Cα=Cβ in the allyl group is formed (step VII), the C2–Cγ bond between the allyl group and the phenyl ring is formed (step VIII), the first stage of the dearomatisation of the phenyl ring starts through the formation of the localized C3–C4 bond (step IX), the dearomatisation of the phenyl ring continues through the formation of the second localized C2′–C3′ bond in the phenyl ring and this step ends the Claisen rearrangement of APhE. The BET analysis performed for the M052x data (IRC from the TS to APhE) also shows five steps of the reaction and a very similar topology of the ELF for the TS.

The breaking of the carbon–oxygen bond from the ELF-perspective is a complicated process that depends on the DFT functional used. For a number of points on the IRC path the DFT (B3LYP) calculations show the fluctuating electron density between C and O atoms (started in a step I and clearly visible in a step II). Such a mechanism seems to be correctly represented by two formal resonance hybrids with a heterolytically broken bond, C⁺O⁻, C⁻O⁺. The application of the M052x functional yields a simpler picture where the breaking of the C–O bond causes the formation of the non-bonding monosynaptic basin V₃(O). Those results show that the choice of the DFT functional may be crucial for the qualitative description of the breaking of the carbon–oxygen bond.

Finally, we may answer the questions posed at the beginning of our paper. (1) The redistribution of the electron density in APhE is not as simple as usually depicted (see Scheme 1). The formation of a new bond requires a supply of electron density, usually from neighbouring bonds, thus the picture of the electron flow is very complicated (see Scheme 3). (2) Given that the term “synchronous mechanism” refers to breaking and formation of the chemical bonds at the same moment of the reaction path (for instance in the TS), our study shows that in the case of the Claisen rearrangement of APhE the mechanism is asynchronous. In the transition structure (step V) the new C2–Cγ bond between the allyl group and the phenyl ring is not yet formed but the Cα–O bond is already entirely broken (step III). The process of concentrating the electron density in the C2⋯Cγ region continues and in the vicinity of the Cα core the degree of electron localization is high enough to observe the local attractor V(Cα) and its basin. (3) The double C=C bonds in the six-membered ring are formed in the final steps of the reaction after the Cα–O bond is broken, the C=C bond in the allyl group is translated to another position and the C2–Cγ bond is formed.

The presented picture of the evolution of chemical bonds in the Claisen rearrangement of APhE rules out a pericyclic mechanism, because the electron density flow does not take place in a cyclic, one-way curve. In this context a recent study by Domingo^54,55 who also refuted the pericyclic mechanism for the Diels–Alder reaction between ethylene and butadiene is worth mentioning.

Acknowledgements

The authors gratefully acknowledge the Wroclaw Centre for Networking and Supercomputing (WCSS) for the allocation of computer time on the BEM Cluster and also the Academic Computer Centre in Gdańsk (CI TASK) for the allocation of computer time on the Tryton Cluster. The Marie Curie European Reintegration Grant supported the work of S.B. – contract No. MERG-CT-2004-006330. “The authors are solely responsible for the information communicated and it does not represent the opinion of The European Community. The European Community is not responsible for any use that might be made of data appearing therein”. Special thanks to Piotr Skoluda for editing this document.

References

1. A. M. Martin Castro, Chem. Rev., 2014, 104, 2939.
2. L. Claisen, Chem. Ber., 1912, 45, 3157.
3. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.
4. B. Silvi and A. Savin, Nature, 1994, 371, 683.
5. A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088.
6. B. Silvi, J. Mol. Struct., 2002, 614, 3.
7. A. Savin, THEOCHEM, 2005, 727, 127.
8. A. Savin, J. Chem. Sci., 2005, 117, 473.
9. R. Thom, Stabilité Structurelle et Morphogénèse, InterEditions, Paris, 1972.
10. D. Roca-López, V. Polo, T. Tejero and P. Merino, Eur. J. Org. Chem., 2015, 4143.
11. D. Roca-López, V. Polo, T. Tejero and P. Merino, J. Org. Chem., 2015, 80, 4076.
12. V. Polo and J. Andrés, J. Comput. Chem., 2005, 26, 1427.
13. I. M. Ndassa, B. Silvi and F. Volatron, J. Phys. Chem. A, 2010, 114, 12900.
14. X. Krokidis, S. Noury and B. Silvi, J. Phys. Chem. A, 1997, 101, 7277.
15. X. Krokidis, B. Silvi and M. E. Alikhani, Chem. Phys. Lett., 1998, 292, 35.
16. X. Krokidis, B. Silvi, C. Dezarnaud-Dandine and A. Sevin, New J. Chem., 1998, 22, 1341.
17. X. Krokidis, R. Vuilleumier, D. Borgis and B. Silvi, Mol. Phys., 1999, 96, 265.
18. S. Yamabe, S. Okumoto and T. Hayashi, J. Org. Chem., 1996, 61, 6218.
19. O. Wiest, K. A. Black and K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10336.
20. M. J. S. Dewar and C. Jie, J. Am. Chem. Soc., 1989, 111, 511.
21. M. M. Davidson, I. H. Hillier and M. A. Vincent, Chem. Phys. Lett., 1995, 246, 536.
22. H. Y. Yoo and K. N. Houk, J. Am. Chem. Soc., 1994, 116, 12047.
23. M. P. Meyer, A. J. DelMonte and D. A. Singleton, J. Am. Chem. Soc., 1999, 121, 10865.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004.
25. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
26. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
27. K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
29. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724.
30. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
31. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213.
32. P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209.
33. M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163.
34. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654.
35. R. C. Binning Jr and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206.
36. J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016.
37. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223.
38. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976.
39. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193.
40. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081.
41. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009.
43. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
44. K. Fukui, J. Phys. Chem., 1970, 74, 4161.
45. K. Fukui, Acc. Chem. Res., 1981, 14, 363.
46. S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597.
47. ChemCraft, version 1.7, G. A. Andrienko, http://www.chemcraftprog.com.
48. B. Gómez, P. K. Chattaraj, E. Chamorro, R. Contreras and P. Fuentealba, J. Phys. Chem. A, 2002, 106, 112227.
49. A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088.
50. S. Noury, F. Colonna, A. Savin and B. Silvi, J. Mol. Struct., 1998, 450, 59.
51. B. Silvi, Phys. Chem. Chem. Phys., 2004, 6, 256.
52. S. Noury, F. Colonna, A. Savin and B. Silvi, J. Mol. Struct., 1998, 450, 59.
53. B. Silvi, J. Mol. Struct., 2002, 614, 3.
54. L. R. Domingo, Org. Chem.: Curr. Res., 2013, 2, 120.
55. L. R. Domingo, RSC Adv., 2014, 4, 32415.

---