Structure, formation, thermodynamics and interactions in 9-carboxy-10-methylacridinium-based molecular systems

Abstract

9-Carboxy-10-methylacridinium chloride and trifluoromethanesulfonate, the parent compounds for a wide range of chemiluminogenic salts of practical importance, were synthesized and thoroughly investigated to address problems concerning structural and thermodynamical issues of these cognitively interesting molecular systems. Under various conditions of crystallization, the title salts disclosed three types of crystals: one built from the monomeric form of cations and two containing homoconjugated cations. The title compounds made the first described derivatives of acridine, expressing homoconjugated cationic forms, both in crystalline solid and gaseous phases. The monocrystals were characterized, employing X-ray crystallography and spectroscopic methods such as MALDI-TOF MS, ESI-QTOF MS, NMR and UV-Vis. X-ray crystallography studies revealed the occurrence of the three different molecular architectures, in which not only the counter ions and stoichiometry are different, but also the space group and number of molecules in the unit cell. The energetics and intermolecular interactions occurring within the crystals were explored, applying crystal lattice energy calculations and Hirshfeld surface analysis. In order to elucidate the thermodynamics and origin of the experimentally revealed forms, computations based on the density functional theory were performed, assuming vapour and liquid phases.

---

Introduction

Derivatives of acridine-9-carboxylic acid (ACA) are a widely investigated and applied group of compounds, due to their ability for effective luminescence in aqueous and organic environments,^1–4 as well as their interesting physicochemical properties.^5–7 ACA, the parent molecule in this family of compounds, makes a simple heteroaromatic system, differing from its hydrocarbon analogue, anthracene-9-carboxylic acid, by the presence of an electron-attracting nitrogen atom in the central aromatic ring at the para position to the carboxyl group. The endocyclic N atom present in ACA causes a slight change in the π-electronic energy levels, as compared to those in anthracene-9-carboxylic acid, and diminution of charge transfer from the aromatic ring system to the carboxyl fragment.⁵ Theoretical studies carried out on the ACA molecule indicated that in the ground state, the carboxyl group is oriented at an angle of about 55° relative to the plane of the acridine moiety, while in the excited state (S₁), the –COOH fragment twists, which is accompanied by the flattening of the molecular arrangement.⁵ In the aqueous liquid phase, ACA, in addition to its neutral form, may appear as zwitterions or monocations, depending on the acidity of the environment.⁵

The compounds under study, containing the N-methylated ACA moiety, are the simplest and oldest acridinium derivatives investigated in the context of the chemiluminescence phenomenon.⁸ 9-Carboxy-10-methylacridinium cations (CMA) form the structural base of a wide range of chemiluminogenic compounds that have been widely employed as labels and indicators, specially designed molecular systems utilized in medical diagnostics and trace analysis.⁹ However, derivatives of CMA are also interesting from the cognitive point of view. CMA, similar to ACA and related molecular systems, can occur in liquid phases in various forms, depending on the degree of their ionization.¹⁰ The structural similarity of CMA to betaines and isonicotinic acids is an intriguing fact in the context that the latter compounds are able to interact effectively with biological molecules through the formation of complexes, or by a wide range of short-range interactions.¹¹ Like other carboxylic acids, molecules of CMA are prone to the formation of H-bonded forms involving the carboxyl group, which opens up opportunities for the molecules to occur in various structural forms.

The molecular architecture and the intermolecular interactions occurring in various phases in the group of quaternary salts containing 9-carboxy-10-methylacridinium or hydrogen bis(9-carboxy-10-methylacridinium) cations and chloride or trifluoromethanesulfonate (triflate) anions, were the main tasks of the presented work. The abovementioned molecular systems adopt various crystalline forms, denoted as 1, 2 and 3, which contain structural moieties that originate from CMA chemiluminogenic salts of practical importance.^1,9 We focused primarily on the investigation of various crystalline forms with the participation of CMA, since we were interested in the number of structural variants and under what conditions they appear in solid, gaseous and liquid phases. We assumed that an extensive analysis of the structural problems concerning CMA-based cationic forms would be helpful in disclosing the factors determining the chemical and physicochemical properties of a wide range of related acridinium salts. Since CMA makes one of the products secreted upon chemiluminescence of acridinium esters and sulphonamides, the structural study presented here may also shed some light on the mechanism of this complicated process, which has been studied by us for a long time.^2,12,13 In this work we employed a broad set of experimental methods, such as single crystal X-ray crystallography and spectroscopic techniques including UV-Vis, ¹H and ¹³C NMR, MALDI-TOF and ESI-QTOF mass spectrometry. Moreover, we also applied various theoretical tools, such as determination of Hirshfeld surfaces, calculation of crystal lattice energies, as well as computations at the level of density functional theory (DFT). All these approaches provided us with a chance to take a deep look at the intermolecular interactions occurring among neighboring fragments of molecules and cations in various forms, energetics of cohesion forces in crystals and the “molecular shapes”, characteristic of crystalline solid phases. Quantum chemistry calculations disclosed information concerning structural and thermodynamic aspects of the investigated compounds, their stabilities in the gaseous and liquid phases and enabled us to propose a pathway leading to the formation of the CMA-based molecular systems described here.

Experimental

Single crystal X-ray diffraction analysis and refinement

Two acridinium salts, namely 9-carboxy-10-methylacridinium chloride (CMACl) and 9-carboxy-10-methylacridinium trifluoromethanesulfonate (CMATfO), were prepared and analysed for chemical identity, as given in ESI.† The compounds were subjected to crystallization under various conditions; CMACl was dissolved in DI water (UP class), acidified with HCl and the solution was heated to boiling, then cooled to 298 K and left aside for gradual evaporation of the solvent, resulting in the crystals of the compound 1, namely, 9-carboxy-10-methylacridinium chloride dihydrate. In addition, CMACl was dissolved in an ethanol/water phase (1/9 v/v) and left at 298 K to enable the growth of crystals of the compound 2, namely hydrogen bis(9-carboxy-10-methylacridinium) chloride dihydrate, for X-ray diffraction studies. Similarly, CMATfO was dissolved in an ethanol/water mixture (1/9 v/v), filtered and left aside at room temperature to obtain good quality crystals of hydrogen bis(9-carboxy-10-methylacridinium) trifluoromethanesulfonate (3).

Diffraction measurements were performed using an Oxford Diffraction Gemini R ULTRA Ruby CCD diffractometer with MoKα (λ = 0.71073 Å) radiation. Data collection and cell refinement were carried out with CrysAlis CCD and data reduction with CrysAlis RED software,¹⁴ applying multiscan absorption corrections (empirical absorption correction based on spherical harmonics, implemented in the SCALE3 ABSPACK scaling algorithm). The SHELXS-97 package was used to solve the structures by direct methods, and SHELXL-97 to carry out refinements by full-matrix least-squares on F².¹⁵ The H-atoms bound to carboxylic oxygen atoms in 2 and 3 were located in a Fourier-difference map and refined freely with occupancy factors of 0.5. The H-atom bound to carboxylic oxygen atom in 1 was located in a Fourier difference map and refined as riding with U_iso(H) = 1.5U_eq(O). In all cases, the water H atoms were located in a Fourier-difference map, restrained by DFIX command 0.85 for O–H distances and by DFIX 1.39 for H⋯H distances and refined as riding with U_iso(H) = 1.5U_eq(O). All other H-atoms were positioned geometrically, with C–H = 0.93 Å and 0.96 Å for the aromatic and methyl H-atoms, respectively, and constrained to ride on their parent atoms with U_iso(H) = xU_eq(C), where x = 1.2 for the aromatic H-atoms and x = 1.5 for the methyl H-atoms. All interactions demonstrated were found by PLATON program.¹⁶ To prepare molecular graphics, ORTEPII,¹⁷ PLUTO-78¹⁸ and Mercury¹⁹ programs were employed.

Crystal lattice energies

The lattice energies (E_L), reflecting the global energetics of interactions within crystals, were obtained using X-ray structures of investigated compounds 1–3. We performed calculations employing the General Utility Lattice Program (GULP, version 4.0), which is based on the force field methods approach.²⁰ The GULP computations allow for evaluation of the lattice energy as the sum of three components: the energy of the long-range Coulomb interactions (E_el) and energies of the dispersive (E_d) and repulsive (E_r) interactions (eqn (1)):

E_L = E_el + E_d + E_r (1)

The Coulomb energy was calculated according to the expression given by Coulomb's law. Relative atomic partial charges, necessary for prediction of E_el values, were obtained at the density functional theory (DFT) level²¹ by reproducing the electrostatic potential around the molecules (ESP fit charges).²² DFT single-point computations were conducted in the gas phase for aggregates of molecules preserving their geometries and their relative arrangement, as in the crystal phase. In these calculations, the M06-2X functional²³ was employed, together with the 6-31++G** basis set.²⁴ Calculations were carried out using the Gaussian 09 program.²⁵ Two-body short-range interactions, contributing as E_d and E_r terms to the lattice energy, were described by the Buckingham potential available within GULP (eqn (2)):

−C₆/R⁶ + A exp(−R/ρ) (2)

In the above expression, C₆, A and ρ denote the atomic parameters for the pairs of interacting atoms and R represents the interatomic distances between atoms in the reference cell and atoms in the neighbouring cells. Potential parameters describing interactions involving the F atom were obtained from a report by Mayo et al.,²⁶ whereas parameters for the remaining atoms were obtained from a report by Filippini et al.²⁷ Such an approach was demonstrated to be successful in the prediction of the sublimation energies for related acridinium derivatives.^7,28

Hirshfeld surface analysis

The investigation of packing modes and intermolecular interactions in crystals was carried out using Hirshfeld surfaces to partition the crystal space. Hirshfeld surfaces and fingerprint plots facilitate the comparison of intermolecular interactions in building different supramolecular motifs in the crystal structure. Molecular geometries, taken directly from resolved crystal structures of 1–3, were used for generating the Hirshfeld surfaces and two-dimensional fingerprint plots with the assistance of the Crystal Explorer 3.1 program.²⁹ Complementary two-dimensional mappings, which quantitatively summarize the types of intermolecular contacts experienced by chemical entities in the bulk are also presented.

Spectroscopic measurements

¹H and ¹³C NMR spectra for compounds 1–3 in deuterium oxide, dimethyl sulfoxide-d₆, acetonitrile-d₃ and methanol-d₄ were recorded at room temperature using a Varian Unity 500 Plus spectrometer with a 5 mm PFG probe attached. Additionally, molecular systems presenting various forms in the solid crystalline phase (1 and 2), were subjected to ¹H NMR experiments in CD₃OD at standard (298 K) and lowered temperature (233 K). The signals of protons in ¹H NMR spectra were assigned with the aid of ¹H–¹H COSY spectra and the carbon-13 signals were assigned with the assistance of ¹H–¹³C HETCOR (ghmbc) spectra and ACD HNMR/CNMR software,³⁰ respectively. The NMR data are summarized in Table S1 (ESI†) and selected spectra are presented in Fig. S2 and S3 (ESI†).

The mass spectra of 1–3 were recorded employing a Biflex III MALDI-TOF mass spectrometer, working in the positive polarity mode with the 150–600 m/z scan range and the attenuation of the laser beam set at 60%. The samples of 1–3 (3–5 mg) were dissolved in the solution of dihydroxybenzoic acid (DHBA) in water. Additionally, samples of 1–3 were dehydrated (denoted as 1dh, 2dh, 3dh) and dissolved in a non-aqueous matrix (DHBA/anhydrous acetonitrile) and the above mixtures were also subjected to MALDI-TOF MS experiments. Results obtained for 1, 2 and 3 and 1dh, 2dh, 3dh are summarized in Tables S2 and S3 (ESI†), and exemplary mass spectra are presented in Fig. S2 (ESI†).

The ionization constant (pK_a), denoting protolytic dissociation of the monocationic (c) to zwitterionic (z) form of 1 (K_a = [1z][H₃O⁺]/[1c]) was obtained by spectrophotometric acid–base titration at 298 K in water–ethanol (9 : 1, v : v) solutions (Table S4 and Fig. S3, ESI†). To a stirred solution of 1 (2.00 ml, 2.50 × 10⁻⁵ M) in DI H₂O (UP-grade), concentrated hydrochloric acid was gradually added in 10–100 μl portions until the final volume of 4.00 ml was attained. The actual pH of the mixtures with c(HCl) <0.1 M was determined using a portable pH-meter (GPX-105s, Elmetron, Poland). The acidity constants (H₀) were determined instead of pH for the highly acidic mixtures,^31,32 using the mass concentration of HCl in the cell, established gravimetrically after each addition. The electronic absorption UV-Vis spectra for each solution were recorded using a Lambda 40 UV-Vis spectrophotometer (Perkin-Elmer, USA) in the range of 300–500 nm (slit = 1 nm). The registered spectra were multiplied by the dilution coefficient d (d = V_i/V₀, where V_i is the volume of the actual solution, in ml; V₀ is the volume of the starting solution, 2.00 ml). To calculate the values of pK_a by monitoring changes in absorbance at selected wavelengths, the Henderson–Hasselbalch equation, implemented in Spectra Data Lab software,³³ was applied. This method relates pH and pK_a to the equilibrium concentrations of dissociated [A⁻] and non-dissociated form [HA] of the acid, according to the following equation (eqn (3)):³⁴

pH = pK_a + log([A⁻]/[HA]) (3)

The medium effects associated with the high content of acid in concentrated HCl solutions were corrected according to the Haldna method.³⁵

Computations

Unconstrained geometry optimizations of isolated cations and their dimeric forms involved in 1–3 complexes with counter ions (Cl⁻, CF₃OSO₂⁻) and water molecules were carried out at the DFT level of theory²¹ using gradient techniques³⁶ and the 6-31G** basis set.³⁷ The calculations were carried out with the B3LYP functional, in which Becke's nonlocal exchange³⁸ and the Lee–Yang–Parr correlation functionals³⁹ were applied. After completion of each optimization, the Hessian (second derivatives of the energy as a function of the nuclear coordinates) were calculated to assess whether stationary structures had been obtained.^21,37b The harmonic vibrational frequencies were then derived from the numerical values of these second derivatives and used to obtain the Gibbs' free energy contributions at 298.15 K and standard pressure with the aid of a built-in computational program of statistical thermodynamics routines.⁴⁰ All quantum chemical calculations were performed using Gaussian 09²⁵ program, while the plots showing the molecular structures were generated with the aid of the ChemCraft program.⁴¹

Results and discussion

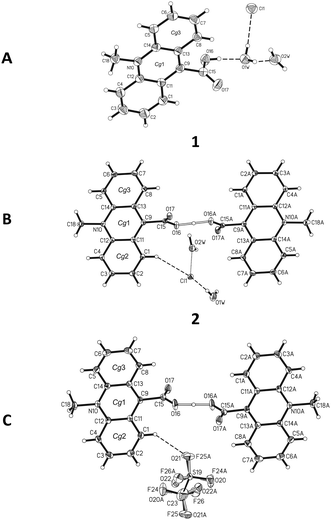
Crystal architecture riddles

9-Carboxy-10-methylacridinium chloride dihydrate (1). Compound 1, whose molecular structure is depicted in Fig. 1A, crystallizes in the monoclinic P2₁/n space group with four ion pairs and eight water molecules in the unit cell (Table S5, ESI†). The bond lengths and angles characterizing the geometry of the acridine moiety in 1, are similar to other already reported salts.^42–48 The acridine ring system is almost planar (the average deviation from planarity is 0.0239(3) Å), while the carboxyl group is twisted at an angle of 89.6(1)°, relative to the acridine skeleton. The mean planes of adjacent acridinium moieties are either parallel or inclined at an angle of 25.5(1)° in the crystal lattice. The packing of ions and water molecules in 1 is affected by O–H⋯O, O–H⋯Cl and π–π stacking intermolecular interactions and contacts (Fig. 1, 2 and Fig. S4, Tables S6, S7, ESI,† CCDC 981470). The carboxylic hydrogen atom involved in each cation interacts with one water molecule through the O–H⋯O hydrogen bond (length 2.471(3) Å). The water molecule linked to the cation is further H-bonded to another water molecule and chloride anion, with lengths of 2.666(4) and 3.041(2) Å, respectively. Each water molecule not directly H-bonded to the cation participates in O–H⋯Cl hydrogen bonding with two chloride anions (lengths 3.121(3) and 3.133(3) Å). The above described interactions are infinitely repeated and result in a ladder-like chain running along the [010] direction (Fig. 2A). Three water molecules and two chloride anions, participating in the above-mentioned chains, are arranged in characteristic five-membered rings of the R₅³(10) motif. Inversely oriented parallel chains are tied together in the sheet, formed by the intermolecular π–π stacking interactions between adjacent acridinium moieties (Fig. 2B). The crystal lattice of 1 is further stabilized by non-specific dispersive interactions between inversely oriented parallel sheets (Fig. 2C).

Fig. 1 The molecular structure of crystalline compound 1 (structure A), 2 (structure B) and 3 (structure C) showing the atom labeling scheme. Displacement ellipsoids are drawn at the 25% probability level and H-atoms are shown as small spheres of arbitrary radius. Cg1 and Cg2 and Cg3 denote the ring centroids. The O–H⋯O, O–H⋯Cl, O–H⋯Cl, C–H⋯Cl hydrogen bonds and O⋯Cl contacts are represented by dashed lines.

Fig. 2 The supramolecular architecture in the crystal of 1: (A) the ladder-like chain running along the [010] direction; (B) the single layer stabilized by the π–π stacking interactions between aromatic rings of adjacent acridinium moieties; (C) the global framework of ions and water molecules in the crystal in parallel sheets. [Symmetry codes: (i) −x + 1/2, y − 1/2, −z + 3/2; (ii) x, y − 1, z; (iii) −x, −y, −z + 1; (iv) −x, −y + 1, −z + 1.]

Hydrogen bis(9-carboxy-10-methylacridinium)chloride dihydrate (2). Compound 2, whose molecular arrangement is demonstrated in Fig. 1B, crystallizes in the monoclinic P2₁/n space group with two ion pairs and four water molecules in the unit cell (Table S5, ESI†). In the homoconjugated cation of hydrogen bis(9-carboxy-10-methylacridinium) involved in this compound, symmetric O–H⋯O hydrogen bonding occurs (length 2.435(3) Å), in which the H-atom is located directly in the inversion centre. The chloride anion is found in two spatial positions, related by the inversion centre, with site occupancy factors of 0.5. The bond lengths and angles characterizing the geometry of the acridine moieties in the cation are characteristic of acridinium salts.^42–48 The two acridine ring systems are almost planar (the average deviation from planarity is 0.0311(3) Å) and parallel (0.0(0)°). The carboxyl groups are twisted at an angle of 84.8(1)° with respect to the relevant acridine skeletons. Acridinium moieties of adjacent cations are either parallel (remain at an angle of 0.0(1)°) or inclined at an angle of 23.6(1)°. The predominant role in the packing of ions and water molecules in the crystals of 2 is played by O–H⋯Cl, C–H⋯O, C–H⋯Cl, π–π and Cl⋯O intermolecular interactions and contacts (Fig. 1, 3 and Fig. S5, Tables S8–S10, ESI,† CCDC 981472). Each homoconjugated cation links two chloride anions via C–H⋯Cl interactions (lengths 3.560(3) and 3.735(3) Å). In turn, each chloride anion interacts with two water molecules by O–H⋯Cl hydrogen bonds (lengths 2.904(2) and 2.937(3) Å) and with one water molecule via O⋯Cl contact. Water molecules interact with neighbouring water molecules via O–H⋯O hydrogen bonds (length 2.820(4) Å), while cations interact by O–H⋯O (carbonyl) (length 3.117(4) Å) and C–H⋯O (length 3.519 Å) bonds. Repetition of some of the above described O–H⋯O, O–H⋯Cl and C–H⋯Cl interactions brings about the formation of infinite chains of ions and water molecules running along the [010] direction (Fig. 3A). Parallely oriented chains are tied by π–π stacking interactions between aromatic rings of adjacent acridinium moieties (Fig. 3B) and C–H⋯Cl hydrogen bonds between the H-atoms of methyl groups of cations and chloride anions into a sheet spread out in the [110] plane. Alternately oriented sheets constitute the crystal lattice of 2, which is stabilized by the network of Cl⋯O contacts between chloride anions and water molecules, as well as C–H⋯O interactions involving H-atoms of the acridinium fragments and water molecules (Fig. 3C).

Fig. 3 The supramolecular architecture in the crystal structure of 2: (A) complex chain built of ions and crystal water molecules running along the [010] direction; (B) single layer stabilized by the π–π stacking interactions between rings of neighboring acridinium moieties spread out in the [110] plane; (C) inversely oriented sheets linked by the network of O⋯Cl contacts between chloride anions and water molecules [symmetry codes: (i) x, y + 1, z; (ii) −x + 2, −y, −z + 1; (iv) −x + 1, −y + 1, −z + 1; (v) −x + 1, −y, −z + 1; (vi) −x + 3/2, y − 1/2, −z + 1/2].

Hydrogen bis(9-carboxy-10-methylacridinium)trifluoromethane-sulfonate (3). Compound 3, whose molecular structure is demonstrated in Fig. 1C, crystallizes in the triclinic P1̄ space group with one ion pair in the unit cell (Table S5, ESI†). In the homoconjugated hydrogen bis(9-carboxy-10-methylacridinium) cation found in this compound, similar to some other acid salts of carboxylic acids,^49–52 symmetric O–H⋯O hydrogen bonding occurs, in which the H-atom is located directly in the inversion centre (length 2.449(2) Å). The triflate anions (CF₃OSO₂⁻) occupy two positions, with occupancy factor of 0.5 for S19, O21–22, C23, F24–26 and S19A, O21A–O22A, C23A, F24A–F26A, related to the inversion centre. The bond lengths and angles, characterizing the geometry of the acridinium moieties in the cation, are similar to other acridinium-based derivatives.^42–45 Two acridine ring systems in the cation are almost planar (the average deviation from planarity is 0.0505(3) Å) and parallel (0.0(0)°). The carboxyl groups are twisted at an angle of 84.2(1)° relative to the relevant acridine skeleton. Acridinium moieties of adjacent cations are parallel in the crystal lattice, remaining at an angle of 0.0(1)°.

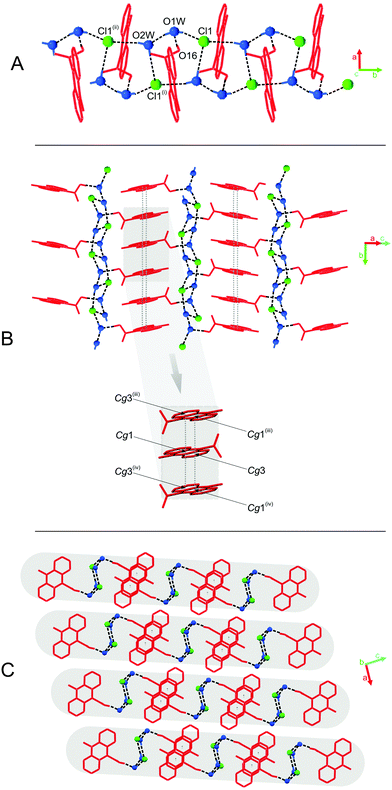
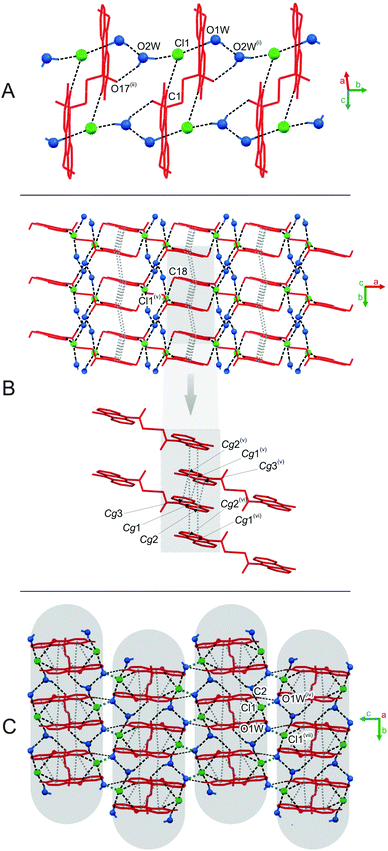
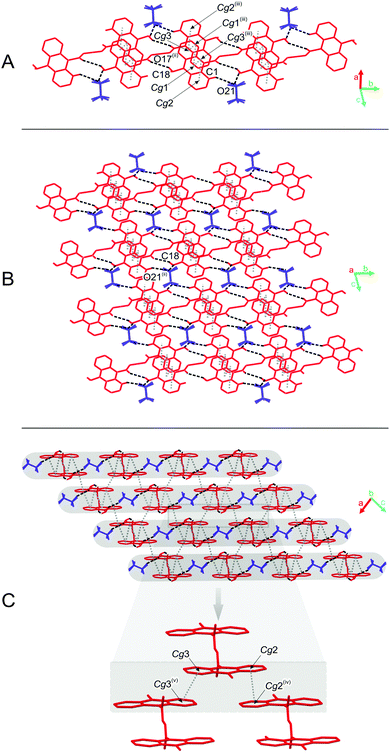
The predominant role in the packing of ions in the crystal of 3 is played by C–H⋯O and π–π intermolecular interactions (Fig. 1, 4 and Fig. S6, Tables S11 and S12, ESI,† CCDC 981471). Each homoconjugated cation interacts with neighbouring cations and anions through weak C–H⋯O hydrogen bonds involving the methyl H-atom and carbonyl oxygen atom (length 3.199 Å) or methyl or acridine skeleton H atoms and O atoms of triflate anions (lengths of 3.360(20) and 3.370(30) Å, respectively).

Repetition of the above mentioned C–H⋯O interactions brings about the formation of endless chains of ions running along the [001] direction (Fig. 4A). Parallely oriented chains are linked by the network of C–H⋯O (involving methyl H atoms and O atoms of anions) and π–π intermolecular interactions (between aromatic rings of neighbouring acridinium moieties) forming layers spreading along the (011) plane (Fig. 4B). Parallely oriented layers are stabilized by the network of π–π intermolecular interactions between aromatic rings of adjacent acridinium moieties, which results in the formation of a continuous multi-layered framework of ions in the crystal (Fig. 4C).

Fig. 4 Supramolecular architecture in the crystal of 3: (A) infinite chain built of homoconjugated cations and anions running along [010] direction; (B) single layer of ions spread out in [101] plane; (C) multilayered framework of ions [symmetry codes: (ii) x, y − 1, z; (iii) −x + 2, −y + 1, −z; (iv) −x + 2, −y + 1, −z + 1; (v) −x + 3, −y + 1, −z].

Cambridge structural database analysis of O–H⋯O hydrogen bond. To have an insight on how the geometric parameters of O⋯H⋯O hydrogen bonds occurring in homoconjugated hydrogen bis(9-carboxy-10-methylacridinium) cations involved in compounds 2 and 3 relate to those in other compounds containing ions of such type, we carried out a search in the Cambridge Structural Database (version 5.32) using the program CONQUEST. The geometrical query with the limiting criteria of no polymeric structures, no errors, no powder structures and only organics with 3D coordinates determined, is depicted in Fig. S7 (ESI†). Among 25 structures found, 23 possessed the hydrogen atom placed strictly in the middle of the O⋯H⋯O interaction (DIST1 = DIST2). Among the homoconjugated cations found, only 3 represented nitrogen-containing heteroaromatic systems.

The scattergrams correlating lengths of hydrogen bonds (DIST1 and DIST2) and histograms imaging the distribution of the O⋯O distances (DIST3) in homoconjugated cations of 23 aromatic carboxylic systems are demonstrated in Fig. S8 (ESI†). Analysis of the data stored in the Cambridge Structural Database and summarized in the figures discloses that the lengths of the symmetrical O⋯H⋯O hydrogen bonds span from 1.21 to 1.24 Å, and O⋯O distances from 2.422 to 2.480 Å. The hydrogen bond lengths and O⋯O distances in 2 and 3, equal to 1.22, 1.22 and 2.435(3), 2.449(2) Å, respectively, fall within the range of the above determined values.

Global and local interactions characterizing the crystal lattices

Energetics of the crystal lattices. An important thermodynamic characteristic of crystalline compounds is the crystal lattice energy, E_L, which reflects the strength of cohesion forces occurring within this kind of solid phase. Theoretical cohesive energies may be compared with the lattice energies, assessed on the basis of experimental data (enthalpies of sublimation). In the past, employing the same computational methodology as in the current study, we predicted E_L for a series of phenyl acridine-9-carboxylates and satisfactory correlations with the experimental data were disclosed.⁷ The theoretical lattice energies were also obtained for several 9-phenoxycarbonyl-10-methylacridinium triflates containing CMA as a structural fragment.⁷ However, for these compounds, similar to the case of compounds 1, 2 and 3, experimental thermodynamic characteristics were not available. In such cases, computer-aided simulations appear to be the only strategy to gain information regarding the thermodynamic properties of investigated crystals. The E_L values characterizing 1–3, calculated together with the electrostatic (E_el), dispersive (E_d) and repulsive (E_r) contributions to E_L, are summarized in Table 1.

Table 1 Theoretical lattice energies (E_L) calculated using GULP and contributions to the lattice energies: E_el (Coulomb energy), E_d and E_r (dispersion and repulsion energy, respectively, calculated according to Buckingham's potential). All values are in kJ mol⁻¹

Compound no.	E el	E d	E r	E L = Eel + Ed + Er
a Values calculated for lattices, neglecting the presence of water molecules.
1	−548.5	−281.3	254.9	−575.0
	−358.1^a	−150.7^a	48.2^a	−460.5^a
2	−312.3	−471.7	248.6	−535.4
	−240.0^a	−290.5^a	98.6^a	−432.0^a
3	−398.1	−355.6	100.6	−653.1

---

Predicted high values of E_L reflect the substantial ionic character of lattices investigated herein (for comparison, purely molecular crystals of phenyl acridine-9-carboxylate derivatives studied previously were characterized by E_L of magnitude around −160 kJ mol⁻¹).⁷

The strongest cohesion force was found for 3 (E_L equals 653 kJ mol⁻¹). The lattice of compound 1 is less stable than the lattice of 3 by ca. 80 kJ mol⁻¹ (E_L equals to −575 kJ mol⁻¹), whereas the lattice of 2 is less stable by almost 120 kJ mol⁻¹, when compared to 3 (E_L is equal to −535 kJ mol⁻¹).

Various thermodynamic stabilities of the investigated compounds result from different contributions of E_el, E_d and E_r to their total lattice energy. For 1, we have predicted the largest Coulombic term, E_el, among investigated crystals, which constitutes the dominant contribution to E_L for this compound (−548 kJ mol⁻¹). Values of E_el obtained for crystals containing the homoconjugated forms of cations are smaller by about 240 kJ mol⁻¹ (2) and 150 kJ mol⁻¹ (3).

Compound 2, which appears to be the least stable among the investigated crystals, is distinguished from the others because of the high value of the dispersion term (−472 kJ mol⁻¹), which surpasses its electrostatic term (−312 kJ mol⁻¹). In contrast, dispersive attractions, represented by the E_d term in the case of 1 and 3, are smaller than the coulombic forces. It may also be noted that the E_d term in 3 assumes a similar value to E_el calculated for this compound (−398 vs. −356 kJ mol⁻¹) and both terms significantly overcome repulsive forces within the crystal lattice (E_r = 101 kJ mol⁻¹). Regarding repulsion, compounds involving chloride anions and water molecules (1, 2) exhibit almost identical E_r terms, ca. 250 kJ mol⁻¹.

To estimate the influence of water molecules on the cohesive forces occurring within the crystalline solid phases of 1 and 2, we performed additional calculations involving crystals, from which we removed the water. Resulting E_L values along with the corresponding contributions (labelled with superscript a) are shown in Table 1.

When comparing the E_L and E^a_L values collected in Table 1, it can be observed that neglecting water molecules leads to the destabilization of crystals 1 and 2 by 115 and 103 kJ mol⁻¹, respectively. Despite a similar decrease in the total cohesive forces within 1 and 2 upon the removal of water, the changes in the individual components of E_L are not uniform. Thus, reducing E_el in 1 amounts to 190 kJ mol⁻¹, while in 2, it amounts to 72 kJ mol⁻¹ (Table 1). In turn, the larger decrease in E_d takes place in 2 compared to 1 (180 vs. 131 kJ mol⁻¹). Taking into account the sum of the E_el and E_d values, it can be estimated that co-crystallized water molecules introduce attractive interactions into the crystal lattices equal to −321 kJ mol⁻¹ (1) and −253 kJ mol⁻¹ (2). Moreover, water molecules also exert significant repulsive effects, which in the case of 1, amounts to 207 kJ mol⁻¹ and in the case of 2 – to 150 kJ mol⁻¹. Interestingly, removing water from 2 yields the E_r value of 98.6 kJ mol⁻¹, which is almost identical to that predicted for 3, and also involves the homoconjugated CMA cation. According to the above findings, it can be inferred that the interplay between attractive and repulsive effects, due to the presence of water molecules, results in the enhancement of the cohesive forces within 1 and 2; however, this effect does not seem to be the main factor determining the stability of CMA-based crystals investigated here.

The Hirshfeld surfaces. The Hirshfeld molecular surfaces divide the crystal into regions, where the electron distribution of a sum of spherical atoms for the molecule dominates the corresponding sum over the crystal.^53,54 Thus, they reflect the directions and strength of intermolecular interactions within the crystal, mapped with different properties: the distance from the Hirshfeld surface to the nearest nucleus outside the surface (d_e), the corresponding distance to the nearest nucleus inside the surface (d_i) and a normalized contact distance (d_norm), shape index and curvedness (Fig. 5 and Fig. S9, ESI†). The 2D plots of d_ivs. d_e map the quantitative contribution and relative strength (color coded) of different intermolecular interactions occurring within the crystal structures (Fig. S10 and S11, ESI†).

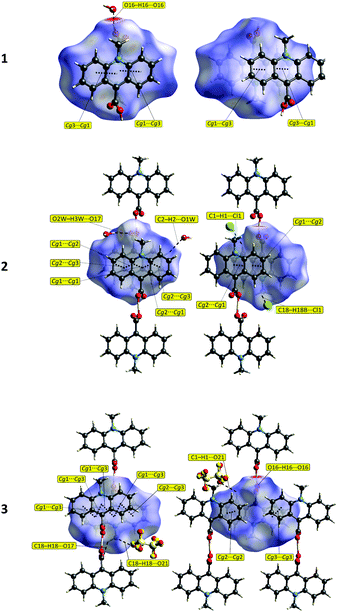Fig. 5 The Hirshfeld surfaces (front (left) and reverse (right) views) of the 9-carboxy-10-methylacridinium moieties reflecting the normalized contact distances (d_norm) with selected interactions.

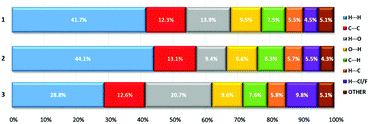
The analysis of the Hirshfeld surfaces mapped by the d_norm property verified the presence of both hydrogen bonds and π–π interactions listed by the PLATON programme (Fig. 5 and Tables S6–S12, ESI†). For the molecular systems investigated (1–3), the π–π interactions are represented by relatively large, flat areas in the curved surfaces (Fig. S9, ESI†). For 1, the strong O–H⋯O hydrogen bond between O16 and O1W marked on the d_norm surface as the red region, is also present in the d_e and d_i surfaces (Fig. 5 and Fig. S9, ESI†). In the case of compounds 2 and 3, weak hydrogen bonds of type C–H⋯O and C–H⋯Cl are marked as pale red areas. The large red regions marked on the maps reflect short distances between O atoms, external and internal to the surface (d_e and d_i, respectively), as well as the presence of mutual H atoms. All the abovementioned interactions are presented in the two-dimensional fingerprint plots (d_e/d_i) (Fig. S10 and S11, ESI†). The majority of the surfaces arise from the contribution of H⋯H interactions (from ca. 29% for 3 up to ca. 44% for 2) (Fig. 6 and Fig. S10 and S11, ESI†), which is characteristic of molecular crystals.⁵⁴ For 1, the O16–H16⋯O1W hydrogen bond between the acridinium cation and water molecule is represented by a single long spike (d_i between 0.6 and 1.2) in the O⋯H and H⋯O fingerprint plots (Fig. S10 and S11, ESI†). For 2 and 3, such spikes do not occur; however, smaller spikes (d_i values in the range of 1.1–1.6) indicating the presence of C–H⋯O hydrogen bonds among water molecules and CMA moieties, or among CMA moieties themselves, are observed. Calculations for all compounds, performed with the assistance of the PLATON programme, disclose no signs of the existence of C–H⋯π interactions, which is further confirmed by the lack of characteristic wing motifs in the appropriate C⋯H and H⋯C fingerprint plots (Fig. S11, ESI†). The acridinium acid moieties are involved in π–π type contacts, which are illustrated by the presence of green areas of the C⋯C contributions to the Hirshfeld surfaces (Fig. S11, ESI†).

Fig. 6 Main contributions to the Hirshfeld surfaces from specific pairs of atom-types for 9-carboxy-10-methylacridinium moieties involved in compounds 1–3. Contributions denoted as “other” are for all compounds: C⋯O, O⋯C, C⋯N, N⋯C, H⋯N, N⋯H, O⋯O, O⋯N, N⋯O; in addition for 1: C⋯Cl and for 3: N⋯F.

The relatively high amounts of the Cl⋯H and H⋯Cl contacts for 1 (4.5%) suggest the presence of a C–H⋯Cl interaction between the acridinium moiety and the chloride ion; however, such an interaction was not found by the PLATON programme. In the case of compound 2, the presence of the above-mentioned interactions is confirmed by both PLATON and the Hirshfeld surface (Cl⋯H and H⋯Cl fingerprint plot, Fig. S11, ESI†). Relatively high contributions of H⋯F and F⋯H interactions (9.8%) disclosed for 3, presumably result from the occurrence of disordered anionic fragments (CF₃OSO₂⁻), in which the oxygen atoms may exchange with the fluorine atoms.

Spectroscopic features

¹H and ¹³C NMR spectra recorded for compounds 1, 2 and 3 show a similar pattern to that observed for previously investigated symmetric ACA derivatives (Fig. S2 and S3, ESI†).⁵⁵

The most deshielded protons, located in the spatial proximity of the nitrogen and oxygen atoms (H1/H8 and H4/H5, respectively (Fig. 1 and Scheme S2, ESI†)), are manifested by the signals appearing in the form of two clear doublets. The remaining aromatic protons of the acridine ring system appear as two distinct triplet systems; these are, in order of increasing shielding, H3/H6 and H2/H7, respectively (Table S1A, ESI†).

In general, the results of the ¹H NMR experiments performed in various liquid phases (deuterium oxide, acetonitrile-d₃, methanol-d₄ and dimethylsulphoxide-d₆), do not suggest the existence of more than one form of the cations involved in 1–3, or their mutual interconversion is too fast in comparison to the experiment time scale. Such a statement can be strictly drawn from the spectra, which present only clear and well-shaped signals of all protons involved in the systems investigated, as well as no changes in their intensity or shape upon lowering the temperature (in CD₃OD) (Fig. S2B, ESI†). This observation differentiates the behaviour of the compounds investigated in liquid environment from their behaviour in the crystalline solid or in the gas phase (discussed below), where various forms of these molecular systems are observed. Similar conclusions can be drawn from ¹³C NMR spectra, recorded for 1–3 in deuterium oxide and dimethylsulphoxide-d₆ (Table S1B and Fig. S3, ESI†). The latter resemble the spectra obtained for other quaternary derivatives of acridine-9-carboxylic acid investigated by us.⁵⁵

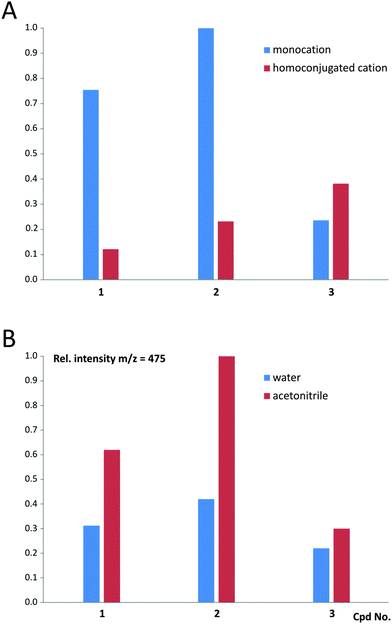
The MALDI-TOF mass spectra recorded for 1–3 (Table S2 and Fig. S12, ESI†) indicate that in the case of 1 and 2, the monocationic form prevails over the homoconjugated form of CMA in the gas phase; however, for 3 the situation seems to be reversed (Fig. 7 and Table S3, ESI†). Contents of the homoconjugated cations in the gas phase increase in the order of 1, 2 and 3, which reveals that cations involved in 1 (appearing in a crystalline solid phase in the monomeric form) and 3 (appearing in a crystalline solid phase in the homoconjugated form) are characterized by the lowest and the highest amounts of the homoconjugated cation, respectively. This allows us to conclude that the molecular systems under investigation are characterized by the occurrence of equilibrium between the two above-mentioned forms, and their population in the gas phase depends on the chemical environment and experimental conditions. The latter statement is supported by the comparison of the population of monocationic vs. homoconjugated forms, characterizing cations 1–3 when a protic (water) vs. non-protic (acetonitrile) medium is used for preparation of samples (Fig. 7 and Table S3, ESI†). The experiments reveal that the amount of the monocationic form of CMA decrease in anhydrous conditions, compared to aqueous conditions, indicating the occurrence of equilibrium between both forms in the gaseous phase. High-resolution UPLC/ESI-QTOF mass spectra were additionally recorded for 1 and 3 (see Fig. S13 and S14 and text below, ESI†).

Fig. 7 The cations involved in compounds 1, 2 and 3 in the gas phase found in the MALDI-TOF mass spectra. (A) The relative intensities (normalized) of the signals of monocationic form (m/z = 238) and homoconjugated cationic form (as a sum of signals of m/z = 475, 497 and 513). (B) The relative intensities (normalized) of the signals derived from homoconjugated cationic forms (m/z = 475) in the presence of various solvents used for sample preparation.

To understand the origin of the unique behaviour of CMA in the solid phase, one should take into account the composition of the solutions used for crystal growth. Since CMA contains groups that are able to participate in protolytic transformations, its actual form in aqueous solutions depends on the acidity of the environment (pH/H₀). The protolytic forms of CMA are characterized by different spectral properties that allowed us to determine the ranges of pH/H₀ in which these species are thermodynamically stable, by performing spectrophotometric UV-Vis acid–base titrations (Table S4 and Fig. S15, ESI†). In solutions of high acidity (H₀ < −2.0) CMA exists in the mono-protonated form (monocation, Fig. 8). In solutions of lower acidity (−2.0 < H₀/pH < 2.0) the monocationic form coexists with the zwitterionic one (Fig. 8); the pK_a value of this protolytic equilibrium is 0.05 ± 0.01 (Table S4, ESI†). The pK_a values calculated at various wavelengths from the UV-Vis spectra, change slightly in a systematic manner, which likely arises from the changes in the ionic strength of the titrated solutions.

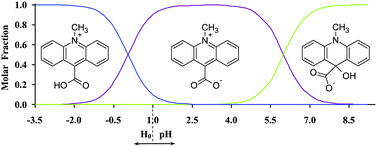Fig. 8 Mole fractions of the forms of 1versus pH/H₀ estimated based on the experimentally determined first ionization constant (pK_a (1) = 0.05) and the theoretically predicted second ionization constant (pK_a (2) = 6.0). See also Table S4 and Fig. S13 (ESI†).

The equilibrium between the monocationic and zwitterionic forms, characterized by a pK_a value of 1.72, was assessed in the past in the aqueous solutions containing 3-carboxy-1-methylpyridinium cation, which is structurally related to CMA.⁵⁶ The zwitterionic form of CMA is thermodynamically stable in solutions of low acidity and it transforms to a pseudo-base form in neutral and basic environments (Fig. 8), in a similar fashion to other 10-methylacridinium derivatives.⁵⁷ Since the crystals of 1–3 were grown in protic solutions of various acidity, the co-existence of monocationic and zwitterionic forms in such media is of special interest for understanding the origin of formation of CMA-based homoconjugated cations; this is discussed below.

Computational predictions

Structural considerations. Calculations carried out at the DFT level of theory for the reagents in the gaseous phase enabled us to propose the structures of monomeric (1a–1c) and homoconjugated (2a–2e, 3a–3c) forms of CMA, that might be involved in 1–3 (Fig. S16, ESI†). Other forms, including classical dimeric ones (containing two O–H⋯O hydrogen bonds) were also considered, but were not included in the further analysis because they are highly energetic (thermodynamically unstable). The structural and thermodynamic data summarized in Table 2 and Table S14 (ESI†) concern the possible vapour phase complexes that may be formed with the participation of CMA, chloride or triflate anions and water molecules. Optimization of the monomeric structures leads to the most thermodynamically stable form, 1a (Table 2). The enthalpy and Gibbs free energy differences (Δ_relH and Δ_relG, respectively) of the latter structure and the two less stable monomeric forms (1b, 1c) are substantial, assuming values of 292.2, 292.5 (Δ_relH) and 291.8, 288.4 (Δ_relG) kJ mol⁻¹, respectively.

Table 2 Structural features and thermodynamic data for conformers of the compounds 1–3

Entity	Method^a	Geometry of the O–H⋯O hydrogen bond				Angle (°)				ΔHrel	ΔGrel	μ
		O–H	H⋯O	O⋯O	<(OHO)	A	B	C	D
a DFT – the DFT(B3LYP)/6-31G** level of theory. b A, between the mean plane of the first acridine nucleus (C1–C14, N10) and the second acridine nucleus (C1A–C14A, N10A); B, between the mean planes delineated by C15, O16, O17 and C15A, O16A, O17A; C, between the mean plane of the first acridine nucleus (C1–C14, N10 or C1A–C14A, N10A) and the mean plane of the carbonyl group of the same acridine nucleus (C15, O16, O17 or C15A, O16A, O17A); D, between the mean plane of the first acridine nucleus (C1–C14, N10 or C1A–C14A, N10A) and the mean plane of the carbonyl group of the second acridine nucleus (C15A, O16A, O17A or C15, O16, O17). c μ represents the dipole moment of the compounds (indicated in Fig. S16, ESI), in D. d ΔHrel and ΔGrel represent the enthalpy and the Gibbs' free energy of a given conformers (indicated in Fig. S16, ESI) relative to the enthalpy and the Gibbs' free energy of 1a form; ΔHrel and ΔGrel values, in kJ mol^−1. e ΔHrel and ΔGrel represent the enthalpy and the Gibbs' free energy of a given conformer (indicated in Fig. S16, ESI) relative to the enthalpy and the Gibbs' free energy of 2b form; ΔHrel and ΔGrel values, in kJ mol^−1. f ΔHrel and ΔGrel represent the enthalpy and the Gibbs' free energy of a given conformer (indicated in Fig. S16, ESI) relative to the enthalpy and the Gibbs' free energy of 2d form; ΔHrel and ΔGrel values, in kJ mol^−1. g ΔHrel and ΔGrel represent the enthalpy and the Gibbs' free energy of a given conformer (indicated in Fig. S16, ESI) relative to the enthalpy and the Gibbs' free energy of 3a form; ΔHrel and ΔGrel values, in kJ mol^−1.
1a	X-ray							89.6
	DFT							51.5				17.6
1b	DFT							58.5		292.2^d	291.8^d	11.0
1c	DFT							57.6		292.5^d	288.4^d	11.5
2a	X-ray	1.220	1.220	2.435	180	0.0	0.0	84.8	84.8
	DFT	1.068	1.419	2.486	176	3.8	61.4	64.5/69.2	67.3/60.9	27.4^e	29.9^e	11.5
2b	DFT	1.047	1.472	2.513	172	49.2	74.8	66.6/72.7	38.8/38.5			29.1
2c	DFT	1.056	1.448	2.498	172	55.6	75.2	71.0/73.3	40.3/38.5	2.6^f	−0.9^f	28.6
2d	DFT	1.038	1.517	2.492	154	60.3	72.6	68.8/75.3	44.4/82.2			6.9
2e	DFT	1.117	1.320	2.434	174	47.3	77.6	69.2/70.7	38.5/34.4			14.9
3a	X-ray	1.220	1.220	2.449	180	0.0	0.0	88.2	88.2
	DFT	1.042	1.509	2.485	153	51.5	72.3	78.8/79.3	50.3/82.5			7.2
3b	DFT	1.052	1.456	2.502	172	52.3	73.4	74.0/69.7	38.0/42.7	13.5^g	5.5^g	37.3
3c	DFT	1.158	1.261	2.416	174	44.1	76.7	68.2/68.4	39.2/38.1			4.0

---

The computational studies carried out on the homoconjugated forms of CMA enabled us to propose the three types of structure: linear (2a, 2c and 3b), bent (2b, 2d and 3a) and flat (2e and 3c) (Fig. S16, ESI†). Linear and bent forms refer to the hydrogen bond (O–H⋯O) geometry; the flat form refers to the anion⋯cation–H–cation⋯anion geometry. Regarding the homoconjugates, type 2 and 3 (the bent structures) are characterized by small values of the dipole moment and are thermodynamically preferred in the gas phase (Table S14, ESI†). In both types of salts, i.e., the ones comprised of Cl⁻ and CF₃SO₃⁻ counter anions (2d and 3a, respectively, Fig. S16, ESI†), the more stable bent structures are also characterized by lower values of the dipole moment (Table 2). However, in the case of complexes composed of the homoconjugated cation, chloride anion and two molecules of water (structures 2a and 2b, Fig. S16, ESI†), the dipole moment assumes substantially higher values (11.5 and 29.1, respectively), although the energetically favourable arrangement is also bent (2b). The latter feature likely results from the replacement of the Cl⁻ and H₂O moieties towards one of the N atoms of the acridine ring system (in the case of 2b), while in the linear complex (2a), the Cl⁻ and H₂O remain in a central position, i.e., in the vicinity of the H-bond, binding both CMA moieties. In the case of negatively charged molecular complexes containing two anions (2e and 3c, Fig. S16, ESI†), the more stable structure is flat, with the anions shifted towards the nitrogen atoms (N10 and N10A). In the case of the linear homoconjugated forms (2a, 2c, 3b, Fig. S16, ESI†), the O⋯H–O hydrogen bond is slightly shorter, compared to the length specified for the bent arrangements (2b, 2d, 3a, Fig. S16, ESI†) although the enthalpy and Gibbs free energies of such complexes are higher (Table 2 and Table S14, ESI†). The geometry of hydrogen bonding in the homoconjugated cations resembles that determined in the case of the crystalline solid phases (2 and 3). However, the H-atom involved is insignificantly shifted towards one of the oxygen atoms, resulting in the formation of slightly unsymmetrical hydrogen bonding (Table 2 and Fig. S16, ESI†). As was discussed above, the stability of the optimized complexes is controlled mainly by the electrostatic interactions occurring among the positively charged N atoms and CF₃SO₃⁻ or Cl⁻ anions. In the bent complexes (2d, 3a, Fig. S16, ESI†), the N⁺⋯A⁻ distances are relatively short, attaining the values of 4.045/7.808 Å for CF₃SO₃⁻ and 3.686/7.680 Å for Cl⁻, respectively, while in the case of the linear complexes (2c, 3b, Fig. S16, ESI†), shorter (comparable to the above ones) and longer N⁺⋯A⁻ distances were predicted (5.228/15.878 Å for CF₃SO₃⁻ and 4.319/14.121 Å for Cl⁻). The situation is different in the case of complexes containing molecules of water; in the flat structure 2a, the distances are comparable (7.539 and 7.360 Å for CF₃SO₃⁻ and Cl⁻, respectively), while in the bent complex 2b, these distances are similar to those found for the linear ones, attaining values of 4.265 and 14.403 Å, respectively. The latter effect is presumably a consequence of a distinct shift of the chloride anion, together with water molecules, towards one of the nitrogen atoms (N10 or N10A), followed by the bending of the whole molecular arrangement.

Generally, DFT calculations indicate that the incorporation of water molecules into the investigated molecular complexes is manifested in the thermodynamic stabilization of resultant structures; linear complexes are less stable than the bent ones by about 27.2 and 29.7 kJ mol⁻¹ (respective differences in enthalpy and Gibbs free energy). In the case of the chloride complex, this effect is not distinctly pronounced and the linear architecture is less stable than the bent one by 2.5 kJ mol⁻¹ (enthalpy). In the linear complex 2a the N10⋯O(w) distances are comparable and are distributed quite symmetrically (values of 5.769, 6.657, 6.771 and 10.661 Å), while in the bent complex 2b, a distinct shift of water molecules towards the acridinium N atom is observed (values of 4.149, 14.917, 4.653 and 15.934 Å).

The vapour phase-optimized structure of the monomeric form, associated with two molecules of water and the chloride counter ion (1a), closely resembles the architecture characterizing the crystalline solid phase (1). As was mentioned above, the latter form is also energetically favoured among considered monocationic forms, since the other ones are less stable by about 290 kJ mol⁻¹ (Table S14 and Fig. S16, ESI†).

Pathways of formation of the homoconjugated cations. Calculations of basic thermodynamic data (enthalpies and Gibbs free energies) carried out at the DFT level of theory for the reagents in gaseous and liquid phases (water and ethanol), enabled us to propose a pathway of formation of the homoconjugated CMA-based forms involved in compounds 2 and 3. The formation of the homoconjugated cation and the zwitterionic form of CMA (CMA/z) is energetically more favourable than the formation of the dimer, consisting of two CMA cations (data not shown). The formation of the homoconjugated form is thermodynamically probable, as the enthalpy (Δ_r,298H°) and Gibbs free energy (Δ_r,298G°) attain the values of −178.6 and –132.1 kJ mol⁻¹, respectively (Table 3). In the case of the dimeric form, the calculated Δ_r,298H° and Δ_r,298G° energies are much higher, expressing values of 64.4 and 112.0 kJ mol⁻¹, respectively. Taking into account the transformation pathways leading to the formation of the homoconjugated forms involved in 2 and 3, as well as the above-discussed findings (Spectroscopic features section), we considered the possible processes that may explain the experimental observations. Scheme 1 presents probable transformation pathways involving various forms of CMA in a protic environment (water/ethanol). Step I denotes the equilibrium, that may occur between the zwitterionic and the ‘pseudobase’⁸ forms of CMA; step II shows the formation of the homoconjugated cation from the above two forms; step III represents the equilibrium between zwitterionic and monocationic forms of CMA with the participation of the hydronium ion; step IV is the formation of the homoconjugated cation from the zwitterionic and monocationic forms of CMA.

Table 3 Thermodynamic data (in kJ mol⁻¹) for consecutive steps of formation of hydrogen-bis(9-carboxy-10-methyacridinium) cation^a

Step^b	Phase	Method	ΔH	ΔG
a ΔH and ΔG denote enthalpy and Gibbs free energy of the reaction (step), respectively. b For possible pathways of formation of the title cation see Scheme 1.
I	Gaseous	DFT/6-31G**	−78.0	−27.7
	Liquid	DFT (PCM-H2O)/6-31G**		34.5
		DFT (PCM-CH3CH2OH)/6-31G**		31.9
II	Gaseous	DFT/6-31G**	−100.6	−104.4
	Liquid	DFT (PCM-H2O)/6-31G**		−72.6
		DFT (PCM-CH3CH2OH)/6-31G**		−73.3
III	Gaseous	DFT/6-31G**	−358.7	−353.0
	Liquid	DFT (PCM-H2O)/6-31G**		−144.0
		DFT (PCM-CH3CH2OH)/6-31G**		−150.7
IV	Gaseous	DFT/6-31G**	−178.6	−132.1
	Liquid	DFT (PCM-H2O)/6-31G**		−38.0
		DFT (PCM-CH3CH2OH)/6-31G**		−41.4

---

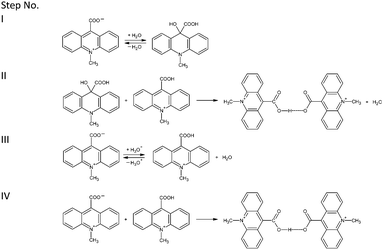Scheme 1 Probable pathways of formation of homoconjugated bis(9-carboxy-10-methylacridinium) cations proposed at the level of the DFT method.

The theoretically predicted thermodynamic data for possible transformation pathways summarized in Table 3, indicate that the above described steps are probable only in the gaseous phase. In the liquid phase (H₂O or CH₃CH₂OH), step I seems to be thermodynamically unfavourable (positive value of Gibbs free energy). Predicted thermodynamic data suggest that formation of the homoconjugated cations presumably takes place according to the transformation steps denoted as III and IV (Scheme 1). These pathways underline our above-stated findings, indicating that the formation of homoconjugated cations of CMA occurs in solid crystalline and gaseous phases.

Conclusions

The quaternary acridinium salts of cognitive and practical interest, namely 9-carboxy-10-methylacridinium chloride (CMACl) and 9-carboxy-10-methylacridinium trifluoromethansulfonate (CMATfO), were synthesized and subjected to thorough experimental and theoretical investigations. Various crystalline forms of the above CMA-based salts, encoded as compounds 1, 2 and 3, were investigated with the aid of single crystal X-ray diffraction analysis, crystal lattice energy calculations, the determination of Hirshfeld surfaces, MALDI-TOF and ESI-QTOF mass spectrometry, ¹H and ¹³C NMR and UV-Vis spectroscopy, as well as quantum chemistry methods based on the density functional theory (DFT). Geometry, spatial architecture of the entities ordered in the crystalline forms, intermolecular interactions occurring in the solid and gaseous phases, as well as the thermodynamics and their origin are also elucidated in the work.

Compounds 1–3 presented in Fig. 1 are in general similar in terms of molecular geometry to other acridinium salts investigated by us, being characterized by the planar acridine ring system and a carboxyl group twisted at approximately right angles, relative to the acridine nucleus. Chlorides 1 and 2 crystallize in the monoclinic space group, while the triflate 3 crystalizes in the triclinic space group. As was detected using the PLATON program, the predominant role in the crystal packings of 1–3 is played by hydrogen bonds of various strength (O–H⋯O, C–H⋯O), or halogen (X)-containing specific intermolecular interactions, such as O–H⋯X and C–H⋯X. Parallely oriented aromatic layers in the crystals are stabilized by the network of π–π contacts and non-specific dispersive interactions that occur between aromatic rings of adjacent acridinium moieties, resulting in the formation of characteristic multi-layered frameworks. In the homoconjugated forms 2 and 3, symmetric O–H⋯O hydrogen bonding occurs, in which the H-atom is located directly in the inversion centre. The observed features of the crystalline networks are responsible for major differences in conformation, H-bond patterns and calculated lattice energies, characterizing the crystalline solid phases of the investigated systems. The reason for the observed physicochemical features of the crystalline solids presumably lies in the presence or absence of water molecules and fluorine atoms involved in a complex network of short-range interactions revealed in 1, 2 and 3.

Computational methods implemented in the GULP program, used for evaluation of the crystal lattice energies, provided the thermodynamic characteristics of the systems. Theoretically predicted lattice energies (E_L, Table 1) reveal that the lattices characterizing 1–3 significantly differ in terms of their stability, i.e., compound 3 appears as the one forming the most stable crystals and compound 2, the least stable. In 1, the major attractive force occurring within the crystal lattice was found to be electrostatic (E_el). Here, the dispersive term (E_d) is almost entirely suppressed by the repulsion term (E_r). In turn, dispersion dominates in E_L assessed for crystals of 2, whereas in crystals of 3, E_el and E_d contributions to E_L express comparable magnitude. The influence on the thermodynamic stability of crystals, exerted by water molecules within the lattices of 1 and 2, was also elucidated. In general, the presence of H₂O within the crystal structures is manifested by the increase in total cohesive forces by more than 100 kJ mol⁻¹; however, this effect, when compared to the large E_L values, seems not to be of fundamental importance for the stabilization of the crystal lattices of 1 and 2.

The analysis of the Hirshfeld surfaces designated for 1–3 verified the presence of hydrogen bonds and π–π contacts, commonly occurring within the investigated molecular systems (Fig. 5 and 6). The red or pale red areas on the surfaces correspond to various types of hydrogen bonds and indicate shorter or longer mutual distances of the selected atoms. The O–H⋯O and C–H⋯O interactions are represented by longer or shorter single spikes on the fingerprint plots, according to the relative energy of the above interactions, while π–π contacts are represented by large flat regions characterizing the Hirshfeld surfaces.

Spectroscopic methods, such as MALDI-TOF MS, ESI-QTOF MS, ¹H and ¹³C NMR and UV-Vis, allowed us to get further insight into the structures of 1–3 in gaseous and liquid phases. The mass spectra revealed that in the gas phase, the equilibrium occurs between the monocationic and homoconjugated forms of CMA, where their population depends on the experimental conditions; hydrated cations, involved in crystals of 1 and 2, were not observed in the MS experiments. ¹H and ¹³C NMR spectra obtained for 1–3 in various liquid phases (D₂O, DSO-d₆, CD₃OD, CD₃CN) and at different temperatures (298 K and 233 K), disclosed that forms of CMA are not distinguishable by this method, or one form is present under the conditions of experiments. Spectrophotometric acid–base titration of 1 (built of the monocationic form of CMA in crystalline solid phase), performed in an aqueous environment, revealed that CMA may exist in the monocationic or zwitterionic forms under the conditions of crystal growth, which gives rise to the formation of the homoconjugated cations found in crystals of 2 and 3.

According to quantum chemistry calculations (DFT) conducted for 1–3 in the gas phase, the structural data obtained theoretically are comparable to the experimental findings (single crystal X-ray crystallography, Tables 2, 3 and Table S13, ESI†). Thermodynamic stability of the homoconjugated cations relates to the O–H⋯O hydrogen bond length, as well as attractive electrostatic interactions occurring among the oppositely charged groups of atoms (the N atoms experiencing a deficit of electron density, and the Cl⁻ or CF₃OSO₂⁻ anions). The above-mentioned features of the investigated molecular systems are also reflected in their various dipole moments. Based on the DFT approach, we proposed a possible pathway for the formation of CMA-based forms studied here. Calculated thermodynamic data emphasize the experimental findings, revealing that the formation of the homoconjugated forms of CMA is likely to occur in crystalline solid and liquid phases.

Acknowledgements

Financial support is acknowledged from the State Funds for Scientific Research through National Science Centre grants No. DEC-2012/05/B/ST5/01680 (contract No. UMO-2012/05/B/ST5/01680). Computer time was granted from Wroclaw Centre for Networking and Supercomputing (WCSS, Poland) under grants no. 196 and 215 and the Tri-City Academic Computer Centre in Gdansk (TASK, Poland). This research was also supported in part by PL-Grid Infrastructure. BZ acknowledges financial support from the European Social Fund within the project “The development program of the University of Gdansk in areas of Europe 2020 (UG 2020)”. The authors would thank to MSc Paweł Wityk for his valuable help in recording of UPLC/ESI-QTOF MS spectra.

References

1. K. Smith, J.-J. Yang, Z. Li, I. Weeks and J. S. Woodhead, J. Photochem. Photobiol., A, 2009, 203, 72.
2. K. Krzymiński, A. D. Roshal, B. Zadykowicz, A. Białk-Bielińska and A. Sieradzan, J. Phys. Chem. A, 2010, 114, 10550.
3. A. Roda and M. Guardigli, Anal. Bioanal. Chem., 2012, 402, 69.
4. A. Natrajan and D. Sharpe, Org. Biomol. Chem., 2013, 11, 1026.
5. J. Dey, J. L. Haynes III, I. M. Warner and A. K. Chandra, J. Phys. Chem. A, 1997, 101, 2271.
6. K. Krzymiński, A. D. Roshal and A. Niziołek, Spectrochim. Acta, Part A, 2008, 70, 394.
7. K. Krzymiński, P. Malecha, P. Storoniak, B. Zadykowicz and J. Błażejowski, J. Therm. Anal. Calorim., 2010, 100, 207.
8. M. W. Cass, E. Rapaport and E. H. White, J. Am. Chem. Soc., 1971, 94, 3168.
9. L. J. Kricka, Anal. Chim. Acta, 2003, 500, 279.
10. Y. Kitamura, T. Iwasaki, M. Saito, M. Mifune, Y. Saito, K. Sato, C. Yomota and K. Tanamoto, J. Food Hyg. Soc. Jpn., 2006, 47, 232.
11. Z. Dega-Szafran, A. Kartusiak and M. Szafran, J. Mol. Struct., 2006, 785, 160.
12. J. Rak, P. Skurski and J. Błażejowski, J. Org. Chem., 1999, 64, 3002.
13. K. Krzymiński, A. Ożóg, P. Malecha, A. D. Roshal, A. Wróblewska, B. Zadykowicz and J. Błażejowski, J. Org. Chem., 2011, 76, 1072.
14. CrysAlis CCD and CrysAlis RED, Oxford Diffraction Ltd., Yarnton, England, 2008.
15. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
16. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148.
17. C. K. Johnson, ORTEP II, Report ORNL-5138, Oak Ridge National Laboratory, Oak Ridge, TN, USA, 1976.
18. S. Motherwell and S. Clegg, PLUTO-78, Program for Drawing and Molecular Structure, University of Cambridge, UK, 1978.
19. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. Van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466.
20. (a) J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629; (b) J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291.
21. Density functional methods in chemistry, ed. J. K. Labanowski and J. K. Andzelm, Springer, New York, 1991.
22. (a) U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129; (b) B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comput. Chem., 1990, 11, 431.
23. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
24. (a) R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724; (b) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian. Inc., Wallingford CT, 2013.
26. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897.
27. G. Filippini and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 868.
28. B. Zadykowicz, K. Krzymiński, P. Storoniak and J. Błażejowski, J. Therm. Anal. Calorim., 2010, 101, 429.
29. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2012.
30. A. Williams, S. Bakulin and S. Golotvin, NMR Prediction Software, Advanced Chemistry Development, Toronto, 2001, http://www.acdlabs.com.
31. K. Pigoń and Z. Ruziewicz, Physical chemistry: phenomenological basics, PWN, Warsaw, 2005, vol. 1, p. 334.
32. R. A. Cox and K. Yates, Can. J. Chem., 1981, 59, 2116.
33. A. O. Doroshenko, Spectral Data Lab Software, Kharkiv, 1999.
34. J. Reijenga, A. van Hoof, A. van Loon and B. Teunissen, Anal. Chem. Insights, 2013, 8, 53.
35. (a) Ü. Haldna, Prog. Phys. Org. Chem., 1990, 18, 65; (b) Ü. Haldna and A. Murshak, Comput. Chem., 1988, 8, 201.
36. Modern Electronic Structure Theory: Geometry Optimization on Potential Energy Surfaces, ed. H. B. Schlegel, World Scientific Publishing, Singapore, 1994.
37. (a) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213; (b) Ab Initio Molecular Orbital Theory, ed. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Wiley, New York, 1986.
38. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
39. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
40. M. J. S. Dewar and G. P. Ford, J. Am. Chem. Soc., 1977, 99, 7822.
41. ChemCraft, Version 1.6 (build 350), http://www.chemcraftprog.org.
42. D. Trzybiński, K. Krzymiński, A. Sikorski, P. Malecha and J. Błażejowski, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o826.
43. D. Trzybiński, K. Krzymiński, A. Sikorski and J. Błażejowski, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o906.
44. D. Trzybiński, K. Krzymiński, A. Sikorski and J. Błażejowski, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o1313.
45. D. Trzybiński, K. Krzymiński and J. Błażejowski, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o2773.
46. M. Mirzaei, H. Eshtiagh-Hosseini, M. Bazargan, F. Mehrzad, M. Shahbazi, J. T. Mague, A. Bauzá and A. Frontera, Inorg. Chim. Acta, 2015, 438, 135.
47. H. Eshtiagh-Hosseini, M. Mirzaei, S. Zarghami, A. Bauzá, A. Frontera, J. T. Mague, M. Habibi and M. Shamsipur, CrystEngComm, 2014, 16, 1359.
48. M. Mirzaei, H. Eshtiagh-Hosseini, Z. Karrabi, K. Molčanov, E. Eydizadeh, J. T. Mague, A. Bauzá and A. Frontera, CrystEngComm, 2014, 16, 5352.
49. G. E. Bacon and N. A. Curry, Acta Crystallogr., 1960, 13, 717.
50. L. Manojlović and J. C. Speakman, Acta Crystallogr., Sect. B: Struct. Sci., 1968, 24, 323.
51. J. C. Speakman, Struct. Bonding, 1972, 12, 141.
52. N. K. Kalsbeek and S. Larsen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 1005.
53. J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627.
54. P. Panini, T. P. Mohan, U. Gangwar, R. Sankolli and D. Chopara, CrystEngComm, 2013, 15, 4549.
55. K. Krzymiński, P. Malecha, B. Zadykowicz, A. Wróblewska and J. Błażejowski, Spectrochim. Acta, Part A, 2011, 78, 401.
56. M. L. Black, J. Phys. Chem., 1955, 59, 670.
57. J. W. Bunting, V. S. F. Chew, S. B. Abhyankar and Y. Goda, Can. J. Chem., 1984, 62, 351.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, chemical data and canonical structures of the investigated crystals (1–3) (Schemes S1 and S2) and their precursors (Fig. S1), crystal data and structure refinement for 1–3 (Table S5), parameters of hydrogen bondings found in 1–3 (Tables S6, S8 and S11), parameters of π–π interactions (Tables S7, S9 and S12), parameters of Cl⋯O contacts (Table S10), crystal packing in 1–3 (Fig. S4–S6), CSD database data (Fig. S7 and S8), chemical shifts of 1–3 in ¹H and ¹³C NMR spectra (Table S1, Fig. S2, S3), MS data (Tables S2, S3 and Fig. S12–S14), the Hirshfeld surfaces representing distances external and internal to the surface for 1–3 (Fig. S9) and fingerprint plots of acridinium moieties in 1–3 (Fig. S10, S11), spectrophotometric titration data for 1 (Fig. S15 and Table S4) structural parameters of 1–3 (Table S13) and thermodynamic data for monomeric and dimeric conformers of 1 and 2 (Table S14) and the DFT structures (Fig. S16). CCDC 981470–981472. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6nj00725b

---