Stimuli-responsive behavior of composites integrating thermo-responsive gels with photo-responsive fibers†
Olga
Kuksenok‡
and
Anna C.
Balazs
*
Chemical Engineering Department, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: balazs@pitt.edu
First published on 9th November 2015
Abstract
Materials that could be reconfigured multiple times into different shapes with the use of different stimuli could dramatically impact manufacturing processes. As a step toward creating such useful, adaptive materials, we use computational modeling to design a composite that integrates a thermo-responsive polymer gel and photosensitive fibers. The gel displays a lower critical solution temperature (LCST), and thus, shrinks at elevated temperatures. The elastic fibers are functionalized with spirobenzopyran (SP) chromophores, which become hydrophobic under blue light. If these chromophores are uniformly distributed in this LCST gel (without the embedded fibers), then both light and heat produce the same effect on the sample, causing the gel to undergo a uniform collapse. When the SP-functionalization is confined to fibers that are embedded in the gel, the material displays distinctly different behavior in the presence of light and heat. In particular, samples anchored to a surface bend in one direction when illuminated and in the opposite direction when heated. When the sample is detached from the surface, then the composites shrink like an accordion when heated and bend like a caterpillar when illuminated. Common to both the tethered and untethered samples, one material displays a distinct response to the different stimuli. Hence, our findings indicate how a given sample can be fashioned into different shapes through the use of separate stimuli. Overall, our results point to a robust method for controllably reconfiguring the morphology of compliant composites and amplifying the effects of external environmental cues (light or temperature) on the behavior of these systems.
Conceptual insightsUsing computational modeling, we designed new, physically-realizable composites that integrate functionalized, photo-responsive fibers with thermo-responsive gels. If the fibers were passive elements, the materials would already exhibit valuable attributes, with the strong fibers acting as a skeleton that reinforces the “muscle” provided by the responsive, active gel. The complexity and potential functionality of the material is, however, increased when the fibers are also stimuli-responsive and thus, constitute active elements. Via our model, we uncovered the cooperative interactions that control the reorganization of the responsive fibers and the morphological changes of the gel in the presence of light, heat and the combination of the two stimuli. These studies provide insight into the complex mechanisms by which multiple stimuli interact with an adaptive material to produce different forms of reconfiguration and actuation. The findings thus reveal the distinct advantage offered by these hybrid materials: a single composite yields access to a range of dynamic responses and structures. On a conceptual level, our results provide guidelines for combining different types of stimuli-responsive components to create adaptive materials that can be controllably and repeatedly actuated to display new dynamic behavior and large-scale motion. |
I. Introduction
The aim of 4D printing is to create materials that can dynamically alter their morphology, and hence, time becomes the fourth dimension that characterizes the structure of the material.1,2 To achieve such reconfigurability, the printed materials typically encompass stimuli-responsive components. With the introduction of the appropriate environmental cue, these materials can be driven to controllably change their shape, and thus, their functionality. Materials that can be configured and reconfigured multiple times into different shapes with the use of different stimuli could revolutionize manufacturing processes. In particular, the ability to reconfigure a material into a new shape, without building a new part, would contribute significantly to the recyclability and sustainability of the system.The challenge, however, is creating materials that are both strong and malleable in the presence of the external stimuli. Ideally, the system should also display distinctly different behavior in the presence of different stimuli, and thus, exhibit a plurality of functions. Fiber-filled gels constitute useful candidates for creating strong, reconfigurable materials since the fibers impart a degree of stiffness and the polymers impart the required malleability.3 Such fiber-filled polymeric materials can be created via direct ink writing methods and other 3D printing techniques.4 Alternatively, these composites can be fabricated by forming a gel around sterically-stabilized fibers dispersed in solution or creating a gel around an array of anchored posts.5 Herein, we use a new computational approach to simulate the behavior of thermo-responsive gels that encompass arrays of photo-responsive fibers, and thereby, demonstrate that this system can display exceptional reconfigurability.
As we show below, the application of light and heat produces distinctly different responses in these gel–fiber composites, and hence, these stimuli can provide orthogonal means of regulating the overall properties of the material. Thus, a single composite can display multiple functionalities. In particular, light can be used to promote a specific shape and functionality, while heat can be used to produce a different response. Notably, significant progress has recently been made in designing shape-memory polymers that change their shape upon application of external stimuli;6 however, the shapes of these materials are typically pre-programmed during their fabrication. The composites described here allow one to re-program their shape and functionality “on demand”, so that the reconfigurations are dynamically prescribed through the external stimuli (which could be applied either serially or simultaneously).
We also show that the presence of multiple functionalized fibers enables the amplification of small-scale signals into large-scale responses. Since the fibers extend from the surface of the gel (Fig. 1a), they could be harnessed to transfer a signal from the composite to the surrounding media. In previous studies,5 we showed that elastic posts embedded in a thermo-responsive hydrogel and immersed in a binary fluid could transmit a chemo-mechanical signal between the two fluid layers, and thus, control the dynamic behavior of the entire system. As indicated by the findings described below, the introduction of photosensitive fibers (posts) allows one to use light to transfer signals from the gel to the fluids, and thus, control the dynamic behavior of the system remotely and non-invasively.
More generally, the creation of materials that are simultaneously adaptive, flexible, lightweight and strong would open new routes for producing the next generation of smart sensors, coatings, textiles and structural components. On a more fundamental level, the coupling of multiple responsive components and multiple stimuli could open the door to new, emergent behavior.
II. Model
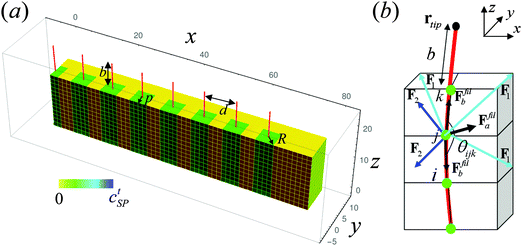
The gel-based composite considered here is shown schematically in Fig. 1a, revealing the fibers (or posts) partially embedded in a gel layer. Our computational approach to modeling this material captures the dynamics of the gel, the motion of the elastic posts embedded in the gel and the functionalization of the posts with spirobenzopyran chromophores. Below, we describe each aspect of this hybrid model.A. Modeling the gel and posts
The gel is modeled using our recently developed three-dimensional “gel lattice spring model” or gLSM,7 which combines a finite element approach for the spatial discretization of the elastodynamic equations and a finite difference approximation for modeling reaction–diffusion events occurring in the gel. The details of the formulation of the gLSM in three dimensions, as well as the validation of the approach can be found in the ref. 7. Originally, the gLSM7–10 was developed to simulate the dynamics of self-oscillating gels undergoing the Belousov–Zhabotinsky chemical reaction, the so-called “BZ gels”.11,12 We later modified this model to simulate the dynamics of photo-responsive gels functionalized with spirobenzopyran chromophores.13 The findings from a number of computational studies using the gLSM approach7,14–16 are in a good agreement with corresponding experimental results.7,14–17 Hence, the gLSM7–10 has proven to be a powerful approach for predicting the behavior of a variety of chemo-responsive gels.Within the framework of the gLSM,8,9 we take the total energy of the chemo-responsive gels as the sum of the energy of the polymer–solvent interaction, UFH, and elastic energy associated with the deformation of the gel, Uel. The first term is written in the following Flory–Huggins form:18
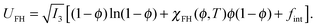 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[B with combining circumflex]](https://www.rsc.org/images/entities/b_char_0042_0302.gif) is an invariant of the left Cauchy–Green (Finger) strain tensor
is an invariant of the left Cauchy–Green (Finger) strain tensor ![[B with combining circumflex]](https://www.rsc.org/images/entities/b_char_0042_0302.gif) , which characterizes the volumetric changes in the deformed gel.20 The local volume fraction of polymer in the deformed state, ϕ, and undeformed state, ϕ0, are related as9ϕ = ϕ0I3−1/2.
, which characterizes the volumetric changes in the deformed gel.20 The local volume fraction of polymer in the deformed state, ϕ, and undeformed state, ϕ0, are related as9ϕ = ϕ0I3−1/2.
The elastic energy contribution, Uel, describes the rubber elasticity of the cross-linked network,18,21 and is proportional to the crosslink density, c0:
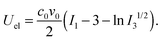 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[B with combining circumflex]](https://www.rsc.org/images/entities/b_char_0042_0302.gif) .20
.20
Eqn (1) and (2) yield the following constitutive equation for the chemo-responsive gels:8,9
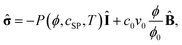 | (3) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e111.gif) is the dimensionless stress tensor measured in units of v0−1kT, and cSP denotes the dimensionless concentration of the chromophores in the spiro form, which in turn defines the photo-mechanical response of the gel around the functionalized posts as detailed further below. (For non-functionalized posts or within the gel matrix, we set cSP = 0.)
is the dimensionless stress tensor measured in units of v0−1kT, and cSP denotes the dimensionless concentration of the chromophores in the spiro form, which in turn defines the photo-mechanical response of the gel around the functionalized posts as detailed further below. (For non-functionalized posts or within the gel matrix, we set cSP = 0.)
The isotropic pressure, P(ϕ,cSP,T), in eqn (3) is defined as:
| P(ϕ,cint,T) = −(ϕ + ln(1 − ϕ) + χ(ϕ,T)ϕ2) + c0v0ϕ(2ϕ0)−1 + πint(cSP). | (4) |
Within the gLSM,7–10 we describe the dynamics of a chemo-responsive gel within the framework of the two-fluid model.21–23 Both the respective polymer and solvent velocities, v(p) and v(s), contribute to the total velocity as v = ϕv(p) + (1 − ϕ)v(s), where ϕ and 1 − ϕ are the respective volume fractions of the polymer and solvent. The system is incompressible, i.e., ∇·v = 0. We further assume there is no collective motion and that only the polymer–solvent inter-diffusion contributes to the gel dynamics;8,9,24,25 therefore, we neglect the total velocity of the polymer–solvent system, and set v = 0.
The volume fraction of polymer, ϕ, obeys the following continuity equation:
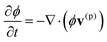 | (5) |
v(p) = Λ0(ϕ/ϕ0)−3/2(1 − ϕ)∇·![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e111.gif) . . | (6) |
Within the framework of the model, a 3D deformable gel is represented by a set of general linear hexahedral elements26,27 (see Fig. 1a and b). Initially, the sample is undeformed and consists of (Lx − 1) × (Ly − 1) × (Lz − 1) identical cubic elements (Fig. 1a), where Li is the number of nodes in the i-direction, i = x, y, z; the linear size of the elements in the undistorted state is set to Δ = 1.
We assume that the nodes that make up the posts are attached to the gels nodes, i.e., the posts (or fibers) can only move together with the gel nodes.5 We define the fiber energy as:5
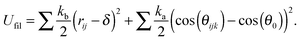 | (7) |
The schematic in Fig. 1b illustrates all the forces acting on the node common to the gel and post marked j. There are four types of forces acting on such a node.5 The first two contributions (marked in aqua and blue) represent forces arising from interactions with the neighboring gel elements and the second two contributions (in black) are due to interactions with the neighboring posts' nodes. Forces marked F1 represent spring-like elastic forces acting between this node and all the next-nearest and next-next-nearest neighboring nodes (for simplicity, only three of these contributions are shown (in aqua) in Fig. 1b). Forces marked F2 (in blue) represent the contributions from the isotropic pressure within all the gel elements containing this node; these forces include both osmotic and elastic contributions.7 The contributions from the forces that account for the post energy (eqn (7)) are marked by black arrows. The spring-like elastic forces that act between the nearest neighbor nodes within the post and describe the contribution from the first term in eqn (7) are marked as Ffilb in Fig. 1b. These forces restore the length of the bond in the post to its equilibrium length, δ.5 The force marked Ffila accounts for the contribution from the second term in eqn (7). This force ensures that the angle between each of the two neighboring bonds sharing a common node remains close to its equilibrium value and controls the stiffness28 of the post.
Since the dynamics of the polymer network is assumed to be purely relaxational,22 the velocity of node n of the element m is proportional to the total force acting on this node and is calculated as:7,9
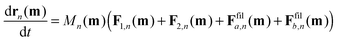 | (8) |
B. Modeling the functionalization of elastic posts with spirobenzopyran chromophores
We model the functionalization of the posts by accounting for the corresponding variation of the gel's properties within a radius R around the post. Specifically, if the position of the center of the gel's element, rC, at t = 0 satisfies the condition rC < R, we assume that the total concentration of the spirobenzopyran chromophores within this element is cSPt. We further assume that these chromophores are anchored onto the polymer network.29,30Recent experimental studies showed that in the absence of light and in acidic aqueous solutions, the spirobenzopyran chromophores are primarily in the open ring form (the protonated merocyanine form, or McH) and are hydrophilic, while illumination with blue light causes the isomerization of these chromophores into the closed ring conformation (the spiro form, or SP), which is hydrophobic.29,30 The SP form is unstable in the absence of light, and hence, in the dark undergoes spontaneous conversion back to the stable, hydrophilic McH form as:
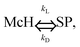 | (9) |
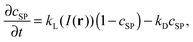 | (10) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) SP = (1 + kD/kL(I))−1.
SP = (1 + kD/kL(I))−1.
For this chemo-responsive SP-functionalized gel, we specify the last term in eqn (1) describing the energy of the polymer–solvent interaction as:13
| fint(ϕ, cSP) = α(1 − ϕ)cSP | (11) |
The uniform photo-responsive gel (no posts) can attain a steady-state if the following two conditions are satisfied: (1) the concentration of the chromophores in the spiro form has reached the photo-stationary value, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) SP, and (2) the elastic stresses are balanced by the osmotic pressure. This equilibrium degree of swelling, λeq (
SP, and (2) the elastic stresses are balanced by the osmotic pressure. This equilibrium degree of swelling, λeq (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) SP,T), depends only on temperature and on
SP,T), depends only on temperature and on ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) SP and can be found as detailed in ref. 13.
SP and can be found as detailed in ref. 13.
The physical origin of the photo-induced volume change of the SP-functionalized gels is distinctly different from the gel collapse that results from a direct light-induced heating.31,32 Experiments have shown that the temperature of the SP-functionalized gels remains constant during the illumination29 and it is the light-induced ring closure of the chromophores that results in the shrinking of the gels.
C. Simulation parameters and their relationships to the experimental values
For a set of reference parameters, we chose the dimensionless values that are based on the available experimental data. Namely, we chose poly(N-isopropylacrylamide) (PNIPAAm) as the host gel because there is experimental data on the heat-induced volume phase transitions of this lower critical solution temperature (LCST) gel19 and there is experimental data on the behavior of SP-functionalized PNIPAAm gels.29 For the parameters characterizing the properties of this thermo-responsive gel, we set ϕ0 = 0.114, and c0 = 7.2 × 10−4; these parameters match experimental values given in ref. 19. For the gel–solvent interaction parameters, we set χ1 = 0.518 and calculated χ0(T) as specified above using the following values for the changes in the enthalpy and entropy per monomeric unit of the network:19 δh = −12.4 × 10−14 and δs = −4.7 × 10−16. Again, these parameters describe PNIPAAm, which shrinks upon heating.19Within the patterned region around the functionalized posts, we set the total concentration of chromophores to cSPt = 0.2, and the interaction parameter that describes the photo-induced decrease in the hydration of the polymer network to α = 8.25 × 10−2.13 For the reference values of the forward and backward reaction rates, we used kL = 0.5 and kD = 0.05, respectively;13 at these values, the photo-stationary concentration of the chromophores in the spiro form is ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) SP ≈ 0.91. (The latter value is within the range provided in ref. 33, where researchers demonstrated that the isomerization from the McH to the SP form in the photo-stationary state ranged from 82% to 98%, depending on the specific spirobenzopyran derivatives that were used.)
SP ≈ 0.91. (The latter value is within the range provided in ref. 33, where researchers demonstrated that the isomerization from the McH to the SP form in the photo-stationary state ranged from 82% to 98%, depending on the specific spirobenzopyran derivatives that were used.)
As noted above, the parameters describing the SP-functionalized gels were based on the available experimental data.29 Using these parameters, we could quantitatively reproduce certain experimentally observed effects of light on volume phase transitions in SP-functionalized gels. Specifically, similar to the experimental observations,29 we demonstrated the following three important effects:13 (1) the shrinking of the illuminated sample up to 20% in its linear size at T = 20 °C, (2) significantly smoother volume phase transitions in the presence of light, and (3) a bell-shaped curve for the relative degree of swelling in light with respect to that in the dark as a function of temperature.
Here, we relate our reference value of the spontaneous ring closure, kD = 0.05, to the experimental value of ∼10−2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and thereby, set our dimensionless unit of time to be T0 ≈ 5 s.13 In addition, we take the dimensionless unit of length to be L0 = 30 μm.13
33 and thereby, set our dimensionless unit of time to be T0 ≈ 5 s.13 In addition, we take the dimensionless unit of length to be L0 = 30 μm.13
The size of our simulation sample (see Fig. 1a) is chosen to be 60 × 8 × 14 nodes (using the notation in ref. 7). As initial conditions for the simulations described below, we chose the concentrations of the chromophores in the spiro form, cSP, to be zero. The size of each element is taken to be a cube with side λeq (0,20) = 1.31; this equilibrium value is calculated as described in ref. 13 in the dark at T = 20 °C for the above values of ϕ0 and c0.
In all the simulations described below, the distance between the posts is seven elements and the length of the posts extending over the surface of the gel is b = 9.5. Initially, the posts are in the upright position, aligned along the z-direction (Fig. 1a). The size of the region functionalized with the chromophores is set to R = 3 and the distance between the row of posts and the front face of the sample is p = 2 elements (unless specified otherwise).
With the above scaling (and taking the size of each element to be initially λeq (0,20) = 1.31), these characteristic dimensions correspond to the following dimensional values. The sample size is 2.3 mm × 0.3 mm × 0.5 mm in the absence of illumination. The dimensionless total length of a post, taking into account the above value of λeq (0,20), is 26.53 ∼0.8 mm, with ∼0.3 mm extending over the surface of the gel; the distance from the row of posts to the front face of the sample is ∼0.08 mm, and the radius of functionalization is ∼0.12 mm. We consider sufficiently thin samples so that we can neglect the attenuation of light through the thickness of the gel.
III. Results and discussion
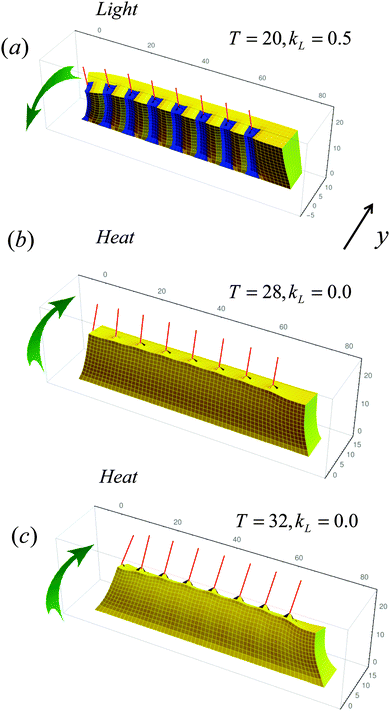
The integration of the thermo-responsive gel and the photo-responsive fibers yields a composite that displays distinctly different behavior in response to light and to heat. We first consider the scenario where the bottom of the composite is grafted to an underlying surface. Starting from the initial, unperturbed state of this system (Fig. 1a), illumination of the composite with blue light causes the fibers to bend towards the negative y-direction (Fig. 2a). On the other hand, when this sample is heated (in the absence of blue light), the fibers now bend in the opposite direction, i.e., towards the positive y-direction (Fig. 2b and c). The images in Fig. 2 represent the late time, steady-state behavior of the system and clearly show that the composite displays a different shape in response to the different stimuli, and hence, the shape can be tailored by exposing the material to different environmental cues.This behavior is all the more striking given that a thermo-responsive gel (without the fibers) containing a uniform distribution of the spirobenzopyran chromophores displays the same behavior when illuminated with blue light or heated: the entire gel shrinks in size. Namely, blue light causes the chromophores to convert to the spiro (SP) form, which is hydrophobic, and thus, drives a uniformly functionalized hydrogel to collapse. For an LCST polymer network, the gel will also collapse with increases in temperature. Hence, both stimuli produce the same effect on the system. (Images from simulations of the surface-anchored, stimuli-responsive gels without posts are given in Fig. S1 in the ESI.†)
The structural variation shown in Fig. 2 is due to localizing the chromophores solely on the fibers. Hence, when the sample is illuminated, the shrinking is confined to specific regions of the material, and thus, produces a distinct morphological pattern. When the sample is not illuminated, all the chromophores are in the open-ring McH form (i.e., CSP = 0). Consequently, the patterning around the fibers remains “hidden” and does not affect the collapse of the gel when the sample is heated in the “dark”. In effect, the application of blue light exposes this hidden pattern, and thereby, affects the bending of the posts and configuration of the sample.
The behavior displayed in Fig. 2 is also due to the specific placement of the functionalized fibers within the gel. In particular, these posts are placed relatively close to the front of sample (see Fig. 1a). In all the cases in Fig. 2, the posts bend towards the more collapsed regions. For the illuminated sample in Fig. 2a, the more collapsed regions are on the front face of the sample since this region contains the highest concentration of chromophores. Thus, the fibers bend towards the negative y-direction (i.e., away from the back of the sample). In contrast, when the sample is heated, the stiff fibers attached to the front face of the gel limit the flexibility and shrinkage of the regions around the fibers. Thus, the more collapsed regions are in the back of the sample. Consequently, the fibers bend in the positive y-direction (Fig. 2b and c). The deflection of these posts increases at higher temperatures (Fig. 2c) due to the greater temperature-induced collapse of the LCST polymer network in the back of the sample.
To quantify the dynamic behavior of these composites, we plot the temporal evolution of the y-coordinate of the tip of the central post (the fourth post from the left) at different environmental conditions. (While the temporal evolution of the other posts follows similar dynamics, posts 1 and 2 display more distinct bending due to their location near the end of the gel, as shown in Fig. S2, ESI.†) The red curve in Fig. 3a corresponds to the illuminated sample in Fig. 2a and the blue curve corresponds to the heated sample (with T = 28 °C) in Fig. 2b. The black line in Fig. 3a provides a point of reference; it indicates the y-coordinate of the tip of the central post for an equilibrated sample held in the dark at T = 20 °C. These plots clearly show that the fibers are deflected in opposite directions when the composite is exposed to the different stimuli (light and heat).
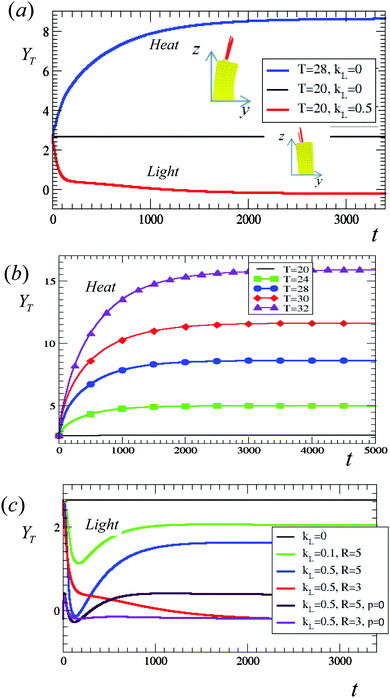 | ||
| Fig. 3 (a) Evolution of the y-coordinate of the tip of the middle fiber for the simulation in Fig. 2a (red curve) and simulation in Fig. 2b (blue curve). (b) Effect of temperature on the evolution of the y-coordinate of the tip of the middle fiber. The values of temperature are given in the legend; here, we set kL = 0.5. (c) Effect of light on the evolution of the y-coordinate of the tip of the middle fiber for different arrangements and levels of functionalization of the fibers. The values of the kL and R are given in the legend; the distance from the row of fibers to the front face of the sample is p = 2 in all of the cases except for the brown and maroon curves marked p = 0. Here, we set T = 20 °C. In (a–c), the black line marks the equilibrium position of the tips in our reference case (a non-illuminated sample held at T = 20 °C). The insets show side views of the corresponding samples after they have reached the equilibrium degree of swelling. In all the simulations, the length of the fibers extending out of the gel is 9.5 and the length of the fiber buried within the gel is 17.03 dimensionless units. | ||
The plot in Fig. 3b underscores the observation in Fig. 2b and c that the deflection of the tips can be controlled by varying temperature; namely, an increase in temperature produces a more pronounced deflection of the posts. (The upper curve in Fig. 3b at T = 32 °C corresponds to the simulation shown in Fig. 2c.) Notably, the bending of the samples in the positive y-direction upon heating is robust; at all temperatures considered here, the posts bend in the same direction, and hence, all the curves in Fig. 3b lie above the black line, which indicates the y-position of the tips at equilibrium at T = 20 °C.
Similarly, Fig. 3c shows that the effect of bending in the negative y-direction upon illumination is also robust and is observed at different radii of spirobenzopyran functionalization around the posts, light intensities, and even different placement of the posts. Correspondingly, all the curves in Fig. 3c lie below the black line (for the equilibrated, non-illuminated sample at T = 20 °C).
The plots in Fig. 3c specifically reveal the effect of varying R, the radius of spirobenzopyran functionalization around the posts. Notably, the larger radius of functionalization, R = 5 (blue curve), leads to the faster and more pronounced deflection of the post's tip at early times; however, at later times, the deflection is more pronounced for the reference case, R = 3 (red curve). (This case is shown in Fig. 2a.) In the reference case, we set the distance between the posts and the front face of the sample to be p = 2 elements (Fig. 1a).
At early times, the behavior of the illuminated samples is dominated by the response of the photo-responsive region around the posts; this area shrinks and causes the posts to bend in the negative y-direction. Since the photo-responsive region is larger for R = 5 than R = 3, the R = 5 sample initially shows a more pronounced bending than the R = 3 composite. At later times, however, the entire gel achieves the equilibrium degree of swelling, and hence, the configuration of the posts is controlled by the global behavior of the gel. In the absence of the posts, an illuminated sample that contains a uniform distribution of SP would show a uniform collapse (similar to the uniform collapse of the temperature-responsive gel). Embedded in this globally collapsed gel, the bending of the posts would be similar to their bending in the heated sample. The SP-functionalized domains in the R = 5 case occupy a sufficiently large region in the sample relative to the R = 3 sample. This increase in R yields an effectively more homogeneous sample; this results in a more global response of the gel, and the partial straightening of the posts. For R = 3, the functionalized region around the posts is sufficiently small that the bending of the posts toward the negative y-direction is due to the localized response of this more heterogeneous sample.
When R = 1, the size of the collapsed region is significantly smaller than the rest of the swollen sample (Fig. S3c and d, ESI†). Hence, the effect of the functionalization on the fibers is small and correspondingly, the fibers show the smallest deflection of the cases considered here.
The intensity of the light can also be used to tailor the deflection of the fibers in the illuminated samples. For R = 5, Fig. 3c shows that the deflection is more pronounced for the higher intensity, and correspondingly, higher value of the reaction rate coefficient, kL = 0.5, than at kL = 0.1 (as seen by comparing the respective blue and green curves). A higher light intensity leads to higher photo-stationary values of the chromophores, and hence, results in a larger degree of shrinking.13
Finally, the deflection of the illuminated fibers in the negative y-direction persists even when these filaments are placed directly at the front face of the sample (at the front node of the element 1, marked as p = 0 in the legend in Fig. 3c). Consistent with the observation at p = 2, this bending is somewhat more pronounced for R = 3 than for R = 5 because the smaller values of R = 3 allows us to access a more localized response of the sample (see corresponding images in Fig. S4, ESI† and recall that we characterize the bending by the motion of the middle fiber).
All the plots in Fig. 3 indicate that under illumination, the fibers robustly deflect in the negative y-direction, while heating the sample causes the posts to deflect in the positive y-direction. It is of interest to consider the behavior of the system in the presence of both stimuli, and thus, potentially provide another route for tailoring the morphology of the system. Fig. 4a shows the effect of applying both stimuli simultaneously to the same sample. As a point of reference, the red and blue curves show the deflection of the central tip in the y-direction solely under light and upon heating, respectively. (These curves are the same as in Fig. 3a.) If the samples are now heated in the presence of light, the posts initially deflect towards the negative y-direction, behaving similar to samples illuminated at T = 20 °C. At later times, however, due to the heat, the tips begin to deflect towards the positive y-direction. This effect is stronger for the higher temperatures considered here. Hence, the curve in Fig. 4a for kL = 0.5 at T = 28 °C (in maroon) lies higher than that for the T = 24 °C (in green).
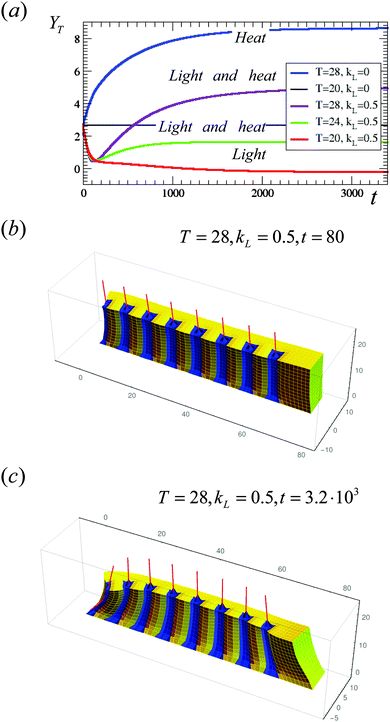 | ||
| Fig. 4 (a) Evolution of the y-coordinate of the tip of the middle fiber for the cases involving the simultaneous application of light and heat; the green and maroon curves correspond to T = 24 °C and T = 28 °C, respectively. Red, blue and black lines are the same as in Fig. 3a. (b and c) Morphology of the sample under light (kL = 0.5) at T = 28 °C at early time (t = 80) in (b) and at late time (t = 3.2 × 103) in (c). | ||
The morphology of the composites that are both illuminated and heated to T = 28 °C is shown at early times and at late times in Fig. 4b and c, respectively. At early times, only the functionalized areas around the posts are significantly collapsed, and the structure of the composite in Fig. 4b resembles that in Fig. 2a. At later times (Fig. 4c), the shrinking of the entire sample upon heating leads to a straightening out of the row of posts from the early time configuration, where the fibers were bent towards the negative y-direction Since in this case the difference between the degree of swelling within the functionalized and non-functionalized regions is smaller, the gel is less effective at driving the preferential bending of the composite. Since an increase in temperature causes a more uniform collapse of the gel, a higher temperature results in a more pronounced straightening of the posts after the initial deflection. Notably, Fig. 2a, b and 4c indicate that the application of light, heat, or the combination of these stimuli, provide distinctly different means of controlling the morphology of a given sample.
While the composites described above exhibit considerable reconfigurability, their movement is restricted by their attachment to the substrate. To harness the full range of motion that could be exhibited by these materials, we remove the constraint of anchoring the bottom layer to the surface; now, the samples are completely untethered. With the fibers initially arranged as in Fig. 1a, we again find that the samples display distinctly different behavior under light and heat. Fig. 5 shows the dramatic structural transformation and actuation that can be achieved by exposing the sample to blue light. Namely, at early times (Fig. 5a), the sample shrinks around the posts, similar to the behavior in Fig. 2a. At late times, however, the collapsed regions of this untethered sample act like hinges and drive the entire system to bend towards the front face of the sample (Fig. 5b). In effect, the material coarsely mimics the lateral dexterity of a caterpillar, as it bends its body into an arch. This biomimetic, stimuli-responsive motion could prove highly useful for creating joints that can be made to bend and unbend with light and thus, could be an essential component for new adaptive devices, including flexible robots.
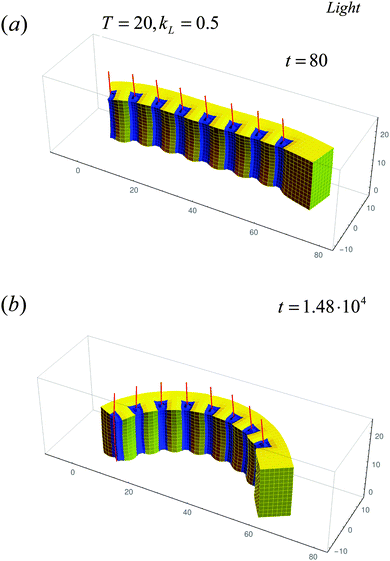 | ||
| Fig. 5 Evolution of the untethered sample under the light (kL = 0.5) at T = 20 °C at early time (t = 80) in (a) and at late time (t = 1.48 × 104) in (b). | ||
The free, untethered sample responds to heat (Fig. 6) in a distinctly different manner than to light. The motion now more closely resembles the contraction of an accordion. Namely, with the shrinking of the entire sample, the distance between the posts becomes significantly smaller (Fig. 6b and Fig. S5, ESI†). Note that these fibers are still slightly deflected in the positive y-direction.
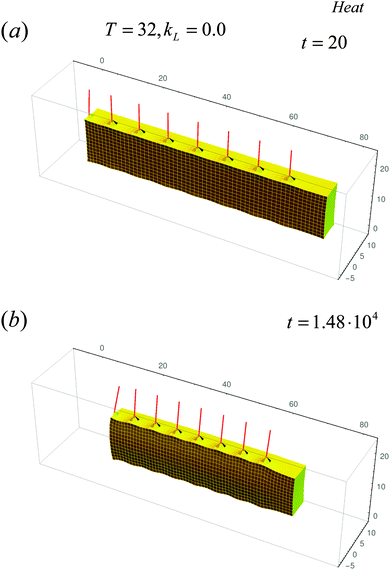 | ||
| Fig. 6 Evolution of the untethered sample in the dark at high temperature T = 32 °C at early time (t = 20) in (a) and at late time (t = 1.48 × 104) in (b). | ||
To characterize the motion of this free sample, in Fig. 7a we plot both the x-coordinate and the y-coordinate of the “terminal” post (left-most post marked as post 1 in Fig. S2, ESI†). The deflection of each post in the free sample depends on its position within the gel; we choose the terminal post to characterize the sample's motion since it displays the most pronounced deflection. Fig. 7a shows the time evolution of the x- and y-coordinates of the terminal post for the cases in Fig. 5 (black curves marked “light”) and Fig. 6 (blue curves marked “heat”). (The solid curves indicate the trajectories of the x-coordinate, while the dashed lines mark the trajectories of the y-coordinate.) This figure highlights the distinctly different temporal evolution of the heated and illuminated samples. While the trajectory of the post's tip in light corresponds to the curving of the sample, the trajectory upon heating corresponds to the shrinking of the sample (decrease in the x-coordinate) and deflection in the positive y-direction.
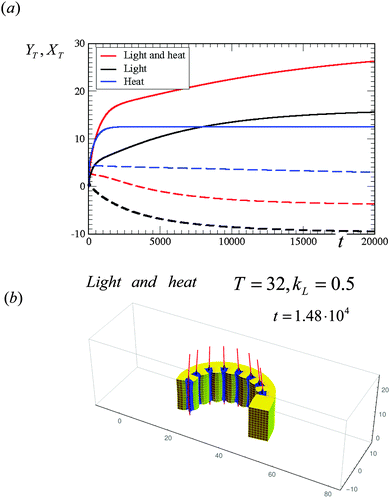 | ||
| Fig. 7 (a) Evolution of the x-coordinates (solid lines) and y-coordinates (dashed lines of the same color) of the tip of the left-most (terminal) fiber for the following cases: black lines (marked “light” in legend) correspond to the simulation in Fig. 5, blue curves (marked “heat”) correspond to the simulation in Fig. 6, and red curves (marked “light and heat”) correspond to T = 32, kL = 0.5 (see (b)). (b) Evolution of the untethered sample under light (kL = 0.5) and at late time (t = 1.48 × 104). | ||
The simultaneous application of both stimuli by heating the illuminated sample to T = 32 °C has a significant affect: it combines both the observed caterpillar-like bending and the accordion-like contraction of the sample (Fig. 7b). Importantly, however, the presence of both stimuli amplifies the bending of the sample, as can be seen by comparing Fig. 7b and 5b (taken at the same simulation time) and the respective trajectories for all these scenarios of the x- and y-coordinates (Fig. 7a). This case illustrates how the coupling of orthogonal stimuli can intensify the response of the system, and thereby, yield pronounced actuation.
IV. Conclusions
In carrying out these studies, our aim was to design composites that could be dynamically and repeatedly “programmed” via external stimuli. We specifically focus on systems that integrate thermo-responsive gels with photo-responsive fibers in an effort to create composites that are both highly reconfigurable and mechanically strong. The introduction of the photo-responsive moieties has the advantage that the composite's structure can be reconfigured both remotely and non-invasively. Furthermore, illumination can be localized to certain regions of the sample, permitting actuation of specified areas, and thus, enabling control over local motion. We expressly concentrate on functionalization with spirobenzopyran chromophores because the temperature of the sample remains constant during the light-induced collapse of the gel.29 Namely, in this system, illumination does not lead to a heating of the sample;29 this behavior allows us to exploit the localized shrinking that occurs only in the functionalized regions when the patterned sample is illuminated.It is important to recall that light and heat have the same effect on thermo-responsive gels (without the fibers) that contain uniform distributions of SP chromophores throughout the sample: both stimuli drive the gel to undergo uniform shrinkage. By localizing the SP-functionalization solely on the embedded fibers, we could design composites that exhibit a distinct response to the different stimuli. Namely, these composites can encompass patterns that remain “hidden” in the absence of the light (even at elevated temperatures) and become “developed” only under illumination. Thus, light provides a means of tailoring the shape of the sample that could not be achieved by simply heating the material.
We observed that the anchored composites bend in one specific direction under the influence of heat and bend in the opposite direction in the presence of light. In effect, heat and light provide orthogonal means of regulating the properties of these composites. The distinctive behavior in the presence of light or heat arises from a difference between a local versus global response. In particular, the localized shrinking around the posts that occurs when the sample is illuminated causes the posts (and sample) to bend in one way. On the other hand, the entire sample collapses when it is heated and this global response dictates the behavior of the system, driving the fibers to bend in the opposite direction. This effect is robust and can be modulated by changing the light intensity or temperature.
The free samples (which are not anchored to the surface) also responded to light and heat in distinctly different ways. Here, the light allowed the fibers to act as hinges, which promoted the large-scale bending of the sample. By turning the light on and off, this sample could undergo a bending and unbending that could be harnessed to grip and release a microscopic object. In this scenario, the combination of light and heat lead to a more pronounced bending and hence, both stimuli could be used to great effect in regulating the gripping behavior of the sample.
Since the top portions of the fiber are not bound to the gel, they have greater lateral mobility then the lower, bound sections. Thus, the tops of the fibers can amplify the response of the system to the external stimuli. In particular, if the system is immersed in a fluid, the fibers can transmit the motion of the gel into the surrounding media, and thus, be harnessed to perform additional tasks.5,34 Hence, the system provides a useful means of transmitting signals between different media.
In future studies, we will consider other arrangements of the partially embedded fibers, which can facilitate the design of reconfigurable hand-like structures that could serve as novel grippers. For example, we will simulate two parallel rows of functionalized fibers within the thermo-responsive gel. When this sample is illuminated, the “fingers” would move apart and be splayed away from each other. When the sample is heated, however, the fingers would come together. Hence, the combination of light and temperature could be used to manipulate the motion of the “hand”. We will also consider cases where the fibers are entirely encased in the gel; we anticipate that our findings would be qualitatively similar to the systems considered here. In particular, for systems involving fully encased fibers, the bending of the anchored and free samples will show the same trends as observed for the respective cases involving the partially embedded fibers. Overall our findings provide a route for creating strong, temporally programmable materials that can effectively self-reconfigure in response to different external cues and thus, exhibit different functionality in different environments.
Acknowledgements
We gratefully acknowledge financial support from the Army Research Office under grant number W911NF-13-0489 for studies towards applications in 4D printing and the United States Department of Energy under grant number DE-FG02 90ER45438 for the development of models for SP-functionalized gels. We also thank Prof. Ralph Nuzzo and Jennifer Lewis for helpful conversations.References
- Q. Ge, H. J. Qi and M. L. Dunn, Appl. Phys. Lett., 2013, 103, 131901 CrossRef.
- S. Tibbits, Archit. Des., 2014, 84, 116 Search PubMed.
- J. R. Capadona, K. Shanmuganathan, D. J. Tyler, S. J. Rowan and C. Weder, Science, 2008, 319, 1370 CrossRef CAS PubMed.
- J. A. Lewis, Adv. Funct. Mater., 2006, 16, 2193 CrossRef CAS.
- X. M. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Nature, 2012, 487, 214 CrossRef CAS PubMed.
- M. Behl, J. Zotzmann and A. Lendlein, Adv. Polym. Sci., 2010, 226, 1 CrossRef CAS.
- O. Kuksenok, V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041406 CrossRef PubMed.
- V. V. Yashin and A. C. Balazs, Science, 2006, 314, 798 CrossRef CAS PubMed.
- V. V. Yashin and A. C. Balazs, J. Chem. Phys., 2007, 126, 124707 CrossRef PubMed.
- V. V. Yashin, O. Kuksenok and A. C. Balazs, Prog. Polym. Sci., 2010, 35, 155 CrossRef CAS.
- R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134 CrossRef CAS.
- R. Yoshida, T. Sakai, Y. Hara, S. Maeda, S. Hashimoto, D. Suzuki and Y. Murase, J. Controlled Release, 2009, 140, 186 CrossRef CAS PubMed.
- O. Kuksenok and A. C. Balazs, Adv. Funct. Mater., 2013, 23, 4601 CrossRef CAS.
- O. Kuksenok, V. V. Yashin, M. Kinoshita, T. Sakai, R. Yoshida and A. C. Balazs, J. Mater. Chem., 2011, 21, 8360 RSC.
- I. C. Chen, O. Kuksenok, V. V. Yashin, R. M. Moslin, A. C. Balazs and K. J. Van Vliet, Soft Matter, 2011, 7, 3141 RSC.
- P. Yuan, O. Kuksenok, D. E. Gross, A. C. Balazs, J. S. Moore and R. G. Nuzzo, Soft Matter, 2013, 9, 1231 RSC.
- R. Yoshida, M. Tanaka, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 2000, 104, 7549 CrossRef CAS.
- T. L. Hill, An Introduction to Statistical Thermodynamics, Addison-Weley, Reading, MA, 1960 Search PubMed.
- S. Hirotsu, J. Chem. Phys., 1991, 94, 3949 CrossRef CAS.
- R. J. Atkin and N. Fox, An Introduction to the Theory of Elasticity, Longman, New York, 1980 Search PubMed.
- A. Onuki, Adv. Polym. Sci., 1993, 109, 63 CrossRef CAS.
- B. Barriere and L. Leibler, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 166 CrossRef CAS.
- M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001 CrossRef.
- J. Boissonade, Chaos, 2005, 15, 023703 CrossRef CAS PubMed.
- T. Roose and A. C. Fowler, Bull. Math. Biol., 2008, 70, 1772 CrossRef PubMed.
- I. M. Smith and D. V. Griffiths, Programming the Finite Element Method, Wiley, Chichester, England, 2004 Search PubMed.
- O. C. Zienkiewicz and R. L. Taylor, The Finite Element Method, Butterworth-Heinemann, Oxford, England, 2000 Search PubMed.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750 CrossRef CAS.
- A. Szilagyi, K. Sumaru, S. Sugiura, T. Takagi, T. Shinbo, M. Zrinyi and T. Kanamori, Chem. Mater., 2007, 19, 2730 CrossRef CAS.
- T. Satoh, K. Sumaru, T. Takagi and T. Kanamori, Soft Matter, 2011, 7, 8030 RSC.
- A. Suzuki and T. Tanaka, Nature, 1990, 346, 345 CrossRef CAS.
- A. Suzuki, Adv. Polym. Sci., 1993, 110, 199 CrossRef CAS.
- T. Satoh, K. Sumaru, T. Takagi, K. Takai and T. Kanamori, Phys. Chem. Chem. Phys., 2011, 13, 7322 RSC.
- A. Shastri, L. M. McGregor, Y. Liu, V. Harris, H. Q. Nan, M. Mujica, Y. Vasquez, A. Bhattacharya, Y. T. Ma, M. Aizenberg, O. Kuksenok, A. C. Balazs, J. Aizenberg and X. M. He, Nat. Chem., 2015, 7, 447 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mh00212e |
| ‡ Present address: Department of Materials Science and Engineering, Clemson University, Clemson, SC 29634, USA. |
| This journal is © The Royal Society of Chemistry 2016 |