Block copolymer compatibilizers for ternary blend polymer bulk heterojunction solar cells – an opportunity for computation aided molecular design

Abstract

In this review article, we discuss some recent developments in the context of the use of block copolymers (BCP) as compatibilizers in ternary blend organic photovoltaic devices. At the outset, we review some of the salient experimental studies and highlight the successes achieved in using BCPs to improve the long-term stability of the donor–acceptor based devices. We suggest that the physico-electro-chemical properties of BCP compatibilizers may be targeted as a hitherto less-explored handle to modulate the morphology and device characteristics of such systems. In this regard, we propose that coarse-grained computer simulation tools, despite being limited in their ability to capture complex interaction features and crystallization phenomena, can serve as a guide to narrow and/or identify parametric regions where morphologies desirable for better exciton and charge transport can be achieved. Furthermore, we suggest that the output of the morphological predictions can be combined with coarse-grained device simulation approaches to identify the overall photovoltaic properties of the ternary blends containing such BCP compatibilizers. Together, such computational studies can serve to connect the molecular structure and electronic properties of the BCP to the overall device properties and, thereby, to enable a rational molecular design of BCP compatibilizers for organic photovoltaic devices.

---

1 Introduction

1.1 Bulk heterojunction solar cells

Recently, there has arisen a significant interest in organic photovoltaic (OPV) and organic light emitting devices (OLED) based on conjugated polymers.^1–9 In contrast to inorganic silicon and germanium based materials, organic materials with appropriate chemistries allow for processing techniques such as spin coating^10–12 and roll-to-roll fabrication,^13,14 which facilitate deployment over large surface areas. Moreover, many of the materials used in organic electronic applications possess large optical absorption coefficients, which enable thinner films for devices. In view of such advantages, it is widely believed that OPVs and OLEDs hold the key to scalable, low cost, sustainable energy devices.

The mechanisms underlying charge transport in OPVs exhibit significant differences from their inorganic counterparts.^2,15,16 Inorganic materials possess high dielectric constants, and hence photogenerated excitons directly separate into free charge carriers (electrons and holes). In contrast, OPVs typically involve materials with low dielectric constants, and hence the binding energies of photogenerated excitons (electron–hole pair) preclude direct separation into free electrons and holes. As a consequence, excitons have to travel to an electron-donor/electron-acceptor material interface where the differences in the energy levels of the donor and acceptor molecules lead to a dissociation and separation of the excitons into electrons and holes.

The above-discussed mechanistic features impose a number of constraints and challenges for the design of OPVs.^17–27 At a materials level, the challenge has been to develop appropriate electron donors and acceptors that simultaneously possess the desirable features of suitable energy level offsets, light adsorption capabilities and charge mobilities. Moreover, the presence of two or more materials within OPVs places some unique constraints on the morphological aspects. Indeed, the life-time of the generated excitons is believed to be of the order of pico/nanoseconds, which constrains the donor–acceptor interfaces to be within an order of 10 nm to facilitate charge carrier generation. Further, once the exciton dissociates into electrons and holes, the charge carriers require continuous morphological pathways to the respective electrodes.

Motivated by the above morphological requirements, significant interest has arisen in bulk heterojunction (BHJ) device configurations, which are characterized by continuously percolating donor and acceptor domains permeating the film.^{17,18,21,22,24,28–36} The expectation is that, if the size scale of the domains can be tuned to the order of exciton diffusion length, the presence of many donor–acceptor interfaces would facilitate efficient exciton dissociation. Moreover, the existence of an interpenetrating network of domains would enable the transport of dissociated free electrons and holes to their respective electrodes. Based on such considerations, it is widely believed that optimized BHJ morphologies hold the key to the design of efficient OPV devices.

Typically, organic photovoltaic BHJ cells are fabricated by either mixing a conjugated polymer (donor) with acceptor C₆₀ molecules (or their derivatives) or by blending a donor and an acceptor conjugated polymer.^17,25,30 Often such components are either immiscible or partially miscible, which leads to phase separation into domains that are separated by interfaces with different degrees of intermixing.^37,38 Moreover, in many cases, the donors and/or acceptors themselves also crystallize within such domains.³⁹ An outstanding issue is that the morphologies resulting in such conditions often correspond to metastable states formed enroute to the true equilibrium of phase separated domains.⁴⁰ Not surprisingly, many experiments have reported that the performance of the device degrades with time due to the resulting evolution of the morphologies.^41–43 More pertinently, processing conditions such as thermal/solvent annealing,^44–48 solvent used for casting etc.⁴⁹ have also been observed to exert a sensitive effect on the morphology and device characteristics.^18,50 As a result, there has arisen significant interest in strategies that can enhance the long-term stability of the devices through a stabilization of the morphologies.

1.2 Ternary blend solar cells with block copolymer compatibilizers

In the context of BHJ solar cells, block copolymers (BCPs) have recently emerged as materials of interest for stabilizing the desired morphological features.^23,51–56 Block copolymers are macromolecules comprised of two or more covalently bound homopolymer chains. The incompatibility between the blocks often drives the morphological segregation of the components, but the presence of a covalent bond precludes bulk phase separation into macroscopic domains. As a result, such materials self-assemble into nanoscopic domains with a morphology that is controlled by the volume fraction of the different blocks and the temperature (i.e. the degree of incompatibility between the blocks). A vast body of literature has studied the morphology of such systems for different parametric conditions.⁵⁷

Not surprisingly, a number of studies have also explored the use of BCPs in the context of OPVs. One strategy envisions the self-assembly of block copolymers merely as a means to achieve ordered morphologies within which the donors and/or acceptors can be introduced.^58–62 A different strategy envisions the use of functional block copolymers containing one or more semiconductor blocks to simultaneously achieve the morphological and the electronic characteristics desired in OPVs.^{23,24,53,63–73} Such interest stems from the fact that the self-assembly of such conjugated block copolymers leads to morphologies that simultaneously possess length scales on the order of the exciton diffusion length and continuous pathways that can enable charge extraction. Moreover, such morphologies are equilibrium microstructures and, in contrast to donor–acceptor mixtures, are not expected to coarsen with aging. In line with such expectations, a number of recent studies have demonstrated the successful fabrication of devices based on all conjugated block copolymers.^{23,24,53,63–73} While the efficiencies of such devices have lagged behind the conventional donor–acceptor blends, considerable opportunities remain and are actively being pursued to engineer the molecular and electronic structure of the components to enhance the resulting performance.

A third strategy of application of BCPs in OPVs borrows the idea of solid-state block copolymer compatibilizers, which have long been pursued to control the domain sizes in the context of commodity polymer blends.^74,75 Therein, surfactant-like block copolymers, comprised of two or more blocks designed to exhibit preferential interaction with the different components in the mixture, have played an important commercial role in stabilizing the blended morphologies. When dissolved in the blend, the copolymers migrate to the domain interfaces⁷⁶ and, by a combination of the reduction in interfacial tension⁷⁷ and a suppression of coalescence of the droplets, ensure both a stabilization of the domains and smaller domain sizes.⁷⁸

Despite the immense popularity of copolymer compatibilizers in other contexts, it was only in 2006 that pioneering experiments by Sivula et al. demonstrated the design and use of block copolymers in OPV applications.⁷⁹ Explicitly, they synthesized a block copolymer comprised of poly(3-hexylthiophene) (P3HT) repeat units in one segment and fullerene pendants in the other segment as a compatibilizer for P3HT:PCBM based OPVs. They compared the morphologies and the performance of devices fabricated with and without the compatibilizers. While the as-cast morphologies exhibited similar characteristics, annealing of the blends in the absence of compatibilizers resulted in growth of domain sizes and a degradation of the device performance. In contrast, by the addition of a suitable amount of compatibilizer, the authors demonstrated that they could lower the interfacial energy between the donors and acceptors such that no detectable phase segregation was observed after annealing. Relevantly, they also demonstrated that such a device exhibited no degradation in properties even after annealing over a period of ten hours (cf.Fig. 1).

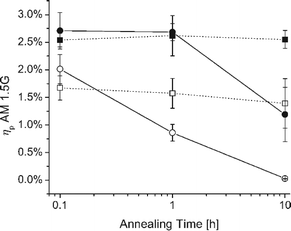Fig. 1 (Adapted with permission from Sivula et al.⁷⁹) Average power conversion efficiency of 1 : 1 P3HT/PCBM solar cells as a function of annealing time before (open circles and squares) and after (closed circles and squares) deposition of the aluminum electrode. Circles represent standard P3HT:PCBM devices, while squares represent devices made with 17 wt% of BCP included in the active layer.

In a later study,⁸⁰ Wudl and coworkers synthesized a donor–acceptor diblock copolymer based on a P3HT rod block and C₆₀ chromophores using a reversible addition fragmentation chain transfer (RAFT) polymerization strategy and studied the influence of various concentrations of the compatibilizer on the morphologies and the device properties of the resulting BHJ cells. Their study demonstrated an almost 35% increase in the device efficiency for a film that contained 5 wt% compatibilizer. Lee et al.⁸¹ investigated a similar system of a blend of P3HT:PCBM and a compatibilizer P3HT-b-C₆₀ based on side-chain fullerenes. They demonstrated that the domain sizes in the P3HT:PCBM blend increased with increasing annealing times, whereas the compatibilized mixtures maintained a bicontinuous network morphology during the annealing process. They suggested that the preferential location of the copolymer at the interface between the P3HT and PCBM phases inhibited the macrophase separation under annealing.

The above seminal studies have since sparked an intense interest in the synthesis and use of a variety of block copolymer compatibilizers in BHJ OPV devices.^82–85 A number of initial studies were based on diblock copolymer compatibilizers whose one block was P3HT and whose other block contained C₆₀ in either a side chain, pendant or end-capped form.^81,86–89 However, more recently, interest has arisen in other kinds of chemistries and architectures for serving as compatibilizers. In an early study, Tsai and coworkers used a coil-rod-coil triblock copolymer poly(4-vinyltriphenylamine)-b-poly(3-hexylthiophene)-b-poly(4-vinyltriphenylamin) (PTPA-P3HT-PTPA) as a surfactant for P3HT/PCBM based solar cells.⁹⁰ The morphologies were shown to become modulated by the volume fraction of the compatibilizer, and, moreover, the aggregation of PCBM was shown to become reduced. Such morphological changes were shown to lead to an enhancement in the power conversion efficiency of the device. Hadziioannou and coworkers^82,87,91 studied a variety of P3HT based compatibilizers and demonstrated that the BCP can lead to a range of morphological effects (which include increased crystallinity of P3HT, reduced agglomeration of PCBM etc.) that translate to better device performances. Yuan⁹² compared two liquid crystalline copolymer compatibilizers and showed that the self-assembly of the liquid crystalline block enhances the crystallization and ordering of P3HT chains and improves the efficiency of exciton separation of the active layer. Other studies have examined compatibilizers such as P3HT-PEO,⁹³ P3HT-PTCNE (and their triblock version)⁹⁴ and PS-b-P3HT⁹⁵ and have demonstrated similar morphological effects on P3HT-PCBM blends, which reflect in enhanced device performance and thermal stability. A slightly different strategy⁹⁶ was pursued by Jo and coworkers, in which a fullerene-end-capped poly(ethylene glycol) (PEG-C₆₀) was used in a P3HT/PC61BM blend. The PEG-C₆₀ molecules migrated to the surface of the P3HT/PC61BM active layer and induced a segregation of PC61BM to the top surface. The authors demonstrated that such segregation increased the VOC and improved the stability of the OPV by protecting the active layer from oxygen.

Most of the above-discussed studies were based on the most popular combination of donors and acceptors, viz., P3HT/PCBM solar cells. However, more recently, several studies have expanded the compatibilizer concept to other donor–acceptor combinations.^97,98 Frechet and coworkers⁹⁹ synthesized poly(3-hexylthiophene)-block-poly(bismide perylene acrylate) copolymer for use in poly(3-hexylthiophene):perylene diimide blend solar cells and reported an almost three fold improvement in performance relative to the uncompatibilized blend. Greenham and coworkers synthesized a fully conjugated diblock copolymer (P3HT-b-PFTBTT),⁹⁸ used it in a donor–acceptor mixture of the individual blocks and showed enhanced thermal stability relative to the uncompatibilized blend. Kim et al.¹⁰⁰ developed a graft architecture compatibilizer, poly(3-hexylthiophene)-graft-poly(2-vinylpyridine) (P3HT-g-P2VP), that was shown to lead to an enhancement of the mechanical and thermal stabilities of BHJ layers composed of a P3HT donor and various kinds of fullerene acceptors. Interestingly, they demonstrated that the P3HT-g-P2VP copolymer had better compatibilizing efficiency and enhanced mechanical and thermal stabilities when compared to linear type P3HT-b-P2VP. Green and coworkers fabricated BHJ solar cells using blends of poly(3-hexylthiophene) (P3HT) donor, indene-C₆₀ bisadduct (ICBA) acceptor, and an all-conjugated random copolymer (RCP) additive.¹⁰¹ By optimizing the RCP loading, they showed that power conversion efficiencies up to 20% higher than those of a binary P3HT:ICBA mixture can be achieved. The improved device characteristics were rationalized as a consequence of RCP induced improvement in the degree of structural order of the BHJ fibrillar network and the extent of microphase separation between P3HT and ICBA.

It is evident from the above discussion that significant strides have been achieved in the past decade in the use of block copolymer compatibilizers in OPV devices. In almost all cases, favorable morphological effects have been noted, and have ranged from diminished phase separation, enhanced thermal stability, increased crystallization of P3HT, reduced agglomeration of PCBM etc. In many cases, such morphological effects have also translated to better photovoltaic performance as reflected in the efficiencies, short circuit currents and fill factors. Inspired by such successes, similar strategies are also starting to be pursued in the context of hybrid organic–inorganic solar cells.¹⁰²

1.3 Molecular design of block copolymeric compatibilizers: motivation

Despite the impressive progresses reported, the design and use of block copolymer compatibilizers in OPVs has remained more driven by advances in synthetic chemistry alone rather than being informed by the expected physico-electronic effects on the morphology and the device properties of the donor–acceptor blend. However, even with a limited palette of chemistries, a substantial number of physical parameters can be modulated to influence the morphologies and the resulting properties of the OPV devices. For instance, one can vary the volume fraction of the blocks in the copolymer, the molecular weight of the copolymer relative to the donor and/or acceptors, and possibly even the architecture of the copolymer (i.e. effect architectural modifications to create triblock, graft and random copolymer versions). In this regard, a particularly attractive feature of ternary donor–acceptor blends containing block copolymer compatibilizers is that, with appropriate annealing protocols, morphological features consistent with thermodynamic equilibrium can be achieved. Pertinently, in contrast to binary donor–acceptor blends where the equilibrium often corresponds to macroscopically phase separated domains, ternary blends can exhibit more complex equilibrium morphologies, which can be modulated by the physical parameters discussed above.¹⁰³

Excepting a few instances, block copolymer compatibilizers have mainly been targeted for modulating the morphology of the donor–acceptor blend. In this context, we note that significant interest has recently arisen in organic ternary blends based on electron donor or acceptor additives meant to enhance the absorption wavelengths compared to the primary donor–acceptor mixture.^104–108 A number of studies have shown that the use of such ternary components can also exert significant influence on other device characteristics such as the open circuit voltage.¹⁰⁹ While considerable research is ongoing in the design and exploration of various candidates as the ternary component and the mechanisms are still not completely resolved,^110–112 block copolymer compatibilizer additives represent a less explored avenue to achieve the features and properties desired in the above new developments. Indeed, as discussed earlier, by choosing the interactions/chemistry of the BCP with the donor and acceptor components in an appropriate manner, equilibrium morphologies with controlled distribution of the BCPs additives within donors and acceptor phases can be achieved. For instance, for optimal charge transfer, it maybe desired that the third component of the ternary blend be located at the interface between that of the donor and acceptor. If the blocks of the compatibilizer are chosen selective to the donor and acceptor respectively (a surfactant like configuration), such an objective can be easily facilitated using BCPs. Additionally, if the optoelectronic characteristics of the BCP are chosen appropriately, energy cascades that reduce charge recombination can be achieved.^113–115 Such considerations suggest that, with appropriate choice of the electronic properties of the copolymer blocks, the BCP compatibilizers can potentially be used to actively modulate the photo-electronic properties and thereby the resulting device characteristics.

The parameter space accompanying ternary blends with BCP compatibilizers is vast, rendering it intractable to navigate through an exclusively experimental program. We suggest that, through appropriate combination of computational tools and experimental measurements, it may be possible to rationally target morphologies possessing desirable characteristics for OPV applications. Motivated by such considerations, in the next section, we briefly review the different scales of computational tools used for studying BHJ devices and identify a possible set of tools to design such BCP compatibilizers for facilitating both morphological and device level control.

2 Computer simulations of BHJ based OPV devices

There have been significant developments in computational approaches that both facilitate fundamental understanding and aid in the materials discovery/device fabrication of OPV materials. Below, for ease of discussion, we classify the computational approaches into four broad levels:

(i) Quantum simulations: approaches based on density functional theory and quantum-dynamics based methods have been utilized¹¹⁶ to investigate the electronic structure and photoelectric processes of individual, or at most, a small number of molecular species. Such simulations have been utilized in the design of next generation polymer donors with the small optical band gaps and large transition dipole moments required to promote photon absorption across the solar spectrum.^117,118 They have also been utilized to predict the ionization potentials, electron affinities, reorganization energies, and intramolecular/intermolecular electronic coupling of donors and acceptors etc.^119–121 To maintain brevity of this article, we do not discuss these developments further, and instead refer the reader to comprehensive reviews/articles on this topic.^116,122,123

(ii) Atomistic simulations: methodologies that embody chemically realistic descriptions of the molecules and corresponding force fields remain the most accurate framework for capturing the influence of molecular structure on the properties of systems. Not surprisingly, such simulations have been extensively used in the context of OPVs to study the detailed structure and packing characteristics of donors and/or acceptors at the nanoscale level.^124–129 For instance, Cheung et al.¹³⁰ used classical MD simulations to study the interlayering and arrangement of low molecular weight P3HT and connected their observations to the charge mobilities in such systems. Similar in spirit molecular packing studies¹³¹ were effected on PBTTT (poly(2,5-bis(3-alkylthiophen-2-yl)thieno[3,2-b]thiophene)) to identify the mechanistic origins of their hole transport properties. More recently, Alexiadis et al. used such simulations¹²⁶ to extensively characterize the conformational and configurational behavior of P3HT molecules in both crystalline and amorphous configurations. A number of other studies have used similar approaches to probe the packing and arrangement of molecules and the related impact on charge transfer etc.^132–136

(iii) Mesoscopic/coarse-grained simulations: even with the present advances in computational power, atomistically detailed models are only capable of studying a small number of molecules and for time scales of the order of a few nanoseconds at most. Such time scales are insufficient to accommodate the phase separation of the mixture, and, moreover, the length scales are limited in their ability to capture mesoscale order, which may result in the context of binary and ternary blends. In this regard, significant interest has arisen in the development of coarse-graining strategies and models that can capture the longer length and time scale characteristics of OPV systems. One class of such coarse-grained models strives to maintain a strong connection to the atomistic scale by envisioning coarse-grained sites to rigorously represent a collection of atomistic units. Often, the potentials governing the interactions between such coarse-grained sites are explicitly obtained using smaller scale simulations of atomistic descriptions.¹³⁷ In an early study in this regard,^138,139 Lee et al. developed a multiscale simulation framework that included coarse-grained (CG) simulations followed by reverse mapping (i.e. reintroduction of atomistic details) to study the morphology evolution in BHJ films comprising P3HT and PCBM. A phase-separated blend film with the fibrillar P3HT structure was observed in their CG simulations, and, by reintroducing the atomistic details, they showed strong π–π interactions between the thiophene rings at the atomistic level. Faller and coworkers presented coarse-grained models^140–142 in which collections of atoms from a physically accurate atomistic model were rigorously mapped onto a smaller number of coarse-grained units. They effected such coarse-graining for P3HT and P3HT/fullerene-C₆₀ mixtures, and used it to study the evolution and cluster formation in C₆₀ of the binary blends upon lowering the temperature (cf.Fig. 2). In recent studies, Jayaraman and coworkers^143,144 used such coarse-grained models to elucidate the influence of side chain length and positioning on the morphology of blends of 2,5-bis(3-alkylthiophen-2-yl) thieno[3,2-b]thiophene, BTTT, and fullerene derivative based acceptors. Bredas and coworkers used similar coarse-grained models to study¹⁴⁵ mixtures of P3HT with a variety of acceptors to identify the connection between the chemical structure and the mesoscale structure of such mixtures. A number of other studies have used similar models to probe the nanomorphology,^146–148 the role of annealing protocols^149,150 and the mechanical properties¹⁵¹ of such OPV donor–acceptor mixtures.

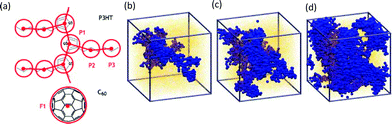Fig. 2 (Adapted with permission from Huang et al.¹⁴¹): (a) Chemical structures of P3HT and C₆₀ with coarse-grained site types depicted and labeled; (b)–(d) snapshots of the simulation configuration of the system with P3HT : C₆₀ = 1.27 : 1 (w/w) at t = 0 ns (b), t = 30 ns (c), and t = 135 ns (d). The C₆₀ molecules in the largest cluster are highlighted in blue and all other particles in the system shown as dots.

While the above “intermediate” scale coarse-grained models have had a significant impact in developing an understanding of the morphological features of OPV mixtures and the underlying connection to the chemical details, such models are still too detailed and computationally expensive to effect a parametric study of the morphologies resulting in ternary blends. Moreover, the formation and identification of microphase separated morphologies, which are ordered on nanometer length scales, proves to be a challenge within such methodologies. In this regard, we note that, in the context of multicomponent polymer melts and solutions, considerable success has been achieved in predicting the equilibrium morphological characteristics through the use of “highly” coarse-grained models.¹⁵² Such a framework employs simplistic micromechanical models that embody the main characteristics of the system and use generic and tractable intra- and intermolecular interactions to capture the essential physics. While such a framework can be implemented within different methodologies,^153,154 in section 2.1 below, we discuss approaches that are based on a field-theory framework that proves especially convenient for computational implementation and, in many instances, also yields results that are quantitatively consistent with experiments. We suggest that such a computational framework holds promise for the design, based on morphological considerations, of block copolymer compatibilizers for ternary blends in OPV applications.

(iv) Macroscopic/continuum level device simulations: such studies have focused on device properties, which result from the interplay between the mesoscopic morphologies and the electronic properties of the constituents. We discuss these further in section 2.4 and highlight their potential role in enabling an extra layer of molecular design of BCP compatibilizers.

Computer aided design of OPVs is truly a multiscale problem such that no single scale of simulation method can effectively address all the underlying issues.¹⁵⁵ While significant progress has been achieved in the development of efficient methodologies in the different scales discussed above, connecting them to implement a multiscale program of designing OPVs remains a holy grail. In the following sections, we concern ourselves mainly with the computational design of ternary blend OPVs (containing block copolymer compatibilizers) with the desired morphological features and device characteristics. Using such a context as a framework, we discuss how the tools developed in the level (iii) above can be used to study the equilibrium phase behavior. We suggest that such tools can be used in conjunction with experiments to identify physical parameter combinations likely to result in ternary blend morphologies of interest. In section 2.4, we review some of the recent work in the continuum models in level (iv) above which allow one to translate the mesoscale morphological characteristics to device characteristics. We suggest that such advances can be combined with the morphology tools to enable the design of BCP compatibilizers that can result in optimal performance characteristics. Since there are a number of excellent review articles on the individual computational aspects discussed above, we restrict our discussion only to the most relevant works.

2.1 Field theory approaches for multicomponent conjugated polymeric materials

In the context of polymeric systems, field-theory approaches have been extensively used for cataloging the morphological phase behavior of block copolymer melts consisting of conformationally flexible polymer chains.^152,156 In such a framework, the conformation of each molecule is parameterized by a continuous variable, and a continuum limit of the Hookean spring energy is ascribed to characterize the intramolecular interactions. Nonbonded interactions are usually enforced as simple contact forces between the different monomers and are supplemented by a constraint of overall incompressibility, which enforces the hard core interactions in an approximate manner. Despite its simplicity, the exact analytical treatment of the statistical mechanics of such a model is not tractable. However, in the limit where thermal fluctuations can be neglected (often corresponding to the limit of very long polymer chains and/or concentrated systems), accurate results can be obtained by using a mean-field approximation supplemented by a numerical solution.^152,157 In the last two decades, a number of approaches have been proposed to facilitate efficient and highly accurate numerical solutions of such field theories – notably, such approaches have demonstrated remarkable quantitative agreement with experiments.^158,159

In contrast to flexible copolymers, the polymers used in OPV applications usually contain at least one semiconductor/conjugated polymeric component, which renders the molecule either rigid (rodlike) or semiflexible. The presence of such materials leads to a significant impact on the morphological characteristics exhibited by such systems. For instance, early experimental studies on rod-coil block copolymers, which contain a rod-like rigid component linked to a flexible coil-like component, demonstrated self-assembly into a number of liquid crystalline morphologies such as smectic, columnar, arrowhead and zigzag phases.^160,161 Motivated by such experiments, a number of theoretical studies (based on field theory framework) undertook to examine the influence of conformational rigidity on the morphological phase behavior of block copolymers. The first such investigations employed approximations based on scaling arguments and/or assumptions of weakly segregated morphologies to study the formation of liquid crystalline and microphase order in rod-coil BCPs.^162–167 Mean-field theories (commonly termed as self consistent field theory, SCFT, in this context) for the phase behavior of rod-coil block copolymers were later developed to eliminate the assumptions accompanying the earlier works and to delineate the interplay between liquid crystalline ordering and the formation of microphase separated morphologies.^168–173 Numerical calculations based on such theories indicated, in agreement with experimental observations, that the phase behavior of rod-coil BCPs exhibit significant differences from their coil–coil counterparts. Explicitly, in contrast to the morphologies seen in the latter case (such as hexagonally arranged cylinders, body-centered cubic spheres etc.), mostly lamella like morphologies are predicted in the context of rod-coil BCPs.^170,174 More recent studies have developed efficient numerical approaches to study the mean-field theories accompanying rod-coil copolymers^175,176 and their multiblock variants,¹⁷⁷ as well as to elucidate the effects of external confining surfaces.¹⁷⁸

The conjugated polymer donors and acceptors typically utilized in OPVs often possess a finite value persistence length, L_P, whose value relative to the contour length L of the molecule depends on both the chemistry of the molecule and the molecular weight. Depending on the ratio L_P/L, a molecule can be rendered anywhere from flexible (L_P/L ≪ 1) to rod-like (L_P/L ≫ 1). Motivated by such conformational characteristics of different conjugated polymers, more recent works have investigated the morphological phase behavior of BCPs containing semiflexible blocks. Unfortunately, for such systems, the numerical framework accompanying the mean-field theory becomes substantially more complex. Creative numerical methods^179–181 have been proposed to enable the solution of such equations to probe morphologies in three spatial dimensions.^182,183 In recent studies,^184–186 Chen and coworkers used such a framework to elucidate the morphologies of diblock copolymers containing semiflexible blocks and identified a variety of complex microphase separated morphologies that resemble those seen in coil–coil diblock copolymers.

In the context of BCPs containing semiflexible blocks, hybrid methods, which embed the statistical features of a SCFT within a second simulation framework (i.e., Monte Carlo,¹⁸⁷ Brownian dynamics,¹⁸⁸etc.) and allow for efficient computations for semiflexible polymers, have also been developed. Such hybrid methods incorporate the same model framework underlying the field theoretic approach and hence provide results that match the solution of SCFT except insofar as including additional effects native to the second simulation framework (for instance, fluctuation effects). Kumar and Ganesan utilized self-consistent Brownian dynamics to investigate the equilibrium phase behavior of a semiflexible-flexible BCP (see Fig. 3).¹⁸⁹ They were able to capture (see Fig. 3) the morphological changes resulting from a transition from the flexible chain (L_p/L = 0.02) to the rod-like limit (L_p/L = 1.0). Daoulas and coworkers used similar ideas to develop a coarse-grained model to study the phase behavior of P3HT, demonstrated that their model can describe uniaxial and biaxial nematic mesophases and reproduced the experimentally observed effect of molecular weight on phase behavior. They used such morphologies as input for studying charge transport properties and showed the importance of chain ends and orientational correlations.^190,191

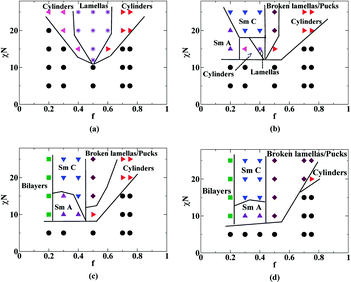Fig. 3 (Adapted with permission from Kumar et al.¹⁸⁹): Phase behavior of semiflexible-flexible BCPs:¹⁸⁹ (a) L_p/L = 0.02; (b) L_p/L = 0.2; (c) L_p/L = 0.5; (d) L_p/L = 1.0. The results presented here span the range from a completely flexible chain (L_p/L = 0.02) to the rod-like limit (L_p/L = 1.0). f and x denote the volume fraction of the coil and the Flory interaction parameter between the rods and coils.

2.2 Open issues underlying the application of coarse-grained models to OPVs

It is evident from the above discussion that considerable advances have occurred in the context of the highly coarse-grained models for enabling accurate predictions of the morphologies of multicomponent polymer systems exhibiting the conformational rigidity characteristic of the conjugated molecules used in OPV applications. Despite the attractiveness of such computational methodologies, some outstanding limitations remain in translating the advances to OPVs. Primarily, most of the coarse-grained approaches (including many of the “intermediate” resolution methods discussed in the section 2), are capable of modeling only amorphous materials. However, crystallization is prevalent in conjugated polymers, and, in many cases, the performance of devices has been observed to be sensitively dependent on the degree of crystallinity.^192–196 Unfortunately, the model simplifications accompanying such coarse-grained methods, which enable long time and length-scale simulations, also eliminate the critical features of interactions that drive crystallization phenomena. To date, the accurate incorporation of such crystallization effects within models for self-assembly of conjugated polymers remains a significant, but unfulfilled goal.

Along the above lines, another limitation of coarse-grained models is in their insufficient ability (in the current forms) to capture the complexity of the intermolecular interactions that accompany the materials used in OPV applications. For instance, the most commonly used donor material, P3HT, exhibits directional π–π interactions, which prove important for self-assembly.^197,198 While approximate approaches have been proposed to mimic such interactions,^190,191 the quantitative ability to render such complex physics within such simple force fields remains an open issue. A similar issue relates to the influence of the electrodes and their interactions with the components in modulating the morphologies of the donor–acceptor systems. While approaches exist to model the influence of confining surfaces within the coarse-grained models discussed in the preceding section,¹⁷⁷ their reasonableness in the context of OPV materials and electrodes remains to be validated.

Another important challenge for coarse-grained methods is in connecting the parameters accompanying such models to experimental systems. While a vast body of literature has developed a framework for connecting the parameters appearing in the field theoretical models of flexible di- and multiblock block copolymers to the experimental results of scattering,¹⁹⁹ contact angle and interfacial segregation measurements, there is considerably less clarity on the corresponding framework for conformationally rigid polymers especially when characterized by orientational interactions.^172,174 Recently, remarkable progress has been achieved in adapting rigorous coarse-graining formalisms for use with atomistic simulations to extract the interaction parameters and potentials accompanying coarse-grained models.^200–205 While such approaches still need to be refined for characterizing multicomponent interactions,^203,206 nevertheless, in situations where accurate atomistic force fields exist, such coarse-graining methodologies hold hope for circumventing complex experimental measurements to parameterize such models.

Finally, most of the above discussion centered on a simulation framework capable of studying the equilibrium characteristics of polymeric systems. While modifications necessary to address dynamics and kinetic effects have recently been proposed,^188,207,208 such a framework has not been implemented for conjugated polymers and their multicomponent versions. As a consequence, the applicability of such tools to conventional donor–acceptor BHJ devices remains limited.

2.3 Design of copolymer compatibilizers for OPVs based on morphology considerations: outlook and a case-study

Coarse-grained computational methods (especially the field-theoretic approaches discussed in the previous section) have long served as a useful tool for studying the equilibrium properties of ternary blend systems containing surfactants and polymeric compatibilizers. Specifically, a number of initial studies were concerned with mixtures consisting of two immiscible homopolymers and a relatively small amount of block copolymer.^77,209,210 Such researches have quantified the changes in the interfacial properties of the polymer blend systems that result from block copolymer additives as a function of the sequence, architecture and molecular weights of the compatibilizers.

More recently, interest has arisen in the complete equilibrium (morphological) phase behavior of ternary polymer blends containing flexible block copolymers and two other flexible polymeric components.^211–219 A part of the interest in ternary blends has arisen from seeking to understand whether additional polymeric components can be used to modulate the self-assembly patterns that arise in diblock copolymers. For instance, in the context of a mixture of a symmetric AB diblock copolymer and a polymer blend of A and B components (of equal volume fractions), it has been found that novel bicontinuous microemulsion (BμE) morphologies, which are equilibrium nanoscale structures possessing percolating domains, can be achieved at appropriate concentrations of block copolymers.²¹¹ While much of the parametric space of such ternary blends remains to be explored in theoretical studies, preliminary reports suggest that expanding the sequence and architecture of the copolymer in such blends can potentially enable access to a number of complex morphologies.^212–219

We suggest that field-theoretic methods with appropriate models that make allowance for the conjugated nature of the polymers (section 2.1) can serve as a useful framework for the computation-aided molecular design of block copolymer compatibilizers for ternary blend based OPV applications. At least two possible kinds of molecular design studies may be facilitated by such computational approaches. At one level, adapting the formalism of the earlier studies discussed above,^77,209,210 it may be possible to design the architecture and sequence of block copolymer compatibilizers to facilitate the largest possible reduction in interfacial tension between the donor and acceptor components. A second direction, following the approach of the more recent studies discussed above,^211–219 would be to seek the novel morphologies that can arise in the context of mixtures of BCPs with donor and acceptor components. While the discussion in section 2.2 does highlight some challenges underlying the application of such simulation approaches to OPV systems, nevertheless, a judicious combination of experiments and model simplifications may enable simulations to identify or narrow parametric regions for creating equilibrium morphologies that may hold the most potential for enhanced device characteristics.

Motivated by the above considerations, in recent works,^{103,220–222} we used a class of hybrid field-theoretic methods to investigate the influence of BCP additives on the equilibrium morphologies and interfacial properties of conjugated polymer donor/fullerene acceptor blends. The theoretical framework was pursued in conjunction with the experimental system of poly(thieno[3,4-b]-thiophene-co-benzodithiophene) (PTB7), PTB7-b-polynaphthalene diimide (PTB7-b-PNDI), and phenyl-C61-butyric acid methyl ester (PCBM).²²² As a model for the system of interest, we considered a blend of semiflexible homopolymers (a model for the conjugated polymer donor), semiflexible-flexible block copolymers (a model for the BCP additive), and explicit solvent particles (a model for the PCBM acceptor). Our interests were specifically drawn towards the BμE morphologies seen in the context of ternary blends of flexible polymers. Due to the percolating and bicontinuous nature of their domains, we hypothesized that such morphologies may possess characteristics desired for organic photovoltaic applications. However, whereas such BμE morphologies had been achieved by the addition of BCP compatibilizers to flexible polymer blends, it remained an outstanding question whether BCP additives can be utilized to achieve bicontinuous morphologies also in the case of blends of conjugated polymer donors and fullerene acceptors.

To address the above issue, we utilized a coarse-grained, hybrid computational framework to identify a broad range of parametric conditions (volume percentage of block copolymer, relative molecular weights of block copolymers and donors etc.) that result in morphological characteristics like that of the BμE.²²¹ In addition, by calculating the morphological quantities that characterize the bicontinuous phases for different parameter combinations, we elucidated how to design and blend the various blend components to give rise to bicontinuous morphologies with the smallest domain sizes and most compositionally pure donor and acceptor domains.

To explore the experimental correspondence of the above simulation predictions, we parameterized the simulation model for the experimental system by using contact angle measurements to quantify the interactions between the different components.²²¹ While such a method is approximate, earlier studies had demonstrated its applicability to blends of semiflexible conjugated polymers with fullerenes.²²³ Using such parameters and the simulations results, we were able to guide the experimental search for achieving thermally stable, bicontinuous donor/acceptor morphologies by the use of all-conjugated BCP additives (see Fig. 4).²²² Such results demonstrated that complex and desirable equilibrium donor/acceptor morphologies can indeed be facilitated using block copolymer compatibilizers in ternary blends and, moreover, mesoscopic simulation techniques can serve as an effective means to predictively target the parameters that favor the formation of such morphologies.

Fig. 4 (Adapted with permission from Kipp et al.²²²) Cross-sectional TEM images of thermally annealed thin films for different volume fractions ϕPTB7-b-PNDI of the block copolymer PTB7-b-PNDI: (A) ϕPTB7-b-PNDI = 0.3; (B) ϕPTB7-b-PNDI = 0.4; (C) ϕPTB7-b-PNDI = 0.5; (D) ϕPTB7-b-PNDI = 0.6. Panel C shows the bicontinuous morphology whereas panels A, B and D show droplet-like morphologies where only the dark or light domains are continuous. The scale bar is 1 μm. The insets show the volumetric density of PNDI resulting from SCMF simulations to match the experiments.

2.4 Computer simulations of device characteristics of OPVs

While the hybrid field-theoretic methods discussed in section 2.1 may aid in designing donor/acceptor morphologies, unfortunately, they do not provide a direct handle to discern whether such morphologies facilitate optimal device performance. To truly facilitate the molecular design of BCP compatibilizers, such a framework for predicting morphology needs to be coupled to methodologies that can predict the device properties that may result from such morphologies. However, despite the considerable progress achieved surrounding the quantum mechanics/density functional theory based approaches for predicting the optoelectronic properties of individual or even clusters of molecules, until a few decades ago, there were not many approaches to translate such advances to the prediction of device properties of OPVs, especially involving the BHJ framework. In the past two decades, however, considerable advances have occurred in the context of simulations that use either continuum-level drift-diffusion models or a lattice-based kinetic Monte Carlo approach to identify the influence of the morphologies of donors and acceptors upon device characteristics. Below, we review the developments in these contexts and suggest the means by which they can be incorporated in the work-flow for the design of block copolymer compatibilizers for ternary blend OPVs. A number of excellent and comprehensive reviews exist on these topics,^224–231 and hence our discussion is necessarily brief.

2.4.1 Drift-diffusion models. Drift-diffusion (DD) models constitute a continuum approach to characterize the device characteristics of OPV systems.^230,232 Such models embody the physics of the transport of charge carriers driven by both the electric field and the gradient in charge carrier concentrations within a continuum reaction–diffusion framework while accounting for (in OPV devices) the generation of excitons, their dissociation into electrons and holes, and the subsequent transport of electrons and holes to the electrodes. Such processes are also often augmented by physics that quantify the diffusion, decay, photogeneration, and dissociation of excitons, as well as the influence of bimolecular recombination of electrons and holes and the presence of charge traps. Such equations are solved in conjunction with the Poisson equation for the electrostatic potential in terms of the local density of charge carriers.

In an early study,²³³ Barker et al. developed a one-dimensional DD model for the physics of a bilayer cell (including charge photogeneration, injection, drift, diffusion, recombination and the effect of space charge on the electric field) and showed good agreement with experimental observations of the dependency of the open-circuit voltage on the incident light intensity. Subsequently,²³⁴ Koster et al. developed a model, which included bimolecular recombination and a temperature- and field-dependent generation of free charges, and computed the current density–voltage characteristics. Buxton and Clarke extended such ideas²³⁵ to a two-dimensional device model to characterize the influence of features such as domain size and order upon the current–voltage characteristics. Subsequent works by Williams and Walker²³⁶ and Maturova et al.^237–239 presented refined two dimensional models in which the physics of the dissociation and decay processes were treated in a more accurate manner. In a related work, Hwang and Greenham^240,241 augmented the DD models to incorporate a better description of charge traps, solved for non steady state features of such models and demonstrated excellent agreement with experiments. A number of subsequent studies have proposed refinements to the DD model to provide a better representation of exciton generation rate, boundary conditions at electrodes etc.²³⁰

The above DD models have been applied in the context of the complex BHJ morphologies that arise in multicomponent polymeric donor–acceptor OPV systems.^235,242 Buxton–Clarke pioneered such studies by using a Flory–Huggins Cahn–Hilliard model to determine the morphology of an active layer consisting of a donor–acceptor block copolymer under various conditions. They used such morphologies as an input to the DD models to elucidate the dependence of the device characteristics on the morphological features.²³⁵ A similar approach was adopted by Shah and coworkers to study the role of anisotropic charge transport accompanying conjugated rod-coil BCPs.²⁴³ Such studies have demonstrated that morphology-level simulations and device-level simulations can be coupled in sequence to investigate the influence of physically meaningful and experimentally-realizable morphologies on device performance.

2.4.2 Kinetic Monte Carlo models. Lattice based kinetic Monte Carlo methods^231,244 founded on the more fundamental models of exciton and charge carrier hopping^123,245,246 have emerged as a popular alternative to DD models for investigating the charge transport and device characteristics of OPVs and BHJ devices. Watkins et al.²⁴⁷ developed one of the earliest versions of such a lattice model to investigate the dependence of internal quantum efficiency (IQE) on the interfacial area of the of BHJ morphologies and demonstrated the IQE to be sensitive to the length scale of phase separation of the morphology. In a subsequent work,²⁴⁸ Marsh and coworkers proposed a refined version of such a lattice KMC model that accounted for features such as dark injection at the electrodes, electrostatic interactions, energetic disorder, and polaronic effects. Yang and Forrest²⁴⁹ developed a more comprehensive model in which the effects of optical interference, energetic disorder and exciton/carrier transport were all considered. They quantified the exciton dissociation, charge collection and external quantum efficiencies as a function of the morphology. Subsequent works have refined such models even further by including improved descriptions of charge injection and correlations in site energies.²⁵⁰ Most recently, Meng et al. presented a model²⁵¹ that coupled Monte Carlo simulations with the Poisson equation to deal with a nonuniform electrostatic potential that depends on the charge distribution (cf.Fig. 5). Their simulations reproduced the experimental current–voltage curves in the dark and under illumination.

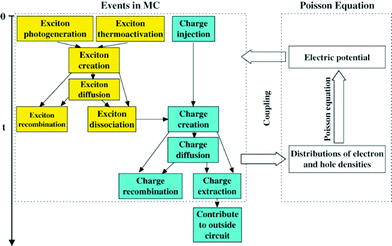Fig. 5 (Adapted with permission from Meng et al.²⁵¹) Schematic representation of the kinetic Monte Carlo simulation approach proposed in Meng et al.²⁵¹

Most of the above studies have been concerned with the morphologies generated from a lattice gas model of phase separation for binary mixtures, in which the electron donor and acceptor sites are assumed to occupy sites on a cubic lattice and their interactions are tuned to produce varying degrees of phase separation.²⁵² More recently, Walker and coworkers used the KMC simulations to evaluate the use of triply-periodic, bicontinuous gyroid and diamond morphologies in OPV applications.²⁵³ The authors found that the regularly-sized, perfectly percolating domains of such structures promoted efficient exciton dissociation and minimized charge recombination. However, the bicontinuous morphologies were shown to have a lower than expected benefit over the disordered morphologies produced from Ising models. Moreover, idealized columnar morphologies outperformed both the disordered and bicontinuous morphologies.

A different approach to modeling was adopted by Nelson and others^254,255 in which Monte Carlo algorithms were used to simulate the morphologies adopted by polymer chains in a polymer-blend film and then to simulate the drift transport of charges through the polymer chains. They were able to quantify the differences in the morphology arising between mutually attractive (termed homophilic in their work) and repulsive (heterophilic) polymeric systems and the resulting impact on charge transport. Based on their results, they concluded that the connectivity and morphology adopted by polymer chains needs to be incorporated in the modeling of organic solar cells.

2.5 Challenges underlying models of device properties

While substantial progress has occurred in the last two decades in the context of the DD and KMC models, a number of limitations still remain in translating such results to experimental situations. A primary challenge is the lack of a more fundamental framework for determining the parameters that accompany the transport rates in DD and KMC models, especially in situations involving multicomponent systems. While proposals have been presented to parameterize such models based on judicious experiments,^230,256 there are unresolved issues regarding the dependence of such properties on the local structure of the molecules, morphology, crystallinity of the phases, interfacial organization etc. More fundamentally, the changes in optoelectronic properties resulting from covalently linking two different molecules is still not fully understood, but critically influences the properties of BCP based materials. As a consequence, to date, most models are forced to rely on pure material properties and some reasonable assumptions regarding the interfaces and mixed regions, which may or may not accord with physical observations.^{105,110–112}

Despite the above shortcomings, coarse-grained transport models have enabled several insights regarding the influence of different morphological aspects on the device characteristics of OPVs. For instance, such models have clarified the role of interfacial areas, domain widths, tortuosities, interfacial zones between donors and acceptors etc. upon the device properties.^247,252 Inspired by such successes, in the next section we propose that the molecular design of copolymer compatibilizers can be further informed by such device models when used in conjunction with the morphology tools discussed earlier.

2.6 Design of copolymer compatibilizers for OPVs based on device considerations: outlook and a case study

Coupling the morphology simulations discussed in section 2.1 with the device-level simulations discussed in sections 2.4.1 and 2.4.2 may facilitate a framework for the computational design of BCP based ternary blends motivated by device property considerations. While there are still a number of unresolved issues regarding the dependence of the local optoelectronic properties upon the individual material characteristics and the morphology, nevertheless, by employing simple physical models for such features, one can account for the photoelectronic properties of the active layer and their dependence on the morphology within the DD and the lattice KMC models. Using the morphologies resulting from the methods discussed in section 2.1 as input to such simulations, a characterization of device properties for varying physical parameters can be effected to enable the design of compatibilizers.

Along the above lines, in a recent work,²⁵⁷ we combined the results of the morphology studies discussed in section 2.3 with device level simulations²⁵⁸ to investigate the performance of ternary blend organic solar cells based on the BCP additives. Specifically, our studies focused on two broad questions: “Which among the different morphologies observed in donor–acceptor-conjugated BCP based ternary blend systems possess features optimal for device characteristics?” “How do the photoelectronic properties of the BCP compatibilizers interplay with morphology to influence the overall device performance?”

To address the above questions, we used the hybrid field-theoretic simulations discussed in section 2.1 to predict the morphologies resulting for different combinations of ternary blend compositions, block copolymer compositions etc. Such morphologies were then combined with a KMC simulation framework for device characteristics to study the overall performance. As a simple model for treating the energy levels, we stochastically selected the occupation energy of each donor/acceptor site from a Gaussian density of states with an expected value equal to the composition-averaged HOMO of donors/LUMO of acceptors at that site. Similarly, we calculated a blend-averaged HOMO of donors (HOMO_blend) and LUMO of acceptors (LUMO_blend), which we utilized to calculate the electric field across the device active layer: F = F_applied + HOMO_blend − LUMO_blend where F_applied is the applied electric field. These methods for calculating the distribution of site energies and F match the “organic alloy model” for well-mixed two donor and two acceptor systems recently proposed by Khlyabich et al.²⁵⁹ Such methods allowed us to approximate the influence of the BCP additive on the density of states in the vicinity of the interface and the open-circuit voltage.^260–262 However, in some instances, the open-circuit voltage has been demonstrated to “pin” to the higher HOMO (lower LUMO) of ternary blend systems based on two donors (acceptors).²⁶³ Accordingly, we also investigated a model incorporating such pinning.

As our base case for studies, we considered a BCP constituted of two components whose energy levels matched respectively with the donor and acceptor of the blend. In such a context, our studies indicated that the bicontinuous morphologies containing percolating domains with interweaving interfaces gave rise to highly efficient charge separation (see Fig. 6(a)). However, blend formulations with higher BCP loadings and smaller domain sizes led to higher exciton dissociation efficiencies (albeit, at the cost of slightly lower charge separation efficiencies). These results suggested that for donors and acceptors with small exciton diffusion lengths but slow charge recombination, high BCP loadings may be required to achieve the maximum optimal device performance. In contrast, for donors and acceptors with large exciton diffusion lengths but fast charge recombination, the bicontinuous morphologies that form at low BCP loadings may be sufficient to achieve the optimal device performance.

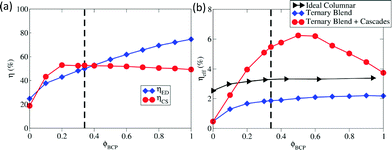Fig. 6 (Adapted from the results of Kipp et al.²⁵⁷) Simulated device performance characteristics of ternary blend systems. (a) Exciton dissociation (η_ED) and charge separation efficiency (η_CS) as a function of the blend composition of BCP (ϕ_BCP). (b) Device efficiencies (η_eff) for ideal columnar morphologies and ternary blend morphologies with and without appropriately tuned energy cascades. The ideal columnar morphologies were designed to have the same interfacial area per volume as the ternary blend morphologies for a given ϕ_BCP. The dashed black lines indicate the ϕ_BCP corresponding to the onset of bicontinuous phases.

We also examined²⁵⁷ the device characteristics of ternary blend morphologies for a model system of compatibilizers in which the energy levels are such that either donor or acceptor energy cascades are present at the interface between domains. The resulting device performance of such ternary blends was seen to reflect the combined influence of morphology and energy cascades, and, in some instances, outperformed the idealized columnar morphologies (which did not possess such energy cascades) proposed as optimal for BHJ devices (see Fig. 6(b)). Moreover, the influence of such energy cascades on the device fill factor was found to be especially strong since the cascade provided the energetic drive to separate charges at the interface, and the electric field was then only responsible for sweeping the charges out of the active layer. Together, such results suggested that the use of BCP additives in ternary blend systems may represent a unique strategy to actively exploit the combined influence of photoelectronic properties and morphology on the device characteristics.

Admittedly, the implementation of KMC device simulation methods for ternary blend systems is still at a relatively early stage due to a lack of clarity on how the local mixing and volume fractions influence many of the photoelectronic properties such as energy levels, photon adsorption, charge mobilities etc. Nevertheless, our study indicates that, by using physically reasonable models, it may be possible to delineate the combined roles of morphology and photoelectronic properties on the overall device characteristics. Using such computations, it may become possible to design BCP compatibilizers to target optimal device performance even if they may otherwise lack the ability to form what are usually deemed as optimal BHJ morphologies.

3 Summary and conclusions

In this review article, we discussed some of the recent developments in the context of the use of BCP compatibilizers in OPV devices based on the BHJ framework. While numerous successful experimental demonstrations exist in this regard, most such studies were concerned with the use of BCPs to improve the long-term stability of the donor–acceptor based OPV devices. After a brief review of such studies, we suggested that the physico-electro-chemical properties of BCP compatibilizers may be used as an as-yet unexplored handle to tune the device characteristics. In this regard, we pointed to the studies of ternary blends in the context of flexible copolymers to suggest that similar approaches may be utilized to target novel morphologies, which may hold the promise for better exciton and charge transport. Secondly, we suggested that, by appropriately choosing the BCPs electronic properties, an active control over the different photovoltaic processes can be exerted.

While success in the above efforts will heavily depend on synthetic advances for being able to create BCPs of different chemistries and electronic properties, we suggested that computational methods can serve as a useful tool to guide the physical properties to be targeted by the experiments. In this regard, we propose that coarse-grained morphology tools, despite not being at a stage where the complex conformational and interaction features can be incorporated, can serve as a guide for narrowing parametric regions for desirable morphologies. Since the device properties ultimately determine whether a morphology is relevant, the morphologies resulting from such coarse-grained tools should be combined with device simulations to identify the overall device properties. Such computational studies can serve to connect the molecular structure and electronic properties of the BCP to the overall device properties and thereby enable a rational, molecular design of BCP compatibilizers for OPV devices.

Acknowledgements

This work was supported in part by a grant from Robert A. Welch Foundation (Grant F1599 to VG and C1888 to RV), National Science Foundation (CBET-1264583, DMR-1306844) and US Army Research Office under grant W911NF-13-1-0396. The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing computing resources that have contributed to the research results reported within this paper.

References

1. T. Ameri, G. Dennler, C. Lungenschmied and C. J. Brabec, Energy Environ. Sci., 2009, 2, 347–363.
2. P. W. M. Blom, V. D. Mihailetchi, L. J. A. Koster and D. E. Markov, Adv. Mater., 2007, 19, 1551–1566.
3. C. J. Brabec, S. Gowrisanker, J. J. M. Halls, D. Laird, S. J. Jia and S. P. Williams, Adv. Mater., 2010, 22, 3839–3856.
4. L. T. Dou, J. B. You, Z. R. Hong, Z. Xu, G. Li, R. A. Street and Y. Yang, Adv. Mater., 2013, 25, 6642–6671.
5. M. Gratzel, Acc. Chem. Res., 2009, 42, 1788–1798.
6. H. Hoppe and N. S. Sariciftci, J. Mater. Res., 2004, 19, 1924–1945.
7. A. Pivrikas, N. S. Sariciftci, G. Juska and R. Osterbacka, Prog. Photovoltaics, 2007, 15, 677–696.
8. D. Wohrle and D. Meissner, Adv. Mater., 1991, 3, 129–138.
9. H. X. Zhou, L. Q. Yang and W. You, Macromolecules, 2012, 45, 607–632.
10. A. Hadipour, B. de Boer, J. Wildeman, F. B. Kooistra, J. C. Hummelen, M. G. R. Turbiez, M. M. Wienk, R. A. J. Janssen and P. W. M. Blom, Adv. Funct. Mater., 2006, 16, 1897–1903.
11. D. J. Lipomi, B. C. K. Tee, M. Vosgueritchian and Z. Bao, Adv. Mater., 2011, 23, 1771–1775.
12. J. Wu, H. A. Becerril, Z. Bao, Z. Liu, Y. Chen and P. Peumans, Appl. Phys. Lett., 2008, 92, 263302.
13. F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2009, 93, 465–475.
14. R. Sondergaard, M. Hosel, D. Angmo, T. T. Larsen-Olsen and F. C. Krebs, Mater. Today, 2012, 15, 36–49.
15. A. Goetzberger, C. Hebling and H. W. Schock, Mater. Sci. Eng., R, 2003, 40, 1–46.
16. C. Waldauf, M. C. Scharber, P. Schilinsky, J. A. Hauch and C. J. Brabec, J. Appl. Phys., 2006, 99, 104503.
17. C. J. Brabec, M. Heeney, I. McCulloch and J. Nelson, Chem. Soc. Rev., 2011, 40, 1185–1199.
18. D. Chen, A. Nakahara, D. Wei, D. Nordlund and T. P. Russell, Nano Lett., 2011, 11, 561–567.
19. B. Kippelen and J.-L. Bredas, Energy Environ. Sci., 2009, 2, 251–261.
20. A. C. Mayer, S. R. Scully, B. E. Hardin, M. W. Rowell and M. D. McGehee, Mater. Today, 2007, 10, 28–33.
21. K. A. Mazzio and C. K. Luscombe, Chem. Soc. Rev., 2015, 44, 78–90.
22. J. Nelson, Curr. Opin. Solid State Mater. Sci., 2002, 6, 87–95.
23. R. A. Segalman, B. McCulloch, S. Kirmayer and J. J. Urban, Macromolecules, 2009, 42, 9205–9216.
24. M. Sommer, S. Huettner and M. Thelakkat, J. Mater. Chem., 2010, 20, 10788–10797.
25. B. C. Thompson and J. M. J. Frechet, Angew. Chem., Int. Ed., 2008, 47, 58–77.
26. X. Yang and J. Loos, Macromolecules, 2007, 40, 1353–1362.
27. X. N. Yang, J. Loos, S. C. Veenstra, W. J. H. Verhees, M. M. Wienk, J. M. Kroon, M. A. J. Michels and R. A. J. Janssen, Nano Lett., 2005, 5, 579–583.
28. S. H. Park, A. Roy, S. Beaupre, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–302.
29. M. C. Scharber, D. Wuhlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. L. Brabec, Adv. Mater., 2006, 18, 789–794.
30. C. J. Brabec, S. Gowrisanker, J. J. M. Halls, D. Laird, S. Jia and S. P. Williams, Adv. Mater., 2010, 22, 3839–3856.
31. M. T. Dang, L. Hirsch and G. Wantz, Adv. Mater., 2011, 23, 3597–3602.
32. C. Mueller, T. A. M. Ferenczi, M. Campoy-Quiles, J. M. Frost, D. D. C. Bradley, P. Smith, N. Stingelin-Stutzmann and J. Nelson, Adv. Mater., 2008, 20, 3510–3515.
33. H. Hoppe and N. S. Sariciftci, J. Mater. Chem., 2006, 16, 45–61.
34. B. Walker, C. Kim and T.-Q. Nguyen, Chem. Mater., 2011, 23, 470–482.
35. H. Hoppe, M. Niggemann, C. Winder, J. Kraut, R. Hiesgen, A. Hinsch, D. Meissner and N. Sariciftci, Adv. Funct. Mater., 2004, 14, 1005–1011.
36. H. Hoppe and N. S. Sariciftci, J. Mater. Chem., 2006, 16, 45–61.
37. W. L. Ma, C. Y. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617–1622.
38. Y. Gu, C. Wang and T. P. Russell, Adv. Energy Mater., 2012, 2, 683–690.
39. T. A. Bull, L. S. C. Pingree, S. A. Jenekhe, D. S. Ginger and C. K. Luscombe, ACS Nano, 2009, 3, 627–636.
40. M. Jorgensen, K. Norrman, S. A. Gevorgyan, T. Tromholt, B. Andreasen and F. C. Krebs, Adv. Mater., 2012, 24, 580–612.
41. Y. Kim, S. A. Choulis, J. Nelson, D. D. C. Bradley, S. Cook and J. R. Durrant, Appl. Phys. Lett., 2005, 86, 063502.
42. T. Wang, A. J. Pearson, D. G. Lidzey and R. A. L. Jones, Adv. Funct. Mater., 2011, 21, 1383–1390.
43. M. O. Reese, A. M. Nardes, B. L. Rupert, R. E. Larsen, D. C. Olson, M. T. Lloyd, S. E. Shaheen, D. S. Ginley, G. Rumbles and N. Kopidakis, Adv. Funct. Mater., 2010, 20, 3476–3483.
44. Y. H. Kim, C. Sachse, M. L. Machala, C. May, L. Mueller-Meskamp and K. Leo, Adv. Funct. Mater., 2011, 21, 1076–1081.
45. T. Wang, A. D. F. Dunbar, P. A. Staniec, A. J. Pearson, P. E. Hopkinson, J. E. MacDonald, S. Lilliu, C. Pizzey, N. J. Terrill, A. M. Donald, A. J. Ryan, R. A. L. Jones and D. G. Lidzey, Soft Matter, 2010, 6, 4128–4134.
46. H. Yan, S. Swaraj, C. Wang, I. Hwang, N. C. Greenham, C. Groves, H. Ade and C. R. McNeill, Adv. Funct. Mater., 2010, 20, 4329–4337.
47. H.-L. Yip and A. K. Y. Jen, Energy Environ. Sci., 2012, 5, 5994–6011.
48. S. Bertho, I. Haeldermans, A. Swinnen, W. Moons, T. Martens, L. Lutsen, D. Vanderzande, J. Manca, A. Senes and A. Bonfiglio, Sol. Energy Mater. Sol. Cells, 2007, 91, 385–389.
49. M. A. Ruderer, S. Guo, R. Meier, H.-Y. Chiang, V. Koerstgens, J. Wiedersich, J. Perlich, S. V. Roth and P. Mueller-Buschbaum, Adv. Funct. Mater., 2011, 21, 3382–3391.
50. S. Lizin, S. Van Passel, E. De Schepper, W. Maes, L. Lutsen, J. Manca and D. Vanderzande, Energy Environ. Sci., 2013, 6, 3136–3149.
51. S. S. Sun, Sol. Energy Mater. Sol. Cells, 2003, 79, 257–264.
52. P. D. Topham, A. J. Parnell and R. C. Hiorns, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1131–1156.
53. U. Stalmach, B. de Boer, C. Videlot, P. F. van Hutten and G. Hadziioannou, J. Am. Chem. Soc., 2000, 122, 5464–5472.
54. A. de Cuendias, R. C. Hiorns, E. Cloutet, L. Vignau and H. Cramail, Polym. Int., 2010, 59, 1452–1476.
55. I. Botiz and S. B. Darling, Mater. Today, 2010, 13, 42–51.
56. S. B. Darling, Energy Environ. Sci., 2009, 2, 1266–1273.
57. F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38.
58. P. Docampo, S. Guldin, M. Stefik, P. Tiwana, M. C. Orilall, S. Huettner, H. Sai, U. Wiesner, U. Steiner and H. J. Snaith, Adv. Funct. Mater., 2010, 20, 1787–1796.
59. B. W. Boudouris, C. D. Frisbie and M. A. Hillmyer, Macromolecules, 2008, 41, 67–75.
60. K. M. Coakley, Y. X. Liu, M. D. McGehee, K. L. Frindell and G. D. Stucky, Adv. Funct. Mater., 2003, 13, 301–306.
61. J. I. Lee, S. H. Cho, S.-M. Park, J. K. Kim, J. K. Kim, J.-W. Yu, Y. C. Kim and T. P. Russell, Nano Lett., 2008, 8, 2315–2320.
62. E. J. W. Crossland, M. Kamperman, M. Nedelcu, C. Ducati, U. Wiesner, D. M. Smilgies, G. E. S. Toombes, M. A. Hillmyer, S. Ludwigs, U. Steiner and H. J. Snaith, Nano Lett., 2009, 9, 2807–2812.
63. K. Nakabayashi and H. Mori, Macromolecules, 2012, 45, 9618–9625.
64. K. Li, Z. Li, K. Feng, X. Xu, L. Wang and Q. Peng, J. Am. Chem. Soc., 2013, 135, 13549–13557.
65. Y. Lee and E. D. Gomez, Macromolecules, 2015, 48, 7385–7395.
66. R. H. Lohwasser and M. Thelakkat, Macromolecules, 2012, 45, 3070–3077.
67. K. Van De Wetering, C. Brochon, C. Ngov and G. Hadziioannou, Macromolecules, 2006, 39, 4289–4297.
68. Y. Tao, B. Ma and R. A. Segalman, Macromolecules, 2008, 41, 7152–7159.
69. A. Yassar, L. Miozzo, R. Gironda and G. Horowitz, Prog. Polym. Sci., 2013, 38, 791–844.
70. C. Guo, Y.-H. Lin, M. D. Witman, K. A. Smith, C. Wang, A. Hexemer, J. Strzalka, E. D. Gomez and R. Verduzco, Nano Lett., 2013, 13, 2957–2963.
71. R. S. Kularatne, H. D. Magurudeniya, P. Sista, M. C. Biewer and M. C. Stefan, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 743–768.
72. M. Sommer, S. M. Lindner and M. Thelakkat, Adv. Funct. Mater., 2007, 17, 1493–1500.
73. U. Scherf, A. Gutacker and N. Koenen, Acc. Chem. Res., 2008, 41, 1086–1097.
74. U. Sundararaj and C. W. Macosko, Macromolecules, 1995, 28, 2647–2657.
75. C. W. Macosko, P. Guegan, A. K. Khandpur, A. Nakayama, P. Marechal and T. Inoue, Macromolecules, 1996, 29, 5590–5598.
76. P. Cigana, B. D. Favis and R. Jerome, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 1691–1700.
77. Y. Lyatskaya, D. Gersappe, N. A. Gross and A. C. Balazs, J. Phys. Chem., 1996, 100, 1449–1458.
78. K. S. Anderson and M. A. Hillmyer, Polymer, 2004, 45, 8809–8823.
79. K. Sivula, Z. T. Ball, N. Watanabe and J. M. J. Frechet, Adv. Mater., 2006, 18, 206–210.
80. C. Yang, J. K. Lee, A. J. Heeger and F. Wudl, J. Mater. Chem., 2009, 19, 5416–5423.
81. J. U. Lee, J. W. Jung, T. Emrick, T. P. Russell and W. H. Jo, J. Mater. Chem., 2010, 20, 3287–3294.
82. C. Renaud, S.-J. Mougnier, E. Pavlopoulou, C. Brochon, G. Fleury, D. Deribew, G. Portale, E. Cloutet, S. Chambon, L. Vignau and G. Hadziioannou, Adv. Mater., 2012, 24, 2196–2201.
83. P. Cheng and X. Zhan, Mater. Horiz., 2015, 2, 462–485.
84. H.-C. Liao, P.-H. Chen, R. P. H. Chang and W.-F. Su, Polymer, 2014, 6, 2784–2802.
85. J. Liu and Y. Han, Polym. Bull., 2012, 68, 2145–2174.
86. M. Raissi, H. Erothu, E. Ibarboure, H. Cramail, L. Vignau, E. Cloutet and R. C. Hiorns, J. Mater. Chem. A, 2015, 3, 18207–18221.
87. D. Deribew, E. Pavlopoulou, G. Fleury, C. Nicolet, C. Renaud, S.-J. Mougnier, L. Vignau, E. Cloutet, C. Brochon, F. Cousin, G. Portale, M. Geoghegan and G. Hadziioannou, Macromolecules, 2013, 46, 3015–3024.
88. M. H. Yun, J. Kim, C. Yang and J. Y. Kim, Sol. Energy Mater. Sol. Cells, 2012, 104, 7–12.
89. J. U. Lee, J. W. Jung, T. Emrick, T. P. Russell and W. H. Jo, Nanotechnology, 2010, 21, 105201.
90. J.-H. Tsai, Y.-C. Lai, T. Higashihara, C.-J. Lin, M. Ueda and W.-C. Chen, Macromolecules, 2010, 43, 6085–6091.
91. N. Sary, F. Richard, C. Brochon, N. Leclerc, P. Leveque, J.-N. Audinot, S. Berson, T. Heiser, G. Hadziioannou and R. Mezzenga, Adv. Mater., 2010, 22, 763–768.
92. K. Yuan, L. Chen and Y. Chen, J. Mater. Chem. C, 2014, 2, 3835–3845.
93. J. Chen, X. Yu, K. Hong, J. M. Messman, D. L. Pickel, K. Xiao, M. D. Dadmun, J. W. Mays, A. J. Rondinone, B. G. Sumpter and S. M. Kilbey II, J. Mater. Chem., 2012, 22, 13013–13022.
94. H. Fujita, T. Michinobu, S. Fukuta, T. Koganezawa and T. Higashihara, ACS Appl. Mater. Interfaces, 2016, 8, 5484–5492.
95. Z. Sun, K. Xiao, J. K. Keum, X. Yu, K. Hong, J. Browning, I. N. Ivanov, J. Chen, J. Alonzo, D. Li, B. G. Sumpter, E. A. Payzant, C. M. Rouleau and D. B. Geohegan, Adv. Mater., 2011, 23, 5529–5535.
96. J. W. Jung, J. W. Jo and W. H. Jo, Adv. Mater., 2011, 23, 1782–1787.
97. J. E. Slota, E. Elmalem, G. Tu, B. Watts, J. Fang, P. M. Oberhumer, R. H. Friend and W. T. S. Huck, Macromolecules, 2012, 45, 1468–1475.
98. R. C. Mulherin, S. Jung, S. Huettner, K. Johnson, P. Kohn, M. Sommer, S. Allard, U. Scherf and N. C. Greenham, Nano Lett., 2011, 11, 4846–4851.
99. S. Rajaram, P. B. Armstrong, B. J. Kim and J. M. J. Frechet, Chem. Mater., 2009, 21, 1775–1777.
100. H. J. Kim, J.-H. Kim, J.-H. Ryu, Y. Kim, H. Kang, W. B. Lee, T.-S. Kim and B. J. Kim, ACS Nano, 2014, 8, 10461–10470.
101. A. Li, J. Amonoo, B. Huang, P. K. Goldberg, A. J. McNeil and P. F. Green, Adv. Funct. Mater., 2014, 24, 5594–5602.
102. Y. Shi, F. Li and Y. Chen, New J. Chem., 2013, 37, 236–244.
103. D. Kipp and V. Ganesan, J. Phys. Chem. B, 2014, 118, 4425–4441.
104. T. Ameri, P. Khoram, J. Min and C. J. Brabec, Adv. Mater., 2013, 25, 4245–4266.
105. Q. An, F. Zhang, J. Zhang, W. Tang, Z. Deng and B. Hu, Energy Environ. Sci., 2016, 9, 281–322.
106. L. Lu, M. A. Kelly, W. You and L. Yu, Nat. Photonics, 2015, 9, 491–500.
107. T. Liu, L. Huo, X. Sun, B. Fan, Y. Cai, T. Kim, J. Y. Kim, H. Choi and Y. Sun, Adv. Energy Mater., 2016, 6, 1502109.
108. B. M. Savoie, S. Dunaisky, T. J. Marks and M. A. Ratner, Adv. Energy Mater., 2015, 5, 1400891.
109. S. A. Mollinger, K. Vandewal and A. Salleo, Adv. Energy Mater., 2015, 5, 1501335.
110. P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2012, 134, 9074–9077.
111. L. Yang, H. Zhou, S. C. Price and W. You, J. Am. Chem. Soc., 2012, 134, 5432–5435.
112. R. A. Street, D. Davies, P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2013, 135, 986–989.
113. H. Cha, D. S. Chung, S. Y. Bae, M.-J. Lee, T. K. An, J. Hwang, K. H. Kim, Y.-H. Kim, D. H. Choi and C. E. Park, Adv. Funct. Mater., 2013, 23, 1556–1565.
114. M. C. Chen, D. J. Liaw, Y. C. Huang, H. Y. Wu and Y. Tai, Sol. Energy Mater. Sol. Cells, 2011, 95, 2621–2627.
115. C. Groves, Energy Environ. Sci., 2013, 6, 1546–1551.
116. C. Risko, M. D. McGehee and J.-L. Bredas, Chem. Sci., 2011, 2, 1200–1218.
117. J. Gierschner, J. Cornil and H.-J. Egelhaaf, Adv. Mater., 2007, 19, 173–191.
118. G. L. Gibson, T. M. McCormick and D. S. Seferos, J. Am. Chem. Soc., 2012, 134, 539–547.
119. G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350.
120. G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 16866–16881.
121. T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820.
122. S. Difley, L. P. Wang, S. Yeganeh, S. R. Yost and T. Van Voorhis, Acc. Chem. Res., 2010, 43, 995–1004.
123. J. Nelson, J. J. Kwiatkowski, J. Kirkpatrick and J. M. Frost, Acc. Chem. Res., 2009, 42, 1768–1778.
124. K. Do, D. M. Huang, R. Faller and A. J. Moule, Phys. Chem. Chem. Phys., 2010, 12, 14735–14739.
125. S. Dag and L. W. Wang, J. Phys. Chem. B, 2010, 114, 5997–6000.
126. O. Alexiadis and V. G. Mavrantzas, Macromolecules, 2013, 46, 2450–2467.
127. C. Melis, L. Colombo and A. Mattoni, J. Phys. Chem. C, 2011, 115, 576–581.
128. J. E. Northrup, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245202.
129. D. L. Cheung and A. Troisi, Phys. Chem. Chem. Phys., 2008, 10, 5941–5952.
130. D. L. Cheung, D. P. McMahon and A. Troisi, J. Phys. Chem. B, 2009, 113, 9393–9401.
131. P. Brocorens, A. Van Vooren, M. L. Chabinyc, M. F. Toney, M. Shkunov, M. Heeney, I. McCulloch, J. Cornil and R. Lazzoroni, Adv. Mater., 2009, 21, 1193–1198.
132. T. B. Singh, N. S. Sariciftci, H. Yang, L. Yang, B. Plochberger and H. Sitter, Appl. Phys. Lett., 2007, 90, 213512.
133. C. I. Wang, C. H. Hsu, C. C. Hua and S. A. Chen, J. Polym. Res., 2013, 20, 188.
134. C. I. Wang and C. C. Hua, J. Phys. Chem. B, 2015, 119, 14496–14504.
135. D. L. Cheung and A. Troisi, J. Phys. Chem. C, 2010, 114, 20479–20488.
136. R. C. I. MacKenzie, J. M. Frost and J. Nelson, J. Chem. Phys., 2010, 132, 064904.
137. T. T. To and S. Adams, Phys. Chem. Chem. Phys., 2014, 16, 4653–4663.
138. C.-K. Lee, C.-W. Pao and C.-W. Chen, Energy Environ. Sci., 2013, 6, 307–315.
139. C.-K. Lee, C.-W. Pao and C.-W. Chu, Energy Environ. Sci., 2011, 4, 4124–4132.
140. D. M. Huang, R. Faller, K. Do and A. J. Moule, J. Chem. Theory Comput., 2010, 6, 526–537.
141. D. M. Huang, A. J. Moulé and R. Faller, Fluid Phase Equilib., 2011, 302, 21–25.
142. D. M. Huang, A. J. Moule and R. Faller, Fluid Phase Equilib., 2011, 302, 21–25.
143. E. Jankowski, H. S. Marsh and A. Jayaraman, Macromolecules, 2013, 46, 5775–5785.
144. H. S. Marsh, E. Jankowski and A. Jayaraman, Macromolecules, 2014, 47, 2736–2747.
145. N. R. Tummala, S. Mehraeen, Y.-T. Fu, C. Risko and J.-L. Bredas, Adv. Funct. Mater., 2013, 23, 5800–5813.
146. J. H. Yap, T. T. To and S. Adams, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 270–279.
147. K. N. Schwarz, T. W. Kee and D. M. Huang, Nanoscale, 2013, 5, 2017–2027.
148. C.-K. Lee, O. Wodo, B. Ganapathysubramanian and C.-W. Pao, ACS Appl. Mater. Interfaces, 2014, 6, 20612–20624.
149. C.-K. Lee and C.-W. Pao, J. Phys. Chem. C, 2014, 118, 11224–11233.
150. J.-M. Y. Carrillo, R. Kumar, M. Goswami, B. G. Sumpter and W. M. Brown, Phys. Chem. Chem. Phys., 2013, 15, 17873–17882.
151. S. E. Root, S. Savagatrup, C. J. Pais, G. Arya and D. J. Lipomi, Macromolecules, 2016, 49, 2886–2894.
152. G. H. Fredrickson, V. Ganesan and F. Drolet, Macromolecules, 2002, 35, 16–39.
153. C. Du, Y. Ji, J. Xue, T. Hou, J. Tang, S.-T. Lee and Y. Li, Sci. Rep., 2015, 5, 16854.
154. Y. Ji, C. Du, X. Xu, T. Hou and Y. Li, Mol. Simul., 2016, 42, 836–845.
155. C. Poelking, K. Daoulas, A. Troisi and D. Andrienko, P3ht Revisited: From Molecular Scale To Solar Cell Devices, 2014, vol. 265, pp. 139–180.
156. M. W. Matsen, J. Phys.: Condens. Matter, 2002, 14, R21–R47.
157. F. Drolet and G. H. Fredrickson, Phys. Rev. Lett., 1999, 83, 4317–4320.
158. H. D. Ceniceros and G. H. Fredrickson, Multiscale Model. Simul., 2004, 2, 452–474.
159. S. W. Sides and G. H. Fredrickson, Polymer, 2003, 44, 5859–5866.
160. J. T. Chen, E. L. Thomas, C. K. Ober and S. S. Hwang, Macromolecules, 1995, 28, 1688–1697.
161. J. T. Chen, E. L. Thomas, C. K. Ober and G. P. Mao, Science, 1996, 273, 343–346.
162. A. Halperin, Macromolecules, 1990, 23, 2724–2731.
163. A. N. Semenov, Mol. Cryst. Liq. Cryst., 1991, 209, 191–199.
164. D. R. M. Williams and G. H. Fredrickson, Macromolecules, 1992, 25, 3561–3568.
165. R. Holyst and M. Schick, J. Chem. Phys., 1992, 96, 721–729.
166. C. Singh, M. Goulian, A. J. Liu and G. H. Fredrickson, Macromolecules, 1994, 27, 2974–2986.
167. M. Reenders and G. ten Brinke, Macromolecules, 2002, 35, 3266–3280.
168. D. Duchs and D. Sullivan, J. Phys.: Condens. Matter, 2002, 14, 12189.
169. M. W. Matsen, J. Chem. Phys., 1996, 104, 7758–7764.
170. V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2004, 120, 5824–5838.
171. M. Shah, V. Pryamitsyn and V. Ganesan, Macromolecules, 2008, 41, 218–229.
172. Y. Tao, B. D. Olsen, V. Ganesan and R. A. Segalman, Macromolecules, 2007, 40, 3320–3327.
173. Q. Wang, Soft Matter, 2011, 7, 3711–3716.
174. B. D. Olsen, M. Shah, V. Ganesan and R. A. Segalman, Macromolecules, 2008, 41, 6809–6817.
175. Y. A. Kriksin and P. G. Khalatur, Macromol. Theory Simul., 2012, 21, 382–399.
176. W. Song, P. Tang, F. Qiu, Y. Yang and A.-C. Shi, J. Phys. Chem. B, 2011, 115, 8390–8400.
177. G. Yang, P. Tang, Y. Yang and Q. Wang, J. Phys. Chem. B, 2010, 114, 14897–14906.
178. J.-Z. Chen, Z.-Y. Sun, C.-X. Zhang, L.-J. An and Z. Tong, J. Chem. Phys., 2008, 128, 074904.
179. W. Song, P. Tang, H. Zhang, Y. Yang and A.-C. Shi, Macromolecules, 2009, 42, 6300–6309.
180. W. Song, P. Tang, F. Qiu, Y. Yang and A.-C. Shi, Soft Matter, 2011, 7, 929–938.
181. W. Song, P. Tang, F. Qiu, Y. Yang and A.-C. Shi, Soft Matter, 2011, 7, 929–938.
182. J. Gao, W. Song, P. Tang and Y. Yang, Soft Matter, 2011, 7, 5208–5216.
183. Y. Jiang and J. Z. Y. Chen, Phys. Rev. Lett., 2013, 110, 138305.
184. Y. Jiang and J. Z. Y. Chen, Phys. Rev. B, 2013, 88, 042603.
185. Y. Jiang and J. Z. Y. Chen, Phys. Rev. Lett., 2013, 110, 138305.
186. S. Li, Y. Jiang and J. Z. Y. Chen, Soft Matter, 2014, 10, 8932–8944.
187. F. A. Detcheverry, H. Kang, K. C. Daoulas, M. Mueller, P. F. Nealey and J. J. de Pablo, Macromolecules, 2008, 41, 4989–5001.
188. B. Narayanan, V. A. Pryamitsyn and V. Ganesan, Macromolecules, 2004, 37, 10180–10194.
189. N. A. Kumar and V. Ganesan, J. Chem. Phys., 2012, 136, 101101.
190. P. Gemuenden, C. Poelking, K. Kremer, D. Andrienko and K. C. Daoulas, Macromolecules, 2013, 46, 5762–5774.
191. P. Gemuenden, C. Poelking, K. Kremer, K. Daoulas and D. Andrienko, Macromol. Rapid Commun., 2015, 36, 1047–1053.
192. D. R. Kozub, K. Vakhshouri, L. M. Orme, C. Wang, A. Hexemer and E. D. Gomez, Macromolecules, 2011, 44, 5722–5726.
193. S. Nilsson, A. Bernasik, A. Budkowski and E. Moons, Macromolecules, 2007, 40, 8291–8301.
194. R. H. Lohwasser, G. Gupta, P. Kohn, M. Sommer, A. S. Lang, T. Thurn-Albrecht and M. Thelakkat, Macromolecules, 2013, 46, 4403–4410.
195. F. Liu, Y. Gu, J. W. Jung, W. H. Jo and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1018–1044.
196. D. Deribew, E. Pavlopoulou, G. Fleury, C. Nicolet, C. Renaud, S.-J. Mougnier, L. Vignau, E. Cloutet, C. Brochon, F. Cousin, G. Portale, M. Geoghegan and G. Hadziioannou, Macromolecules, 2013, 46, 3015–3024.
197. C. K. Lee, C. C. Hua and S. A. Chen, Macromolecules, 2011, 44, 320–324.
198. C. Melis, L. Colombo and A. Mattoni, J. Phys. Chem. C, 2011, 115, 576–581.
199. F. S. Bates, Science, 1991, 251, 898–905.
200. J. Baschnagel, K. Binder, P. Doruker, A. A. Gusev, O. Hahn, K. Kremer, W. L. Mattice, F. Muller-Plathe, M. Murat, W. Paul, S. Santos, U. W. Suter and V. Tries, Advances In Polymer Science: Viscoelasticity, Atomistic Models, Statistical Chemistry, 2000, vol. 152, pp. 41–156.
201. A. Chaimovich and M. S. Shell, J. Chem. Phys., 2011, 134, 094112.
202. A. R. A. Khajeh, K. Shankar and P. Choi, ACS Appl. Mater. Interfaces, 2013, 5, 4617–4624.
203. W. G. Noid, J. Chem. Phys., 2013, 139, 090901.
204. C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357–4366.
205. M. Praprotnik, L. Delle Site and K. Kremer, Annu. Rev. Phys. Chem., 2008, 59, 545–571.
206. Q. Sun and R. Faller, J. Chem. Theory Comput., 2006, 2, 607–615.
207. G. H. Fredrickson, J. Chem. Phys., 2002, 117, 6810–6820.
208. D. M. Hall, T. Lookman, G. H. Fredrickson and S. Banerjee, Phys. Rev. Lett., 2006, 97, 114501.
209. T. A. Vilgis and J. Noolandi, Macromolecules, 1990, 23, 2941–2947.
210. Y. Lyatskaya, D. Gersappe and A. C. Balazs, Macromolecules, 1995, 28, 6278–6283.
211. G. H. Fredrickson and F. S. Bates, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 2775–2786.
212. M. Banaszak and M. D. Whitmore, Macromolecules, 1992, 25, 249–260.
213. G. Pandav and V. Ganesan, Macromolecules, 2013, 46, 8334–8344.
214. M. W. Matsen, Macromolecules, 1995, 28, 5765–5773.
215. R. Wang, W. Li, Y. Luo, B.-G. Li, A.-C. Shi and S. Zhu, Macromolecules, 2009, 42, 2275–2285.
216. M. D. Whitmore and J. D. Vavasour, Acta Polym., 1995, 46, 341–360.
217. P. K. Janert and M. Schick, Macromolecules, 1997, 30, 3916–3920.
218. Y. G. Jeong, S. Ramalingam, J. Archer, S. W. Hsu and C. W. Paul, J. Phys. Chem. B, 2006, 110, 2541–2548.
219. J. Huh and W. H. Jo, J. Chem. Phys., 2002, 117, 9920–9926.
220. D. Kipp, R. Verduzco and V. Ganesan, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 884–895.
221. D. Kipp, O. Wodo, B. Ganapathysubramanian and V. Ganesan, ACS Macro Lett., 2015, 4, 266–270.
222. D. Kipp, J. Mok, J. Strzalka, S. B. Darling, V. Ganesan and R. Verduzco, ACS Macro Lett., 2015, 4, 867–871.
223. J. U. Lee, J. W. Jung, T. Emrick, T. P. Russell and W. H. Jo, J. Mater. Chem., 2010, 20, 3287–3294.
224. C. Groves, Energy Environ. Sci., 2013, 6, 3202–3217.
225. F. Yang and S. R. Forrest, ACS Nano, 2008, 2, 1022–1032.
226. P. K. Watkins, A. B. Walker and G. L. B. Verschoor, Nano Lett., 2005, 5, 1814–1818.
227. J. Nelson and R. E. Chandler, Coord. Chem. Rev., 2004, 248, 1181–1194.
228. L. Meng, Y. Shang, Q. Li, Y. Li, X. Zhan, Z. Shuai, R. G. E. Kimber and A. B. Walker, J. Phys. Chem. B, 2010, 114, 36–41.
229. G. Li, L. Liu, F. Wei, S. Xia and X. Qian, IEEE J. Photovoltaics, 2012, 2, 320–340.
230. T. Kirchartz and J. Nelson, Multiscale Modelling of Organic and Hybrid Photovoltaics, 2014, vol. 352, pp. 279–324.
231. C. Groves and N. C. Greenham, Multiscale Modelling of Organic and Hybrid Photovoltaics, 2014, vol. 352, pp. 257–278.
232. B. K. Crone, P. S. Davids, I. H. Campbell and D. L. Smith, J. Appl. Phys., 2000, 87, 1974–1982.
233. J. A. Barker, C. M. Ramsdale and N. C. Greenham, Phys. Rev. B, 2003, 67, 075205.
234. L. J. A. Koster, V. D. Mihailetchi, H. Xie and P. W. M. Blom, Appl. Phys. Lett., 2005, 87, 203502.
235. G. A. Buxton and N. Clarke, Modell. Simul. Mater. Sci. Eng., 2007, 15, 13.
236. J. Williams and A. B. Walker, Nanotechnology, 2008, 19, 424011.
237. K. Maturova, R. A. J. Janssen and M. Kemerink, ACS Nano, 2010, 4, 1385–1392.
238. K. Maturova, S. S. van Bavel, M. M. Wienk, R. A. J. Janssen and M. Kemerink, Nano Lett., 2009, 9, 3032–3037.
239. K. Maturova, S. S. van Bavel, M. M. Wienk, R. A. J. Janssen and M. Kemerink, Adv. Funct. Mater., 2011, 21, 261–269.
240. I. Hwang and N. C. Greenham, Nanotechnology, 2008, 19, 424012.
241. I. Hwang, C. R. McNeill and N. C. Greenham, J. Appl. Phys., 2009, 106, 094506.
242. Y. M. Nam, J. Huh and W. H. Jo, Sol. Energy Mater. Sol. Cells, 2010, 94, 1118–1124.
243. M. Shah and V. Ganesan, Macromolecules, 2010, 43, 543–552.
244. C. Groves, Energy Environ. Sci., 2013, 6, 3202–3217.
245. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Bredas, Chem. Rev., 2007, 107, 926–952.
246. J. L. Bredas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003.
247. P. K. Watkins, A. B. Walker and G. L. B. Verschoor, Nano Lett., 2005, 5, 1814–1818.
248. R. A. Marsh, C. Groves and N. C. Greenham, J. Appl. Phys., 2007, 101, 083509.
249. F. Yang and S. R. Forrest, ACS Nano, 2008, 2, 1022–1032.
250. R. G. E. Kimber, E. N. Wright, S. E. J. O'Kane, A. B. Walker and J. C. Blakesley, Phys. Rev. B, 2012, 86, 235206.
251. L. Meng, D. Wang, Q. Li, Y. Yi, J.-L. Brédas and Z. Shuai, J. Chem. Phys., 2011, 134, 124102.
252. C. R. McNeill, S. Westenhoff, C. Groves, R. H. Friend and N. C. Greenham, J. Phys. Chem. C, 2007, 111, 19153–19160.
253. R. G. E. Kimber, A. B. Walker, G. E. Schroder-Turk and D. J. Cleaver, Phys. Chem. Chem. Phys., 2010, 12, 844–851.
254. J. M. Frost, F. Cheynis, S. M. Tuladhar and J. Nelson, Nano Lett., 2006, 6, 1674–1681.
255. R. Noriega, A. Salleo and A. J. Spakowitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16315–16320.
256. R. C. I. MacKenzie, C. G. Shuttle, M. L. Chabinyc and J. Nelson, Adv. Energy Mater., 2012, 2, 662–669.
257. D. Kipp and V. Ganesan, Macromolecules, 2016, 49(14), 5137–5144.
258. D. Kipp and V. Ganesan, J. Appl. Phys., 2013, 113, 234502.
259. P. P. Khlyabich, A. E. Rudenko, B. C. Thompson and Y.-L. Loo, Adv. Funct. Mater., 2015, 25, 5557–5563.
260. P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2011, 133, 14534–14537.
261. P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2012, 134, 9074–9077.
262. R. A. Street, D. Davies, P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2013, 135, 986–989.
263. N. Felekidis, E. Wang and M. Kemerink, Energy Environ. Sci., 2016, 9, 257–266.

---