Open Access Article
Open Access ArticleElectrochemical DNA biosensors based on long-range electron transfer: investigating the efficiency of a fluidic channel microelectrode compared to an ultramicroelectrode in a two-electrode setup†
M.-C.
Horny
ad,
M.
Lazerges
b,
J.-M.
Siaugue
c,
A.
Pallandre
d,
D.
Rose
a,
F.
Bedioui
b,
C.
Deslouis
a,
A.-M.
Haghiri-Gosnet
d and
J.
Gamby
*ad
aSorbonne Universités, UPMC Univ Paris 06, CNRS, Laboratoire Interfaces et Systèmes Electrochimiques, 4 place Jussieu, F-75005, Paris, France. E-mail: Jean.gamby@lpn.cnrs.fr
bUTCBS, U 1022 INSERM, UMR 8258 CNRS, Paris Sciences Lettres University, Ecole Nationale Supérieure de Chimie de Paris, 11 rue Pierre et Marie Curie, 75005 Paris, France and Sorbonne Paris Cité, Université Paris Descartes, Faculté de Pharmacie de Paris, 4 avenue de l'observatoire, 75006 Paris, France
cSorbonne Universités, UPMC Univ Paris 06, CNRS, UMR 8234, Laboratoire PHysico-chimie des Electrolytes et Nanosystèmes InterfaciauX (PHENIX), 4 place Jussieu, F-75005, Paris, France
dCentre de Nanosciences et de Nanotechnologies, CNRS, Univ. Paris-Sud, Université Paris-Saclay, C2N – Marcoussis, 91460 Marcoussis, France
First published on 23rd September 2016
Abstract
Here, we describe the transposition of an ultramicroelectrode (UME) setup into a microfluidic chip configuration for DNA biosensors. The hydrodynamic properties of the fluidic channel microelectrode were screened with an [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− redox couple by cyclic voltammetry to provide a basis for further biological processes. A 23-base DNA probe was self-assembled into a monolayer on gold microelectrodes both in classical configuration and integrated in a microfluidic setup. Special interest was focused on the DNA target mimicking the liver-specific micro-ribonucleic acid 122 (miRNA122). Long-range electron transfer was chosen for transducing the hybridization. This direct transduction was indeed significantly enhanced after hybridization due to DNA-duplex π-stacking and the use of redox methylene blue as a DNA intercalator. Quantification of the target was deduced from the resulting electrical signal characterized by cyclic voltammetry. The limit of detection for DNA hybridization was 0.1 fM in stopped flow experiments, where it can reach 1 aM over a 0.5 μL s−1 flow rate, a value 104-fold lower than the one measured with a conventional UME dipped into an electrolyte droplet under the same analytical conditions. An explanation was that forced convection drives more biomolecules to the area of detection even if a balance between the speed of collection and the number of biomolecules collected has been found. The latter point is discussed here along with an attempt to explain why the sensor has reached such an unexpected value for the limit of detection.
1. Introduction
A key consideration for biosensors is the limit of detection imposed by the molecular level changes in the expression of biomolecules to be able to perform reliable diagnostics before symptoms of a disease appear. In the context of a new generation of cheap and portable biosensors, biomolecules present in vivo at physiological levels have to be detected quickly while maintaining high specificity.In recent years, research studies have focused on micro-ribonucleic acids (miRNAs) as they have been detected in serum and plasma of humans at stable and reproducible levels.1 Indeed, being specific regulators of gene expression under baseline conditions, miRNAs have more pronounced functions in case of stress or disease, decreasing or increasing their levels in serum and plasma,2 thus opening the possibility of using miRNAs as diagnostic biomarkers of various diseases.3–5 They have also been shown to allow precise differentiation and classification of cancers.6,7 For instance, miRNA122 is only produced by liver cells in case of injury (hepatitis, alcoholism, obesity).8 Commonly, miRNA detection studies use real-time PCR (polymerase chain reaction).9 Although PCR is a powerful technique, it has limitations due to protocol times, cost, accurate quantification, and the need for complete fine tuning of the temperature during multiple stages of hybridization/denaturation; thus it still requires further development to improve its robustness.2,8,10
DNA hybridization is more and more chosen as the most prized method compared to direct sequencing due to a better understanding of the long range electron transfer mechanism through DNA duplex π-stacking.11 The electronic coupling within its inner core of a stacked array of heterocyclic aromatic base pairs is very sensitive to local disruptions such as mismatches, making a DNA biosensor particularly sequence specific. In a DNA biosensor, the target sequence is recognized by a complementary DNA probe and hybridized. The hybridization of two basis according to Watson and Crick's rules12 is converted into an electrical signal.
In order to be efficient, three key steps have to be controlled in a DNA biochip: (i) probe immobilization on a solid substrate, (ii) hybridization (or recognition) of the complementary target strand and (iii) conversion of the hybridization event into a physical signal (i.e. transduction). The strategies to achieve probe immobilization, target recognition and detection are numerous. A plethora of biosensors can be found in the literature, which differ in the biological process followed, the choice of transduction exploited, and the electrode material used. The literature has a significant number of papers that classify and compare different kinds of biosensors. In the domain of probes grafted on a solid substrate for direct hybridization with an unlabelled DNA target by using electrochemical transduction, a wide range of concentrations are reported in the literature from femtomolar to attomolar and even zettomolar concentrations. For instance, Riccardi et al.13 achieved a 2 × 10−16 M limit of detection by monitoring the changes in oxidation of gold polypyrrole due to DNA hybridization. Differential pulse voltammetry (DPV) was used for direct DNA oxidation on a conducting polymer leading to 10−17 M (ref. 14) and 10−15 M limits of detection with genomic DNA on polydeoxycytidine.15 Non-faradic biosensors coupled with impedance techniques for screening the interface charge density have reached a 10−18 M limit of detection on GaN nanowires16 and a 10−20 M limit of detection on boron-doped diamond with a polyethyleneimine layer.17 Chen et al.10 have reported a 10−16 M limit of detection with their nanogap sensor with sandwich arrays of gold/SiO2/gold using long-range electron transfer toward the redox indicator.
In this work, a traditional two-electrode configuration setup comprising a gold ultramicroelectrode (UME) and a large counterelectrode inspired by the work of Lazerges et al.18 is compared to its counterpart integrated into a microfluidic system. The combined use of a microband electrode and a fluidic channel termed a channel microelectrode offers (i) the obtention of a fast steady state current response (around one millisecond) due to a very thin diffusion layer compared to the convection layer and (ii) a way to drastically improve the efficiency of the sensor in terms of the volume of the analytes and system dynamics with easy manipulation of samples.19–25 These aims are achieved by the use of an [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− redox couple in a channel microelectrode during the immobilization and hybridization steps in order to set an equilibrium potential at 0 V as both microelectrodes are in gold. DNA hybridization is followed by cyclic voltammetry (CV) with the redox couple allowing surface property analysis, such as surface modification, when binding events of target DNA occur on the sensor surface. The selectivity of the electrochemical DNA biosensor using an UME was already verified in a previous study using the same protocol scheme where a double-stranded DNA (miR122) had a single mismatch in the sequence.26
2. Materials and methods
2.1. Chemicals
Sodium chloride (NormaPur), methylene blue (Alfa Aesar), potassium ferricyanide(III), and potassium hexacyanoferrate(II) (Sigma-Aldrich) were used in the experiments without further purification. The thiol-labeled DNA probe (P) and complementary target (T) were purchased from Integrated DNA Technologies (Belgium). Their sequences are shown in Table 1. The target DNA used mimics the fragment of interest miRNA-122 for the diagnosis of liver cells in case of injury (hepatitis, alcoholism, obesity).| Name | Sequence |
|---|---|
| P | 5′-thiol C6-CAA ACA CCA TTG TCA CAC TGC-3′ |
| T | 5′-GCA GTG TGA CAA TGG TGT TTG-3′ |
2.2. Microfluidic chip fabrication
All lithographic masks were designed using L-Edit software (Tanner EDA). The device was microfabricated by assembling an upper PDMS part with a microchannel and a lower part containing gold microelectrodes patterned on a glass substrate. Glass substrates were cleaned with a piranha solution (H2SO4/H2O2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) prior to use. The glass slides were then spin-coated with AZ5214 resin followed by inverted lithography on an MJB4 aligner. Substrates were then cleaned by a reactive ion etching (RIE) process to remove all resin residues and then metallized with a 200 nm layer of gold on top of a 20 nm titanium layer followed by a classic lift-off process.
1) prior to use. The glass slides were then spin-coated with AZ5214 resin followed by inverted lithography on an MJB4 aligner. Substrates were then cleaned by a reactive ion etching (RIE) process to remove all resin residues and then metallized with a 200 nm layer of gold on top of a 20 nm titanium layer followed by a classic lift-off process.
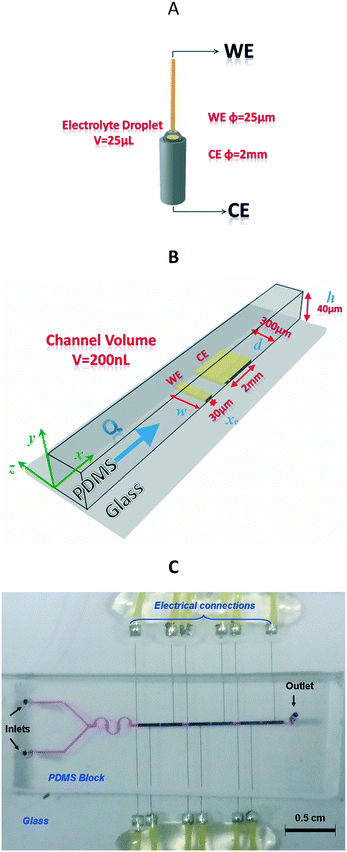
The fluidic circuit is obtained from a master mold made of SU-8. Fabrication of the mold starts with the cleaning of the silicon wafer and lithography of a 16 μm thick layer of SU-8. A 1 cm thick layer of PDMS is poured onto the SU-8 master mold to obtain a negative replica after curing the fluidic network at 70 °C overnight. The PDMS and the glass substrates with the electrodes are washed with isopropanol and dried with nitrogen. Then, the PDMS part is treated with nitrogen plasma to favor the adhesion of the PDMS onto the glass slide. The manual alignment of the PDMS and electrodes is performed under binocular conditions for the correct electrode alignment on the microfluidic channel (see Fig. 1C).
2.3. Ultra-microelectrode fabrication
The 25 μm ultra-microelectrode (UME) was home-made using 99.99% pure Goodfellow gold wire sealed in glass capillaries. The counterelectrode was a 2 mm diameter gold wire sealed in a Teflon cylinder (Metronic, France). The gold UME was polished with 3 μm silicon carbide disks and rinsed with deionized water.2.4. Probe immobilization and target hybridization
The DNA probe immobilization was performed by incubating the UME electrode for two hours in a 500 μL volume of 10 μg mL−1 DNA probe diluted in 0.5 M NaCl. Then the UME electrode was rinsed with deionized water. Between probe immobilization and target recognition, the UME is in contact for 30 minutes with 0.5 M NaCl to test the stability of the self-assembled monolayer (SAM). Target hybridization was performed in a 500 μL solution of DNA target of decreasing concentration in 0.5 M NaCl solution for 30 minutes followed by rinsing with 0.5 M NaCl solution. An [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− redox couple and a methylene blue (MB) redox catalyst were added to a 0.5 M NaCl solution for electrochemical detection.ss-DNA probe immobilization in a microfluidic chip was performed by circulating a 0.15 μM DNA probe in 0.5 M NaCl and then stopping the flow for two hours. The flushing and the test of stability of the SAM are the same as for the UME. High frequency electric impedance spectroscopy (HFEIS) measurements were performed to estimate the probe density (see the ESI†). A value of 1.1 × 10−11 mol cm−2 SAM coverage was found to roughly match the 4.47 × 10−10 mol cm−2 experimental value found for close-packed short-thiol SAM on gold by Rouhana et al.27
Hybridization was performed under various flow conditions with samples of target DNA of increasing concentrations in 0.5 M NaCl for 30 minutes.
2.5. Electrochemical detection
For the electrochemical measurement, the UME was immersed in a 25 μL electrolyte drop, while for the microfluidic chip, a flow of 0.2 μL s−1 was selected.Cyclic voltammetry was performed using the two-electrode setup displayed in Fig. 1A. For simplicity, this design will be called the conventional UME setup (Fig. 1A) in contrast to the microfluidic setup (Fig. 1B and C).
Please note that the thiol-gold bond is formed spontaneously on the surface of both the WE and CE, and thus both electrodes are functionalized with ss-DNA probes. However, for several reasons, the measured current at each step (bare gold, ss-DNA immobilization or ds-DNA hybridization) will be mainly attributed to the WE current response (see Fig. 2). First, the CE was intentionally positioned after the WE (vs. flow), in order to favour DNA-probe immobilization and then DNA-target hybridization on the WE. Second, as the counter-electrode (6 × 10−3 cm2 surface area) in the fluidic channel is about 66-fold larger than that of the working microelectrode (9 × 10−5 cm2), it can be considered as a pseudo reference since its current density variation is lower compared to that of the working microelectrode.
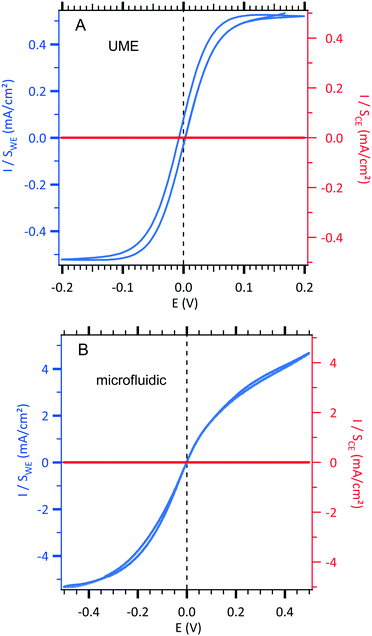 | ||
| Fig. 2 Sigmoidal voltammograms of an equimolar solution of 3 mM [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− and 0.5 M NaCl centred at zero potential with the two configurations (see Fig. 1). The current densities of the working electrode (WE, left axis in blue) and the counterelectrode (CE, right axis in red) are normalized according to each electrode area. (A) Conventional UME set-up as illustrated in Fig. 1A. Cyclic voltammetric response of an UME as a WE electrode using 10 mV s−1 as the scan rate. B. Microfluidic setup as illustrated in Fig. 1B. Cyclic voltammetric response of a WE microband electrode using 0.05 μL s−1 as the fixed value of the flow rate and 10 mV s−1 as the scan rate. | ||
2.6. Apparatus
Cyclic voltammetry measurements were performed using EC-lab software from Biologic SP-300 electrochemical station. Both setups have a two electrode configuration. The scan rate was set to 10 mV s−1 for the microfluidic setup to obtain quasi-identical forward and backward waves. For the conventional configuration, a scan rate of 25 mV s−1 was selected.High frequency electric impedance spectroscopy (HFEIS) measurements were performed by coupling a frequency response analyser (Solartron FRA 1255B) with a dielectric interface (Solartron DI 1296A) to the apparatus. The frequency range used for measurements was varied from 1 MHz to 0.1 Hz. The sinusoidal AC signal excitation between microelectrodes is set to 100 mV peak to peak, since DC was fixed at 0 V.
The microfluidic setup was connected to a programmable syringe pump allowing a flow rate in the range from 0.01 μL s−1 to 5 μL s−1.
3. Results and discussion
3.1. Hydrodynamic conditions in the microfluidic channel and mass transport to the microelectrode
The high aspect ratio (d/h) of the fluidic channel (h and d are the height and width of the channel, respectively) ensures a quasi one-dimensional Poiseuille flow. The only velocity component is vx in the flow direction, which depends on y, the coordinate orthogonal to the two parallel planes with a well-known developed parabolic profile, as follows: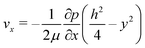 | (1) |
One can define the volumetric flow rate Q as follows:
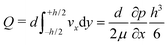 | (2) |
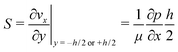 | (3) |
This results in the following relation between Q and S:
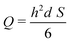 | (4) |
The concentration distribution of a solute obeys the mass transport equation:
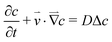 | (5) |
The diffusion–convection term is reduced to 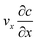 and the diffusion term to
and the diffusion term to 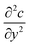 .
.
The solution of eqn (4) when the electrode acts as an ideal mass sink is obtained with the boundary conditions c = 0 on the electrode and ∂c/∂y = 0 on the insulating areas.
Given these conditions, L. P. Reiss and T. J. Hanratty28 have predicted the limiting diffusion current to a thin rectangular microelectrode of width w and length xe placed crosswise to the flow direction:
| Ilim = 0.807nFc∞D2/3xe2/3wS1/3 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), c∞ is the concentration of electroactive species (mol cm−3) and D is the diffusion coefficient of the electroactive species (cm2 s−1). xe, w, h and d are the dimensions (μm) shown in Fig. 1B.
485 C mol−1), c∞ is the concentration of electroactive species (mol cm−3) and D is the diffusion coefficient of the electroactive species (cm2 s−1). xe, w, h and d are the dimensions (μm) shown in Fig. 1B.
Eqn (6) implies that the diffusion layer thickness is small enough with respect to h so that vx within is approached by its linear approximation, as follows:
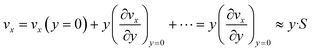 | (7) |
For consistency, y is taken here as a local orthogonal coordinate from the wall (i.e. y and vx are null at the wall).
Compton29 has proposed an equivalent expression as a function of the volumetric flow rate (see eqn (1)):
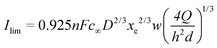 | (8) |
Therefore, for both eqn (6) and (8) to be valid, it is required that the diffusion layer which develops from the leading edge of the microelectrode (i.e. for x = 0) remains very small at its leaving edge, i.e. for x = xe.
The local diffusion layer thickness is defined as follows:30,31
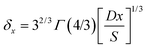 | (9) |
In Nernst layer approximation and using Fick's law, eqn (6) or (8) can be obtained from eqn (9) by a straightforward integration.
Therefore, from eqn (9) and (4), one can also check whether the used microelectrode fulfills the condition of a sufficiently small diffusion layer thickness at x = xe.
As an example, for Q = 10−3 cm3 s−1 corresponding to the higher imposed volumetric flow rate, and with D = 10−5 cm2 s−1, xe = 30 μm, h = 40 μm and d = 300 μm, one obtains δxe ∼ 2.5 μm.
This value corroborates the above assumption of a linear velocity profile within the diffusion layer. For much lower Q values, this assumption could not be justified.
In a first step, a test experiment was conducted with a fast redox system. To this end, an equimolar solution of 3 mM [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− and 0.5 M NaCl was introduced into our designed microchip flow channel containing the two-microelectrode setup under laminar flow conditions. The results are displayed in Fig. 2.
Sigmoid shape voltammograms are observed as expected for a laminar flow. They are centred at zero potential. Indeed, in this two-electrode setup, the working electrode and the counterelectrode are made from the same metal and are immersed in the same electrolyte containing the redox couple. Indeed, the 2 mm gold counterelectrode (very high area compared to the 30 μm gold working electrode) can be considered as a pseudo-reference electrode allowing a feeble potential drift during measurements.
In order to compare the currents from the conventional setup and the microfluidic setup, the obtained current curves, IWE, were normalized with the surface of each working electrode (Sconventional = 1.96 × 10−5 cm2 and Smicrofluidic = 9.0 × 10−5 cm2) resulting in a comparable current density, JWE, at a given potential (in mA cm−2) as shown in Fig. 2. Moreover, in each configuration, the current density, JWE, on the working electrode is compared to the one on each counterelectrode, JCE, which is negligible. The scan rate was optimized at 10 mV s−1 to obtain a steady state current response and to minimize the gap between the forward and backward current curves. Moreover, the qualitative difference in the fluidic voltammogram (non-symmetric), where the reduction current is slightly higher than the oxidation current, is due to the difference between the diffusion coefficients of [Fe(III)(CN)6]3− (D = 6.6 × 10−6 cm2 s−1) and [Fe(II)(CN)6]4− (D = 5.6 × 10−6 cm2 s−1) in NaCl as supporting electrolytes. For instance, the theoretical ratio between the diffusion coefficients ((DFe(III)/DFe(II))2/3) is equal to 1.12 that is close enough to the 1.15 experimental ratio between the limiting current in reduction (Ilim,reduction at −0.4 V) and the limiting current in oxidation (Ilim,oxidation at +0.4 V) according to eqn (6).
To analyse the hydrodynamics in the fluidic channel microelectrode, a flow rate of increasing value was imposed. The results are shown in Fig. 3. The limiting current plateau is flow dependent as the diffusion layer near the microelectrode is controlled by the forced convection. While the voltammogram of the UME (Fig. 2A) shows the expected S-shape, the one corresponding to the fluidic channel microelectrode (Fig. 2B) indicates an apparent more sluggish reaction. The cathodic plateau current for example is attained below −0.4 V, whereas this is achieved at −0.1 V for the UME. The more plausible explanation is the larger value of the ohmic drop between the WE and CE in the fluidic channel. High frequency electric impedance spectroscopy (HFEIS)32 measurements were performed to estimate the ohmic resistance (see eqn S2 in the ESI†).
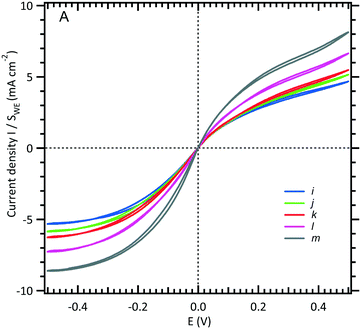 | ||
| Fig. 3 Limiting current intensity response of a WE microchannel electrode vs. volumetric flow rates (see Fig. 1B). The channel is filled with an equimolar solution of 3 mM [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− and 0.5 M NaCl. The scan rate is fixed at 10 mV s−1, and five flow rates are shown here: (i) 0.05, (j) 0.08, (k) 0.1, (l) 0.2, and (m) 0.5 μL s−1. | ||
In Fig. 4, the intensity of the reduction plateau current that has been normalized with eqn (6) is plotted against the volumetric flow rate, (Q)1/3. It can be observed that the deviation with respect to the value given by eqn (6) in the low flow rate range is significant. A similar behaviour was observed by Ordeig et al.33 in their simulation with a gold microelectrode. They ascribed this low flow rate behaviour to the effect of edge diffusion at the microelectrodes and channel wall effects which were not taken into account in eqn (6) or (8) at lower flow rates.
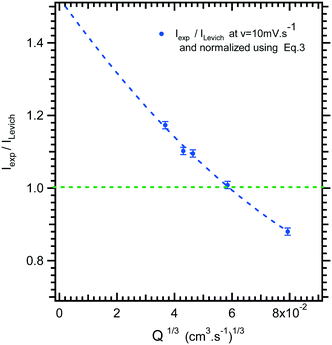 | ||
| Fig. 4 Limiting current ratio between experimental current, Iexp, and Levich equation current, ILevich, as a function of the 1/3 volumetric flow rate for the microfluidic setup. | ||
3.2. DNA hybridization protocol with the conventional UME
Thiols adsorb on gold substrates building self-assembled monolayers (SAMs) according to eqn (10).212R-SH(aq) + 2Au(s) → 2RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) - -![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au(s) + H2(g) Au(s) + H2(g) | (10) |
The use of thiol micromolar concentrations minimizes the contributions of any added impurities to the adsorption kinetics21 onto which reproducibility and stability of the measurements are critically dependent. Moreover, with a micromolar concentration, a full monolayer is built within two hours.27 A value of 1.1 × 10−11 mol cm−2 SAM coverage was found (see the ESI†). DNA hybridization detection is based on long range electron transfer through the DNA double strand via π-stacking as described previously. The [Fe(III)(CN)6]3−/[Fe(II)(CN)6]4− redox couple was use to discriminate a single strand DNA immobilized from a double strand hybridized. Indeed, DNA is wrapped within a negatively charged sugar phosphate backbone which prevents diffusion of the also negatively charged redox complex inside the SAM. However, the current density before hybridization (red curve, Fig. 5A) is not zero probably due to edge effects and holes in the SAM. After hybridization (blue curve, Fig. 5B), the current–voltage slope is steeper indicating that hybridization occurred. The DNA hybridization response sensitivity was obtained with the use of a MB redox intercalator. In brief, methylene blue (MB) is used as both a redox catalyst and a DNA-duplex organic intercalator having an affinity constant of 106 M−1. The MB reduction step is reversible with a redox potential of 0 (vs. NHE) that is lower than that of [Fe(III)(CN)6]3− reduction. The electrons jump from the gold electrode to the intercalated MB and are then accepted by the ferrocyanate in solution. The MB oxidized form is regenerated for a further electrochemical reduction. The LOD determination and standard deviation on measurements will be discussed in section 3.3.1.
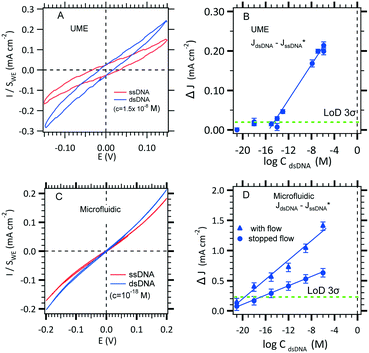 | ||
| Fig. 5 Effect of hybridization on cyclic voltammetry current with the two configurations. A. Two electrodes in the UME configuration where the kinetic current on a 25 μm diameter microelectrode is obtained for Fe(II)/Fe(III) (3 mM) MB (10−8 M) in 0.5 M NaCl in the absence and in the presence of a DNA target. B. LOD determination using the conventional UME set-up (see Fig. 1A) recorded at −0.1 V (see panel A). C. Effect of increasing hybridization target concentrations on the microchannel electrode sensor for a working flow rate of 0.5 μL s−1. D. LOD determination using the microfluidic set-up (see Fig. 1C) with several pairs of microelectrodes (blue circles) recorded at −0.2 V (see panel C). | ||
3.3. Hybridization detection in the microfluidic setup
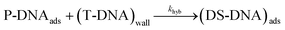 | (11) |
The hybridization rate is expressed as follows:
| rhyb = khyb·ΓP·[T]0 | (12) |
As shown in eqn (11) and (12), the partial order of reaction for each reactant is one and the global order is two. As a consequence, the observed hybridization rate, robs, between T-DNA and P-DNA can be viewed as a second order reaction, with robs in M s−1 and kobs in M−1 s−1 representing the observed hybridization kinetic rate constant.
We consider, from time t = 0, the concentration of T at the wall which is lower than the concentration of T in the bulk, i.e. 0 < [T]0 ≤ [T]bulk, because the hybridization reaction is considered as slow. However, at infinite time t∞ (i.e. 30 minutes at least for the hybridization time step in our experiments), the concentration at the wall tends to the bulk concentration, [T]0 = [T]bulk, and because any P was hybridized (ΓP)=0, the hybridization rate tends to zero.
As a consequence, the concentration of DS at infinite time, [DS]t=∞, is equal to the initial concentration of (ΓP)t=0, and then the measured current corresponding to the hybridization step at infinite time becomes proportional to the initial concentration, (i)t=∞ ∝ (ΓP)t=0.
The dehybridization rate of DS, rdes, is proportional with the double stranded DNA concentration and it is considered as a zero order reaction since the amount of the adsorbed DS-DNA on the gold microelectrode can be considered as unchanged:
| rdes = kdes | (13) |
As a consequence, the ratio (kdes/khyb) is defined as the equilibrium dissociation constant, KD, which is given in M. We also consider that the dehybridization rate is negligible in comparison with the hybridization rate, as follows:
| rdes ≪ rhyb | (14) |
The transport of target T is described in the analyte stream according to eqn (5) with the obtained value for the diffusion coefficient of T-DNA being around 10−11 m2 s−1 which is much lower than that of the redox probe, that is in accordance with an expected thin diffusion layer (DT-DNA ≪ DFe(III)).
The flow entrance on the sensor is described as a radial velocity vector. At the outlet, the outflow condition used is given as follows:
| n·(−D∇C) = 0 | (15) |
The hybridization of target DNA at the functionalized surface gives rise to a net flux at the corresponding boundaries as follows:
| NT = −rhyb + rdes = −rhyb | (16) |
The hybridization rate depends on the target concentration in the stream and it was taken into account in numerical calculations where two Comsol Multiphysics modules were coupled (surface reaction and transport of diluted species). In other words, hybridization of targets on the probe creates a concentration gradient which permits the diffusion of species to the surface. Indeed, diffusion dominates near the sensor while convection predominates further. The analytical resolution of this problem gives a diffusion layer thickness for x = xe that varies with the flow rate using eqn (9) and (4) as follows.
The calculation reveals that the depletion zone is thinner than the sensor surface, as follows:
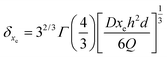 | (17) |
As listed in Table 2, the δxe value corresponding to each imposed volumetric flow rate can be deduced.
| Q (μL s−1) | δ x e (μm) | V (μL) | N B (number of targets) | ||
|---|---|---|---|---|---|
| 10−14 M | 10−16 M | 10−18 M | |||
| Static | 31.2 | 0.009 | 4.2 × 104 | 4.2 × 102 | 4.2 |
| 0.2 | 0.91 | 360 | 1.4 × 105 | 1.4 × 103 | 14 |
| 0.5 | 0.67 | 900 | 1.9 × 105 | 1.9 × 103 | 19 |
| 0.8 | 0.57 | 1440 | 2.3 × 105 | 2.3 × 103 | 23 |
Finally, the flow through the depletion zone can be approximated as follows:
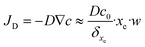 | (18) |
An example of calculation is tested below for 10 fM as initial concentration, 0.2 μL s−1 as flow rate, a binding-site density, bm, equal to 6.7 × 1012 sites cm−2 calculated from the value of SAM's coverage given in section 3.2 and, the equilibrium dissociation constant of DNA at room temperature that is taken equal to KD = koff/kon = 10−11 M.36 Consequently, one can estimate that 4.1 molecules per second will reach the sensor surface at this working concentration and this flow rate. In other words, 0.24 seconds between binding events can be estimated. As the dehybridization rate constant was supposedly negligible due to the strongly bound DNA duplex at room temperature,37 the expected number of target molecules to be bound to the sensor is given by eqn (19).
| NB = JD·t | (19) |
By taking into account these data, a number of molecules (7.6 × 103) can be estimated during a hybridization time step of 30 minutes. Moreover, the target molecules collected are only those in the thin diffusion layer. The goal is to select an accurate flow in our device configuration that will allow a sufficient number of DNA targets to be captured and sensed in 30 minutes reaction time. Although taller channels enable faster flows and quicker measurements, they reduce the relative fraction of biomolecules collected and thus increase the volume of reaction (V) needed. It is obvious that the detection limit imposed by the sensor is related to the local concentration at which one molecule will be bound to the sensor. To this aim, the theoretical number of targets for different initial concentrations and various flow rates are calculated and then listed in Table 2.
As shown in Table 2, it is necessary to strike a balance between a slow flow where all target molecules could be collected and a fast flow where target molecules are swept away before they can enter the diffusion layer and be collected. It is obvious that a fast flow increases the volume of solution discarded which is a disadvantage when expensive biological samples are used. Another reason for the choice of an intermediary flow rate is that the SAM on gold (thiol-Au) is a fragile system. Indeed, the risk of SAM degradation could increase and distort the probe current measurement. As a consequence, for the next experiments, a flow rate of 0.5 μL s−1 was selected because it discards less than 1 mL of solution with an expected theoretical LOD between 1 × 10−18 and 1 × 10−16 M.
To gain confidence with the experimental results, the standard deviation (SD) on each experimental point was calculated using the definitions established by Armbruster et al.38 In our case, blank current density measurements, JssDNA, were recorded (30 minutes in the presence of single-stranded DNA in 0.5 M NaCl without target DNA). Then, the current density, JdsDNA, was measured after the hybridization of the double stranded DNA (30 minutes in 0.5 M NaCl with target DNA). Finally, the difference between JdsDNA and JssDNA was plotted with the DNA target concentration, and the LOD was estimated by taking the intersection between the linear section of the experimental data and 3-fold of the SD line. As shown in Fig. 5B and D, the error bars were generated using the standard deviation of the means of the difference between the ssDNA current density and the blank current density obtained with the conventional and microfluidic configurations. The obtained experimental LODs are summarized in Table 3 where a subfemtomolar and an attomolar concentration can be reached as it was theoretically estimated for stopped flow and with flow, respectively (see Tables 2 and 3).
| Setup | Conventional UME | Microfluidic stopped flow | Microfluidic with flow |
|---|---|---|---|
| Q (μL s−1) | — | — | 0.5 |
| LOD (M) | 10−14 | 10−16 | 10−18 |
Conclusions
We describe here the transposition of a conventional two-electrode set-up into a microfluidic one allowing the increase in the system's dynamics and thus the increase in the number of DNA targets hybridizing on the sensor achieving 1 aM as the LOD. This unexpected LOD is due to a forced convection which diminishes the diffusion layer thickness and results in a faster collection of the DNA targets toward the sensor. Thus, more targets are collected and contribute to the increase of the hybridization signal.The advantages of the microfluidic setup in comparison with the UME conventional setup are an easy to use two-electrode configuration for fast screening and a more efficient control of the distance between electrodes. Indeed, there is less risk of damage to the SAM of single-stranded DNA by manipulating the microelectrode, thus decreasing the standard deviation of blank measurements. Another advantage of the electrobiochip described here is the possibility of multi-detection for parallel analysis of numerous miRNAs especially relevant in the case where a cancer manifests through multiple miRNAs, generating a map of miRNA concentration changes.
Acknowledgements
This work was supported by the LabEx MiChem part of French state funds managed by the ANR within the Investissements d'Avenir programme under reference ANR-11-IDEX-0004-02. The authors would also like to thank the “Centre de Nanosciences et de Nanostructures” for its financial support through the clean room facilities in Marcoussis, France.References
- Q. Shi, X. Yang and D. L. Mendrick, Biomarkers Med., 2013, 7, 307 CrossRef CAS PubMed.
- E. Van Rooij, Circ. Res., 2011, 108, 219 CrossRef CAS PubMed.
- T. Adachi, M. Nakanishi, Y. Otsuka, K. Nishimura, G. Hirokawa, Y. Goto, H. Nonogi and N. Iwai, Clin. Chem., 2010, 56, 1183 CAS.
- X. Ji, R. Takahashi, Y. Hiura, G. Hirokawa, Y. Fukushima and N. Iwai, Clin. Chem., 2009, 55, 1944 CAS.
- G. A. Calin, C. D. Dumitru, M. Shimizu, R. Bichi, S. Zupo, E. Noch, H. Aldler, S. Rattan, M. Keating, K. Rai, L. Rassenti, T. Kipps, M. Negrini, F. Bullrich and C. M. Croce, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15524 CrossRef CAS PubMed.
- A. M. Gurtan and P. A. Sharp, J. Mol. Biol., 2013, 425, 3582 CrossRef CAS PubMed.
- A. Lujambio and S. W. Lowe, Nature, 2012, 482, 347 CrossRef CAS PubMed.
- L. Moldovan, K. E. Batte, J. Trgovcich, J. Wisler, C. B. Marsh and M. Piper, J. Cell. Mol. Med., 2014, 18, 371 CrossRef CAS PubMed.
- B. S. Ferguson, S. F. Buchsbaum, J. S. Swensen, K. Hsieh, X. Lou and H. T. Soh, Anal. Chem., 2009, 81, 6503 CrossRef CAS PubMed.
- X. Chen, S. Roy, Y. Peng and Z. Gao, Anal. Chem., 2010, 82, 5958 CrossRef CAS PubMed.
- S. O. Kelley, E. M. Boon, J. K. Barton, N. M. Jackson and M. G. Hill, Nucleic Acids Res., 1999, 27, 4830 CrossRef CAS PubMed.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737 CrossRef CAS PubMed.
- C. D. S. Riccardi, H. Yamanaka, M. Josowicz, J. Kowalik, B. Mizaikoff and C. Kranz, Anal. Chem., 2006, 78, 1139 CrossRef CAS PubMed.
- K. Arora, N. Prabhakar, S. Chand and B. D. Malhotra, Sens. Actuators, B, 2007, 126, 655 CrossRef CAS.
- E. Alipour, M. H. Pournaghi-Azar, M. Parvizi, S. M. Golabi and M. S. Hejazi, Electrochim. Acta, 2011, 56, 1925 CrossRef CAS.
- C. P. Chen, A. Ganguly, C. Y. Lu, T. Y. Chen, C. C. Kuo, R. S. Chen, W. H. Tu, W. B. Fischer, K. H. Chen and L. C. Chen, Anal. Chem., 2011, 83, 1938 CrossRef CAS PubMed.
- J. Weng, J. Zhang, H. Li, L. Sun, C. Lin and Q. Zhang, Anal. Chem., 2008, 80, 7075 CrossRef CAS PubMed.
- M. Lazerges, V. T. Tal, P. Bigey, D. Scherman and F. Bedioui, Sens. Actuators, B, 2013, 182, 510 CrossRef CAS.
- J. S. Rossier, M. A. Roberts, R. Ferrigno and H. H. Girault, Anal. Chem., 1999, 71, 4294 CrossRef CAS PubMed.
- K. Stulik, C. Amatore, K. Holub, V. Marecek and W. Kutner, Pure Appl. Chem., 2000, 72, 1483 CrossRef CAS.
- C. Amatore, C. Sella and L. Thouin, J. Electroanal. Chem., 2006, 593, 194 CrossRef CAS.
- I. Streeter, N. Fietkau, J. Del Campo, R. Mas, F. X. Munoz and R. G. Compton, J. Phys. Chem. C, 2007, 111, 12058 CAS.
- D. Suwatchara, M. C. Henstridge, N. V. Rees and R. G. Compton, J. Phys. Chem. C, 2011, 115, 14876 CAS.
- H. Wang, Y. Liu, C. Liu, J. Huang, P. Yang and B. Liu, Electrochem. Commun., 2010, 12, 258 CrossRef CAS.
- M. Faure, A. Pallandre, S. Chebil, I. Le Potier, M. Taverna, B. Tribollet, C. Deslouis, A.-M. Haghiri-Gosnet and J. Gamby, Lab Chip, 2014, 14, 2800 RSC.
- A. Nassi, F. X. Guillon, A. Amar, B. Hainque, S. Amriche, D. Maugé, E. Markova, C. Tsé, P. Bigey, M. Lazerges and F. Bedioui, Electrochim. Acta, 2016, 209, 269 CrossRef CAS.
- L. L. Rouhana, M. D. Moussallem and J. B. Schlenoff, J. Am. Chem. Soc., 2011, 133, 16080 CrossRef CAS PubMed.
- L. P. Reiss and T. J. Hanratty, AIChE J., 1963, 9, 154 CrossRef CAS.
- R. G. Compton, A. C. Fisher, R. G. Wellington, P. J. Dobson and P. A. Leigh, J. Phys. Chem., 1993, 97, 10410 CrossRef CAS.
- M. A. Lévêque, Ann. Mines, 1928, 13, 283 Search PubMed.
- S. C. Ling, J. Heat Transfer, 1963, 85, 230 CrossRef.
- M. Faure, B. Sotta and J. Gamby, Biosens. Bioelectron., 2014, 58, 61 CrossRef CAS PubMed.
- O. Ordeig, N. Godino, J. Del Campo, F. X. Muñoz, F. Nikolajeff and L. Nyholm, Anal. Chem., 2008, 80, 3622 CrossRef CAS PubMed.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Nat. Biotechnol., 2008, 26, 417 CrossRef CAS PubMed.
- J. Newman, in Electroanalytical Chemistry, ed. Bard A., Dekker, New York, 1973, vol. 6 Search PubMed.
- P. W. Stevens, M. R. Henry and D. M. Kelso, Nucleic Acids Res., 1999, 27, 1719 CrossRef CAS.
- T. E. Ouldridge, A. A. Louis and J. P. K. Doye, J. Chem. Phys., 2011, 134, 085101 CrossRef PubMed.
- D. A. Armbruster and T. Pry, Clin. Biochem. Rev., 2008, 29(Suppl 1), S49 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6lc00869k |
| This journal is © The Royal Society of Chemistry 2016 |