Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Additively manufactured MEMS multiplexed coaxial electrospray sources for high-throughput, uniform generation of core–shell microparticles
D.
Olvera-Trejo
ab and
L. F.
Velásquez-García
*c
aMicrosystems Technology Laboratories, Massachusetts Institute of Technology, Cambridge, MA, USA
bTecnológico de Monterrey, Monterrey, NL, Mexico. E-mail: daniel.olvera.trejo@itesm.mx
cMicrosystems Technology Laboratories, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: velasquez@alum.mit.edu
First published on 3rd October 2016
Abstract
This study reports the first MEMS multiplexed coaxial electrospray sources in the literature. Coaxial electrospraying is a microencapsulation technology based on electrohydrodynamic jetting of two immiscible liquids, which allows precise control with low size variation of the geometry of the core–shell particles it generates, which is of great importance in numerous biomedical and engineering applications, e.g., drug delivery and self-healing composites. By implementing monolithic planar arrays of miniaturized coaxial electrospray emitters that work uniformly in parallel, the throughput of the compound microdroplet source is greatly increased, making the microencapsulation technology compatible with low-cost commercial applications. Miniaturized core–shell particle generators with up to 25 coaxial electrospray emitters (25 emitters cm−2) were fabricated via stereolithography, which is an additive manufacturing process that can create complex microfluidic devices at a small fraction of the cost per device and fabrication time associated with silicon-based counterparts. The characterization of devices with the same emitter structure but different array sizes demonstrates uniform array operation. Moreover, the data demonstrate that the per-emitter current is approximately proportional to the square root of the flow rate of the driving liquid, and it is independent of the flow rate of the driven liquid, as predicted by the theory. The core/shell diameters and the size distribution of the generated compound microparticles can be modulated by controlling the flow rates fed to the emitters.
Introduction
Electrospraying, i.e., the atomization of liquids using high electric fields, is an electrohydrodynamic phenomenon first described in the literature in at least the 16th century1 and investigated for over one hundred years.2 In the 1960s, G. I. Taylor presented a theoretical model that describes the shape of the free surface of the liquid phase under the effect of a high electrical field as conical, and this became known as the Taylor cone.3 Electrospraying typically entails the injection of a liquid through a metal capillary that is biased at a high voltage with respect to a counter electrode. For a specific range of applied electrical field and injected flow rates, the electrified meniscus forms a Taylor cone that ejects from its apex an extremely thin and steady jet that breaks up into very fine droplets with low size spread.Coaxial electrospraying is the electrohydrodynamic atomization of two immiscible liquids that are fed using concentric flow structures, e.g., capillaries. In coaxial electrospraying, the menisci of both liquids adopt a conical shape, and a compound jet of two co-flowing coaxial liquids is formed downstream, which eventually breaks up into core–shell particles (the outer liquid of the compound jet forms the shells of the particles and the inner liquid of the compound jet forms the cores of the particles). Unlike traditional, i.e., uniaxial, electrospraying, which has been used to produce microstructured materials since at least three decades ago,4 the study of coaxial electrospraying only spans about a decade. As a matter of fact, the first report on the generation of monodisperse core–shell particles via coaxial electrospraying was published in 2002,5 followed in 2003 by the first study of the scaling laws that describe the dependence of the emitted current on the flow rates and the physical properties of the liquids.6
Coaxial electrospraying is a very promising microencapsulation technique because (i) it is easy to implement, (ii) it can operate at room temperature and at atmospheric pressure, (iii) it does not require a series of steps in the encapsulation process, (iv) it can generate compound droplets with a narrow size distribution, and (v) it can be used to encapsulate a great variety of materials; therefore, coaxial electrospraying is compatible with a wide range of biomedical and engineering applications. For example, coaxial-electrosprayed core–shell and hybrid core–shell micro/nanoparticles are actively investigated for drug delivery, tissue engineering, and plastic surgery.7 One of the most common applications of the technology is the fabrication of hard shell microspheres using polymeric materials, which has been successfully demonstrated as an effective mechanism for drug delivery control.8,9 Microencapsulation by electroatomization is also a promising technique for generating particles made of FDA-approved polymers,10–12 and for production with precise control of the core–shell geometry of drug-loaded microcapsules.13 Moreover, core–shell microcapsules fabricated by coaxial electrospraying can have embedded microactuators, e.g., electrically sensitive hydrogel beads that can regulate the release profile of the molecules encapsulated within the core of the particles.14 In addition, coaxial electrospraying has been used to encapsulate ceramic particles with polymers15 because ceramic–polymeric composites are promising as dental biomaterials and can also be used in bone grafts. Beyond biomedical applications, the encapsulation of active lipophilic compounds using coaxial electrospraying can be applied in the food, pharmaceutical, and flavouring industries with the purpose of increasing the stability and lifetime of the active compounds.16 Furthermore, coaxial electrospraying has been employed for the synthesis of micrometer-sized hollow hemispherical TiO2 particles that enhance the light-harvesting efficiency of dye-sensitized solar cells.17 In addition, self-healing micro/nanostructured materials have demonstrated encapsulating liquid monomers inside polymer fibers via electroatomization.18
Standard coaxial electrospray sources have very low throughput because they have only one emitter, which is operated in the cone-jet emission mode. Moreover, a coaxial electrospray emitter is restricted to low flow rates because this allows for complete solvent evaporation when a polymeric solution is used as core and/or shell feedstock. In addition, increasing the flow rates fed to the emitter increases the diameter of the particles, which could cause adverse effects in a given application. Increasing the bias voltage can increase the throughput of the emitter, although at the expense of the size uniformity of the particles generated. Consequently, the existing coaxial electrospray sources are only suitable for high-end applications and research. An approach to increase the throughput of a coaxial electrospray source without affecting the size variation of the emitted compound microparticles is to implement arrays of coaxial emitters that operate in parallel. However, unlike uniaxial electrospraying, of which numerous demonstrations of multiplexed MEMS devices exist in the literature,19–23 to the best of the authors' knowledge, no miniaturized array sources have been reported; this is probably due to the inherent three-dimensionality of the emitter geometry and the hydraulic network required to attain uniform array operation, which is at odds with the planar nature of traditional microfabrication. However, 3D printing has recently been used to demonstrate a variety of microsystems, including microfluidics.24–26 In particular, stereolithography (SLA), which is an additive manufacturing process that creates freeform solid objects from the photopolymerization of a resin using ultraviolet light, can be used to create MEMS multiplexed uniaxial electrospray sources at a small fraction of the cost per device and fabrication time associated with silicon-based counterparts.27 Herein, using high-resolution stereolithography in their manufacture, the first MEMS multiplexed coaxial electrospray sources in the literature are reported. The characterization of devices with the same emitter structure but different array sizes evidences uniform array operation, demonstrating the feasibility of the reported approach to generate core–shell particles in great quantities via electroatomization, which is compatible with low-cost commercial applications.
Experimental
Device design
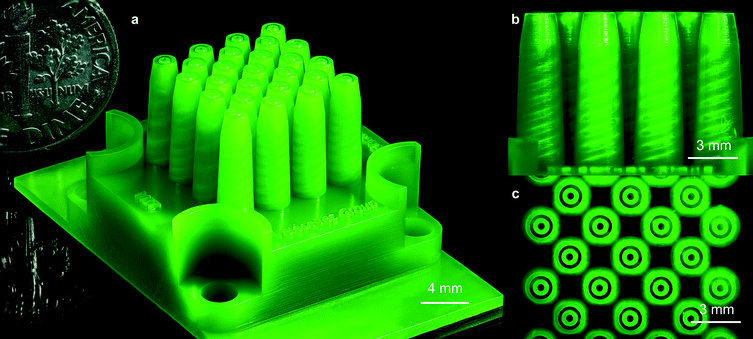
A schematic of one of the MEMS multiplexed coaxial electrospray sources is shown in Fig. 1, and the specifications of the design are listed in Table 1. Arrays of 1, 4, 9, 16, and 25 emitters occupying an active area equal to 1 cm2 were fabricated, sharing the same emitter specifications. Each device has a 7 mm by 24.25 mm by 24.25 mm frame with four through-holes that are utilized to clamp the device to a chuck with liquid feedthroughs using M4 screws; the through-holes are protected by curved spill guards. The microfluidic devices have two identical liquid reservoirs with a capacity of 0.2 mL each; the inner liquid reservoir provides the feedstock for the core layer of the particles, while the outer liquid reservoir provides the feedstock for the shell layer of the particles (Fig. 1a). The liquid reservoirs have inlet channels that open to the bottom of the microfluidic device. The ceilings of the liquid reservoirs are supported by an array of rounded square columns that avoid ceiling overhangs greater than 750 μm, which could result in collapse of the liquid reservoirs. Each reservoir feeds a microchannel embedded within each conical emitter that ends in a coaxial nozzle (Fig. 1b); in the case of the outer liquid reservoir, the channels are embedded within the support columns (Fig. 1c).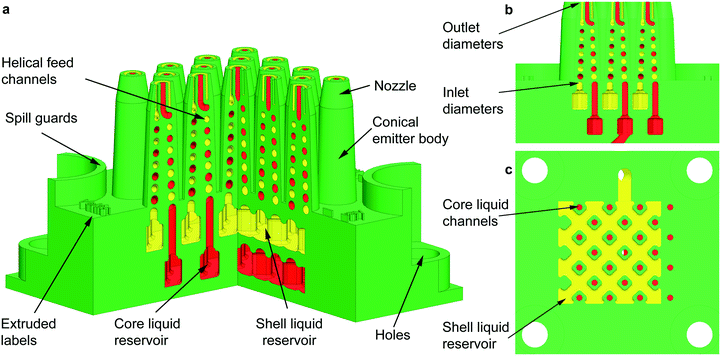 | ||
| Fig. 1 (a) Intersected cross-section of a 3D schematic of a planar array of 25 coaxial electrospray emitters. The hydraulics for the inner and outer liquids are coloured in red and yellow, respectively, whereas the structural (i.e., printed) material is coloured in green. (b) Lateral cross-section of the central emitter row of the schematic shown in Fig. 1a; the diameter of the tapered channels goes from 750 μm at the inlet of the channel to 450 μm at the outlet of the channel. (c) Top cross-section of the outer liquid reservoir; honeycomb structures are formed by square, rounded columns with bored inner channels to transport the liquid feedstock of the core layer. | ||
| Feature | Dimension |
|---|---|
| Inlet diameter of helical microchannel [μm] | 700 |
| Outlet diameter of helical microchannel/emitter spout [μm] | 450 |
| Emitter height [mm] | 9.35 |
| Nozzle height [mm] | 2 |
| Average gyration diameter of helical microchannel [mm] | 1.6 |
| Length of helical microchannel [mm] | 19 |
| Volume of each internal liquid reservoir [mL] | 0.2 |
The two microchannels inside each emitter define a double conical helix that is congruent, i.e., the channels are spirals of equal shape and size on a conical surface that differ by a translation along the axis. The helical structure implements within a small footprint and emitter height a large hydraulic impedance per liquid feed, which is a critical parameter for the stability and uniformity of electrospray array operation.21,28,29 In addition, each helical microchannel is a converging tapered pipe with the purpose of decoupling the pressure required to fill in the emitter and the pressure needed to cause dripping. For a circular pipe, the maximum pressure before dripping, PD, is given by PD = 4γ/ΦID, where γ is the surface tension of the liquid and ΦID is the inner diameter of the pipe. In a straight pipe, the fill-in pressure is the same pressure that would cause dripping at the other end of the channel. However, in a tapered pipe the two pressures are decoupled, and in a converging tapered pipe, the fill-in pressure is smaller than the dripping pressure. Using tapered channels greatly facilitates the filling in of multiplexed electrospray devices without causing dripping.27
Each emitter nozzle consists of two concentric conical tubes (i.e., a central tube with a circular cross-section and a concentric tube with an annular cross-section) that have the same hydraulic diameter DH (for the outer tube, DH = OTOD − OTID, where OTOD and OTID are the outer and internal diameter of the tube, respectively). The hydraulic diameter of the inner/outer fluid hydraulics at the nozzle spouts is equal to 450 μm, which is the smallest diameter that would result in printed devices with unclogged channels across the whole array. The hydraulic diameter of the microchannels at the emitter spouts is also an order of magnitude larger than the pixelation of the 3D printer. The walls of the conical tubes are 250 μm thick. The conical shape of the emitter body and nozzle enhances the electrical field over the liquid menisci, and the rounded fillet at the internal tube tip also improves the continuous feeding of the outer liquid. Having a small emitter tip results in a lower onset voltage V because the electrical field required to trigger electrospray emission corresponds to having the electrostatic pressure equal to the surface tension pulling; therefore, εoEn2 ∼ 8γ/ΦID for an electrospray emitter capillary with inner diameter ΦID, where εo is the permittivity of free space, En ∼ V/ΦID is the normal surface electric field acting on the meniscus, and V is the bias voltage.30
Device fabrication
The devices were fabricated using a high-resolution SLA printer (pixelation ∼25 μm) with a layer height equal to 25 μm and absolute tolerances in the x–y and z directions equal to 50 μm and 125 μm, respectively. The MEMS multiplexed coaxial electrospray sources are made of an opaque green, ABS-like material based on the epoxy resin SOMOS, with a tensile modulus equal to 2.1 GPa, a Shore D hardness of 85, and an elongation to break equal to 6.1%. Each device starts as a computer-aided design (CAD) file that is exported in STL format with a dimensional tolerance equal to 2.5 μm (i.e., an order of magnitude smaller than the pixelation of the printer). Then, the STL file is transformed into a set of cuts that are transferred to the stereolithography 3D printer. The printer creates, layer by layer, the microfluidic device using an array of diodes and a puddle of the photosensitive resin. After printing, the uncured resin within the hydraulics or on the surface of the device is removed using isopropanol. Finally, any particles within the hydraulics are removed using an ultrasonic bath at 45 °C with a solution of deionized water mixed with isopropanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) for 10 minutes. A 3D-printed MEMS multiplexed coaxial electrospray source with 25 emitters in 1 cm2 is shown in Fig. 2, which includes a US dime coin for reference (Fig. 2a). The helical channels make 3.5 revolutions with a pitch of half of the spiral diameter and a tapered spiral of 2.2° (Fig. 2b). Fig. 2c is a top view of the active area of the device, showing the array of coaxial nozzles.
1 v/v) for 10 minutes. A 3D-printed MEMS multiplexed coaxial electrospray source with 25 emitters in 1 cm2 is shown in Fig. 2, which includes a US dime coin for reference (Fig. 2a). The helical channels make 3.5 revolutions with a pitch of half of the spiral diameter and a tapered spiral of 2.2° (Fig. 2b). Fig. 2c is a top view of the active area of the device, showing the array of coaxial nozzles.
Working liquids
In coaxial electrospraying, the driving liquid is pulled by the electrostatic forces, pushing the other, i.e., driven, liquid by transferring the electrical stress through viscosity. The driving liquid has the smaller electrical relaxation time, te = εrεo/K, of the two liquids fed to the emitter, where εr and K are the relative electrical permittivity and the electrical conductivity of the liquid, respectively. In general, a coaxial electrospray emitter with the driven liquid as outer liquid and the driving liquid as inner liquid can operate stably over a wider range of flow rates compared to the opposite combination.31 In this work, a solution of deionized water mixed with isopropyl alcohol (DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP) or ethylene glycol (EG) were used as driving liquids and sesame oil (SO) was used as driven liquid. Specifically, unless otherwise noted, device versions with 1, 4, and 9 emitters were tested as core–shell particle generators using a DIW
ISP) or ethylene glycol (EG) were used as driving liquids and sesame oil (SO) was used as driven liquid. Specifically, unless otherwise noted, device versions with 1, 4, and 9 emitters were tested as core–shell particle generators using a DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution as inner liquid and SO as outer liquid, while device versions with 1, 4, 9, 16, and 25 emitters were tested using EG as inner liquid and SO as outer liquid. The flow rates of the driving liquid were varied in the range from 0.5 to 2.5 mL h−1, and the driven liquid flow rates were set at 0.0 (uniaxial electrospraying of the driving liquid), 0.10, 0.25, and 0.50 mL h−1.
1 v/v solution as inner liquid and SO as outer liquid, while device versions with 1, 4, 9, 16, and 25 emitters were tested using EG as inner liquid and SO as outer liquid. The flow rates of the driving liquid were varied in the range from 0.5 to 2.5 mL h−1, and the driven liquid flow rates were set at 0.0 (uniaxial electrospraying of the driving liquid), 0.10, 0.25, and 0.50 mL h−1.
Experimental apparatus and testing procedure
A schematic of the apparatus utilized for the experimental characterization of the 3D-printed microfluidic devices is shown in Fig. 3. The two working liquids are loaded into syringes that are controlled by a Dual Syringe 33 Harvard Pump, Holliston, MA, USA. The syringes are connected to tubes and fittings that are attached to the liquid feedthroughs of an aluminium chuck, and the microfluidic device is clamped to the same chuck using screws. The electrospray source is configured as a triode (i.e., emitter array, extractor electrode, and collector electrode), which decouples the bias voltage required to form a single, stable Taylor cone on each spout from the downstream specifications of the emission.28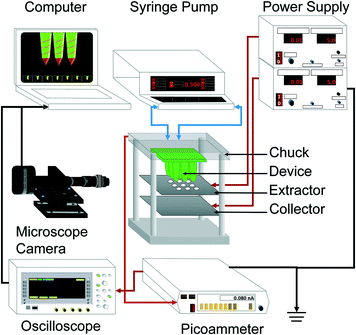 | ||
| Fig. 3 Schematic of the experimental apparatus used in the characterization of the 3D-printed MEMS coaxial electrospray devices. | ||
The extractor electrode, i.e., a laser-cut 250 μm-thick 304 stainless steel plate with circular apertures that line up with the axes of the coaxial electrospray emitters of the device, is also integrated to the chuck using screws; a multiplexed electrospray source with a proximal extractor electrode, where each aperture is concentric to an emitter, can attain large array utilization, because each emitter is shielded from electric field shadowing caused by the neighboring emitters. Similarly, the collector electrode is a laser-cut 250 μm-thick 304 stainless steel plate affixed to the chuck using screws. The aluminium chuck is grounded, while negative bias voltages between 4.0 kV and 6.5 kV are applied to the extractor and collector electrodes using a dual output Gamma High Voltage, 20 W, 1 mA Power Supply, Ormond Beach, FL, USA; the devices were tested in air under standard conditions. The emitted current is measured with a 485 Keithley picoammeter, Cleveland, OH, USA, and recorded with a DS6000 Rigol oscilloscope, Beaverton, OR, USA; the picoammeter is protected by a 5 MΩ high-voltage resistor in series. For each device, the per-emitter current I and per-emitter flow rate Q were estimated by dividing the total measured current and set flow rate of the device by its number of emitters, respectively; this approach to estimating the per-emitter current from MEMS multiplexed electrospray sources has also been employed by other research groups.21 Uniform emitter operation across the array was assumed because all emitters have an identical design and are seeing the same electric field; this assumption was experimentally confirmed by the flow rate vs. current data collected from array sources with between 1 and 25 emitters (see the section: per-emitter current-flow rate characteristics). There is probably a spread in the output from each emitter because of the small variations in the flow rates (the hydraulic impedances of the emitters are very similar but not identical) and because of the direct correlation between the emitted current and emitter flow rate in the cone-jet mode; these variations even out more effectively in the per-emitter estimates from larger arrays.
During the experiments, the nozzles were constantly monitored with a 5 MP CCD colour digital camera attached to a 12× zoom microscope lens. Before feeding any working liquids to a microfluidic device, a priming/purging process was performed with the purpose of removing any solid residues inside its hydraulic network. A 20 mL syringe loaded with isopropyl alcohol was connected to each reservoir inlet port of the device; the liquid was manually fed through the emitters until homogenous jets crossing the emitter array were observed.
Characterization of the spread in the sizes of the core–shell particles generated by the break-up of the coaxial jets with different combinations of driving/driven liquid flow rates was conducted using optical images from an AmScope Infinity Plan EPI Fluorescent Microscope, Irvine, CA, USA. Each sample of compound droplets was collected on a glass slide coated with the translucent oleophobic film, Fusso TabletPC, API Corp., Tokyo, Japan, right on top of the collector electrode, and special care was taken to make sure that the droplets were only collected while the devices were operating steadily in cone-jet mode. In each case, 200 droplets selected at random were measured to estimate the average and standard deviation of the outer and inner droplet diameters for a given combination of flow rates. In these experiments, the driving liquid was EG, the driven liquid was SO, and the optical images were collected using white light. However, some samples were collected using EG mixed with rhodamine B (coloured red) as driving liquid, and SO mixed with fluorescein (coloured green) as driven liquid, and the pictures were collected using coloured light as an alternative approach to visualizing the structure of the compound droplets. Droplets were also collected in a concave slide filled with water; however, no statistics for the droplet sizes were calculated because the constant movement of the droplets in the liquid made the pictures blurry.
Optimization of extractor bias voltage
It was determined experimentally that when the DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution and SO flow rates are set at 0.30 mL h−1 and 0.10 mL h−1, respectively, and the extractor electrode is positioned 6.4 mm from the emitter spouts, steady emission in cone-jet mode is achieved on each emitter for extractor bias voltages between −5.4 and −6.3 kV. Similarly, if the extractor electrode is positioned 4.5 mm from the emitter spout(s), a stable Taylor cone can be generated for the wider range of bias voltage between −4.2 and −5.9 kV. However, if the extractor electrode is positioned 2.6 mm from the emitter spout(s), the range of bias voltages that generate a stable Taylor cone is narrowed to −4.5 to −4.8 kV. The extractor bias voltage and position of the extractor electrode do not seem to have a significant influence on the per-emitter current for a given flow rate; however, for a given bias voltage, the electrical field acting on the Taylor cone increases as the separation distance between the emitter spout(s) and the extractor electrode decreases, which has a significant influence on the formation of the Taylor cone. Based on these observations, all devices were characterized using a separation of 4.75 mm between the emitter nozzle and the extractor electrode, with a bias voltage of −5 kV. Running the microfluidic devices in a triode configuration with a collector bias voltage equal to −5 kV results in a small fraction of the droplets deposited on the surface of the extractor electrode facing the emitter spouts, while the great majority of the droplets pass through the apertures of the extractor plate to be collected on the surface of the collector electrode facing the extractor electrode.
1 v/v solution and SO flow rates are set at 0.30 mL h−1 and 0.10 mL h−1, respectively, and the extractor electrode is positioned 6.4 mm from the emitter spouts, steady emission in cone-jet mode is achieved on each emitter for extractor bias voltages between −5.4 and −6.3 kV. Similarly, if the extractor electrode is positioned 4.5 mm from the emitter spout(s), a stable Taylor cone can be generated for the wider range of bias voltage between −4.2 and −5.9 kV. However, if the extractor electrode is positioned 2.6 mm from the emitter spout(s), the range of bias voltages that generate a stable Taylor cone is narrowed to −4.5 to −4.8 kV. The extractor bias voltage and position of the extractor electrode do not seem to have a significant influence on the per-emitter current for a given flow rate; however, for a given bias voltage, the electrical field acting on the Taylor cone increases as the separation distance between the emitter spout(s) and the extractor electrode decreases, which has a significant influence on the formation of the Taylor cone. Based on these observations, all devices were characterized using a separation of 4.75 mm between the emitter nozzle and the extractor electrode, with a bias voltage of −5 kV. Running the microfluidic devices in a triode configuration with a collector bias voltage equal to −5 kV results in a small fraction of the droplets deposited on the surface of the extractor electrode facing the emitter spouts, while the great majority of the droplets pass through the apertures of the extractor plate to be collected on the surface of the collector electrode facing the extractor electrode.
Optimization of collector bias voltage (droplet statistics)
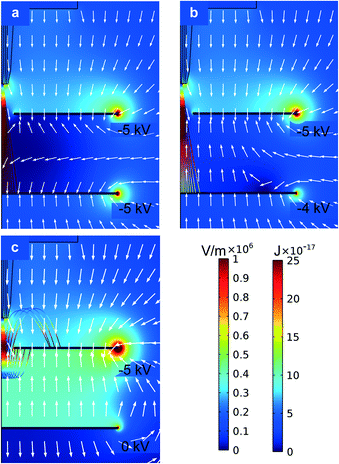
The bias voltage applied to the collector electrode and the separation between this electrode and the extractor electrode were investigated. By varying the two bias voltages, the electric field in the space between the two electrodes can be optimized to accumulate the particles on the surface of the collector electrode facing the emitters. Two-dimensional axisymmetric electrostatic simulations of an emitter facing a proximal extractor electrode with a concentric aperture, and a distal collector electrode with a parametric sweep of the collector bias voltage between 0 and −6 kV were carried out using the commercial software Comsol Multiphysics. In these simulations the chuck was grounded and the extractor electrode was biased at −5 kV, matching the value used in the experimental electrical characterization. Rough estimates of the trajectories of the droplets are also shown, assuming typical values of the mass and specific charge of the particles generated and a dashpot model for the drag caused by air. Fig. 4a corresponds to the case where both plates have the same bias voltage, i.e., −5 kV; although the magnitude of the electrical field in the space between the electrodes is close to zero, the electrical field vectors within this region point to the collector electrode, pushing the charged particles transmitted through the extractor electrode to the collector electrode. Fig. 4b corresponds to the case where the bias voltage on the collector electrode is equal to −4 kV, resulting in electric field lines within the inter-electrode region pointing toward the surface of the extractor electrode facing the collector plate, pushing back the charged droplets transmitted through the extractor electrode. The kinetic energy of the particles at the collector surface is smaller when the collector electrode is biased at −4.0 kV, compared to the case where the collector electrode bias voltage is set at −5.0 kV; the particles do not reach the collector electrode if grounded (Fig. 4c). The simulation results suggest that the collector bias voltage should be about −4 kV (or larger in magnitude, i.e., more negative) when the bias voltage applied to the extractor electrode is −5 kV, to be able to accumulate the droplets on top of the collector electrode instead of pushing the droplets back onto the surface of the extractor plate facing the collector electrode. It was verified experimentally that the compound microdroplets started to accumulate on the collector electrode when the applied voltage was −4.0 kV for DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP and −4.5 kV for EG. The experimental results indicate that the inertia of the droplets and the viscous drag significantly influence their trajectory; a more refined model is needed to gain further understanding of the dynamics of the particles. After trial and error, it was found that positioning the collector electrode 6 mm and 15 mm away from the extractor electrode was adequate to collect the particles with DIW–ISP cores and with EG cores, respectively. The dissimilarity is possibly due to the higher viscosity of EG, which forms a longer jet before it breaks up into droplets.
ISP and −4.5 kV for EG. The experimental results indicate that the inertia of the droplets and the viscous drag significantly influence their trajectory; a more refined model is needed to gain further understanding of the dynamics of the particles. After trial and error, it was found that positioning the collector electrode 6 mm and 15 mm away from the extractor electrode was adequate to collect the particles with DIW–ISP cores and with EG cores, respectively. The dissimilarity is possibly due to the higher viscosity of EG, which forms a longer jet before it breaks up into droplets.
Glass slides coated with translucent oleophobic film were used to collect the compound droplets and run statistics to characterize their size spread. The contact angle of the sesame oil on this film, measured with a Ramé-Hart goniometer, Succasunna, NJ, USA, with DROPimage Advanced software, is estimated as 85°. The collected droplets are hemispherical. To collect the compound microparticles, a glass slide coated with oleophobic film is put on top of the collector electrode, a −5 kV bias voltage is applied on the collector electrode, and the droplets are collected for 2 seconds; longer deposition times result in collision and agglomeration of the particles, making their measurement unfeasible. In addition, to further reduce the number of particles generated for a given running time, single-emitter devices were employed to collect the core–shell particle samples. Inspection of the collected samples suggests that the total volume of each compound droplet is not altered by the collection process; therefore, the average shell diameter of the corresponding spherical droplets before collection can be estimated from the measured average outer diameter of the hemispherical compound particles. Similarly, the average inner diameter of the spherical droplets before collection can be quantified from the estimated shell diameter and the ratio of inner/outer flow rates fed to each emitter.
Results
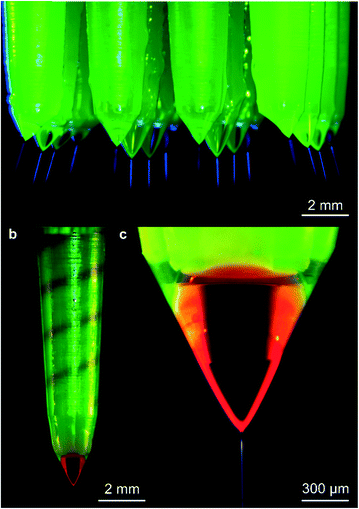
Fig. 5 shows examples of microfabricated coaxial electrospray sources operating in steady cone-jet mode. In Fig. 5a, the inner liquid is EG and the outer liquid is SO, while in Fig. 5b and c, the driving liquid is EG dyed with rhodamine B and the driven liquid is SO mixed with fluorescein. In Fig. 5b, the coloured EG can be seen filling in the inner helical microchannel within the emitter, and the interface between the two liquids is visible near the edge of the external cone. In Fig. 5c, the interface of both immiscible liquids can also be observed, as well as the coaxial jet emitted from the cone apex; the diameter of the jet is approximately equal to 10 μm.The per-emitter current measurements obtained from a variety of 3D-printed MEMS devices, working liquids, and flow rates are summarized in Fig. 6. Fig. 6a shows the current versus time for uniaxial (i.e., no SO flow rate) and coaxial electrospray of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution (1 mL h−1) as driving liquid and SO (0.125 mL h−1) as driven liquid, using a single-emitter device. Fig. 6b, c, and e show the per-emitter current versus per-emitter driving liquid flow rate characteristics for various emitter array sizes and driving liquids, using SO as driven liquid: in Fig. 6b, the driving liquid is DIW
1 v/v solution (1 mL h−1) as driving liquid and SO (0.125 mL h−1) as driven liquid, using a single-emitter device. Fig. 6b, c, and e show the per-emitter current versus per-emitter driving liquid flow rate characteristics for various emitter array sizes and driving liquids, using SO as driven liquid: in Fig. 6b, the driving liquid is DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
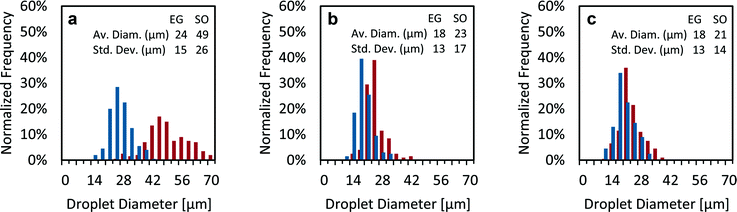
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution, while in Fig. 6c and e, the driving liquid is EG. Fig. 6d and f are column charts that show the per-emitter current versus the per-emitter EG flow rate of the data shown in Fig. 6c and e, respectively; each bar corresponds to the per-emitter current measured from a different device. Examples of the core–shell particles generated by the 3D-printed MEMS coaxial electrospray sources are shown in Fig. 7; the driving liquid is EG mixed with rhodamine B, with a flow rate equal to 1.0 mL h−1 (Fig. 7a) or 2.0 mL h−1 (Fig. 7b), and the driven liquid is SO mixed with fluorescein with a flow rate equal to 1.0 mL h−1. Fig. 8 shows three droplet size distributions estimated from the metrology of optical images, conducted as explained in the Experimental section, using EG as driving liquid and SO as driven liquid; the average inner diameter and outer diameter with their corresponding standard variations are included.
1 v/v solution, while in Fig. 6c and e, the driving liquid is EG. Fig. 6d and f are column charts that show the per-emitter current versus the per-emitter EG flow rate of the data shown in Fig. 6c and e, respectively; each bar corresponds to the per-emitter current measured from a different device. Examples of the core–shell particles generated by the 3D-printed MEMS coaxial electrospray sources are shown in Fig. 7; the driving liquid is EG mixed with rhodamine B, with a flow rate equal to 1.0 mL h−1 (Fig. 7a) or 2.0 mL h−1 (Fig. 7b), and the driven liquid is SO mixed with fluorescein with a flow rate equal to 1.0 mL h−1. Fig. 8 shows three droplet size distributions estimated from the metrology of optical images, conducted as explained in the Experimental section, using EG as driving liquid and SO as driven liquid; the average inner diameter and outer diameter with their corresponding standard variations are included.
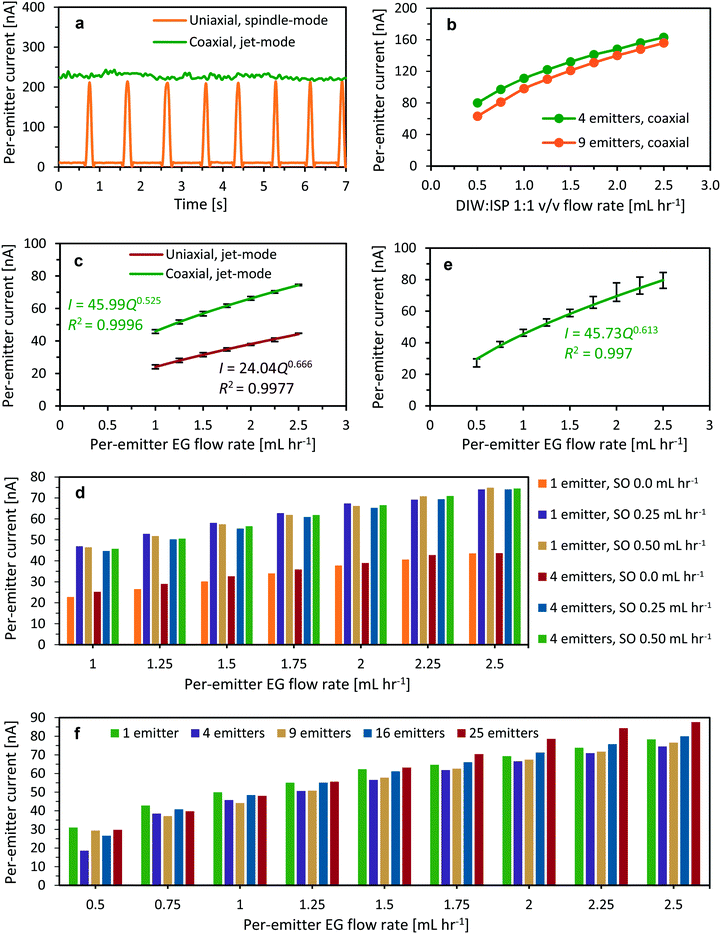 | ||
Fig. 6 (a) Per-emitter current versus time for uniaxial (dripping mode) and coaxial electrospray (cone-jet mode) of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1 ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution (1 mL h−1) as driving liquid and SO (0.125 mL h−1) as driven liquid. (b) Per-emitter current versus per-emitter flow rate for coaxial electrospray of DIW 1 v/v solution (1 mL h−1) as driving liquid and SO (0.125 mL h−1) as driven liquid. (b) Per-emitter current versus per-emitter flow rate for coaxial electrospray of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1 ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution covered by SO (0.25 mL h−1). (c) Per-emitter current versus per-emitter EG flow rate for devices working as uniaxial or coaxial electrospray sources (SO flow rates equal to 0.0, 0.25, and 0.50 mL h−1). (d) Clustered column chart of the per-emitter current versus per-emitter EG flow rate shown in Fig. 6c. (e) Per-emitter current versus per-emitter EG flow rate for devices working as coaxial electrospray sources with an SO flow rate equal to 0.50 mL h−1. (f) Clustered column chart of the per-emitter current versus EG flow rate shown in Fig. 6d. In Fig. 6d and f, each bar corresponds to the current measurement from a different device. 1 v/v solution covered by SO (0.25 mL h−1). (c) Per-emitter current versus per-emitter EG flow rate for devices working as uniaxial or coaxial electrospray sources (SO flow rates equal to 0.0, 0.25, and 0.50 mL h−1). (d) Clustered column chart of the per-emitter current versus per-emitter EG flow rate shown in Fig. 6c. (e) Per-emitter current versus per-emitter EG flow rate for devices working as coaxial electrospray sources with an SO flow rate equal to 0.50 mL h−1. (f) Clustered column chart of the per-emitter current versus EG flow rate shown in Fig. 6d. In Fig. 6d and f, each bar corresponds to the current measurement from a different device. | ||
Discussion
Dry electrical characterization
Before any wet tests were performed, dry single-emitter devices were characterized to determine the magnitude of the leakage current through the dielectric while the bias voltage between the chuck and the extractor electrode was set at −5 kV. These measurements are representative of all devices tested because the parts of the device that interface with the chuck, with the screws for clamping the device to the chuck, and with the screws for integrating the electrodes to the device are identical; in addition, the emitters do not touch the extractor electrode. From these measurements, an average leakage current equal to 3 nA was measured, which is an order of magnitude smaller than the smallest currents measured in single-emitter devices in the wet experiments. Therefore, the majority of the currents measured in the wet experiments correspond to the current carried by the spray(s), which allows comparison of the per-emitter currents as a way to assess the uniformity of the operation across the array.Array filling-in uniformity (driving liquid)
A series of experiments using 4-emitter devices operating in uniaxial cone-jet mode (i.e., without feeding the outer liquid to the devices) were conducted to explore the influence of the surface tension on the uniform filling in of the inner flow hydraulics of the devices; this is a very important practical matter, given the intention of the work to greatly increase the throughput of the coaxial electrospray source through emitter multiplexing. Using a solution of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 6
ISP 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v as inner liquid, uniform operation across the emitter array was achieved for per-emitter flow rates larger than 2 mL h−1, i.e., steady cone-jet emission was observed simultaneously in all emitters. Similar devices were tested with DIW
1 v/v as inner liquid, uniform operation across the emitter array was achieved for per-emitter flow rates larger than 2 mL h−1, i.e., steady cone-jet emission was observed simultaneously in all emitters. Similar devices were tested with DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP solutions of 3
ISP solutions of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v and 1
1 v/v and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, which resulted in steady cone-jet emission for per-emitter flow rates above 0.5 mL h−1 and 0.1 mL h−1, respectively. The same test was repeated with a similar device using EG as inner liquid, resulting in stable array operation for per-emitter flow rates above 0.2 mL h−1. If a device is supplied with a per-emitter flow rate smaller than the reported minimum values, in all cases, only a fraction of the emitters developed a meniscus, which resulted in spray emission from a fraction of the array when the extractor electrode was energized. These values are not related to the minimum flow rate for stable cone-jet operation,32 but to the minimum flow rate needed to create a filling-in pressure within the device, such that all the emitters develop a meniscus. It is speculated that the minimum filling-in flow rate is related to the surface tension of the liquid and to non-idealities in the devices, e.g., the spread in the dimensions of the hydraulics. For example, the experiments with DIW
1 v/v, which resulted in steady cone-jet emission for per-emitter flow rates above 0.5 mL h−1 and 0.1 mL h−1, respectively. The same test was repeated with a similar device using EG as inner liquid, resulting in stable array operation for per-emitter flow rates above 0.2 mL h−1. If a device is supplied with a per-emitter flow rate smaller than the reported minimum values, in all cases, only a fraction of the emitters developed a meniscus, which resulted in spray emission from a fraction of the array when the extractor electrode was energized. These values are not related to the minimum flow rate for stable cone-jet operation,32 but to the minimum flow rate needed to create a filling-in pressure within the device, such that all the emitters develop a meniscus. It is speculated that the minimum filling-in flow rate is related to the surface tension of the liquid and to non-idealities in the devices, e.g., the spread in the dimensions of the hydraulics. For example, the experiments with DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP solutions show that the minimum flow rate for filling in the device decreases for decreasing values of surface tension (the surface tension values at 20 °C of the DIW
ISP solutions show that the minimum flow rate for filling in the device decreases for decreasing values of surface tension (the surface tension values at 20 °C of the DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, 3
1 v/v, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, and 6
1 v/v, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v mixtures are 26.0 mN m−1, 31.5 mN m−1, and 39.8 mN m−1, respectively).33 The minimum filling-in flow rate values were taken into account for planning the wet electrical characterization of the devices as coaxial electrospray sources.
1 v/v mixtures are 26.0 mN m−1, 31.5 mN m−1, and 39.8 mN m−1, respectively).33 The minimum filling-in flow rate values were taken into account for planning the wet electrical characterization of the devices as coaxial electrospray sources.
Spraying modes
In general, a coaxial electrospray emitter can operate in different spraying modes, according to the magnitude of the electrostatic field and flow rate fed to the emitter. For a given flow rate, increasing the magnitude of the electrostatic field results in operating the emitter in the dripping mode, the spindle mode, the cone-jet mode, or the multi-jet mode.34 However, core–shell microdroplets can only be generated in cone-jet mode.In the dripping mode, the bias voltage causes an electrostatic force on the meniscus that is smaller than the hydrodynamic forces, the surface tension forces, and gravity. The dripping mode is identified by a seemingly random fluctuation in the emitted current. In the spindle mode, the electrical stresses are large enough to form a cone, but no continuous emission takes place; instead, this regime has a characteristic pulsed operation as the stressed meniscus varies its volume between emission events (the meniscus accumulates liquid until a jet is emitted, which depletes the volume of the meniscus, eventually causing the emission to stop; a new cycle follows, starting with accumulation of liquid within the meniscus). In the cone-jet mode, the strength of the electric field is large enough to trigger the formation of the Taylor cone, which produces core–shell particles via the breakup of the coaxial jet emitted by its apex. The cone-jet mode is very stable and the emission current is constant, even after hours of continued emission, which is in striking contrast to the pulsed operation of the spindle mode or the randomly fluctuating emission of the dripping mode. Further increasing the bias voltage leads to the unstable multi-jet mode, when more than one jet is emitted from the surface of the meniscus; this regime is associated with wide variation in the size of the electrosprayed particles.35 Most of the data collected in the wet experiments correspond to operation in cone-jet mode; however, Fig. 6a shows an interesting experimental behaviour obtained while investigating single and coaxial electrospray emission of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution flowing at 1.0 mL h−1, using a single-emitter device. Without an SO flow rate, no stable uniaxial electrospray emission was achieved; instead, operation in spindle mode takes place. Nonetheless, once the SO flow rate is set at 0.125 mL h−1, the emission becomes stable, in the cone-jet mode. In the dripping mode, the hydraulic and electrical forces are unbalanced,31 but the experiment suggests that the higher viscosity of the SO film surrounding the DIW
1 v/v solution flowing at 1.0 mL h−1, using a single-emitter device. Without an SO flow rate, no stable uniaxial electrospray emission was achieved; instead, operation in spindle mode takes place. Nonetheless, once the SO flow rate is set at 0.125 mL h−1, the emission becomes stable, in the cone-jet mode. In the dripping mode, the hydraulic and electrical forces are unbalanced,31 but the experiment suggests that the higher viscosity of the SO film surrounding the DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solution stabilizes the emission process.
1 v/v solution stabilizes the emission process.
Per-emitter current-flow rate characteristics
A significant deviation in the per-emitter flow rate versus current characteristics was observed while comparing the coaxial electrospray data from 4-emitter and 9-emitter devices using DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP 1
ISP 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v as driving liquid (Fig. 6b). At DIW
1 v/v as driving liquid (Fig. 6b). At DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP flow rates equal to 0.5 mL h−1, 1.0 mL h−1, and 2.0 mL h−1, while the SO flow rate is held constant at 0.25 mL h−1, the 9-emitter device generates 21%, 12%, and 5% less current per emitter than the 4-emitter device, respectively. The data suggest that the magnitude of the driving liquid flow rate influences the uniformity of the emission across the array, where higher flow rates imply more uniform operation. Inspection of the emitters using a macro lens at 12× magnification revealed that for low flow rates, not all the emitters of the device were fed by the inner liquid, which resulted in array subutilization (i.e., only a fraction of the emitter array would be active). The partial filling in of the emitter array is probably caused by small differences in hydraulic impedance across the emitters, worsened by the fact that the inner liquid used in the experiments did not wet as well the resin that makes up the microfluidic devices. Visual inspection of the emitters that were fed by both inner and outer liquids revealed partially engulfing Taylor cones (i.e., the outer liquid did not completely surround the inner liquid); this causes intermittent breakup of the shell layer at the Taylor cones, which results in emission of droplets without shells. Partial engulfing takes place because the interfacial tension between the inner and outer liquids does not accomplish the dynamic conditions to guarantee complete engulfing.31 When the per-emitter flow rate increases, all emitters of the array can be successfully filled in, and the partial engulfing at the Taylor cones also disappears.
ISP flow rates equal to 0.5 mL h−1, 1.0 mL h−1, and 2.0 mL h−1, while the SO flow rate is held constant at 0.25 mL h−1, the 9-emitter device generates 21%, 12%, and 5% less current per emitter than the 4-emitter device, respectively. The data suggest that the magnitude of the driving liquid flow rate influences the uniformity of the emission across the array, where higher flow rates imply more uniform operation. Inspection of the emitters using a macro lens at 12× magnification revealed that for low flow rates, not all the emitters of the device were fed by the inner liquid, which resulted in array subutilization (i.e., only a fraction of the emitter array would be active). The partial filling in of the emitter array is probably caused by small differences in hydraulic impedance across the emitters, worsened by the fact that the inner liquid used in the experiments did not wet as well the resin that makes up the microfluidic devices. Visual inspection of the emitters that were fed by both inner and outer liquids revealed partially engulfing Taylor cones (i.e., the outer liquid did not completely surround the inner liquid); this causes intermittent breakup of the shell layer at the Taylor cones, which results in emission of droplets without shells. Partial engulfing takes place because the interfacial tension between the inner and outer liquids does not accomplish the dynamic conditions to guarantee complete engulfing.31 When the per-emitter flow rate increases, all emitters of the array can be successfully filled in, and the partial engulfing at the Taylor cones also disappears.
Further wet characterization of the devices involved EG as driving liquid instead of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ISP to ensure full engulfment, even at low per-emitter flow rates (e.g., EG has an interfacial tension with olive oil at 20 °C equal to 11.95 mN m−1, while ISP has an interfacial tension with olive oil at 20 °C equal to 0.05 mN m−1).34Fig. 6c shows the per-emitter current versus per-emitter flow rate of EG for three different per-emitter SO flow rates (0.0, 0.25, and 0.50 mL h−1), using single-emitter and four-emitter devices. The data show that the per-emitter current-versus-flow rate scaling law that governs standard (i.e., uniaxial) electrospraying also applies to the coaxial electrospraying case; however, the data also show that in coaxial electrospraying, the flow rate that influences the emitted current is only that of the driving liquid (Fig. 6d). In Fig. 6c and d, the per-emitter current is approximately proportional to the square root of the per-emitter flow rate of the driving liquid, which is in agreement with the scaling laws for both uniaxial and coaxial cone-jet electrospray emission reported in the literature.5,32 This result might be explained by the fact that the SO is very inefficient at transporting charge; therefore, for practical purposes, the SO only supplies dielectric material that surrounds the conductive material, similar to operating a standard electrospray emitter in air. The per-emitter current varies by less than 2% across corresponding data points with the same per-emitter driving liquid flow rate (Fig. 6d). However, even though the exponents of the power-law fits in Fig. 6c are similar, there is a significant increase in the scaling constants, i.e., from 24.04 for uniaxial electrospraying to 45.99 for coaxial electrospraying. In addition, the current per emitter in coaxial cone-jet mode (i.e., both inner and outer liquids are fed to the emitters) is about twice the current per emitter in uniaxial cone-jet mode (i.e., only the inner liquid is fed to the emitters); this is an unexpected and counterintuitive result that needs to be further investigated. To the best of the authors' knowledge, there are no reports in the literature of similar experiments that can be contrasted with these results. The authors do not have a good explanation for the striking difference in current emitted between operating the emitters in coaxial cone-jet mode and operating the emitters in uniaxial cone-jet mode. However, they speculate that sesame oil might be transporting charge, given that uniaxial electrospraying of SO at 0.25 ml h−1 with the extractor collector at −5 kV operates in the dripping mode.
ISP to ensure full engulfment, even at low per-emitter flow rates (e.g., EG has an interfacial tension with olive oil at 20 °C equal to 11.95 mN m−1, while ISP has an interfacial tension with olive oil at 20 °C equal to 0.05 mN m−1).34Fig. 6c shows the per-emitter current versus per-emitter flow rate of EG for three different per-emitter SO flow rates (0.0, 0.25, and 0.50 mL h−1), using single-emitter and four-emitter devices. The data show that the per-emitter current-versus-flow rate scaling law that governs standard (i.e., uniaxial) electrospraying also applies to the coaxial electrospraying case; however, the data also show that in coaxial electrospraying, the flow rate that influences the emitted current is only that of the driving liquid (Fig. 6d). In Fig. 6c and d, the per-emitter current is approximately proportional to the square root of the per-emitter flow rate of the driving liquid, which is in agreement with the scaling laws for both uniaxial and coaxial cone-jet electrospray emission reported in the literature.5,32 This result might be explained by the fact that the SO is very inefficient at transporting charge; therefore, for practical purposes, the SO only supplies dielectric material that surrounds the conductive material, similar to operating a standard electrospray emitter in air. The per-emitter current varies by less than 2% across corresponding data points with the same per-emitter driving liquid flow rate (Fig. 6d). However, even though the exponents of the power-law fits in Fig. 6c are similar, there is a significant increase in the scaling constants, i.e., from 24.04 for uniaxial electrospraying to 45.99 for coaxial electrospraying. In addition, the current per emitter in coaxial cone-jet mode (i.e., both inner and outer liquids are fed to the emitters) is about twice the current per emitter in uniaxial cone-jet mode (i.e., only the inner liquid is fed to the emitters); this is an unexpected and counterintuitive result that needs to be further investigated. To the best of the authors' knowledge, there are no reports in the literature of similar experiments that can be contrasted with these results. The authors do not have a good explanation for the striking difference in current emitted between operating the emitters in coaxial cone-jet mode and operating the emitters in uniaxial cone-jet mode. However, they speculate that sesame oil might be transporting charge, given that uniaxial electrospraying of SO at 0.25 ml h−1 with the extractor collector at −5 kV operates in the dripping mode.
Fig. 6e shows the characteristic per-emitter current versus per-emitter flow rate of EG using 3D-printed devices between 1 and 25 emitters, a per-emitter SO flow rate equal to 0.50 mL h−1, and a per-emitter EG flow rate between 0.5 mL h−1 and 2.5 mL h−1. Uniform operation across the array for all array sizes and flow rates is achieved (Fig. 6f), which demonstrates that the proposed 3D-printed MEMS multiplexed devices can be used to greatly increase the compound microparticle throughput of the state-of-the-art coaxial electrospraying sources. These experiments further confirm that the per-emitter current I transported by the coaxial jet scaled with a per-emitter driving liquid flow rate Q is relatively close to a square-root power dependence.
Microdroplet size distribution and throughput
Adjusting the flow rates fed to the 3D-printed coaxial sources can be used to control the structure of the core–shell microparticles produced. In the sets analysed (Fig. 8), the narrowest size distribution is found when the ratio of the EG flow rate to the SO flow rate is the largest (Fig. 8c, EG flow rate to SO flow rate equal to 5), in agreement with the work of López-Herrera et al.6 When the driving liquid is the inner flow and its flow rate is significantly larger than the flow rate of the driven liquid, the core volume and the full droplet volume are governed by the break-up of the inner jet; in this case, the average diameter of the spherical droplets exhibits a linear dependence on the inner liquid flow rate.6 Comparing Fig. 8b and c, i.e., when the outer liquid flow rate is increased 2.5 times from 0.10 to 0.25 mL h−1 while the inner flow rate is kept constant at 0.5 mL h−1, the core diameter has the same average value and standard deviation, while the average shell diameter and associated standard deviation exhibit a 10% and 21% increase, respectively. Given that the volume of the droplets is not affected by the collection process, the shell diameter of the spherical droplets before collection (i.e., as produced by the source) is equal to the shell diameter of the deposited hemispherical droplets divided by 21/3. Therefore, the average shell diameter of the spherical droplets in Fig. 8a, b, and c is estimated at 39 μm, 18 μm, and 17 μm, respectively. Consequently, from the estimated average shell diameter and the ratio of the inner/outer flow rates fed to each emitter, the average core diameter of the spherical droplets in Fig. 8a, b, and c is estimated at 31 μm, 16 μm, and 16 μm, respectively. Even though the inner and outer diameters of the compound jet can be estimated as a function of the flow rates,36 to the best of the authors' knowledge there are no studies that correlate the jet structure with the size of electrosprayed core–shell particles shaped as spheres or as lentils.Using the estimated average shell diameter of the spherical droplets from the smallest droplets measured (Fig. 8c), i.e., 17 μm, results in a per-emitter production of ∼68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 droplets per second, with an EG flow rate equal to 0.50 mL h−1 and an SO flow rate equal to 0.1 mL h−1. Therefore, a 25-emitter source should produce close to ∼1
800 droplets per second, with an EG flow rate equal to 0.50 mL h−1 and an SO flow rate equal to 0.1 mL h−1. Therefore, a 25-emitter source should produce close to ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720
720![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compound droplets per second using the same per-emitter flow rates.
000 compound droplets per second using the same per-emitter flow rates.
Future work
Two important issues should be addressed to greatly improve the applicability of the reported 3D-printed compound droplet source technology, i.e., (i) extending the chemical compatibility of the sources to solvents of relevance to applications of interest, and (ii) demonstrating means for collecting the compound droplets that are compatible with applications of interest.The devices reported in this work are made of a green-toned epoxy resin via SLA, but equivalent working devices were successfully printed and operated using other SLA printable resins. However, one of the more significant limitations of SLA is the narrow choice of available materials and the restrictive physical/chemical properties of these materials. Unfortunately, the reported devices are not resistant to a plurality of solvents, including tetrahydrofuran, chloroform, and acetone; consequently, the applicability of such devices is limited in applications such as drug delivery. Nonetheless, PVA and PEO are biocompatible and biodegradable polymeric materials that can be dissolved in water and/or ethanol; given that the reported SLA-printed devices are compatible with such solvents, it should be possible to use these polymers as feedstocks to make compound droplets for drug release applications. As a matter of fact, PVA has been used to fabricate compound microspheres for insulin delivery using coaxial electrospraying.37
The MEMS multiplexed coaxial electrospray sources require 3D printing of nonporous structures with high resolution. There is a number of exciting research possibilities to make the devices out of better materials if other additive manufacturing approaches are considered. A first possibility is to micromold metallic devices using the lost-wax process,38 using SLA-printed wax masters; even though SLA printable wax resins are commercially available, significant process development will be required to manufacture complex internally-fed metallic microfluidics. A second possibility for manufacturing more resilient devices is using Direct Metal Laser Sintering (DMLS), which is a 3D printing technology that can produce nonporous metallic components by melting metal powders.39 However, the resolution of DMLS printing is significantly lower than that of SLA printing (the pixelation of DMLS printers is around 100 μm, versus the ∼25 μm pixelation of cost-competitive, commercial high-resolution SLA printers), which should impact the emitter density that is achievable. A third possibility for microfluidic devices compatible with a wider range of feedstock is using fused filament formation (FFF),40 which is a 3D printing technology based on the extrusion of thermoplastic filaments. The resolution of FFF printing is significantly coarser than that of SLA printing (layer height >0.1 mm and width of the imprint >0.2 mm are typical), which will affect the emitter density, but the choice of materials is significantly better, e.g., PEEK and polypropylene, and FFF printed parts can be watertight.
Several approaches for collecting the compound droplets are suggested. The sources emit the compound droplets as a spatial array of droplet bunches; if the electrostatic lens stack is modified to attain individual emitter actuation and emitter beam collimation, the source can be used as a ‘dot matrix’ printing head to create the particles on demand and deposit them in specific locations. The imprints can create single-layer structures if the droplets are not intended to be agglomerated – similar to what was demonstrated in the droplet metrology experiments, or could create multi-layered structures if the shell of the deposited particles is solid, e.g., made of a polymer solution that dries out or is made of a photosensitive resin that is cured as the particles are generated. It is also possible to collect the compound droplets in a solvent to manufacture a compound droplet feedstock. Although the compound droplets generated in this work were successfully collected in water, a systematic exploration of the maximum droplet concentration and the optimization of the feedstock solvent for a given compound droplet shell material need to be conducted. Perhaps the manufacture of such droplet feedstock would be facilitated if triaxial electrospray emitters41 are used to generate core–shell–shell particles, where the outer shell layer is made of the solvent used to disperse the compound particles. These more advanced microfluidics are also more complex but should be compatible with 3D printing.
Conclusions
The first MEMS multiplexed coaxial electrospray sources in the literature have been reported. Core–shell particle generators with up to 25 coaxial electrospray emitters (25 emitters cm−2) were 3D-printed using stereolithography. The characterization of devices with the same emitter structure but different array sizes demonstrates uniform array operation, validating a microencapsulation technology compatible with low-cost, large-market applications, e.g., drug delivery, food processing, self-healing composites, and dye-sensitized solar cells. The data demonstrate that the per-emitter current is approximately proportional to the square root of the flow rate of the driving liquid, and it is independent of the flow rate of the driven liquid. The diameter and distribution of the generated core–shell particles can be modulated by controlling the flow rates fed to the emitters and the collector bias voltage.Acknowledgements
This research has been partially funded by the Tecnológico de Monterrey and MIT Nanotechnology Program.References
- W. Gilbert, On the magnet and magnetic bodies, and on that great magnet the Earth, Peter Short, London, 1628 Search PubMed.
- J. Zeleny, Phys. Rev., 1914, 3, 69–91 CrossRef.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1964, 280, 383–397 CrossRef.
- J. Xie, J. Jiang, P. Davoodi, M. P. Srinivasanb and C. Wang, Chem. Eng. Sci., 2015, 125, 32–57 CrossRef CAS PubMed.
- I. G. Loscertales, A. Barrero, I. Guerrero, R. Cortijo, M. Marquez and A. M. Gañán-Calvo, Science, 2002, 295, 1695–1698 CrossRef CAS PubMed.
- J. M. López-Herrera, A. Barrero, A. López, I. G. Loscertales and M. Márquez, J. Aerosol Sci., 2003, 34, 535–552 CrossRef.
- K. S. Kumar, V. B. Kumar and P. Paik, J. Nanopart., 2013, 2013, 24 Search PubMed.
- K. K. Kim and D. W. Pack, Volume I Biological and Biomedical Nanotechnology, Springer US, Boston, MA, 2006, pp. 19–50 Search PubMed.
- Q. Xu, H. Qin, Z. Yin, J. Huac, D. W. Pack and C. Wang, Chem. Eng. Sci., 2013, 104, 330–346 CrossRef CAS PubMed.
- N. Bock, M. A. Woodruff, D. W. Hutmacher and T. R. Dargaville, Polymers, 2011, 3, 131 CrossRef CAS.
- N. Bock, T. R. Dargaville and M. A. Woodruff, Prog. Polym. Sci., 2012, 37, 1510–1551 CrossRef CAS.
- J. Xie, W. J. Ng, L. Y. Lee and C. H. Wang, J. Colloid Interface Sci., 2008, 317, 469–476 CrossRef CAS PubMed.
- L. Zhang, J. Huang, T. Si and R. X. Xu, Expert Rev. Med. Devices, 2012, 9, 595–612 CrossRef CAS PubMed.
- H. Yang, X. Qiao, W. Hong and L. Dong, J. Microelectromech. Syst., 2013, 22, 509–518 CrossRef CAS.
- M. Nangrejo, Z. Ahmad and M. Edirisinghe, J. Microencapsulation, 2010, 27, 542–551 CrossRef CAS PubMed.
- S. Y. Koo, K. H. Cha, D. Song, D. Chung and C.-H. Pan, Int. J. Food Sci. Technol., 2014, 49, 733–739 CrossRef CAS.
- J. Xi, Q. Zhang, D. Myers, Y. Sun and G. Cao, J. Nanophotonics, 2012, 6, 063511 CrossRef.
- S. Sinha-Ray, D. D. Pelot, Z. P. Zhou, A. Rahman, X.-F. Wu and A. L. Yarin, J. Mater. Chem., 2012, 22, 9138–9146 RSC.
- X. Wang, J. W. Cooper, C. S. Lee and D. L. DeVoe, Lab Chip, 2004, 4, 363–367 RSC.
- L. F. Velásquez-García, A. I. Akinwande and M. A. Martinez-Sanchez, J. Microelectromech. Syst., 2006, 15, 1272–1280 CrossRef.
- W. Deng, J. F. Klemic, X. Li, M. A. Reed and A. Gomez, J. Aerosol Sci., 2006, 37, 696–714 CrossRef CAS.
- R. Krpoun and H. R. Shea, J. Micromech. Microeng., 2009, 19, 045019 CrossRef.
- F. A. Hill, E. V. Heubel, P. Ponce de Leon and L. F. Velásquez-García, J. Microelectromech. Syst., 2014, 23, 1237–1248 CrossRef CAS.
- K. V. Wong and A. Hernandez, ISRN Mech. Eng., 2012, 2012, 10 Search PubMed.
- H. Gong, A. T. Woolley and P. Nordin, Lab Chip, 2016, 16, 2450–2458 RSC.
- S. Waheed, J. M. Cabot, N. P. Macdonald, T. Lewis, R. M. Guijt, B. Paull and M. C. Breadmore, Lab Chip, 2016, 16, 1993–2013 RSC.
- L. F. Velásquez-García, J. Microelectromech. Syst., 2015, 24, 2117–2127 CrossRef.
- L. F. Velásquez-Garcia, A. I. Akinwande and M. A. Martinez-Sanchez, J. Microelectromech. Syst., 2006, 15, 1260–1271 CrossRef.
- R. Krpoun, K. L. Smith, J. P. W. Stark and H. R. Shea, Appl. Phys. Lett., 2009, 94, 163502 CrossRef.
- P. D. Prewett and G. L. R. Mair, Focused Ion Beams from Liquid Metal Ion Sources, Wiley, 1991 Search PubMed.
- F. Mei and D.-R. Chen, Aerosol Air Qual. Res., 2008, 8, 218–232 CAS.
- J. Fernandez de la Mora, J. Fluid Mech., 1994, 260, 155–184 CrossRef CAS.
- G. Vazquez, E. Alvarez and J. M. Navaza, J. Chem. Eng. Data, 1995, 40, 611–614 CrossRef CAS.
- X. P. Chen, L. B. Jia, X. Z. Yin, J. Cheng and J. Lu, Phys. Fluids, 2005, 17, 032101 CrossRef.
- J. Perel, A. Y. Yahiku, J. F. Mahoney, H. L. Daley and A. Sherman, J. Spacecr. Rockets, 1971, 8, 702–709 CrossRef.
- A. G. Marin, I. G. Loscertales, M. Marquez and A. Barrero, Phys. Rev. Lett., 2007, 98, 014502 CrossRef PubMed.
- B. Felice, M. P. Prabhakaran, M. Zamani, A. P. Rodríguez and S. Ramakrishna, Polym. Int., 2015, 64, 1722–1732 CrossRef CAS.
- C. Chung, Y.-J. Chen, P.-C. Chen and C.-Y. Chen, Precis. Eng. Manuf., 2015, 16, 2033–2039 CrossRef.
- L.-C. Zhang and H. Attar, Adv. Eng. Mater., 2016, 18, 463–475 CrossRef CAS.
- P. J. Kitson, M. H. Rosnes, V. Sans, V. Dragone and L. Cronin, Lab Chip, 2012, 12, 3267–3271 RSC.
- W. Kim and S. S. Kim, Anal. Chem., 2010, 82, 4644–4647 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |