Comparison of capacitive and radio frequency resonator sensors for monitoring parallelized droplet microfluidic production

Abstract

Scaled-up production of microfluidic droplets, through the parallelization of hundreds of droplet generators, has received a lot of attention to bring novel multiphase microfluidics research to industrial applications. However, apart from droplet generation, other significant challenges relevant to this goal have never been discussed. Examples include monitoring systems, high-throughput processing of droplets and quality control procedures among others. In this paper, we present and compare capacitive and radio frequency (RF) resonator sensors as two candidates that can measure the dielectric properties of emulsions in microfluidic channels. By placing several of these sensors in a parallelization device, the stability of the droplet generation at different locations can be compared, and potential malfunctions can be detected. This strategy enables for the first time the monitoring of scaled-up microfluidic droplet production. Both sensors were prototyped and characterized using emulsions with droplets of 100–150 μm in diameter, which were generated in parallelization devices at water-in-oil volume fractions (φ) between 11.1% and 33.3%.Using these sensors, we were able to measure accurately increments as small as 2.4% in the water volume fraction of the emulsions. Although both methods rely on the dielectric properties of the emulsions, the main advantage of the RF resonator sensors is the fact that they can be designed to resonate at multiple frequencies of the broadband transmission line. Consequently with careful design, two or more sensors can be parallelized and read out by a single signal. Finally, a comparison between these sensors based on their sensitivity, readout cost and simplicity, and design flexibility is also discussed.

---

1 Introduction

Microfluidic droplet generation has been of significant interest in the production of novel advanced materials, because it has enabled chemical synthesis and crystallization in confined droplets.^1,2 These droplet systems offer enhanced control over the reaction conditions, improved homogeneity, consistent sample to sample reproducibility and new reaction paths that are not possible at the macro-scale. Examples of applications that have been demonstrated using this technology include nanocrystals,¹ active pharmaceutical ingredients,³ microporous annealed particle gels,⁴ microcapsules,⁵ quantum dots⁶ and nanoparticles⁷ among others. Industries such as foods, pharmaceuticals, fine chemicals, and cosmetics, etc., will benefit from a low variability emulsification technique that allows at the same time, the possibility of performing chemical reactions inside the droplets.^1,2

The limited production of droplet microfluidics is one of the key challenges that refrain the use of microfluidics in industrial processes. Therefore, moving such technologies from laboratory experiments into industrially competitive methodologies has become of great interest to the community, to see novel developments become commercial products.^1,2,8–10 Traditional scale-up procedures and parallelization of microfluidic droplet generators (i.e. scale-out) are two approaches to achieve industrially relevant scales of production.¹ On one hand, traditional scale-up methodologies involve increasing the reactor size to increase the production volume.¹¹ However, increasing the reactor size also alters basic reaction physics such as heat and mass transfer, which strongly influence the quality of the final products. On the other hand, parallelization of hundreds of microfluidic droplet generators into integrated devices does not involve modifying the size of the reactors and thus the physics relative to the miniaturization are conserved.¹ Nevertheless, these parallelization benefits come at the cost of serious engineering challenges in design, operation robustness, and fabrication of parallelization devices.⁸

In recent years, steps have been taken towards the creation of parallelization systems to increase the volume production of single droplet-generator devices.^{2,8–10,12,13} However, these demonstrations have shown at most production volumes of a few liters per hour,^10,13 which are still insufficient to meet industrial demands or to compete with other emulsification methods with production rates up to 20 000 L h⁻¹.¹⁴ Therefore, another hierarchical level of parallelization is needed to create a competitive and sustainable production plant. As a consequence, current parallelization systems will become modules that are going to be in turn parallelized to achieve the desired scaled-up in production. These modules must ensure the formation of droplets of controlled size and distribution, and maintain the production of such materials within the established tolerances required for each application. In droplet microfluidics, these tolerances are commonly kept within coefficients of variation below 5% to enable precise droplet-to-droplet consistency.¹⁵

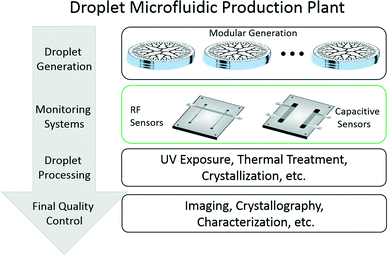
A successful implementation of a complete droplet microfluidic production plant for μ-reaction technologies (μRT) is depicted in Fig. 1. Parallelization modules for droplet generation are only one of the components needed to scale up these technologies. Monitoring systems for droplet generation, post-generation processing, and final quality control are also important elements to consider in the realization of a scaled-up manufacturing plant based on droplet microfluidics.

Fig. 1 Vision of a droplet microfluidic production plant for μ-reaction technologies. This picture shows some of the future challenges and components of a droplet microfluidics manufacturing plant. Monitoring systems can be integrated with the droplet generation devices or can be placed as a serial step as drawn above.

Concerning the monitoring of droplet generation, a complete infrastructure of sensors is needed to detect operational problems in the parallelized systems. These problems may arise from scenarios such as: sudden channel clogging by contaminants, progressive channel fouling by the products of the reaction that get trapped at the walls, air leakages in the system, or any other possible issues at the fluid supply level that may lead to defective droplet generation. These sensors can be placed at any of the hierarchical levels of parallelization, especially in those where we still have the ability to correct the problem or to avoid the generation of wasteful material that may contaminate the product in a shared output. For example, these sensors may look at the production of entire parallelization modules in a plant. If one of these modules fails, a possible corrective action in this level of the hierarchy is to replace the faulty module for another one. In lower hierarchical levels, these sensors may monitor groups of generators within a module or even single droplet generators within a group, where valves or actuators may be triggered to close that section and fix the issue.

Image processing¹⁶ is one method that can be used to monitor the production of droplets in microfluidics. First, an optical image of the generated droplets is taken using both suitable cameras and optics. Then this picture is analyzed by a processing unit, which runs several algorithms to determine the droplet morphology and velocimetry.¹⁶ After the image processing is completed, the resulting information can then be used to trigger a particular action like turning on an alert, adjusting the flow rates, and closing valves or other actuators. Although this method is accurate and reliable, it is also difficult to implement in parallelization systems due to the limited field of view that a lens can resolve. A monitoring system based on image processing will require either a system that can move the camera from one location to another or a costly setup consisting of several cameras.

Another approach is to take advantage of the difference in the dielectric properties of common fluids such as air, oil and water (ε_oil ≈ 2–3 and ε_water ≈ 80.4), which enables accurate electrical detection of the water-in-oil volume fraction (φ) in emulsions. This information can then be used to evaluate the water content in several collection channels, and detect whether or not they are all operating under stable conditions. Electrical sensors based on capacitive measurements or radio frequency resonators measurements (s-parameters) are two different approaches that can be used to analyze the water-in-oil content in microfluidic emulsions.^17–20

Although both methods rely on impedance measurements (Z = R + jX), capacitive sensors measures directly the reactive part of the impedance, whereas the RF resonator measurements (s-parameters) look at the signals of the power transmitted and reflected between two ports, to obtain the resonant frequency of the resonator. Impedance measurements at frequencies from 10⁻⁶ to 10⁷ Hz can be done reliably using the first method. However, at higher frequencies (10⁷ to 10¹¹ Hz) parasitic impedances by cables, connectors, etc., become more important and the second approach is preferred.²¹

Previously, capacitive measurements in microfluidics were reported to detect the size and speed of individual droplets as they were generated by a single droplet generator.¹⁷ Other example applications of capacitive sensors in this field, include non-invasive cell counting devices for flow cytometry applications,^18,22 and cellular activity identification and monitoring in single-cell studies.²³ Radio frequency resonators have also been used in microfluidics, as water-cut sensors to detect the water volume fraction in crude oil that occurs naturally during oil extraction.²⁴ They were used to obtain the dielectric properties of various solvents (e.g. methanol, ethanol, chloroform, etc.²⁵), and to analyze sugar and salt concentrations in solutions.^19,20 These applications are all based on the same principle of operation, which takes advantage of the dielectric properties of the various liquid mixes to produce a measurable capacitance change or frequency shift.

In this paper, we propose for the first time a monitoring system based on electrical measurements (i.e. capacitance or s-parameters) that can assist in keeping droplet production within established process control limits. Our approach consists of placing several of these sensors in different sections within a module and in every module within a plant, to detect faulty parallelization devices. If a section or an entire module fails (i.e. produces polydisperse droplets), the effective permittivity of the emulsions will change from one section or module to another and differential measurements between these sensors can then be used to identify the module responsible for the problem.

The implementation of both types of sensors, in this work, enabled us to establish a point of comparison between these technologies and identify their strengths and weakness for this particular application. Our intention is not to study the dielectric properties of the emulsions but to provide a detection platform, which can be integrated into the parallelization chips, for the monitoring of microfluidic emulsion generation at large scales. In this sense, we present capacitive sensors and RF resonator sensors as two candidates suitable for the required monitoring.

2 Description of the system

Three devices were designed and fabricated in this work. The first device is a microfluidic emulsion generator, in which parallelized droplet generators are run simultaneously to generate microfluidic emulsions with controlled water-in-oil content. The output from this device was then sent to either the capacitive sensor (Fig. 4A) or the RF resonators (Fig. 4B) for monitoring. Comparing both methods, under the same flow conditions and procedures, enable us to contrast the differences between both approaches.

2.1 Emulsion generation

Prior to this work, flow-focusing generators were studied for parallelization using CFD simulations in COMSOL Multiphysics.^26,27 Their dimensions were chosen because they showed little droplet-size dependency on slight flow rate variations.¹⁰ By grouping these generators in sections on multiple layers, we were able to parallelize 512 microfluidic droplet generators successfully in a single device (Fig. 2A).¹⁰ Using this device, we achieved production rates as high as 1 L h⁻¹ of water-in-oil droplets. Our characterization also showed that the least droplet size variability was obtained for O : W ratios of 5 : 1, and water flow rates of ∼1 mL h⁻¹ per generator.

Fig. 2 Production of microfluidic emulsions in parallelization systems. A) Picture of the parallelization device with 512 generators. B) Representative section with 16 generators that was used in our tests.

In this work, we used the same flow regimes as before, but only a representative section of that parallelization system is used for demonstration purposes (Fig. 2B). Since this section behaves in the same way as our former parallelization device, the characterization obtained in this work will also be relevant for larger parallelization systems that are composed of two or more of these sections. One of the advantages of working with this representative unit is our ability to manipulate the flow rates accurately, in order to produce droplet streams with controlled water-in-oil volume fractions to test our sensors. If the water volume fraction, in this particular system, is too large (e.g. >35%) the emulsion generation becomes unstable and significant size variation is observed (see Fig. 3A).

Fig. 3 Droplet generation of polydisperse vs. monodisperse droplet streams. A) Shows a parallelization device in which droplet production is polydisperse due to either unstable flow or clogging problems. B) Shows a uniform and monodisperse droplet production.

The design of this representative section consists of five layers: the first two layers are for droplet generation, the next two are for liquid distribution, and the last one is used to enclose the microfluidic device. The generation layers are comprised of 8 droplet generators each, which were parallelized using a fractal distribution network. This embodiment of our parallelization system produces water-in-dodecane droplets of approximately 150 μm at total flow rates of between 100–160 mL h⁻¹. More details about the fabrication and design of the parallelization devices can be found elsewhere.¹⁰

2.2 Capacitive sensor

The second microfluidic device built is the capacitive sensor depicted in Fig. 4A. This chip has a ∼4 mm-wide and ∼700 μm-deep microfluidic channel that is sandwiched between two thin films (50 μm) of PMMA. The capacitor's plates are then placed on the top and on the bottom of a microfluidic channel to serve as a capacitive sensor.²⁸ The capacitance of the sensor depends on the dielectric properties of the liquid traveling through the channel embedded in between the electrodes. For a parallel plate configuration, the capacitance of the system is given by the simple parallel plate equation:where ε₀ is the permittivity of free space, ε_eff is the effective permittivity of the dielectric in between the electrodes, A is the plates overlapping area, and d is the distance separating them. In this design, however, the capacitor's dielectric material is a combination of the fluids present in the micro-channel (e.g. water, dodecane), the two thin PMMA films and the channel walls. All of which contribute to the effective permittivity of the sensor.

Fig. 4 Prototypes of the parallel plate capacitive sensor and the RF resonator sensors. A) The parallel plate capacitive sensor is formed by two electrodes placed on top and bottom of a microfluidic channel. The insets show the top view and the cross-section of the sensor. B) Prototype of the RF resonator sensors. Two resonators are put together and read with only one measurement instrument, enabling parallelized monitoring. The insets show the top view and the cross-section of the sensor.

In this parallel plate configuration, the capacitance is also directly proportional to the overlapping area of the electrodes and inversely proportional to their separation. The dimensions of the electrodes (4.1 mm-wide by 20 mm-long) were selected such as the impedance measurements, in any case, fall in between a measurable capacitance range (1 to 15 pF). Since the separation (800 μm) was determined by the thickness of the PMMA layers used (middle layer 700 μm and thin films 2 × 50 μm), the main design variables were restricted to the selection of the dimensions of the electrodes. This dependency also drives the dimensions (i.e. cross-sectional area) of the microfluidic channel.

2.3 Radio frequency sensor

A radio frequency T-resonator is comprised of an open-end transmission stub and feed lines that together form a T-pattern.^24,29–31 This open-ended stub resonates at odd integer multiples of their quarter wavelength frequency,²⁹ and their response is given by:where L is the length of the stub, n is the order of resonance (n = 1, 3, 5,…), c is the speed of light, f is the frequency, and ε_eff is the effective permittivity.

Unlike the capacitive sensors that require one probe per monitoring channel, two or more microwave resonators can share the broadband transmission line to monitor different channels in parallel with only one measurement probe.

Changing the length of the stub also changes the resonant frequency of the resonator (see eqn (2)). Thus, two different stub lengths correspond to two different resonant frequencies (i.e. two detection bands). If the lengths of the stubs are carefully selected, multiple resonators can be read independently using a single transmission without interference issues. For this reason, our design (shown in Fig. 4B) consists of two T-shape radio frequency resonators with different lengths (i.e. 8 mm and 16 mm) that are interconnected through a single feed line. Using this dual band capability, we were able to successfully monitor two groups of 16 microfluidic droplet generators independently with a single measurement.

In our prototype shown in Fig. 4B, our double resonator lines are laid down on top of 400 μm-wide and 1000 μm-deep microfluidic channels that carry the emulsions under test. A ground plate is placed on the bottom surface of the microfluidic chip to enable the RF resonator measurements. The resonant frequency of the T-resonators depends on the dielectric properties of the fluids passing through the micro-channels. If the effective permittivity of the emulsion changes over time, the resonant frequency of the sensors will also shift indicating the issue.

Since the effective permittivity of the sensor is the result of the combination of multiple layers and materials (i.e. PMMA, dodecane, water), we used FEM simulation to get an accurate solution of the frequency response and to determine the appropriate dimensions of such resonators (Fig. 7). More details of the simulation can be found elsewhere.³⁰

3 Fabrication

The three microfluidic devices were fabricated using the same fabrication method and therefore, the emulsion generator device and the sensors device can be integrated into a single microfluidic chip. The reason for making them independently is the possibility of manipulating the tube that connects the generation device to the sensors device in order to simulate channel clogging.

The fabrication process begins with the micro-milling of channels into thin sheets of PMMA using an LPKF Protomat S103 PCB plotter. This tool can either route or cut through the PMMA sheets to generate micro-channels and through-holes. Once the machining process was completed, the composing layers were stacked together and aligned mechanically using metallic pins and tight through-holes. These layers were then put in between two glass slides and compressed at high temperature for bonding. We used an Instron 5900-Series stress tester fitted with a temperature-controlled chamber, to heat the stack to 150 °C while applying a uniform load of 15 N cm⁻² for 30 min. After this time, the temperature was dropped to 50 °C while the pressure remained constant for another 15 min. Finally, the pressure is removed and the microfluidic chips are left to cool down to room temperature.

After bonding, the corresponding metal layers of the sensor devices were placed and patterned on the chips' surfaces as required by each design following the next procedure. First, a copper foil tape (3M-1194) was laid down on the top and bottom surfaces of the devices, and then we used a 1.06 μm-fiber laser cutter (Universal laser cutter PLS6MW) to etch through the copper tape without damaging the PMMA substrate underneath. After, the undesired copper tape parts are removed from the surface, leaving behind only the patterns of interest. We used low power (i.e. 10% of this 40 W laser cutter at speeds of 240 mm s⁻¹) to avoid localized heating zones that could damage the plastic underneath. Using this technique, the minimum feature size (metal line) that was achieved is approximately 200 μm – an acceptable dimension for most applications in microfluidics.

The 1.06 μm laser wavelength cuts mainly through metals and ceramics, and does not affect common plastics and glass. As a result, this technique enables the integration thick metal lines into many fabrications process and substrates in microfluidics. Inkjet printing and laser sintering of metallic inks,²⁴ is an alternative method to deposit the desired metal lines and it is also compatible with current manufacturing procedures in microfluidics. This technique can potentially reduce the cost of mass production of the sensors and produce cleaner metal lines at better resolutions.³² Other methods for depositing metal lines like sputtering and PVD are costly and the resulting layers retain residual stresses that often makes them crack and delaminate on semi-flexible substrates. Finally, to provide a robust interface to characterize the sensors at a wide range of frequencies, we soldered standard SMA connectors to both sensor devices as shown in Fig. 4.

4 Experimental results

4.1 Materials and methods

For characterization and testing of the monitoring systems, emulsions of DI water in dodecane (≥99%) were prepared using the parallelization device described above (Fig. 2B). A 2% (w/w) surfactant mixture of 70% Span-20 and 30% Span-80 was added to the continuous phase to improve the stability of the emulsion. The electrical properties of PMMA and the fluids used to characterized these prototypes are shown in Table 1. The properties of the PMMA were previously obtained using a material analyzer (Agilent 4991 A) for 1 GHz and was found to have a dielectric constant of 2.65 and a loss tangent of 0.015.²⁴

Table 1 Material properties of the materials used. These values were used to run the simulations on ANSYS

Material	ε r	tan δ
PMMA	2.65	0.015
Water	80.4	0.15
Dodecane	2.0	0.15

---

The sensitivity of the sensors was studied with microfluidic emulsions of different water-in-oil volume fractions, ranging from 11.1% to 33.3%. The dodecane solution and the DI water were infused into the parallelization device using two syringe pumps (Harvard Apparatus 703007) at controlled flow rates. The different percentages of water-in-oil content were produced by keeping the flow rate of dodecane constant to 80 mL h⁻¹ and varying the water flow rate from 10 to 40 mL h⁻¹. Every channel under test (e.g. one for capacitive sensor and two for the RF resonator sensors) received the emulsions generated by a group of 16 generators (see Fig. 2B), ensuring the experiments were performed following similar conditions.

4.2 Capacitive sensing

Capacitive measurements were performed using a Keysight LCR meter E4980A for a frequency range of 50 to 2 MHz. The results of six measurements for channels containing only water, dodecane, air and some of the emulsions tested are shown in Fig. 5. Error bars were plotted; however, they cannot be easily distinguished due to the low variability of the sensor. In this graph, we can see that the magnitude of the capacitance for a channel full of water is approximately 11 pF whereas a channel filled with dodecane or air has a capacitance of 2.27 pF and 1.5 pF respectively. These values determine the dynamic range of the sensor (Cp_dodecane ≤ Cp_emulsion ≤ Cp_water), since the effective permittivity of the system depends mainly on the contribution of both water and oil volume fractions in the emulsions.

Fig. 5 Microfluidic capacitive sensing. Capacitance measurements are plotted for channels containing 100% air, 100% water, 100% dodecane and stable emulsions with water content (φ) of 16.7%, and 33.3% and 44.4%.

The change in capacitance at the different water volume fractions is shown in Fig. 6. As expected, due to the non-linear behavior of the ε_eff in emulsion,³³ the increment in capacitance becomes more significant at larger water volume fractions. Using this sensor, changes as little as 2.4% in the water content showed capacitance increments of 150 fF. These magnitudes can easily be detectable using our LCR meter or other integrated circuits controlled with LabView®.³⁴

Fig. 6 Capacitance measurements of emulsions containing different water-in-oil volume fractions (φ). As expected, the graph shows that the effective permittivity of the emulsions does not change linearly with an increase water content.

Important characteristics of the dielectric properties of W/O emulsions under flow have previously been studied.³³ For example, it was observed that processes like flocculation and coalescence influence the dielectric properties of a W/O emulsion.³³ When flocs are formed, or the emulsions are non-spherical, measuring the permittivity of the system in one direction differs from that obtained in another direction. To compensate for this shape dependency, Boyle included a shape factor (i.e. the axial ratios of the droplets) in his prediction of the ε_eff of the mix.³⁵ Measuring the emulsions at stable flow conditions usually prevents flocculation and sets a particular shape factor that leads in general to lower permittivity values.³³

Similarly, the dielectric properties of the emulsions also vary depending on the measurement frequency. On one hand, if the permittivity of emulsions is measured at static or low-frequency conditions, a phenomenon called interfacial polarization or Maxwell–Wagner relaxation occurs at the interface between the water and oil domains.³³ This polarization happens because the ions in the water-phase cannot penetrate into the oil domain and thus create a charge separation at the W/O interface that opposes the external electric field. These dipoles increase the effective permittivity of the system, which yields larger capacitances. On the other hand, if the measurements are performed at frequencies above a critical frequency value, the ions in the water-phase cannot reach the interphase before the electric field changes direction. In such case, no interfacial polarization occurs, and the measured capacitances do not get amplified by this phenomenon. In general, the permittivity of an emulsion depends on many factors like volume fraction, flocculation, coalescence, droplet size dispersity, interfacial polarization, and shape factor of the droplets.

Our capacitance sensor reads the resulting average of many droplets passing through the channel (i.e. water volume fraction in the emulsion) and cannot predict whether or not an emulsion is either polydisperse or monodisperse from a single reading. However, if we observe at different locations over time, we can detect any changes in the permittivity of the emulsion (due to any of the factors mentioned above) and pinpoint the section or modules where the change has occurred. Once the problem module has been identified, it can be deactivated or replaced minimizing the impact on the overall system.

It is also important to notice that electrical fields interacting with droplets in an emulsion can alter their stability, modify their interfacial tension, and lead to droplet coalescence.^36–38 For example, electro-coalescence in microfluidics has been achieved using low-frequency AC and short DC pulses that create abrupt surface tension instabilities leading to droplet coalescence.^36,37 In these demonstrations, voltages as low as 1 V-DC for a pulse period of 100 ms were used to drive droplet coalescence.³⁷ Similarly, on electro-wetting on a dielectric (EWOD) systems, low frequencies (≤20 Hz) and high voltages (i.e. V = 50 V) were also used for active mixing of reagents in droplets.³⁸ Since our measurements were done using frequencies sweeps from 20 Hz to 2 MHz and low voltages (i.e. 1 V), no abrupt interfacial changes were created and no droplet coalescence was observed.

4.3 RF sensing

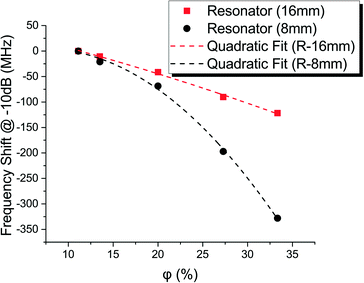
The RF sensors were characterized following the same procedure as the capacitive sensor for comparison purposes. A PNA network analyzer E8363C was used to quantify the magnitude of the power transmitted from port 1 to port 2 (S₂₁-parameter) for frequencies between 1 to 7 GHz. The measured and simulated S₂₁-parameters for channels filled with dodecane, water, and air are plotted in Fig. 7. Here, the frequency response of each resonator, in this double T design, can be associated with one of the two frequency notches observed. In accordance with eqn (2), the curve describing response for channels filled with water is shifted >1 GHz to the left of the response for channels filled with dodecane. This difference in the frequency responses gives the dynamic range for our RF resonator sensors. Also, the experimental results followed closely our FEM simulations, and the small discrepancies are probably due to either fabrication tolerances or slight variations in the dielectric properties of the materials (e.g. relative permittivity and loss tangent).

Fig. 7 Dual band microfluidic RF sensing. The graph shows the magnitude of the “s₂₁-parameters” as a function of frequency for channels containing 100% air, 100% water, 100% dodecane and their corresponding FEM simulations (performed on ANSYS electromagnetic suite).

The frequency shift measured at different water-in-oil volume fractions is plotted in Fig. 8. Although in this graph the two resonators apparently show different sensitivities, they both behave relative to their resonant frequency at which they were designed. When normalized against the frequency response of a channel filled with water, they both show similar relative sensitivities (Fig. 9).

Fig. 8 Frequency shifts measured at −10 dB at the different water-in-oil volume fraction emulsions tested. Although both resonators apparently show different sensitivities, they behave similarly when normalized to their resonant frequency.

Fig. 9 Comparison of the normalized sensitivity between the capacitive and RF resonator sensors. The sensors were normalized to the response of 100% water. Both of these sensing approaches produced comparable sensitivities with ≈10% perceptual dynamic ranges for emulsions with water volume fraction between 11.1% and 33.3%.

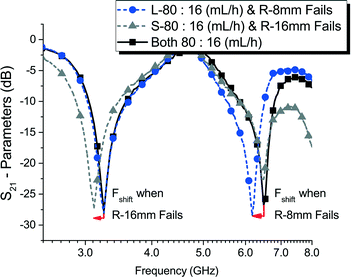
Finally, to prove frequency independence between both T-resonator frequency bands, and demonstrate our monitoring strategy. Clogging in parallelization systems was emulated by suddenly disrupting the flow in one of the monitoring channels in the RF sensing device (Fig. 10). First, two emulsion streams with 16.7% water volume fraction were generated at 80 mL h⁻¹ of dodecane and 16 mL h⁻¹ of water using two parallelization devices. These streams were then sent to the microfluidics channels in the RF resonators device and their fundamental response (“s₂₁-parameters”) was continuously recorded. During operation, we alternatively closed one of the tubings feeding the microfluidic channels to make them fail individually. When the channel with the short resonator was closed, only the higher band showed a frequency shift while the other remained at normal operation readings. Similarly, when the channel with the longer resonator was closed, the frequency shift was observed only at the lower band. This experiment demonstrates that even though the resonators work together, their operation is independent of each other.

Fig. 10 RF monitoring of emulsions (frequency_axis in log scale). The line with squared symbols shows the frequency response of both monitoring bands as an emulsion flows through the sensor. This emulsion was obtained at flow rates of 80 mL h⁻¹ of dodecane and 16 mL h⁻¹ of water. We then alternatively closed one of the tubings feeding the microfluidic channels to make them fail. When the channel with the short resonator was closed only the higher band showed a frequency shift. Similarly, when the channel with the long resonators was closed only the lower band shifted. This demonstrates their independence.

5 Comparison and discussion

Both the capacitive and the RF resonators sensors, show clear readings that can be used to monitor stable emulsion generation if different locations are measured over time and their readouts are compared. The readings of both types of sensors were found to be non-linear, yielding greater changes at higher water volume fractions. This trend is due to the fact that the effective relative permittivity (ε_eff) of the emulsion does not change linearly with the water content.³³ The responses for both sensor devices (curves in Fig. 6 and 8) were fitted to quadratic functions showing their close dependency on the permittivity of the emulsions. When the responses of both capacitive and RF resonator sensors were normalized, we observed very similar sensitivities between their responses (see Fig. 9).

Although the sensitivity of the sensors drops considerably for water-in-oil volume fractions below 10%, the droplets generators used for parallelization are commonly operated above this volume fraction in the dripping regime (i.e. low capillary and Webber numbers).^9,10,13,39 In this flow regime, the droplet formation is more controllable than in jetting regime,^40–42 favoring the parallelization process. Both capacitive and RF resonator sensors can be used to monitor droplet generation of any droplet-size as long as the water-in-oil volume fraction is kept above 10%.

These sensors are not able to describe the droplet size distribution of the generated droplets directly from the permittivity readings. However, if previous dielectric and optical characterizations are performed and the sensors are calibrated to detect a particular response, this technique provides a fair estimation of the initial quality of the emulsions. Alternately, permittivity measurements across different parallelization devices within a plant can also be used to determine atypical permittivity readings in any of the devices.

In terms of readability, the capacitive sensors are simpler to read using either LCR meters or integrated circuits.³⁴ In the case of the RF resonator sensors, commercially available multi-frequency analyzers, based on conventional transmission line measurements can be used, however their cost is usually higher than capacitive measurement systems. If only a differential measurement is required, like in this application, the resonators can be incorporated to oscillator circuits in order to obtain the frequency shifts, enabling a cost effective monitoring solution.⁴³

Unlike the capacitive sensors in which one set of probes is needed per monitoring channel, the RF resonator sensors were successfully parallelized in a double T configuration – where two channels can be monitored at the same time using a single probe. Although both resonators worked independently in this multi-frequency system, the lossy nature of the dielectric properties of oil and water limits the number of channels that can be parallelized in a single device. If more channels were added, the harmonic frequencies of one resonator may interfere with the fundamental frequency of the others. However, when a narrower detection region of the emulsion's permittivity is of interest, a smaller dynamic range is required for each sensor and many more resonators could be parallelized with careful design. In such case, monitoring of several locations in a single module is possible using a single measurement signal.

In general, microfluidic channels with large cross-sectional areas are preferred for this application because they can handle the large flows from parallelization systems and avoid coupling problems that can affect the generation stage. However, it is not desirable to make them too large because the system loses the advantages of miniaturization, which could be needed for further processing steps downstream. In this regard, the RF sensor is less dependent on the channel geometry than the capacitive sensor. According to eqn (2), the main frequency notch of the T-resonator depends mainly on the length of the stub and not as much in the other dimensions. Modifying the dimensions of the microfluidic channels will only modify the effective permittivity (ε_eff), which in turn will shift the resonant frequency. However, this shift can be accounted for and still produce a readable signal. On the contrary, the readout of the capacitive sensor depends heavily on the dimensions of the microfluidic channel (eqn (1)), separation distance and the overlapping area. Therefore, modifying the dimensions of the channel completely modifies the overall magnitude of the capacitance. This characteristic makes designing capacitive sensors less flexible than designing RF resonators. Also, the wide and shallow micro-channels needed for the capacitive sensors are more difficult to fabricate on flexible substrates because they tend to collapse.

6 Conclusions

In this paper, we present and study both capacitive and RF resonator sensors as two candidates, which can continuously monitor microfluidic droplet production in parallelization systems. We have compared both sensors in terms of sensitivity, parallelization potential, cost and readability, and design flexibility.

Permittivity-based sensors represent a more viable solution than optical-based sensors towards the monitoring of the production of large scale droplet generation. Especially, because these sensors can be integrated at a low cost and can also be parallelized to monitor several locations in a scaled-out system.

To characterize these sensors, water-in-oil microfluidic emulsions were generated using a scaled-up microfluidic chip comprised of 16 parallelized microfluidic droplet generators. Capacitance differences of ≈1 pF were obtained between emulsions containing 11.1% and 33.3% water-in-oil volume fraction. Similarly, the RF resonators showed frequency shifts between 120 and 390 MHz for the same variation of the water content. When normalized, both the capacitive and the RF resonator sensors show similar sensitivities. One noticeable difference between these sensors is their operation frequencies. Capacitive measurements cannot be made at high frequencies (>10⁷ Hz) and therefore, RF resonator measurements come as an effective method to detect permittivity variations at high sampling rates.

During droplet production, these sensors can be used to quickly detect any changes in the permittivity of the emulsions, which combine the effects of volume fraction, dispersity, interfacial polarization, and shape factor in order to assist control engineers to take quick decisions such as closing or replacing a parallelization module in order to avoid sources of waste.

In this paper, we also discussed a rapid fabrication process that allows the integration of thick metal lines on polymer substrates with great accuracy using a 1.06 μm laser cutter. Inkjet printing and laser sintering of metallic inks is another fabrication method that can enable enhanced reproducibility and improved precision to manufacture these sensors in mass production.

To date, scale up of parallelization of microfluidic droplet generators has received considerable attention by the community, however, other challenges related to this scale-up goal, such as monitoring systems for quality control and post-generation processing methods require more attention. The microfluidic sensors presented here, serve as a proof of concept and they are the first step towards implementation of a monitoring system for scaled-up microfluidic droplet generation.

References

1. T. W. Phillips, I. G. Lignos, R. M. Maceiczyk, A. J. deMello and J. C. deMello, Lab Chip, 2014, 14, 3172–3180.
2. G. T. Vladisavljević, N. Khalid, M. A. Neves, T. Kuroiwa, M. Nakajima, K. Uemura, S. Ichikawa and I. Kobayashi, Adv. Drug Delivery Rev., 2013, 65, 1626–1663.
3. R. A. Leon, W. Y. Wan, A. Z. M. Badruddoza, T. A. Hatton and S. A. Khan, Cryst. Growth Des., 2013, 14, 140–146.
4. D. R. Griffin, W. M. Weaver, P. O. Scumpia, D. Di Carlo and T. Segura, Nat. Mater., 2015, 14, 737–744.
5. C.-X. Zhao, Adv. Drug Delivery Rev., 2013, 65, 1420–1446.
6. A. M. Nightingale and J. C. de Mello, ChemPhysChem, 2009, 10, 2612–2614.
7. E. Chan, A. Alivisatos and R. Mathies, J. Am. Chem. Soc., 2005, 127, 13854–13861.
8. C. Holtze, J. Phys. D: Appl. Phys., 2013, 46, 114008.
9. T. Nisisako, T. Ando and T. Hatsuzawa, Lab Chip, 2012, 12, 3426–3435.
10. D. Conchouso, D. Castro, S. A. Khan and I. G. Foulds, Lab Chip, 2014, 14, 3011–3020.
11. M. Zlokarnik, Scale-up in Chemical Engineering, John Wiley & Sons, Inc., 2nd edn, 2006.
12. R. Dangla, S. C. Kayi and C. N. Baroud, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 853–858.
13. H.-H. Jeong, V. R. Yelleswarapu, S. Yadavali, D. Issadore and D. Lee, Lab Chip, 2015, 4387–4392.
14. D. J. McClements, Food Emulsions: Principles, Practice, and Techniques, CRC Press LLC, 1999.
15. A. Jillavenkatesa, S. J. Dapkunas and L.-S. H. Lum, Particle Size Characterization, 2001.
16. A. S. Basu, Lab Chip, 2013, 13, 1892–1901.
17. C. Elbuken, T. Glawdel, D. Chan and C. L. Ren, Sens. Actuators, A, 2011, 171, 55–62.
18. S. Zheng, M. Liu and Y.-C. Tai, Biomed. Microdevices, 2007, 10, 221–231.
19. J. Shao, G. Manandhar, B. Arigong and H. Zhang, Microw. Opt. Technol. Lett., 2012, 54, 2691–2694.
20. S. Pinon, D. L. Diedhiou, A. Boukabache, V. Conedera, D. Bourrier, A.-M. Gue, G. Prigent, E. Rius, C. Quendo, B. Potelon and J.-F. Favennec, Microwave Symposium Digest (MTT), 2012 IEEE MTT-S International IS -, 2012, pp. 1–3.
21. F. Kremer and A. Schönhals, in Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, 2012.
22. S. Gawad, K. Cheung, U. Seger, A. Bertsch and P. Renaud, Lab Chip, 2004, 4, 241.
23. T. Sun and H. Morgan, Microfluid. Nanofluid., 2010, 8, 423–443.
24. G. Mckerricher, D. Conchouso, B. S. Cook, I. G. Foulds and A. Shamim, Microwave Symposium (IMS), 2014 IEEE MTT-S International IS - SN - VO -, I, 2014, pp. 1–3.
25. A. A. Abduljabar, D. J. Rowe, A. Porch and D. A. Barrow, IEEE Trans. Microwave Theory Tech., 2014, 62, 679–688.
26. D. Conchouso, E. Rawashdeh, D. Castro, A. Arevalo and I. G. Foulds, Proceedings of the 2013 COMSOL Conference, Rotterdam, 2013.
27. D. Conchouso, E. Al Rawashdeh, A. Arevalo, D. Castro and I. G. Foulds, Proceedings of the 2013 COMSOL Conference, Rotterdam, 2013.
28. D. Conchouso, A. Arevalo, D. Castro and I. G. Foulds, Nano/Micro Engineered and Molecular Systems (NEMS), 2016 IEEE 11th International Conference on, Matushima Bay and Sendai, 2016.
29. K. P. Latti, M. Kettunen, J. P. Strom and P. Silventoinen, IEEE Trans. Instrum. Meas., 2007, 56, 1845–1850.
30. D. Conchouso, G. Mckerricher, D. Castro, A. Arevalo and I. G. Foulds, 2015 COMSOL Conference, Grenoble, France, 2015.
31. D. Conchouso, A. Arevalo, G. Mckerricher, D. Castro and I. G. Foulds, Nano/Micro Engineered and Molecular Systems (NEMS), 2016 IEEE 11th International Conference on, Matsushima Bay and Sendai, 2016.
32. H. Sirringhaus, T. Kawase, R. H. Friend, T. Shimoda, M. Inbasekaran, W. Wu and E. P. Woo, Science, 2000, 290, 2123–2126.
33. T. Skodvin, T. Jakobsen and J. Sjöblom, J. Dispersion Sci. Technol., 1994, 15, 423–448.
34. H. Omran, M. Arsalan and K. N. Salama, Sens. Actuators, A, 2014, 216, 43–51.
35. M. H. Boyle, Colloid Polym. Sci., 1985, 263, 51–57.
36. K. Ahn, J. Agresti, H. Chong, M. Marquez and D. A. Weitz, Appl. Phys. Lett., 2006, 88, 264105.
37. C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 89, 134101.
38. P. Paik, V. K. Pamula and R. B. Fair, Lab Chip, 2003, 3, 253–259.
39. J. Guzowski, P. M. Korczyk, S. Jakiela and P. Garstecki, Lab Chip, 2011, 11, 3593–3595.
40. A. S. Utada, L. Y. Chu, A. Fernandez-Nieves, D. R. Link, C. Holtze and D. A. Weitz, MRS Bull., 2007, 32, 702–708.
41. S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366.
42. A. S. Utada, Science, 2005, 308, 537–541.
43. T. J. Warnagiris, Microw. J., 2000, 140.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6lc00693k

---