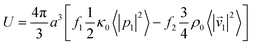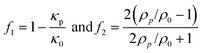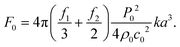Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic-field devices for the ultrasonic manipulation of microparticles
Bruce W.
Drinkwater
*
Department of Mechanical Engineering, University of Bristol, Bristol, BS8 1TR, UK. E-mail: b.drinkwater@bristol.ac.uk
First published on 26th May 2016
Abstract
The use of acoustic radiation forces in lab-on-a-chip environments has seen a rapid development in recent years. Operations such as particle sieving, sorting and characterisation are becoming increasingly common with a range of applications in the biomedical sciences. Traditionally, these applications rely on static patterns of ultrasonic pressure and are often collectively referred to as ultrasonic standing wave devices. Recent years have also seen the emergence of devices which capitalise on dynamic and reconfigurable ultrasonic fields and these are the subject of this review. Dynamic ultrasonic fields lead to acoustic radiation forces that change with time. They have opened up the possibility of performing a wide range of manipulations such as the transport and rotation of individual particles or agglomerates. In addition, they have led to device reconfigurability, i.e. the ability of a single lab-on-a-chip device to perform multiple functions. This opens up the possibility of channel-less microfluidic devices which would have many applications, for example in biosensing and microscale assembly. This paper reviews the current state of the field of dynamic and reconfigurable ultrasonic particle manipulation devices and then discusses the open problems and future possibilities.
I. Introduction
This paper reviews published research on dynamic and reconfigurable ultrasonic manipulators. The definition of a dynamic device adopted here is one in which the acoustic field is altered dynamically for the purpose of micro-particle manipulation. The paper starts by briefly reviewing static-field ultrasonic devices which have found widespread use in lab-on-a-chip (LOC) applications, such as microparticle sorting. These static-field devices form the basis for the more recent emergence of dynamic devices. Of course, this is not a one way process and research on both static and dynamic field concepts is now proceeding in parallel. As the number and functionality of available devices increases seemingly exponentially, it becomes progressively harder for academic and industrial researchers to understand what the most appropriate device for a given application is. This review aims to bring clarity to this confusion. The approach adopted here is to discuss the physical principles of the different devices and explore what functions each can perform, setting them in the context of the current LOC applications. The dynamic devices are then classified into the scheme proposed in Fig. 1. Within this classification scheme three broad classes of device are defined: in-plane manipulators, beam manipulators and planar arrays. The paper compares and contrasts these devices and concludes by considering what future developments, both in device science and practical application, might be possible.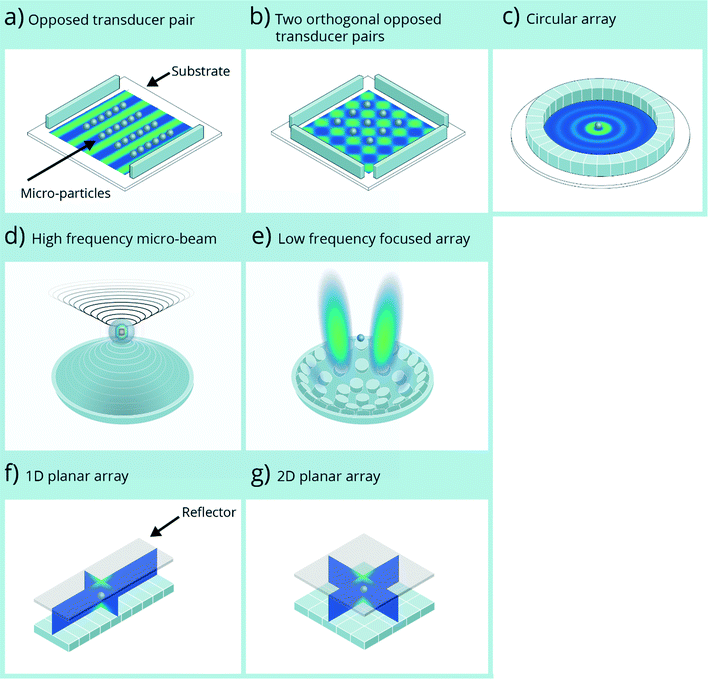 | ||
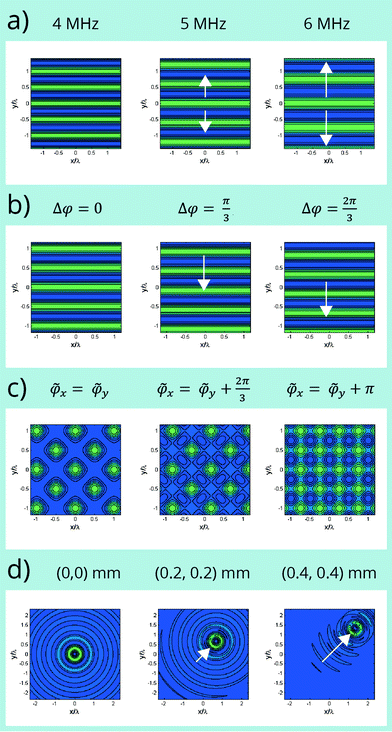
| Fig. 1 Schematic representations of the different dynamic ultrasonic micro-scale manipulators. With the exception of d) the acoustic fields are shown as normalised Gor'kov potentials of dense particles in water. In a)–c) the frequency has been lowered to enable the field to be more clearly visualised; d) shows the pressure field at based on the 30 MHz device of Lee et al.79 and the particle is approximately to scale w.r.t. the transducer; e) is based on the device of Baresch et al.;39 f) and g) show half wavelength resonances in the vertical direction and are based on the devices of Glynne-Jones et al.86 and Qui et al.88 respectively. | ||
A. Devices using static acoustic fields
Although the focus of this review is on dynamic-field devices, it is important to set their development in the context of the alternatives; namely static-field manipulation devices. It is also important to stress that the purpose of a device is to fulfil a function required by an application. In general if a simpler device can fulfil that function, it will be a better and more reliable solution. The key point here is that dynamic reconfigurability comes at the cost of complexity, therefore such devices should only be used when an application demands. In this section the key static field devices are described and examples of where they have solved specific LOC application challenges are given.Ultrasonic standing wave devices that create a static acoustic field have now found wide-spread application in LOC devices (see reviews by Coakley et al.,1 Laurell et al.,2 Wiklund3 and Glynne-Jones et al.4). A common configuration is to excite a resonance in a fluid-filled chamber or channel. Typically, the chamber has a simple planar geometry and a simple mode shape is selected in which the mode has local near-1D properties.4 This resonant operation means that very efficient devices, in terms of acoustic force applied for a given input power, can be made if the system has low damping. In turn, this means that these devices can often by driven with a sinusoidal signal of a few volts and <0.1 W of input power. However, the acoustic field is fixed by the resonant mode-shape, which is a characteristic of the geometry (and acoustic properties) of the device, hence the use of the term static. Any specific device will have an infinite number of possible modes to choose from, however, typically a single, low-order mode with a simple mode-shape is selected. Such modes are preferable as they are the easiest to excite and are sufficient to perform operations such as agglomeration and separation. The other shared attribute of these devices is that the wavelength, λ, of the ultrasound is commonly set to be significantly larger than the objects being manipulated (or more strictly, ka ≪ 1, where k = 2π/λ, and, a, is the size of the particle, e.g. the radius in the case of a sphere). In this Rayleigh regime, the forces act to move dense and stiff particles (e.g. cells in water) to the pressure nodes. More strictly the acoustic radiation force is governed by a contrast factor which is a function of the particle and host density and compressibility. The forces are then proportional to the gradient of the Gor'kov energy potential as discussed in section 1.C.5
Cell agglomeration for tissue engineering is an area that has attracted particular attention.6–8 In a typical device, an agglomeration of cells in a liquid cell culture medium, is held at a node of a planar (or strictly a near-planar) standing wave. The planar acoustic field leads to the production of a planar tissue construct. The benefit of ultrasonic forces in these applications is that the agglomerate is formed in a three-dimensional scaffold-less environment which is thought to be a reasonable approximation to the situation in vivo. Many of these devices have been built on a microfluidic scale, in combination with microfluidic flows. One or more of the chamber dimensions, e.g. the channel width, is set to an integer multiple of half the acoustic wavelength to produce the desired resonance. Frequencies in the MHz range are required for microfluidic lengthscales, leading to wavelengths and hence channel dimensions of the order of 100's of micrometers (e.g. in water λ/2 = 375 μm at 2 MHz). A particularly compelling microscale filtering application was shown in Petersson et al.9 in which red blood cells are separated from lipids (fat particles). The mixture flows along a microfluidic channel containing a half-wavelength planar standing wave field and because of their differing density and compressibility with respect to the host fluid, the red blood cells move towards the nodes and the lipids towards the antinodes. The red blood cells and lipids are then separated spatially and flow out through different channels. Perhaps the most commercially developed application is in flow cytometry in which standing waves due to a low-order channel resonance are used to produce precise alignment of particles in a flow cell, prior to spectral analysis.10,11 In a development of this concept a standing wave device was used to measure the acoustic impedance of cells (independent of their size) by monitoring the balance between flow and the acoustic radiation forces.12 This is one of a number of emerging characterisation applications in biomedicine which capitalise on the links between cell type and mechanical properties.
Fixed patterns of standing waves have also been formed across chambers with dimensions >10λ for applications such as patterning13 and larger-scale filtration.14 In cell patterning the area of interest typically has dimensions of the same order as a small glass microscope cover slide (e.g. 10 mm diameter circle). There has also been interest in using ultrasound to seed particles prior to cell growth. For example, Gesellchen et al.15 used ultrasonic standing waves to align Schwann cells and demonstrated that the nerve cells, growing from a ganglion follow this ultrasonically produced alignment. Very similar devices have also been used to assemble inorganic materials, for example, fibre reinforced composites16–18 and to assemble micro- and nano-structures.19–21 On a similar scale, Böhm et al.14 demonstrated a filter to remove bio-matter from water at flow rates of up to 58 L per day. Here a standing wave was formed in a filtration chamber of dimensions ≥10λ, through which the contaminated water flowed. Filtration is achieved as the bio-matter remains trapped at the nodes of the standing wave field.
Static-field devices based on travelling waves have also been proposed. Destgeer et al. use the acoustic radiation forces of a travelling surface acoustic wave (SAW) to perturb particles from a flow; the larger particles are perturbed by a greater distance and hence can be separated.22 Others have used travelling waves to create streaming effects to move particles in microfluidic systems.23
B. From static to dynamic-field devices
The thought that dynamic-field devices can do more than static-field devices is attractive and this review will explore what has been achieved in this direction and what might be possible in the future. For example, Marx24 recently reviewed the rapid development of dynamic cell manipulation technologies for biomedical applications. As a minimum a single dynamic device might be able to perform the function of multiple static devices – this attribute could be called reconfigurability. At the other extreme a future dynamic device might be able to independently manipulate many thousands of particles and assemble them into arbitrary configurations – imagine an all-acoustic version of a 3D printer. The devices in the previous section were static by design and, for example, the standing wave devices were operated at a resonant frequency of the device chamber/channel. The simplest method for creating a dynamic device is to use multiple transducers and to change the ultrasonic field by switching off/on the excited transducers. For example, Llewellyn-Jones et al.25 integrated an ultrasonic assembly stage in to a 3D printer and demonstrated the printing of glass-fibre composite layers. As shown in Fig. 2, the field (and hence the pattern of fibres) can be changed mid-print by switching between differently oriented transducer pairs. In these devices the efficiency benefits of resonant operation are maintained but some reconfigurability is added. A more sophisticated method of introducing dynamic-fields, which again capitalises on the benefits of resonant operation is to use mode switching in which the acoustic field within the device is rapidly switched between resonant modes (achieved first in air26 and then in water27). The net force on a particle is then the time average of the modal contributions. This approach relies on the switching being performed faster than the time constant associated with particle motion.28 It has also been shown that rapid sweeping of the frequency in a narrow band about the resonant frequency of a channel can lead to significantly improved trapping stability and consistency.29 Again the net force on the particles is the time average across the frequency sweep, which is then less affected by other localised parasitic device resonances.An alternative and much more versatile approach to creating a dynamic-field capability is to move to non-resonant device operation. However, whilst non-resonant operation frees the device from the constraint of operating at a specific resonant mode, in as many dimensions as required, it inevitably reduces the efficiency of the device. This means that greater applied voltages and power levels are needed to achieve a given level of force. The extent to which the device efficiency is reduced in a non-resonant device depends on the damping (e.g. quality or Q-factor) of the resonant device to which it is compared. Note that, for a system with low damping, the Q-factor is the amplification at resonance w.r.t. static forcing. For example, resonant devices manufactured from low damping materials can have, Q > 10, suggesting greater than ten-fold efficiency differences.4 However, it is worth noting that non-resonant devices capable of producing 90 kPa per Volt have been reported meaning that operation below 10 V would be suitable for many LOC applications where typically hundreds of kPa are required.30
In static standing wave devices it has been shown that temperature changes greater than a few degrees can have a major detrimental effect on the acoustic field.31 Non-resonant devices are by design less sensitive to changes in the device resonances, so potentially are less sensitive to temperature effects. However, such results are device specific and require careful measurement in a given device or application. The other cost is complexity: both of the device itself and the electronics required to control it. However, rapid progress in microscale manufacture and embedded electronics means that a range of LOC scale dynamic devices can already be built and operated with modest resources.
C. Acoustic radiation forces on particles
Before proceeding further the acoustic radiation forces, which are the basis of the devices that form the subject of this review are briefly described. Fundamentally, the propagation of an acoustic or ultrasonic wave results in acoustic radiation forces on objects and the acoustic streaming of fluids. These are second order effects, caused by nonlinearities in the governing physics. Lord Rayleigh developed the first understanding of acoustic streaming32 and the acoustic radiation force on a plane obstacle due to a propagating wave.33,34 The basic phenomena had been known for some years prior to this when Kundt observed that dust particles moved to the nodes of an acoustic standing wave generated in a glass tube – he used these observations to infer the speed of sound in various gases.35 However, the modern understanding of acoustic radiation forces started with King who developed analytical expressions for the force on a rigid sphere in an inviscid fluid in plane standing and travelling wave fields.36 When the particle diameter is substantially smaller than the incident wavelength (i.e. ka ≪ 1), the scattering is simplified to a sum of monopole and dipole contributions and analytical expressions for the force result. Further development of this basic result produced an analytical solution for compressible spheres37 which was then was generalised to arbitrary acoustic fields by Gor'kov.5 Gor'kov elegantly described the forces as resulting from a potential field, U, (see also Bruus28). In this way the acoustic radiation force,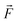 , can be found as
, can be found as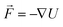 | (1) |
where 〈|p1|2〉 and
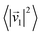 are the mean squared pressure and particle velocity respectively at the object, a is the radius of the spherical object, ρ and κ are density and compressibility respectively and the subscripts denote the particle, ‘p’, or host, ‘0’ properties. Note that for a fluid
are the mean squared pressure and particle velocity respectively at the object, a is the radius of the spherical object, ρ and κ are density and compressibility respectively and the subscripts denote the particle, ‘p’, or host, ‘0’ properties. Note that for a fluid 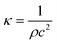 .
.
It should be noted that eqn (1) only accounts for gradient forces which arise due to gradients of acoustic pressure and particle velocity in standing and propagating wave fields. However, it does not include the scattered force due to the reflection (i.e. scattering) of propagating plane waves (i.e. with no gradient) from the object. It should be further noted that scattering forces have been shown to be small in most microfluidic applications.38,39 However, for larger particles (i.e. ka > 1) in travelling wave fields the scattering terms can be significant.22 Another limitation of eqn (1) is that it does not account for the secondary radiation forces that occur when particles become closely spaced.2,40 Although eqn (1) has these and other deficiencies from a theoretical perspective, for small and widely spaced particles, it is capable of describing the vast majority of experimental observations.
Analysis of the acoustic radiation force on larger spherical particles (i.e. ka ≥ 1) has been developed37,41 and more recently extended to various non-spherical particles42 and shells.43–45 Note that shells are of particular practical importance as they act as contrast and drug delivery agents in medical ultrasonics. Numerical techniques have meant that the shape and size of particles that can now be analysed is almost limitless (see for example, Glynne-Jones et al.46). However, with a few exceptions47 and despite recent advances in computational power, the numerical methods are still limited to the solution of simplified versions of the full coupled governing equations. The most common numerical approach, which broadly follows Gor'kov's analytical approach, is to integrate the second order acoustic pressures around a boundary that encloses the particle,
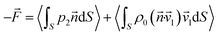 | (2) |
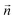 is the normal of that surface. The problem can then be dramatically simplified for an inviscid fluid as the second order pressure, p2, can be obtained from first order terms as37
is the normal of that surface. The problem can then be dramatically simplified for an inviscid fluid as the second order pressure, p2, can be obtained from first order terms as37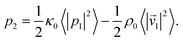 | (3) |
Acoustic streaming, is a family of effects that are an integral part of any acoustic manipulation device.51,52 However, in the majority of devices discussed in this paper, streaming is unwanted and researchers operate in regimes where the acoustic radiation forces dominate over the streaming induced drag. This means that, whilst streaming in inevitably present, its presence does not strongly affect the operation of the devices. Readers should see Wiklund et al. for examples of applications where streaming is beneficial, i.e. fluid pumping or microstreaming mediated drug delivery.53 The use of streaming for LOC-based particle manipulation is also an active area and recently very high frequency (over 200 MHz) focused beams were used to harness combined streaming and radiation forces to cause agglomeration of sub-micron polystyrene particles.23
II. Classification of dynamic manipulation devices
The following classification scheme, shown schematically in Fig. 1, draws together the dynamic devices into three broad groups: in-plane, beam and planar array manipulators. The aim of this paper is to explore the functionality of the different classes of device and explore their suitability for current and future applications. Within each class, device functionality is described approximately chronologically. However, this chronological description also maps onto the progression towards devices that are increasingly dynamic and reconfigurable. A large proportion of the research to-date uses the in-plane devices with beam devices attracting growing interest. Both classes of device have seen biomedical application. It should be noted that at present very few examples of planar arrays are present in the literature, however, they were thought to be sufficiently different from the in-plane devices to warrant their own class and a hence separate discussion.A. In-plane manipulators
In-plane manipulators are characterised by transducers arranged around the periphery of a plane, manipulation occurring in that plane within a central chamber. Various examples of in-plane manipulation devices are shown schematically in Fig. 1(a)–(c). From this figure and also the summary Table 1 it is immediately apparent that the complexity of the fields produced and the range of fields possible are dependent on the number of transducers employed. As more transducers are used and hence more complex fields are achievable, device reconfigurability and functionality increases; i.e. complex operations become possible. The section below charts this development in functionality and sets this in the context of current application challenges.| Authors | Number of transducers (wave type) | Control method | Particles | Size (dia.), μm | Freq., MHz | Wavelength, μm |
|---|---|---|---|---|---|---|
| Takeuchi & Yamanouchi, 1994 (ref. 59) | 2 (SAW) | Travelling waves | Glass | 100 | 49 | 80 |
| Saito et al., 2002 (ref. 54) | 4 (SAW) | Mode hopping | Euglena | Ø10, length 30–50 | 2–4 | 750–375 |
| Paramecia | Ø30, length 150–200 | |||||
| Haake & Dual, 2005 (ref. 55) | 4 (BW) | Frequency shift, amplitude modulation | Polymer | 26–74 | 1–3 | 1500–500 |
| Haake et al., 2005 (ref. 56) | 4 (BW) | Frequency shift | MCF10A | 15 | 1.2–2.2 | 1250–682 |
| HL60 | 20 | |||||
| Wood et al., 2009 (ref. 58) | 4 (SAW) | Frequency shift | Latex | 0.5–2 | 32.4 | 112–124 |
| Courtney et al., 2011 (ref. 62) | 4 (BW) | Phase shift | PS | 10 | 5 | 304 |
| Orloff et al., 2011 (ref. 65) | 2 (SAW) | Phase shift | Latex | 3 | 91 | 46 |
| Meng et al., 2011 (ref. 64) | 4 (SAW) | Phase shift | MB | 0.87 | 19.8 | 200 |
| Breast cancer cell MDA MB 453 | 10 | |||||
| Ding et al., 2012 (ref. 57) | 4 (SAW) | Frequency shift | PS | 2–15 | 18.5–37 | 100–200 |
| Bovine RBC | 6 | |||||
| C. elegans | Length 300 | |||||
| Tran et al., 2012 (ref. 66) | 4 (SAW) | Frequency modulation | Silicone oil | 10 | 34.5–37 | 100 |
| Human RBC | 6–8 | |||||
| Human WBC | 14 | |||||
| Bernassau et al., 2012 (ref. 69) | 7 (BW) | Phase shift | PS | 10 | 4 | 375 |
| MDCK | — | |||||
| Guo et al., 2014 (ref. 67) | 4 (SAW) | Amplitude modulation (incoherent) | HEK 293 T, HeLa S3, HMVEC | ∼15 | 13.35–13.45 | ∼300 |
| Courtney et al., 2014 (ref. 71) | 64 (BW) | Independent phase shifts | PS | 45–90 | 2.35 | 640 |
The most simple in-plane manipulators use opposing pairs of transducers, each pair generating a standing wave as shown in Fig. 1(a) and (b).54–56 The transducer dimensions in the plane of operation are designed to be large compared to the wavelength (i.e. L ≫ λ) so, when excited with a simple continuous sinusoid, they will emit near plane waves. A single opposed pair generates a pseudo-1D acoustic standing wave field (i.e. p(x) = P0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kx)sin(ωt)) which leads to small (i.e. ka ≪ 1), dense and stiff microparticles becoming trapped in a series of nodal lines, with the force given by
cos(kx)sin(ωt)) which leads to small (i.e. ka ≪ 1), dense and stiff microparticles becoming trapped in a series of nodal lines, with the force given by
F(x) = F0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kx), sin(2kx), | (4) |
Two orthogonal opposed pairs generate a grid-like pattern of nodes due to the interference of the two orthogonal, pseudo-1D fields. The first such devices used piezoelectric elements to excite bulk waves (BW) in a fluid-filled chamber. Here, the exciting sine wave is swept from low to high frequency passing through a sequence of simple chamber resonances. As the frequency increases, so the nodal lines are compressed about the centre of the device (as the nodes become more closely spaced at higher frequencies). Due the resonant nature of the operation of these devices, the field is much more intense at the specific resonant frequencies, in effect limiting the operation to these frequencies and hence to a fixed sequence of patterns. Using this approach it is possible to cause a variety of objects including cells and micro-organisms to be transported or become concentrated towards the centre of a device. However, if the manipulation chamber is positioned off-centre (i.e. near one of the transducers) the particle motion is a translation as well as a compression of the nodal lines.57
Wood et al.58 demonstrated a device incorporating two opposed pairs of interdigital transducers (IDTs) arranged as a square using a classic microfluidic SAW chip design. As the acoustic field in the fluid is generated by leakage of energy from a surface or Lamb wave in the substrate, so it is most intense near the surface. It should be noted that this device builds on earlier work which explored the use of SAW technology for droplet transport and mixing.59–61 The approach is to deposit metallic IDT electrodes onto a lithium niobate (LiNbO3) piezoelectric substrate and, in order to inhibit reflections from the ends of the substrate, add absorbing material to the surface. This means that each of the transducer elements can be thought of as emitting into a free-field in the plane of operation. Under these free-field conditions, the pseudo-1D force from a pair of identical transducers becomes,
F(x) = F0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kx + Δφ), sin(2kx + Δφ), | (5) |
Courtney et al.62 added a non-reflective boundary condition to a bulk-wave device with a square arrangement of transducers as shown in Fig. 1(b). This was achieved through the addition of matching layers to the front surface of the piezoelectric transducers and the use of a highly absorbing backing material. Note that other approaches have been explored to create non-resonant manipulation devices include angling the transducers to inhibit reflection into the central region63 and operating at the first through-thickness resonance of the piezo-element to create an efficient transmission line.30 With chamber resonances removed, Fig. 3(b) shows that the relative phase, Δφ, between opposed transducer elements can then be used to control the location of the nodes. This approach leads to the ability to apply an arbitrary translation to the line or grid patterns within the plane of operation.
In bulk wave devices the motion is generated directly in the fluid, therefore, the ultrasonic field exists over the entire depth of the device. Intriguingly, Scholz et al. recently showed that, although unintended, the energy in many bulk wave devices is also higher near the substrate.18 However, further work is needed to see if this is a general effect or a device-specific result. Conversely, there are applications such as tissue engineering in which the positioning of objects away from the substrate is also beneficial and so further work is required to design devices and transduction to facilitate this.
Microfluidic in-plane manipulators have also been used to manipulate cells and small organisms.64,65,57 Tran et al. showed that human red blood cells (hRBCs) can be translated at speeds of up to 10 mm s−1 in the SAW version of this type of device.66 Similarly, Fig. 4 shows how bulk wave devices using phase control have been used to generate complex tartan-like cell patterns (using C2C12 cells) by depositing lines of cells, waiting for cell adherence, before reconfiguring the acoustic field and depositing further cells.15 Collectively, this body of research on cell manipulation suggests that the acoustic pressure levels required for manipulation do not have a measureable detrimental effect on cell viability. However, whilst these results are encouraging, cell viability in dynamic-field devices must be treated on a device-by-device basis until stronger evidence emerges. It is also apparent that the use of polymer spheres (e.g. polystyrene or latex) acts as a reliable model for cell manipulation performance.
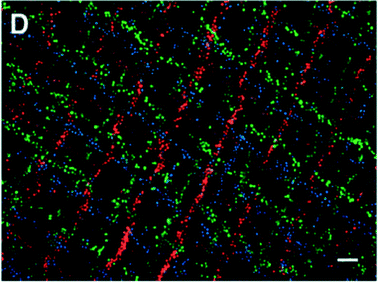 | ||
| Fig. 4 Adapted from Fig. 2 in Gesellchen et al.15 with permission from the Royal Society of Chemistry. Composite of fluorescent micrographs taken after patterning fluorescently labelled C2C12 cells. Cells are stained with MitoTracker Red, MitoTracker Green and Hoechst 33342, scale bar 100 μm. | ||
Guo et al. carefully controlled the distance between two cells (various cell types) in a single potential well within a 4-transducer device.67 This functionality has significant potential for cell communication and interaction studies. The field was switched on for short periods during which two initially separated cells were caused to move together by small amounts, until eventually they were brought into contact at the centre of the trap. This approach capitalises on the microfluidic nature of the device, which means that the particle inertia is negligible and so the motion of the particles stops with the ultrasonic actuation. This demonstrates a new operational mode for these devices (amplitude modulation) which, in this case, led to precise control of cell–cell separation. However, it should be noted that this device applies a device-scale forcing, i.e. the same forcing is applied to objects in each pressure node within the device. This limitation comes from the low number of transducers.
As the number of independent transducers increases, so does the range of patterns possible and the degree of reconfigurability achievable. For example, the 4-transducer devices can be excited to reconfigure the field between two pressure distribution extremes by adjusting the average phase of the two pairs (where 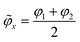 ,
,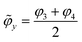 and φ1...4 are the phases of the individual transducers). As shown in Fig. 3(c) this enables this type of device to produce a diagonal cross-like pattern of Gor'kov potential minima when
and φ1...4 are the phases of the individual transducers). As shown in Fig. 3(c) this enables this type of device to produce a diagonal cross-like pattern of Gor'kov potential minima when ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) x =
x = ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) y and a dot-like pattern when
y and a dot-like pattern when ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) x =
x = ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) y + π. If the transducer pairs are excited at differing frequencies (or by using unsynchronised signal generators) then the pairs become independent and at long times
y + π. If the transducer pairs are excited at differing frequencies (or by using unsynchronised signal generators) then the pairs become independent and at long times 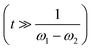 the dot-like pattern is formed. Under these conditions the force is simply given by,68
the dot-like pattern is formed. Under these conditions the force is simply given by,68
F(x, y) = Fx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kxx + Δφx) + Fy sin(2kxx + Δφx) + Fy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kyy + Δφy). sin(2kyy + Δφy). | (6) |
Inspired by the Bessel-shaped traps used in optical tweezing,70 Courtney et al.71 used 64-elements arranged in a circle to generate first order (m = 1) Bessel-shaped acoustic fields,
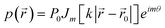 | (7) |
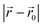 and
and 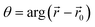 are respectively the radial distance and angle w.r.t. to a Bessel function centred on
are respectively the radial distance and angle w.r.t. to a Bessel function centred on 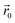 . Assuming a distribution of peripherally located elements, such as in the circular arrangement shown in Fig. 1(c), the translation of the Bessel function centre is achieved by the application of a phase delays such that
. Assuming a distribution of peripherally located elements, such as in the circular arrangement shown in Fig. 1(c), the translation of the Bessel function centre is achieved by the application of a phase delays such that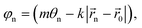 | (8) |
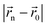 , and
, and 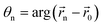 are respectively the radial distance and the angle between the element and the Bessel function centre. In eqn (8), the first term produces a field that approximates an mth order Bessel function and the second part translates its centre. Note, as the number of array elements increases, so the field becomes a closer approximation to a true Bessel function. As shown in Fig. 3(d) these fields are attractive as they consist of a low potential central node surrounded by a high potential circle, which forms a uniform two-dimensional trap. This also leads to a more efficient device as the high intensity acoustic field is concentrated (i.e. focused) in a small region of the chamber. Using this approach, a particle trapped at the central node can be moved to an arbitrary location as shown in Fig. 3(d). By linear superposition, multiple Bessel traps can be generated and moved independently.72,73 However, interference between the traps means that, as the Bessel function shaped traps approach, they interfere and the trapping is lost. The authors were able to show that controlled approaches of the order of a wavelength were possible and that the number of independent traps that could be generated depended on the number of elements used. In order to finally bring particles together the authors used higher order Bessel functions that have a larger central nodal region and then by progressively lowering the Bessel function order brought the particles to a central point. If, for example, this array device was combined with amplitude modulation, a number of different cell–cell interaction studies would be possible at different locations within the same device.
are respectively the radial distance and the angle between the element and the Bessel function centre. In eqn (8), the first term produces a field that approximates an mth order Bessel function and the second part translates its centre. Note, as the number of array elements increases, so the field becomes a closer approximation to a true Bessel function. As shown in Fig. 3(d) these fields are attractive as they consist of a low potential central node surrounded by a high potential circle, which forms a uniform two-dimensional trap. This also leads to a more efficient device as the high intensity acoustic field is concentrated (i.e. focused) in a small region of the chamber. Using this approach, a particle trapped at the central node can be moved to an arbitrary location as shown in Fig. 3(d). By linear superposition, multiple Bessel traps can be generated and moved independently.72,73 However, interference between the traps means that, as the Bessel function shaped traps approach, they interfere and the trapping is lost. The authors were able to show that controlled approaches of the order of a wavelength were possible and that the number of independent traps that could be generated depended on the number of elements used. In order to finally bring particles together the authors used higher order Bessel functions that have a larger central nodal region and then by progressively lowering the Bessel function order brought the particles to a central point. If, for example, this array device was combined with amplitude modulation, a number of different cell–cell interaction studies would be possible at different locations within the same device.
Rotation of objects has also been achieved and Schwarz et al.74 showed the controlled rotation of non-spherical objects such as glass fibres in a 4-transducer device. They controlled the relative phase of the two opposing pairs of transducer, as per Fig. 3(c), which resulted in a sequence of acoustic fields that then produced rotation of a small cylinder. Hong et al. generated an acoustic vortex (i.e.eqn (7)) in a circular array device, as shown in Fig. 1(c), and observed that microscopic objects trapped at the central vortex core were subject to rotation due to transfer of orbital angular momentum.75 These examples suggest that controlled micro-centrifugation is possible in an LOC environment although this functionality has yet to be fully exploited.
B. Beam manipulators
The second major class of dynamic manipulator uses propagating beams to trap and move microparticles as shown in Fig. 1(d) and (e) and summarised in Table 2. The use of beams for micro-manipulation was suggested theoretically by Wu and Du76 and then explored experimentally using two counter-propagating focused beams from 3.5 MHz, 12 mm diameter, 24 mm focal length transducers.77 Latex particles with a diameter of 270 μm and clusters of frog's eggs were trapped, however, in these first experiments no movement of the trapped particles was performed. The focused transducers emit converging fields which interfere to produce a standing wave, i.e. similar in principle to the 1D in-plane manipulator shown in Fig. 1(a), except now with a 3D manipulation capability due to the stronger lateral forces caused by the focusing. The disadvantage of this approach is that the need for two, relatively bulky, focused transducers makes observation of the trapped objects challenging. For this reason, these devices have seen little practical application. As with the other devices discussed so far, the acoustic wavelength remains larger than the particle (i.e. the Rayleigh scattering regime) and the manipulation forces can be described by the Gor'kov model. A variant on this simple beam device was realised by Yamakoshi and Noguchi who trapped particles in a channel at the focus of two propagating beams driven out of phase.78 In this configuration a nodal line (and hence trapping) is created between the transducers in the direction of propagation. There is no trapping in the propagation direction, but the presence of the channel constrains the particles.| Author | Particles | Size (dia.), μm | Frequency, MHz | Wavelength, μm | No. elements |
|---|---|---|---|---|---|
| Wu, 1991 (ref. 77) | Latex | 270 | 3.5 | 429 | 2 |
| Frog's eggs | — | ||||
| Yamakoshi & Noguchi, 1998 (ref. 78) | PS | 30 | 5 | 304 | 2 |
| Lee et al., 2009 (ref. 79) | Lipid drop | 126 | 30 | 50 | 1 |
| Lee et al., 2011 (ref. 81) | K562 leukaemia cell | 10 | 200 | 7.5 | 1 |
| Zheng et al., 2012 (ref. 83) | PS | 45 | 26.3 | 57 | 64 |
| Hwang et al., 2014 (ref. 80) | PS | 5 | 193 | 8 | 1 |
| Baresch et al., 2016 (ref. 39) | PS | 190–390 | 1.15 | 1304 | 127 |
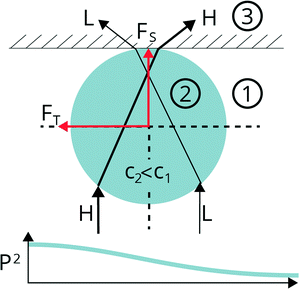
Acoustic beam-based manipulators analogous to optical tweezers70 have recently been explored.79 These use a focused acoustic beam with a high frequency and a low F-number (F-number = focal length/aperture size) to cause trapping effects at the focus. This has made possible the trapping and manipulation of single cells opening up a range of new applications which have only just begun to be explored. Crucially these beam devices are single-sided and so permit simple optical access for imaging. In a typical configuration the ultrasonic transducer is mounted below a horizontal plane on which both manipulation and imaging occur (i.e. the microscope mounted above). For example, Hwang et al.80 used a trapped functionalised micro-bead to probe the mechanical properties of cells thereby transforming the beam device into a stiffness measurement device. The use of high frequencies (up to 200 MHz has been demonstrated) and hence micrometre-scale focal spot sizes, has led to the use of the term micro-beam to describe these devices in which the wave-particle interactions are in a regime where the object is comparable to, or larger than, the wavelength (i.e. the Mie scattering regime).81 Ray models, based on a high frequency approximation, have been used to provide insight into the micro-beam manipulation process. As can be seen in Fig. 5, the micro-beam transducer emits a series of rays which are reflected and refracted by the particle. Part of the momentum of the refracted rays is transferred to the particle and this causes objects of lower velocity than the surrounding fluid (such as lipids in water) to be drawn to the high amplitude focus. Excellent experimental agreement with the ray model was achieved for relatively large (2a = 105 μm) lipid drops and wavelengths of 50 μm.82 This demonstrates that the forces exerted by micro-beam devices can be accurately calibrated, which is important in many applications, particularly those involving cells. Micro-beam manipulation, has now been demonstrated experimentally using frequencies from 30–200 MHz on a wide selection of particles including lipid drops and various cells.81 Once trapped, the particle can be manipulated by physical movement of the transducer or through use of an array.83
At present, despite several clear biological application demonstrations, the use of micro-beam devices has been low. The author speculates that this is due to two factors; the challenge and expense of manufacturing ultrasonic transducers to operate at these frequencies and the expense and experimental difficulties associated with generation and amplification of high voltages at these frequencies. However, it is reasonable to think that reliable and less expensive systems will become available in the coming years. One obvious driver is that performance approaching optical tweezing could be possible, but without the need for a high power laser and hence the associated laser safety requirements.
To date, the high frequency (Mie scattering regime) micro-beam devices all manipulate the particles against a surface or membrane. Recently Baresch et al.39 developed an array based beam manipulator which is capable of creating a stable 3D trap. Unlike the micro-beam devices, their array device operates in the Rayleigh regime (i.e. ka ≪ 1) and creates a type of focused acoustic vortex which is shaped as a first order Bessel-function at the focus. As can be seen in Fig. 1(e), this device can be thought of as a 3D version of the 2D array device developed by Courtney et al.,71 both devices operating in the low frequency regime and both generating first order Bessel-shaped fields. However, the Baresch et al. device operates into a free-field and so is non-resonant in all three-dimensions. Although they only demonstrated an axial manipulation capability this approach naturally leads naturally to full 3D manipulation. Given that 30 MHz is common in medical imaging arrays, e.g. in ophthalmological applications, it can be expected that a range of interesting micro-scale beam devices suitable for LOC operation will emerge in the coming years.84
C. Planar array manipulators
This section describes devices known as planar arrays or lateral manipulators. Fig. 1(f) and (g) show 1D and 2D planar arrays in which resonance is used in one direction and manipulation is achieved in a line or plane orthogonal to that direction (see Table 3 for a summary of the key publications). The concept was introduced by Kozuka et al.85 who created a one-dimensional manipulator based on this principle by placing a reflector parallel to a 2.19 MHz 1D array with 30 mm separation. They observed that if a small number of the array elements were excited then 80 μm alumina particles collected in the nodes which form a line between the activated elements and the reflector. By slowly switching the activated elements along the array, the particles could be made to move laterally, following the activated elements. Glynne-Jones et al.86 demonstrated a similar concept but now on a microfluidic scale. They used a 1D array to create a half-wavelength resonance in a 300 μm channel and demonstrated that 10 μm polystyrene spheres could be transported along the device. They were able to show that the agglomeration and transport effects originate directly from the velocity term in the Gor'kov potential function (eqn (1)) which acts to pull particles laterally into the centre of the node. However, they also observed that the relatively shallow gradients typically established in the lateral direction gave rise to relatively weak manipulation forces (lateral force was 2.3 pN and the force in the vertical resonant direction was 206 pN). The result being that only slow lateral manipulation was achieved. It is worth noting that a similar planar resonator approach was implemented to manipulate matter in air and bring two millimetre-sized objects together.87 Recently Qui et al.88 extended this idea to two-dimensions by creating resonances between the elements of a 7.5 MHz, screen-printed 36-element 2D array and a glass reflector. They were able to demonstrate 2D manipulation of an agglomerate of 10 μm polystyrene spheres. This device is attractive as it was manufactured with readily available micro-fabrication techniques which would lend themselves to scale-up. The recent development of an optically transparent transduction system also offers the potential to overcome the poor quality bight field imaging that is one drawback of these devices (the planar arrangement means that the transducer surfaces are always imaged with the particles).89 In an interesting hybrid device, Guo et al.68 used a 4-transducer SAW device to position particles in a horizontal plane and a planar resonance (in conjunction with streaming) to move them against gravity and hold them in the vertical direction. This combined forcing approach creates a new route to limited 3D manipulation which could be useful for biomedical applications such as scaffold assembly in tissue engineering.| Author | Number of transducers (geometry) | Control method | Particles | Size (dia.), μm | Frequency, MHz | Wavelength, μm |
|---|---|---|---|---|---|---|
| Kozuka et al., 1996 (ref. 85) | 15 (1D array) | Aperture movement | Alumina | 80 | 2.19 | 685 |
| Glynne-Jones et al., 2012 (ref. 86) | 12 (1D array) | Aperture movement | PS | 10.3 | 2.52 | 595 |
| Qui et al., 2015 (ref. 88) | 36 (2D grid array) | Aperture movement | PS | 10 | 7.52 | 199 |
| Guo et al., 2016 (ref. 68) | 4 (Square) | Phase & amplitude | PS | 4.2–10.1 | 13 | 300 |
| 3T3 and HeLa S3 cells | — |
III. Discussion and future prospects
Dynamic-field devices offer the prospect of high levels of control over the position of multiple micro-scale objects and are well suited to integration into LOC environments. Table 4 summarises the current capabilities of the manipulation devices covered by this review and arranged according to the classification scheme shown in Fig. 1. The simpler dynamic-field devices, such as the 4-transducer devices, have now been demonstrated on applications that require operations such as translation of the acoustic radiation force field.15,25 In parallel with this application development of the simpler devices, more complex devices have emerged that have new functionalities.73 These devices are only just starting to find application, and the section below discusses their potential.81| Class | Figure | Sub-class | Field shape | Manipulation methods | Manipulation capability | Independent motion | Wavelength range, μm | Cells tested |
|---|---|---|---|---|---|---|---|---|
| In-plane | 1(a) | 2-Element | Lines | Phase | 1D translation | No | 46–1500 | Yes |
| Frequency | 1D stretch | |||||||
| 1(b) | 4-Element | Grid | Phase | 2D translation | No | Yes | ||
| Frequency | 2D stretch | |||||||
| Amplitude | 2D translation | |||||||
| 1(c) | Array | Wide range | Phase | 2D arbitrary | Yes | 375–640 | Yes | |
| Beam | 1(d) | Mie Regime | Focused | Phase | 2D arbitrary | Yes | 8–57 | Yes |
| 1(e) | Rayleigh regime | Focused first-order Bessel-beam | Phase | 3D arbitrary | Yes | 304–1304 | Yes | |
| Planar array | 1(f) and (g) | 1D or 2D | Local resonance | Amplitude (on/off) | 2D arbitrary (limited by element size) | Yes | 199–703 | Yes |
The simple in-plane devices (see Fig. 1(a) and (b)), either using SAW or bulk waves, have seen the greatest research interest and have now been extensively demonstrated in the widest range of LOC application scenarios. Some of this technology, for example the classic 2- and 4-element SAW and bulk wave devices, is now moving to maturity. These devices have been demonstrated in assembly operations that require a single pattern with a single particle type, i.e. no dynamic manipulation. This now includes numerous examples in tissue engineering6,90 and materials assembly.20,18 Given that these devices are now in wide-spread use by the research community, the focus of the current work is on their application and their integration with other electronics, microfluidics or other LOC systems. Indeed, their inherent integratability is emerging as a strong point of ultrasonic manipulation technology. However, the addition of a manipulation or reconfiguration capability leads to the possibility of performing multiple and more sophisticated operations within a single device. Application examples of these dynamic devices are growing and include the creation of co-cultures in tissue engineering,15 the careful control of cell–cell distances as a biological research tool,67 or dynamically shaping composite materials.25
This paper has described the wide range of manipulation functionalities now possible with dynamic-field devices (i.e.Table 4). Exactly how this increased functionality will be best deployed to solve application challenges is uncertain. One example is the user driven manipulation seen in optical tweezers in which the operator views and controls the manipulation on a microscope. However, another alternative is completely automated operation in which particles are manipulated in a closed LOC environment.91 A key enabler here is that the electronics required to drive and control these acoustic manipulation systems have the potential to be both miniaturised and integrated. However, the challenge of achieving this new functionality within a LOC environment remains one of the open problems in micro-particle manipulation. Courtney et al.73 made some progress in this direction when they used an array to trap up to three 90 μm polystyrene spheres and moved them independently using a superposition of first-order Bessel shaped fields. In this device, the particle separation had to be maintained at above a wavelength, or interference between the traps caused the trapping to be lost. The use of an array with many elements, all of which need to be controlled, makes the devices and the electronics more complex. This means that these devices will only see widespread usage if the expense of these systems can be justified. Given this expense, there are now challenges in the design of robust dynamic devices with the minimum level of complexity necessary to solve the emerging application challenges. In this way devices with limited, application specific reconfigurability, will emerge.
In the future, more sophisticated control strategies may emerge to overcome current limitations in the range of acoustic fields that can be produced and hence lead to even more versatile manipulation capabilities. One possible approach is to cast the manipulation challenge as an optimisation problem.92,93 Here a design requirement, such as point-like or other shaped traps, is encapsulated in an objective function. The parameter space, e.g. the amplitudes and phases of the excitation signals, is then exhaustively searched for optimal solutions. This approach can potentially open up new manipulation capabilities, however, it is preferable to use well-formulated analytical expressions for device control, assuming they are tractable.
Device performance is governed by operating frequency as this sets the texture of the acoustic field, in a similar way to how it determines resolution in imaging. This analogy is a close one and it seems reasonable to assume that future acoustic manipulation devices will be diffraction limited. This means that the acoustic field will contain no features smaller than the point spread function of the device, which, taking the example of the circular in-plane devices would be the size of the central maxima of the zeroth order Bessel function (i.e. 0.76λ). For high-frequency micro-beam devices this performance limit is extremely small (i.e. λ = 5 μm in water at 200 MHz), but manufacturing difficulties mean that most of the micro-beam devices manufactured to date have been monolithic, manipulation only being possible by mechanically moving the transducer. It is easy to imagine that in the future multiple micro-beams or array-based micro-beams could be used to undertake very sophisticated manipulations.
Despite the spatial resolution limit, significant progress has been made in the manipulation of clusters of particles. Much of this is due the presence of secondary radiation forces which cause multiple particles to be held tightly within a trap due to attractive acoustic inter-particles forces.2 For example, Lee et al.94 trapped and manipulated a hexagonal arrangement of lipid microspheres (80 μm) at the focus of a 24 MHz ring-shaped micro-beam manipulator. In this case the hexagon aligned with the first side-lobe of the focused field. On a larger scale, Fig. 6 shows results from Owens et al.95 in which many spheres and hexagons are assembled in close-packed arrangements at a nodal plane, due to a combination of self-assembly (i.e. as close-packing is energetically optimal) and secondary radiation forces, which cause the particles to be attracted to each other.
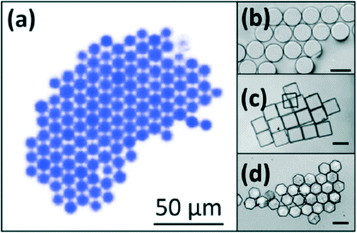 | ||
| Fig. 6 Adapted from Fig. 8 in Owens et al.95 with permission from the Royal Society of Chemistry. Micrographs of acoustically assembled colloidal crystallites. (a) Fluorescent micrograph of 10 μm spheres assembled into a hexagonally close packed arrangement. (b) Optical micrograph of 50 × 10 μm circular tiles assembled into a hexagonally close packed arrangement. (c) Optical micrograph of 50 × 10 μm square tiles assembled into a square close packed arrangement. (d) Optical micrograph of 50 × 10 μm hexagonal tiles assembled into a hexagonally close packed arrangement. Scale bars are 50 μm. | ||
The above discussion suggests the potential for using ultrasonic manipulation in combination with other assembly modalities, e.g. self-assembly. To date these hybrid approaches have garnered relatively little attention, but the relevant literature is reviewed by Glynne-Jones and Hill.96 The simultaneous operation of optical and acoustic manipulation devices has attracted the most attention, perhaps due to the complementary size of the objects these techniques can most easily manipulate; optical tweezers performing best in the 0.1–10 μm range and acoustic devices being most commonly deployed from 1 μm upwards.70,97 More recently, Chen et al. used a combination of acoustic radiation forces and forces due to the electrical field present in a SAW device to produce a new patterning effect in silver nano-rods which included starbursts patterns at the nodes.19 This is particularly interesting as it suggests a route by which ultrasonic manipulation could be extended to nano-scale applications. This is an important area as recent years have seen much interest in the use of nano-scale additives for a wide range of applications including drug delivery and improved mechanical performance.98
Crane et al. describes the huge diversity of micro- and nano-scale manipulation challenges facing modern manufacturing, both in the biomedical and engineering sectors.99 It is apparent that ultrasonic manipulation is yet to take its place alongside such technologies such as physically contacting micro-grippers and dielectriphoresis (DEP). To date the main industrial applications for ultrasound in assembly have been limited to alignment with respect to sensors, aggregation, and to a lesser extent patterning. However, the reconfigurable ultrasonic manipulation tools that have emerged in recent years have many advantages over current manipulation technologies. Perhaps the most important advantage of acoustic methods is their ability to manipulate a very wide range of materials including handling cells without causing damage. This ability to handle cells without damage stems from the relatively low energies associated with ultrasonic particle manipulation, e.g. acoustic pressures in the range 10–100 kPa are reported to be sufficient which, assuming plane travelling waves equates to a low intensity of 0.07–7 nW μm−2. Given the emerging capabilities of ultrasonic manipulation devices described here and the rapidly expanding requirements for micro- and nano-assembly, it seems highly likely that the use of ultrasonic devices will increase dramatically over the coming years.
Acknowledgements
The author was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) EP/G012067/1. No new data were generated during this research. The author would like to thank Matt Sutton and Tom Llewellyn-Jones, University of Bristol for their assistance with the figure design.References
- W. T. Coakley, J. J. Hawkes, M. A. Sobanski, C. M. Cousins and J. Spengler, Analytical scale ultrasonic standing wave manipulation of cells and microparticles, Ultrasonics, 2000, 38(1), 638–641, DOI:10.1016/S0041-624X(99)00151-1.
- T. Laurell, F. Petersson and A. Nilsson, Chip integrated strategies for acoustic separation and manipulation of cells and particles, Chem. Soc. Rev., 2007, 36(3), 492–506, 10.1039/b601326k.
- M. Wiklund, Acoustofluidics 12: Biocompatibility and cell viability in microfluidic acoustic resonators, Lab Chip, 2012, 12(11), 2018, 10.1039/c2lc40201g.
- P. Glynne-Jones, R. J. Boltryk and M. Hill, Acoustofluidics 9: Modelling and applications of planar resonant devices for acoustic particle manipulation, Lab Chip, 2012, 12(8), 1417–1426, 10.1039/c2lc21257a.
- L. P. Gor'kov, On the forces acting on a small particle in an acoustical field in an ideal fluid, Sov. Phys. Dokl., 1962, 6(9), 773–775 Search PubMed.
- L. A. Kuznetsova, D. Bazou, G. Edwards and W. T. Coakley, Multiple three dimensional mammalian cell aggregates formed away from solid substrata in ultrasound standing waves, Biotechnol. Prog., 2009, 25(3), 834–840, DOI:10.1021/bp.164.
- D. Bazou, A. Castro and M. Hoyos, Controlled cell aggregation in a pulsed acoustic field, Ultrasonics, 2012, 52(7), 842–850, DOI:10.1016/j.ultras.2012.01.005.
- S. Li, P. Glynne-Jones, O. G. Andriotis, K. Y. Ching, U. S. Jonnalagadda, R. O. C. Oreffo and R. S. Tare, Application of an acoustofluidic perfusion bioreactor for cartilage tissue engineering, Lab Chip, 2014, 14(23), 4475–4485, 10.1039/c4lc00956h.
- F. Petersson, A. Nilsson, C. Holm, H. Jonsson and T. Laurell, Continuous separation of lipid particles from erythrocytes by means of laminar flow and acoustic standing wave forces, Lab Chip, 2005, 5(1), 20–22, 10.1039/b405748c.
- G. Goddard and G. Kaduchak, Ultrasonic particle concentration in a line-driven cylindrical tube, J. Acoust. Soc. Am., 2005, 117(6), 3440–3447, DOI:10.1121/1.1904405.
- C. Koch, M. Brandstetter, B. Lendl and S. Radel, Ultrasonic Manipulation of Yeast Cells in Suspension for Absorption Spectroscopy with an Immersible Mid-Infrared Fiberoptic Probe, Ultrasound Med. Biol., 2013, 39(6), 1094–1101, DOI:10.1016/j.ultrasmedbio.2013.01.003.
- P. Augustsson, J. T. Karlsen, H.-W. Su, H. Bruus and J. Voldman, Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping, Nat. Commun., 2016, 7, 11556, DOI:10.1038/ncomms11556.
- J. Shi, D. Ahmed, X. Mao, S.-C. S. Lin, A. Lawit and T. J. Huang, Acoustic tweezers: patterning cells and microparticles using standing surface acoustic waves (SSAW), Lab Chip, 2009, 9(20), 2890–2895, 10.1039/b910595f.
- H. Böhm, L. G. Briarty, K. C. Lowe, J. B. Power, E. Benes and M. R. Davey, Quantification of a novel h-shaped ultrasonic resonator for separation of biomaterials under terrestrial gravity and microgravity conditions, Biotechnol. Bioeng., 2003, 82, 74–85, DOI:10.1002/bit.10546.
- F. Gesellchen, A. L. Bernassau, T. Déjardin, D. R. S. Cumming and M. O. Riehle, Cell patterning with a heptagon acoustic tweezer - application in neurite guidance, Lab Chip, 2014, 19, 2266–2275, 10.1039/c4lc00436a.
- M. Saito and Y. Imanishi, Host-guest composites containing ultrasonically arranged particles, J. Mater. Sci., 2000, 35(10), 2373–2377, DOI:10.1023/A:1004745927648.
- F. G. Mitri, F. H. Garzon and D. N. Sinha, Characterization of acoustically engineered polymer nanocomposite metamaterials using x-ray microcomputed tomography, Rev. Sci. Instrum., 2011, 82(3), 034903, DOI:10.1063/1.3553207.
- M.-S. Scholz, B. W. Drinkwater, T. M. Llewellyn-Jones and R. S. Trask, Counterpropagating wave acoustic particle manipulation device for the effective manufacture of composite materials, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2015, 62(10), 1845–1855, DOI:10.1109/TUFFC.2015.007116.
- Y. Chen, X. Ding, S.-C. Steven Lin, S. Yang, P. Huang, N. Nama and T. J. Huang, Tunable nanowire patterning using standing surface acoustic waves, ACS Nano, 2013, 7(4), 3306–3314, DOI:10.1021/nn4000034.
- R. R. Collino, T. R. Ray, R. C. Fleming, C. H. Sasaki, H. Haj-Hariri and M. R. Begley, Acoustic field controlled patterning and assembly of anisotropic particles, Theor. Appl. Mech. Lett., 2015, 5, 37–46, DOI:10.1016/j.eml.2015.09.00.
- M. Caleap and B. W. Drinkwater, Acoustically trapped colloidal crystals that are reconfigurable in real time, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(17), 6226–6230, DOI:10.1073/pnas.1323048111.
- G. Destgeer, B. H. Ha, J. H. Jung and H. J. Sung, Submicron separation of microspheres via travelling surface acoustic waves, Lab Chip, 2014, 14(24), 4665–4672, 10.1039/C4LC00868E.
- D. J. Collins, Z. Ma and Y. Ai, Highly Localized Acoustic Streaming and Size-Selective Submicrometer Particle Concentration Using High Frequency Microscale Focused Acoustic Fields, Anal. Chem., 2016, 88(10), 5513–5522, DOI:10.1021/acs.analchem.6b01069.
- V. Marx, Biophysics: using sound to move cells, Nat. Methods, 2014, 12(1), 41–44, DOI:10.1038/nmeth.3218.
- T. M. Llewellyn-Jones, B. W. Drinkwater and R. S. Trask, 3D printed components with ultrasonically arranged microscale structure, Smart Mater. Struct., 2016, 25(2), 02LT01, DOI:10.1088/09641726/25/2/02LT01.
- E. Trinh, J. Robey, N. Jacobi and T. G. Wang, Dual-temperature acoustic levitation and sample transport apparatus, J. Acoust. Soc. Am., 1986, 79(3), 604612, DOI:10.1121/1.393450.
- P. Glynne-Jones, R. J. Boltryk, N. R. Harris, A. W. J. Cranny and M. Hill, Mode-switching: a new technique for electronically varying the agglomeration position in an acoustic particle manipulator, Ultrasonics, 2010, 50(1), 68–75, DOI:10.1016/j.ultras.2009.07.010.
- H. Bruus, Acoustofluidics 7: The acoustic radiation force on small particles, Lab Chip, 2012, 12(6), 1014–1021, 10.1039/c2lc21068a.
- O. Manneberg, B. Vanherberghen, B. Onfelt and M. Wiklund, Flow-free transport of cells in microchannels by frequency-modulated ultrasound, Lab Chip, 2009, 9(6), 833–837, 10.1039/b816675g.
- A. Grinenko, C.-K. Ong, C. R. P. Courtney, P. D. Wilcox and B. W. Drinkwater, Efficient counter-propagating wave acoustic micro-particle manipulation, Appl. Phys. Lett., 2012, 101(23), 233501, DOI:10.1063/1.4769092.
- P. Augustsson, R. Barnkob, S. T. Wereley, H. Bruus and T. Laurell, Automated and temperature-controlled micro-PIV measurements enabling long-term-stable microchannel acoustophoresis characterization, Lab Chip, 2011, 11(24), 4152–4164, 10.1039/c1lc20637k.
- L. Rayleigh, On the Circulation of Air Observed in Kundt's Tubes, and on Some Allied Acoustical Problems, Philos. Trans. R. Soc. London, 1884, 175, 1–21, DOI:10.1098/rstl.1884.0002.
- L. Rayleigh, On the momentum and pressure of gaseous vibrations, and on the connexion with the virial theorem, Philos. Mag., 1905, 10(6), 364–374, DOI:10.1080/14786440509463381.
- R. T. Beyer, Radiation pressure—the history of a mislabeled tensor, J. Acoust. Soc. Am., 1978, 63(4), 1025–1030, DOI:10.1121/1.381833.
- A. Kundt, III. Acoustic experiments, Philos. Mag., 1868, 35(234), 41–48, DOI:10.1080/14786446808639937.
- L. V. King, On the Acoustic Radiation Pressure on Spheres, Proc. R. Soc. A, 1934, 147(861), 212–240, DOI:10.1098/rspa.1934.0215.
- K. Yosioka and Y. Kawasima, Acoustic radiation pressure on a compressible sphere, Acustica, 1955, 5(3), 167–173 Search PubMed.
- G. T. Silva, Acoustic radiation force and torque on an absorbing compressible particle in an inviscid fluid, J. Acoust. Soc. Am., 2014, 136(5), 2405–2413, DOI:10.1121/1.4895691.
- D. Baresch, J.-L. Thomas and R. Marchiano, Observation of a single-beam gradient force acoustical trap for elastic particles: acoustical tweezers, Phys. Rev. Lett., 2016, 116(2), 024301, DOI:10.1103/PhysRevLett.116.024301.
- D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves, Nat. Commun., 2015, 6, 8686, DOI:10.1038/ncomms9686.
- T. Hasegawa and K. Yosioka, Acoustic-Radiation Force on a Solid Elastic Sphere, J. Acoust. Soc. Am., 1969, 46(5), 1139–1143, DOI:10.1121/1.1911832.
- W. Wei, D. B. Thiessen and P. L. Marston, Acoustic radiation force on a compressible cylinder in a standing wave, J. Acoust. Soc. Am., 2004, 116(1), 201–208, DOI:10.1121/1.1753291.
- P. L. Marston, Shape oscillation and static deformation of drops and bubbles driven by modulated radiation stresses—Theory, J. Acoust. Soc. Am., 1980, 67(1), 15–26, DOI:10.1121/1.383798.
- T. Hasegawa, Y. Hino, A. Annou, H. Noda, M. Kato and N. Inoue, Acoustic radiation pressure acting on spherical and cylindrical shells, J. Acoust. Soc. Am., 1993, 93(1), 154–161, DOI:10.1121/1.405653.
- F. G. Mitri, Acoustic radiation force acting on elastic and viscoelastic spherical shells placed in a plane standing wave field, Ultrasonics, 2005, 43(8), 681–691, DOI:10.1016/j.ultras.2005.03.002.
- P. Glynne-Jones, P. P. Mishra, R. J. Boltryk and M. Hill, Efficient finite element modelling of radiation forces on elastic particles of arbitrary size and geometry, J. Acoust. Soc. Am., 2013, 133(4), 1885–1893, DOI:10.1121/1.4794393.
- A. Grinenko, P. D. Wilcox, C. R. P. Courtney and B. W. Drinkwater, Acoustic radiation force analysis using finite difference time domain method, J. Acoust. Soc. Am., 2012, 131(5), 3664–3670, DOI:10.1121/1.3699204.
- M. Settnes and H. Bruus, Forces acting on a small particle in an acoustical field in a viscous fluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(1), 016327, DOI:10.1103/PhysRevE.85.016327.
- J. T. Karlsen and H. Bruus, Forces acting on a small particle in an acoustical field in a thermoviscous fluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(4), 043010, DOI:10.1103/PhysRevE.92.043010.
- A. A. Doinikov, Acoustic radiation force on a spherical particle in a viscous heat-conducting fluid. I. General formula, J. Acoust. Soc. Am., 1997, 101(2), 713–721, DOI:10.1121/1.418035.
- P. B. Muller, M. Rossi, Á. G. Marín, R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Ultrasound-induced acoustophoretic motion of microparticles in three dimensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88(2), 023006, DOI:10.1103/PhysRevE.88.023006.
- R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Acoustic radiation- and streaming-induced microparticle velocities determined by microparticle image velocimetry in an ultrasound symmetry plane, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(5), 056307, DOI:10.1103/PhysRevE.86.056307.
- M. Wiklund, R. Green and M. Ohlin, Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices, Lab Chip, 2012, 12(14), 2438, 10.1039/c2lc40203c.
- M. Saito, N. Kitamura and M. Terauchi, Ultrasonic manipulation of locomotive microorganisms and evaluation of their activity, J. Appl. Phys., 2002, 92(12), 7581, DOI:10.1063/1.1522813.
- A. Haake and J. Dual, Contactless micromanipulation of small particles by an ultrasound field excited by a vibrating body, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 117(5), 2752–2760, DOI:10.1121/1.1874592.
- A. Haake, A. Neild, G. Radziwill and J. Dual, Positioning, displacement, and localization of cells using ultrasonic forces, Biotechnol. Bioeng., 2005, 92(1), 8–14, DOI:10.1002/bit.20540.
- X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang and T. J. Huang, On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(28), 11105–11109, DOI:10.1073/pnas.1209288109.
- C. D. Wood, J. E. Cunningham, R. D. O'Rorke, C. Wälti, E. H. Linfield, A. G. Davies and S. D. Evans, Formation and manipulation of two-dimensional arrays of micron-scale particles in microfluidic systems by surface acoustic waves, Appl. Phys. Lett., 2009, 94(5), 054101, DOI:10.1063/1.3076127.
- M. Takeuchi and K. Yamanouchi, Ultrasonic micromanipulation of small particles in liquid, Jpn. J. Appl. Phys., Part 1, 1994, 33(5), 3045–3047, DOI:10.1143/JJAP.33.3045.
- A. Wixforth, C. Strobl, C. Gauer, A. Toegl, J. Scriba and Z. V. Guttenberg, Acoustic manipulation of small droplets, Anal. Bioanal. Chem., 2004, 379(7–8), 982–991, DOI:10.1007/s00216-004-2693-z.
- L. Y. Yeo and J. R. Friend, Ultrafast microfluidics using surface acoustic waves, Biomicrofluidics, 2009, 3(1), 012002, DOI:10.1063/1.3056040.
- C. R. P. Courtney, C.-K. Ong, B. W. Drinkwater, A. L. Bernassau, P. D. Wilcox and D. R. S. Cumming, Manipulation of particles in two dimensions using phase controllable ultrasonic standing waves, Proc. R. Soc. A, 2011, 468(2138), 337–360, DOI:10.1098/rspa.2011.0269.
- T. Kozuka, T. Tuziuti, H. Mitome, T. Fukuda and F. Arai, Control of position of a particle using a standing wave field generated by crossing sound beams, in 1998 IEEE Ultrasonics Symposium. Proceedings (Cat. No. 98CH36102), IEEE, 1998, vol. 1, pp. 657–660, DOI:10.1109/ULTSYM.1998.762234.
- L. Meng, F. Cai, Z. Zhang, L. Niu, Q. Jin, F. Yan and H. Zheng, Transportation of single cell and microbubbles by phase-shift introduced to standing leaky surface acoustic waves, Biomicrofluidics, 2011, 5(4), 044104, DOI:10.1063/1.3652872.
- N. D. Orloff, J. R. Dennis, M. Cecchini, E. Schonbrun, E. Rocas, Y. Wang and J. C. Booth, Manipulating particle trajectories with phase-control in surface acoustic wave microfluidics, Biomicrofluidics, 2011, 5(4), 044107, DOI:10.1063/1.3661129.
- S. B. Q. Tran, P. Marmottant and P. Thibault, Fast acoustic tweezers for the two-dimensional manipulation of individual particles in microfluidic channels, Appl. Phys. Lett., 2012, 101(11), 114103, DOI:10.1063/1.4751348.
- F. Guo, P. Li, J. B. French, Z. Mao, H. Zhao, S. Li and T. J. Huang, Controlling cell–cell interactions using surface acoustic waves, Proc. Natl. Acad. Sci. U. S. A., 2014, 112(1), 43–48, DOI:10.1073/pnas.1422068112.
- F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li and T. J. Huang, Three-dimensional manipulation of single cells using surface acoustic waves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(6), 1522–1527, DOI:10.1073/pnas.1524813113.
- A. L. Bernassau, F. Gesellchen, P. G. A. MacPherson, M. Riehle and D. R. S. Cumming, Direct patterning of mammalian cells in an ultrasonic heptagon stencil, Biomed. Microdevices, 2012, 14(3), 559–564, DOI:10.1007/s10544-012-9633-z.
- K. C. Neuman and S. M. Block, Optical trapping, Rev. Sci. Instrum., 2004, 75(9), 2787–2809, DOI:10.1063/1.1785844.
- C. R. P. Courtney, B. W. Drinkwater, C. Demore, S. Cochran, A. Grinenko and P. D. Wilcox, Dexterous manipulation of microparticles using Bessel-function acoustic pressure fields, Appl. Phys. Lett., 2013, 102(12), 123508, DOI:10.1063/1.4798584.
- A. Grinenko, P. D. Wilcox, C. R. P. Courtney and B. W. Drinkwater, Proof of principle study of ultrasonic particle manipulation by a circular array device, Proc. R. Soc. A, 2012, 468(2147), 3571–3586, DOI:10.1098/rspa.2012.0232.
- C. R. P. Courtney, C. Demore, H. Wu, A. Grinenko, P. D. Wilcox, S. Cochran and B. W. Drinkwater, Independent trapping and manipulation of microparticles using dexterous acoustic tweezers, Appl. Phys. Lett., 2014, 104(15), 154103, DOI:10.1063/1.4870489.
- T. Schwarz, G. Petit-Pierre and J. Dual, Rotation of non-spherical micro-particles by amplitude modulation of superimposed orthogonal ultrasonic modes, Proc. R. Soc. A, 2013, 133(3), 1260–1268, DOI:10.1121/1.4776209.
- Z. Y. Hong, J. Zhang and B. W. Drinkwater, Observation of Orbital Angular Momentum Transfer from Bessel-Shaped Acoustic Vortices to Diphasic Liquid-Microparticle Mixtures, Phys. Rev. Lett., 2015, 214301, DOI:10.1103/PhysRevLett.114.214301.
- J. Wu and G. Du, Acoustic radiation force on a small compressible sphere in a focused beam, Proc. R. Soc. A, 1990, 87(3), 997–1003, DOI:10.1121/1.399435.
- J. Wu, Acoustical tweezers, Proc. R. Soc. A, 1991, 89(5), 2140–2143, DOI:10.1121/1.400907.
- Y. Yamakoshi and Y. Noguchi, Micro particle trapping by opposite phases ultrasonic travelling waves, Ultrasonics, 1998, 36(8), 873–878, DOI:10.1016/S0041-624X(98)00013-4.
- J. Lee, S.-Y. Teh, A. Lee, H. H. Kim, C. Lee and K. K. Shung, Single beam acoustic trapping, Appl. Phys. Lett., 2009, 95(7), 73701, DOI:10.1063/1.3206910.
- J. Hwang, C. Lee, K. Lam, H. Kim, J. Lee and K. K. Shung, Cell membrane deformation induced by a fibronectin-coated polystyrene microbead in a 200-MHz acoustic trap, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2014, 61(3), 399–406, DOI:10.1109/TUFFC.2014.2925.
- J. Lee, C. Lee, H. H. Kim, A. Jakob, R. Lemor, S.-Y. Teh and K. K. Shung, Targeted cell immobilization by ultrasound microbeam, Biotechnol. Bioeng., 2011, 108(7), 1643–1650, DOI:10.1002/bit.23073.
- J. Lee, C. Lee and K. K. Shung, Calibration of sound forces in acoustic traps, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2010, 57(10), 2305–2310, DOI:10.1109/TUFFC.2010.1691.
- F. Zheng, Y. Li, H.-S. Hsu, C. Liu, C. Tat Chiu, C. Lee and K. K. Shung, Acoustic trapping with a high frequency linear phased array, Appl. Phys. Lett., 2012, 101(21), 214104, DOI:10.1063/1.4766912.
- G. R. Lockwood, D. H. Turnbull, D. A. Christopher and F. S. Foster, Beyond 30 MHz - applications of high-frequency ultrasound imaging, IEEE Eng. Med. Biol. Mag., 1996, 15, 60–71, DOI:10.1109/51.544513.
- T. Kozuka, T. Tuziuti, H. Mitome and T. Fukuda, Acoustic micromanipulation using a multi-electrode transducer, in MHS’96 Proceedings of the Seventh International Symposium on Micro Machine and Human Science, IEEE, Nagoya, Japan, 1996, pp. 163–170, DOI:10.1109/MHS.1996.563418.
- P. Glynne-Jones, C. Demore, C. Ye, Y. Qiu, S. Cochran and M. Hill, Array-controlled ultrasonic manipulation of particles in planar acoustic resonator, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2012, 59(6), 1258–1266, DOI:10.1109/TUFFC.2012.2316.
- D. Foresti, M. Nabavi, M. Klingauf, A. Ferrari and D. Poulikakos, Acoustophoretic contactless transport and handling of matter in air, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(31), 12549–12554, DOI:10.1073/pnas.1301860110.
- Y. Qiu, H. Wang, S. Gebhardt, A. Bolhovitins, C. E. M. Demore, A. Schonecker and S. Cochran, Screen-printed ultrasonic 2-D matrix array transducers for microparticle manipulation, Ultrasonics, 2015, 62, 136–146, DOI:10.1016/j.ultras.2015.05.010.
- G. Brodie, Y. Qiu, S. Cochran, G. Spalding and M. MacDonald, Optically transparent piezoelectric transducer for ultrasonic particle manipulation, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2014, 61(3), 389–391, DOI:10.1109/TUFFC.2014.2923.
- K. A. Garvin, D. C. Hocking and D. Dalecki, Controlling the spatial organization of cells and extracellular matrix proteins in engineered tissues using ultrasound standing wave fields, Ultrasound Med. Biol., 2010, 36(11), 1919–1932, DOI:10.1016/j.ultrasmedbio.2010.08.007.
- J. A. Grieve, A. Ulcinas, S. Subramanian, G. M. Gibson, M. J. Padgett, D. M. Carberry and M. J. Miles, Hands-on with optical tweezers: a multitouch interface for holographic optical trapping, Opt. Express, 2009, 17(5), 3595, DOI:10.1364/OE.17.003595.
- A. Marzo, S. A. Seah, B. W. Drinkwater, D. R. Sahoo, B. Long and S. Subramanian, Holographic acoustic elements for manipulation of levitated objects, Nat. Commun., 2015, 6, 8661, DOI:10.1038/ncomms9661.
- J. Greenhall, F. Guevara Vasquez and B. Raeymaekers, Ultrasound directed self-assembly of user-specified patterns of nanoparticles dispersed in a fluid medium, Appl. Phys. Lett., 2016, 108(10), 103103, DOI:10.1063/1.4943634.
- C. Lee, J. Seob Jeong, J. Youn Hwang, J. Lee and K. Kirk Shung, Non-contact multi-particle annular patterning and manipulation with ultrasound microbeam, Appl. Phys. Lett., 2014, 104(24), 244107, DOI:10.1063/1.4884938.
- C. E. Owens, C. W. Shields, D. F. Cruz, P. Charbonneau and G. P. López, Highly parallel acoustic assembly of microparticles into well-ordered colloidal crystallites, Soft Matter, 2016, 12(3), 717–728, 10.1039/C5SM02348C.
- P. Glynne-Jones and M. Hill, Acoustofluidics 23: acoustic manipulation combined with other force fields, Lab Chip, 2013, 13(6), 1003–1010, 10.1039/c3lc41369a.
- G. Thalhammer, R. Steiger, M. Meinschad, M. Hill, S. Bernet and M. Ritsch-Marte, Combined acoustic and optical trapping, Biomed. Opt. Express, 2011, 2(10), 2859–2870, DOI:10.1364/BOE.2.002859.
- G. Bao, S. Mitragotri and S. Tong, Multifunctional Nanoparticles for Drug Delivery and Molecular Imaging, Annu. Rev. Biomed. Eng., 2013, 15(1), 253–282, DOI:10.1146/annurev-bioeng-071812-152409.
- N. B. Crane, O. Onen, J. Carballo, Q. Ni and R. Guldiken, Fluidic assembly at the microscale: progress and prospects, Microfluid. Nanofluid., 2013, 14(3–4), 383–419, DOI:10.1007/s10404-012-1060-1.
| This journal is © The Royal Society of Chemistry 2016 |