Inertial focusing in non-rectangular cross-section microchannels and manipulation of accessible focusing positions

Abstract

Inertial focusing in microfluidic channels has been extensively studied experimentally and theoretically, which has led to various applications including microfluidic separation and enrichment of cells. Inertial lift forces are strongly dependent on the flow velocity profile and the channel cross-sectional shape. However, the channel cross-sections studied have been limited to circles and rectangles. We studied inertial focusing in non-rectangular cross-section channels to manipulate the flow profile and thus the inertial focusing of microparticles. The location and number of focusing positions are analyzed with varying cross-sectional shapes and Reynolds number. We found that the broken symmetry of non-equilateral triangular channels leads to the shifting of focusing positions with varying Reynolds number. Non-rectangular channels have unique mapping of the focusing positions and the corresponding basins of attraction. By connecting channels with different cross-sectional shapes, we were able to manipulate the accessible focusing positions and achieve focusing of microparticles to a single stream with ∼99% purity.

---

Introduction

Inertial microfluidics provides methods for passive and high-throughput micro-particle manipulation including particle focusing, separation and ordering.^1–4 It is also used to manipulate flow streams, for example, to mix fluids^5,6 or to modify the flows to a specific shape.^7–9 Among the inertial effects leading to these applications, inertial focusing has been studied most extensively and the mechanism leading to distinct focusing positions in micro-channels is relatively well understood.^1,10,11 These focusing positions are determined by the balance of the two inertial lift forces: shear-gradient lift force and wall-effect lift force.^10–12 Breaking of symmetry in channel cross sections gives clear changes in focusing positions. While the focusing position is an annulus in a circular capillary,^11,13 there are four focusing positions in a square channel (Fig. 1a and b).^1,10,11 In rectangular channels with an aspect ratio approximately larger than 4/3, the number of focusing positions reduces again from four to two (Fig. 1c). In rectangular channels, particles first migrate toward the long channel faces by the shear-gradient lift force.^10,14 Then, the dominant wall-effect lift force causes the particles to migrate along the long channel faces to the focusing positions.^10,14 Other than shear-gradient and wall-effect lift forces, the rotation-induced lift force can affect the migration of particles.¹⁵ For our system, the particles can rotate to match the local vorticity of the flow such that the effect, which depends on a mismatch with the local shear rate, is expected not to be dominant. The directions of the combined inertial lift forces divide the channel cross-section into several basins of attraction that lead to each attractor, namely, the focusing positions. As a result, the particles located in each basin of attraction at the inlet will end up at the corresponding focusing positions. The basins of attraction for square and rectangular channels are shown in Fig. 1b and c.

Fig. 1 Inertial focusing positions and schematic of force fields in channels with various cross-sectional shapes: (a) circle, (b) square, and (c) rectangle. F_w (red arrow) is the wall-effect lift force and F_s (blue arrow) is the shear-gradient lift force. The green arrow indicates the expected trajectories. The white dashed lines are boundaries of basins of attraction for focusing positions. (d) Cross-sectional images of the non-rectangular channels studied (scale bar, 20 μm).

The current understanding of inertial microfluidics is largely based on inertial effects in circular microcapillaries and micro-channels with rectangular cross-sections mainly because they are the most widely available type of microfluidic channels.^1,10,11,14 Nevertheless, there were several cases that non-rectangular microfluidic channels were used for specific applications. For example, the flow channels of the multilayer on-chip valves¹⁶ utilized rounded flow channels and haptotactic gradients of protein¹⁷ were generated with triangular channels. However, there has been no significant investigation of taking advantage of the channel cross-sectional shape in the microfluidics community. Inertial focusing, as shown from the difference between square channels and rectangular channels, is strongly dependent on the channel cross-sectional shape, yet studies have been conducted only with circular and rectangular channels. We studied inertial focusing in micro-channels with a non-rectangular cross-section to better understand the mechanism of inertial focusing and provide more degrees of freedom in the manipulation of particles in microfluidic channels.

Inertial microfluidic systems have design parameters such as channel length, width, height and curvature, by which one can manipulate focusing positions and secondary flows to control particles or flows. In addition, one can vary the channel aspect ratio to guide particles focused to a specific position.^14,18 The connection of different aspect-ratio rectangular channels with carefully designed fluidic resistances can result in particles migrating to specific focusing positions.¹⁸ In this study, we show that the variation of cross-sectional shape can be a new control parameter. More specifically, we demonstrated focusing particles to specific positions in the cross-sections using various cross-sectional shapes. Moreover, matching focusing positions and basins of attraction of channels with different cross-sectional shapes allows selection of the focusing position.

Inertial focusing has been suggested as a method for focusing cells for flow cytometry, where focusing of cells in a tight spot is critical for accurate measurement.^19,20 Inertial focusing is especially attractive due to the capability of focusing cells without the use of sheath flow. Because simple straight rectangular channels have more than one focusing position, curved channels, such as spiral channels, asymmetric curved channels, or pillar structures were introduced to reduce the number of focusing positions using drag force induced by a secondary flow.^21–23 However, drag also acts more non-uniformly across particles of different sizes leading to focusing dispersion as a function of size such that it was necessary to further focus particles downstream with a straight channel.²⁴ In addition, for some implementations, while particles are focused with better accuracy, the focusing position near a side wall results in difficulty in analysis due to light scattered from the side wall.²⁴ Therefore, it is more desirable to focus particles in the centerline of the channel in one dimension using a low aspect ratio channel.²⁵ A secondary flow induced by serial stepped channels can destabilize the focusing position in the lower portion of the channel and reduce the focusing position to a single point. However, the strength of secondary flow does not scale the same way as the inertial lift forces; therefore, careful design and determination of proper operational flow rates which are dependent on the particle size are required. We fabricated channels with varying cross-sections and controlled accessible inertial focusing positions in nonrectangular cross-section channels to focus the particles in a single focusing position without using secondary flows.

Results and discussion

Inertial focusing and ordering in non-rectangular cross-section channels

We built microchannels with non-rectangular cross sections and observed inertial focusing and ordering of microparticles. Three different cross-sectional shapes were built: the half-circle and the wide and narrow triangles (with 90° and 70.6° apex angles) as shown in Fig. 1d. The details of the fabrication of the non-rectangular microchannel and the side-view channels can be found in the experimental section and in the ESI† (Fig. S1). Inertial focusing positions of dilute solutions of micro-particles (9.9 μm diameter) were observed using fluorescence microscopy and high-speed imaging from the top view and side view (Fig. 2). Confocal microscopy was used to confirm the focusing position in the cross-sections. The length of the channels was 4 cm, and the measurements were made just before the outlet to ensure that the particles approach a steady-state configuration. The particle Reynolds number (R_P) was about 2.0 in all cases. We used conventional definitions of R_P and Reynolds number (Re): , where a is the particle diameter, H is the hydraulic diameter, ρ and μ are the density and dynamic viscosity of the fluid, and U is the average velocity of the fluid.

Fig. 2 Inertial focusing of microparticles in non-rectangular channels. (a) Half-circular channel. (b) Wide triangular channel. (c) Narrow triangular channel (R_p = ∼2.0). Fluorescence images and high-speed capture images are taken from the top view (left) and side view (middle) (scale bar, 50 μm). Confocal microscopy (right) is used to confirm the focusing positions in the cross-section.

In Fig. 2a, the fluorescent streak images and high speed images from the half-circular channel show a single focusing position in the top view and two focusing positions in the side view. The confocal microscopy image (Fig. 2, right) clearly shows the two focusing positions near the top and bottom channel walls. In addition to focusing of microparticles, ordering can be observed from the high speed images (below the fluorescence images). Inertial ordering results from inter-particle hydrodynamic interactions mediated through the wall-reflected disturbance flow.^1,2 The focusing and ordering behavior in the half-circular channel is similar to those in the low-aspect-ratio rectangular channels.^10,14 The difference is that the top focusing position (marked with a blue arrow) is further away from the top wall than the bottom focusing position (marked with a red arrow).

The triangular channels show unique focusing behaviors. The fluorescence images show a single line from the top view and two lines from the side view (Fig. 2b and c). High speed images reveal that there are actually three focusing positions in the top view of the channel. The focusing positions are close to each other and overlap so that they are observed as a single line in the top-view fluorescence images. Three focusing positions near the middle of the channel faces are most probable considering the three-fold symmetry of triangles. However, the observations from the top and side views alone cannot rule out other possible focusing position configurations. The confocal microscope images showing the y–z plane confirm that actually the three focusing positions are located near the channel face. The focusing positions of the two triangular channels with different angles are slightly different; the top focusing positions are closer to the apex of the triangle in the wide triangular channels. The focused particles in the triangular channels also show a regular, self-assembled pattern that is similar to those from rectangular channels. In addition, non-spherical particles such as red blood cells are known to show alignment in the rotation angle.¹ We found similar but unique ordering with a three-fold symmetry in triangular channel cross-sections (Fig. S2†).

Focusing with varying R_p

We observed inertial focusing in non-rectangular channels with varying particle Reynolds number. The statistics of particle positions in the y- and z-coordinates are shown in Fig. 3. The data are collected near the outlet of the channel using a microscope system equipped with a high-speed camera. The number of particles that are analyzed is 3000 for each R_P, and the bin size of the histogram is 1 μm. In general, particles are randomly distributed at low particle Reynolds number, which is expected for Stokes flow, and the particle focusing positions can be identified more clearly as the peaks become sharper with increasing R_P.

Fig. 3 Statistics of particle positions with R_P (total N = 3000). The normalized count (P) is shown for the top view and the side view. (a) Half-circular channels. (b) Wide triangular channels. (c) Narrow triangular channels. The schematics represent two-stage focusing dynamics and the shift of the focusing positions according to the R_P changes.

Fig. 3a shows the statistics for the half-circular channels. From both the side view and the top view, the statistics clearly show the peaks that indicate the focusing positions. The number and the position of the peaks match with the fluorescence data from Fig. 2a. In the statistics from the top view, the peak appears at the center and it becomes narrower with increasing R_P. In the statistics from the side view, two peaks become clear for R_p > 0.23, which corresponds to the top focusing positions and the bottom focusing positions. The peak representing the bottom focusing position (z/H ∼ 0.2) appears at smaller R_P than the peak representing the top focusing position (z/H ∼ 0.7). It is well known that inertial migration in rectangular channels occurs in two stages: fast migration towards the long channel face and slow migration towards the center of the long channel faces, i.e., the focusing positions.^10,11,14,15 We also find that inertial migration in the half-circular channel occurs in two stages as in the case for the rectangular channels. If we compare the top view and side view data with R_p = 0.0091, 0.091, and 0.23, we can find that the peaks are narrower in the side view, which means fast migration in the z direction. Due to the similarity of the flow velocity profile with the low aspect-ratio rectangular channels, inertial migration and focusing behavior are very similar in the half-circular channel. We can infer, as we did in rectangular channels, that the migration speed is faster towards the top and bottom of the channel due to the strong shear-gradient lift force, and then the migration is dominated by the wall-effect lift force that further pushes the particles toward the center of the channel face. Furthermore, the broken symmetry of the half-circular channels leads to differences between the top focusing position and the bottom focusing position. The curvature in the top channel wall leads to a wider particle distribution for the top focusing position in the side view (R_P = 0.23 and 0.46) and a shift of the peak center. After the particle focus tightly at the focusing position (R_P > 0.91), the peaks in the side view do not show significant differences.

Fig. 3b and c show the statistics for the triangular channels. With increasing R_P, the peaks representing the focusing position become clear and the positions and number of peaks agree with the results shown in Fig. 2b and c. Inertial focusing in the triangular channels shares the same two-stage focusing characteristics. Similar to the half-circular channel, the peaks appear first in the side views with R_P as low as 0.10. The peak in the top view become clear when R_P > 1.0, and individual peaks become distinguishable at even higher R_P. These results are, in part, due to the fact that the focusing positions are closer to each other in the top views than the side views and the peaks overlap significantly in the top view. More importantly, the difference in the onset of the peak appearance originated from the focusing dynamics in the microfluidic channels: fast migration towards the wall and then slow migration to the focusing positions. This focusing dynamics can also elucidate the fact that the peaks for the bottom focusing position are sharper than the top focusing position in the side view.

A unique characteristic of inertial focusing in triangular channels is the fact that the top two inertial focusing positions shift significantly with increasing R_P. Unfortunately, we could not increase the R_P beyond 4.0 with the triangular channels due to channel delamination from high pressure. We could not check experimentally whether the focusing position will continue shifting towards the bottom vertices with increasing R_P, and if the shift stops, how will this affect the focusing position. The use of microfluidic channels that can withstand high pressure^26,27 may help address this issue. However, it wouldn’t be easy to build side view channels with these rigid materials. Analysis with 3D imaging such as the holographic method^28,29 or mirror embedded channel³⁰ is expected to not only resolve the side view problem but also better understand focusing mechanisms.

We used two different triangular cross-sections to investigate the effect of lift forces by controlling the cross-sectional symmetry. A narrow triangular channel, with angles of 70.6° and 54.7°, has a cross-section similar to an equilateral triangle that has three-fold axial symmetry, while the wide triangular channel has only left and right mirror symmetry. The symmetry of the channel affects the focusing position and several important observations are noted here. 1. The bottom focusing positions are located at the center of the bottom channel face and do not shift with varying R_P because of the mirror symmetry (left and right). 2. The top focusing positions appear near the center of the side channel face (∼0.4–0.5 (z/H)) in the narrow triangular channels, while they appear significantly off the center of the side channel face (∼0.6–0.7 (z/H)) in the wide triangular channels. 3. The shift of the top focusing position is from near the vertex to the center of the side channel face. This tendency is also confirmed with finite element method (FEM) simulation of the flow and particle interactions, which is described in the next section. The shift of the focusing position with Reynolds number was observed in square channels, but in this case, the shift is in the radial direction only due to the difference in scaling of the two lift forces with Reynolds number.³¹ Here, we also observe that the focusing position shifts in the circumferential direction due to broken symmetry. The migration in the circumferential direction and the location of the focusing position is dominated by the wall-effect lift force.

We observed similar focusing behavior with 7 μm particles (Fig. S3†): two focusing positions are found in half-circular channels, and three focusing positions that shift with varying R_P are found in triangular channels. The exact mechanism of the focusing position shift is beyond the scope of this study and will be left for a future study. However, the observed shift of the focusing position implies that the balance of the two wall-effect lift forces from nearby channel walls changes with the Reynolds number. These triangular channels thus can provide a good platform for studying the inertial lift forces separately.

Inertial lift force in the cross-section

The simulated force plot for a triangular channel with R_P = 2.7, top right local regions of a triangle with R_P = 1.4 and 2.7, and a half-circular channel with R_P = 6.5 are shown in Fig. 4. The length and the direction of the arrow represents the relative magnitude and direction of the lateral force, respectively, at the tail position of the arrow. These force maps also represent the particle motions in the cross-section and support the two-step focusing dynamics described in the previous section. In Fig. 4a, the force plot demonstrates two equilibrium positions marked by red circles, agreeing with the experimental results (three in total if the whole triangle is considered) shown in Fig. 2b and 3b. The arrows point out a distinct location for the bottom equilibrium position. Similar to the square channel force map,³¹ there are stable equilibrium positions and unstable equilibrium positions. Near the stable equilibrium position, or the focusing positions, the arrows are only directed towards the focusing positions, while the arrows point towards and away near the unstable focusing positions or saddle points. To precisely locate the top right equilibrium position, force plots (R_P = 1.4 and 2.7) with finer binning (1 μm) around the potential region marked by a blue dash triangle are drawn in Fig. 4b. The top inset (R_P = 2.7) shows that the equilibrium position is close to the bottom right corner, while the bottom one (R_P = 1.4) demonstrates that the equilibrium position is shifted in the top left direction. The result is coincident with the experimental one showing that the equilibrium position moves towards the bottom right when R_P is increased. In Fig. 4c, top and bottom equilibrium positions in the middle line of the half circle can be predicted by considering the flow of the arrows, agreeing with the experiment in Fig. 2a and 3a.

Fig. 4 Force plot of a particle with a 10 μm diameter in the cross-sectional plane of a wide triangular channel and a half circular channel calculated using COMSOL Multiphysics. (a) Force plot for right half plane of the wide triangular channel with R_P = 2.7. (b) Force plot for the region marked by a blue dashed triangle in (a) with R_P = 1.4 and 2.7. (c) Force plot for right half plane of the half circular channel with R_P = 6.5. In all figures, red circles represent the estimated equilibrium positions following arrow plots of force.

Single-stream particle focusing

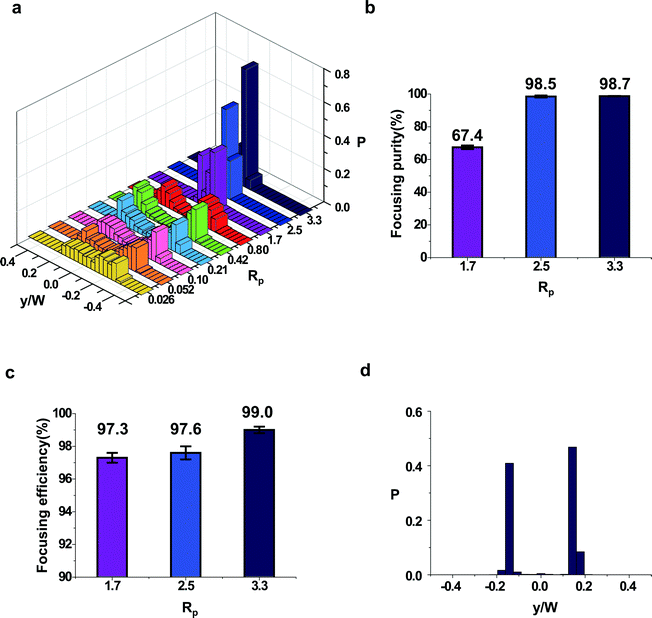
As shown in the previous sections, the inertial focusing position is dependent on the channel cross-sectional shape, which implies that the cross-sectional shape can be a control parameter for manipulation of particles in microfluidic channels. In addition to simple manipulation of the number and location of focusing positions using non-rectangular channels, connecting the microfluidic channels with different cross-sectional shapes can lead to the control of accessible focusing positions. As a demonstration, we built an inertial microfluidic device that can focus particles in a single focusing position, which is applicable to the field of flow cytometry to align cells without sheath fluid. The single-stream focusing device is a straight channel with engineered variation in cross-section as shown in Fig. 5a. The cross-sectional shape changes from a rectangle (2.5 cm long) to a triangle (1 cm long) and then to a half circle (1 cm long). As shown in the schematics in Fig. 5a, this device consecutively reduces the number of accessible focusing positions from 2 out of 2 in rectangular cross-section to 2 out of 3 in triangular cross-section and 1 out of 2 in half-circular cross-section. When channels with different cross-sectional shapes are connected, the focusing positions and the corresponding basins of attraction in the different channels do match one to one. The laminar nature of the finite Reynolds number flows leads to mapping of focusing positions in the upstream channel to new basins of attraction in the downstream channel (Fig. 5a and S4†). The stitched fluorescence image (top view) taken from the inlet to the outlet shows how the particles migrate in the device (Fig. 5b). In the single-stream focusing device, particles are first focused at two equilibrium positions in the rectangular channel (Fig. 5a(i)). As the channel cross-section is changed to a triangle, already focused particles in the rectangular channel enter the basins of attraction of the top two focusing positions, and then the particles migrate to the top focusing positions (Fig. 5a(ii)). Finally, the particles focused at the top two focusing positions enter the half-circular channel and migrate to the top focusing position (Fig. 5a(iii)). As a result, the bottom focusing position in a half-circular channel becomes inaccessible for the particles. Fig. 5c and d clearly show that the particles are not found in the bottom focusing position in the triangular channel and the half circular channel. From the top view, the two lines in the triangular channel become a single line in the half-circular channel. Normally, a top view fluorescence image from a triangular channel gives a single fluorescent line that is actually three overlapped focusing positions, but the separated two lines can be found in the single-stream focusing device because the bottom focusing position is inaccessible for the particles. The connection of the channels was fairly smooth and the streamlines are not disturbed by vortex formation, which may occur at the connecting positions. More detailed information and the 3D shape of the connection section can be found in the ESI† (Fig. S5). Due to an abrupt change in the channel cross section, an entrance effect is expected to be observed. The entrance length is fairly small for most microchannels and we have a few hundred micrometer entrance length for the experimental conditions. Considering each section is longer than 10 mm, we expect that the influence on the particle manipulation is not significant.

Fig. 5 (a) Focusing mechanism and channel design for single-stream focusing. The cross-sectional shape changes from a rectangle to a triangle and then to a half-circle. The particles are focused at two equilibrium positions in the rectangular channels (i). The focused particles in the rectangular channel migrate to the top two equilibrium positions in the triangular channel (ii). The focused particles in the triangular channel migrate to the top equilibrium position of the half-circular channel (iii) (scale bar, 20 μm). (b) The connected fluorescence image shows how the particles are finally focused into a single focusing position after passing through the whole channel. Fluorescence images and high speed capture images of the top view (c) and side view (d) of the channel. The particles are excluded from the middle (bottom) equilibrium position in the triangular channel and focused in a single stream at the outlet. The particle Reynolds number of the experimental data is 2.9 at the rectangular channel, 3.8 at the triangular channel and 2.8 at the half-circular channel (scale bar, 50 μm).

Fig. 6 shows the statistics of the particle positions in the single-stream focusing device. With increasing R_p, particles near the outlet (in the half-circular channel) are found tightly focused at the channel center (Fig. 6a). As expected, particles cannot be focused at the low R_p. In the intermediate R_P regime (R_P ∼ 0.21–0.80), particles are found in two streams, which means that the two streams from the top two focusing positions in the triangular channel did not fully merge into a single stream. This result means that the half-circular channel part is not of sufficient length to focus the particles into a single stream line for R_P ∼ 0.21–0.80. At higher R_P (R_P > 2.5), particles are focused in a single stream demonstrating the feasibility of the single-stream focusing device for applications in preparing the samples for flow cytometry.^25,32 In Fig. 6b, we calculated the ratio of the particles focused within a ±7 μm range (∼1.4D) from the center of the channel, where D is the particle diameter. About 99% of the particles are focused within the range with R_p > 2.5.

Fig. 6 Statistics of the particle positions in the single stream focusing device. (a) Distribution of the particle positions in the half-circular channel with varying R_P (N = 800). (b) Fraction of focused particles within ±0.7 × D from the channel center. D indicates the particle diameter (N = 3000). (c) The ratio of particles focused at the top focusing position in the half-circular channel (N = 3000). (d) Distribution of the particle positions at the triangular channel region (R_P = 3.3, N = 3000).

While the width of the stream is still large at R_P < 1.7, most particles are in the upper half of the half circular channel. We calculated the ratio of the particles found at the top focusing position of the half-circular channel (Fig. 6c). Here, we focused the microscope at the top of the channel and distinguished the position of the particles by the amount of blur in the particle image. At R_P = 1.7, particles were distributed rather broadly (Fig. 6a); however, 97.3% of the particles are still found in the top focusing position (Fig. 6c). The ratio becomes larger: 97.6% with R_p = 2.5 and 99.0% with R_p = 3.3. Fig. 6d shows the statistics of particle positions in the triangular channel part of the single-stream focusing device. At the triangular channel, 99.1 ± 0.2% of the particles are found at the side (top focusing positions) and rarely found in the middle (bottom focusing position, R_p = 3.3). This ratio is almost the same as the ratio of the particles found at the top focusing positions in the half-circular channel (Fig. 6c). The statistics show that focused particles at the rectangular channel migrate exclusively to the top two focusing positions of the triangular channel. This single-stream focusing device demonstrates the feasibility of use with flow cytometry and can be further optimized by changing the total length, length fraction of the different channel cross-sections, and the channel cross-section size. The particle concentration was 0.05% throughout the experiments. Particle–particle hydrodynamic interactions lead to rearrangement of the particles.² Especially, a high particle concentration can increase the ratio of expelled particles from the focusing position, and it will reduce the efficiency of particle manipulation. It is expected that the focusing efficiency and the purity will be worse with a high particle concentration. It is crucial to determine the appropriate sample concentration.

Experimental

Fabrication of non-rectangular cross-section channels

Non-rectangular PDMS channels are fabricated by conventional soft lithography techniques and the molds are fabricated by various fabrication techniques described below. Fig. 1d shows the images of the channel cross-sections. Half-circular channel molds were made by photoresist reflow. A positive photoresist (AZ 50XT, AZ electronic materials) was patterned and hard baked at 130 °C, which is above glass transition temperature of the photoresist. The polydimethylsiloxane (PDMS) molded from the rounded photoresist mold³³ was bonded using air plasma onto a glass slide³⁴ to form a half-circular channel. Triangular channel molds with a 70.6 degree angle were made by Si anisotropic etch with potassium hydroxide (KOH). A SiN layer was used for the etch mask, which was removed with reactive ion etching (RIE) after the KOH etching. This v-groove on Si served as the master mold, and the PDMS mold replicated from the master mold was used for the channel mold. The triangular channel molds with a 90 degree angle were made by a similar method. An isopropyl alcohol (IPA) and KOH mixture (300 mL of IPA, in DI water) was used for Si anisotropic etch. Adding IPA to KOH can alter the etching rate for the Si crystal plane to give a 90° angle.

Fabrication of the single-stream focusing device

We connected the channels with varied cross-sectional shapes for single-stream focusing (rectangle, triangle with 70.6 degrees, and half-circle as shown in Fig. 5a). First, a triangular channel mold was constructed with UV-glue by capillary molding. For this process, a triangular PDMS channel (1 cm) was used as a mold for the UV-glue. Then, a rectangular channel was patterned using SU-8 resist (SU-8 3025, MicroChem) on top of the triangular channel mold. Finally, the half circular channel (1 cm) was patterned using AZ 50XT and rounded by a reflow process at 130 °C. The reflow of the AZ resist not only provides rounded half-circular cross-sections but also results in a smooth connection between different channels. After the channel mold was fabricated, conventional PDMS molding and plasma bonding were used to build the microchannel devices.

Experimental setup and measurements

Our experiment was observed from the top and side views of the channel. The top-view channel was made by bonding PDMS³³ and a glass slide with oxygen plasma treatment.³⁴ The process of fabrication of the side-view channel is depicted in Fig. S1.†

We used 9.9 μm particles (Thermo fluoro-max™) for most of the experiments. This particle is green fluorescent (excitation 468 nm, emission 508 nm) with a particle density of 1.05 g cm⁻³. The particle is dispersed in DI water with 1% Tween 20 (Sigma-Aldrich) to prevent aggregation of particles. To prevent the particles from sedimenting in water, we matched the density of the particles and that of water by adding NaCl. The particle concentration in the solution was 0.05–0.1 weight percent.

Particle suspensions were injected using a syringe pump (Harvard Apparatus PHD ULTRA CP syringe pump) with the volumetric flow rate controlled. With the fluid density matched with the particle, no significant particle sedimentation was observed in the syringe or in the fluidic channel.

Particle dynamics is observed by using an optical microscope (Nikon eclipse Ti-U), a digital high speed camera (Phantom v7.3) and a fluorescence illuminator (Nikon intenslight C-HGFIE). We found the particle positions in the channel by using a MATLAB code which implements a Circular Hough Transform algorithm. It detects the sudden change of image gradient at both sides of a particle. It senses the center of the transition position as the center of the particles.

FEM simulation

We numerically calculated the lift force of a particle (a = 10 μm) in the wide triangular channel with 45° side angle and half circular channel using COMSOL Multiphysics. The full 3D Navier–Stokes equations are solved in the particle frame of reference, where the particle is stationary inside the channel, by setting the walls of the channel moving backward. The inlet and outlet boundary conditions of the channel are set to be fully developed laminar inflow and outflow, respectively, to isolate one particle. In the simulation program, the velocity of the walls and the slip velocity at the surface of the particle, corresponding to the particle velocity and angular velocity, respectively, are iteratively updated until the drag in the flow direction and torque in all directions applied on the particle are negligible. We then integrated the total force per area across the particle surface to obtain the lateral lift forces. Because of symmetry, the model with a particle at each position of the grid binned by 2.5 μm in the right half domain of the triangle and half circle is simulated to achieve force plots across the entire cross-sectional plane. The triangular case is simulated at R_P = 1.4 and 2.7 for the study of R_P-dependent equilibrium position, while the half circular one is executed at R_P = 6.5 because there is no R_P dependence regarding experimental observation and the force plot can be clearly illustrated with a large force induced by a large flow rate. More details can be found in the ESI.†

Conclusions

We investigated unique inertial focusing phenomena within microchannels with non-rectangular cross-sections. Half circular channels and triangular channels show one focusing position each near the channel faces. As expected from previous studies of inertial focusing, the particle focusing have two stages: a fast radial migration due to the shear-gradient lift force and then a slow circumferential migration due to the wall-effect lift force. Interestingly, focusing positions in triangular channels shift significantly along the channel face with increasing R_P. This unexpected shift of focusing position cannot be seen in the rectangular channels where the wall-effect lift forces from nearby walls are always balanced. We believe the shift is evidence that the wall-effect lift force scaling with R_P is a function of the distance from the channel wall; however, the exact mechanism of the shift needs to be elucidated in a future study. The variations in location of focusing positions using the cross-sectional shapes can be a new control parameter for particle manipulations in microfluidics. We suggest a new concept of basins of attraction for this manipulation technique. The mapping of the focusing position and the corresponding basins of attraction is unique in the channels with various cross-sections. The connection of the channels with different cross-sectional shapes allows the control of accessible focusing positions. We demonstrated the manipulation of accessible focusing positions by sequentially connecting a rectangular channel, a triangular channel and a half-circular channel. The resulting device can be utilized for focusing of particles in a single cross-sectional position with an efficiency of ∼99%.

Acknowledgements

This work was supported by a grant from the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2012R1A2A2A03046642, NRF-2015M2A2A4A02044826). D. D. acknowledges financial support from the Office of Naval Research Young Investigator Program (Grant no. N000141210847). We thank Dong Ki Yoon for supporting confocal microscopy measurements.

References

1. D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897.
2. W. Lee, H. Amini, H. A. Stone and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413–22418.
3. D. R. Gossett, W. M. Weaver, A. J. Mach, S. C. Hur, H. T. K. Tse, W. Lee, H. Amini and D. Di Carlo, Anal. Bioanal. Chem., 2010, 397, 3249–3267.
4. N. Pamme, Lab Chip, 2007, 7, 1644–1659.
5. A. P. Sudarsan and V. M. Ugaz, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7228–7233.
6. A. D. Stroock, S. K. Dertinger, A. Ajdari, I. Mezic, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651.
7. D. Dendukuri, D. C. Pregibon, J. Collins, T. A. Hatton and P. S. Doyle, Nat. Mater., 2006, 5, 365–369.
8. J. K. Nunes, C. Y. Wu, H. Amini, K. Owsley, D. Di Carlo and H. A. Stone, Adv. Mater., 2014, 26, 3712–3717.
9. D. Dendukuri, S. S. Gu, D. C. Pregibon, T. A. Hatton and P. S. Doyle, Lab Chip, 2007, 7, 818–828.
10. H. Amini, W. Lee and D. Di Carlo, Lab Chip, 2014, 14, 2739–2761.
11. D. Di Carlo, Lab Chip, 2009, 9, 3038–3046.
12. E. S. Asmolov, J. Fluid Mech., 1999, 381, 63–87.
13. G. Segre and A. Silberberg, Nature, 1961, 189, 209–210.
14. D. R. Gossett, H. T. K. Tse, J. S. Dudani, K. Goda, T. A. Woods, S. W. Graves and D. Di Carlo, Small, 2012, 8, 2757–2764.
15. J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132.
16. M. A. Unger, H. P. Chou, T. Thorsen, A. Scherer and S. R. Quake, Science, 2000, 288, 113–116.
17. J. Park, D. H. Kim, G. Kim, Y. Kim, E. Choi and A. Levchenko, Lab Chip, 2010, 10, 2130–2138.
18. J. Zhou, P. V. Giridhar, S. Kasper and I. Papautsky, Lab Chip, 2013, 13, 1919–1929.
19. M. E. Piyasena and S. W. Graves, Lab Chip, 2014, 14, 1044–1059.
20. A. Givan, in Flow Cytometry Protocols, ed. T. S. Hawley and R. G. Hawley, Humana Press, 2011, ch. 1, vol. 699, pp. 1–29.
21. R. Aman, K. G. Amit, N. Sunitha, C. Dino Di, F. E. Jon and T. Mehmet, New J. Phys., 2009, 11, 075025.
22. J. M. Martel and M. Toner, Phys. Fluids, 2012, 24, 032001.
23. A. J. Chung, D. Pulido, J. C. Oka, H. Amini, M. Masaeli and D. Di Carlo, Lab Chip, 2013, 13, 2942–2949.
24. J. Oakey, R. W. Applegate, E. Arellano, D. Di Carlo, S. W. Graves and M. Toner, Anal. Chem., 2010, 82, 3862–3867.
25. A. J. Chung, D. R. Gossett and D. Di Carlo, Small, 2013, 9, 685–690.
26. E. Sollier, C. Murray, P. Maoddi and D. Di Carlo, Lab Chip, 2011, 11, 3752–3765.
27. E. J. Lim, T. J. Ober, J. F. Edd, S. P. Desai, D. Neal, K. W. Bong, P. S. Doyle, G. H. McKinley and M. Toner, Nat. Commun., 2014, 5.
28. Y. Frauel, T. J. Naughton, O. Matoba, E. Tajahuerce and B. Javidi, Proc. IEEE, 2006, 94, 636–653.
29. T. Zhang and I. Yamaguchi, Opt. Lett., 1998, 23, 1221–1223.
30. J. Koh, J. Kim, J. H. Shin and W. Lee, Appl. Phys. Lett., 2014, 105, 114103.
31. D. Di Carlo, J. F. Edd, K. J. Humphry, H. A. Stone and M. Toner, Phys. Rev. Lett., 2009, 102, 094503.
32. X. Wang, M. Zandi, C.-C. Ho, N. Kaval and I. Papautsky, Lab Chip, 2015, 15, 1812–1821.
33. J. R. Anderson, D. T. Chiu, H. Wu, O. J. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27–40.
34. M. K. Chaudhury and G. M. Whitesides, Langmuir, 1991, 7, 1013–1025.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5lc01100k

---