Coupled molecular design diagrams to guide safer chemical design with reduced likelihood of perturbing the NRF2-ARE antioxidant pathway and inducing cytotoxicity

Abstract

The NRF2-ARE antioxidant pathway is an important biological sensing and regulating system that responds to xenochemicals. NRF2 senses chemically-caused production of reactive oxygen species (ROS) and electrophilic interactions with chemical species. Upon NRF2 activation, the expression of a wide array of genes will be upregulated to counteract oxidative or electrophilic insults. However, when the external disruption exceeds the inherent resilience of the biological system, cellular damage can occur, eventually leading to cytotoxicity. Induced NRF2 activity in in vitro assays is therefore a signal that a man-made chemical may cause unwanted cellular activity. This was the motivation to derive a chemical design strategy to minimize the risk that new chemicals would perturb this pathway. We constructed a logistic regression model using design variables derived from density functional theory (DFT) calculations and physical properties. The model showed excellent predictive power to distinguish between NRF2-active and inactive chemicals based on the EPA ToxCast high throughput screen (HTS) assay data (tested in the concentration range of 10⁻³–10² μM). External evaluation showed that the area under the curve (AUC) for the receiver operating characteristic (ROC) of the model is 0.81 and the precision is 0.90. Combining this model with a previously developed cytotoxicity model, we developed a probabilistic design diagram to guide chemical design with the twin goals of minimizing NRF2 antioxidant pathway activity and cytotoxicity. This work initiated a simultaneous design strategy against two toxicity pathways of interest in molecular design research.

---

1. Introduction

The fourth principle of green chemistry states that “chemical products should be designed to preserve their desired function while minimizing their toxicity”.¹ This idea leads to the desire among chemists to seek design solutions to reduce the likelihood of chemicals perturbing various toxicity pathways. In this report, we chose the NRF2-ARE antioxidant pathway as a target for study. NRF2 (Nuclear factor E2-Related Factor 2) is a bZip transcription factor and a member of Cap ‘n’ Collar family of regulatory proteins.^2,3 At the basal level, NRF2 is repressed by Kelch-like ECH-associated protein 1 (Keap1) and constantly undergoes ubiquitin-assisted degradation.^4,5 Upon stimulation initiated by redox active or electrophilic chemicals, signaled by the presence of reactive oxygen species (ROS), the Keap1–NRF2 interaction is destabilized or the degradation of NRF2 is hindered. In either case, free NRF2 forms a transcription factor that causes upregulation of anti-oxidation genes via the antioxidant response element (ARE).^6–8 The resulting detoxifying enzymes are upregulated to both reduce ROS levels and clear xenobiotics.^9,10 At low levels of perturbation (low xenobiotic concentration, short exposure durations), NRF2 activation can effectively protect the cell from the effects of ROS or electrophilic attacks. This is considered to be a protective mechanism to help an organism adaptively respond to this type of insult. The NRF2-ARE pathway was thus proposed as a potential therapeutic target for anti-oxidation intervention.^10–13 However, at greater levels of exposure, the protection mechanism can be overwhelmed and adverse consequences may follow. Oxidative stress provides a well-known example of tipping over the inherent redox balance in the biological system due to the pressure from ROS. NRF2–Keap1 is responsible for sensing this event.^5,14–16 The adverse effects of oxidative stress have been linked to multiple clinical syndromes including neurodegenerative diseases, cancer, arthritis, atherosclerosis and inflammatory diseases.^3,17–21 Therefore, man-made chemicals should be designed to minimize the likelihood of generating ROS. The NRF2–Keap1 is used as a biosensor in this study to gauge the potential of a chemical inducing ROS generation and posing an electrophilic threat. It should be noted that certain chemicals may bypass the NRF2–Keap1 monitor but still be involved in ROS generation. Those cases deserve separate treatment and are not considered this research endeavor.

Three critical components are needed to build a predictive model of NRF2 activity to be used in green molecular design. First, we need a reliable biological assay that probes the chemically induced activation of the NRF2-ARE pathway. In vitro high throughput screening (HTS) methods answer this need. HTS is a cost-effective technology to examine how chemicals disrupt biological pathways and hence potentially lead to adverse health outcomes. It embodies a paradigm shift in toxicology from using in vivo to using in vitro and in silico testing approaches, as described by the U.S. National Research Council (NRC) in their report on Toxicity Testing in the 21st Century.^22,23 In order to evaluate practical approaches to implement the “Tox21” vision, the U.S. National Toxicological Program (NTP), the U.S. Environmental Protection Agency (EPA) and the NIH National Center for Advancing Translational Sciences (NCATS) collaboratively forged a collaborative research partnership. This Tox21 partnership is using HTS methods to test thousands of chemicals in a wide variety of cells, pathways and technologies, relevant to many aspects of chemical toxicity.^24–29 The NRF2-ARE antioxidant pathway has been probed using the ToxCast/Tox21 assay battery. Second, we need to construct a design variable space with physically meaningful and accurately calculable parameters. Physical observables and chemically intuitive variables are preferred because of their accessibility from experimental measurements. Additionally, these design variables should also encapsulate mechanistic information regarding the molecular initiating events that lead to the toxicity endpoint of interest. Thirdly, the predictive model needs to be built so that the design variable space can be made searchable and the inverse function of the model can be presented in a probabilistic and complete manner. This requires a careful design of the modeling algorithm.

Previously, acute aquatic toxicity,^30,31 mutagenicity/carcinogenicity³² and cytotoxity³³ have been investigated as single target toxicity endpoints to derive green molecular design strategies. In this report, we present for the first time in molecular design research a coupled design diagram that simultaneously considers two design goals, in this case the minimization of both cytotoxity and the NRF2-ARE pathway perturbation. This attempt is motivated by the significance that certain chemicals can induce one toxic response without the other. With the progress of molecular design research, it is anticipated that more and more models can and will be linked together to provide a comprehensive design strategy.

2. Methods

2.1. Toxicity data resource

The U.S. EPA Toxicity ForeCaster (ToxCast™) program release³⁴ contains two assays that were designed to monitor chemicals perturbing the NRF2-ARE toxicity pathway: ATG_NRF2_ARE_CIS_up (subsequently abbreviated as ATG_NRF2) and Tox21_ARE_BLA_agonist_ratio (subsequently abbreviated as Tox21_ARE).

ATG_NRF2 is part of a multiplexed assay using an inducible reporter that measures mRNA for gain-of-signal activity at the transcription factor-level as they relate to the gene NFE2L2. This is one of 52 assay component measured or calculated from the ATG_CIS assay. Activity is detected with fluorescence intensity signals by reverse transcription polymerase chain reaction (RT-PCR) and capillary electrophoresis technology. Activity is quantified by the level of mRNA reporter sequence unique to the cis-acting reporter gene response element ARE, which is responsive to the endogenous human nuclear factor, erythroid 2-like 2 [GeneSymbol:NFE2L2|GeneID:4780|Uniprot_SwissProt_Accession:Q16236]. The assay is cell-based and uses HepG2, a human liver cell line, with measurements taken at 24 hours after chemical dosing in a 24-well plate.³⁵

Tox21_ARE uses an inducible reporter to measure gain-of-signal activity related to the gene NFE2L2. The assay measures beta-lactamase induction, as detected with fluorescence intensity signals by GAL4 beta-lactamase reporter gene technology. Changes to fluorescence intensity signals produced from an enzymatic reaction involving the key substrate [CCF4-AM] are indicative of changes in transcriptional gene expression due to agonist activity regulated by NRF2. The assay is cell-based, producing a single-readout that uses HepG2, with measurements taken at 24 hours after chemical dosing in a 1536-well plate.²⁹

The two assays were tested on chemicals with similar concentration ranges, approximately 10⁻³–10² μM (see Fig. S1 in ESI†). Consequently, our predictive model is strictly applied to the likelihood for chemicals incurring biological responses over this particular concentration range. The testing outcome concordance between these two assays is 0.73 (see Fig. S2 in ESI†). Cytotoxicity was also examined in the ToxCast data. Assay data related to cytotoxicity were used to construct a cytotoxicity model that was linked to the NRF2-ARE toxicity pathway model. Detailed description of the cytotoxicity model is provided in our recent publication.³³

2.2. Chemical selection

Four criteria were set for chemical selection in the following analyses:

1. Molecular weight < 1000. The bioavailability for chemicals with molecular weight greater than 1000 is negligible.³⁶

2. Single compound with a definite structure, excluding geometrical and optical isomers and mixtures. The molecular mechanisms for mixtures can be complex, and are not considered here.

3. Containing no metal elements. The calculation of electronic properties of metals is significantly more challenging than for organics, so the focus here is on the latter.

4. Concordant testing outcomes between ATG_NRF2 and Tox21_ARE assays (both positive or both negative). Concordance is required because both assays have false positives and false negatives, so chemicals with concordant behavior are more likely to be correctly assigned.³⁷

A total of 1261 chemicals satisfied these four criteria. Binary hit calls provided in the ToxCast release³⁴ were used to categorize chemicals into two classes: chemicals detected to be not perturbing the NRF2-ARE toxicity pathway (inactive) and otherwise (active). The chemical membership distribution is biased towards the inactive chemicals, which account for ∼72% of the total sample population.

All chemical data were evenly split into training and test sets with the same ratio between active and inactive chemicals for cross-validation and external evaluation. The first treatment of the chemical structures is to remove counter-ions from the molecules using the open-source OpenBabel chemistry toolbox.³⁸ Subsequently, 3D structures with the lowest energy conformation were generated using the ChemAxon Marvin calculator plugin.³⁹

2.3. Generation and selection of design variables

Seven design variables were generated and examined in this study: molecular softness (SOF), electrophilicity index (EPH), ionization potential (IP), electron affinity in the aqueous phase (EA.aq), polarizability (PLRZ), radical stability energy (RSE) and log P (log water–octanol partition coefficient). log P was calculated using the ChemAxon Marvin calculator plugin.³⁹ The remaining variables were computed based on DFT implemented in Gaussian 09 rev.D.01.⁴⁰ Boese and Martin's τ-dependent hybrid functional⁴¹ and basis set 6-31+G(d) were used for full geometry optimization. Vertical IP and electron affinity (EA) were calculated in vacuum. The species with an extra electron were then transferred into the implicit aqueous environment based on a universal solvation model⁴² to obtain vertical EA.aq. SOF and EPH were derived according the following formulas.⁴³

SOF = 1/(IP − EA) (1)

EPH = (IP + EA)²/8(IP − EA) (2)

Radical stability energy (RSE) is defined as the reaction energy for the reaction:

where MH is a generic presentation of a chemical with H being a hydrogen atom and M˙ is the leftover radical after one hydrogen atom is removed from MH.

The numerical distribution of each design variable is plotted in ESI Fig. S3.†

2.4. Mechanistic rationales for design variables

The molecular initiating event for NRF2 activation is the chemical modification of thiol groups on Keap1.^7,8 Such modification can be effected through a covalent interaction or a redox mechanism. SOF is a quantitative variable that describes the likelihood for covalent interaction.⁴⁴ Covalent interactions account for a number of toxicological events including the activation of NRF2-ARE pathway and cytotoxicity.^5,45 Therefore, it is reasonably included in the predictive model design. For the redox event, EA.aq describes the energy gain of a chemical after acquiring one electron. Here, it can viewed as a measure of the potential of a chemical stripping one electron from critical biological molecules in the aqueous phase. The higher the EA.aq value, the higher is the reactivity of a chemical. It was within the original design variable consideration, but discarded later because of its inferior predictive power compared to other preserved variables (see Table S1 in ESI†). In order for xenobiotics to interact with Keap1 inside a cell, they must permeate the membrane. log P has been frequently used to estimate such likelihood and has shown acceptable predictivity in quantitative structure–activity relationship (QSARs) of acute aquatic toxicity.⁴⁶ Subsequent to molecular transport into a cell, xenobiotics proceed to interact with biological targets. This process is driven at least partially by induced electric dipole moments and dispersion forces.⁴⁷ Polarizability (PLRZ) is a physical quantity that describes the relative tendency towards molecular electron cloud distortion under the influence of an external electric field. This reflects the energy alteration during a molecular recognition process. This provides the physical basis for including PLRZ in the predictive model.

The last variable to mention is radical stability energy (RSE). It approximates the degree to which a chemical is liable to form reactive radicals, which is the trigger for releasing the NRF2–Keap1 interaction. However, the low predictive power of this variable in the model suggests that direct radical activation is not the dominant mechanism of NRF2 activation in chemicals included in this study. It is consistent with the fact that HepG2 cell lines do not possess full metabolic activities^48–50 and that biotransformation is an important avenue for generating reactive radicals.^51,52

2.5. Predictive model construction and design probability derivation

The predictive model for this work is built on the logistic regression algorithm.⁵³where π(X) denotes the probability for a chemical not perturbing the NRF2-ARE toxicity pathway (benign probability) and X denotes the design variables. The predictive power of the seven design variables were assessed using ROC AUC analysis (see ESI Table S1†). The three most predictive variables (PLRZ, SOF and log P) were selected based on LASSO regularization⁵⁴ for the predictive model construction. The logistic regression model was trained on ∼600 chemicals with 10-fold cross validation, i.e. chemicals were randomly partitioned into 10 equal sized groups and a single group is retained as validation set for the model built upon the other nine groups in rotation until every group has been tested. Then the established model was externally tested on the remaining ∼600 chemicals.

Model construction, data analysis, graphics and design diagrams in this study were coded using the Python programming language and the R statistical computing environment.^55–67

3. Results and discussion

3.1. Performance evaluation for the predictive model

We used the following measures to evaluate the performance of the logistic model:

precision = truepositive/(truepositive + falsepositive) (5)

accuracy = (truepositive + truenegative)/all (6)

Because we are interested in producing ‘safer’ chemicals in the design process, we define chemicals that do not perturb the NRF2-ARE antioxidant pathway as positive in this study. Therefore, type I error is the focus of interest from the green design perspective. Precision measures the probability that a chemical will be a true positive relative to the fraction of chemicals that are predicted to be positive. This probability is of high interest to green chemists. It should be maximized for the purpose of safer chemical design. Accuracy is a measure of the balanced performance of the model. Given that the overall rate for a chemical to be inactive against the NRF2-ARE pathway is imbalanced, the ROC AUC (equivalent to the balanced accuracy) is a more robust measure for the overall classification accuracy of the predictive model. The model performance is summarized in Table 1.

Table 1 Model performance evaluation

Measure	Precision	Accuracy	ROC AUC
Cross validation	0.86 ± 0.04	0.80 ± 0.03	0.81 ± 0.04
External evaluation	0.90	0.78	0.81

---

From Table 1, one can see that three performance indicators are in reasonable agreement. Additionally, the cross-validation and external evaluation results agree well with one other. This suggests that the classifier has reasonable forward predictive performance and can be used for deriving green design probabilities for novel chemicals.

3.2. NRF2-ARE pathway and cytotoxicity

Phase II enzymatic detoxification is triggered by electrophilic and redox-active species, and among other actions serves to maintain a stable intracellular environment.^68,69 When chemical perturbations exceed the cellular recovery capacity, molecular damage can result that could eventually lead to cell death. Therefore, a correlation is expected to exist between NRF2-ARE pathway perturbation and cytotoxicity. For the purpose of comparison, the NRF2-ARE and cytotoxicity assay results³³ are summarized in Table 2. There is an 82% concordance between the two assays, among which 30% of chemicals cause positive responses in both assays. 99 chemicals (∼14%) specifically invoke cytotoxicity without perturbing the NRF2-ARE pathway and 23 chemicals (∼3%) solely activate the NRF2-ARE system.

Table 2 Confusion table between NRF2-ARE pathway perturbation and cytotoxicity. Number of chemicals (in percentage)

		NRF2-ARE	NRF2-ARE
		Positive	Negative
Cytotox	Positive	209 (30.0%)	99 (14.3%)
Cytotox	Negative	23 (3.3%)	364 (52.4%)

---

Mechanistically, the NRF2-ARE pathway activation can be triggered by either covalent or redox modifications of the thiol groups on Keap1.^15,16 Cytotoxicity can be induced by multiple causes including cell membrane disruption, activation of specific signaling pathways or DNA modification.^70,71 Given the multitude of mechanisms of cytotoxicity, it is of interest to investigate the differences between chemicals that induce only one or both of NRF2-ARE activity and cytotoxicity. The following statistical discussion will focus on the chemicals that only cause cytotoxicity (cytotox group, 99 chemicals) or incur both cytotoxicity and NRF2-ARE response (cytotox + ARE group, 209 chemicals).

Table 3 shows the calculated ROC AUC^72,73 and p-values from a Mann–Whitney U test⁷⁴ for the three design variables (SOF, PLRZ and log P) used in the logistic model. In accordance with the Mann–Whitney U test, SOF strongly suggests that the two groups of chemicals (cytotox and cytotox + ARE group) are drawn from two unequivalent distributions. This is consistent with the ROC AUC result, where SOF exhibits the highest discriminative power among the three design variables. The overlaid SOF histogram (Fig. 1) further illustrates that the distributions of the two chemical groups are staggered, with the cytotox group slightly shifted to the left. Based on the analysis, it follows that the two groups of chemicals have differential selectivity toward invoking the NRF2-ARE pathway and cytotoxicity. The distributions are not totally separated, which is an indication that SOF is not solely responsible for separating the two groups.

Fig. 1 Histogram overlay for SOF. Color coding: yellow—chemicals causing both cytotoxicity and perturbing the NRF2-ARE pathway, green—chemicals only causing cytotoxicity, vertical blue bar—median value for chemicals causing cytotoxicity only, vertical red bar—median value for chemicals perturbing the NRF-ARE pathway and incurring cytotoxicty.

Table 3 Design variables analysis for distinguishing chemicals causing both cytotoxicity and NRF2-ARE activity vs. chemicals only inducing cytotoxicity

Design variable	ROC AUC	p-Value for Mann–Whitney U test
SOF	0.64	2.7 × 10^−5
PLRZ	0.53	0.19
log P	0.55	0.04

---

Many processes leading to toxicity are driven by chemical reactivity toward critical biological targets including DNA, enzymes, lipids and others, and thus should be able to be described by chemical design variables. In the current case, SOF was found to be helpful in discriminating between the cytotox and cytotox + ARE chemical groups. This can be understood from Pearson's HSAB theory⁷⁵—acid–base reactions preferentially occur between chemicals with a similar level of softness/hardness. Since covalent bond formation plays a crucial role in chemical initiation of cytotoxicity and the NRF2-ARE pathways, it is thus plausible to expect certain discriminative power from SOF in distinguishing the two classes of interest. In a biochemical interaction, active functional groups on proteins and DNA normally act as nucleophiles, while xenobiotics often act as electrophiles.^76,77 The sulfhydryl groups on protein cysteine residues are generally softer than the amino and hydroxy groups on nucleic acids.⁷⁸ In rapidly dividing cells, cytotoxicity has been attributed to chemical modification of DNA.^79,80

Interactions between chemicals and critical proteins can also lead to cytotoxicity.⁴⁵ The thiol group is an important functional unit on many proteins, and is responsible for sensing a variety of the chemical signals. The NRF2 activation mechanism is an example of the thiol group functioning as a molecular switch.⁸¹ Therefore, it is reasonable that chemicals with a preference to induce only cytotoxicity may initiate this event primarily through reacting with DNA, which is a ‘harder–harder’ interaction. On the other hand, chemicals that cause both cytotoxicity and NRF2-ARE activity are more likely to achieve this effect through modifying thiol groups,⁸¹ which is a ‘softer–softer’ interaction. Thus, it is observed that the SOF distribution for the cytotox chemical group is shifted to the left (harder) compared to the cytotox + ARE group.

3.3. Probabilistic design diagram

The full design diagram is composed of two parts (Fig. 2). The left panel depicts the probability of chemicals not activating NRF2-ARE and the solution to any probability in the design variable space. The right panel is the design diagram for reducing the likelihood of causing cytotoxicity.³³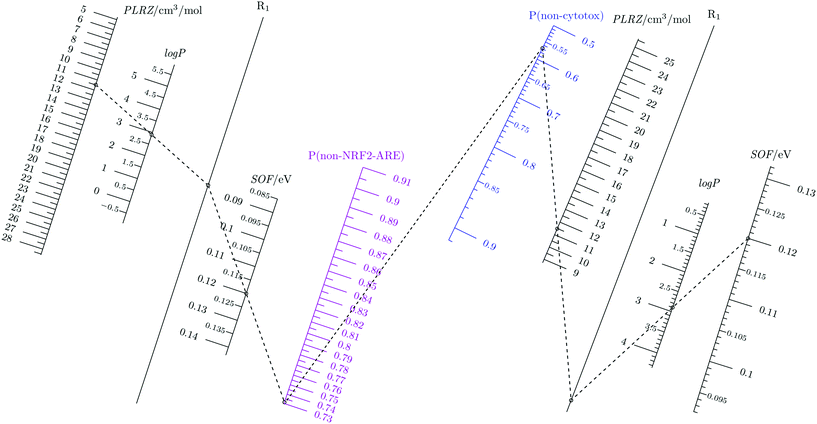

Fig. 2 Coupled nomograms for NRF2-ARE activity and cytotoxicity.³³ P(non-NRF2-ARE): probability of not activating NRF2-ARE (purple). P(non-cytotox): probability of not inducing cytotoxicity (blue). The benign probability axis is colored while other design variables axes are printed black. R1 indicates an auxiliary axis. The numerical range of each design variable axis are calculated using 5 to 95 percentiles of numerical data to produce probabilities corresponding to the range of the benign probability axis. Benign probability above 50% is considered for the green molecular design purpose.

Given the high concordance between cytotoxicity and NRF2-ARE activation, one would expect to observe a degree of similarity between the two diagrams. However, its should be kept in mind that the concordance matrix (Table 2) possesses non-zero off-diagonal elements. This means that the predicted probabilities may vary between the two toxicity endpoints. To obtain a design solution with a target probability of not stimulating the NRF2-ARE pathway and not causing cytotoxicity, one can simply start from desired probabilities for each endpoint and work out values for design variables on the diagrams. A sample solution is given in Fig. 2, using dotted lines. In this example, suppose we have planned probabilities for a chemical not perturbing the NRF2-ARE pathway (73%) and the probability of not incurring cytotoxicity (58%). We start by identifying the positions of these two probabilities on their corresponding probability axes and link them with a dotted line. Next, we put dots on the desired values for softness (0.12) and log P (2.9) on the design variable axes because those values fit into the feasible design space. Then we connect those dots on the design variable axes with the dots on the probability axes and we arrive at the values for polarizability. This case study shows the different probabilities for non-cytotoxic and non-NRF2-ARE activity for the same set of values of the design variables. Of course, users have the freedom to choose any three fixed points on either diagram to determine the last unknown parameter (either a design variable or a probability). One can also work on one side of the diagram first to determine the benign probability and then to check its probability of not invoking the other endpoint by filling those numbers on the other half of the diagram.

4. Conclusions

We have trained a classifier based on the logistic regression algorithm to identify chemicals that do not disrupt the NRF2-ARE antioxidant pathway in the concentration range of 10⁻³–10² μM. The overall performance of this model is 0.81 for ROC AUC and 0.90 for precision, as assessed using an external validation set. Based on this model, we derived a probabilistic diagram to guide molecular design to reduce the chance for chemicals perturbing the NRF2-ARE pathway. In addition, we statistically demonstrated that molecular softness (SOF) possess information in distinguishing the distributions between chemicals that cause cytotoxicity, with or without activating NRF2. This effect was mechanistically rationalized as the preferential interaction between chemicals and either DNA or proteins. Further, we coupled the NRF2-ARE activity and cytotoxicity to arrive at a linked diagram to provide more comprehensive information for chemists in designing safer chemicals. This coupled diagram is the first such toxicity-oriented multi-objective initiative in the molecular design literature. We foresee that linking multiple toxicity endpoints is a general trend in the future of safer chemical design research.

EPA disclaimer

The views expressed in this paper are those of the authors and do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency.

Acknowledgements

This research is supported by the NSF Division of Chemistry and the Environmental Protection Agency under Grant No. 1339637. The authors would like to thank for the helpful discussions with Dr Cong Li, Dr Terrence Kavanagh, Dr Jakub Kostal, and Dr Philip Coish. The authors acknowledged the computational support provided by Dr William Jorgensen, Dr Julian Tirado-Rives and Yale high performance computing platform. PTA would like to recognize funding support from QAFCO.

References

1. P. T. Anastas and J. C. Warner, Green Chemistry: Theory and Practice, Oxford University Press, New York, USA, 1998.
2. P. Moi, K. Chan, I. Asunis, A. Cao and Y. W. Kan, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 9926–9930.
3. M. O'Connell and J. Hayes, Biochem. Soc. Trans., 2015, 43, 687–689.
4. M. Kobayashi and M. Yamamoto, Antioxid. Redox Signaling, 2005, 7, 385–394.
5. Q. Ma, Annu. Rev. Pharmacol. Toxicol., 2013, 53, 401–426.
6. F. Hong, K. E. Sekhar, M. L. Freeman and D. C. Liebler, J. Biol. Chem., 2005, 280, 31768–31775.
7. V. O. Tkachev, E. B. Menshchikova and N. K. Zenkov, Biochemistry, 2011, 76, 407–422.
8. Q. Ma and X. He, Pharmacol. Rev., 2012, 64, 1055–1081.
9. P. Talalay, M. J. D. E. Long and H. J. Prochaska, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 8261–8265.
10. M. K. Kwak, N. Wakabayashi and T. W. Kensler, Mutat. Res., 2004, 555, 133–148.
11. C. R. Wolf, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2941–2943.
12. K. N. Lewis, J. Mele, J. D. Hayes and R. Buffenstein, Integr. Comp. Biol., 2010, 50, 829–843.
13. T. Suzuki, H. Motohashi and M. Yamamoto, Trends Pharmacol. Sci., 2013, 34, 340–346.
14. K. W. Kang, S. J. Lee and S. G. Kim, Antioxid. Redox Signaling, 2005, 7, 1664–1673.
15. J. W. Kaspar, S. K. Niture and A. K. Jaiswal, Free Radicals Biol. Med., 2009, 47, 1304–1309.
16. T. Nguyen, P. Nioi and C. B. Pickett, J. Biol. Chem., 2009, 284, 13291–13295.
17. I. Casetta, V. Govoni and E. Granieri, Curr. Pharm. Des., 2005, 11, 2033–2052.
18. F. Giacco and M. Brownlee, Circ. Res., 2010, 107, 1058–1070.
19. N. Maicas, M. L. Ferrándiz, R. Brines, L. Ibáñez, A. Cuadrado, M. I. Koenders, W. B. van den Berg and M. J. Alcaraz, Antioxid. Redox Signaling, 2011, 15, 889–901.
20. M. Valko, C. J. Rhodes, J. Moncol, M. Izakovic and M. Mazur, Chem.-Biol. Interact., 2006, 160, 1–40.
21. E. Kansanen, S. M. Kuosmanen, H. Leinonen and A. L. Levonenn, Redox Biol., 2013, 1, 45–49.
22. H. Sun, M. Xia, C. P. Austin and R. Huang, AAPS J., 2012, 14, 473–480.
23. D. Krewski, M. Westphal, M. Al-Zoughool, M. C. Croteau and M. E. Andersen, Annu. Rev. Public Health, 2011, 32, 161–178.
24. D. J. Dix, K. A. Houck, M. T. Martin, A. M. Richard, R. W. Setzer and R. J. Kavlock, Toxicol. Sci., 2006, 95, 5–12.
25. F. S. Collins, G. M. Gray and J. R. Bucher, Science, 2008, 319, 906–907.
26. R. S. Judson, K. A. Houck, R. J. Kavlock, T. B. Knudsen, M. T. Martin, H. M. Mortensen, D. M. Reif, D. M. Rotroff, I. Shah, A. M. Richard and D. J. Dix, Environ. Health Perspect., 2009, 118, 485–492.
27. S. J. Shukla, R. Huang, C. P. Austin and M. Xia, Drug Discovery Today, 2010, 15, 997–1007.
28. R. Kavlock, K. Chandler, K. Houck, S. Hunter, R. Judson, N. Kleinstreuer, T. Knudsen, M. Martin, S. Padilla, D. Reif, A. Richard, D. Rotroff, N. Sipes and D. Dix, Chem. Res. Toxicol., 2012, 25, 1287–1302.
29. M. S. Attene-Ramos, N. Miller, R. Huang, S. Michael, M. Itkin, R. J. Kavlock, C. P. Austin, P. Shinn, A. Simeonov, R. R. Tice and M. Xia, Drug Discovery Today, 2013, 18, 716–723.
30. A. M. Voutchkova, J. Kostal, J. B. Steinfeld, J. W. Emerson, B. W. Brooks, P. Anastas and J. B. Zimmerman, Green Chem., 2011, 13, 2373–2379.
31. J. Kostal, A. Voutchkova-Kostal, P. T. Anastas and J. B. Zimmerman, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6289–6294.
32. J. Kostal, A. Voutchkova-Kostal, B. Weeks, J. B. Zimmerman and P. T. Anastas, Chem. Res. Toxicol., 2012, 25, 2780–2787.
33. L. Q. Shen, R. Judson, F. Menlikov, J. Roethle, A. Gudibanda, J. B. Zimmerman and P. T. Anastas, Green Chem., 2016, 18, 4461–4467.
34. U. EPA, ToxCast & Tox21 Summary Files Released Dec. 2014, http://www.epa.gov/chemical-research/toxicity-forecaster-toxcasttm-data.
35. M. T. Martin, D. J. Dix, R. S. Judson, R. J. Kavlock, D. M. Reif, A. M. Richard, D. M. Rotroff, S. Romanov, A. Medvedev, N. Poltoratskaya, M. Gambarian, M. Moeser, S. S. Makarov and K. A. Houck, Chem. Res. Toxicol., 2010, 23, 578–590.
36. S. C. DeVito and R. L. Garrett, Designing Safer Chemicals. Green Chemistry for Pollution Prevention, American Chemical Society, Washington DC, USA, 1996.
37. K. Mansouri, A. Abdelaziz, A. Rybacka, A. Roncaglioni, A. Tropsha, A. Varnek, A. Zakharov, A. Worth, A. M. Richard, C. M. Grulke, D. Trisciuzzi, D. Fourches, D. Horvath, E. Benfenati, E. Muratov, E. B. Wedebye, F. Grisoni, G. F. Mangiatordi, G. M. Incisivo, H. Hong, H. W. Ng, I. V. Tetko, I. Balabin, J. Kancherla, J. Shen, J. Burton, M. Nicklaus, M. Cassotti, N. G. Nikolov, O. Nicolotti, P. L. Andersson, Q. Zang, R. Politi, R. D. Beger, R. Todeschini, R. Huang, S. Farag, S. A. Rosenberg, S. Slavov, X. Hu and R. S. Judson, Environ. Health Perspect., 2016, 124, 1023–1033.
38. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
39. Marvin Calculator Plugins, Calculator Plugins were used for structure property prediction and calculation, Marvin 6.3.4, 2013, ChemAxon (http://www.chemaxon.com).
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian∼09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
41. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
42. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
43. R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
44. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
45. J. A. Hinson and D. W. Roberts, Annu. Rev. Pharmacol. Toxicol., 1992, 32, 471–510.
46. M. D. Cronin, Curr. Comput.-Aided Drug Des., 2006, 2, 405–413.
47. D. M. Quinn, H. K. Nair, J. Seravalli, K. Lee, T. Arbuckle, Z. Radić, D. C. Vellom, N. Pickering and P. Taylor, in London Dispersion Interactions in Molecular Recognition by Acetylcholinesterase, ed. D. M. Quinn, A. S. Balasubramanian, B. P. Deoctor and P. Taylor, Springer, 1995.
48. J. V. Castell, R. Jover, C. P. Martínez-Jiménez and M. J. Gómez-Lechón, Expert Opin. Drug Metab. Toxicol., 2006, 2, 183–212.
49. M. T. Donato, A. Lahoz, J. V. Castell and M. J. Gómez-Lechón, Curr. Drug Metab., 2008, 9, 1–11.
50. S. N. Hart, Y. Li, K. Nakamoto, E. A. Subileau, D. Steen and X. Zhong, Drug Metab. Dispos., 2010, 38, 988–994.
51. B. K. Park, N. R. Kitteringham, J. L. Maggs, M. Pirmohamed and D. P. Williams, Annu. Rev. Pharmacol. Toxicol., 2005, 45, 177–202.
52. Handbook of Experimental Pharmacology, ed. G. Born, P. Cuatrecasas and H. Herken, Springer-Verlag, 1993, vol. 105.
53. P. McCullagh and J. A. Nelder, Generalized Linear Models, Chapman & Hall/CRC, London, United Kingdom, 2nd edn, 1989.
54. R. Tibshirani, J. R. Stat. Soc. Series B: Methodol., 1996, 58, 267–288.
55. T. E. Oliphant, Comput. Sci. Eng., 2007, 9, 10–20.
56. K. J. Millman and M. Aivazis, Comput. Sci. Eng., 2011, 13, 9–12.
57. R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2013.
58. E. Jones, T. Oliphant, P. Peterson, et al., SciPy: Open source scientific tools for Python, 2001, http://www.scipy.org/, [Online; accessed 2016-01-24].
59. S. van der Walt, S. Colbert and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 22–30.
60. pandas: Python Data Analysis Library, Online, 2012, http://pandas.pydata.org/.
61. F. Pérez and B. E. Granger, Comput. Sci. Eng., 2007, 9, 21–29.
62. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
63. L. Roschier, PyNomo - a program to create nomographs with Python, 2009, http://sourceforge.net/projects/pynomo/.
64. J. Friedman, T. Hastie and R. Tibshirani, J. Stat. Softw., 2010, 33, 1–22.
65. N. Simon, J. Friedman, T. Hastie and R. Tibshirani, J. Stat. Softw., 2011, 39, 1–13.
66. H. Wickham, ggplot2: Elegant Graphics for Data Analysis, Springer-Verlag, New York, 2009.
67. T. Sing, O. Sander, N. Beerenwinkel and T. Lengauer, Bioinformatics, 2005, 21, 3940–3941.
68. T. Iyanagi, Int. Rev. Cytol., 2007, 35–112.
69. C.-H. Chen, Activation and Detoxification Enzymes. Functions and Implications, Springer-Verlag, New York, 2012.
70. D. V. Parke, Regul. Toxicol. Pharmacol., 1982, 2, 267–286.
71. D. G. Deavall, E. A. Martin, J. M. Horner and R. Roberts, J. Toxicol., 2012, 2012, 1–13.
72. A. P. Bradley, Pattern Recogn., 1997, 30, 1145–1159.
73. T. A. Lasko, J. G. Bhagwat, K. H. Zou and L. Ohno-Machado, J. Biomed. Inf., 2005, 38, 404–415.
74. H. B. Mann and D. R. Whitney, Ann. Math. Stat., 1947, 18, 50–60.
75. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539.
76. J. A. H. Schwöbel, Y. K. Koleva, S. J. Enoch, F. Bajot, M. Hewitt, J. C. Madden, D. W. Roberts, T. W. Schultz and M. T. D. Cronin, Chem. Rev., 2011, 111, 2562–2596.
77. R. M. LoPachin and T. Gavin, Free Radical Res., 2016, 50, 195–205.
78. S. Magesh, Y. Chen and L. Hu, Med. Res. Rev., 2012, 32, 687–726.
79. E. K. Weisburger, Annu. Rev. Pharmacol. Toxicol., 1978, 18, 395–415.
80. P. O'Brien, Chem.-Biol. Interact., 1991, 80, 1–41.
81. W. D. Holtzclaw, A. T. Dinkova-Kostova and P. Talalay, Adv. Enzyme Regul., 2004, 44, 335–367.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/C6GC02073A

---