Sustainable, inexpensive and easy-to-use access to the super-reductant e^˙−_aq through 355 nm photoionization of the ascorbate dianion—an alternative to radiolysis or UV-C photochemistry

Abstract

We have investigated and exploited a new photochemical route to hydrated electrons, which are among the strongest reductants known and can even be used for direct carbon dioxide and nitrogen fixation. Our electron precursor is the ascorbate dianion, which we photoionize with a 355 nm laser. The method is instrumentally much simpler and far less accompanied by health and safety issues than is pulse radiolysis. Advantages over other photoionizable substrates or systems comprise the favourably long operating wavelength, at which many additives do not absorb anymore; the low price and nonexisting biohazards of this naturally occurring electron precursor; and the lack of visible absorption as well as the nonreactivity of the ionization by-product, the ascorbate radical, which greatly simplifies the mechanistic and kinetic studies of subsequent reactions. To illustrate the usefulness of this electron source, we have prepared a number of radical anions (through scavenging the electrons) including several that are inaccessible by the usual photochemical route for mechanistic or thermodynamic reasons, obtained their calibrated absorption spectra, and in one case investigated their green-light photochemistry. As proof of its applicability to environmental remediation, we have successfully utilized this electron generator to detoxify a model compound for halogenated organic waste.

---

1 Introduction

A sarcasm often ascribed to Liebig¹ but actually some 150 years older and due to Kunckel² ridicules the idea of a universal solvent (i.e., one capable of dissolving everything) by asking how to store it. The same dilemma would seem to exist for a universal reductant, but here the loophole is to release it from a stable precursor only on demand and in situ.

The hydrated electron e^˙−_aq comes close to being such a universal reductant in a medium of biological and environmental importance, because its standard potential of −2.9 V (ref. 3) empowers it to reduce “nearly everything”. Relevant examples start with the preparation of radical anions that cannot be obtained through excitation of their parent compounds,⁴ continue with the degradation of pharmaceutical pollutants,^5–7 rise to the detoxification of halogenated^8–12 as well as nonhalogenated¹³ persistent organic waste, and finally culminate in the fixation of molecular nitrogen¹⁴ or carbon dioxide.¹⁵ These highly promising applications raise the question of suitable precursors for e^˙−_aq, which decomposes even its own solvent, water, on a millisecond timescale.³

Radiolysis is an effective means to liberate the super-reductant e^˙−_aq from water itself^5,6,12,13 but affords several other reactive intermediates as well,³ thus complicating the systems; furthermore, the generation of ionizing radiation incurs safety and security hazards and is technically demanding in its time-resolved version. Much easier to handle is the access to e^˙−_aq through photoionization. Many simple species such as iodide,^11,14,15 sulfite,^7–9 hexacyanoferrate,¹⁰ and even water¹⁶ have been employed for that purpose but require excitation by UV-C light, which is often strongly absorbed by the substrates intended to react with e^˙−_aq or by other ingredients of the samples. The other extreme is provided by electron sources as recently found by us,^17,18 which need only green light to produce e^˙−_aq but are multicomponent systems in a microheterogeneous medium.

An important step towards a compromise between chemical simplicity and favourable operating wavelength has been taken by Johnston et al., who used the UV-A (355 nm) photoionization of 4,4′-dimethoxy stilbene in acetonitrile or dimethylformamide, their objective being a general route to the radical anions of additives through capture of the expelled electrons.⁴ However, the electrons attach chemically to these two solvents,^19,20 and the strong absorptions of the stilbene radical cation—the photoionization by-product—obliterate the UV and visible range, so have to be removed by adding also a nucleophile; the former effect made it impossible to obtain calibrated spectra, and both features increase the mechanistic complexity.

In our quest for a way to transfer this technique to water, where e^˙−_aq is an extremely well-characterised and relatively long-lived unique species,³ we discovered that the ascorbate dianion Asc²⁻, which we had previously utilized as a sacrificial donor in catalytic photoionization cycles,^17,18,21,22 can itself be ionized with a 355 nm laser. Being a bioavailable and completely nontoxic substance, this extremely inexpensive precursor obviously provides sustainable access to e^˙−_aq, and its photoionizability in the UV-A avoids all potential issues associated with radiolysis or UV-C excitation. As we will show, its ionization by-product Asc˙⁻ also causes no problems, neither through its absorption nor through its reactivity; this contrasts favourably both with the above-mentioned stilbene (or the multitude of other organic compounds that are photoionizable with 355 nm but bring with them the same difficulties) and with NADH, which despite its price would also qualify as a sustainable near-UV source of e^˙−_aq but perturbs the spectra by strong and time-dependent absorptions over the whole observation range owing to a protonation equilibrium of its radical.²³

In this work, we have thoroughly characterized the 355 nm photoionization of Asc²⁻ and developed it into a routine method for preparing precisely defined concentrations of radical anions. This approach immediately yields reliably calibrated absorption spectra of these species and, in consequence of the virtual nonreactivity of the counter-radical Asc˙⁻, opens the way to investigate their subsequent thermal reactions or their photochemistry as if in an isolated system. Our examples include radical anions that cannot be obtained through electron-transfer quenching of their excited parent compounds because of competing photochemical reactions or because they lie too high in energy, as well as radical anions for which this standard route is viable but gives spectra that are complicated by the absorptions of earlier intermediates or are difficult to calibrate because of incomplete charge separation. Finally, we demonstrate the value of our new electron source for environmentally-relevant application by decomposing chloroacetate, a popular model reaction for the elimination of halogenated organic pollutants from drinking water.⁸

2 Results and discussion

2.1 The method

2.1.1 Asc²⁻ as an electron source in the near UV. Ascorbic acid Asc²⁻ acid is dibasic with pK_a values of 4.25 and 11.79 in water;²⁴ hence, its fully protonated form plays no role under physiological conditions or in more basic medium. Its oxidation yields the monoanion radical Asc˙⁻ regardless of pH, because the more highly protonated forms of this radical are too acidic (the pK_a value of AscH˙ is −0.45).²⁴ Deprotonation facilitates the oxidation, with the standard potentials being 0.70 V and 0.05 V for the couples Asc²⁻˙/AscH⁻ and Asc˙⁻/Asc²⁻.²⁴

While the ascorbate monoanion AscH⁻ can be photoionized at 254 nm (ref. 25) but no longer at 308 nm or 355 nm,^21,22 we recently observed that the red shift of the absorption band by about 40 nm (see, the ESI†) and the decrease of the redox potential associated with the second deprotonation step suffice to extend the photoionizability of the dianion Asc²⁻ not only to 308 nm but also to 355 nm.²² In this section, we present a comprehensive investigation of this ionization at the latter wavelength in the near UV.

The transient absorption spectrum of a strongly basic ascorbate solution directly after a 355 nm laser flash is the superposition of two bands (see the main plot of Fig. 1a). The first, with the maximum at 720 nm and extending over the whole visible range, clearly belongs to the hydrated electron e^˙−_aq, as follows from the known spectral characteristics and the complete removal of this band when the solution is saturated with the specific electron scavenger N₂O.³ The second, centered at 360 nm and with a full width at half maximum of only 50 nm, is due to the ascorbate radical Asc˙⁻; it is identical to the signal we observed when we photoionized Asc²⁻ with 308 nm (ref. 22) or employed ascorbate to quench oxidizing radicals.^22,26 To separate the two bands, we first recorded the electron spectrum free from absorbances of any other species by photoionizing mere water at the same pH with 266 nm.¹⁶ Scaling the result of that control experiment C(λ) with a factor n to match the experimental spectrum of the ascorbate sample E(λ) in the region above 500 nm yields the spectral contribution of e^˙−_aq, and taking the difference E(λ) − nC(λ) then yields that of Asc˙⁻. This straightforward procedure does not rely on any assumptions, and is obviously valid at all points of time after the laser flash.

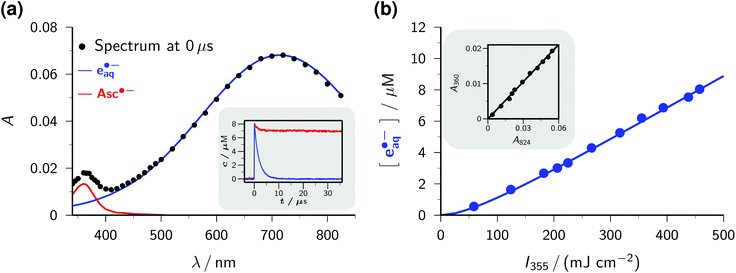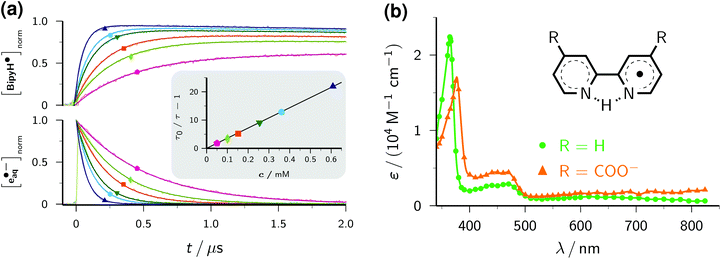
Fig. 1 Near-UV (355 nm) photoionization of an argon-saturated 5 mM solution of Asc²⁻ (pH 12.7). (a) Main plot, decomposition of the absorption spectrum immediately after a laser flash of intensity 450 mJ cm⁻². Dots, experimental absorptions E(λ); blue curve, contribution of e^˙−_aq, i.e., scaled spectrum nC(λ) of e^˙−_aq obtained by two-photon ionization of water at 266 nm (without ascorbate); red curve, contribution of Asc˙⁻, i.e., E(λ) − nC(λ). Inset, concentration traces for e^˙−_aq and Asc˙⁻ under the same experimental conditions; the laser is fired at time 0 μs. (b) Main plot, dependence of the electron concentration [e^˙−_aq] on the laser intensity I₃₅₅. The blue curve represents a fit with a biphotonic model.²⁷ Inset, linear dependence of the absorptions at 824 nm (A₈₂₄, e^˙−_aq only) and at 360 nm (A₃₆₀, e^˙−_aq and Asc˙⁻). For further explanation, see the text.

The main plot of Fig. 1b displays the dependence of the electron yield on the laser intensity. For instrumental reasons, we observed e^˙−_aq not at its spectral maximum but at 824 nm.²² To obtain the electron concentrations, we used the widely accepted molar absorption coefficient at maximum, 22 700 M⁻¹ cm⁻¹,²⁸ which after application to C(λ) gave values of 16 900 M⁻¹ cm⁻¹ and 1500 M⁻¹ cm⁻¹ at 824 nm and 360 nm. The intensity dependence exhibits only a minute upward curvature, but the negative intercept when it is fitted by a straight line clearly identifies the ionization as biphotonic,²⁹ as described by eqn (1),

The extremely small molar absorption coefficient of Asc²⁻ at 355 nm, only 40 M⁻¹ cm⁻¹, might suggest this electron source to be very inefficient. However, Fig. 1b demonstrates that under our experimental conditions up to 8 μM of e^˙−_aq are generated (maximum energy density of the laser flash, 450 mJ cm⁻²). This is equivalent to the electron yield with a dose of about 30 Gy, that is, in a typical pulse radiolysis experiment.³

Plotting the absorbances at 360 nm (Asc˙⁻ and e^˙−_aq) versus those at 824 nm (e^˙−_aq only) gives a straight line, as can be seen in the inset of Fig. 1b. The ejection of a hydrogen atom, a process frequently competing with photoionization,^30,31 is structurally impossible for the substrate Asc²⁻. The absence of any additional transients thus militates for stoichiometric equivalence between e^˙−_aq and Asc˙⁻, which in turn determines the molar absorption coefficient of Asc˙⁻ at 360 nm to be 4500 M⁻¹ cm⁻¹, identical to our result in the 308 nm photoionization of Asc²⁻ (ref. 22) and agreeing closely with the average of previously reported values (3700 M⁻¹ cm⁻¹ (ref. 24) and 4900 M⁻¹ cm⁻¹ (ref. 32)).

The inset of Fig. 1a finally shows the time dependence of the post-flash concentrations at our highest laser intensity. Within less than 10 μs, e^˙−_aq disappears completely whereas [Asc˙⁻] only decreases by about 10 percent and then remains constant. This classifies the bimolecular recombination of e^˙−_aq and Asc˙⁻ as a minor pathway and is indicative of the high stability of Asc˙⁻. The hardly changing concentration of Asc˙⁻ and the insignificance of self-termination at micromolar concentrations of e^˙−_aq (ref. 3) explain why we found the time dependence of [e^˙−_aq] to be indistinguishable from a monoexponential decay. A fit gave an electron life of 1.8 μs, which leaves ample margin for scavenging e^˙−_aq with an additive Q to give the radical anion Q˙⁻. On one hand, the competition by this process drives back the recombination of e^˙−_aq and Asc˙⁻ still further; on the other hand, Q˙⁻ necessarily lies lower in energy and because of its size diffuses less rapidly than does e^˙−_aq, so reacts even more slowly with Asc˙⁻, as it is reflected by the fact that we encountered no problems caused by a recombination of Q˙⁻ and Asc˙⁻ in any of our experiments. Ultimately, the radical Asc˙⁻—a key intermediate in radical-scavenging cascades of human metabolism—is either reduced to recover Asc²⁻ or further oxidized to give dihydroascorbate, which is also completely nontoxic.²⁴ The substrate Asc²⁻ also does not participate in any other way than by photoionization: neither is its excited state quenched by Q, nor is its ground state reduced by Q˙⁻. In conjunction, these properties make the ascorbate system an almost ideal electron source, featuring a nonreactive precursor and a noninterfering, quasi-stable by-product.

2.1.2 Stern–Volmer analysis of radical anion formation through scavenging of e^˙−_aq. For illustration, we have chosen 2,2′-bipyridine Bipy, which is known to react rapidly with e^˙−_aq.³ Even at our very high pH, the primarily formed radical anion is immediately monoprotonated to give the neutral radical BipyH˙ (for the formula, see Fig. 2b), which then undergoes disproportionation.³³ Obtaining a calibrated absorption spectrum of BipyH˙ by the traditional photochemical method (excitation of Bipy in the UV-B or UV-C followed by intersystem crossing and electron transfer from a suitable donor to the triplet) is made difficult by the very similar spectra of the triplet and the radical;³⁴ furthermore, we found that laser flash photolysis at 308 nm or 266 nm also generates some amount of e^˙−_aq through photoionization of the triplet, so produces not only an additional amount of BipyH˙ that is difficult to quantify but also unwanted absorptions due to its radical cation. The ascorbate access to BipyH˙ circumvents all these problems because it uses 355 nm.

Fig. 2 (a) Stern–Volmer analysis for scavenging e^˙−_aq with 2,2′-bipyridine Bipy, with quencher concentration/symbols/colour being 5.0 × 10⁻⁵ M/pentagons/pink, 1.0 × 10⁻⁴ M/diamonds/light green, 1.5 × 10⁻⁴ M/squares/orange, 2.6 × 10⁻⁴ M/inverted triangles/dark green, 3.6 × 10⁻⁴ M/circles/cyan, and 6.1 × 10⁻⁴ M/triangles/dark blue. The concentrations of e^˙−_aq (bottom) and of BipyH˙ (top), both normalized to the initial electron concentration, were obtained with the procedures explained in the text; solid lines are best fits of the functions also given there, with the same electron lifetime τ for the corresponding pairs of traces, and extrapolated back to the middle of the laser pulse. Inset, Stern–Volmer plot based on τ, with the same colour code for the quencher concentrations as in the main plot, and the unquenched lifetime τ₀ (trace not shown). (b) Calibrated absorption spectra of BipyH˙ (green, circles) and BipyH˙(COO⁻)₂ (orange, triangles) and structural formulae of the radicals. The curves are spline fits through the data points. For further details, see the text.

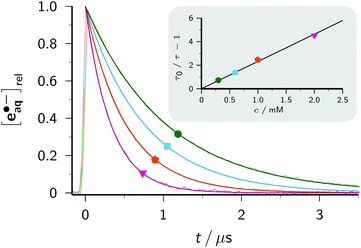
With this method, the electron decay, normalized to the concentration immediately after the laser flash, is extracted by forming the expression (A − A_∞)/(A₀ − A_∞), where A is the time-dependent absorbance at the observation wavelength for e^˙−_aq, with A₀ and A_∞ being its initial post-flash and its final value, respectively. This analysis relies merely on a constant stoichiometric relationship between the decrease of e^˙−_aq and the increase of the absorbing product(s) through scavenging, therefore is not restricted to first-order kinetics. Complications can arise when the radical anion is not stable. In that case, the contributions of it and of its subsequent products to A should be minimized by choosing a suitable observation wavelength. Obviously, this is facilitated by the intense, yet very broad, absorption band of e^˙−_aq, which provides a window at least 300 nm wide for sensitive monitoring. In the case of BipyH˙, as well as for all other systems investigated in this work, our usual detection wavelength (824 nm) turned out to be adequate. The normalized electron decays are represented perfectly by fit functions exp(−t/τ), as seen in the lower part of the main plot of Fig. 2a. The Stern–Volmer plot (inset of the figure) is linear and gives a rate constant of 2.38 × 10¹⁰ M⁻¹ s⁻¹ for the scavenging of e^˙−_aq by Bipy, in good agreement with values obtained by pulse radiolysis (1.9…2.5 × 10¹⁰ M⁻¹ s⁻¹).³

For any additive concentration, the above measurement at the reference wavelength allows the straightforward removal of the time-dependent contribution of e^˙−_aq and the initial one of Asc˙⁻ from the transient absorption at any other wavelength by using the spectrum of Fig. 1a. The subsequent fast decrease of Asc˙⁻ caused by its recombination with e^˙−_aq—a minor effect even in the absence of an additive, as the inset of Fig. 1a evidences—can be eliminated in an equally simple manner because it is an apparent first-order decay with the same time constant τ as that of the electron and an amplitude determined by competition kinetics; however, for a sufficiently large additive concentration even this correction is unnecessary as the amplitude becomes negligibly small. Under these circumstances, a series of wavelength-dependent traces recorded with the same concentration directly yields the uncalibrated absorption spectrum of the radical anion as the cross section at a constant post-flash time.

Provided that on the timescale of the radical anion rise its decay can be approximated by a first-order rate law with the apparent rate constant k, the corrected absorption at wavelength λ divided by (A₀ − A_∞) at the reference wavelength λ_ref equals the ratio r of molar absorption coefficients of the radical anion at λ and e^˙−_aq at λ_ref times the function {exp(−kt) − exp(−t/τ)}(1 − τ/τ₀)/(1 − kτ). The upper part of the main plot of Fig. 2a demonstrates that the experimental data at 365 nm, corresponding to the maximum of the BipyH˙ spectrum, can be fitted with r as the global parameter and local k. This system thus exhibits the expected Stern–Volmer behaviour, and through the described kinetic analysis at a single wavelength, the absorption spectrum is calibrated. Fig. 2b displays the result. We found a significantly lower molar absorption coefficient at maximum (ε₃₆₅ = 22 100 ± 600 M⁻¹ cm⁻¹, average of 10 measurements with different concentrations of Bipy and/or e^˙−_aq) than that reported in the literature (about 30 000 M⁻¹ cm⁻¹).³³ As can be perceived in Fig. 2a, the decrease of BipyH˙ is quite slow; many of the radical anions studied in this work were completely stable during the observation period, so for them, the described analysis was even simpler (k = 0 in the above formula).

The derivative 2,2′-bipyridine-4,4′-dicarboxylate Bipy(COO⁻)₂ is widely used as a ligand in highly efficient photovoltaic cells, where it acts as an anchor of ruthenium-based light harvesting compounds to a semiconductor surface.³⁵ The absorption of a photon transforms such a complex into its metal-to-ligand charge-transfer (MLCT) state, which is best described as possessing an oxidized metal atom and a radical-anion ligand.³⁶ A characterization of the radical anion should thus help understand the influence of the ligand on the overall photo process. Yet, only scarce experimental information about non-complexed Bipy(COO⁻)₂ can be found in the literature. From density-functional calculations, it was concluded that the carboxylic groups exert only an electron withdrawing effect with little consequence for the electronic and spectral properties.³⁷ We, therefore, assume that Bipy(COO⁻)₂, which exclusively exists in its doubly deprotonated form under our experimental conditions,³⁸ behaves analogously to Bipy upon reduction, that is, forms the radical species BipyH˙(COO⁻)₂. Despite the Coulombic repulsion that e^˙−_aq experiences with Bipy(COO⁻)₂ as opposed to Bipy, we found only a moderate reduction of the scavenging rate, to 1.83 × 10¹⁰ M⁻¹ s⁻¹. The spectra of BipyH˙ and BipyH˙(COO⁻)₂ (Fig. 2b) are very similar, but the main band of the dicarboxylate-substituted radical is slightly red-shifted and substantially less intense (ε₃₇₅ = 17 600 M⁻¹ cm⁻¹).

2.2 Examples illustrating the advantages of the method

2.2.1 Circumventing reactions that interfere with direct radical anion generation. The two compounds of this section, valerophenone VP and 2-hydroxy-2-methyl propiophenone HMP (for the molecular skeletons, see Fig. 3a), serve as archetypal examples of substrates that decompose rapidly and efficiently through Norrish-II and Norrish-I processes upon the absorption of a photon. This property makes bimolecular quenching of their excited states not a very attractive route to their radical anions because it would dictate impractically high quencher concentrations to suppress the products of their monomolecular decay. A related case is provided by cinnamate with its extremely short-lived excited state, but will be dealt with in the next section because its radical anion is also very high-lying energetically.

Fig. 3 (a) Calibrated absorption spectra and structural formulae of the radical anions of VP (green circles) and HMP (orange diamonds). Ascorbate concentration, laser intensity, and substrate concentration: 5 mM, 450 mJ cm⁻², and 3.1 × 10⁻⁴ M (VP); 9 mM, 123 mJ cm⁻², and 7.9 × 10⁻⁵ M (HMP). The curves are spline fits through the experimental data points. (b) Reaction schemes upon excitation of VP and HMP. For further explanation, see the text.

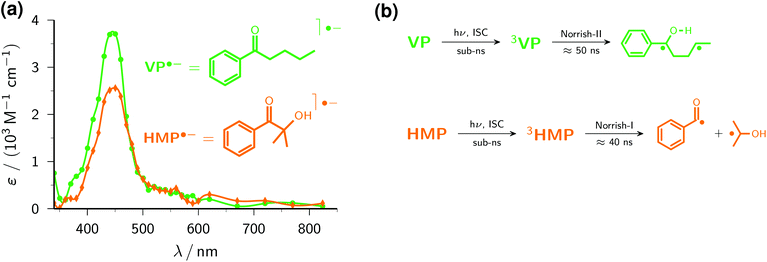
The photophysics and photochemistry of VP in aqueous solution have been thoroughly studied, both experimentally³⁹ and computationally.⁴⁰ After excitation of VP, intersystem crossing occurs on a subnanosecond timescale; subsequently, intramolecular hydrogen abstraction (Fig. 3b) limits the lifetime of the triplet to about 50 ns. The resulting biradical ultimately affords cleavage and cyclization products.

Johnston et al.⁴ already utilized the capture of electrons ejected from 4,4′-dimethoxy stilbene in acetonitrile to obtain the uncalibrated spectrum of the valerophenone radical anion VP˙⁻ in that medium. Our ascorbate method is more than simply an extension to aqueous solution, because it simultaneously provides the electron scavenging rate, 1.85 × 10¹⁰ M⁻¹ s⁻¹, and the calibrated radical anion spectrum (ε₄₄₅ = 3700 M⁻¹ cm⁻¹) through Stern–Volmer analysis described in the preceding section. In water, the spectrum of VP˙⁻ (see, Fig. 3a) is blue-shifted by 35 nm compared to acetonitrile, a solvatochromic effect reported for other carbonyl radical anions as well.⁴¹ Control experiments without Asc²⁻ gave no detectable absorptions in the wavelength range of interest, which shows the spectrum of Fig. 3a to be free from contaminations by transients formed through direct excitation of VP.

The popular polymerization initiator HMP has also been extensively investigated with regard to its photochemistry.^42,43 In water, its triplet is again formed within subnanoseconds and decomposes on a timescale of some 40 ns by α-cleavage (Fig. 3b) to give the initiator species proper.⁴⁴

Despite its low molar absorption coefficient at the laser wavelength (ε₃₅₅ ≈ 15 M⁻¹ cm⁻¹; for the spectrum, see the ESI†), the excitation of HMP alone at a concentration sufficient for quantitative scavenging of e^˙−_aq (5 × 10⁻⁴ M) yields appreciable transient absorptions at our usual laser level. To minimize these spectral contaminations, we reduced both the laser intensity and the maximum HMP concentration. The former entails a lower degree of Asc²⁻ ionization (Fig. 1b), which can be easily compensated for by raising the Asc²⁻ concentration until the desired sensitivity is reached; the latter decreases the amount of e^˙−_aq trapping (to two-thirds in this case), which is accommodated by Stern–Volmer analysis without deterioration of the precision. The slightly higher rate constant for scavenging e^˙−_aq by HMP, 2.22 × 10¹⁰ M⁻¹ s⁻¹, is in accordance with the slightly smaller molecular size compared to VP; as Fig. 3a shows, the spectral shapes and peak positions of HMP˙⁻ and VP˙⁻ are very similar, but the maximum molar absorption coefficient of HMP˙⁻ is noticeably smaller (ε₄₅₀ = 2600 M⁻¹ cm⁻¹).

2.2.2 Access to energy-rich radical anions. The number of electron donors capable of quenching the excited states of compounds with very negative reduction potentials is severely limited, for simple thermodynamic reasons. Our route via the extremely strong reductant e^˙−_aq circumvents this problem by removing the necessity of generating a radical cation in addition to the desired radical anion, at the same time avoiding absorptions or secondary reactions caused by the presence of this by-product.
1,5-Naphthalene disulfonate. We have recently presented an in-depth investigation of 1,5-naphthalene disulfonate NDS²⁻ (standard potential, −1.97 V)⁴⁵ as the key ingredient for a highly efficient catalytic cycle of green-light ionization.²¹ To obtain the calibrated spectrum of the radical anion NDS˙³⁻, two-laser experiments and a three-component spectral separation were necessary in our earlier study. Not only does the simplicity of our new procedure compare very favourably with this, but especially noticeable is that significant differences between the two spectra arise only at wavelengths where we previously had to apply massive corrections for perturbing absorptions by other species.
Cinnamate. The standard potential of cinnamate CA⁻ (for the molecular formula, see Fig. 5) in water is unknown but can be approximated by that of styrene in dimethylformamide (−2.36 V) because the carboxylate substituent has a negligible Hammett constant.⁴⁶ In addition to the thermodynamic demands arising from this very negative potential, a photoinduced electron transfer to the excited state *CA⁻ faces the competition with extremely rapid deactivation through cis–trans isomerization.

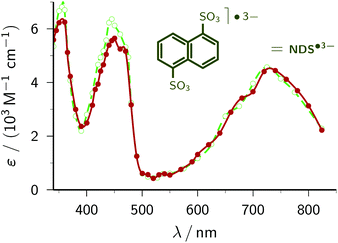Fig. 4 Comparison of the calibrated absorption spectra of NDS˙³⁻ as reported previously by us²¹ (green; open circles and dashed line) and obtained by the method of this work (red; solid circles and solid line). The curves are spline fits. The structural formula of NDS˙³⁻ is given above the spectra. For further explanation, see the text.

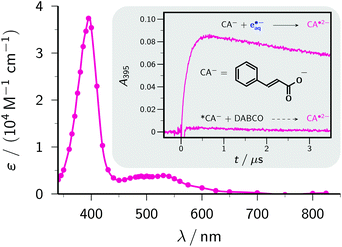Fig. 5 Main plot, calibrated absorption spectrum of the radical anion CA˙²⁻. The solid curve is a spline fit through the data points (circles). Inset, comparison of absorption traces at the absorption maximum, 395 nm, in experiments with electron-transfer quenching of the excited state *CA⁻ (obtained through excitation of CA⁻ with 308 nm; concentration of *CA⁻, 2.7 × 10⁻⁵ M, as determined by actinometry with benzophenone-4-carboxylate²⁷) with 0.5 M DABCO, and with scavenging of 6.3 × 10⁻⁶ M e^˙−_aq, produced through 355 nm photoionization of 5 mM Asc²⁻, by 0.4 mM CA⁻. For further explanation, see the text.

The inset of Fig. 5 illustrates the virtual impossibility of generating the radical anion CA˙²⁻ through electron-transfer quenching of *CA⁻ even with high concentrations of a good donor. The popular quencher DABCO (1,4-diazabicyclo[2.2.2]octane) requires only 0.80 V vs. a normal hydrogen electrode for its oxidation to the radical cation in a polar solvent,⁴⁶ therefore with an energy of about 4 eV for *CA⁻, as estimated from the red edge of the longest-wavelength absorption band of CA⁻, electron transfer from DABCO to *CA⁻ is sufficiently exergonic to be diffusion controlled (k ≈ 10¹⁰ M⁻¹ s⁻¹, as anticipated on the basis of this reasoning; the absence of detectable luminescence made a determination by fluorescence quenching impossible). With a DABCO concentration of 0.5 M and an excited-state lifetime of 50 ps, which is typical for molecules with similar isomerizable structures,⁴⁷ a quenching efficiency of 0.2 is thus expected. However, this experiment (excitation with 308 nm, intensity chosen such that the amount of *CA⁻ quenched by DABCO is similar to the amount of e^˙−_aq obtained by our photoionization of Asc²⁻ and scavenging by ground-state CA⁻) afforded practically no CA˙²⁻. We attribute this to rapid spin-allowed back electron transfer of the radical ion pairs, a general problem with electron-transfer quenching of singlet states.⁴⁸

In contrast, our ascorbate method easily allowed quantitative scavenging of e^˙−_aq by CA⁻, with a rate constant of 1.56 × 10¹⁰ M⁻¹ s⁻¹, and immediately yielded the calibrated spectrum (ε₃₉₅ = 37 000 M⁻¹ cm⁻¹) of CA˙²⁻ displayed as the main plot of Fig. 5.

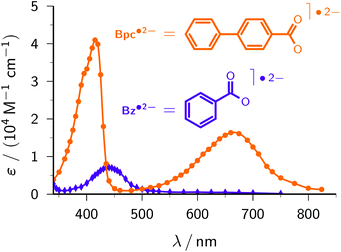
Benzoate. Benzoate Bz⁻ (structural formula, see Fig. 6; standard potential, −2.0 V)⁴⁶ serves to demonstrate another advantage of the ascorbate route to the radical anion Bz˙²⁻. Previous methods to generate Bz˙²⁻ were based on pulse radiolysis;^3,49,50 excitation of Bz⁻ has to resort to UV-C light owing to its absorption properties (see the ESI†). Our lower-energy (UV-A) ascorbate approach turned out to be equally feasible, and gave practically the same rate constant of the reaction between e^˙−_aq and Bz⁻ and the same calibrated absorption spectrum (Fig. 6) as reported in ref. 50. Hence, this model compound highlights that the two-photon ionization of Asc²⁻ can be a much simpler alternative to pulse radiolysis.

Fig. 6 Calibrated absorption spectra of Bz˙²⁻ (violet, diamonds) and Bpc˙²⁻ (orange, circles). The structural formulae are given above the spectra. The curves are spline fits through the data. For further explanation, see the text.

Biphenyl-4-carboxylate. With the same reasoning as for CA⁻, above, we estimate the unavailable standard potential of biphenyl-4-carboxylate Bpc⁻ (structure included in Fig. 6) to be nearly identical to that of the basic compound biphenyl (−2.31 V).⁴⁶ At the very high pH of our experiments, only the deprotonated form Bpc˙²⁻ of the radical anion is present.⁵¹ Comparing the spectrum of Bpc˙²⁻ recorded with our ascorbate method (Fig. 6) with the published one,⁵¹ we found exactly the same intensity ratio of the maxima at 415 nm and 660 nm, 2.5 : 1, but were not able to confirm the—quite untypical—30 nm wide plateau around the former maximum, which might have been due to products of reactions with other species generated by the pulse radiolysis. We obtained a slightly higher molar absorption coefficient at 415 nm, ε₄₁₅ = 41 700 M⁻¹ cm⁻¹vs. 38 000 M⁻¹ cm⁻¹ (literature value recalculated using the currently accepted²⁸ molar absorption coefficient of e^˙−_aq), and a rate constant for the scavenging of e^˙−_aq by Bpc⁻ at pH 12.7 (1.42 × 10¹⁰ M⁻¹ s⁻¹) which, after correction for ionic strength effects with the Brønsted–Bjerrum equation,³ is identical to the reported one (8.96 × 10⁹ M⁻¹ s⁻¹vs. 9 × 10⁹ M⁻¹ s⁻¹ at pH 6.5–7).

2.2.3 Isolated observation of subsequent reactions of radical anions. Many radical anions X˙⁻ absorb in the visible range (see, for instance, Fig. 3–6). Provided that their parent molecules X are transparent in that region, as is the case for all the aforementioned compounds, the ascorbate method can be put to good use, with some generality, as the first block of a two-pulse–two-colour^21,30,52 experiment (355 nm—delay—λ_vis). Because only X˙⁻ experiences the second pulse, its visible-light photochemistry can be studied in isolation by these experiments. Particularly convenient are the absence of time-dependent background signals and the precise knowledge of the concentration of X˙⁻ before the visible pulse.

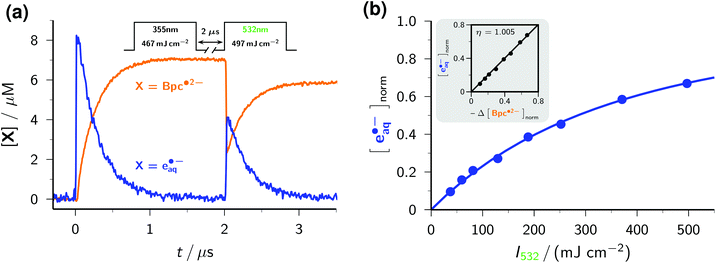
As an example, we have selected the green-light ionization of Bpc˙²⁻ because this process has previously been investigated by pulse radiolysis followed by a laser flash,⁴⁹ and because the calibrated spectrum of this radical anion already was the subject of the preceding section. Fig. 7a displays typical experimental traces. The first laser pulse (355 nm, at 0 μs) acts only on Asc²⁻ and quasi-instantaneously generates e^˙−_aq, which is then scavenged by Bpc⁻ to give Bpc˙²⁻; only the latter is present immediately before the second laser pulse (532 nm, at 2 μs). This second flash bleaches about 70% of Bpc˙²⁻, in the process liberating the same amount of e^˙−_aq. By experiments with the UV-laser blocked or without Bpc⁻, we verified that the green flash alone has no effect on Bpc⁻, on Asc²⁻, and on Asc˙⁻. We further varied the concentration of Bpc˙²⁻ through the intensity of the first pulse (compare Fig. 1b), and the turnover of the photoreaction of Bpc˙²⁻ through that of the second pulse. The results of these control experiments pinpoint Bpc˙²⁻ as the green-light source of e^˙−_aq.

Fig. 7 Green-light ionization of the radical anion Bpc˙²⁻. Graph (a), concentration traces for Bpc˙²⁻ (orange) and e^˙−_aq (blue) in a two-pulse experiment (pulse scheme and parameters given above the traces) on a solution of 2 × 10⁻⁴ M Bpc⁻ and 5 mM Asc²⁻. Main plot of graph (b), dependence of the normalized electron yield [e^˙−_aq]_norm (i.e., concentration of e^˙−_aq produced by the 532 nm laser pulse relative to the concentration of Bpc˙²⁻ immediately before that pulse) as a function of the intensity I₅₃₂ of the green laser pulse. Inset of graph (b), electron formation [e^˙−_aq]_norm as a function of radical anion bleaching −Δ[BPC˙²⁻]_norm, normalization in the same way as above. The slope η of 1 shows the absence of other green-light photochemistry of Bpc˙²⁻ except photoionization. For further explanation, see the text.

The intensity dependence of electron formation by the green pulse (see Fig. 7b) exhibits a linear relationship with zero intercept at low intensities, which is clear evidence for a monophotonic ionization of Bpc˙²⁻,²⁹ and the typical saturation behaviour at high intensities.²¹ The linear plot of e^˙−_aq formation against Bpc˙²⁻ bleaching with a slope of 1 (inset of the figure) establishes that the green-light ionization of Bpc˙²⁻ is not accompanied by side reactions, as we and others already found for this and other aryl radical anions.^18,21,49

To determine the quantum yield of the green-light ionization, we performed relative actinometry with the ruthenium-(tris)bipyridine dication as the reference,^17,18 comparing the spectrophotometrically measured amount of e^˙−_aq produced by the green pulse with the 532 nm induced quantitative formation of the metal-to-ligand charge-transfer excited state of the complex,⁴⁶ monitored through its emission. We obtained a substantially higher quantum yield than reported earlier, 0.15 as opposed to 0.06,⁴⁹ but consider our new value more reliable for two reasons. First, we based our comparison on fits over the whole intensity range both for the ionization and for the reference, which avoids the uncertainties of single-point (i.e., at one excitation intensity only) actinometry. Second, both our calibration of the radical anion spectrum and our determination of the electron yield are based on the molar absorption coefficient of e^˙−_aq, so any uncertainty of this parameter (which was recently found to be significantly higher than previously thought)²⁸ is cancelled.

2.3 Application: detoxification of halogenated waste

Halogenated organic compounds present severe ecological problems because of their toxicity and persistence—hence, accumulation—in the environment. Approaches to their detoxification include oxidative or reductive dehalogenation by using microorganisms, enzymes, or metal complexes;^53,54 recently, cleavage of the carbon–halogen bond by e^˙−_aq generated radiolytically or with UV-C light has received strongly growing attention.^8–12

To test the feasibility of our ascorbate method for this task, we selected the popular model compound chloroacetate ClCH₂COO⁻, which to date is not known to be reducible through photoinduced electron transfer but reacts rapidly with the super-reductant e^˙−_aq in a dissociative electron transfer according to eqn (2).³

ClCH₂COO⁻ + e^˙−_aq → Cl⁻ + ˙CH₂COO⁻ (2)

A Stern–Volmer analysis of the electron decay as a function of the ClCH₂COO⁻ concentration (see Fig. 8) yielded a quenching rate constant of 1.29 × 10⁹ M⁻¹ s⁻¹. Referring both this value and the one reported for pH 11 (8.9 × 10⁸ M⁻¹ s⁻¹)³ to zero ionic strength with the Brønsted–Bjerrum equation³ gave practically identical results (8.1 × 10⁸ M⁻¹ s⁻¹ and 8.3 × 10⁸ M⁻¹ s⁻¹). The independence of the e^˙−_aq concentration immediately after the laser flash shows that the excited state *Asc²⁻ is not quenched even by the highest concentration of ClCH₂COO⁻ used in Fig. 8. Any such direct electron transfer from *Asc²⁻ to ClCH₂COO⁻ would reduce the amount of *Asc²⁻ available for absorbing the second photon (see eqn (1)), so would proportionally reduce the amount of e^˙−_aq ejected. On the basis of these measurements, we estimate the—unknown—lifetime of *Asc²⁻ to be significantly shorter than 1 ns.

Fig. 8 Main plot, traces of the normalized electron concentration monitored at 824 nm for different concentrations of ClCH₂COO⁻ overlaid with best-fit functions of type exp[−t/τ]. Inset, Stern–Volmer plot based on the values of τ determined in the main plot and the unquenched lifetime τ₀ (trace not shown). The same colour codes and labels have been used in both plots (green circle, 0.3 mM; cyan square, 0.6 mM; orange pentagon, 1 mM; pink inverted triangle, 2 mM). For further explanation, see the text.

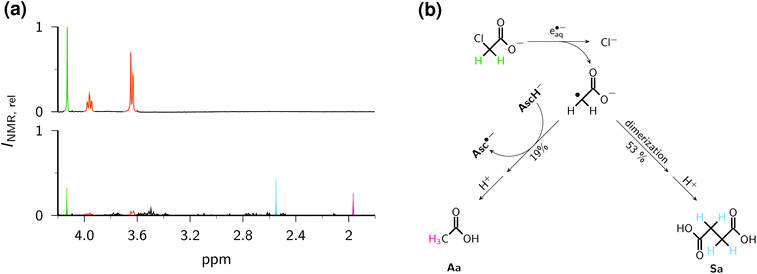
Determination of the further fate of the acetate radical ˙CH₂COO⁻ spectrophotometrically is hampered by its weak molar absorption coefficient in the visible range⁵⁵ and the absence of absorptions by the conceivable (nonaromatic) diamagnetic products in that region. Hence, we resorted to ¹H-NMR spectroscopy to identify and quantify the main products. The photochemical protocol of this experiment comprised irradiating 2 ml of an argon-saturated basic solution (pH 12.7) containing 0.01 M of Asc²⁻ and ClCH₂COO⁻ each in a quartz cuvette (optical pathlength, 1 cm; illuminated volume restricted by the optical setup to one-third of the filled volume) with 355 nm pulses of 191 mJ per pulse at 10 Hz for 15 min under continuous mixing. As workup, we decreased the pH to about 1.0 by adding the required amount of concentrated sulfuric acid to avoid the necessity of recording the NMR spectrum under an inert gas (because of the fast oxidation of ascorbate in strongly basic solution by molecular oxygen),²⁴ and to protonate any remaining starting material as well as products containing carboxylate and/or ascorbate residues. For product identification, we used authentic samples of reference compounds; for quantification, we took the integrals over the pertinent signals in spectra acquired with a sufficiently long relaxation delay.

Relative to the starting solution (Fig. 9a), the irradiation decreased the amount of ClCH₂COO⁻ by 76% and that of Asc²⁻ by 90% (Fig. 9b), whereas control experiments established that ClCH₂COO⁻ is not decomposed under our irradiation conditions when no Asc²⁻ is present. The two main products can be unambiguously identified as acetic acid Aa (s, 1.97 ppm) and succinic acid Sa (s, 2.55 ppm). Taking into account the number of observed protons in each compound, the signal integration reveals that 53% of the acetate radicals dimerize to give Sa and 19% are converted to Aa. The formation of both products is known from studies with the UV-C/sulfite route to e^˙−_aq; there, however, the yield of Aa was considerably higher than that of Sa.⁸ We ascribe the preference of the dimerization product to a much higher radical concentration in our experiments caused by the high energy density of our laser; hence, this process could probably be developed into another general method for the dimerization of alkyl halides in the sense of ref. 56, but metal-free.

Fig. 9 Dechlorination of ClCH₂COO⁻ by e^˙−_aq generated with the ascorbate method. (a), ¹H-NMR spectra of an aqueous solution of 0.01 M Asc²⁻ and ClCH₂COO⁻ before (top) and after (bottom) irradiation, both after the same workup and with the same vertical scale I_NMR,rel. The peak heights do not reflect the intensities (integrals) exactly because of different line widths in the two spectra. (b) Reaction pathways to the two main products Aa and Sa. The same colour coding is used for the corresponding protons in the spectra and in the scheme: green, chloroacetic acid, 4.13 ppm (s); orange, ascorbic acid, 3.64 ppm (d) and 3.96 ppm (m); pink, acetic acid Aa, 1.96 ppm (s); cyan, succinic acid Sa, 2.55 ppm (s). For further explanation, see the text.

Fig. 9c sums up the reaction pathways to the two main products. Not only is an ascorbate-derived species—that is, an excellent electron donor when present as the dianion Asc²⁻, and a good hydrogen atom donor in its monoanionic form—the most plausible candidate for converting the acetate radical into the diamagnetic acetate anion, but this is also corroborated by the fact that the additional amount of Asc²⁻ consumed by this step, 1.19 × 76%, accounts quantitatively for the observed higher turnover of Asc²⁻ with respect to that of ClCH₂COO⁻. This comparison also suggests that hardly any Asc²⁻ is lost by parasitic processes. Although an electron-transfer from Asc²⁻ to the acetate radical to give a stabilized carbanionic species that is subsequently protonated by the aqueous medium is conceivable, we consider a direct atom transfer from the monoanion, which is still present in a 1 mM concentration under our conditions, as more likely.

As is evident from Fig. 9b, further minor products of the dehalogenation process are numerous and possess complicated NMR spectra; besides, reference compounds for their identification are not commercially available. However, the results of this section already demonstrate that the ascorbate method is capable of detoxifying chloro-organics photochemically with UV-A light, which is much less likely to be absorbed by additives or a complex matrix than is UV-C. The application to perfluorinated compounds, which are known to be decomposed by e^˙−_aq generated from inorganic chemicals with UV-C light,^9–11 appears an especially promising extension.

3 Experimental section

Nanosecond laser flash photolysis experiments were carried out with a setup described elsewhere,²¹ with detection of absorption and/or luminescence. For the ascorbate ionizations, we used a frequency-tripled (355 nm) Nd:YAG laser (Continuum SureLite III, 5 ns pulse width), and for the two-pulse experiments of Fig. 7 another frequency-doubled (532 nm) such laser.

All chemicals were obtained in the highest available purity and used as received: acetic acid (glacial), >99.8%, Merck; L(+)-ascorbic acid sodium salt, ≥99%, Carl Roth; benzoic acid p.a., >99%, VK Labor- und Feinchemikalien; biphenyl-4-carboxylic acid, 98%, Alfa Aesar; 2,2′-bipyridine, ≥99%, Aldrich; 2,2′-bipyridine-4,4′-dicarboxylic acid, 98%, Aldrich; chloroacetic acid sodium salt, 98%, Aldrich; cinnamic acid, >99%, Aldrich; deuterium oxide, 99.9% deuteration, Deutero GmbH; disodium 1,5-naphthalene disulfonate hydrate, >98%, TCI; 2-hydroxy-2-methyl propiophenone, 97%, Aldrich; ruthenium-tris(bipyridine)dichloride hexahydrate, 99%, abcr; sodium hydroxide, 99%, Grüssing; succinic acid p.a., ≥99.5%, Aldrich; sulfuric acid, 98%, Carl Roth; valerophenone, 99%, Aldrich. The solvent was Millipore MilliQ purified water (specific resistance, 18.2 MΩ cm).

All solutions were purged with argon (5.0, Air Liquide) for at least 30 minutes before the start and for the whole duration of the experiments. Unless noted otherwise, the pH was 12.7 in all measurements. To avoid oxidation, the sodium ascorbate was always added to the already degassed solution in solid form directly before the measurements. Even when not mentioned explicitly in the main text, control experiments were carried out for every system to ensure that neither photoionization nor other photochemistry occurs without Asc²⁻.

Steady-state absorption and fluorescence spectra were recorded on a Shimadzu UV-2102 spectrophotometer and a Perkin-Elmer LS 50B spectrometer.

The NMR experiments were carried out on a 400 MHz Varian 400 VNMRS spectrometer at 298 K. The intense water signal was suppressed by a PRESAT pulse sequence. Exactly equal volumes were used for the irradiated and the nonirradiated samples; for workup, to each sample was added the same small volume or amount of: first, concentrated sulfuric acid to adjust the pH; second, solid disodium 1,5-naphthalene disulfonate as the reference for quantifying the decrease of ClCH₂COO⁻ and the increase of Aa and Sa; and third, D₂O (10% v/v in the final mixture) for shimming and locking.

4 Conclusions

As has emerged from this work, the ascorbate dianion Asc²⁻ is a very clean source of the hydrated electron e^˙−_aq through its near-UV photoionization: clean in the five-fold sense that this precursor is free from any health hazards; that a great many additives intended to react with e^˙−_aq are transparent at the relatively long ionization wavelength; that the by-product of the ionization (Asc˙⁻) does not absorb in the visible range; that Asc²⁻ cannot be reduced, not even by the super-reductant e^˙−_aq; and that Asc˙⁻ is extremely unreactive, such that the decay of e^˙−_aq is an apparent first-order process. The last four of these properties result in a situation after the disappearance of e^˙−_aq where the system practically contains only the radical anions of the additives at a precisely defined concentration and in apparent isolation. Hence, calibrations of their spectra as well as mechanistic and kinetic studies of their subsequent reactions become extremely easy and reliable. Table 1 compiles the data obtained by this method.

Table 1 Radical anions prepared by the method of this work, rate constants of their generation by the capture of e^˙−_aq, and spectroscopic properties

Radical anion^a	Fig.^b	Rate constant^c (10^10 M^−1 s^−1)	Absorption maximum (nm)	Molar absorption coefficient (M^−1 cm^−1)
a Formal radical anion. The actual charge can differ because of charge-bearing substituents or protonation. b Figure giving the structural formula and spectrum. c At an ionic strength of 0.059 M.
BipyH˙	2b	2.38	365	22 100
BipyH˙(COO^−)2	2b	1.83	375	17 600
VP˙^−	3a	1.85	445	3700
HMP˙^−	3a	2.22	450	2600
NDS˙^3−	4	1.31	355	6500
			450	5700
			730	4500
CA˙^2−	5	1.56	395	37 000
Bz˙^2−	6	0.49	440	7200
Bpc˙^2−	6	1.42	415	41 700
			660	16 700

---

In addition to examples of these uses, we have validated the exploitation of our method in the field of environmental chemistry; we envisage that it should be equally applicable to chemical syntheses involving dissociative electron transfer.⁵⁷ The simplicity of the procedure compares very favourably with radiolysis. Given the inexpensive, user-friendly precursor Asc²⁻ and the low price of current near-UV lasers, it should be within easy reach of every photochemical laboratory to produce the super-reductant e^˙−_aq with its favourably long natural life (≈ 2 μs) in amounts per laser pulse that are comparable to typical pulse radiolysis experiments (≈10 μM).

References

1. J. Hausen, Was nicht in den Annalen steht, Verlag Chemie, Weinheim, 1969.
2. Anonymus, Lancet, 1843, 41, 363–364.
3. G. V. Buxton, C. L. Greenstock, W. P. Heiman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886.
4. N. Mathivanan, L. J. Johnston and D. D. M. Wayner, J. Phys. Chem., 1995, 99, 8190–8195.
5. M. Sánchez-Polo, J. López-Peñalver, G. Prados-Joya, M. A. Ferro-García and J. Riviera-Utrilla, Water Res., 2009, 43, 4028–4036.
6. A. Bojanowska-Czajka, G. Kciuk, M. Gumiela, S. Borowiecka, G. Nacz-Jawecki, A. Koc, J. F. Garcia-Reyes, D. S. Ozbay and M. Trojanowicz, Environ. Sci. Pollut. Res., 2015, 22, 20255–20270.
7. X. Liu, T. Zhang, L. Wang, Y. Shao and L. Fang, Chem. Eng. J., 2015, 260, 740–748.
8. X. Li, J. Ma, G. Liu, J. Fang, S. Yue, Y. Guan, L. Chen and X. Liu, Environ. Sci. Technol., 2012, 46, 7342–7349.
9. Z. Song, H. Tang, N. Wang and L. Zhu, J. Hazard. Mater., 2013, 262, 332–338.
10. L. Huang, W. B. Dong and H. Q. Hou, Chem. Phys. Lett., 2007, 436, 124–128.
11. H. Park, C. D. Vecitis, J. Cheng, W. Choi, B. T. Mader and M. R. Hoffmann, J. Phys. Chem. A, 2009, 113, 690–696.
12. Y. Peng, S. He, J. Wang and W. Gong, Radiat. Phys. Chem., 2012, 81, 1629–1633.
13. N. Liu, G. Xu, M. Wu, X. He, L. Tang, W. Shi, L. Wang and H. Shao, Res. Chem. Intermed., 2013, 39, 3727–3737.
14. J. R. Christianson, D. Zhu, R. J. Hamers and J. R. Schmidt, J. Phys. Chem. B, 2014, 118, 195–203.
15. L. Zhang, D. Zhu, G. M. Nathanson and R. J. Hamers, Angew. Chem., Int. Ed., 2014, 53, 9746–9750.
16. M. Goez and V. Zubarev, Chem. Phys., 2004, 307, 15–26.
17. M. Goez, C. Kerzig and R. Naumann, Angew. Chem., Int. Ed., 2014, 53, 9914–9916.
18. C. Kerzig and M. Goez, Chem. Sci., 2016, 7, 3862–3868.
19. S. C. Doan and B. J. Schwartz, J. Phys. Chem. B, 2013, 117, 4216–4221.
20. I. A. Shkrob and T. W. Martin, J. Phys. Chem. A, 2012, 116, 1746–1757.
21. C. Kerzig and M. Goez, Phys. Chem. Chem. Phys., 2014, 16, 25342–25349.
22. C. Kerzig and M. Goez, Phys. Chem. Chem. Phys., 2015, 17, 13829–13836.
23. B. Czochralska and L. Lindqvist, Chem. Phys. Lett., 1983, 101, 297–299.
24. M. B. Davies, J. Austin and D. A. Partridge, Vitamin C: Its Chemistry and Biochemistry, The Royal Society of Chemistry, Cambridge, 1991.
25. N. Getoff, In Vivo, 2013, 27, 565–570.
26. C. Kerzig, S. Henkel and M. Goez, Phys. Chem. Chem. Phys., 2015, 17, 13915–13920.
27. M. Goez and C. Kerzig, Angew. Chem., Int. Ed., 2012, 51, 12606–12608.
28. P. M. Hare, E. A. Price and D. M. Bartels, J. Phys. Chem. A, 2008, 112, 6800–6802.
29. U. Lachish, A. Shafferman and G. Stein, J. Chem. Phys., 1976, 64, 4205–4211.
30. R. W. Redmond, J. C. Scaiano and L. J. Johnston, J. Am. Chem. Soc., 1990, 112, 398–402.
31. R. Hermann, G. R. Mahalaxmi, T. Jochum, S. Naumov and O. Brede, J. Phys. Chem. A, 2002, 106, 2379–2389.
32. B. H. J. Bielski and H. W. Richter, Ann. N. Y. Acad. Sci., 1975, 258, 231–237.
33. Q. G. Mulazzani, S. Emmi, P. G. Fuochi, M. Venturi, M. Z. Hoffman and M. G. Simic, J. Phys. Chem., 1979, 83, 1582–1590.
34. Y. P. Tsentalovich, O. B. Morozova, A. V. Yurkovskaya and P. J. Hore, J. Phys. Chem. A, 1999, 103, 5362–5368.
35. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740.
36. P. S. Braterman, A. Harriman, G. A. Heath and L. J. Yellowlees, J. Chem. Soc., Dalton Trans., 1983, 1801–1803.
37. F. Labat, P. P. Lainé, I. Ciofini and C. Adamo, Chem. Phys. Lett., 2006, 417, 445–451.
38. M. K. Nazeeruddin and K. Kalyanasundaram, Inorg. Chem., 1989, 28, 4251–4259.
39. R. G. Zepp, M. M. Gumz, W. L. Miller and H. Gao, J. Phys. Chem. A, 1998, 102, 5716–5723.
40. L. Shen and W.-H. Fang, J. Org. Chem., 2011, 76, 773–779.
41. T. Shida, S. Iwata and M. Imamura, J. Phys. Chem., 1974, 78, 741–748.
42. L. Lecamp, B. Youssef, C. Bunel and P. Lebaudy, Polymer, 1997, 38, 6089–6096.
43. C. Decker, Macromol. Rapid Commun., 2002, 23, 1067–1093.
44. J. Eichler, C. Herz, I. Naito and W. Schnabel, J. Photochem., 1980, 12, 225–234.
45. A. P. Shestov and N. A. Osipova, Sb. Statei, Nauchn.-Issled. Inst. Organ. Poluprod. i Krasitelei, 1961, 2, 13–45.
46. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, Taylor and Francis, Boca Raton, 3rd edn, 2006.
47. G. L. Duveneck, E. V. Sitzmann, K. B. Eisenthal and N. J. Turro, J. Phys. Chem., 1989, 93, 7166–7170.
48. G. J. Kavarnos and N. J. Turro, Chem. Rev., 1986, 86, 401–449.
49. P. Natarajan and R. W. Fessenden, J. Phys. Chem., 1989, 93, 6095–6100.
50. D. M. O'Donnel, PhD thesis, University of Notre Dame, 2010.
51. Y. Yamamoto, J. Chem. Soc., Perkin Trans. 2, 1994, 1555–1559.
52. M. Sakamoto, X. Cai, S. S. Kim, M. Fujitsuka and T. Majima, J. Phys. Chem. A, 2007, 111, 223–229.
53. P. Bhatt, M. S. Kumar, S. Mudliar and T. Chakrabarti, Crit. Rev. Environ. Sci. Technol., 2007, 37, 165–198.
54. M. Bressan, N. d'Alessandro, L. Liberatore and A. Morvillo, Coord. Chem. Rev., 1999, 185–186, 385–402.
55. P. Neta, M. Simic and E. Hayon, J. Phys. Chem., 1969, 73, 4207–4213.
56. M. R. Prinsell, D. A. Everson and D. J. Weix, Chem. Commun., 2010, 46, 5743–5745.
57. A. Houmam, Chem. Rev., 2008, 108, 2180–2237.

---

Footnotes

† Electronic supplementary information (ESI) available: Ground-state spectra of pertinent compounds. See DOI: 10.1039/C6GC01113F

‡ These authors contributed equally to this work.

---