Open Access Article
Open Access ArticleMultidimensional high harmonic spectroscopy of polyatomic molecules: detecting sub-cycle laser-driven hole dynamics upon ionization in strong mid-IR laser fields
Barry D.
Bruner
*a,
Zdeněk
Mašín
b,
Matteo
Negro
c,
Felipe
Morales
b,
Danilo
Brambila
b,
Michele
Devetta
 c,
Davide
Faccialà
d,
Alex G.
Harvey
b,
Misha
Ivanov
b,
Yann
Mairesse
e,
Serguei
Patchkovskii
b,
Valeria
Serbinenko
b,
Hadas
Soifer
af,
Salvatore
Stagira
d,
Caterina
Vozzi
c,
Nirit
Dudovich
*a and
Olga
Smirnova
*b
c,
Davide
Faccialà
d,
Alex G.
Harvey
b,
Misha
Ivanov
b,
Yann
Mairesse
e,
Serguei
Patchkovskii
b,
Valeria
Serbinenko
b,
Hadas
Soifer
af,
Salvatore
Stagira
d,
Caterina
Vozzi
c,
Nirit
Dudovich
*a and
Olga
Smirnova
*b
aDepartment of Physics of Complex Systems, Weizmann Institute of Science, Rehovot 76100, Israel. E-mail: nirit.dudovich@weizmann.ac.il; Fax: +972 8934 4109; Tel: +972 8934 6290
bMax Born Institute for Nonlinear Optics and Short Pulse Spectroscopy, Max-Born-Strasse 2 A, 12489 Berlin, Germany
cIstituto di Fotonica e Nanotecnologie-CNR, Milan 20133, Italy
dDipartimento di Fisica, Politecnico di Milano, Milan 20133, Italy
eCELIA, Université de Bordeaux-CNRS-CEA, UMR5107, F33405 Talence, France
fStanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
First published on 26th September 2016
Abstract
High harmonic generation (HHG) spectroscopy has opened up a new frontier in ultrafast science, where electronic dynamics can be measured on an attosecond time scale. The strong laser field that triggers the high harmonic response also opens multiple quantum pathways for multielectron dynamics in molecules, resulting in a complex process of multielectron rearrangement during ionization. Using combined experimental and theoretical approaches, we show how multi-dimensional HHG spectroscopy can be used to detect and follow electronic dynamics of core rearrangement on sub-laser cycle time scales. We detect the signatures of laser-driven hole dynamics upon ionization and reconstruct the relative phases and amplitudes for relevant ionization channels in a CO2 molecule on a sub-cycle time scale. Reconstruction of channel-resolved complex ionization amplitudes on attosecond time scales has been a long-standing goal of high harmonic spectroscopy. Our study brings us one step closer to fulfilling this initial promise and developing robust schemes for sub-femtosecond imaging of multielectron rearrangement in complex molecular systems.
1 Introduction
The ability to manipulate and probe the evolution of electronic wavepackets on their natural time-scale has been the focus of attosecond science for the past two decades. Application of strong (1013 to 1014 W cm−2) infrared fields in attosecond spectroscopy gives access to phenomena evolving on a sub-laser cycle time scale1 – well below 2.6 fs for 800 nm wavelength fields.One of the fastest phenomena is photoionization – electron removal from an atom or a molecule using attosecond XUV pulses2–4 or strong IR laser fields.5–8 Much experimental and theoretical effort in the attosecond community has been devoted to understanding and reconstructing ionization times from experimental observations.2–8 Electron removal creates a hole in an atomic or molecular system, and the evolution of the hole upon ionization is a prominent example of the sub-cycle time-scale dynamics. This evolution can be driven by spin–orbit interaction,9,10 a laser field,11,12 or pure electronic correlations.13 It can also arise from strongly non-equilibrium initial conditions created by ultrashort excitation inducing complex hole dynamics,14 which may involve electron correlations.15
Among the most exciting advances in atto-science is high harmonic generation (HHG) spectroscopy. It allows one to combine sub-Angstrom spatial with attosecond temporal resolution, holding the potential of resolving the structure of electronic wavefunctions as they evolve in time.11,12,16–21 HHG spectroscopy exploits the built-in pump-probe process. Ionization acts as a pump: it removes an electron and creates a hole in the system, launching non-equilibrium dynamics. Driven by the laser field, the liberated electron returns to the parent ion (electron–ion recollision) and probes it via radiative recombination.22 The emitted attosecond burst of light takes a snapshot of the system, probing the evolved wavefunction. HHG spectroscopy is not limited by the duration of the driving laser pulse. The dynamics only start when the electron is detached from the system, and probed as the electron recollides. The spatial resolution is given by the de-Broglie wavelength of the returning electron.23,24 High harmonic spectroscopy has been used to resolve ultrafast electronic,11,12,16–19,25 chiral26 and nuclear27–34 dynamics in molecules and to visualize the structure of molecular orbitals.35–38
A unique property of high harmonic spectroscopy is its ability to time-resolve the interference between multiple quantum pathways in the response of a multielectron system to the ionizing pulse, encoding their relative phases.16–18 These phases, in turn, encode the underlying multielectron rearrangement during ionization. However, the high temporal resolution and interferometric sensitivity of HHG spectroscopy come with a clear trade-off. The main parts of the experiment – the pump-probe delay, the fundamental field's intensity and wavelength – cannot be independently controlled. They are all coupled by the light–matter interaction and are dictated by the recollision mechanism.
In conventional multidimensional ultrafast spectroscopy, the coherent evolution of the system is excited and probed by a sequence of pulses with independently controllable time delays between them. The spectrum is spread into multiple dimensions where the full dynamical picture can be more easily understood.39 In contrast, in conventional HHG spectroscopy, these independent controls are not available, and the complex multielectron response is mapped into a 1D experimental observable – the HHG spectrum.
Disentangling the underlying dynamics requires a multi-dimensional approach, capable of separating the contributions of different ionization pathways, reminiscent of how multidimensional spectroscopy has been used for mapping energy transfer and coupling between electronic and vibrational states.40,41 In the absence of such controls, HHG cannot advance to be a robust tool for probing complex multielectron dynamics in molecular systems.
In this paper we describe advanced HHG spectroscopy, demonstrating the ability to resolve complex dynamics of multielectron rearrangement in CO2 molecules. In prior work, we have employed similar schemes for separating the spatial and temporal information in HHG from molecules.7 In addition, we have applied these schemes to calibrate the intrinsic pump-probe delay in HHG spectroscopy by reconstructing ionization and recombination times.7,42–44
Here, we introduce the idea of a laser-driven intra-molecular interferometer and exploit it to detect core rearrangement dynamics during ionization. The interferometer is created by sub-cycle laser driven dynamics inside the molecular ion between ionization and recombination. It is naturally built into molecules interacting with strong IR fields, and is particularly simple for longer wavelengths of the driving laser field.
Laser induced dynamics in the molecular ion result in new HHG pathways (channels), where ionization and recombination involve two different states of the ion.11 In this work we first show that the 2D HHG spectroscopy is particularly sensitive to such channels. Second, we use these channels to perform reconstruction of sub-cycle ionization dynamics. The reconstruction strategy benefits from the fact that purely laser-driven transitions can be characterized theoretically by solving the Schrödinger equation for laser-driven bound dynamics in the ion, between ionization and recombination. Therefore, the new HHG pathways associated with these dynamics can serve as a reference – the analogue of a local oscillator in heterodyne-style detection. The interference of these “reference” pathways with “signal” pathways evolving towards the same HHG recombination channels records the contribution of these signal pathways in the harmonic spectrum. These contributions can include additional interactions leading to inter-channel coupling, such as electron correlations during strong field ionization,45–47 which can introduce nontrivial amplitudes and phases between different ionization channels.
For longer wavelengths of the driving field, laser-driven dynamics in the molecular ion is dominated by laser-induced polarization of different ionic states. The “virtual” transitions between the ionic states associated with polarization are phase-locked to the driving field. Thus, the reference pathways of the intra-molecular interferometer become particularly simple. We focus our analysis of the multidimensional HHG spectra on this regime.
The paper is organized as follows. Section 2 describes the essential high harmonic channels and their interference in mid-IR fields. Section 3 provides the background for “reading” the information recorded in 2D HHG spectra. Section 4 describes the experimental results. Section 5 describes the theoretical analysis of 2D HHG spectra, demonstrates the contribution of laser-driven HHG channels and performs the reconstruction of sub-cycle ionization dynamics from experimental 2D spectra.
2 Encoding electronic dynamics in molecular HHG spectra
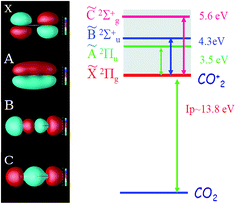
The CO2 molecule represents a complex system in which strong field ionization can leave the ion in four different states (ground,![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , and three excited Ã,
, and three excited Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ,
, ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ), as shown in Fig. 1. For clarity, in the remainder of the paper we shall omit the tilde in the notations of these states. The strength of each ionization channel depends exponentially on the corresponding ionization potential, but also very strongly on the structure of the Dyson orbital associated with each channel.17,48,49
), as shown in Fig. 1. For clarity, in the remainder of the paper we shall omit the tilde in the notations of these states. The strength of each ionization channel depends exponentially on the corresponding ionization potential, but also very strongly on the structure of the Dyson orbital associated with each channel.17,48,49
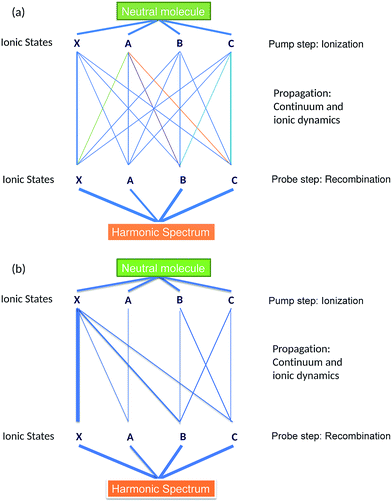
The four ionization channels give rise to at least four recombination channels: XX, AA, BB, CC, where the second letter labels the recombination channel. We call these channels “direct” (or “diagonal”), because the state of the ion does not change between ionization and recombination. As detailed in ref. 11, the laser field can also couple the different states of the ion between ionization and recombination and lead to additional cross-channels. For example, the ionization channel X now leads to four HHG channels XX, XA, XB, XC – one direct and three cross-channels. Note that the three cross-channels arise even in the absence of real excitations from the state X – in this case, they reflect polarization of the ionic core at the moment of recombination.
The observed signal is the result of the coherent addition of all pathways, leading to a particular recombination channel, as shown schematically in Fig. 2(a). Ab initio calculations of laser-driven dynamics in the ion and recombination amplitudes open the opportunity to recover the less well-known pathways in the network of channels. The interferometer becomes simpler in the long wavelength limit, as shown in Fig. 2(b). Here we briefly summarize the dominant channel-resolved contributions to the HHG spectra, a more detailed analysis will appear in Section 5 of the paper.
The XX channel usually dominates the HHG signal, since the ionization potential for this channel is significantly lower than for other direct channels, such as AA, BB, CC. The disparity between these channels is further accentuated in mid-IR fields, where the strong field ionization is expected to leave an even smaller fraction of molecular ions in the excited state. Thus, we expect smaller contributions of the AA, BB and CC channels to the HHG spectrum. These contributions interfere with cross-channels XA, XB and XC, which all originate from X and are associated with the laser-induced dynamics between the states X, A, B, C between ionization and recombination. These channels are mostly associated with “virtual” transitions, which reflect the laser-induced polarization of state X. The contributions of these cross-channels to HHG spectra are on par with the contributions of direct AA, BB, CC channels. The cationic states B and C are strongly coupled by the laser field, which leads to significant population transfer between these states and results in relatively important contributions from CB and BC HHG channels. Finally, channels AX, BX, CX are much weaker than XA, XB, XC due to their lower ionization rates.
Thus, the pathways XA, XB, and XC form the analogue of the reference, locked by the driving laser field to the XX channel. They heterodyne the “unknown” signal encoded in the pathways AA, BB, CC. Ab initio calculations of the laser-driven dynamics and recombination matrix elements yield an accurate reference and open the possibility to decode the unknown signal – the initial ionic superposition state formed during the ionization step. In principle, this can be performed for each harmonic and thus the dynamics of the initial ionic superposition state can be mapped with sub-cycle resolution.
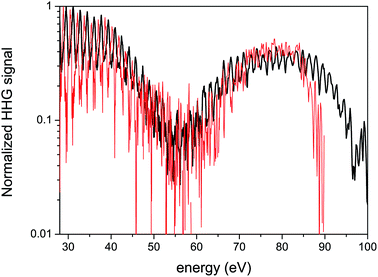
While strong field interaction with CO2 molecules is described by multi-channel dynamics, its rich complex nature has not yet been fully resolved experimentally. One major limitation is imposed by the interplay between the structural and dynamical information in the HHG spectrum. Sample experimental spectra appear in Fig. 3, where aligned CO2 molecules were probed using HHG for two laser intensities. The experimental set-up and the molecular alignment mechanism used to obtain such spectra will be discussed in more detail in Section 3. The stand-out feature is the pronounced minimum around 55 eV, with a width of about 15 eV. This is a well known structural feature associated with so-called two center interference in the recombination step of HHG.37
Much effort has been directed toward resolving these types of structural signatures in the HHG spectra of CO2 (ref. 36 and 37) and N2,19,35,50,51 aimed at extracting the spatial information of the participating orbitals. The interplay between the spatial and the temporal features in HHG spectra has been studied in CO2 and N2O by systematic scans of the laser wavelength and intensity.16,52,53 For particular experimental conditions, it has been shown that the strong field dynamics scales with the laser intensity while the structural information contained in the HHG spectrum remain unchanged.16,54 This is also seen in Fig. 3 – as the intensity of the fundamental field increases, the basic features of the 1D spectra appear very similar, except for an extension of the cut-off. The details of the complex multi-channel dynamics remain elusive, their presence is not apparent.
Extracting dynamical information from the HHG spectrum is one of the primary challenges in HHG spectroscopy. Measurements of dynamical interference attributed to two independently evolving ionization channels in these molecules have also been reported.7,54–56 The coupling between different channels can leave its signature in the HHG polarization state11 and in the interference between HHG signals from long and short trajectories.25 In the next section we show that applying a two-colour multidimensional scheme allows us to record the complex multielectron dynamics, which leaves clear fingerprints in the HHG spectrum.
3 Increasing the dimensionality of HHG measurements
3.1 Two-colour gating of HHG signals
Our multidimensional method is based upon HHG generated by two-colour, orthogonally polarized fields. The concepts behind these experiments have been described in detail previously.7,8,42–44,56 For a concise overview of the most pertinent concepts, we refer the reader to ref. 56 as a starting point. Here in Sections 3.1 and 3.2, we provide a brief introduction for the benefit of the reader.A fundamental, high intensity field dictates the basic properties of the interaction while a weak phase-locked second harmonic field, in an orthogonal polarization, serves as a subcycle gate. The second harmonic field perturbs the dynamics of the continuum electron, controlling the direction and magnitude of the lateral kick imparted to the electron before it recollides. A large kick in the lateral direction means that the probability of electron recombination to the parent ion is lowered and therefore the HHG signal is suppressed.
As we vary the two-colour phase delay ϕ between the fields, we modulate this kick, leading to clear sinusoidal oscillations of the signal at each harmonic order. Optimization of the HHG yield in this two-colour configuration selects a very specific condition for ionization: it remains virtually unaffected by the perturbative second harmonic field, especially in the long-wavelength limit.43 Thus it is essential that the perturbing field is sufficiently weak. Under these conditions, the overall HHG yield depends weakly on ϕ, such that the amplitude of the ϕ-dependent modulation is small compared to the average HHG yield. This allows us to extract a key observable of the experiment – the optimal two-colour delay, ϕmax, that maximizes the high harmonic yield for each harmonic.
Scanning the two-colour delay increases the dimensionality of the measurement and helps to resolve the dynamical information driven by the interaction. The optimal delay ϕmax depends on the strong field parameters that define each electron trajectory – the ionization time and recollision time. Therefore, the modulation phase of each channel serves as a “label” which identifies the underlying dynamics. When the dynamics evolve along several channels, each channel is modulated according to its characteristic phase ϕmax. The HHG spectrum records the interference of these modulations, encoding the relative phases and amplitudes dictated by the hole dynamics.
3.2 Single channel dynamics
When ionization occurs from a single isolated channel, the 2D measurement provides a universal fingerprint, which offers an important calibration tool. Representative examples of single-channel ionization in Krypton gas are shown in Fig. 4. The 2D HHG spectra were recorded for different laser wavelengths and intensities, and ϕmax was extracted as a function of harmonic energy for each measurement. The variation of ϕmax with energy follows the same basic curve for all measurements. As the electron energy increases, there is a gradual monotonic increase in ϕmax over nearly the entire range of the HHG spectrum. The exact shape of the curve can be robustly predicted as a function of a single parameter, the well known Keldysh parameter defined as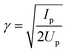 , where Up is the electron ponderomotive energy and Ip is the ionization potential. The Keldysh parameter encompasses the important experimental parameters that determine the single channel response, namely the laser wavelength, intensity, and the ionization potential. The relations between the three data sets can be seen more clearly by re-scaling the HHG energy over a range set between zero and unity, where the minimum energy (zero) corresponds to Ip and the maximum to the classical HHG cut-off (Fig. 4(b)). These concepts were confirmed experimentally for a number of other simple atomic systems as well.44 The single-channel response can be considered as the basic reference for decoding more complex electronic dynamics involving multiple ionization channels.
, where Up is the electron ponderomotive energy and Ip is the ionization potential. The Keldysh parameter encompasses the important experimental parameters that determine the single channel response, namely the laser wavelength, intensity, and the ionization potential. The relations between the three data sets can be seen more clearly by re-scaling the HHG energy over a range set between zero and unity, where the minimum energy (zero) corresponds to Ip and the maximum to the classical HHG cut-off (Fig. 4(b)). These concepts were confirmed experimentally for a number of other simple atomic systems as well.44 The single-channel response can be considered as the basic reference for decoding more complex electronic dynamics involving multiple ionization channels.
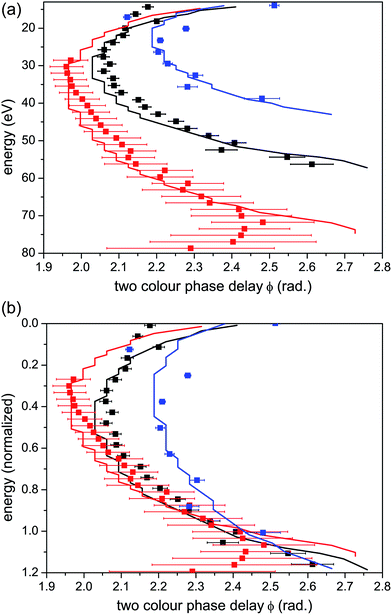 | ||
| Fig. 4 Single channel ionization in Krypton. (a) Optimal two-colour phase delay ϕmaxvs. harmonic energy and (b) vs. harmonic energy normalized to the classical HHG cut-off. Experimental data are shown as scatter graphs and theoretical calculations are shown as solid lines. Calculated values for ϕmax are found by solving for the times of ionization and recombination within the strong field approximation, propagating the semiclassical electron in the two-colour field and solving for the optimal ϕ. These methods are described in more detail in ref. 44. Red curves: laser wavelength = 1434 nm, intensity = 9 × 1013 W cm−2, corresponding to Up = 16.9 eV and γ = 0.64. Black curves: laser wavelength = 1300 nm, intensity = 7 × 1013 W cm−2, corresponding to Up = 11.5 eV and γ = 0.78. Blue curves: laser wavelength = 800 nm, intensity = 1.3 × 1014 W cm−2, corresponding to Up = 7.8 eV and γ = 0.95. | ||
3.3 Two channel interference
How can we link the 2D measurement with the underlying dynamics and multi-channel contributions? Consider the case of two ionization channels,7 when the HHG signal can be written as:Atot = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ1) + A2 exp(iφ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ2), exp(iφ2), | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Δφ) with Δφ the phase difference φ2 − φ1. The amplitudes of each channel are themselves modulated by the two-colour field, varying sinusoidally with respect to the relative two-colour phase delay ϕ, and labelled by their optimal two-colour phase delays ϕmax,1 and ϕmax,2. Such a modulation is then mapped, via the interference Δφ between channels, into the total signal modulation having an optimal phase ϕtotmax.
cos(Δφ) with Δφ the phase difference φ2 − φ1. The amplitudes of each channel are themselves modulated by the two-colour field, varying sinusoidally with respect to the relative two-colour phase delay ϕ, and labelled by their optimal two-colour phase delays ϕmax,1 and ϕmax,2. Such a modulation is then mapped, via the interference Δφ between channels, into the total signal modulation having an optimal phase ϕtotmax.
One mechanism that leads to deviations from the single channel response, as observed in our experiment, arises under two conditions. The first requires a comparable contribution of the two channels – A1 ∼ A2, so that their interference is visible. In contrast, when one of the channels completely dominates the interaction, the total signal will follow the single-channel response.
The second condition requires substantial variation of the relative phase, Δφ ∼ π. A dramatic shift of ϕtotmax can originate from a destructive interference between the two channels.7,56 In this case the interference becomes a differential measurement, mapping small phase differences between ϕmax,1 and ϕmax,2 into a significant phase jump observed in ϕtotmax.
Consider the interference between two direct channels, when the total signal is the coherent sum of two independent channels induced separately by the strong laser field. The relative phases between the two channels can be approximated by17
| Δφ = (Ip2 − Ip1)τ + (φr2 − φr1). | (2) |
A different picture could be expected when the two channels are coupled, so that the laser field can induce real (population transfer) or virtual (polarization) transitions between the channels, during the time-delay between ionization and recombination. For a sufficiently strong coupling field, the contribution of the two coupled channels may become comparable anywhere in the HHG spectrum. In addition, the laser-induced A2 will vary relative to A1 from one harmonic to another. Therefore, the condition A1 ∼ A2 can be achieved over a large spectral range, not only near the cut-off or a structural minimum. As a result, a smooth deviation from the single channel response over a large spectral range, rather than discrete phase jumps in ϕmax, might be expected.
In Section 5 we show that while all diagonal channels have very similar ϕmax, the laser-driven cross-channels lead to a different optimization of the two-colour delay. Fundamentally, it is related to the entanglement between the electron and the ion. For a given harmonic order, laser-driven “real” or “virtual” transitions in the ion are correlated to changes in the continuum electron trajectory leading to this harmonic. Consider, for example, channels XX and XC. The ionization time is the same for these two channels, but the recombination times are different due to a different final state, C (instead of X), with a different Ip (mathematically, this leads to an extra phase accumulated in the XC channel upon transition to the state C). Since the optimal two-colour delay depends on both ionization and recombination times, the pair of times corresponding to the XX channel will optimize ϕmax for the XX channel, but the shift of the recombination time in the XC channel for the same ionization time as in XX will inevitably lead to a different value of ϕmax for the XC channel. The magnitude of this effect and its appearance in the spectrum depends on the value of ΔIp between the two coupled channels.
While this general assessment of multichannel interference provides an essential background for our overview of the experimental results in Section 4, Section 5 rigorously analyzes the contributions of the individual direct and cross channels and uses this analysis to reveal the dynamics recorded in experimental 2D spectra.
3.4 Measurement and control of the laser driven dynamics
We explore multiple channels in HHG spectroscopy using a fundamental wavelength in the mid-IR regime.57 The cut-off frequency scales linearly with Up = I/4ω02 with I being the laser intensity and ω0 the laser frequency. Increasing the fundamental wavelength (i.e. decreasing the frequency) greatly increases the HHG spectral bandwidth and therefore the available spatial resolution and dynamical range provided in HHG spectroscopy.58–60High harmonics are generated by focusing a 20 fs, 1480 nm, 1.3 mJ self-stabilized tunable optical parametric amplifier (OPA) laser source into a pulsed gas jet. The harmonic spectra were measured with a flat field XUV spectrometer consisting of a spherical variable line space grating focusing onto a micro channel plate coupled to a phosphor screen and imaged with a CCD camera. The second harmonic (SH) gating field is produced using a thin (typical thickness 100 μm) BBO (βBaB2O4) nonlinear crystal in a type-I phase matching configuration, which ensures that the SH field is orthogonally polarized with respect to the fundamental field. The group velocity walk off between the beams is compensated using a birefringent crystal (calcite) and IR-coated glass wedges. The sub-cycle delay ϕ of the SH field relative to the fundamental field is controlled by translation of the glass wedges.
The use of the pulsed gas jet at moderate backing pressure (∼3–4 bars) produces a supersonic expansion of molecules that are rotationally cooled upon entering the vacuum chamber.61 For laser-induced molecular alignment,62 we split off a small portion of the 800 nm Ti:S beam that is used to pump the OPA. The pulses are stretched to 100 fs in order to improve the efficiency of the alignment. The energy in the alignment beam is approximately 250 μJ, with a focused intensity of ∼4 × 1013 W cm−2. The polarization of the alignment beam relative to the generating beam is set with a zero-order half-wave plate. The alignment and two-colour generating beams are collinearly combined using a dichroic mirror. Spatial filtering and mode matching of all beams is achieved using irises placed near the entrance to the vacuum chamber.
In this work we control the key parameters of our dynamical imaging scheme – the sub-cycle laser driven dynamics between ionization and recombination – by modifying the fundamental laser field intensity and the dipole couplings between different states of the ion. The latter is achieved by variation of the molecular alignment angle.
The alignment pulse excites a rotational wavepacket in the molecular ensemble that undergoes periodic revivals for linear molecules such as CO2. Changing the polarization of the strong probe pulse relative to the polarization of the aligning pulse allows one to probe the molecular ensemble at different alignment angles. The alignment distribution displays cylindrical symmetry around the axis defined by the polarization direction of the alignment pulse.37
Calculations show that the X-channel ionizes most strongly for all alignment angles due to its lower Ip. However, for the channels with higher Ip, the interplay of their electronic structure and the molecular alignment angle plays a significant role in defining the angular dependence of the ionization rate. For example, for molecules aligned perpendicular to the HHG generating field, the A-channel has a higher ionization rate than the B-channel, whereas for parallel alignment, ionization from the B-channel dominates over the A-channel despite its higher Ip.17,49 Thus, the alignment angle affects the relative contributions of the individual channels, and therefore modulates the phase and amplitude of their interference.
Multidimensional HHG scans were recorded for two fundamental field intensities and two alignment directions. The polarization of the alignment pulse was set parallel or perpendicular to the polarization of the fundamental field that drives HHG, while the fundamental field and its SH are orthogonally polarized. The two-colour field was delayed by 21.2 ps relative to the alignment pulse, which corresponds to the half-revival time for CO2. Under these alignment conditions, HHG spectra were recorded as a function of the relative phase delay ϕ between the strong fundamental and weak second harmonic fields. The experiment was performed at two intensities of the generating field: ∼1.0 × 1014 W cm−2 and ∼1.3 × 1014 W cm−2, which we will refer to as the “low” and “high” intensity scans, respectively.
4 Experimental results
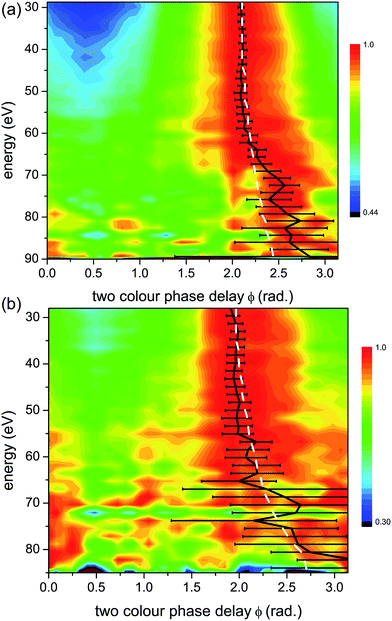
To facilitate the visualization of the optimal two-colour delay, which maximises HHG yield for each harmonic, we perform a normalization of 2D HHG spectra. Specifically, for each photon energy, the HHG yield is normalized to its maximal value, achieved at ϕmax. Fig. 5 shows the 2D plots of the normalized HHG energy as a function of the relative two-colour phase delay ϕ for the case of perpendicular alignment. By normalizing the 2D HHG spectrum along the ϕ-axis, such that for each harmonic the magnitude of the signal is equal to one at ϕ = ϕmax, the dependence of ϕmaxversus photon energy is easier to visualize.Both the high (Fig. 5(a)) and low (Fig. 5(b)) intensity scans produce similar results, with a slow, monotonic increase in ϕmax with respect to energy. Since the Ip of the X-channel in CO2 is nearly the same as that of Krypton, we expect them to have the same characteristic 2D HHG spectrum.
As a confirmation, in Fig. 5 and 6 we plot the expected ϕmax for a single channel with the same Ip as the X-channel of CO2. The single channel calculation is based on a model that relies only on the strong field approximation for predicting ϕmax (see Fig. 4). This model was used for calculating the predicted HHG signal dependence on the two-colour phase delay in our prior work on single channel dynamics in atomic systems.44 The experiment measures the relative two-colour phase ϕ only. We calibrate the absolute value of ϕmax for CO2 by assuming that the X-channel dominates the signal for low harmonic energies. This is a reasonable assumption based on the concepts presented in Section 3.3. The absolute value of ϕmax for a single channel (the X-channel) can then be calculated using the model, and used to calibrate the absolute value of ϕmax for the entire harmonic spectrum.7,44 Once the absolute ϕmax is determined, we can see that for both intensities in perpendicularly aligned CO2, the measured signal closely follows the single X-channel response over the entire HHG spectral range. A small deviation from the single channel response appears near the cut-off, in particular for high intensity. Contributions from additional channels, in particular the A state of the cation, only appear in this region of the HHG spectrum.
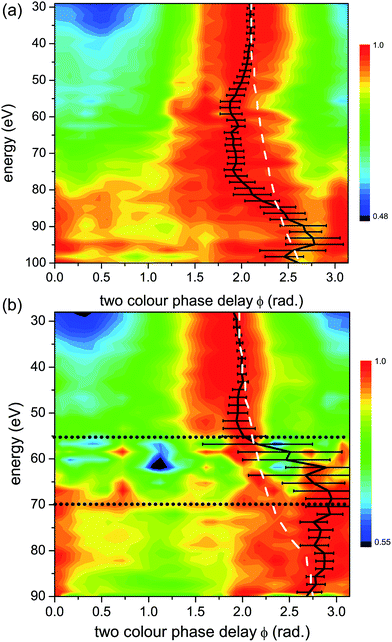 | ||
| Fig. 6 Normalized experimental 2D colour plots of HHG signal vs. relative two-colour phase delay ϕ for high (1.3 × 1014 W cm−2) (a) and low (1.0 × 1014 W cm−2) (b) intensities of the strong 1480 nm generating field for parallel alignments (alignment field polarization is parallel to that of the generating field). Bold black lines: maximum two-colour phase ϕmax, with experimental error bars. White dashed lines: calculated maximum two-colour phase for a single ionization channel with the same Ip as the X-channel in CO2 (13.8 eV), as in Fig. 5. The horizontal grey dotted lines in panel (b) mark the energy region, from 55 eV to 70 eV, where the non-normalized experimental HHG signal is extremely weak, making reliable assignment of ϕmax in this region very challenging. | ||
A significantly different response is observed as we rotate the molecular system to be parallel to the strong fundamental field. Fig. 6 shows the normalized HHG energy as a function of the relative two-colour phase delay for the two intensities. For the low intensity, the HHG signal is suppressed almost completely in the structural minimum around 55 eV in this range. In contrast, for the high intensity, the HHG signal is suppressed by over an order of magnitude in this region of the spectrum, but the remaining signal is still well within the sensitivity of the measurement. For both intensities, ϕmax deviates significantly from the expected single channel dynamics, except at very low harmonic energies. Importantly, comparing the high (Fig. 6(a)) and low (Fig. 6(b)) intensities shows a dramatic difference. In particular, at higher energies, we observe a pronounced shift in ϕmax of about 1.5 radians near 70 eV for the low intensity, and near 95 eV for the high intensity. This feature is similar to the phase shift observed in our earlier experiments performed at 800 nm.7 The shift around 75 eV at high intensity has a different origin as will be discussed below.
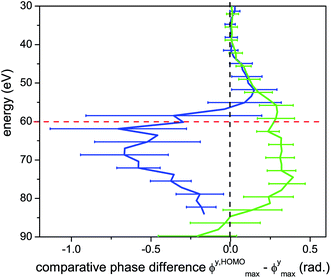
A more direct comparison between the experimental data and the expected single channel response appears in Fig. 7. Here we plot the comparative phase difference between ϕmax extracted from the high and low intensity measurements and the calculated phase, ϕXmax associated with the single channel (channel X) response. For low harmonics, ϕmax follows the single channel case for both intensities. Above 45 eV, the two curves sharply diverge. For the low intensity, ϕXmax − ϕmax shifts toward larger values of ϕ compared with a single channel, having the largest deviation at 70 eV. At high intensity ϕXmax − ϕmax shifts towards the opposite direction, having the maximal deviation at 75 eV. The comparative phase difference with respect to energy is a key indicator for the multichannel dynamics that are encoded in the 2D spectrum. Note that for low intensity and parallel alignment the non-normalized experimental HHG signal is extremely weak in the energy region from 55 eV to 75 eV, thus reliable assignment of ϕmax in this region becomes very challenging. This region is indicated by horizontal lines in Fig. 6(b).
We note that modulations of the HHG spectrum due to structural features, such as the minimum near 55 eV in aligned CO2, do not hinder the detection of multichannel dynamics in our experiment. In fact, the structurally-based reduction of the signal from the HOMO relative to the deeper orbitals leads to more comparable amplitude contributions between the channels.17,54 This leads to larger and more easily measurable shifts in ϕmax56 and increases the sensitivity of the measurement to the channels with higher Ip.
In the following section, we analyze the 2D HHG response and the encoded dynamics in greater detail. We identify the contribution of different channels, analyze their coupling, and describe the approach which allows us to decode the relative phases of the different cationic channels formed at the ionization step, with sub-cycle time-resolution.
5 Theoretical analysis of the experimental 2D HHG spectra
5.1 The AZUR method
In the time domain, the HHG process can be understood as a sequence of several events which happen within a single half-cycle of the fundamental field: ionization, laser-driven dynamics in the ion accompanied by electron propagation in the continuum, and finally recombination. Formally, the opportunity to factorize the whole quantum process into a sequence of these events in the time domain comes from the application of the saddle point method to evaluate the multiple integrals describing the HHG signal, including the coupling between the different channels (see e.g.ref. 63).The detailed tutorial description of the method we use in this paper is available on the arXiv.64 Here we give a brief summary for the benefit of the reader.
For each half cycle j of the laser field, the sequence of the three steps in the HHG process can be formalized as a product of two vectors and two matrices. The ionization step generates a vector of complex amplitudes Aj, with j labelling the half-cycle. Recombination is described by the vector Rj, which contains recombination matrix elements for each final state of the ion. The two matrices, describing laser-driven dynamics in the continuum and in the cation between ionization and recombination are Zj (for the electron) and Uj (for the ion) (see e.g.ref. 63). Note that factorization of the full propagator into the product of Zj and Uj is an approximation. For the recombination step, this approximation is motivated by short duration of the recollision event. The laser field is “frozen” during recombination, so that real transitions between the states of the ion do not occur during this time. The same approximation is, however, questionable during the ionization step. The tunnelling electron departs with low energy and can strongly interact with the ion within the ionization window, leading to correlation-driven processes in strong-field ionization45,46 and potentially to changes in the amplitudes and phases of the ionization vector Aj. As we will discuss in the next section, the experimental results may allow us to check the validity of this approximation.
The complete signal is given by the time-dependent induced dipole as follows:
| Dj(t) = RjUjZjAj | (3) |
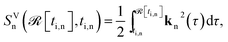 | (4) |
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) [ti,n]). Here
[ti,n]). Here ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [ti,n],
[ti,n], ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) [ti,n] are the real and imaginary parts of the complex ionization time ti,n, kn(τ) = kt,n + A(τ), A(t) is the vector potential of the laser field, and kt,n is the complex saddle point solution for the electron canonical momentum, specified for every moment of recombination t.
[ti,n] are the real and imaginary parts of the complex ionization time ti,n, kn(τ) = kt,n + A(τ), A(t) is the vector potential of the laser field, and kt,n is the complex saddle point solution for the electron canonical momentum, specified for every moment of recombination t.
The recombination vector is a row, with entries given by the corresponding recombination dipoles Rn = rn(kn(t), θ). These depend on the channel n, the channel-specific electron kinetic momentum at the recombination kn(t), and the molecular alignment angle θ. Note that in orthogonally polarized two-colour fields, kn(t) modifies the recombination angle for every half cycle. This is why we keep the information about the molecular alignment angle and the vector kn(t) in the argument of Rn.
The diagonal continuum propagation matrix Z has elements Znn = exp(−iSVn(t,![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [ti,n]))apropn(t,ti,n), which describe the laser-driven electron dynamics and contain the Volkov action and the pre-factor apropn describing the spreading of the electron wave-packet. Finally, the matrix U describes laser-driven dynamics in the ion. Its respective matrix elements are the amplitudes of laser-induced transitions between ionic states m and n: umn(t,
[ti,n]))apropn(t,ti,n), which describe the laser-driven electron dynamics and contain the Volkov action and the pre-factor apropn describing the spreading of the electron wave-packet. Finally, the matrix U describes laser-driven dynamics in the ion. Its respective matrix elements are the amplitudes of laser-induced transitions between ionic states m and n: umn(t, ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) [ti,n]) (see ref. 63), with the energies of the ionic states calculated from the ground state energy of the neutral. The whole expression, described in eqn (3), has to be read from right to left, following the standard convention of quantum mechanics and the Hebrew tradition, hence the name AZUR.
[ti,n]) (see ref. 63), with the energies of the ionic states calculated from the ground state energy of the neutral. The whole expression, described in eqn (3), has to be read from right to left, following the standard convention of quantum mechanics and the Hebrew tradition, hence the name AZUR.
The full high harmonic dipole comes from summing over all odd and even half-cycles of the fundamental field, D(t) = D(t)jo + D(t)je. In linearly polarized fields and for a symmetric ground state, Dj+1(t) = −Dj(t + π/ω). However, in two-colour fields this symmetry between the two consecutive half-cycles of the fundamental is broken, leading to the generation of even harmonics. In molecules, the two successive half cycles jo = 2k − 1 and je = 2k may also correspond to different ionization and recombination angles. Note also that all saddle point solutions depend on the two-colour delay ϕ. Thus, the full high harmonic dipole becomes a function of the two-colour phase delay ϕ. We suppress the index describing this dependence to simplify notations.
Now consider the auxiliary dipole vectors including all steps except the recombination: 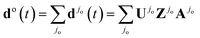 and
and 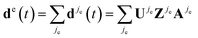 . In our method, we first calculate the Fourier transforms of the auxiliary dipole vectors separately for even and odd half-cycles, yielding do,e
. In our method, we first calculate the Fourier transforms of the auxiliary dipole vectors separately for even and odd half-cycles, yielding do,e![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (N) =
(N) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [do,e(t)], and then include the recombination step. To this end, we multiply odd and even components of the auxiliary frequency domain dipole vectors do,e
[do,e(t)], and then include the recombination step. To this end, we multiply odd and even components of the auxiliary frequency domain dipole vectors do,e![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (N) by the respective recombination vectors for odd Rjo(N,θjo) and even half-cycles Rje(N,θje), where Ro,e are taken at the respective different recombination angles θo,e and energies Nω. Thus, finally the HHG light is given by
(N) by the respective recombination vectors for odd Rjo(N,θjo) and even half-cycles Rje(N,θje), where Ro,e are taken at the respective different recombination angles θo,e and energies Nω. Thus, finally the HHG light is given by
D(N,θ,ϕ) = Ro(N,θo)do![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (N) + Re(N,θe)de (N) + Re(N,θe)de![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (N). (N). | (5) |
To calculate this expression we need to know the respective vectors and matrices.
The ionization vector is obtained using the method described in ref. 49 and describes strong -field ionization for uncoupled X, A, B, and C channels. Both phase and amplitude corrections to these quantities, which may arise e.g. due to channel coupling during ionization, are the targets of reconstruction from the experimental data.
The recombination matrix elements are calculated using the ab initio R-matrix method (UKRMol), and specifically its recent extension to photoionization from aligned molecules.65,66 We have developed two photoionization models. The first model (for full details see ref. 65, model 3) uses a sophisticated modelling of correlation/polarization but uses a version of UKRmol which limits the calculation in several parameters. Subsequently, in collaboration with J. Gorfinkiel, we have significantly improved on the codes which has allowed us to refine the original model and to generate more accurate photoionization dipoles. The new model differs from the original one in several aspects.
First, the original model used a description of the continuum based on Gaussian-type (GTO) continuum basis functions with angular momentum up to L = 5. In the new model we have been able to include continuum functions with L = 6. Inclusion of these functions has significantly extended the upper limit of the energy range for which we are able to generate accurate photoionization dipoles, from approx. 50 eV to approx. 90 eV of photon energy. This extension is crucial for the long wavelength driving laser fields, considered herein. Second, the original model included 96 states in the close-coupling expansion of the scattering wavefunction. In the new model we have included 300 target states spanning the energy range of approx. 30 eV. This has allowed us to further improve the description of polarization/correlation and to further suppress the appearance of unphysical pseudoresonances.
To enable these improvements we have made the following changes to the R-matrix codes. First, we have developed a completely new parallel integral code which is capable of generating the molecular integrals in quadrupole precision. This enabled us to include in our calculations a large number of continuum basis functions without encountering problems with linear dependencies among the diffuse GTO functions. Second, MPI-parallelization of the outer region calculation was implemented. This modification was essential to allow us to include a large number of target states in the calculation. Finally, to generate data for use in HHG calculations, the Dyson orbitals, photoionization dipoles and target transition dipole moments have to be all phase-consistent. Previously, the phase-correction had to be applied manually using a laborious procedure. We have implemented changes to the codes which eliminated a number of arbitrary phases, thus allowing us to automatically generate phase-consistent data.
High quality recombination amplitudes and phases are essential for our HHG calculations due to the interferometric sensitivity of the HHG signal. In the present calculations, we know the recombination dipoles with high accuracy in the region up to 90 eV of photon energy.
The matrix U is also modelled with adequate accuracy. To model laser-driven dynamics of bound states in the CO2 ion we first included around 160 correlated target states (the corresponding dipole couplings and energies were taken from our ab initio R-matrix calculations). Finally, we could show that the four essential states X, A, B, and C are sufficient to describe these dynamics with adequate accuracy (see also ref. 67). We have also checked that the coupling dipoles between these essential states resulting from the quantum chemical calculations based on the CASSCF method yield the same dynamics. These (CASSCF) coupling dipoles (with appropriate phase correction) we have used in the present calculations.
The continuum propagation matrix Z is standard and has been verified over the years in one-electron studies of HHG in atoms, see e.g.ref. 7 and 68.
Having accurate models for the recombination and propagation steps, and using the interferometric sensitivity of the 2D HHG signal allows one to reconstruct the initial conditions dictated by the ionization process. Specifically, we can reconstruct the possibly missing information about the sub-cycle dynamics of multielectron rearrangement during ionization, which occurs in the presence of both correlation-induced and laser-induced coupling between the channels. These dynamics are encoded in the relative phases between different ionic states set up by the ionization process, and also impact the ionization amplitudes. In the following we describe how these quantities can be extracted from the experimental observables of 2D HHG spectroscopy.
5.2 Reconstructing sub-cycle ionization dynamics from 2D HHG spectra
The comparison between theory and experiment allows us to assess the accuracy of the ionization vector used in the calculation. Note that the approximations we have made in describing the ionization step and replacing the exact propagator with UZ are formally equivalent to using a different ionization vector A in eqn (3); given a very large electron oscillation amplitude in an intense IR field, the factorization UZ is appropriate just after the ionization step.The propagator UZ is unitary and performs a well-defined rotation of the initial vector A between ionization and recombination. To find the corrected ionization vector A, we need to perform an additional rotation of the vector d = UZA before applying the recombination operator R, yielding the rotated vector d′. This extra rotation should allow us to match the observed HHG spectrum. Then, performing the back propagation (UZ)−1 of the rotated vector d′ we can determine the corrected ionization vector A′.
We perform the rotation by introducing a diagonal matrix Φ with entries Φnm = ρn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iφn), where n = X, A, B, C, φn ∈ [0, 2π]; only three relative phases matter. In the present analysis, we assume φn to be constant as a function of the photon energy. We also allow for varying the strength of the channels X, A, B, C, by varying ρn. Specific reconstructed values of φn and ρn will be presented and discussed below. In the calculation we ensure that the norm of vector d(t) is preserved upon multiplication by matrix Φ.
exp(−iφn), where n = X, A, B, C, φn ∈ [0, 2π]; only three relative phases matter. In the present analysis, we assume φn to be constant as a function of the photon energy. We also allow for varying the strength of the channels X, A, B, C, by varying ρn. Specific reconstructed values of φn and ρn will be presented and discussed below. In the calculation we ensure that the norm of vector d(t) is preserved upon multiplication by matrix Φ.
Thus, the 2D HHG spectrum for a given angle of molecular alignment θ becomes:
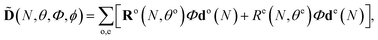 | (6) |
5.3 Details of the HHG calculations
To connect the theoretical analysis to the experiment, we note that the 1D experimental HHG spectra exhibit a strong minimum around 55 eV, associated with the structure of the recombination matrix element correlated to the X state of the cation. In our ab initio calculations of angle-resolved recombination in a CO2 molecule,65 the deep minimum at this energy arises for molecules aligned at 40°, see Fig. 8. Therefore, for our calculations, we coherently add the calculated HHG signals arising from molecules aligned at ±35°, ±40°, and ±45°. We note that high harmonic fields corresponding to “positive” and “negative” alignment angles, e.g. ±40° are different due to the presence of the perturbative second harmonic field. Due to the very weak second harmonic gate field used in the experiment, almost no even harmonic signal was detected. Nonetheless, phases for the parallel high harmonic light for “positive” and “negative” alignment angles are different and they depend on the two-colour delay.The calculations of 2D spectra were performed for a λ = 1480 nm, 4-cycle pulse with constant intensity, for laser field strengths ranging from F = 0.059 a.u. to F = 0.042 a.u. with the step ΔF = 0.001 a.u. Focal averaging is performed using these sets of calculations, for the peak field strengths F = 0.057 a.u. (“high” intensity) and F = 0.051 a.u. (“low” intensity). These fundamental peak field strengths were chosen to match the experimentally observed cut-offs. The second harmonic field strength was set to F2 = 0.14F.
5.4 Channel-resolved contributions to high harmonic spectrum
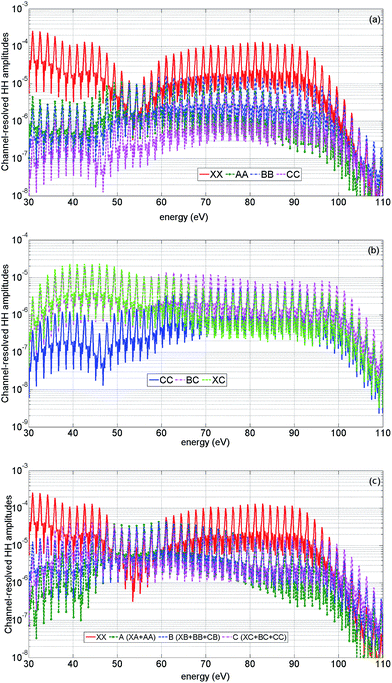
One of the most surprising findings of this work is the sensitivity of the 2D HHG spectra to laser-driven cross-channels. To explain the underlying physics, we start with the analysis of high harmonic channels pertinent to our experiment. These channels can be separated into three groups. The first group includes all diagonal channels: XX, AA, BB, CC (the first letter indicates the ionization channel, the second letter indicates the recombination channel), see Fig. 9(a). The second group of channels includes all channels originating from the X-channel: XX, XA, XB, XC. The cross-channels XA, XB, XC originate mainly due to laser-induced (sub-cycle) polarization, i.e. they are predominately associated with virtual laser-driven transitions between the states of the cation. Finally, the last group of channels represent strongly coupled cross-channels CB and BC: laser-driven transitions between the cationic states B and C that lead to real population transfer. Our following analysis shows that cross-channels leave a mark in the two-dimensional HHG spectrum. The channels recombining to the C-state become particularly visible. Fig. 9(b) illustrates their contributions to the HHG spectrum at the level of amplitudes. Note that due to strong coupling between the B and C states of the cation, direct channels can also bear the signatures of the laser-driven dynamics. For example, the minimum in the CC channel around 46 eV reflects a loss of population in this state due to the laser-driven dynamics between ionization and recombination.It is instructive to group all HHG channels into four groups by recombination: channel XX, channel A (including XA, AA), channel B (including BB, XB, CB) and channel C (including CC, BC, XC), see Fig. 9(c). Comparison of their amplitudes with those of the diagonal channels shown in Fig. 9(a) emphasizes the importance of laser-driven cross-channels.
5.5 Analysis of theoretical 2D spectra
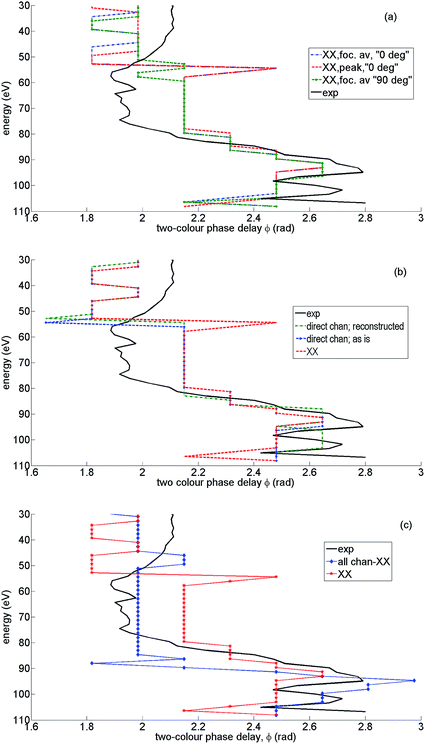
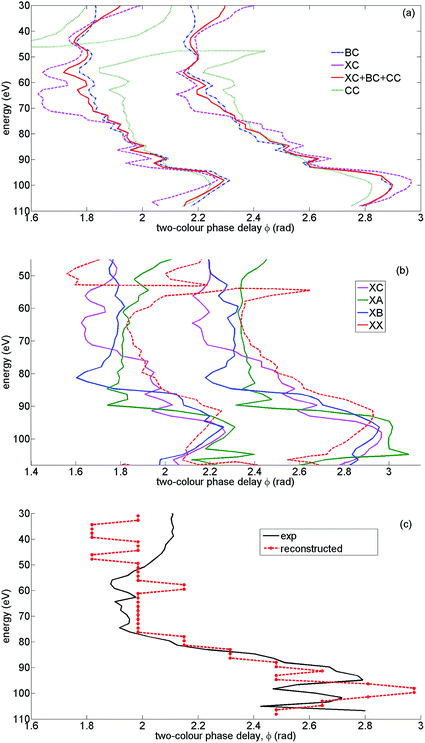
The value of two-colour delay, which corresponds to the maximum of high harmonic intensity for a given harmonic, plays an important role in our analysis. This observable has been introduced and analysed in our earlier work.7,42–44,56 We refer to it as the “optimal two-colour delay” ϕmax. The observed HHG signal results from the coherent addition of many individual channels, as discussed in Section 2. This in turn produces a profile of ϕmaxvs. harmonic energy that is characteristic of the contributing channels and their relative amplitudes and phases. We shall focus on the high intensity case, and demonstrate how to extract each channel contribution. We begin by analyzing ϕmaxvs. harmonic energy for the main high harmonic channel XX. Could the measured profile of ϕmaxvs. harmonic energy be accounted for by a contribution from the XX channel only? We will show that this cannot be the case.Fig. 10(a) shows the optimal two-colour phase for the XX channel at parallel alignment (corresponding in our case to the coherent sum of calculated HHG signals arising from molecules aligned at ±35°, ±40°, and ±45°), perpendicular alignment (corresponding in our case to the coherent sum of calculated HHG signals arising from molecules aligned at 80° and 100°), for high intensity. We also compare ϕmax for the focal averaged results and for the peak intensity (F = 0.057 a.u.), for parallel alignment. These comparisons allow us to identify (i) the characteristic shape ϕmax for the XX channel and (ii) the specific features (jumps) below 60 eV (at 30–35 eV and 50–55 eV), associated with focal averaging and the structure of the XX channel.
The 0.6 rad jump in ϕmax around 55 eV is associated with the structural minimum in recombination to the X-state, but has a purely interference nature. The interference is between the contributions of two adjacent half-cycles. The signal for each half-cycle, as a function of the two-colour delay, is slightly different due to the difference in the recombination angles. Thus, the modulation of the harmonic signal vs. two-colour delay is slightly sheared for the two successive half-cycles. As a result, their interference leads to a differential signal when the half-cycle contribution amplitudes change sign. This can occur in the vicinity of any spectral minimum, either structural, or caused by depletion and a sign change in the laser-driven population amplitude for a particular channel. Better angular averaging involving many more angles (with a smaller step than used here) is likely to smooth out the feature around 55 eV.
While the structural minimum around 55 eV is observed in the 1D spectra for high intensity and parallel alignment (see Fig. 3) it does not manifest itself in the experimental 2D spectra. It also disappears from the theoretical ϕmax trace once all channels are included, see Fig. 11(b). The main message from Fig. 10(a) is that the experimental value of ϕmax (black solid) clearly deviates from ϕmax for the XX channel, most notably in the region of energies from about 55 eV to 80 eV.
Fig. 10(b) shows the optimal two-colour delay corresponding to the 2D spectrum, which includes a coherent sum of only direct channels: XX, AA, BB, CC. Similar to the analysis of the previous paragraph and Fig. 10(a), we can try to fit the experimental ϕmax by taking only the direct channels into account. Once again, we find that the direct channels are insufficient in describing the data – there are only minor deviations of ϕmax that correspond to four direct channels, compared with ϕmax corresponding to a single (XX) channel. Blue dotted and green dashed traces of ϕmax correspond to zero “extra” phases φn (see Section 5.2) and a reconstructed set of phases φn and amplitudes ρn discussed below. In both cases the results are very similar and mostly follow the ϕmax of the XX channel. The only difference is associated with the destructive interference between X and B channels, which is marked by a characteristic jump of ϕmax, and is described in detail in ref. 7 for a 800 nm fundamental field. It coincides with the position of the structural minimum in the XX channel. The key message here is that if we include only diagonal (direct) channels, the ϕmax is virtually indistinguishable from the one corresponding to the XX channel only, apart from the narrow phase jump.
We can now discuss the influence of other channels on the shape of the ϕmax. We proceed with the analysis of parallel alignment (corresponding in our case to a coherent sum of calculated HHG signals arising from molecules aligned at ±35°, ±40°, and ±45°). Fig. 10(c) shows the optimal two-colour phase for all channels except channel XX (blue, diamonds). In this case we apply the reconstructed set of phases φn and amplitudes ρn discussed below. The same figure also shows ϕmax for the XX channel only (red, stars). The comparison with an experimental trace for ϕmax (black, solid) shows that the main channel XX must not dominate in the region of energies from about 55 eV to 80 eV, because the ϕmax corresponding to all channels except channel XX is off-set towards the experimental value. What is the origin of this off-set and what does it tell us?
5.6 The role of laser-driven cross-channels
While all diagonal channels have a very similar ϕmax, the laser-driven cross-channels lead to a different optimization of the two-colour delay. As described in detail in ref. 43 and Section 3.3 of this paper, the optimal two-colour delay is determined by the balance between the optimal ionization and return conditions, which are, in turn, determined by ionization and recombination times. For cross-channels, such as e.g. XB, XC and XA, the ionization and recombination times correspond to different ionization potentials Ip. For direct (diagonal) channels, such as XX they correspond to the same Ip. Therefore, the two-colour delay ϕ = ϕmax that maximises the HHG signal for direct channels, will not be optimal for cross-channels.Fundamentally, this difference is related to the entanglement between the electron and the ion. For a given harmonic order, if a laser-driven “real” or “virtual” transition occurs in the ion, the continuum electron trajectory leading to this harmonic must adjust accordingly. For example, channels XX and XC will have the same ionization time but different recombination times for the same harmonic, due to the extra phase accumulated in the XC channel upon transition to the state C. Since the optimal two-colour delay depends on both ionization and recombination times, the pair of times corresponding to the XX channel will optimize ϕmax for the XX channel, but the shift of the recombination time in the XC channel for the same ionization time as in XX will inevitably lead to a different value of ϕmax for the XC channel. The magnitude of this effect and its appearance in the spectrum depends on the value of ΔIp between the two coupled channels. The strongest deviation of ϕmax from its standard value will be observed for channel XC, because it corresponds to the largest difference in Ip (ΔIp = 5.6 eV) between ionization and recombination channels.
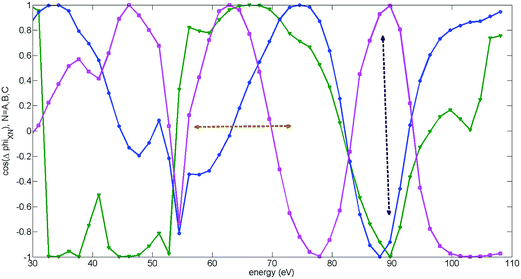
Fig. 11(a) and (b) illustrate this effect. Fig. 11(a) shows contours of the normalized 2D HHG spectrum for channels XC, BC, CC and their coherent sum at the level of 0.95 from its maximal value. The maximal value is unity (i.e. the contour corresponding to 1 is represented by ϕmax itself). By depicting the 2D data as a contour plot, it is easier to visualize the variations in ϕmax over a wide range of harmonic energies. Thus we can see that in the figure, the contour corresponding to channel XC (dashed magenta) shows the largest off-set towards lower values of two-colour delay. The BC channel (dash-dotted blue) corresponds to smaller ΔIp and the effect is smaller. Channel CC (dotted green) follows XX, except for the sharp feature at around 45 eV related to the minimum in its spectrum, in close similarity to that for the XX channel (see Fig. 9(a) and 9(b)). In the region of energies above 45 eV all these channels interfere constructively. Therefore the total signal of channel C, which includes channels XC + CC + BC is also off-set towards lower values of the two-colour delay (solid red contour).
Fig. 11(b) shows that a similar effect is observed for all cross-channels and this effect is indeed proportional to ΔIp. The smaller ΔIp, the longer the time required to accumulate the “extra phase” responsible for the shift of the recombination time. That is why the XA channel shows a significant off-set at the highest harmonics (from 65 eV to 95 eV), the XB channel at lower harmonic energies (from 60 eV to 85 eV), and the XC channel at even lower energies (from 55 eV to 80 eV). The appearance of a similar off-set in the experimental ϕmax signifies the presence of laser-driven channels in the HHG response, as well as their significant strength. The appearance of this off-set in the region of energies from 55 eV to 80 eV emphasises the contribution of the XC channel and consequently all channels recombining to the C state of the ion.
5.7 Physical picture underlying experimental results for high and low intensities
In this subsection we will make direct comparison between the theoretical and experimental 2D spectra to find the set of “extra” phases φn and amplitudes ρn between channels XX, A, B, and C, if they are required.Channels A, B, and C arise once we group all essential channels by recombination (Fig. 9(c)). The channel A includes XA, AA, the channel B includes XB, BB, CB and the channel C includes CC, BC, XC. What is the strategy for finding the possibly missing relative phases between the four different channels XX, A, B and C?
We will follow the variation of the optimal two-colour delay ϕmax to uncover the underlying multielectron dynamics. First of all, as it was pointed out in ref. 7, if ϕmax deviates sharply from the trace corresponding to the XX-channel, it means that there is a destructive interference between XX and another channel. The position of the destructive interference in the spectrum is determined by the evolution of the relative phase between these channels vs. harmonic number, while the magnitude and the “direction” of the deviation of ϕmax depends on the relative weights of the two destructively interfering channels (see Supplementary Information to ref. 7 for details). Thus, in principle, for each harmonic experiencing the phase jump in ϕmax due to destructive interference the relative phase (i.e. ≈π) and relative weight of the two contributing channels could be approximately reconstructed. Such features are definitely observed in the spectra for both high and low intensities (and parallel alignment) and correspond to energies at about 95 eV (high intensity, see also minimum in 1D spectrum in Fig. 3) and 70 eV to 90 eV (low intensity). These phase jumps scale with intensity, as discussed in ref. 7.
In addition to these jumps, for high intensity and parallel alignment the experimental ϕmax smoothly deviates from its XX value towards lower values of the two-colour delay in a broad region of energies from about 55 eV to 80 eV, as extensively discussed above. Fig. 10(c) unambiguously shows that this effect is related to switching between the main channel XX and all other channels: A + B + C. Specifically, the off-set is mainly due to channel C, as discussed in the previous subsection and shown in Fig. 11(a) and (b). The switching can occur in the region of energies where all channels interfere constructively (or very mildly destructively), see Fig. 12. The horizontal double arrow shows the region of energies where A + B + C channels interfere constructively or mildly destructively. The vertical double arrow shows a specific energy, for which the destructive interference between B + A and C channels occurs. For this energy the XX channel has already become unimportant, since it reaches its cut-off, but the C channel with the highest cut-off dominates. The dominance of A + B + C channels before the cut-off may be achieved either due to their constructive interference (this condition defines the relative phases between the channels φn), or, if the constructive interference is still not enough to observe the switching from XX to A + B + C, it requires an additional increase of the weights of the A, B, C channels (this condition approximately determines the amplitudes ρn).
The condition of constructive interference in the region of energies from about 55 eV to 80 eV and destructive interference at about 95 eV allowed us to establish the missing phases between the four recombination channels: φX = 0, φA ≈ 0.4π, φB ≈ 0, φC ≈ −0.12π. The error in this reconstruction is about 0.2π. The condition that the total spectrum must switch from channel XX to A + B + C channels at 55 eV and back at about 80 eV have determined the high harmonic order N-dependent “extra” weights ρn(N) that we have introduced:
| σ = (N − N0)/ΔN, | (7) |
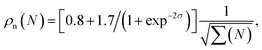 | (8) |
 | ||
| Fig. 13 Normalized two-dimensional HHG spectra of CO2 for parallel alignment. The peak field strength F = 0.057 a.u. (a) and F = 0.051 a.u. (b). The second harmonic field is F2 = 0.14F, the fundamental wavelength is 1480 nm. The results are averaged over the distribution of laser intensities in the focus. Black lines: experimental ϕmax including estimated error in extracting ϕmax for the respective laser intensities, adapted from Fig. 6(a) and (b). For low intensity the non-normalized experimental HHG signal is extremely weak in the energy region from 55 eV to 70 eV, thus reliable assignment of ϕmax in this region becomes very challenging. This spectral region is indicated by grey dotted horizontal lines in Fig. 6(b) and also in panel (b). Outside of this energy region, the theoretical and experimental ϕmax are in excellent agreement. | ||
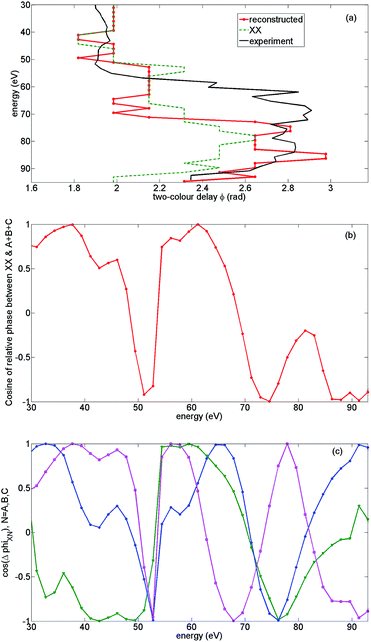
In Fig. 13(a) we show the calculated normalized 2D spectrum for high intensity. The results capture all essential features of the corresponding experimental spectrum in Fig. 6(a), including the deviation from the single-channel picture. A similar comparison is presented for the low intensity case in Fig. 13(b) and (c), showing the same qualitative difference in the 2D spectra between high and low intensities as in the experiment. For low intensity we used the same phases φn and amplitude corrections ρn(N) that we have established from the analysis of theoretical and experimental results for high intensity.
In the low intensity case, the detailed mechanism underlying the deviation of ϕmax from its value corresponding to XX is different from the high intensity case. It is associated with a broad region of destructive interference between XX and all other channels (A + B + C) ranging from 70 eV to 93 eV (see Fig. 14(b) to gauge the cosine of the relative phase between XX and all other channels). This destructive interference is due to a “conveyor” built from the channels A, B, and C “passing” the destructive interference with XX from channel to channel as it “moves” from lower to higher energies in the region from 70 eV to 93 eV, see Fig. 14(c) illustrating this effect. In contrast, in the high intensity experiment the constructive interference is more dominant.
To summarize, the constructive interference between the A, B, and C channels, and the constructive interference between the A + B + C and XX channels together with a markedly different behaviour of ϕmax for laser-driven cross channels allowed us to identify and detect the switching between the XX and A + B + C channels, highlighting the dominance of the C and B channels in the region of energies from 55 eV to 80 eV. These observations allowed us to reconstruct the missing phases φn and weights of the recombination channels ρn.
Overall, our analysis provides clear evidence of the coupled multichannel light–matter interaction that manifests itself in different ways in the low and high intensity experiments.
The resulting 2D HHG spectra for high and low intensities are shown in Fig. 13(a) and (b). These spectra are in good agreement with the experiment, within experimental error bars. Note that for low intensity and parallel alignment the non-normalized experimental HHG signal is extremely weak in the energy region from 55 eV to 75 eV, thus reliable assignment of ϕmax in this region becomes very challenging. This spectral region is indicated by horizontal lines in Fig. 6(b) and 13(b). Outside of this energy region, the theoretical and experimental ϕmax are in excellent agreement.
5.8 Pilot reconstruction of sub-cycle ionization dynamics
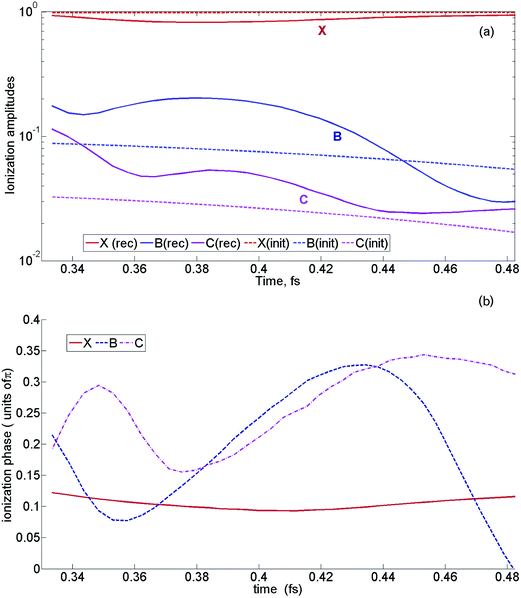
We are now in a position to find the deviation from the original prediction of the sub-cycle ionization amplitudes and phases. However, we note that a full reconstruction of sub-cycle ionization dynamics from the experimental data requires a detailed account of the molecular alignment distribution; here, we have only made illustrative calculations with a limited range of alignment angles.The results of our analysis are shown in Fig. 15, presented in the basis of the field free cationic states. Back-propagation is performed for each harmonic, starting with the real-valued recombination time t = t(N) corresponding to this harmonic, and finishing at the real part of the complex ionization time ti(N) corresponding to the same harmonic. The ionization and recombination times are found for the average ionization potential between the four participating channels. This averaging results in the error in phase reconstruction, contributing to the ∼0.2π error associated with the reconstructed recombination phases. Note that the results are obtained for the so-called short trajectories, relevant for the experiment. Hence, the plateau trajectories correspond to electrons that are ionized well after the peak of the laser field oscillation.
Fig. 15(a) shows the reconstructed ionization amplitude vs. ionization time, corresponding to channels X (red, solid), B (blue, solid), C (magenta, solid) along with the original (initial) sub-cycle amplitudes (dashed), which served as an input for our calculations. Fig. 15(b) shows the respective ionization phases for channels X (red), B (blue), C (magenta).
The reconstructed ionization phases show that channels B and C are generally in phase. States B and C are strongly coupled by the laser field. It makes the ionization process highly non-trivial and puts it outside of the applicability region of standard Keldysh-type strong field ionization theories. In the limit of strongly coupled two-level system, one could think of the two quasi energy states, formed by the “+” and the “−” superposition of B and C states. The results of our reconstruction indicate that the quasi energy state B + C as opposed to B − C was initially populated in our experiment. The B + C quasi energy state has a higher Ip than the state B − C, but its Dyson orbital has asymptotic behaviour that is advantageous for tunneling. Specifically, it extends towards the tunneling barrier, but not in the opposite direction, as would be in the case of the B − C state.
According to our reconstruction, the relative phase between the B and X channels is also small, especially in the high photon energy region, corresponding to early ionization times. This conclusion is in agreement with our earlier observation reported in ref. 16. There, we have followed the evolution of destructive interference in the high harmonic spectrum with laser intensity near the cut-off harmonic and have found that the phase between the X and B channels is close to zero. Our current investigation extends these earlier conclusions to the long-wavelength regime.
In contrast to very minor relative inter-channel ionization phases reconstructed from our experiment, the reconstructed ionization amplitudes (solid curves in Fig. 15(a)) are significantly higher than those expected from single channel strong field ionization theory (dashed curves). This result is not surprising from the point of view of our analysis, since we have increased the contribution of the B and C recombination channels to ensure switching between the dominant channel XX at low harmonic energies to dominant channels A + B + C in the region from 55 eV to 80 eV. The deviation from a single channel model is expected due to strong laser coupling between B and C states, as discussed above. Thus, the experiment suggests that the single-channel model of strong field ionization we have used in our calculations substantially underestimates the relative population of the B and C states.
6 Conclusions
In contrast to standard assumptions, our findings reveal the important role of sub-cycle laser-driven dynamics between cationic states, even for mid-IR driving fields. These dynamics leave a clear fingerprint in the 2D HHG spectra. In general, the optimal phase delay ϕmax is very sensitive to the presence of multiple channels – information that may be hidden in the 1D HHG spectrum. In particular, the dependence of ϕmax on the harmonic number is sensitive to the presence of the laser-driven hole dynamics between ionization and recombination. This property allows one to reconstruct the relative phases between different ionization channels and their relative amplitudes at the moment of ionization, on the sub-cycle time scale. These phases and amplitudes encode the dynamics of multi-electron rearrangement upon strong field ionization. We have found substantial deviations of reconstructed sub-cycle ionization amplitudes from the values predicted by single-channel tunneling theory, which signifies the non-adiabatic nature of the ionization process and may be related to the coupling between the ionization channels, both due to the laser field and also due to correlation-driven interactions during tunnelling. Similar information is present and can be extracted at different intensities and wavelengths of the fundamental field. Additional scans of the wavelength and the intensity of the fundamental field can then be used to reveal the intensity and wavelength-dependent aspects of the dynamics.Our results on the unexpectedly strong contributions of deeper-lying channels to strong-field ionization are pertinent to understanding a wide range of phenomena initiated by ionization in strong IR and mid-IR fields, from laser filamentation and air lasing to multiple ionization and plasma dynamics.
Fundamentally, our study allows us to identify the initial conditions for the hole dynamics – the coherent electronic wavepacket that can be created on multiple potential energy surfaces of a molecule. The role of this coherence in systems with more complex coupled electronic and nuclear dynamics, especially at conical intersections, and the possibility of laser control of these dynamics on the sub-cycle time scale69 are the future challenges of this field.
Authors contributions
B. D. B., M. N., M. D., D. F., C. V., and S. S. performed the experiments. B. D. B., H. S., Y. M., C. V. and S. S. analyzed experimental data. A. G. H. developed the R-matrix code for photo-ionization and photo-recombination and the model for CO2 calculations. Z. M., D. B., and A. G. H. performed R-matrix calculations. Z. M. extended R-matrix codes to high energy region and implemented a phase-consistent approach to photoionization. F. M. and O. S. developed the HHG codes and performed HHG calculations. V. S. contributed at the initial stages of the project. S. P. performed quantum chemical calculations. M. I. and O. S. analysed the experimental and theoretical results and performed the reconstruction. B. D. B., M. I., N. D., and O. S. wrote the paper. All authors discussed the results and provided comments on the manuscript. N. D. and O. S. supervised the project.Acknowledgements
Z. M., F. M. and O. S. gratefully acknowledge the support of Deutsche Forschungsgemeinschaft, project Sm292/5-1, A. G. H. and M. I. gratefully acknowledge the support of Deutsche Forschungsgemeinschaft, project IV152/7-1. The MBI (Z. M., F. M., A. G. H., O. S.) and Polimi (C. V., S. S.) nodes gratefully acknowledge the support of their collaboration via EU ITN MEDEA – AMD-641789-17 project. M. I. gratefully acknowledges the support of EPSRC/DSTL MURI grant EP/N018680/1. The authors gratefully acknowledge the support of their collaboration trough European Cooperation in Science and Technology (COST), program CM1204 XLIC. Prof. Nirit Dudovich is the incumbent of the Robin Chemers Neustein Professorial Chair. N. D. gratefully acknowledges the Minerva Foundation, the Israeli Science Foundation, the European Research Council Starting Research Grant MIDAS, the Crown Photonics Center, and the I-Core Center for financial support. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 641272.References
- F. Krausz and M. Y. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- M. Schultze, M. Fieß, N. Karpowicz, J. Gagnon, M. Korbman, M. Hofstetter, S. Neppl, A. Cavalieri, Y. Komninos, T. Mercouris, C. Nicolaides, R. Pazourek, S. Nagele, J. J. Feist, J. Burgdörfer, A. M. Azzeer, R. Ernstorfer, R. Kienberger, U. Kleineberg, E. Goulielmakis, F. Krausz and V. S. Yakovlev, Science, 2010, 328, 1658–1662 CrossRef CAS PubMed.
- K. Klünder, J. M. Dahlström, M. Gisselbrecht, T. Fordell, M. Swoboda, D. Guénot, P. Johnsson, J. Caillat, J. Mauritsson, A. Maquet, R. Taïeb and A. L'Huillier, Phys. Rev. Lett., 2011, 106, 143002 CrossRef PubMed.
- R. Pazourek, S. Nagele and J. Burgdörfer, Rev. Mod. Phys., 2015, 87, 765–802 CrossRef.
- P. Eckle, A. N. Pfeiffer, C. Cirelli, A. Staudte, R. Dörner, H. G. Muller, M. Büttiker and U. Keller, Science, 2008, 322, 1525–1529 CrossRef CAS PubMed.
- L. Torlina, F. Morales, J. Kaushal, I. Ivanov, A. Kheifets, A. Zielinski, A. Scrinzi, H. G. Muller, S. Sukiasyan, M. Y. Ivanov and O. Smirnova, Nat. Phys., 2015, 11, 503–508 CrossRef CAS.
- D. Shafir, H. Soifer, B. D. Bruner, M. Dagan, Y. Mairesse, S. Patchkovskii, M. Y. Ivanov, O. Smirnova and N. Dudovich, Nature, 2012, 485, 343–346 CrossRef CAS PubMed.
- O. Pedatzur, G. Orenstein, V. Serbinenko, H. Soifer, B. D. Bruner, A. J. Uzan, D. S. Brambila, A. G. Harvey, L. Torlina, F. Morales, O. Smirnova and N. Dudovich, Nat. Phys., 2015, 11, 815–820 CrossRef CAS.
- E. Goulielmakis, Z. H. Loh, A. Wirth, R. Santra, N. Rohringer, V. S. Yakovlev, S. Zherebtsov, T. Pfeifer, A. M. Azzeer, M. F. Kling, S. R. Leone and F. Krausz, Nature, 2010, 466, 739–743 CrossRef CAS PubMed.
- A. Fleischer, H. J. Wörner, L. Arissian, L. R. Liu, M. Meckel, A. Rippert, R. Dörner, D. M. Villeneuve, P. B. Corkum and A. Staudte, Phys. Rev. Lett., 2011, 107, 113003 CrossRef CAS PubMed.
- Y. Mairesse, J. Higuet, N. Dudovich, D. Shafir, B. Fabre, E. Mével, E. Constant, S. Patchkovskii, Z. Walters, M. Y. Ivanov and O. Smirnova, Phys. Rev. Lett., 2010, 104, 213601 CrossRef CAS PubMed.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horný, E. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Wörner, Science, 2015, 350, 790–795 CrossRef CAS PubMed.
- A. I. Kuleff and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124002 CrossRef.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. de Camillis, S. Anumula, L. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Science, 2014, 346, 336–339 CrossRef CAS PubMed.
- J. Leeuwenburgh, B. Cooper, V. Averbukh, J. P. Marangos and M. Ivanov, Phys. Rev. Lett., 2013, 111, 123002 CrossRef PubMed.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972–977 CrossRef CAS PubMed.
- O. Smirnova, S. Patchkovskii, Y. Mairesse, N. Dudovich and M. Y. Ivanov, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16556–16561 CrossRef CAS PubMed.
- O. Smirnova, S. Patchkovskii, Y. Mairesse, N. Dudovich, D. Villeneuve, P. B. Corkum and M. Y. Ivanov, Phys. Rev. Lett., 2009, 102, 063601 CrossRef PubMed.
- S. Haessler, J. Caillat, W. Boutu, C. Giovanetti-Teixeira, T. Ruchon, T. Auguste, Z. Diveki, P. Breger, A. Maquet, B. Carré, R. Taïeb and P. Salières, Nat. Phys., 2010, 6, 200–206 CrossRef CAS.
- P. B. Corkum, Phys. Today, 2011, 64, 36–41 CrossRef CAS.
- O. Smirnova and M. Ivanov, How to for Beginners – Multi-electron Dynamics in HHG, Max Born Institut, 2016, https://www.youtube.com/watch?v=fA2pdLYVkQQ Search PubMed.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994–1997 CrossRef CAS PubMed.
- M. Lein, N. Hay, R. Velotta, J. P. Marangos and P. L. Knight, Phys. Rev. Lett., 2002, 88, 183903 CrossRef CAS PubMed.
- M. Lein, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, R135–R173 CrossRef CAS.
- A. Zaïr, T. Siegel, S. Sukiasyan, F. Risoud, L. Brugnera, C. Hutchison, Z. Diveki, T. Auguste, J. W. Tisch, P. Salières, M. Y. Ivanov and J. P. Marangos, Chem. Phys., 2013, 414, 184–191 CrossRef.
- R. Cireasa, A. E. Boguslavskiy, B. Pons, M. C. H. Wong, D. Descamps, S. Petit, H. Ruf, N. Thiré, A. Ferré, J. Suarez, J. Higuet, B. E. Schmidt, A. F. Alharbi, F. Légaré, V. Blanchet, B. Fabre, S. Patchkovskii, O. Smirnova, Y. Mairesse and V. R. Bhardwaj, Nat. Phys., 2015, 11, 654–658 CrossRef CAS.
- S. Baker, J. S. Robinson, C. A. Haworth, H. Teng, R. A. Smith, C. C. Chirila, M. Lein, J. W. G. Tisch and J. P. Marangos, Science, 2006, 312, 424–427 CrossRef CAS PubMed.
- N. L. Wagner, A. Wüest, I. P. Christov, T. Popmintchev, X. Zhou, M. M. Murnane and H. C. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13279–13285 CrossRef CAS PubMed.
- W. Li, X. Zhou, R. Lock, S. Patchkovskii, A. Stolow, H. C. Kapteyn and M. M. Murnane, Science, 2008, 322, 1207–1211 CrossRef CAS PubMed.
- A. Ferré, D. Staedter, F. Burgy, M. Dagan, D. Descamps, N. Dudovich, S. Petit, H. Soifer, V. Blanchet and Y. Mairesse, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124023 CrossRef.
- A. Ferré, A. E. Boguslavskiy, M. Dagan, V. Blanchet, B. D. Bruner, F. Burgy, A. Camper, D. Descamps, B. Fabre, N. Fedorov, J. Gaudin, G. Geoffroy, J. Mikosch, S. Patchkovskii, S. Petit, T. Ruchon, H. Soifer, D. Staedter, I. Wilkinson, A. Stolow, N. Dudovich and Y. Mairesse, Nat. Commun., 2015, 6, 5952 CrossRef PubMed.
- A. Ferré, H. Soifer, O. Pedatzur, C. Bourassin-Bouchet, B. D. Bruner, R. Canonge, F. Catoire, D. Descamps, B. Fabre, E. Mével, S. Petit, N. Dudovich and Y. Mairesse, Phys. Rev. Lett., 2016, 116, 053002 CrossRef PubMed.
- H. J. Wörner, J. B. Bertrand, D. V. Kartashov, P. B. Corkum and D. M. Villeneuve, Nature, 2010, 466, 604–607 CrossRef PubMed.
- H. J. Wörner, J. B. Bertrand, P. B. Corkum and D. M. Villeneuve, Phys. Rev. Lett., 2010, 105, 103002 CrossRef PubMed.
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867–871 CrossRef CAS PubMed.
- C. Vozzi, F. Calegari, E. Benedetti, J.-P. Caumes, G. Sansone, S. Stagira, M. Nisoli, R. Torres, E. Heesel, N. Kajumba, J. P. Marangos, C. Altucci and R. Velotta, Phys. Rev. Lett., 2005, 95, 153902 CrossRef CAS PubMed.
- C. Vozzi, M. Negro, F. Calegari, G. Sansone, M. Nisoli, S. D. Silvestri and S. Stagira, Nat. Phys., 2011, 7, 822–826 CrossRef.
- T. Kanai, S. Minemoto and H. Sakai, Nature, 2005, 435, 470–474 CrossRef CAS PubMed.
- P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, 1st edn, 2011 Search PubMed.
- M. H. Cho, Chem. Rev., 2008, 108, 1331–1418 CrossRef CAS PubMed.
- F. D. Fuller and J. P. Ogilvie, Annu. Rev. Phys. Chem., 2015, 66, 667–690 CrossRef CAS PubMed.
- H. Soifer, M. Dagan, D. Shafir, B. D. Bruner, M. Y. Ivanov, V. Serbinenko, I. Barth, O. Smirnova and N. Dudovich, Chem. Phys., 2013, 414, 176–183 CrossRef CAS.
- V. Serbinenko and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 171001 CrossRef.
- H. Soifer, B. D. Bruner, M. Negro, M. Devetta, D. Faccialà, C. Vozzi, S. de Silvestri, S. Stagira and N. Dudovich, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 204029 CrossRef.
- L. Torlina, M. Ivanov, Z. B. Walters and O. Smirnova, Phys. Rev. A, 2012, 86, 043409 CrossRef.
- Z. B. Walters and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 161002 CrossRef.
- V. P. Majety and A. Scrinzi, Phys. Rev. Lett., 2015, 115, 103002 CrossRef PubMed.
- J. Muth-Böhm, A. Becker and F. H. M. Faisal, Phys. Rev. Lett., 2000, 85, 2280–2283 CrossRef PubMed.
- R. Murray, M. Spanner, S. Patchkovskii and M. Y. Ivanov, Phys. Rev. Lett., 2011, 106, 173001 CrossRef PubMed.
- P. Salières, A. Maquet, S. Haessler, J. Caillat and R. Taïeb, Rep. Prog. Phys., 2012, 75, 062401 CrossRef PubMed.
- Z. Diveki, R. Guichard, J. Caillat, A. Camper, S. Haessler, T. Auguste, T. Ruchon, B. Carré, A. Maquet, R. Taïeb and P. Salières, Chem. Phys., 2013, 414, 121–129 CrossRef CAS.
- A. Rupenyan, P. M. Kraus, J. Schneider and H. J. Wörner, Phys. Rev. A, 2013, 87, 013401 CrossRef.
- A. Rupenyan, P. M. Kraus, J. Schneider and H. J. Wörner, Phys. Rev. A, 2013, 87, 033409 CrossRef.
- R. Torres, T. Siegel, L. Brugnera, I. Procino, J. G. Underwood, C. Altucci, R. Velotta, E. Springate, C. Froud, I. C. E. Turcu, S. Patchkovskii, M. Y. Ivanov, O. Smirnova and J. P. Marangos, Phys. Rev. A, 2010, 81, 051802 CrossRef.
- Z. Diveki, A. Camper, S. Haessler, T. Auguste, T. Ruchon, B. Carré, P. Salières, R. Guichard, J. Caillat, A. Maquet and R. Taïeb, New J. Phys., 2012, 14, 023062 CrossRef.
- B. D. Bruner, H. Soifer, D. Shafir, V. Serbinenko, O. Smirnova and N. Dudovich, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 174006 CrossRef.
- C. Vozzi, F. Calegari, E. Benedetti, S. Gasilov, G. Sansone, G. Cerullo, M. Nisoli, S. de Silvestri and S. Stagira, Opt. Lett., 2007, 32, 2957–2959 CrossRef CAS PubMed.
- R. Torres, T. Siegel, L. Brugnera, I. Procino, J. G. Underwood, C. Altucci, R. Velotta, E. Springate, C. Froud, I. C. E. Turcu, M. Y. Ivanov, O. Smirnova and J. P. Marangos, Opt. Express, 2010, 18, 3174–3180 CrossRef CAS PubMed.
- C. Vozzi, M. Negro and S. Stagira, J. Mod. Opt., 2012, 59, 1283–1302 CrossRef CAS.
- K. D. Schultz, C. I. Blaga, R. Chirla, P. Colosimo, J. Cryan, A. M. March, C. Roedig, E. Sistrunk, J. Tate, J. Wheeler, P. Agostini and L. F. DiMauro, J. Mod. Opt., 2007, 54, 1075–1085 CrossRef CAS.
- Atomic and Molecular Beam Methods, ed. G. Scoles, Oxford University Press, Inc., 1988, vol. 1 Search PubMed.
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543–557 CrossRef CAS.
- O. Smirnova and M. Ivanov, Attosecond and XUV Physics: Ultrafast Dynamics and Spectroscopy, Wiley-VCH Verlag GmbH and Co. KGaA, 2014, pp. 201–256 Search PubMed.
- O. Smirnova and M. Ivanov, Multielectron High Harmonic Generation: simple man on a complex plane, arXiv:1304.2413, 2013.
- A. G. Harvey, D. S. Brambila, F. Morales and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 215005 CrossRef.
- D. S. Brambila, A. G. Harvey, Z. Mašín, J. D. Gorfinkiel and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 245101 CrossRef.
- F. Morales, I. Barth, V. Serbinenko, S. Patchkovskii and O. Smirnova, J. Mod. Opt., 2012, 59, 1303–1311 CrossRef.
- P. Salières, B. Carré, L. L. Déroff, F. Grasbon, G. G. Paulus, H. Walther, R. Kopold, W. Becker, D. B. Milošecvić, A. Sanpera and M. Lewenstein, Science, 2001, 292, 902–905 CrossRef PubMed.
- M. Richter, F. Bouakline, J. González-Vázquez, L. Martínez-Fernández, I. Corral, S. Patchkovskii, F. Morales, M. Ivanov, F. Martín and O. Smirnova, New J. Phys., 2015, 17, 113023 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |