Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High temperature 35Cl nuclear magnetic resonance study of the LiCl–KCl system and the effect of CeCl3 dissolution
H.
Zhang
and
I.
Farnan
*
Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge, CB2 3EQ, UK. E-mail: if203@cam.ac.uk; Tel: +44 (0)1223 333431
First published on 23rd February 2016
Abstract
This paper examines the dynamics of the LiCl–KCl system over a range of temperatures in order to understand the local structure surrounding chlorine, which is the common ion in these systems, during molten salt pyro-processing. Chlorine-35 nuclear magnetic resonance (NMR) is sensitive to the local environments of the resonant nuclei and their motion on a diffusive timescale. Thus, it is a good probe of the atomic scale processes controlling the viscosities, diffusivities and conductivities of these molten salts. The average isotropic chemical shifts (35Clδ) and spin-lattice relaxation times (T1) of 35Cl in (Li,K)Cl salt mixtures have been obtained over a compositional range of 0–100 mol% KCl with an interval of 10 mol% using high temperature nuclear magnetic resonance (NMR) spectroscopy from room temperature up to 890 °C. The 35Clδ in the two end member salts are consistent with the cation–anion radius ratio as previously measured on the solid halides and the average radius ratio of cation to anion, can be used to explain the variation of 35Clδ with composition. The quadrupolar interaction is found to be responsible for the spin-lattice relaxation of the 35Cl, and the activation energies for T1 relaxation have been obtained for all compositions. The measured T1 (35Cl) activation energies do not vary linearly with composition and peak at 50% KCl, which also coincides with the Chemla point for this system. They also are in good agreement with the values from equivalent conductivity measurements. To investigate the response of the system to solutes, 8 wt% of CeCl3 was added to the pure LiCl as a surrogate actinide. The shift induced was 120 ppm and the activation energy for the T1 (35Cl) increased by a factor of four. This is a promising preliminary result for probing the effect of actinide dissolution on the dynamics of these pyro-processing salts.
1 Introduction
Molten (Li,K)Cl binary salts with eutectic composition (40.9 mol% KCl) are used as an electrolyte in pyrochemical processing to separate actinides from spent nuclear fuel. However, in principle, the thermodynamic activity of the actinide ions in the solvent salt can be tuned using an appropriate mixture of alkali chlorides, which could allow selective extraction of different metals from complex mixtures.1 The composition and temperature of the electrolyte2 can potentially be used to control the interactions of actinides with other ions in the melt in order to get this high separability. The physical consequence of tuning activities is the occurrence of ion–ion interactions, such as the formation of ionic pairs or associates, which decrease the melt conductivity.3–5 Therefore, it is important to know the nature of the ionic species, and their interactions in the melt, in order to predict the physical and chemical properties of the melt precisely when there is a change of conditions, such as temperature, pressure or concentration. This enables the manipulation of the molten salt system with the goal of greater separation efficiency for the actinides.This work forms part of a nuclear magnetic resonance (NMR) study of the pyrochemical process that will eventually include actinide-containing melts. Firstly, we focus on the fundamental microstructure and dynamics of the (Li,K)Cl system, as a basis for future studies of the influence of the lanthanides, actinides and other fission products on the molten salt system. The importance of studying simple molten salt solvents has been exemplified by comparing the self-diffusion rate of F− in (Li,K)F and LiF/YF3 salt systems, where yttrium (in YF3) was shown to promote the formation of bridging F− ions in the mixture.6
A considerable amount of research has been carried out in an attempt to understand the microscopic properties of the alkali chloride solvents and to identify the solution species and their roles in determining the bulk properties. The most relevant works involve structural investigations using neutron scattering and melt dynamics using molecular dynamics simulations.3,7–11 In general, there is a shortening of the inter-ionic distances between metal and chloride ions and a lowering of the co-ordination number of metal ions after melting.7 Neutron scattering studies7 show that this effect is more pronounced in LiCl than in KCl. Partial pair distribution functions derived from molecular dynamics (MD) studies3 of LiCl melts show that the addition of KCl also decreases the Li–Cl distance accompanied by a decrease in the [LiCln]1−n coordination number, and vice versa for K–Cl when mixed with LiCl. These structural details could qualitatively explain the decreasing trend of the ionic (Li+ and K+) diffusion rate and internal mobility (the rate of migration of one species in the melt relative to another) with increasing KCl content in the melt,3,11 but not the different cross-over points of the two properties. Moreover, the magnitude of the calculated conductivity according to the Nernst–Einstein relation is quite similar to the true conductivity in the (Li,K)Cl system, showing that the degree of correlation between the diffusive motions of different ions is not large.3 However, the relative change in the calculated conductivity across different compositions is not as large as for the true conductivity. This indicates that ionic association probably affects the overall charge transport in the system.3
It is common that the conductivity of the molten binary salts is a nonlinear function of the composition expressed as a mole fraction; usually this is a negative deviation from additivity.12 In systems with significant deviation, long-lived complex ions are likely to exist in the mixture such as in CdCl2–KCl.12 Complexes were also proposed to exist in simple alkali halide systems, such as the (Li,K)Cl system,5 although they show only moderate deviations from additivity in their conductivity.5,12 In a recent study of the liquid radial distribution function using MD simulation, an intermediate range chemical ordering of Li+ ions was considered a general property of simple mixtures of lithium halides with other alkali halides such as the (Li,K)Cl and (Li,K)F systems.8,11 Experimentally, Raman spectroscopy detected a new band in the (Li,K)F systems, and it was attributed to the relatively long-lived (LiFx)K configurations compared with pure alkali halides.9,10 Both numerical simulation and Raman spectroscopy evidenced the modification of the ionic structures upon mixing in the (Li,K)F system. However, due to the difficulty of high temperature experiments caused by the corrosiveness of molten LiCl, KCl and their mixtures, there is still a lack of experimental evidence about the potential intermediate, more long-lived structures in (Li,K)Cl molten salts and their effect on dynamic properties such as conductivity.
High temperature NMR is an effective way to monitor the changes in microstructure and dynamics of salts during pyrochemical processing. For example, the identification of the local microstructure and self-diffusion coefficient of specific ions in the molten LiF/KF system has been carried out successfully despite the severe technical challenges posed by their corrosiveness.13 In the work described here, in situ high temperature NMR is used to study atomic scale processes involved in molten (Li,K)Cl salt systems, and the effect of CeCl3 dissolution in eutectic LiCl–KCl. Using NMR spectroscopy, we could observe the chemical shift with the compositional variation to study the ionic environment. One of the most important and useful features of NMR is its ability to probe the molecular motion by measuring the spin-lattice relaxation time, T1, which is determined by the time varied local magnetic/electric fields created by microscopic fluctuations in the liquid. Therefore, it can be used to understand the nature of ionic motion and the rate of change of microstructure in the liquid.
2 Experimental
The hydroscopic nature of halide salts is a known problem. The chloride salts were purchased from Aldrich (KCl, 99.999% anhydrous) and Alfa Aesar (LiCl, CeCl3, 99.995% ultra-dry). The samples with intermediate compositions were first weighed and sealed in glass bottles in an argon glove box (oxygen and moisture contents were both below 1 ppm, in the Department of Chemistry, Cambridge). Weighed samples were kept in desiccators (purged under argon) inside a glove bag under a pureshield argon (99.995%) atmosphere before use. All experiments were carried out within one week of sample preparation. Eleven samples with different concentrations of KCl in the range 0–100 mol% with 10 mol% intervals were produced; and seven CeCl3/LiCl–KCl mixtures with a CeCl3 concentration varying from 0.5% to 40%. The salts were further dried at 200 °C for two hours in situ, with a pre-dried pureshield argon flow in the NMR probe, and were heated to higher temperatures directly from 200 °C. For LiCl–KCl systems, the NMR sample cells were single crystal alumina (sapphire) crucibles with loose fitting lids purchased from Mettler Toledo. After the NMR runs the molten salts were diluted in deionized water, and the solution pH was measured. This showed that the solutions were slightly acidic (pH 5–6); if there had been any interaction with oxygen or moisture during the measurement the pH would have been >7. For the CeCl3/LiCl–KCl (CeCl3–LKE) system, the NMR sample cells were pure fused silica tubes with Swagelok fittings at the open ends.The high temperature NMR (HT NMR) spectra were recorded on a Varian-Chemagnetics Infinity 400 MHz (9.4 T) spectrometer equipped with a 7 mm single channel home-built static probe. The probe could operate at temperatures up to 1500 °C by means of a small electric furnace surrounding the specimen coil, and the magnet and shim coils were protected by a water-cooled jacket around the furnace. The sample temperature was calibrated against the furnace temperature with an R-type thermocouple placed in the sample holder during a non-NMR run, and CsNO3 and CsCl with melting points of 414 °C and 645 °C, respectively, were used as fixed points and detected by 133Cs NMR. The absolute temperature error was less than ±5 °C. It took about 5 minutes for the sample temperature to become stable. The probe could be tuned over a resonant frequency range of 35–105 MHz. For more details, refer to ref. 14. The high temperature probe was operated at 39.197 MHz for 35Cl, and spectra were acquired using a single pulse sequence (Bloch decay). Typically, between 8 and 64 π/2 pulses were acquired with a pulse repetition delay between 0.5 s and 1 s for 35Cl, The chemical shifts were referenced to a NaCl 1 M D2O solution at room temperature for 35Cl. A small, furnace induced, shift of 1.5 ppm was detected by reversing the furnace polarity and is taken into account in all the reported data, but not in the plotted spectra. Spectra were acquired over a range of temperatures below the melting points and for all the samples at temperatures 10 °C to 20 °C above the melting point and additionally at constant temperature (above the highest melting point in the system) of 837 °C LiCl–KCl and 580 °C for the CeCl3–LKE system. Each measurement was carried out 20 minutes after reaching the desired temperature. The inversion recovery pulse sequence was used to measure spin-lattice relaxation times in the melt 20 °C above the liquids for each composition, with a temperature step of 20–30 °C. The investigation of the temperature and compositional effects on the spin-lattice relaxation time was carried out within the temperature range of 636–837 °C for LiCl–KCl (except pure KCl at 837–890 °C), and 580–760 °C for the CeCl3–LKE system.
3 Results
3.1 Chemical shifts
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
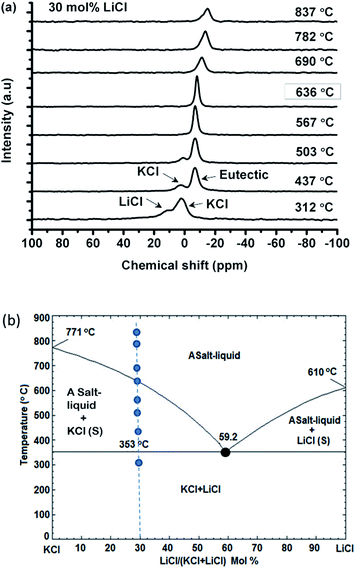
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 437 °C) is much higher than the value calculated from the phase diagram (e.g. about 1.3
1 at 437 °C) is much higher than the value calculated from the phase diagram (e.g. about 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 437 °C) according to the Lever rule. In particular, the 35Cl NMR signal from the solid KCl merges into the eutectic liquid at 567 °C, where the liquid to solid ratio is about 3
1 at 437 °C) according to the Lever rule. In particular, the 35Cl NMR signal from the solid KCl merges into the eutectic liquid at 567 °C, where the liquid to solid ratio is about 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
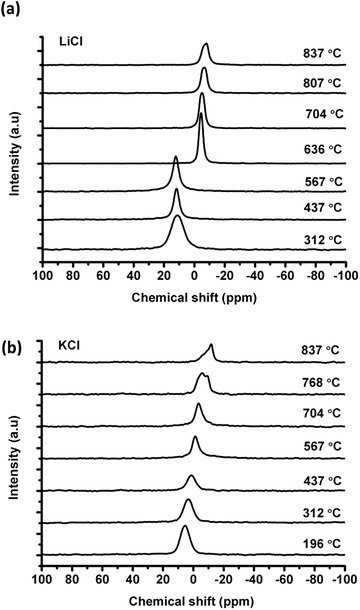
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the phase diagram, before reaching the melting temperature of 636 °C. This could be due to the high mobility of the chloride ions in the liquid, which appear to be exchanging with the rest of the solid KCl before melting (see Discussion).
1 in the phase diagram, before reaching the melting temperature of 636 °C. This could be due to the high mobility of the chloride ions in the liquid, which appear to be exchanging with the rest of the solid KCl before melting (see Discussion).
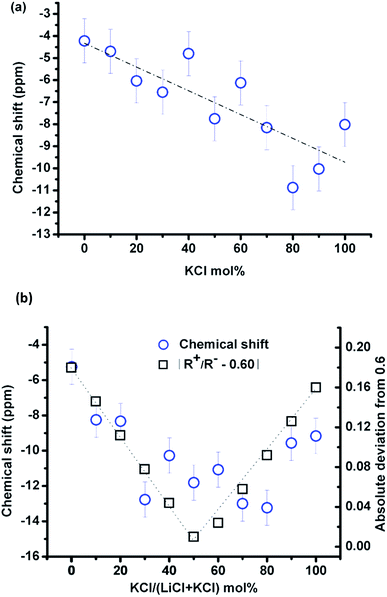
Fig. 3(a) shows the compositional effect of adding KCl to the melt on the chemical shift of 35Cl at 10–20 °C above the corresponding melting point. The Clδ is the weighted average of chlorine ions with different local environments, and it could be taken as a simple additive function of two pure salts in the (Li,K)Cl mixture if the chloride ions have no preferential association in the mixture. The Clδ decreases approximately linearly (least square fitting, the vertical deviation R2 is 64.5%) upon mixing with KCl with a variation of ∼10 ppm across the whole composition. The fitting is just for guidance, as the data become more scattered in the KCl rich zone, possibly due to the migration of the liquid salt towards the cap of the container at high temperature (e.g. in Fig. 1(b)).
The temperature effect on the chemical shift was similar for all compositions (−1.4 ppm/100 °C, e.g. in Fig. 2(a)) in the melt and was not negligible, so the compositional effect was compared at a single temperature of 837 °C, as shown in Fig. 3(b). Despite the small variation of the Clδ with composition and the scattering of the data points, it can be seen that Clδ first decreased and reached a minimum value at about 50 mol% KCl and then increased until pure KCl. This indicates that the effect of composition is nontrivial in the (Li,K)Cl mixture, which will be discussed in Section 4.1.
3.2 Spin-lattice relaxation times, T1
In the melt, the spin-relaxation time, T1, increases with temperature, indicating a decreasing motional correlation time with temperature and, well away from the T1 minimum, the activation energy (Ea) of the motion responsible for the spin-lattice relaxation of Cl− can be calculated from an Arrhenian relationship. The calculated activation energies for the spin-lattice relaxation of 35Cl in pure liquid LiCl and KCl are 0.0826 ± 0.007 eV and 0.1509 ± 0.015 eV, respectively. These agree, within error, with the activation energies of 0.0746–0.0899 eV (LiCl melt) and 0.1414–0.1489 eV (KCl melt), which were obtained in high temperature equivalent conductivity measurements of LiCl and KCl.5,12,15 Here the equivalent conductivity is the product of the specific conductivity and the equivalent volume (of 1 mol), and it refers to a state in which there is always one equivalent of the salt between electrodes at 1.0 cm distance.5,12 Therefore, the activation energy derived from equivalent conductivity is preferred for comparisons of ionic migration. Futhermore, in LiCl and KCl melts, both cations and anions conduct, and their activation energies were taken as the same in a calculation of the conductivity,5,12 which matched the experimental results. 35Cl HT NMR detects the variation of the activation energy for molten salt equivalent conductivity. Thus, the same motional process is underlying both measurements even if their time scales are very different.
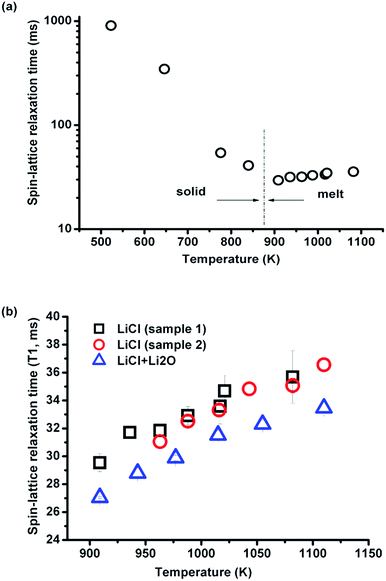
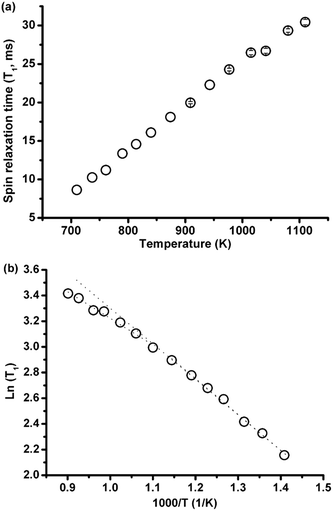
3.2.2.1 Effect of temperature. The spin-lattice relaxation time of 35Cl over a large temperature range of 437–837 °C (710–1110 K) was investigated in eutectic (Li,K)Cl salt. As shown in Fig. 5(a), T1 increases monotonically with temperature. When the data are plotted as ln(T1) against inverse temperature to obtain the activation energy, there appears to be a change in the rate of increase of T1 with temperature above 636 °C (Fig. 5(b)).
The changing rate may be decomposed into two activation energies calculated from ln(T1) vs. 1/T curves, which are 0.231 eV and 0. 171 eV at lower (437–636 °C) and higher (636–837 °C) temperature ranges, respectively. This indicates that the ionic mobility is enhanced at higher temperatures, which is consistent with computational results showing fewer ionic complexes in the (Li,K)Cl eutectic composition, with conductivities closer to the theoretical value of free ions with increasing temperature.16 There is no report on the activation energy variation with temperature in the (Li,K)Cl system, but a similar phenomenon was found in the alkali and alkaline earth halide systems such as CdCl2–KCl.15 In these systems, the decrease in the activation energy for motion suggests the dissociation of the ionic complex, and this indicates there are complexes in the molten (Li,K)Cl system.
3.2.2.2 Effect of composition. Fig. 6 shows the compositional effect on the relaxation time at a constant temperature of 837 °C, and it is compared with the previous study on the variation of equivalent conductivity (Λ) at 800 °C,5 because the activation energy for T1 in two end member salts is comparable with the energy derived from equivalent conductivity.
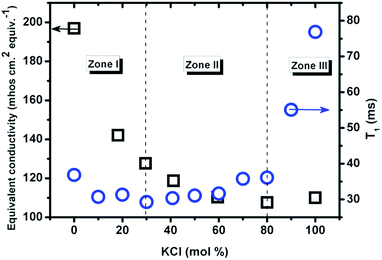 | ||
| Fig. 6 The relaxation time vs. composition at 837 °C (1110 K, circle) measured by NMR in this work; equivalent conductivity vs. composition at 800 °C (1073 K, squares) from ref. 5 (classical AC technique). | ||
The relaxation time of Cl− first decreases upon mixing and reaches a minimum at about 30 mol% KCl, followed by a nontrivial increase, from 29 ms to 36 ms within a wide composition range of 30–80 mol% KCl, and then increases more than two-fold from 80 mol% to pure KCl. The composition with the lowest value of T1 is dependent on temperature and moves to lower KCl concentrations as temperature is increased. This might indicate a change in ionic mobility similar to the Chemla effect.17 According to the relationship between T1 and Λ, the mixture could be divided into 3 zones. In zone I (<30 mol% KCl) the two properties both decrease with increasing KCl mol%. In zone II (30–80 mol% KCl) T1 increases but Λ decreases. In zone III (>80 mol% KCl), both increase with composition. The minimum of equivalent conductivity (80 mol% KCl) indicates a strong chance of formation of complexes or clusters in the mixture.5 Together with the minimum value of T1 at 30 mol% KCl, it means that the (Li,K)Cl system is not a simple mixture of two salts within a certain range of compositions.
The compositional effect on activation energy (Ea) derived from ln(T1) vs. 1/T is shown in Fig. 7 (blue circles). The activation energy calculation is carried out within the same temperature range of 637–837 °C for samples with KCl <70 mol%; and the remainder from 20 °C above the melting point to 837 °C (pure KCl from 837–888 °C). The change of Ea corresponds well to the classification of zones in Fig. 6, and zone II has the higher activation energy than a linear combination of the activation energies of the LiCl and KCl end-members (dashed line), and it reaches a maximum at approximately 40–50 mol% KCl. Moreover, the activation energy obtained from the relaxation time is consistent with the value calculated from the equivalent conductivity (calculated based on the data presented in ref. 5) in the (Li,K)Cl mixture. The maximum activation energy indicates a great chance of forming complexes or clusters in the mixture, which can consume more energy via a transition from complexes to single ions with increasing temperature.
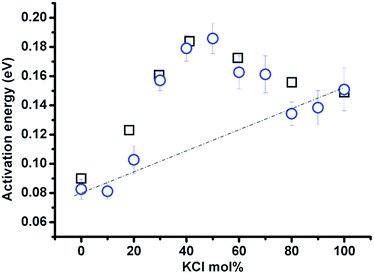 | ||
| Fig. 7 Activation energy for 35Cl in (Li,K)Cl molten salt mixtures calculated according to spin-lattice relaxation time vs. 1/temperature (blue circles); and equivalent conductivity vs. 1/temperature (black squares, equivalent conductivity was calculated from experimental data for specific conductivity and density presented in ref. 5). | ||
3.3 Effect of CeCl3 dissolution
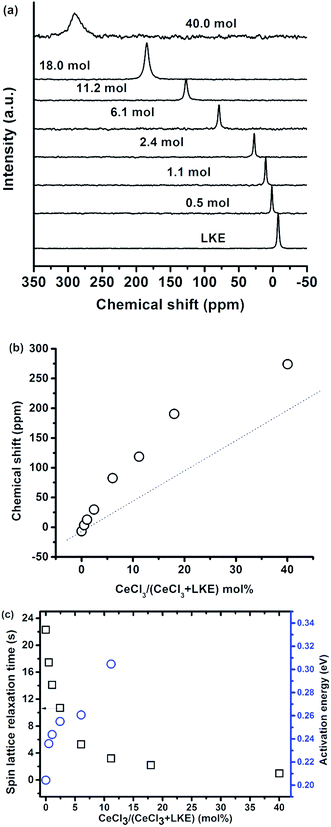
The 35Cl spectra in CeCl3–LKE over a wide range of CeCl3 concentrations is shown in Fig. 8(a) at 580 °C, and the 35Cl peak is shifted from −6.8 ppm in LKE to positive values with increasing CeCl3 concentration (e.g. to 274 ppm in 40 mol% CeCl3). Due to the paramagnetic nature of Ce3+ in CeCl3 the 35Cl resonance was adversely broadened and the chemical shift of 35Cl with CeCl3 higher than 40 mol%. The variation of 35Cl chemical shift as a function of CeCl3 mol% is presented in Fig. 8(b), the dashed line is a guide for the eye presuming the chemical shift of 35Cl is only based on two local environments (Cl− anions from LKE and CeCl3). A non-linear monotonic increase is observed, and this kind of evolution has already been reported in a previous study on LaF3–AF (A = Li, Na, K) systems.18 The non-linearity in this case was attributed to the existence of bridging F− before all the F− are involved in LaFx units in pure LaF3.Fig. 8(c) presents the spin-lattice relaxation time and T1 activation energy variation with CeCl3 concentration.
4 Discussion
4.1 Influences on chemical shift
The chemical shift, Clδ, in KCl (−8 ppm) is more shielded than in LiCl (−4 ppm). This contradicts the empirical finding that the halide chemical shift is more negative for smaller alkali cations in the alkali halides, where the chemical shift is assumed to be controlled by the nearest neighbour interactions.13,19 The difference in chemical shift between the two end-member chloride salts is considerably less than that in LiF and KF (e.g. 70 ppm difference for Fδ).13 This shows that the chemical shift depends on both the size of the cation and anion, and a more detailed study19 found that the chemical shift can be related to the cation-to-anion radius ratio (Rm = R+/R−). With a decrease in this ratio, there is an increase in the shielding of the 35Cl, while deshielding happens when the ratio is <0.6. This parabolic behavior of shielding and deshielding was attributed to changing interaction mechanisms from a first neighbour interaction to a second nearest neighbour induced polarisation19 at Rm = 0.6. The similarity of the Clδ in LiCl and KCl in the current study is because the Rm for KCl and LiCl of 0.76 and 0.42, respectively, are located either side of the turning point at 0.6. The chemical shifts of KF and LiF decrease approximately linearly with a radius ratio of 1.04 and 0.57, respectively, resulting in a chemical shift difference of 70 ppm.The cation-to-anion radius ratio can also explain the variation of the chemical shift with the KCl concentration at constant temperature. Given the cation-to-anion radius ratio in the mixtures is a simple addition of two-end member salts, the ratio increases with the KCl concentration, and a critical value of about 0.6 is obtained at a composition of 50% KCl. The absolute deviation of the cation-to-anion radius ratio from the critical value was plotted in Fig. 3(b), and this trend is consistent with the evolution of Clδ. Therefore, the Clδ in alkali halides such as KCl with Rm > 0.6 is controlled by the first nearest neighbour interaction (the same as 23Na, 87Rb and 133Cs chlorides); while for the small sized Li+, the second nearest neighbour induced polarization will increase the paramagnetic effect resulting in an increase of Clδ in LiCl.
The coalescence of solid and eutectic liquid 35Cl line shapes before reaching the melting point (as shown in Fig. 2(a)) indicates that there could be ionic exchanges between the solid and liquid phases. In a previous study on AlF3–(Na,K)F eutectic systems,20 the total dissolution of AlF3 was found to be at 879 °C by thermal analysis; however, it was cloudy by visual observation, and a clear melt was only observed at approximately 900 °C. The maximum 27Al NMR spectrum was observed at an even higher temperature of 935 °C. These observations show that the melting of the mixture took place over a range of temperature, and involves dissolving/melting processes. In the (Li,K)Cl system a similar process occurred, as the melting process involves the dissolving of the solid into the eutectic before reaching the melting temperature. Moreover, the temperature effect on the Clδ in molten (Li,K)Cl mixtures, where the Clδ decreases slightly (−1.4 ppm/100 °C) with increasing temperature, could be due to the change in the degree of association between the ions. The cations are more tightly bonded to the anions with an increase of temperature, and the coordination number of cations decreases according to MD simulation.3 Therefore, this decrease in chemical shift could be interpreted with more free anions according to a previous study on the fluorine system.13 Alternatively it could be due to thermal expansion, reducing the paramagnetic contribution in the shift causing a reduction in the Cl–Cl interaction.
It is helpful to recall that the NMR spectral life-time is in the range of milliseconds, and species that have shorter lifetimes than this are represented by an average chemical shift. Previous MD simulations8 show that cation ordering, such as Li+–Li+, is the origin of the first sharp diffraction peak in Li halide mixtures. The measurement of the chemical shift of 35Cl would not obtain direct evidence of intermediate range. This is because the residence time of the ions in clusters was estimated to be a few picoseconds,3,11 and the process on this time-scale could contribute to spin-lattice relaxation. However, the increase in activation energy for spin-lattice relaxation is consistent with MD simulations.8,11
4.2 Spin-lattice relaxation mechanism
The NMR spin-lattice relaxation time quantifies the rate of transfer of energy from a nuclear spin system to neighbouring molecules (the lattice) by thermal motion, such as translation, rotation or internal motion of molecules. Thermal motion creates fluctuating magnetic and electric fields at the site of nuclear spins through spin interactions, which could be paramagnetic, dipole–dipole, or for 35Cl, quadrupolar interactions. The purchased salt is of high purity (>99.99%), so the influence of paramagnetic elements on spin-lattice relaxation could be neglected. For spins > 1/2 (I = 3/2 for 35Cl), an electric quadrupolar relaxation mechanism usually dominates the relaxation. The relaxation is due to interaction of Cl nuclei with a fluctuating electric field. The quadrupolar spin-lattice relaxation time under isotropic motion in a liquid is given by:21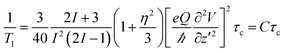 | (1) |
T 1 relaxation is most effective (corresponding to a T1 minimum) at a temperature where ω0τ ≈ 1. Here ω0 is the resonant frequency of nuclei, and τ is the correlation time at this temperature. When ω0τ > 1, the relaxation time increases with increasing correlation time (decreasing temperature), while it decreases when ω0τ < 1. For 35Cl, τ ∼ 1/2πω0 ∼ 4.07 × 10−9 s is expected at T1 minimum. As T1 of 35Cl increases with increasing temperature (Fig. 4) in the melt, this means the relaxation is at the fast motion limit where ω0τ0 ≪ 1 (τ0 ≪ 4.07 × 10−9 s). This confirms the general understanding of the relatively high mobility of the ions in the molten salt reflected in the bulk transport properties, such as conductivity.
In a (Li,K)Cl melt, it is impossible to measure the T1 minimum, so the electric field gradient could not be calculated according to eqn (1), which means that the correlation time corresponding to measurable T1 is unknown. It is impossible to identify the nature of the thermal motion from eqn (1); therefore we calculated the correlation time from thermal motions which may contribute to relaxation, and compared the resulting T1 (according to eqn (1)) with the measured T1 in molten (Li,K)Cl in order to explain our observations indirectly.
We can compare our results on dynamics from nuclear magnetic resonance and molecular dynamics. The correlation time derived from translational motion (diffusion) can be estimated by τt = R02/6D, where R02 is the mean square jump distance and D is the diffusion coefficient. For example in LiCl and KCl at 837 °C, taking the R02 (ref. 3) and D (ref. 22 and 23) from previous work where self-diffusion was measured with radioactive tracers, the estimated translation correlation times τt are about 2.6 ± 0.5 ps and 5.1 ± 1.0 ps, respectively. These are considerably shorter than the τc correlation time at a minimumT1. However, the activation energies derived from spin-lattice relaxation time (0.083 eV and 0.151 eV, respectively) are much less than the energies from self-diffusion of Cl− in LiCl and KCl (0.133 eV and 0.297 eV, respectively calculated from previous measurements.22,23 This precludes self-diffusion as the direct cause of relaxation.
The correlation times derived from the self-exchange velocity calculated from MD simulations3 are consistent with the different T1s in LiCl and KCl. The self-exchange velocity calculates the exchange rate of neighbouring unlike ions, v = (R2 − 〈R2〉)/τ, where R2 is the distance where the radial distribution function (g(r)) between anions and cations crosses unity for the second time; 〈R2〉 is the average separation of unlike ions within R2; and τ is correlation time of this motion (τself-exchange). The τself-exchange for Li+ and K+ at 823 °C are 0.33 ps and 0.56 ps respectively. These values are very close to the correlation times derived from a previous study24 in molten LiBr (0.11 ps) and LiI, which were calculated based on the similarities with the quadrupolar relaxation in liquid metal. The correlation time was interpreted as the average time that the spatial configuration of a group of near neighbours persists.
The radial distribution functions were taken to be the same for Li–Cl at 823, 727 and 627 °C, because the local structure did not change as much as ion dynamics with varying temperature.3 The constants in LiCl calculated from eqn (1) are 8.33, 7.73 and 7.27 × 1013 1/s2 at 823, 727 and 627 °C, respectively, and 2.32 × 1013 1/s2 in KCl at 823 °C, with the correlation time calculated from self-exchange (τ) and measurable spin-lattice relaxation time (T1). The electric field gradient in LiCl increases with increasing temperature, and the calculated Cl electric field gradient (eqn (1)) in LiCl and KCl at 823 °C were 1.34 × 1021 V m−2 and 0.71 × 1021 V m−2, respectively. These values could potentially be compared with force field parameterized ab initio calculations of fluctuating electric field gradients recently published for species in aqueous solution.25 The larger Cl electric field gradient, derived from eqn (1), in LiCl compared with KCl could be due to greater Cl core polarization due to Li, and lead to a shorter T1 in LiCl. This is also consistent with the observation of higher chemical shifts in LiCl than KCl. Therefore, it is most likely that the relaxation is caused by motion of the Cl− to the near neighbour unlike ion sites in the molten salts. The self-exchange velocity is the motional mechanism of the internal mobility,3 which has similar properties to the conductivity, so this could explain the similar activation energies of the relaxation and equivalent conductivity.
4.3 Compositional effect on relaxation time
Fig. 9 compares the calculated T1 according to eqn (1), where the correlation time 35Cl is the weighted average of correlation times calculated based on self-exchange velocities of Li+, K+ with Cl− in the mixture,3 and the electric field gradient in the mixture is a weighted average of two end member salts (823 °C), with measured T1 (837 °C). The actual lower T1 could be due to either the longer correlation time and/or larger electric field gradient than the above weighted average of two properties assumption. The compositional effect on relaxation time and activation energies (Fig. 6–8) shows good evidence for the formation of complexes in (Li,K)Cl molten salt mixtures, which can increase both the correlation time and the electric field gradient.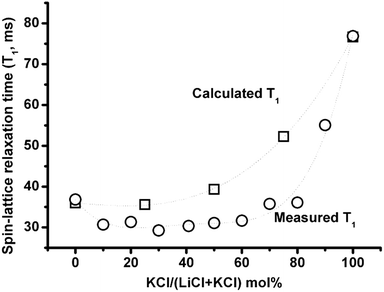 | ||
| Fig. 9 35Cl NMR spin-lattice relaxation times as a function of composition calculated from eqn (1) using a linear weighted average of LiCl and KCl Cl electric field gradients and correlation times (squares) compared with measured values (circles). | ||
Upon addition of KCl (for zone I <30 mol% KCl), both T1 and Λ depend mainly on the LiCl concentration. Upon addition of KCl, the Li–Cl distance decreases and cation association with the anions is longer according to MD simulations.3 These make it more difficult for ions to exchange with near neighbour unlike ions, and increase the chlorine correlation time. Although the addition of KCl could decrease the average electric field gradient, the change is not big enough to compromise the increasing correlation time, so the T1 decreases. The decreased mobility of Li+ and Cl− could lead to the negative deviation of the equivalent conductivity from the addition of the two end member salts. Furthermore, it is worth noting that the final composition of zone I is temperature dependent. Similarly as in zone III (>80 mol% KCl), KCl concentration determines the two properties. The significant increase in T1 is due to the smaller electric field gradient in KCl (eqn (1)), and the slight increase in Λ could be due to the disappearance of clusters.
In zone II (30–80 mol% KCl), the peak value of the activation energy could be related to the formation of intermediate range chemical order on the time scale of picoseconds according to previous studies.8,11 When there are longer-range interactions, such as clustering, in the mixture, these would be able to dissociate more readily into free ions with increasing temperature. This reduces the correlation time and electric field gradient, corresponding to a faster increase in the relaxation time, and results in greater rate of change of liquid structure with temperature and the maximum activation energy in zone II. Moreover, the concentration of LiCl2− and K2Cl+ complexes in the melt calculated using density functional theory16,26 showed a maximum in the range of 37–62 mol% KCl, in a similar plot to Fig. 7, which shows a maximum in 35Cl T1 activation energy at 40–50 mol%. However, the MD simulation showed that the intermediate range complex structure is a cluster of Li+ ions, where the Li+–Li+ distance is shorter than the random ionic mixture in a mixture.8,11 In this study, the effect of overlapping Cl−–Cl− pairs on the 35Cl chemical shift in LiCl was observed, and the change of chemical shift in (Li,K)Cl is determined by cation-to-anion radius ratio in the whole compositional range of molten salts. The maximum activation energy for relaxation in zone II indicates that the complex could be a Li+–Li+ cluster, which is most significant at this compositional range calculated using radial distribution function8,11 determined from molecular dynamics.
4.4 Effect of CeCl3 dissolution
The chemical shift variation of 35Cl with CeCl3 dissolution shows a similar trend to a previous study on a LaF3–ACl system,18 though the deviation from a linear combination of end-member shifts begins at a lower concentration. It indicates the presence of at last three instantaneous chlorine environments almost throughout the whole composition.In Glover and Madden's work,27 the microstructure of molten mixtures of LaCl3 with NaCl and CsCl has been theoretically studied by Raman spectroscopy, to examine the coordination environment around the La3+ ions. In pure molten LaCl3 the La-centred coordination must be linked with a Cl− belonging to the coordination of two or more La3+ ions, from which it is inferred that a bridging Cl− exists in pure LaCl3. Their work showed how the pure melt is broken down by the addition of alkali halides to different extents. This differs from previous studies on LaCl3–AF systems,18 where the bridging F− exists in LaF3–AF mixtures in the same form as in pure LaCl3.
5 Conclusions
High temperature 35Cl NMR measurements of chemical shift and spin-lattice relaxation time can reveal details of the microscopic structure and dynamics of (Li,K)Cl molten salts. The difference in cation-to-anion radius ratio (Rm) can explain the compositional effect on the chemical shift of chlorine at constant temperature in the melt based on second nearest neighbour effects below Rm = 0.6. Thus, the chemical shift in the mixed salt exhibits the same behavior as crystalline alkali halides. Future 35Cl NMR measurements should be able to readily detect the effect of dissolved ions with R+/R− >0.6, such as caesium, an important fission product in spent nuclear fuel reprocessing.It has been shown that the 35Cl spin-lattice relaxation time (T1) is a result of the interaction between the electric quadrupole moment of 35Cl and the fluctuating electric field gradient caused by the rapid ionic exchange calculated by molecular dynamics simulation (self-exchange velocity).3 The Cl motional correlation time responsible for T1 relaxation in LiCl and KCl is on the time scale of picoseconds which is shorter than the time scale of chlorine self-diffusion of tens of ps. The self-exchange rates from MD simulations3 and the measured T1 relaxation times in this work at different temperatures in LiCl yield numerical values for the electric field gradients that could be directly compared with future results derived from ab initio calibrated force field calculations.25 The activation energy for spin-lattice relaxation and equivalent conductivity agree very well, which means that the self-exchange rate model of internal mobility in (Li,K)Cl,3 which has similar collective properties to conductivity is probably accurate.
Microscopic evidence for the variation of the equivalent conductivity of molten salt mixtures with composition was detected. Furthermore, in zone II (30–80 mol% KCl), the maximum activation energy occurs at the same composition for equivalent conductivities and T1 relaxation. This suggests the presence of complexes or clusters in the melt consistent with a greater rate of change of liquid structure with temperature at intermediate compositions.
Acknowledgements
This work was carried out as part of the UK Engineering and Physical Sciences Research Council (EPSRC) funded REFINE consortium (http://www.refine.eng.ed.ac.uk/). We gratefully acknowledge this EPSRC financial support (EP/J000760/1). We also very much appreciate Prof. Brian Ralph for proof-reading the first manuscript.References
- Y. Okamoto, S. Suzuki, H. Shiwaku, A. Ikeda-Ohno, T. Yaita and P. A. Madden, J. Phys. Chem. A, 2010, 114, 4664–4671 CrossRef CAS PubMed.
- M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Phys. Chem. B, 2008, 112, 1177–1183 CrossRef CAS PubMed.
- B. Morgan and P. A. Madden, J. Chem. Phys., 2004, 120, 1402–1413 CrossRef CAS PubMed.
- P. Hebant and G. S. Picard, J. Electrochem. Soc., 1997, 144, 980–983 CrossRef CAS.
- E. R. Van Artsdalen and I. S. Yaffe, J. Phys. Chem., 1954, 59, 118–127 CrossRef.
- A. L. Rollet, V. Sarou-Kanian and C. Bessada, Inorg. Chem., 2009, 48, 10972–10975 CrossRef CAS PubMed.
- V. Danek, Physico-Chemical analysis of molten electrolytes, Elsvier, B. V., Amsterdam, 2006, ch. 1 and 8 Search PubMed.
- M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Phys.: Condens. Matter, 2008, 20, 332101–332105 CrossRef.
- S. A. Kirillov, E. A. Pavlatou and G. N. Papatheodorou, J. Chem. Phys., 2002, 116, 9341–9352 CrossRef CAS.
- S. A. Kirillov, Russ. J. Electrochem., 2007, 43, 901–908 CrossRef CAS.
- M. C. Ribeiro, J. Phys. Chem. B, 2003, 107, 4392–4402 CrossRef CAS.
- H. Bloom and E. Heymann, Proc.-R. Soc. Edinburgh, Sect. A: Math. Phys. Sci., 1947, 188, 392–414 CrossRef CAS.
- A. L. Rollet, S. Godier and C. Bessada, Phys. Chem. Chem. Phys., 2008, 10, 3222–3228 RSC.
- I. Farnan and J. F. Stebbins, J. Am. Chem. Soc., 1990, 112, 32–39 CrossRef CAS.
- J. D. Edwards, C. S. Taylor, A. S. Russell and L. F. Maranville, J. Electrochem. Soc., 1952, 99, 527–535 CrossRef CAS.
- P. Hebant and G. S. Picard, J. Electrochem. Soc., 1997, 144, 980–983 CrossRef CAS.
- M. Chemla and M. Okada, Electrochim. Acta, 1990, 35, 1761–1776 CrossRef CAS.
- A. L. Rollet, S. Godier and C. Bessada, Phys. Chem. Chem. Phys., 2008, 10, 3222–3228 RSC.
- S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1990, 63, 913–919 CrossRef CAS.
- J. H. Barner, C. Bessada and R. W. Berg, Inorg. Chem., 2003, 42, 1901–1907 CrossRef PubMed.
- A. Abragam, Principles of Nuclear Magnetism, Oxford U. P., London, 1961, ch. 8 Search PubMed.
- R. Lenke, W. Uebelhack and A. Klemm, Z. Naturforsch., A: Phys. Sci., 1973, 28, 881–883 CAS.
- J. O. 'M. Bookris, S. R. Richards and L. Nani, J. Phys. Chem., 1965, 69, 1627–1637 CrossRef.
- W. W. Filho, R. L. Havill and J. M. Titman, J. Phys. C: Solid State Phys., 1982, 15, 3617–3625 CrossRef.
- A. Carof, M. Salanne, T. Charpentier and B. Rotenberg, J. Phys. Chem. B, 2014, 118, 13252–13257 CrossRef CAS PubMed.
- P. Hebant and G. S. Picard, J. Mol. Struct., 1995, 358, 39–50 CrossRef CAS.
- W. J. Glover and P. A. Madden, J. Chem. Phys., 2004, 121, 7293–7303 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |