Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assessing corneal biomechanics with Brillouin spectro-microscopy
Guillaume
Lepert
 a,
Ricardo M.
Gouveia
b,
Che J.
Connon
b and
Carl
Paterson
*a
a,
Ricardo M.
Gouveia
b,
Che J.
Connon
b and
Carl
Paterson
*a
aImperial College London, Blackett Laboratory, London, SW7 2BW, UK. E-mail: guillaume.lepert07@imperial.ac.uk
bInstitute of Genetic Medicine, Newcastle University, International Centre for Life, Central Parkway, Newcastle upon Tyne, NE1 3BZ, UK
First published on 6th April 2016
Abstract
A new Brillouin spectro-microscope was designed and built to investigate the mechanical properties of bovine and human corneas. This instrument integrates a single-stage virtually imaged phased array spectrometer with a novel adaptive-optics interferometric filter to achieve unprecedented rejection of the elastic background signal. As a result, highly-resolved, reproducible data from both thin and thick collagen-based materials were obtained. In particular, this technique is capable of rigorously measuring the relative stiffness of different areas of human corneas, thus providing a true non-contact method to characterise the fundamental mechanical features of both live and fixed biological tissue samples.
Brillouin and Raman scattering both constitute useful techniques to study material properties, although through very different regimes. Raman spectroscopy probes intra-molecular vibrational bonds (optical phonons) in the THz range (100 s to 1000 s of cm−1) and reveals information about chemical composition.1 By contrast Brillouin scattering probes bulk acoustic waves (acoustic phonons) at GHz frequencies (∼0.1–1 cm−1) and is linked to viscoelastic properties.2 Brillouin scattering is based on the principle that photons scattered by travelling density fluctuations (spontaneous thermal phonons) acquire a Doppler shift. Measuring this shift is measuring the speed of sound in a given material, which in turn is related to the mechanical properties and moduli of the material.3 Thus, although at a fundamental level the underlying physics is similar, the two techniques address very different needs.
Brillouin spectroscopy is a useful tool in solid mechanics, and has long been used to characterise the mechanical properties of transparent fluids and crystalline solids.4 However, only recently has this technique been applied to the study of organic matter, thanks primarily to the introduction of virtually imaged phased arrays (VIPAs)5in lieu of multi-pass Fabry–Pérot spectrometers,6 and to the realisation that the geometric broadening of the Brillouin spectra arising from focused illumination does not preclude high-NA Brillouin microscopy.7 The invention and widespread adoption of VIPAs in recent years has triggered something of a renaissance for Brillouin scattering by cutting the acquisition times to seconds or less and enabling Brillouin imaging.5 Compared with mechanical methods such as atomic force microscopy (AFM), where measurements require direct interactions between the sample and a probe, Brillouin imaging offers the advantage of a truly local non-contact analysis at microscopic resolution. For example, several recent studies have used Brillouin scattering to characterise the mechanical properties of biological tissues, including live cells,8 components of the extracellular matrix,9 and other natural or synthetic biomaterials.10 Although these developments have yet to be translated to a clinical settings, they show great promise for the diagnosis and treatment of arteriosclerosis plaque11 and keratoconus.12
In the present work we review the fundamentals of Brillouin scattering and introduce a new Brillouin spectro-microscope, dedicated to soft biomaterials, that enables significant advances in suppressing parasitic elastic scattering in aqueous media. This instrument was used to evaluate the mechanical properties of dense collagen type-I gels produced after plastic compression, as well as of corneal tissue of bovine and human origin. The results reported here provide important information about the structure and organisation of the biomaterials analysed. We also address the challenges inherent to this method, notably in relating the measured Brillouin shift to the biomechanical properties evaluated using standard rheological and nano-indentation techniques.
1 Principles and apparatus for Brillouin spectro-microscopy
1.1 Brillouin scattering
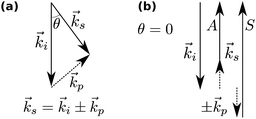
In Brillouin scattering, an incoming photon (angular frequency ωi, wave vector![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i) is inelastically scattered off a travelling thermal phonon (angular frequency ωp, wave vector
i) is inelastically scattered off a travelling thermal phonon (angular frequency ωp, wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) p) at an angle θ, with a new frequency ωs and wave vector
p) at an angle θ, with a new frequency ωs and wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s, as depicted in Fig. 1. In a quantum description, the photon will have either gained or lost a phonon quantum of energy through annihilation or creation of a phonon, respectively referred to as Stokes and anti-Stokes processes. The scattering angle θ is set by the experiment's illumination/collection geometry, which also constrains the phonon wavelength via the conservation of energy and momentum:
s, as depicted in Fig. 1. In a quantum description, the photon will have either gained or lost a phonon quantum of energy through annihilation or creation of a phonon, respectively referred to as Stokes and anti-Stokes processes. The scattering angle θ is set by the experiment's illumination/collection geometry, which also constrains the phonon wavelength via the conservation of energy and momentum: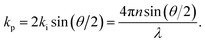 | (1) |
The phonon wavelength is comparable to that of the photons, while the frequency is in general of the order of 10 GHz. In the classical description, the phonon is an acoustic wave, a periodic modulation of density and therefore of refractive index, which can be regarded as a reflective Bragg mirror moving at the speed of sound. Then the above equation is just the Bragg condition; the Stokes/anti-Stokes processes correspond to waves travelling in opposite directions, with the Brillouin shift corresponding to a Doppler shift. The phase velocity vp of the acoustic wave is
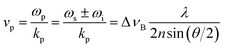 | (2) |
In general, transverse and longitudinal acoustic waves propagate at different velocity, and will give rise to separate peaks in the Brillouin spectrum. However in the back-scattering geometry (θ = 180°) used in this work only longitudinal waves participate in the scattering processes,13 and the spectrum consists of a single Stokes/anti-Stokes doublet.
1.2 Relation of the Brillouin shift to mechanical moduli
The acoustic velocity is correlated to the mechanical moduli of the material. Since we are probing longitudinal waves only, and because the phonon wavelength is much smaller then the material's extent, the relevant moduli is the so-called p-wave or longitudinal modulus M, which is related to the velocity by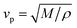 (ρ is the density of the medium). Rheological or nano-indentation techniques measure Young's modulus E, and it would therefore be desirable to be able to relate these two quantities. For a number of reasons this is not straightforward; indeed preliminary comparative experiments14 have shown that the Brillouin modulus is two or three orders of magnitude larger than Young's modulus. First, the acoustic isotropy of highly ordered tissues such as corneal collagen is questionable. Second, M is measured at GHz acoustic frequencies whereas E is a quasi-static measurement. Acoustic dispersion could therefore significantly increase the moduli in the hypersonic regime.15 Thirdly, one may be tempted to use the usual relation3
(ρ is the density of the medium). Rheological or nano-indentation techniques measure Young's modulus E, and it would therefore be desirable to be able to relate these two quantities. For a number of reasons this is not straightforward; indeed preliminary comparative experiments14 have shown that the Brillouin modulus is two or three orders of magnitude larger than Young's modulus. First, the acoustic isotropy of highly ordered tissues such as corneal collagen is questionable. Second, M is measured at GHz acoustic frequencies whereas E is a quasi-static measurement. Acoustic dispersion could therefore significantly increase the moduli in the hypersonic regime.15 Thirdly, one may be tempted to use the usual relation3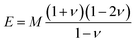 | (3) |
At present, none of these issues have been properly investigated, much less resolved. In what follows we shall therefore not attempt to convert the measured Brillouin shifts into mechanical moduli and use the Brillouin shift ΔvB as the metric.
1.3 Epifluorescence confocal microscope set-up
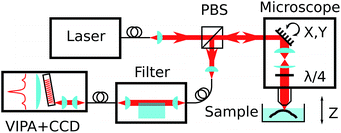
The Brillouin spectro-microscope is schematically depicted in Fig. 2. A frequency-doubled Nd:YVO4 diode-pumped solid-state laser (CNI, MSL-FN-671) operating at λex = 671 nm, coupled into a single-mode polarisation-maintaining fibre (Corning SM600), provided single mode illumination (transverse and longitudinal) with a spectral linewidth smaller than 1 MHz. The fibre output was collimated to a 3 mm diameter beam, reflected off a pair of scanning mirrors (Thorlabs GVS002), and expanded to an 8 mm diameter by two achromatic doublets (focal lengths 75 and 180 mm) to fill the back focal plane of a 20× water dipping microscope objective (Olympus XLUMPLFLN20xW, numerical aperture 0.5). The doublets served as the scan relay optics by imaging the mirrors onto the objective's back focal plane. In addition, a quarter-wave plate inserted just before the objective was used to transform the laser linear polarisation into a circular polarisation. Scattered light was collected by the same objective, descanned by the same mirrors, separated from the excitation light by a polarising beam-splitter, and coupled into a single-mode fibre which also acted as the confocal pinhole. The final imaging resolution was calculated to be 1 × 1 × 5 μm. For depth sectioning, the sample was mounted on a vertical translation stage (Newport MFA-CC).1.4 Suppression of elastic scattering
The elastically-scattered light usually represents a much stronger signal compared to the Brillouin scattering itself. In order to suppress the former, an original wavefront division interferometer was introduced in the system. Light exiting the microscope output fibre was collimated to a 4 mm diameter beam and intersected by a parallelepipedic glass prism such that exactly half of the beam travels above the prism, and half inside. The path difference δ between the two halves depends on the angle θi between the prism and the incident beam. It was calculated as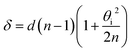 | (4) |
 | (5) |
1.5 VIPA spectrometer
The VIPA (LightMachinery) has a free spectral range of 30 GHz. Light exiting the filter output fibre was collimated to a 0.8 mm diameter and focused on the VIPA entrance window by a 100 mm cylindrical lens. A 400 mm cylindrical lens imaged the VIPA's angular spectrum onto a CCD camera (Andor iXon DU888, operated in non-electron-multiplying mode) with the help of a 50 mm cylindrical lens, orientated orthogonal to the others, to provide focussing along the non-dispersed axis.1.6 Data acquisition and processing
The spectra imaged on the CCD camera were acquired with a typical exposure time of 100 to 1000 ms, increasing with the penetration depth in the sample. Vertical binning was used on the sensor so that one-dimensional spectra were produced without further processing. The beam scanning, sample vertical motion, and interferometer feedback were controlled using a Python-based, custom-made software specifically developed for this purpose (MicroscoPy, pypi.python.org/pypi/MicroscoPy). Raw spectra were stored as a multidimensional array in HDF5 files, alongside position information and other metadata. Data processing was performed using Mathematica. Briefly, the spectral axis was calibrated against reference spectra of water or solid polystyrene, with frequency expressed as a quadratic function of pixel coordinates, and a linear least-square fit to the positions of 3 to 4 Rayleigh peaks and their associated Brillouin peaks. Both the Stokes and anti-Stokes peaks of the brightest interference order were then fitted with a Lorentzian function, and the Brillouin shift was calculated as the average of both the Stokes and anti-Stokes frequencies, making measurements insensitive to laser drift and temperature fluctuations (which can cause a global spectral drift of the order of 1 GHz h−1).1.7 Filter feedback
Unlike the measurement of Brillouin frequency, the interferometric filter is sensitive to frequency drifts (on a timescale of minutes) and requires continuous adjustments to maintain its extinction to the required level. For this purpose, a simple feedback mechanism was incorporated by the addition of a piezoelectric actuator to periodically modulate the interferometer angle to produce a ∼10% modulation in the (post-filtering) elastic amplitude. The latter is measured directly on the acquired spectrum by integrating the pixel intensities around the elastic peak. A digital PID (proportional–integral–differential) control loop was used to keep the prism angle close to its optimum position (corresponding to a minimum in the elastic amplitude), with a time constant of the order of minutes to average out the large fluctuations in the amplitude of the elastic scattering while scanning through the sample.1.8 Preparation of compressed collagen gels
Compressed collagen gels were prepared as described elsewhere.17 Briefly, ice-cold rat tail collagen type-I (2 g L−1 in 0.6% acetic acid; First Link Ltd, UK) was mixed with 10× Modified Essential Medium (MEM; Life Technologies, CA, USA) and neutralised with 1 M NaOH in an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio, respectively, and allowed to gel at 37 °C for 30 min. Polymerised gels were subjected to plastic compression under a 134 g load for 5 min at room temperature by placing the gels between layers of gauze and on top of 10 sheets of filter paper. Plastically-compressed collagen gels were then transferred to a Petri dish onto 3- or 4-gel stacks and washed at room temperature for at least 30 min in distilled water before being analysed by Brillouin microscopy. Chemically-stiffened collagen gels were analysed after fixing the compressed collagen gels in 4% (w/v) paraformaldehyde, with extensive washing in distilled water before imaging. Experiments were performed in triplicate.
1 volume ratio, respectively, and allowed to gel at 37 °C for 30 min. Polymerised gels were subjected to plastic compression under a 134 g load for 5 min at room temperature by placing the gels between layers of gauze and on top of 10 sheets of filter paper. Plastically-compressed collagen gels were then transferred to a Petri dish onto 3- or 4-gel stacks and washed at room temperature for at least 30 min in distilled water before being analysed by Brillouin microscopy. Chemically-stiffened collagen gels were analysed after fixing the compressed collagen gels in 4% (w/v) paraformaldehyde, with extensive washing in distilled water before imaging. Experiments were performed in triplicate.
1.9 Preparation of corneal tissue
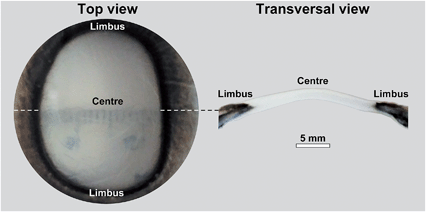
Bovine corneal tissue (depicted in Fig. 3) was isolated from fresh cow eyes obtained from an abattoir (Linden Food Burradon Ltd, UK). The tissue corresponding to the cornea and the surrounding sclera was excised from whole cow eyes, kept on ice during the isolation, incubated with a penicillin–streptomycin solution (1000 U mL−1; Thermo Scientific, MA, USA) for 30 min at room temperature to inhibit bacterial contamination, washed in an excess of phosphate buffered saline (PBS), and kept at 4 °C in either PBS supplemented with 0.025% sodium azide preservative or at room temperature in Carry-C tissue preservation medium (Alchimia, Italy) until further analysis was performed. Human corneal tissues were kindly provided by Dr Francisco Figueiredo, FRCOphth (Royal Victoria Infirmary Newcastle, UK). Tissues remaining from corneal transplant procedures were kept up to 30 days after isolation from cadaveric donors (ages ranging 58–72 years old; male–female donor ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; no prior history of corneal diseases or ocular trauma), in accordance with the Newcastle University and Newcastle-upon-Tyne Hospital Trust Research Ethics Committees’ guidelines. Isolated tissues were then extensively washed in PBS, dried of excess adsorbed liquid, and then maintained at room temperature in Carry-C tissue preservation medium until further analysis was performed. Tissues were imaged in Petri dishes while completely submerged in PBS or Carry-C medium.
1; no prior history of corneal diseases or ocular trauma), in accordance with the Newcastle University and Newcastle-upon-Tyne Hospital Trust Research Ethics Committees’ guidelines. Isolated tissues were then extensively washed in PBS, dried of excess adsorbed liquid, and then maintained at room temperature in Carry-C tissue preservation medium until further analysis was performed. Tissues were imaged in Petri dishes while completely submerged in PBS or Carry-C medium.
1.10 Statistical analysis
The Brillouin shift was measured at eight different z-positions from five distinct collagen gels (n = 5), with differences between average shifts analysed using an unpaired two-tailed Student's t-test, with p = 0.0001 and R2 = 0.91.2 Results and discussion
2.1 Brillouin spectro-microscope assembly and specifications
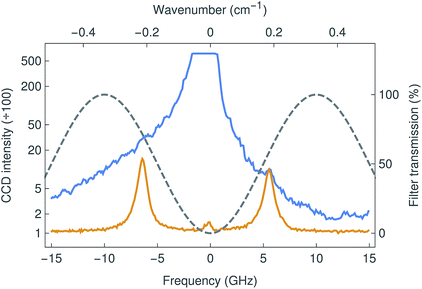
The new Brillouin spectro-microscope was specifically dedicated to study the mechanical properties of soft biological tissues. These systems are characterised by low scattering signals, high elastic backgrounds, and the requirement of sub-GHz resolutions. For this particular instrument we used a λex = 671 nm DPSS laser with high spectral purity and sub-MHz linewidth (Fig. 2). At this wavelength, the Stokes/anti-Stokes components of Brillouin scattering are typically shifted by 5–7 GHz in aqueous media.18 Because such small shifts are inaccessible to grating spectrometers, Brillouin spectrometry has traditionally relied on multi-pass scanning Fabry–Pérot interferometers to achieve both the necessary resolution and fringe contrast; the acquisition time for a single spectrum was measured in minutes or even hours.19 This limitation is overcome by VIPAs, which combine the large dispersive power of the etalon with the spatial dispersion of gratings. They are essentially Fabry–Pérot etalons, dispersing focused light into fringes of equal inclination, with the important difference that the input light is focused by a cylindrical lens in only one direction and enters the etalon through a narrow antireflection-coated window. All of the input light is therefore transmitted, forming a one-dimensional spectrum instead of circular fringes, and resulting in a more efficient device. However, VIPAs have limited finesse (100 at most), and therefore poor fringe contrast (<40 dB), insufficient to resolve (anti-)Stokes Brillouin peaks amidst a strong elastic background, such as that inevitably arising from epi-fluorescence confocal microscopy. This is commonly addressed by cascading two VIPAs in a cross-axis configuration,20 at the cost of reduced throughput and considerable complexity. Another approach involves the absorption of the elastic scattering in hot vapour cells, although this often distorts the Brillouin peaks as well.21In the present work, we used an original adaptive-optics wavefront division interferometer, described above, that enables the interferometric filtering of the elastic scattering, as demonstrated in Fig. 3. With the elastic suppression turned off (interferometer detuned), the signal was overwhelmed by a strong elastic background (blue line) as shown in Fig. 4. By tuning the interferometer to minimise the amplitude of the central elastic peak, the Brillouin Stokes and anti-Stokes components became clearly resolved (orange line). The Brillouin shift was detected at 5.86 ± 0.01 GHz (or 0.195 cm−1), corresponding to a sound velocity of 1475 ± 10 m s−1, as expected for distilled water at 20 °C.22 Furthermore, the elastic suppression ratio exceeded 46 dB, a significantly better outcome compared to other methods currently in use.20,21,23 Consequently, the strong extinction made possible by the interferometric filter allows the implementation of a single-stage VIPA configuration instead, which constitutes, to the extent of our knowledge, a novel development in Brillouin microscopy.
Furthermore, the use of an immersion objective allows the samples to be observed in physiological conditions, as well as enabling several other important benefits for Brillouin imaging. Firstly, it prevents the dehydration of the biological tissues, a parameter that greatly affects their mechanical properties.24 Secondly, it reduces specular reflection at the sample surface, therefore reducing the elastic background. And finally, it limits the loss of resolution normally caused by spherical aberration when focusing deep into thick samples. This issue is particularly relevant in imaging cornea specimens, particularly with bovine origin, where the tissue can be up to 2 mm thick (see below).
2.2 Mechanical properties of high-density collagen gels
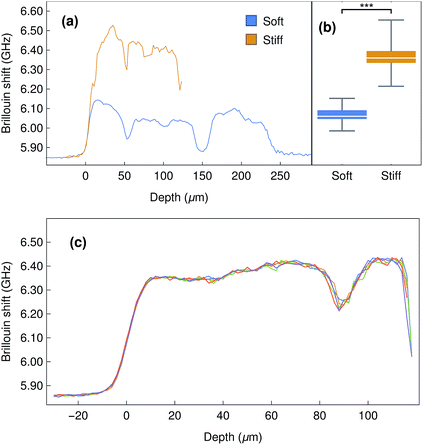
In order to explore the potential uses and limitations of our instrument, we started by evaluating dense collagen gels produced by a plastic compression method. These thin biomaterials have been extensively used as versatile models of connective tissue such as cornea17,24 and skin.25 Furthermore, their mechanical properties (e.g., elastic modulus) have been shown to be highly-defined and dependent on the compression load and duration.24,26,27 As such, collagen gels are relevant as models for the determination of the biomechanical properties of soft materials. The Brillouin shift observed for compressed collagen gels was shown to be very consistent for all gels analysed, both from those in the same stack (4 gels per stack) or between different replicates, with an average shift of 6.06 ± 0.04 GHz (Fig. 5a), and despite the strong elastic background scatter due to the proximity of the interface. In addition, the shifts detected at the surface and within the gels were similar, and their variation smaller than that observed between gels (Fig. 5a). This suggested that the mechanical properties of the compressed collagen gels were uniform between gels and throughout their thickness. Moreover, stiffened collagen gels (crosslinked with paraformaldehyde) showed significantly higher Brillouin shifts of 6.35 ± 0.07 GHz (Fig. 5b), a clear indication that alterations in the stiffness of the collagen gels results in significantly different shifts in Brillouin scatter. Interestingly, the Brillouin profiles also allowed us to determine gross sample depth, with the stiffened collagen gels showing an approximately 50% reduction in thickness compared to the untreated compressed collagen gels. This shrinkage constitutes a common effect of conventional cross-linking methods,28 and may partially account for the increased gel stiffness.2.3 Mechanical properties of corneal tissue
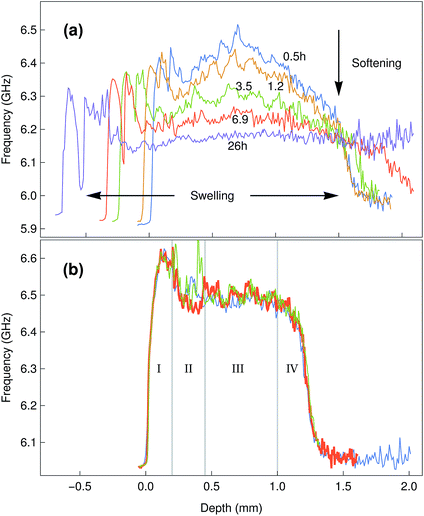
Having determined the Brillouin shift of thin collagen samples, we then evaluated the limitations of the technique for the analysis of thick biological samples. Bovine corneas were used for these experiments, as these tissues are relatively transparent despite the 1.2–1.5 mm thickness of their centre region (Fig. 3). In addition, as the correct evaluation of mechanical properties in biological tissues requires a constant and physiologically-relevant level of tissue hydration, Brillouin spectro-microscopy measurements should be performed in such conditions. Corneas are naturally hyperosmotic, slightly dehydrated tissues in vivo.29 To replicate a dehydration state, whole bovine corneas were immersed in glycerol immediately after isolation, and then washed and kept in PBS to remove the glycerol and evaluate the effects of re-hydration through time on tissue stiffness and thickness (Fig. 6a). The scan series performed throughout the entire depth of the tissues showed that corneas swell progressively, with their thickness almost doubling after 26 h in PBS. This constituted a clear indication of increased hydration well beyond normal in vivo levels.30 Concomitantly, the Brillouin shift measured at all depths of the corneal tissue decreased with time, indicating that the swollen corneas became softer. Specifically, at t = 0.5 h, the corneas showed shifts of 6.3–6.5 GHz at their anterior and 6.5–6.2 GHz at their posterior regions, respectively, whereas at t = 26 h, shifts varied between 6.0 and 6.3 GHz. Furthermore, the pattern of the shifts measured in the swollen corneas indicated a loss of structural integrity within the tissue (Fig. 6a), a common consequence of excessive corneal hydration and oedema.31,32Overall, these results highlighted the importance of performing the measurements in appropriate conditions (i.e., physiological-like) for a given tissue or organ. When measuring the in-depth Brillouin scattering of bovine corneas maintained in Carry-C, a medium specifically developed to preserve corneas in their physiological hydration state, the profiles were remarkably similar to those previously reported for the central regions of human corneas (Fig. 6b).33 In particular, these profiles were divided into four regions (Fig. 6b): an anterior-most peak with 6.5–6.6 GHz shifts corresponding to the corneal epithelium (I), a slope ranging between 6.55 and 6.5 GHz corresponding to the anterior stroma (II), a plateau of shifts of approximately 6.5 GHz corresponding to the posterior stroma (III), and a steep slope corresponding to the posterior-most region of the cornea (IV).34 Furthermore, this pattern was maintained unaltered, along with the natural thickness of the bovine corneal tissue, even after keeping it for more than a week in Carry-C medium.
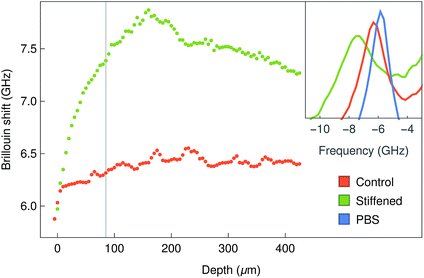
The Brillouin images were also capable of distinguishing differences in stiffness from normal and stiffened-treated corneal tissue. The anterior-most region of the whole bovine corneas fixed with paraformaldehyde showed significantly higher shifts compared to the same region from the untreated tissues (Fig. 7). Moreover, this increase in shift was observed not only at the surface, where the tissue was treated, but also in-depth (Fig. 7, insets), providing information about the range of penetration for such treatment.
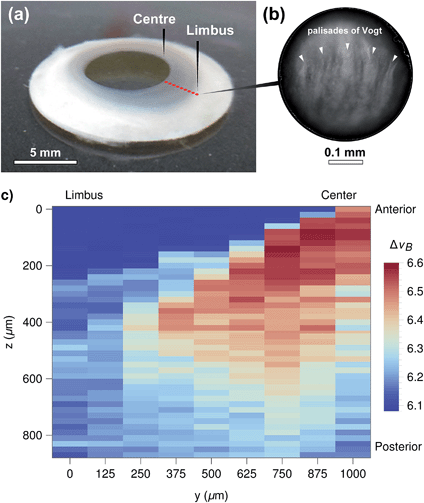
These results also highlight the non-contact nature of Brillouin spectro-microscopy for investigating the mechanical properties in the interior of biological tissues. However, this ability was shown to be limited by the transparency of the material. For example, imaging more opaque areas of the bovine cornea (such as the limbus, Fig. 3) resulted in a considerable reduction in the signal-to-noise ratio at deeper levels of the tissue (data not shown). In contrast, this limitation was not evident in the human cornea, where the (species specific) improved transparency of the limbus (Fig. 8a) still allowed highly-resolved spectra to be obtained. In particular, human corneal tissues maintained in the Carry-C medium were able to be imaged in a sequence of in-depth measurements, thus allowing the assembly of z-scans into 2D heat maps (Fig. 8c). Remarkably, these sequences not only provided a notion of the tissue's morphology, but also the finer differences in stiffness between different regions of the tissue (Fig. 8c: anterior (upper) vs. posterior (lower region); limbus (left) vs. central cornea (right)). Specifically, the values for the Brillouin shift observed in the limbus were lower than those in the central cornea, particularly in the anterior-most region of the tissue. This data was supported by previous, although much less detailed, studies using AFM35 or stress–strain analysis of the cornea.36 Taken together, these results represent a more complete overall view of the stiffness of biological tissues, providing information about the mechanical properties of human corneas of unparalleled accuracy and resolution.
3 Conclusions
In summary, we have introduced a new Brillouin microscope consisting of a fibre-coupled confocal scanning microscope, an interferometric filter to suppress elastic scattering, and a single-stage VIPA spectrometer. The microscope's ability to acquire depth-resolved Brillouin spectra in very thin as well as very thick samples (e.g. in 50μm-thick collagen gels or in bovine corneas up to 2 mm) has been demonstrated, thanks to the interferometric filter that allows sufficient rejection of specular reflections at the sample surfaces.This technique was used to monitor the response of compressed collagen gels and corneal tissue to stiffening (cross-linking) treatments. Brillouin imaging of the limbus in human corneal rings also revealed a clear contrast between the stiffer inner stroma of the centre and the softer limbus. These results validate Brillouin spectro-microscopy as a potent tool for assessing the mechanical properties of soft biomaterials, particularly transparent ones. We thus envisage many possible applications for this technique, including fundamental characterisation studies and as a tool to diagnose the rigidity of many tissues, namely the cornea.
However, the quantification of the absolute stiffness of soft tissues by Brillouin spectroscopy (i.e., using Brillouin shift values to calculate the elastic modulus) constitutes a challenge that remains unresolved.
References
- A. Smekal, Naturwissenschaften, 1923, 11, 873–875 CrossRef CAS.
- L. Brillouin, Ann. Phys., 1922, 17, 88–122 CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley, 8th edn, 2005 Search PubMed.
- G. Benedek and K. Fritsch, Phys. Rev., 1966, 149, 647–662 CrossRef CAS.
- G. Scarcelli and S. H. Yun, Nat. Photonics, 2007, 2, 39–43 CrossRef PubMed.
- R. Mock, B. Hillebrands and J. R. Sandercock, J. Phys. E: Sci. Instrum., 1987, 20, 656–659 CrossRef CAS.
- G. Antonacci, M. R. Foreman, C. Paterson and P. Török, Appl. Phys. Lett., 2013, 103, 221105 CrossRef.
- G. Scarcelli, W. J. Polacheck, H. T. Nia, K. Patel, A. J. Grodzinsky, R. D. Kamm and S. H. Yun, Nat. Methods, 2015, 12, 1132 CrossRef CAS PubMed.
- F. Palombo, C. P. Winlove, R. S. Edginton, E. Green, N. Stone, S. Caponi, M. Madami and D. Fioretto, J. R. Soc., Interface, 2014, 11, 20140739 CrossRef PubMed.
- A. J. Traverso, J. V. Thompson, Z. A. Steelman, Z. Meng, M. O. Scully and V. V. Yakovlev, Anal. Chem., 2015, 87, 7519–7523 CrossRef CAS PubMed.
- G. Antonacci, R. M. Pedrigi, A. Kondiboyina, V. V. Mehta, R. de Silva, C. Paterson, R. Krams and P. Török, J. R. Soc., Interface, 2015, 12, 20150843 CrossRef PubMed.
- G. Scarcelli, S. Besner, R. Pineda and S. H. Yun, Invest. Ophthalmol. Visual Sci., 2014, 55, 4490–4495 Search PubMed.
- R. Vacher and L. Boyer, Phys. Rev. B: Solid State, 1972, 6, 639–673 CrossRef CAS.
- G. Scarcelli, P. Kim and S. H. Yun, Biophys. J., 2011, 101, 1539–1545 CrossRef CAS PubMed.
- K. F. Herzfeld and T. A. Litovitz, Absorption and Dispersion of Ultrasonic Waves, Academic Press, New York and London, 1959 Search PubMed.
- K. Hattori, K. Sakai and K. Takagi, Jpn. J. Appl. Phys., Part 1, 1999, 38, 4932–4935 CrossRef CAS.
- R. M. Gouveia, R. R. Jones, I. W. Hamley and C. J. Connon, Biomater. Sci., 2014, 2, 1222–1229 RSC.
- M. Damzen, Stimulated Brillouin Scattering: Fundamentals and Applications, Institute of Physics, 2003 Search PubMed.
- J. R. Sandercock, Phys. Rev. Lett., 1972, 29, 1735–1738 CrossRef CAS.
- G. Scarcelli and S. H. Yun, Opt. Express, 2011, 19, 10913–10922 CrossRef PubMed.
- Z. Meng, A. J. Traverso and V. V. Yakovlev, Opt. Express, 2014, 22, 5410–5415 CrossRef PubMed.
- W. Marczak, J. Acoust. Soc. Am., 1997, 102, 2776 CrossRef.
- G. Antonacci, G. Lepert, C. Paterson, P. Török and P. Torok, Appl. Phys. Lett., 2015, 107, 061102 CrossRef.
- J. W. Foster, R. R. Jones, C. A. Bippes, R. M. Gouveia and C. J. Connon, Exp. Eye Res., 2014, 127, 37–41 CrossRef CAS PubMed.
- M. E. Smithmyer, L. A. Sawicki and A. M. Kloxin, Biomater. Sci., 2014, 2, 634–650 RSC.
- R. A. Brown, M. Wiseman, C. B. Chuo, U. Cheema and S. N. Nazhat, Adv. Funct. Mater., 2005, 15, 1762–1770 CrossRef CAS.
- R. R. Jones, I. W. Hamley and C. J. Connon, Stem Cell Res., 2012, 8, 403–409 CrossRef CAS PubMed.
- W. J. Howat and B. A. Wilson, Methods, 2014, 70, 12–19 CrossRef CAS PubMed.
- D. W. Leonard and K. M. Meek, Biophys. J., 1997, 72, 1382–1387 CrossRef CAS PubMed.
- Y. L. Kim, J. T. Walsh Jr, T. K. Goldstick and M. R. Glucksberg, Phys. Med. Biol., 2004, 49, 859–868 CrossRef PubMed.
- K. M. Meek, D. W. Leonard, C. J. Connon, S. Dennis and S. Khan, Eye, 2003, 17, 927–936 CrossRef CAS PubMed.
- C. M. Hsueh, W. Lo, W. L. Chen, V. A. Hovhannisyan, G. Y. Liu, S. S. Wang, H. Y. Tan and C. Y. Dong, Biophys. J., 2009, 97, 1198–1205 CrossRef CAS PubMed.
- G. Scarcelli and S. H. Yun, Opt. Express, 2012, 20, 9197–9202 CrossRef PubMed.
- G. Scarcelli, R. Pineda and S. H. Yun, Invest. Ophthalmol. Visual Sci., 2012, 53, 185–190 Search PubMed.
- J. A. Last, S. M. Thomasy, C. R. Croasdale, P. Russell and C. J. Murphy, Micron, 2012, 43, 1293–1298 CrossRef PubMed.
- J. O. Hjortdal, J. Biomech., 1996, 29, 931–942 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |