Influence of a polymer sunscreen additive on the transport and retention of titanium dioxide nanoparticles in water-saturated porous media†
Jessica
Englehart
,
Bonnie A.
Lyon
,
Matthew D.
Becker‡
,
Yonggang
Wang
,
Linda M.
Abriola
and
Kurt D.
Pennell
*
Department of Civil and Environmental Engineering, Tufts University, 200 College Avenue, Medford, Massachusetts 02155, USA. E-mail: kurt.pennell@tufts.edu; Fax: 617 627 3994; Tel: 617 627 3099
First published on 24th November 2015
Abstract
Titanium dioxide nanoparticles (nTiO2) are utilized in an array of consumer products including paints, sunscreens, cosmetics, and food. These products typically contain stabilizing agents that may alter nTiO2 fate when released into the environment. The objective of this study was to investigate the effects of TEGO carbomer, a polymeric stabilizing agent used in sunscreen, on the transport and deposition behavior of nTiO2 in porous media. Aqueous nTiO2 suspensions at pH 5.0 or 7.5 ± 0.2 were introduced into water-saturated columns packed with Federal Fine Ottawa sand. In the absence of carbomer, nTiO2 was not detected in effluent samples at pH 5, which was below the estimated point of zero charge (PZC) of nTiO2 (pH 6.3), while greater than 80% elution of nTiO2 was observed at pH 7.5. The addition of 3 mg L−1 carbomer decreased the PZC from 6.3 to less than 5, and resulted in greater than 94% elution of nTiO2 at pH 5 and 7.5. A nanoparticle transport model that incorporates a first-order, maximum retention capacity term was able to capture column breakthrough and retention data. Model results indicate that the presence of carbomer reduced the average retention capacity of the solid phase from 3.40 to 1.10 μg TiO2 g−1 sand, irrespective of solution chemistry changes. These findings demonstrate the substantial impact that polymeric stabilizing agents can have on the fate of nTiO2 in porous media, potentially enhancing nTiO2 mobility in the environment and reducing the efficiency of filtration systems for nTiO2.
Nano impactTo evaluate the potential for human and ecological exposure to engineered nanomaterials, it is important to consider the impact of stabilizing agents on their environmental fate. This study coupled experimental work with mathematical modeling to investigate the influence of a polymeric sunscreen additive on the transport and deposition behavior of titanium dioxide nanoparticles (nTiO2) in porous media. The transport model was able to predict nanoparticle breakthrough behavior and total retained mass in column experiments, and could be applied in future studies to evaluate different nanomaterials and experimental conditions. The findings demonstrate that the addition of a polymeric sunscreen additive to nTiO2 suspensions could increase their mobility in the environment, increasing the potential for exposure and contamination of drinking water sources. |
1. Introduction
Titanium dioxide (TiO2) is used in a wide range of consumer products including toothpaste and sunscreen, as a food additive and whitener, and as a pigment in paints, plastics, and paper.1,2 Due to the unique and desirable properties of nano-scale TiO2 (nTiO2), the proportion of nano- versus bulk-TiO2 production is expected to increase exponentially over the next decade, with an upper estimate of 2.5 million metric tons of nTiO2 produced by 2025.3 For example, sunscreen manufacturers have demonstrated that by decreasing the primary particle size of TiO2 in sunscreen formulations, the sun protection factor can be improved while minimizing the undesirable skin whitening effect often imparted by TiO2-based UV filters.4The widespread use of nTiO2 in consumer products will inevitably lead to direct or indirect releases to the environment. In a study detailing the lifecycle of nTiO2 in sunscreen, Botta et al.5 found that a substantial amount of nTiO2 residue will disperse into aquatic environments as a result of sunscreen use (up to 30% of the total nTiO2 in the applied sunscreen). Nano-TiO2 contained in food additives or in cosmetic products and sunscreens that are washed off during bathing or cleaning are likely to enter wastewater treatment plants (WWTPs). A recent study by Weir and colleagues estimated a daily loading rate to sewage systems of 0.1 mg nTiO2 per person per day, based on ingestion of nTiO2-containing foods in the United States.2 Although partial removal of nTiO2 in WWTPs has been reported, concentrations of 5–15 μg L−1 as Ti have been measured in wastewater effluents,6,7 demonstrating that nTiO2 will persist and be discharged after treatment. Furthermore, if WWTP biosolids containing nTiO2 are land applied, additional nTiO2 could enter the environment. Release of part per billion (μg L−1) levels of nTiO2 from exterior building paint was shown by Kaegi and colleagues,8 indicating that urban runoff represents another route for nTiO2 to enter the environment.
TiO2 has been classified by the International Agency for Research on Cancer (IARC) as a possible human carcinogen, primarily based on health effects resulting from inhalation.9 nTiO2 ingestion has been linked to Crohn's disease,10 and prior studies have demonstrated nTiO2 toxicity in human and mammalian cells, as well as ecotoxicity including inhibition of algae growth following exposure to nTiO2.11,12 Many factors impact the toxicity of nTiO2,13–15 including crystalline structure (e.g., rutile vs. anatase),16 particle coating, and size, but comprehensive physicochemical characterization is often lacking in nanotoxicity studies making it difficult to correlate nTiO2 properties with observed effects.17 Hence, further research is needed to determine human health impacts and ecological risks associated with nTiO2 in the environment. One critical component of such assessments is a greater understanding of nTiO2 fate and transport under environmentally relevant conditions.
Particle stability and aggregation are important factors in the fate and transport of nTiO2. Jiang et al. found that increasing ionic strength (IS) from 1 to 100 mM NaCl resulted in a 50-fold increase in the hydrodynamic diameter of uncoated nTiO2 with a primary particle size of 15 nm.18 In the same study, the average nTiO2 size was approximately 90 nm when suspension pH was below 4.2 or above 8.2, at a constant IS of 1 mM. The point of zero charge (PZC) of nTiO2 is reported to range from pH 5.5–6.8,18–21 and falls within the pH range observed in the aquatic environment.22 Particle aggregation increases as the pH approaches the PZC, with maximum aggregation occurring at the PZC. In the environment, dissolved natural organic matter (NOM) can stabilize nTiO2 suspensions by reducing particle aggregation, presumably due to steric repulsion.23 Data presented by Domingos and colleagues suggests that, due to the presence of NOM, nTiO2 dispersion and mobility in the environment may occur to a greater extent than predicted based on prior laboratory experiments.23 In addition to naturally occurring stabilizing agents, artificial dispersants are frequently added to nanoparticle suspensions to increase stability and maintain or minimize aggregate size.24,25 Joo et al. observed improved nTiO2 suspension stability in the presence of carboxymethyl cellulose (CMC), where suspensions of uncoated nTiO2 exhibited a PZC of 5.6 while CMC-containing nTiO2 suspensions had a PZC of less than 2.25 An additional study, which evaluated the impact of polyacrylic acid on nTiO2 stability, reported a decrease in the PZC by 0.42–2.08 pH units, depending upon the molecular weight (2000–120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) and concentration (10–100 mg L−1) of added polyacryclic acid.26
000 g mol−1) and concentration (10–100 mg L−1) of added polyacryclic acid.26
Petosa and colleagues demonstrated that polymer-coated (partially cross-linked polyacrylic acid) nTiO2 particles had greater mobility in quartz sands compared to bare nTiO2 for IS ranging from 0.1–100 mM as NaNO3.27 In another study by Joo et al., nearly complete retention of uncoated anatase nTiO2 was reported in quartz sand columns, while the addition of CMC to nTiO2 suspensions (nTiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC ratio of 0.1
CMC ratio of 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) resulted in nanoparticle breakthrough after 1 pore volume (PV), which was attributed to electrosteric stabilization from the adsorption of CMC to the nanoparticles.25 With the exception of a few studies,24,25,27 the majority of previous nTiO2 transport experiments were performed with uncoated nTiO2 or in the absence of stabilizing agents, and did not consider the matrices utilized in most commercial products containing nTiO2. Sunscreens represent a major class of personal care products and potential route of entry for nTiO2 into the environment.5 Thus, in order to predict the fate of nTiO2, it will be important to understand the influence of specific sunscreen additives on stability and transport in the environment. The stabilizing agents considered in previous nTiO2 transport studies include non-ionic and anionic surfactants24 carboxymethyl cellulose,25 and clay particles,28 but the effect of a specific sunscreen additive has not been evaluated. Additionally, very few prior studies measured the amount of retained nTiO2 (i.e., the solid-phase concentration) in column transport experiments28–30 due the difficulties associated with accurately measuring deposited TiO2 concentrations. Measurement of retained mass, however, is critical to experimental mass balance closure and is also important for transport model validation.
1) resulted in nanoparticle breakthrough after 1 pore volume (PV), which was attributed to electrosteric stabilization from the adsorption of CMC to the nanoparticles.25 With the exception of a few studies,24,25,27 the majority of previous nTiO2 transport experiments were performed with uncoated nTiO2 or in the absence of stabilizing agents, and did not consider the matrices utilized in most commercial products containing nTiO2. Sunscreens represent a major class of personal care products and potential route of entry for nTiO2 into the environment.5 Thus, in order to predict the fate of nTiO2, it will be important to understand the influence of specific sunscreen additives on stability and transport in the environment. The stabilizing agents considered in previous nTiO2 transport studies include non-ionic and anionic surfactants24 carboxymethyl cellulose,25 and clay particles,28 but the effect of a specific sunscreen additive has not been evaluated. Additionally, very few prior studies measured the amount of retained nTiO2 (i.e., the solid-phase concentration) in column transport experiments28–30 due the difficulties associated with accurately measuring deposited TiO2 concentrations. Measurement of retained mass, however, is critical to experimental mass balance closure and is also important for transport model validation.
The objective of this research was to investigate the effects of a polymeric stabilizing agent used in sunscreen formulations (carbomer) on the mobility of TiO2 nanoparticles in porous media. Batch studies were carried out to determine the effects of pH and IS on the aggregation, particle size distribution, and zeta potential of nTiO2 in the presence and absence of carbomer. Column experiments were conducted to evaluate the influence of the stabilizing agent on the transport and deposition of nTiO2 in water-saturated quartz sands at pH values of 5.0 and 7.5 ± 0.2. In addition to column effluent samples, nTiO2 solid phase concentrations were measured, allowing for retention profiles and total nTiO2 mass balance to be calculated. A nanoparticle transport model that incorporates a first-order attachment expression and a Langmuirian blocking function was implemented to provide further quantitative interpretation of the experimental results.
2. Materials and methods
2.1. Nanoparticle suspensions
Uncoated TiO2 nanoparticles (99.5%, Aeroxide TiO2 P25) and polymeric stabilizing agent (TEGO Carbomer 341 ER) were obtained from the Evonik Degussa Corporation (Essen, Germany). The nominal nTiO2 particle size provided by the manufacturer was 21 nm, with a reported specific surface area of 15 m2 g−1 and density of 3.8 g cm−3. The crystalline structure of P25 consists of approximately 78% anatase, 14% rutile, and 8% amorphous TiO2.31 The stabilizing agent, TEGO Carbomer 341 ER (hereafter referred to as carbomer), is an acrylates/C10-30 alkyl acrylates cross-polymer with a density of 1.4 g cm−3. The equivalent weight is estimated to be 76 g mol−1 per carboxyl group,32 and using an approximate value of 20 carboxyl groups for this compound, the molecular weight was estimated to be 1500 g mol−1. A high protection sun lotion recipe from Evonik includes 1.5% (w/w) TEGO Sun T 805 G (nTiO2) and 0.2% (w/w) carbomer 341, or a 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w ratio of nTiO2 to carbomer. In the present study, a similar ratio of these components was used for suspensions containing carbomer (10
1 w/w ratio of nTiO2 to carbomer. In the present study, a similar ratio of these components was used for suspensions containing carbomer (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w).
1 w/w).
nTiO2 suspensions were prepared by mixing a pre-weighed mass of dry P25 powder with deionized (DI) water, generating a final suspension concentration of approximately 30 mg L−1. Suspension IS was adjusted to values ranging from 0.01–100 mM using 1 M NaCl. Samples were adjusted to pH 5 using 0.1 M HCl, while pH 7.5 samples were buffered with 1 mM HEPES buffer (Acros Organics, New Jersey). For samples containing stabilizing agent, carbomer was first added to DI water and mixed for ten minutes prior to the addition of nanoparticles, followed by IS and pH adjustment using the same procedure as the samples without stabilizing agent. The final suspensions (including nTiO2) were sonicated for 10 minutes using a Branson Sonifier 450 sonication probe (Branson Ultrasonics, Danbury, CT) with a microtip attachment.
2.2. Nanoparticle characterization
The hydrodynamic diameter and electrophoretic mobility of nTiO2 suspensions were measured with a Malvern ZetaSizer (Malvern, Worcestershire, United Kingdom) using dynamic light scattering (DLS) and laser Doppler velocimetry, respectively. The electrophoretic mobility was then related to the zeta potential (ζ) using the Smoluchowski approximation.33 The particle size distribution, pH, and zeta potential of the influent suspension were monitored at the beginning and end of each column experiment. In batch experiments, DLS measurements were taken one minute after NaCl addition to evaluate the impact of ionic strength on nTiO2 size and zeta potential. Solution pH was monitored using an Orion 3 Star pH Benchtop probe (Thermo Scientific, Waltham, MA). The measured pH values of the nTiO2 suspensions used in column transport studies ranged from 5.0–5.2 and 7.4–7.7 (Table 1). Transmission electron microscope (TEM) images of nTiO2 with and without 3 mg L−1 carbomer were obtained using a JEOL 2100 TEM (JEOL USA, Peabody, MA) and are shown in the ESI† (Fig. S1). Samples were prepared by evaporating several drops of 30 mg L−1 nTiO2 suspensions (at pH 7.5 with 1 mM HEPES buffer) onto a carbon film on 400 square mesh copper grid (Electron Microscopy Sciences, Hatfield, PA).| Column ID | pH | Experimentally determined parameters | Mathematical model fitted parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Suspension additives | C 0 (mg nTiO2 L−1) | Porosity (unitless) | v p (m d−1) | Mass breakthrough (%) | Mass balance (%) | Particle diameterc (nm) | Zeta potential (mV) | k att (1 s−1) | α (unitless) | S max (μg TiO2 g−1 sand) | ||
| a Influent nTiO2 concentration. b Pore-water velocity. c Average of influent particle diameter at beginning and end of pulse injection. d Attachment rate. e Attachment efficiency. f Maximum retention capacity. | ||||||||||||
| 1 | 5.0 | None | 24 | 0.38 | 7.1 | 0 | 85 | 119 | 11 | 3.63 × 10−3 | 0.32 | n/a |
| 2 | 5.0 | None | 24 | 0.36 | 7.8 | 0 | 84 | 116 | 23 | 4.06 × 10−3 | 0.32 | n/a |
| 3 | 7.4 | 1 mM HEPES | 28 | 0.38 | 7.1 | 90 | 98 | 107 | −28 | 2.69 × 10−4 | 0.022 | 2.51 |
| 4 | 7.4 | 1 mM HEPES | 29 | 0.39 | 7.3 | 82 | 93 | 132 | −21 | 5.95 × 10−4 | 0.059 | 4.28 |
| 5 | 5.1 | 3 mg L−1 carbomer | 28 | 0.37 | 7.3 | 104 | 104 | 108 | −32 | 4.08 × 10−4 | 0.031 | 0.34 |
| 6 | 5.1 | 3 mg L−1 carbomer | 28 | 0.38 | 7.4 | 97 | 97 | 109 | −36 | 1.25 × 10−4 | 0.010 | 1.32 |
| 7 | 7.6 | 1 mM HEPES 3 mg L−1 carbomer | 32 | 0.38 | 7.1 | 100 | 103 | 112 | −27 | 3.61 × 10−4 | 0.031 | 0.78 |
| 8 | 7.6 | 1 mM HEPES 3 mg L−1 carbomer | 32 | 0.38 | 7.5 | 94 | 98 | 105 | −36 | 4.50 × 10−4 | 0.036 | 1.82 |
| 9 | 5.2 | 3 mg L−1 carbomer 3 mM NaCl | 24 | 0.38 | 7.2 | 98 | 98 | 129 | −50 | 1.19 × 10−4 | 0.012 | 0.96 |
| 10 | 5.2 | 3 mg L−1 carbomer 3 mM NaCl | 25 | 0.36 | 7.8 | 96 | 96 | 135 | −43 | 7.31 × 10−4 | 0.065 | 0.78 |
| 11 | 7.7 | 1 mM HEPES 3 mg L−1 carbomer 3 mM NaCl | 33 | 0.38 | 7.0 | 97 | 99 | 116 | −38 | 2.78 × 10−4 | 0.024 | 1.42 |
| 12 | 7.7 | 1 mM HEPES 3 mg L−1 carbomer 3 mM NaCl | 33 | 0.37 | 7.6 | 97 | 98 | 124 | −39 | 2.81 × 10−4 | 0.024 | 1.39 |
2.3. Column transport experiments
All column studies were conducted with Federal Fine Ottawa sand (30–140 mesh, d50 = 320 μm) which was obtained from the U.S. Silica Company (Ottawa, IL). The sand was cleaned by soaking in 1.0 M HNO3 solution overnight, rinsing with DI, and was then placed in an ultrasonic bath containing 0.007 M Na2PO4 for at least 10 h, rinsed with DI until pH 7 was reached, and finally oven-dried at 200 °C for 12 h.34 Transport experiments were performed using borosilicate glass columns (10 cm length × 2.5 cm inner diameter, Kontes, Vineland, NJ), which were dry-packed with washed Federal Fine Ottawa sand in 1 cm increments. Both end plates of the column contained a 60-mesh stainless steel screen to support the packed bed and prevent elution of sand grains. Once packing was complete, the column was flushed with CO2 gas for at least 20 minutes to facilitate dissolution of entrapped gas bubbles during water imbibition. A background solution (DI for columns 1–8 or 3 mM NaCl for columns 9–12) was then injected into the column in an upward direction for at least 10 PVs using an ISO-100 Isocratic Pump (Chrom Tech, Apple Valley, MN). Following complete saturation of the column, a non-reactive tracer test was performed to assess water flow and hydrodynamic dispersion within the column. Three PVs of non-reactive tracer solution (1 mM NaBr for columns 1–8, 3 mM NaBr for columns 9–12) were injected at a flow rate of 1 mL min−1, followed by at least two PVs of background solution. The bromide concentration in aqueous samples was measured using a bromide combination electrode (Cole-Parmer, Vernon Hills, IL). Effluent breakthrough curves (BTCs) obtained for the bromide tracer were fit to a dimensionless form of the advection-reactive transport (ADR) equation for each column using the CXTFIT program.35 The average column Peclet number was 148 ± 35, which corresponds to a hydrodynamic dispersion coefficient (DH) of 0.041 ± 0.01 cm2 min−1. A representative model fit to a measured tracer breakthrough curve is shown in Fig. 6.Following the tracer test, a three PV pulse of nTiO2 suspension was injected into the column using a PHD 2000 syringe pump (Harvard Apparatus, Holliston, MA) at a flow rate of 1 mL min−1, followed by at least two PVs of nTiO2-free background electrolyte solution, also at a flow rate of 1 mL min−1. The average Darcy velocity of background electrolyte and nTiO2 injections was 2.8 ± 0.06 m d−1, corresponding to an average pore-water velocity of 7.3 ± 0.3 m d−1. This value is similar to the seepage velocity used by Cai et al. (8 m d−1) in a previous nTiO2 transport study28 to represent flow through coarse aquifer sediments or engineered filtration systems. Column effluent samples were collected continuously (at least five samples per PV) using a Spectrum Labs Spectra/Chrom CF-2 Fraction Collector (Spectrum Laboratories, Inc., Rancho Dominguez, CA). Columns 1–8 were run with a DI water background to first evaluate the role of pH and carbomer addition, and then the effect of background electrolyte (3 mM NaCl) in the presence of carbomer was investigated (columns 9–12). After each experiment, the columns were sectioned into ten 1 cm increments and approximately 2 g of sand from each increment was analyzed to determine the amount of retained nTiO2.
Column effluent and solid samples were oven-dried at 90 °C and then digested in 18.7 M sulfuric acid (2 mL H2SO4 for aqueous samples, 5 mL for solid samples) with a CEM SP-D Discover Microwave Digester (CEM Corporation, Matthews, NC). Acid digestion was conducted at 200 °C for 45 minutes for aqueous samples and 200 °C for 60 minutes for solid samples. After digestion, the samples were diluted to 1 M H2SO4 using DI water and quantified using an Optima 7300 DV Inductively Coupled Plasma Optical Emission Spectrometer, ICP-OES (PerkinElmer, Waltham, MA). Standard curves were prepared from an Ultima Titanium stock standard (1000 mg L−1). The average background titanium concentration of the cleaned Federal Fine Ottawa Sand was 18 μg TiO2 g−1 sand. Titanium was quantified at a wavelength of 336.121 nm, which yielded a detection limit of 12 μg Ti L−1 (equivalent to 20 μg TiO2 L−1), based on the U.S. Environmental Protection Agency method for determining a lowest concentration minimum reporting level.36
2.4. Mathematical modeling
The transport of nTiO2 in the homogeneous saturated packed column can be described by a one-dimensional mass balance equation with first-order particle retention kinetics:34,37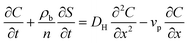 | (1) |
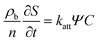 | (2) |
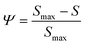 | (3) |
Eqn (1)–(3) were solved with an implicit-in-time and central-in-space finite difference scheme implemented in MATLAB R2010a (The Mathworks Inc., Natick, MA). Pore-water velocity, vp, and hydrodynamic dispersion, DH, terms were independently determined from column tracer data. katt and Smax were then determined by fitting the model to effluent breakthrough data using a non-linear least squares minimization algorithm.38 The transport model (with zero attachment) was also validated against the tracer data fit (that was performed using the CXTFIT program)35 to confirm that it appropriately captured hydrodynamic dispersion.
3. Results and discussion
3.1. Characterization of nTiO2 suspensions
Batch studies were performed to evaluate the effects of solution pH and IS on the zeta potential and mean diameter of nTiO2. By varying the suspension pH from 3.5–11.5 in DI water, the PZC of nTiO2 was estimated to be pH 6.3 (Fig. 1). This value is comparable to the nTiO2 PZC reported in previous studies; 6.0,18 6.8,20 and 6.2.30 The nTiO2 zeta potentials ranged from +36.5 to −48.3 mV over the pH range of 3.5–11.5, with positive zeta potentials for pH values below the PZC and negative zeta potentials for pH values above the PZC. Within one pH unit of the PZC, nTiO2 particles aggregated to become micron-sized (mean nTiO2 diameter = 1.31 ± 0.2 μm for pH 5.7–7.0 in DI water, Fig. 1). The particle size remained below 150 nm when the pH was at least one unit above or below the PZC. Over the pH range of 3.5–4.7, the average particle diameter was 122 ± 21 nm, and for pH values of 7.8–11.5, the average particle diameter was 103 ± 24 nm (Fig. 1).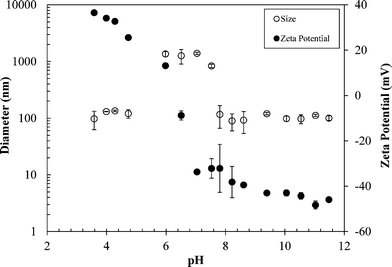 | ||
| Fig. 1 Effect of pH on nTiO2 particle size and zeta potential in DI water. Error bars represent standard deviation of 3 replicate measurements. | ||
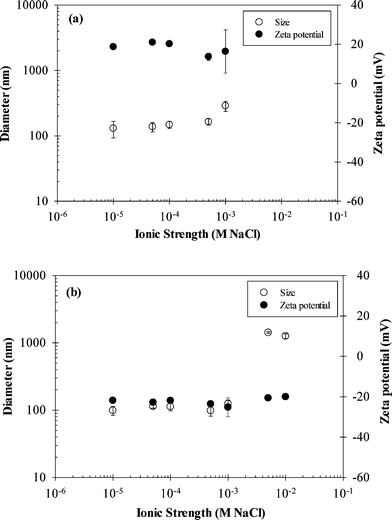
The influence of IS (0.01–10 mM) on the mean particle diameter and zeta potential of nTiO2 suspensions without stabilizing agent at pH 5 and 7.5 is shown in Fig. 2. As expected, the nanoparticles were highly sensitive to changes in solution chemistry in the absence of a stabilizing agent. At pH 5, an increase in nTiO2 particle diameter compared to that in DI water was observed at NaCl concentrations as low as 0.1 mM. When the IS was further increased to 1 mM NaCl, the particle diameter increased more than two-fold (288 ± 50 nm) compared to its value in DI water (112 ± 17 nm). At IS values ≥5 mM NaCl and pH 5, the nTiO2 suspension became unstable, resulting in sedimentation of larger nanoparticle aggregates, and, therefore, unstable size distribution and zeta potential readings. In a previous study using 100% anatase nTiO2 at pH 4.6, Jiang et al. observed a similar trend of increasing nTiO2 size with increasing IS, with substantial aggregation occurring at IS values of 5 mM NaCl and higher.18 In contrast to pH 5 samples, the zeta potential of nTiO2 at pH 7.5 remained relatively constant even when the IS was increased from 0.01 to 10 mM NaCl (mean zeta potential = −22 ± 2.1 mV) in the present study. Although the zeta potential remained stable in pH 7.5 suspensions, particle aggregation was observed and micron-sized aggregates began to form between IS values of 1 mM and 5 mM NaCl.
The addition of 3 mg L−1 carbomer to nTiO2 suspensions resulted in stable particle size and zeta potential for IS values ranging from 0.01 to 100 mM, effectively mitigating the pH effects observed in the absence of carbomer (Fig. 3). At a carbomer concentration of 3 mg L−1, the mean nTiO2 diameter over the entire range of IS was 124 ± 37 nm and 117 ± 37 nm at pH 5 and 7.5, respectively, and the average zeta potential was −42 ± 2 mV and −37 ± 4 mV at pH 5 and 7.5, respectively. The observed differences in mean nTiO2 diameters across IS values were not statistically significant (paired two-tailed t-test, ∝ = 0.05, p-value = 0.50), even though the mean zeta potential values were significantly different (p-value < 0.01). The enhanced stability of nTiO2 suspensions that was observed following the addition of carbomer was likely due to electrosteric repulsion resulting from adsorption of the polymer to the nTiO2 surface. A previous study by Liufu et al. demonstrated that adsorption of polyacrylic acid on nTiO2 occurs by hydrogen bonding and chemical interaction between the TiO2 surface and carboxyl groups of the polymer, which stabilizes nTiO2 suspensions through electrosteric repulsion.26
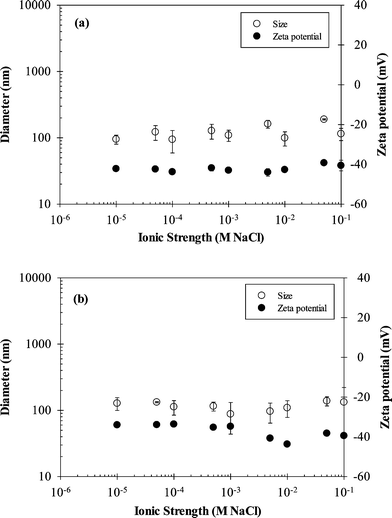 | ||
| Fig. 3 Effect of IS on zeta potential and nTiO2 particle size in the presence of 3 mg L−1 carbomer at (a) pH 5 and (b) pH 7.5. Error bars represent standard deviation of 3 replicate measurements. | ||
3.2. DLVO energy profiles: nanoparticle–nanoparticle interactions
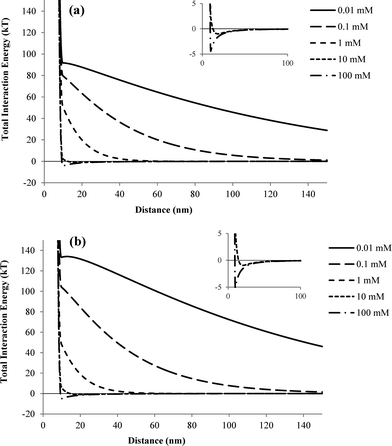
To qualitatively examine the effects of IS on nTiO2 aggregation, Derjaguin–Landau–Verwey–Overbeek (DLVO) interaction energy profiles were calculated for two spherical TiO2 nanoparticles (see ESI† for equations used). For nTiO2 suspensions without a stabilizing agent, the magnitude of the primary energy barrier decreased with increasing IS (ESI,† Fig. S2). For pH 5 suspensions with 0.1 mM NaCl, a repulsive energy barrier existed between two approaching TiO2 nanoparticles (net positive interaction energy). At IS values of 1 mM or higher, a net negative interaction energy was computed, indicating that nTiO2 particles would be attracted to one another. The computed interaction energy profiles were consistent with the observed increase in nTiO2 particle size when the IS was increased above 1 mM (Fig. 2). The interaction energy profiles for an nTiO2 suspension at pH 7.5 were similar to those obtained at pH 5; however, the maximum energy values were slightly higher at pH 7.5 (16.2 versus 14.8 kT at 0.01 mM), and there was a slight repulsive energy at an IS of 1 mM that was not observed at pH 5. Thus, the DLVO interaction energy profiles were consistent with the batch experiment results; specifically, the pH 7.5 suspension was less sensitive to increasing IS, and nTiO2 aggregation was initiated at higher electrolyte concentrations at pH 7.5 compared to pH 5. The primary energy barriers calculated here were on the same order of magnitude as those calculated by Chen et al. (i.e., 10–100 kT).29Traditional DLVO theory does not account for enhanced stability of nanoparticles resulting from the presence of polymers such as carbomer. Therefore, extended DLVO (XDLVO) was used to compute interaction energy profiles for suspensions containing carbomer (Fig. 4). In XDLVO, the total interaction energy includes not only the traditional electronic double layer repulsive energy and van der Waals attractive energy, but also the osmotic and elastic–steric repulsion energies induced by the presence of a polymer layer coating a colloid or nanoparticle.39 The equations and parameters used for XDLVO calculations are provided in ESI† (Table S1). The repulsive energy barriers based on XDLVO calculations reached maximum values of >20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kT at pH 5 and 7.5 for IS values of 0.01–100 mM (Fig. 4, inset). The large primary energy barrier exists within the region of the polymer layer surrounding the particle (d = 0–10 nm), and the repulsive force is primarily due to elastic–steric forces. At both pH 5 and pH 7.5, a secondary energy minimum is observed at IS values of 10 and 100 mM, indicating that, although there is large repulsive energy barrier, attractive forces do exist with higher IS solutions. In comparison, the primary energy barriers obtained using traditional DLVO theory for nTiO2 with carbomer were higher than those obtained for nTiO2 alone (e.g., 63 kT with carbomer versus 15 kT without carbomer at pH 5 and IS = 0.01 mM, ESI† Fig. S2 and S3), but were several orders of magnitude lower than those obtained using XDLVO theory.
000 kT at pH 5 and 7.5 for IS values of 0.01–100 mM (Fig. 4, inset). The large primary energy barrier exists within the region of the polymer layer surrounding the particle (d = 0–10 nm), and the repulsive force is primarily due to elastic–steric forces. At both pH 5 and pH 7.5, a secondary energy minimum is observed at IS values of 10 and 100 mM, indicating that, although there is large repulsive energy barrier, attractive forces do exist with higher IS solutions. In comparison, the primary energy barriers obtained using traditional DLVO theory for nTiO2 with carbomer were higher than those obtained for nTiO2 alone (e.g., 63 kT with carbomer versus 15 kT without carbomer at pH 5 and IS = 0.01 mM, ESI† Fig. S2 and S3), but were several orders of magnitude lower than those obtained using XDLVO theory.
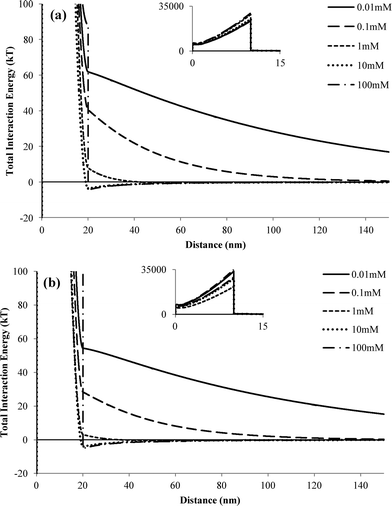 | ||
| Fig. 4 Interaction energy profiles obtained using XDLVO theory for two nTiO2 particles in the presence of carbomer at (a) pH 5 and (b) pH 7.5. Insets show the y-axis on a larger scale. | ||
3.3. DLVO energy profiles: nanoparticle–sand surface interactions
Consideration of interaction energy profiles between an nTiO2 particle and a quartz surface provides a qualitative understanding of the potential for nanoparticle deposition during transport through porous media. Energy profiles obtained using DLVO theory for a spherical nTiO2 particle and a quartz surface (represented as a plane) are shown in ESI† Fig. S4 (calculations provided in ESI). At pH 5, the energy profiles are dominated by a net attractive energy. In contrast, the pH 7.5 profiles indicate positive (repulsive) interaction energies between nTiO2 and the quartz surface (ESI† Fig. S4). At pH 7.5 and 10 mM NaCl, a secondary energy minimum occurs at a separation distance of 16.2 nm, indicating that although there is a repulsive primary energy barrier, attractive forces exist between nTiO2 and the quartz surface, which may contribute to deposition under these conditions.To evaluate the impact of steric repulsion on interaction energy in the presence of a polymer, XDLVO theory was applied to the nanoparticle-quartz surface system.40,41 For this case, the steric interaction energy was calculated between a polymer-coated TiO2 nanoparticle and an uncoated sand grain and summed with the nanoparticle–sand grain electronic double layer repulsive energy and van der Waals attractive energy to obtain the total interaction energy (Fig. 5, see ESI† for equations). The inclusion of steric energy in the XDLVO calculation results in a large positive (repulsive) energy in the region of the polymer layer 0–10 nm from the particle surface, which is consistent with the stabilization of nTiO2 due to an adsorbed polymer coating. In contrast to the interaction energy profiles for nTiO2 and quartz sand in the absence of carbomer (ESI,† Fig. S4), repulsive forces dominate for both pH 5 and 7.5 at low IS (≤1 mM NaCl) when carbomer was present (Fig. 5). Dominant repulsive forces suggest that under these conditions, nTiO2 will not be deposited on porous media, and therefore, the mobility of pH 5 nTiO2 suspensions is expected to be enhanced by the presence of carbomer. For higher IS suspensions (≥10 mM NaCl), a secondary minimum attractive energy was obtained even though a large primary energy barrier existed due to steric repulsion. A similar trend was observed in XDLVO profiles presented by Wang et al. for polyacryclic acid-octylamine-coated quantum dots, with secondary energy minimums observed at IS values of 30 and 100 mM NaCl.42
3.4. Column transport experiments
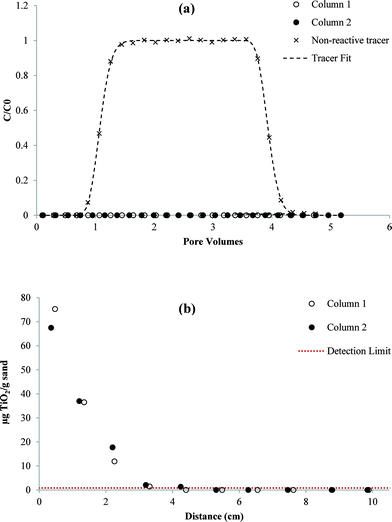
Results of the column transport studies are presented in two parts; nTiO2 effluent BTCs and solid phase retention profiles. The BTCs are plotted as the measured concentration of nTiO2 in effluent samples (C), divided by the influent or applied concentration (C0), versus time, expressed as dimensionless PVs. For each column study, the BTC obtained for a pulse injection of non-reactive tracer is shown as a dashed line for comparison purposes. The retention profiles show the concentration of attached nTiO2 (i.e., solid-phase concentration) as a function of distance from the column inlet (x = 0). Measured nTiO2 effluent BTCs and retention profiles in the presence and absence of carbomer at both pH values are shown in Fig. 6–9. Results obtained for column studies conducted with an IS of 3 mM (NaCl) at both pH values are provided in ESI† (Fig. S5 and S6). Experimental conditions for all of the column studies are summarized in Table 1.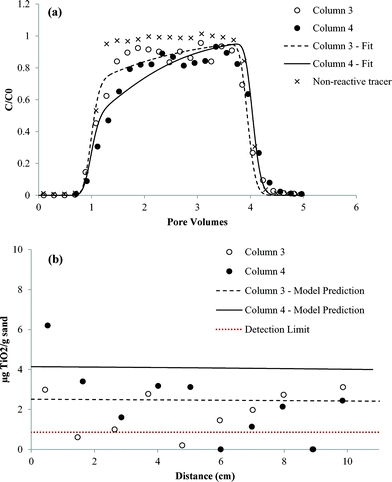 | ||
| Fig. 7 Comparison of experimentally measured and simulated (a) transport and (b) retention of nTiO2 alone at pH 7.4 in Federal Fine (30–140 mesh) Ottawa sand (duplicate columns). | ||
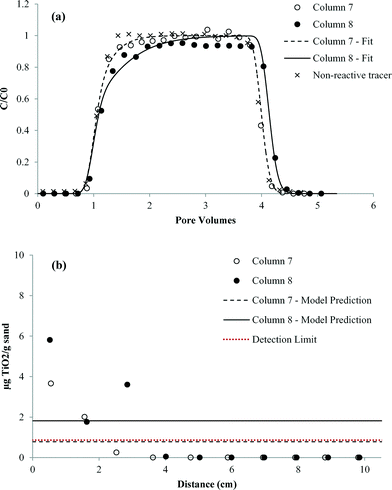 | ||
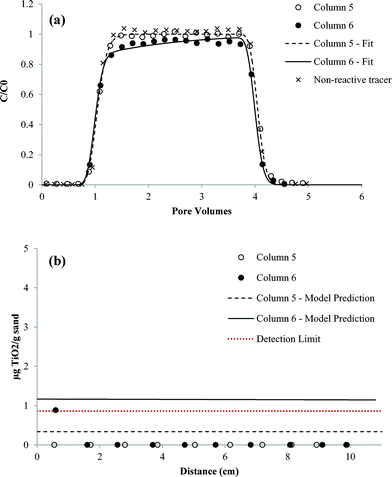
| Fig. 9 Comparison of experimentally measured and simulated (a) transport and (b) retention of nTiO2 with 3 mg L−1 carbomer at pH 7.6 in Federal Fine (30–140 mesh) Ottawa sand (duplicate columns). | ||
When 3 mM NaCl was added to carbomer–nTiO2 suspensions at pH 5.2 and pH 7.7 (columns 9–12, Fig. S5 and S6†), there was minimal change in nTiO2 mobility (<8% change in mass breakthrough) compared to identical column studies performed without NaCl (columns 5–8, Fig. 8 and 9). This finding was consistent with the XDLVO theory, which indicated that nTiO2 particle–particle and particle–surface interaction energy profiles were not sensitive to low electrolyte concentrations in the presence of carbomer (Fig. 4 and 5). Similar to the trend observed for column experiments conducted in the presence of carbomer without NaCl (columns 5–8), the nTiO2 effluent BTC obtained at pH 7.7 with 3 mg L−1 carbomer and 3 mM NaCl (columns 11–12) rose more slowly than the nTiO2 BTC obtained at pH 5.2 under the same conditions (columns 9–10). No measurable nTiO2 retention was observed at pH 5.2, while the solid phase sample collected nearest the column inlet yielded concentrations of 4.8 and 3.0 μg TiO2 g−1 sand in replicate experiments conducted at pH 7.7. Zeta potential values obtained in the presence of carbomer were negative at pH 5–5.2, indicating that the PZC shifted to a pH value lower than 5. Joo et al. observed a similar decrease in the PZC (from pH 5.6 to <2) and enhanced nTiO2 mobility through quartz sand following addition of a different polymer stabilizing agent (carboxymethyl cellulose, MW = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) to nTiO2 suspensions.25
000 g mol−1) to nTiO2 suspensions.25
Collision efficiency (α) values were calculated from the fitted katt values using clean-bed filtration theory:44
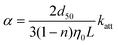 | (4) |
Although the breakthrough behavior was well captured in all cases, the model based upon eqn (1) and (2) with a single (average) Smax value was unable to accurately reproduce the hyper-exponential retention curves exhibited in columns 3–12 (see, for example, Fig. 9b). Although models for mechanical filtration (i.e., straining) of colloidal particles in porous media predict hyper-exponential retention behavior, the measured particle sizes observed in this study were approximately 120 nm, resulting in nTiO2 to porous media diameter (d50 = 350 μm) ratios ranging from 3.0 × 10−4 to 3.9 × 10−4. Typically, straining is considered to be significant when the ratio of particle diameter to grain diameter is greater than 0.05,46 although more recent studies have suggested that straining may be a factor at ratios of 0.002 or 0.008.47,48 Since the nanoparticle![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) grain size diameter ratios were an order of magnitude lower than the reported threshold values, it is unlikely that physical straining contributed to the observed nTiO2 retention. Although the shape of the retention curves was not fully captured, the single-Smax retention model was able to accurately capture the total amount of retained mass in all cases. This result suggests that the maximum capacity for nTiO2 retention varied along the domain, but could be represented by a single average retention parameter.
grain size diameter ratios were an order of magnitude lower than the reported threshold values, it is unlikely that physical straining contributed to the observed nTiO2 retention. Although the shape of the retention curves was not fully captured, the single-Smax retention model was able to accurately capture the total amount of retained mass in all cases. This result suggests that the maximum capacity for nTiO2 retention varied along the domain, but could be represented by a single average retention parameter.
4. Conclusions
The effects of a polymer stabilizing agent, carbomer (a common sunscreen additive), on the transport and retention behavior of nTiO2 in Federal Fine Ottawa sand was investigated using a combination of experimental and mathematical modeling studies. In the absence of carbomer, nTiO2 particles aggregated to become micron-sized within one pH unit of the PZC (pH 6.3). The mean diameter of nTiO2 remained below 150 nm when the pH was at least one unit above or below the PZC (size = 122 ± 21 nm and 103 ± 24 nm, for pH ranges of 3.5–4.7 and 7.8–11.5, respectively). The porous medium possessed a negative zeta potential (e.g., estimated to be −35 mV at pH 5),43 and therefore, when the suspension pH was below the PZC (positive nTiO2 zeta potential), limited TiO2 transport and substantial retention was observed. Conversely, when the suspension pH was above the PZC (negative nTiO2 zeta potential), nTiO2 was not deposited on the negatively charged quartz surfaces, and thus, mobility increased, demonstrating the important role of pH on nTiO2 mobility in the absence of carbomer. When nTiO2 suspensions were amended with 3 mg L−1 carbomer, zeta potential values were negative at pH 5–5.2, indicating that the PZC shifted to a pH value lower than 5. Since this PZC is less than the pH range typically observed in environment systems (i.e., 6–9),22 it is expected that nTiO2 particles will exhibit greater mobility in the presence of stabilizing agents.In the presence of 3 mg L−1 carbomer, greater than 94% effluent mass breakthrough occurred in nTiO2 suspensions, regardless of suspension pH or electrolyte content. The enhanced stability of nTiO2 suspensions following carbomer addition was likely due to increased electrosteric repulsion resulting from adsorption of the polymer to the nanoparticle surface. As a result, the effects of solution pH were overshadowed by the addition of a polymer to nTiO2 suspensions. Simulation of experimental BTCs and retention profiles using a nanoparticle transport model with a first-order kinetic attachment expression and a maximum attachment capacity term adequately described the breakthrough behavior as well as the total amount of retained mass measured in all experiments. However, the model was unable to capture the hyper-exponential nTiO2 retention observed near the column inlet, indicating that there is likely a spatially-variable retention capacity that was not accounted for by the model.
The findings of this study demonstrate the importance of considering the impacts of polymer stabilizing agents on the environmental fate of manufactured TiO2 nanomaterials that are released into the environment from sunscreen and other consumer products containing a dispersing agent in their formulation. More specifically, the addition of product-relevant concentrations of carbomer could alter the system retention capacity substantially, thereby allowing for increased nTiO2 mobility through porous media. Such enhanced transport through porous media or filtration systems could increase the potential for contamination of drinking water sources and risk of human and ecological exposure.
Acknowledgements
Support for this research was provided by grants from the National Science Foundation, Award numbers CBET-0854136 and CBET-1235563. The work has not been subject to NSF review, and therefore, does not necessarily reflect the views of the organization and no official endorsement should be inferred. TEM imaging was performed at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Infrastructure Network (NNIN), which is supported by the National Science Foundation under NSF award no. ECS-0335765. CNS is part of Harvard University.References
- ICIS, ICIS Titanium Dioxide Uses and Market, http://www.icis.com/resources/news/2007/11/07/9076546/titanium-dioxide-tio2-uses-and-market-data/, Accessed February 10, 2014 Search PubMed.
- A. Weir, P. Westerhoff, L. Fabricius, K. Hristovski and N. von Goetz, Environ. Sci. Technol., 2012, 46, 2242–2250 CrossRef CAS PubMed.
- C. O. Robichaud, A. E. Uyar, M. R. Darby, L. G. Zucker and M. R. Wiesner, Environ. Sci. Technol., 2009, 43, 4227–4233 CrossRef CAS PubMed.
- S. Wiechers, P. Biehl, C. Luven, M. Maier, J. Meyer, J. Munzenburg, C. Schulze-Isfort and P. Albers, Cosmet. Toiletries, 2013, 128, 332–339 CAS.
- C. Botta, J. Labille, M. Auffan, D. Borschneck, H. Miche, M. Cabié, A. Masion, J. Rose and J.-Y. Bottero, Environ. Pollut., 2011, 159, 1543–1550 CrossRef CAS PubMed.
- M. A. Kiser, P. Westerhoff, T. Benn, Y. Wang, J. Pérez-Rivera and K. Hristovski, Environ. Sci. Technol., 2009, 43, 6757–6763 CrossRef CAS PubMed.
- P. Westerhoff, G. Song, K. Hristovski and M. A. Kiser, J. Environ. Monit., 2011, 13, 1195–1203 RSC.
- R. Kaegi, A. Ulrich, B. Sinnet, R. Vonbank, A. Wichser, S. Zuleeg, H. Simmler, S. Brunner, H. Vonmont, M. Burkhardt and M. Boller, Environ. Pollut., 2008, 156, 233–239 CrossRef CAS PubMed.
- IARC, IARC Monographs on the Evaluation of Carcinogenic Risks to Humans: Carbon Black, Titanium Dioxide, and Talc, International Agency for Research on Cancer, Lyon, France, 2010 Search PubMed.
- M. C. E. Lomer, R. P. H. Thompson and J. J. Powell, Proc. Nutr. Soc., 2002, 61, 123–130 CrossRef PubMed.
- V. Aruoja, H.-C. Dubourguier, K. Kasemets and A. Kahru, Sci. Total Environ., 2009, 407, 1461–1468 CrossRef CAS PubMed.
- N. B. Hartmann, F. Von der Kammer, T. Hofmann, M. Baalousha, S. Ottofuelling and A. Baun, Toxicology, 2010, 269, 190–197 CrossRef CAS PubMed.
- G. Frenzilli, M. Bernardeschi, P. Guidi, V. Scarcelli, P. Lucchesi, L. Marsili, M. C. Fossi, A. Brunelli, G. Pojana, A. Marcomini and M. Nigro, Mar. Environ. Res., 2014, 100, 68–73 CrossRef CAS PubMed.
- S. Huang, P. J. Chueh, Y.-W. Lin, T.-S. Shih and S.-M. Chuang, Toxicol. Appl. Pharmacol., 2009, 241, 182–194 CrossRef CAS PubMed.
- C.-Y. Jin, B.-S. Zhu, X.-F. Wang and Q.-H. Lu, Chem. Res. Toxicol., 2008, 21, 1871–1877 CrossRef CAS PubMed.
- C. M. Sayes, R. Wahi, P. A. Kurian, Y. Liu, J. L. West, K. D. Ausman, D. B. Warheit and V. L. Colvin, Toxicol. Sci., 2006, 92, 174–185 CrossRef CAS PubMed.
- A. Menard, D. Drobne and A. Jemec, Environ. Pollut., 2011, 159, 677–684 CrossRef CAS PubMed.
- J. Jiang, G. Oberdörster and P. Biswas, J. Nanopart. Res., 2009, 11, 77–89 CrossRef CAS.
- K. A. Dunphy Guzman, M. P. Finnegan and J. F. Banfield, Environ. Sci. Technol., 2006, 40, 7688–7693 CrossRef CAS.
- R. A. French, A. R. Jacobson, B. Kim, S. L. Isley, R. L. Penn and P. C. Baveye, Environ. Sci. Technol., 2009, 43, 1354–1359 CrossRef CAS PubMed.
- N. Solovitch, J. Labille, J. Rose, P. Chaurand, D. Borschneck, M. R. Wiesner and J.-Y. Bottero, Environ. Sci. Technol., 2010, 44, 4897–4902 CrossRef CAS PubMed.
- W. Stumm and J. J. Morgan, Aquatic Chemistry, John Wiley & Sons, New York, 3rd edn, 1995 Search PubMed.
- R. F. Domingos, N. Tufenkji and K. J. Wilkinson, Environ. Sci. Technol., 2009, 43, 1282–1286 CrossRef CAS PubMed.
- I. G. Godinez and C. J. G. Darnault, Water Res., 2011, 45, 839–851 CrossRef CAS PubMed.
- S. H. Joo, S. R. Al-Abed and T. Luxton, Environ. Sci. Technol., 2009, 43, 4954–4959 CrossRef CAS PubMed.
- S. Liufu, H. Xiao and Y. Li, J. Colloid Interface Sci., 2005, 281, 155–163 CrossRef CAS PubMed.
- A. R. Petosa, S. J. Brennan, F. Rajput and N. Tufenkji, Water Res., 2012, 46, 1273–1285 CrossRef CAS PubMed.
- L. Cai, M. Tong, X. Wang and H. Kim, Environ. Sci. Technol., 2014, 48, 7323–7332 CrossRef CAS PubMed.
- G. Chen, X. Liu and C. Su, Langmuir, 2011, 27, 5393–5402 CrossRef CAS PubMed.
- I. Chowdhury, Y. Hong, R. J. Honda and S. L. Walker, J. Colloid Interface Sci., 2011, 360, 548–555 CrossRef CAS PubMed.
- B. Ohtani, O. O. Prieto-Mahaney, D. Li and R. Abe, J. Photochem. Photobiol., A, 2010, 216, 179–182 CrossRef CAS.
- B. Goodrich, BF Goodrich Company Technical Literature: Carbopol Resin Handbook, 1991 Search PubMed.
- R. J. Hunter, Zeta Potential in Colloid Science, Academic Press, New York, 1981 Search PubMed.
- Y. Wang, Y. Li, J. Fortner, J. B. Hughes, L. M. Abriola and K. D. Pennell, Environ. Sci. Technol., 2008, 42, 3588–3594 CrossRef CAS PubMed.
- N. Toride, F. J. Leij and M. T. van Genuchten, The CXTFIT code for estimating trnasport parameters from laboratory or field tracer experiments, U.S. Salinity Laboratory, Agricultural Research Service, U.S. Department of Agriculture, Riverside, CA, 1995 Search PubMed.
- USEPA, Statistical Protocol for the Determination of the Single-Laboratory Lowest Concentration Minimum Reporting Level (LCMRL) and Validation of Laboratory Performance at or Below the Minimum Reporting Level (MRL), Office of Ground Water and Drinking Water, Standards and Risk Management Division, Cincinnati, OH, 2004 Search PubMed.
- I. Toloni, F. Lehmann and P. Ackerer, J. Contam. Hydrol., 2014, 171, 42–48 CrossRef CAS PubMed.
- M. D. Becker, Y. Wang, K. D. Pennell and L. M. Abriola, Environ. Sci.: Nano, 2015, 2, 155–166 RSC.
- G. Fritz, V. Schädler, N. Willenbacher and N. J. Wagner, Langmuir, 2002, 18, 6381–6390 CrossRef CAS.
- T. L. Byrd and J. Y. Walz, Environ. Sci. Technol., 2005, 39, 9574–9582 CrossRef CAS PubMed.
- A. R. Petosa, D. P. Jaisi, I. R. Quevedo, M. Elimelech and N. Tufenkji, Environ. Sci. Technol., 2010, 44, 6532–6549 CrossRef CAS PubMed.
- Y. Wang, H. Zhu, M. D. Becker, J. Englehart, L. M. Abriola, V. L. Colvin and K. D. Pennell, J. Nanopart. Res., 2013, 15, 1805 CrossRef.
- A. Kaya and Y. Yukselen, Can. Geotech. J., 2005, 42, 1280–1289 CrossRef CAS.
- K. Yao, M. T. Mohammad, T. Habibian and C. R. O'Melia, Environ. Sci. Technol., 1971, 5, 1105–1112 CrossRef CAS.
- N. Tufenkji and M. Elimelech, Environ. Sci. Technol., 2004, 38, 529–536 CrossRef CAS PubMed.
- R. Sakthivadivel, Theory and mechanism of filtration of non-colloidal fines through a porous medium, Hydraulic Engineering Lab, University of California Berkeley, 1966 Search PubMed.
- X. Li, T. D. Scheibe and W. P. Johnson, Environ. Sci. Technol., 2004, 38, 5616–5625 CrossRef CAS PubMed.
- S. Xu, B. Gao and J. E. Saiers, Water Resour. Res., 2006, 42, W12S16 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: TEM images; DLVO/XDLVO calculations and parameters; additional transport model equations; DLVO interaction profiles for two nTiO2 particles and for nTiO2-sand grains; BTCs and retention profiles for nTiO2 in the presence of carbomer and 3 mM NaCl. See DOI: 10.1039/c5en00174a |
| ‡ Current address: John and Willie Leone Family Department of Energy and Mineral Engineering and EMS Energy Institute, The Pennsylvania State University, University Park, Pennsylvania 16802, USA. |
| This journal is © The Royal Society of Chemistry 2016 |