 Open Access Article
Open Access ArticleAggregation and sedimentation of magnetite nanoparticle clusters†
P. J.
Vikesland
 *abc,
R. L.
Rebodos
ab,
J. Y.
Bottero
bc,
J.
Rose
bc and
A.
Masion
bc
*abc,
R. L.
Rebodos
ab,
J. Y.
Bottero
bc,
J.
Rose
bc and
A.
Masion
bc
aDepartment of Civil and Environmental Engineering and Institute for Critical Technology and Applied Science (ICTAS), Virginia Tech, Blacksburg, VA, USA. E-mail: pvikes@vt.edu
bCenter for the Environmental Implications of Nanotechnology (CEINT), Duke University, Durham, NC, USA
cInternational Center for the Environmental Implications of Nanotechnology (iCEINT), Aix-en-Provence, France
First published on 24th March 2016
Abstract
Magnetite nanoparticles are redox active constituents of subsurface and corrosive environments. In this study, we characterized the aggregation and sedimentation behavior of well characterized magnetite nanoparticle clusters using dynamic light scattering (DLS), UV-vis-NIR spectroscopy, and small angle X-ray scattering (SAXS). Both unfunctionalized (NaOH-magnetite) and tetramethylammonium hydroxide (TMAOH-magnetite) surface functionalized nanoparticle clusters were employed. TMAOH-magnetite has a slightly smaller primary nanoparticle radius as determined by TEM (4 ± 0.7 nm vs. 5 ± 0.8 for NaOH-magnetite) and a smaller initial DLS determined cluster radius (<30 nm vs. 100–200 nm for NaOH-magnetite). Interestingly, in spite of its smaller initial nanoparticle cluster size, TMAOH-magnetite undergoes sedimentation more rapidly than NaOH-magnetite. This behavior is consistent with the more rapid aggregation of the smaller TMAOH-magnetite clusters as well as their lower fractal dimension, as determined by SAXS. This study illustrates that both nanoparticle cluster size and fractal dimension should be carefully considered when considering the environmental transport and fate of highly aggregated nanoparticles.
Nano impactNanoparticles are often highly aggregated when present in natural water systems. This paper illustrates that the fractal structure of these aggregated (or agglomerated) nanoparticle clusters can affect both cluster–cluster aggregation as well as cluster sedimentation. Using a combination of dynamic light scattering, UV-vis based sedimentation curves, and small angle X-ray scattering we illustrate that cluster size and fractal dimension should be collectively considered when evaluating the fate of highly aggregated nanomaterials. While our study focused explicitly on magnetite nanoparticles, the results are relevant to any other highly aggregated (or agglomerated) system. |
Introduction
The mixed valence iron oxide magnetite (Fe3O4) is commonly found in subsurface and highly corrosive environments.1–5 Over the past fifteen years there has been growing interest in the application of nanoscale magnetite for contaminated groundwater treatment and as a sorbent of metalloid contaminants due to its reductive capacity, high surface area, and superparamagnetic properties.6–12 Magnetite has an inverse spinel crystal structure with a unit cell comprised of 32 O2− anions, 16 Fe3+ cations, and 8 Fe2+ cations. Half of the Fe3+ ions are tetrahedrally (tet) coordinated, while the other half and all of the Fe2+ are octahedrally (oct) coordinated resulting in a (Fe83+)tet(Fe83+Fe82+)octO32 unit cell. The adjacent positioning of Fe3+ and Fe2+ cations in the octahedral layer enables electron hopping due to d orbital overlap between iron atoms.13In aqueous suspensions, magnetite readily aggregates due to a combination of Lifschitz–van der Waals and magnetic forces.6,9,14 The size of these aggregated nanoparticle clusters can be considerable (potentially >1 μm) and thus cluster formation not only affects magnetite transport and delivery, but may also affect reactivity due to the loss of the specific activity of an individual nanoparticle.10,15–18 Aggregation events between individual nanoparticles or between nanoparticle clusters can result either in the formation of irreversibly bound aggregates produced by close contact or in the formation of reversibly bound agglomerates that can be broken by sonication or other mixing processes.19 Whether particles aggregate irreversibly or reversibly is dependent upon the relative magnitudes of the attractive and repulsive forces between the nanoparticles. Because of the challenges associated with experimentally differentiating aggregates from agglomerates and inconsistencies in the literature as to how these terms should be used,20 herein, we refer to irreversibly bound masses of nanoparticles as nanoparticle clusters and the physical process bringing such clusters together as aggregation.
Nanoparticle clusters produced by aggregation processes generally can be considered self-similar fractal structures19,21–23 that can be defined in terms of a fractal dimension (df) that is the power to which the radius of a nanoparticle cluster (R) is raised such that it scales with mass (m):24
| mαRdf | (1) |
The fractal dimension of a cluster can depend on the mechanism by which the aggregation process occurs – namely whether it is diffusion limited cluster aggregation (DLCA) or reaction limited cluster aggregation (RLCA).19,24,25 DLCA or fast aggregation occurs when no net repulsive force is experienced by the particles or clusters. Under these conditions the aggregation rate is solely dependent on the diffusion of the clusters to one another. At high electrolyte concentrations, coagulation in the DLCA regime leads to structures of low fractal dimension (i.e., loose and open aggregates; df ≈ 1.7–1.8).26 For RLCA or slow aggregation, however, additional repulsive forces prevent the clusters from coagulating as readily. The formation of aggregated nanoparticle clusters is therefore dictated by the probability of the clusters adhering to one another. Structures formed by RLCA are more compact and have higher fractal dimensions (df ≈ 2.1–2.2).26 Because of these differences df is often used as a measure to evaluate cluster formation mechanisms.24
Light scattering methods have commonly been used to characterize aggregation processes.27–29 Dynamic light scattering (DLS) is a technique in which temporal fluctuations of scattered light are analyzed to obtain the diffusion coefficient and consequently the hydrodynamic diameter of a given sample. Being a non-invasive technique, DLS was employed herein to characterize the aggregation behavior of magnetite produced both in the presence of tetramethylammonium hydroxide (TMAOH) and in its absence (TMAOH-magnetite and NaOH-magnetite, respectively). An inherent limitation of DLS, however, is that the method requires samples to have low particle concentrations to prevent multiple scattering events from occurring that can lead to inaccurate measurements. Given this restriction, UV-vis-NIR spectroscopy was also utilized to study the aggregation and sedimentation of magnetite at higher particle concentrations. These studies were achieved by monitoring changes in incident light intensity as it passes through a given sample over time. In addition, small angle X-ray scattering (SAXS) was used to probe the smallest nanoparticle sizes as well as the fractal structure of the nanoparticle clusters.
As discussed herein, the aggregation and sedimentation of magnetite clusters was found to be a function of the magnetite surface coating and the fractal dimension of the clusters. This work has relevance not only to studies of magnetite and other iron containing materials, but also any other highly aggregated nanomaterial. As we demonstrate, the fractal dimension of a cluster must be considered when evaluating nanomaterial aggregation and sedimentation in aquatic systems.
Experimental methods
Reagents
Reagent grade chemicals were used without additional purification for all experiments. The following chemicals were used for magnetite synthesis: ferrous chloride tetrahydrate (FeCl2·4H2O; ICN Biomedicals), ferric chloride (FeCl3 anhydrous; Fisher Scientific), sodium hydroxide (NaOH; Fisher Scientific; ≥98.5%), sodium chloride (NaCl; Fisher Scientific), and tetramethylammonium hydroxide pentahydrate (TMAOH·5H2O; Fisher Scientific). All solutions used in the experiments were produced using de-aerated, deionized water (>18.1 MΩ cm) made by boiling for 30 minutes and then sparging with either argon or nitrogen gas for at least 30 minutes while boiling continued. De-aerated water was removed from the heating source, capped, transferred to an anaerobic glovebox (95% N2/5% H2; Coy Laboratory Products) and allowed to cool.Magnetite synthesis
Magnetite nanoparticles were synthesized using a co-precipitation method adapted from Vayssières, et al.30 In brief, in the anaerobic glovebox a mixture of 0.1 M FeCl2 and 0.2 M FeCl3 was added drop-wise (∼1 drop per s) to a well-mixed solution of 1 M NaOH and 1 M NaCl. The final ratio of iron solution to base solution was kept at 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to maintain the pH above 12. Polypropylene containers were used to avoid silicate leaching from glass vessels because of the high pH synthesis conditions. Excess salts were removed by magnetically separating the precipitated nanoparticles and by rinsing with argon-purged, deionized water until the supernatant pH was in the 7–8.5 range. TMAOH functionalized nanoparticles were synthesized using the same co-precipitation method except 1 M TMAOH was used instead of 1 M NaOH. Prepared magnetite stocks were stored in the anaerobic glovebox for periods up to 2 months. The mass concentration of a magnetite stock was gravimetrically determined in triplicate by drying 2 mL of slurry in a 75 °C oven. The final mass of dried sample was converted into an equivalent magnetite mass using the Fe3O4/γ-Fe2O3 gravimetric ratio and assuming 100% conversion of Fe3O4 into γ-Fe2O3.
2 to maintain the pH above 12. Polypropylene containers were used to avoid silicate leaching from glass vessels because of the high pH synthesis conditions. Excess salts were removed by magnetically separating the precipitated nanoparticles and by rinsing with argon-purged, deionized water until the supernatant pH was in the 7–8.5 range. TMAOH functionalized nanoparticles were synthesized using the same co-precipitation method except 1 M TMAOH was used instead of 1 M NaOH. Prepared magnetite stocks were stored in the anaerobic glovebox for periods up to 2 months. The mass concentration of a magnetite stock was gravimetrically determined in triplicate by drying 2 mL of slurry in a 75 °C oven. The final mass of dried sample was converted into an equivalent magnetite mass using the Fe3O4/γ-Fe2O3 gravimetric ratio and assuming 100% conversion of Fe3O4 into γ-Fe2O3.
Characterization of magnetite powders
The morphology and size of nanoparticulate magnetite were characterized using a Philips 420 T TEM operated at 100 keV. Particle slurries were mounted on carbon coated TEM grids (Electron Microscopy Science, Hartfield, PA) and dried in an aerobic environment for a minimum of 48 hours. Collected images were digitally transferred using a slow scan 3086 × 2056 pixel camera. The magnetite particle size was determined by analysis of collected TEM images using the ImageJ software package (NIH, Bethesda, MD). High resolution transmission electron microscope (HRTEM) images were obtained using a FEI Titan scanning/transmission electron microscope (S/TEM) operated at 200 kV. Copper grids (400 mesh) with an ultrathin carbon film on a holey carbon support (Ted Pella, Inc.) were selected for samples investigated with the HRTEM. A representative selection of particle images was obtained from multiple sites on each grid.Small angle X-ray scattering (SAXS)
SAXS experiments were conducted on the ID-02 beamline at the ESRF in Grenoble, France. Collected scattering curves were evaluated to determine both the nanoparticle size as well as the fractal dimension (df) of the magnetite clusters. A q range of 10−0.8–10−2.2 Å−1 was probed with q defined as the wave vector modulus: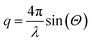 | (2) |
Determination of magnetite cluster–cluster aggregation kinetics
The aggregation behavior of the synthesized magnetite nanoparticle suspensions was studied using an ALV CGS-3 system and established protocols.33,34 This system employs a 22 mW HeNe Laser, an APD-based single photon detector, and an ALV-5000/EPP correlator. The initial size and electrolyte-induced growth of the magnetite clusters were determined by cumulant analysis of dynamic light scattering (DLS) data collected at a 90° scattering angle every 15 seconds for a period of 30–60 minutes.All DLS measurements were conducted at 25 °C and unless otherwise specified at pH = 8.0 ± 0.5. Each sample for analysis was placed in a new prewashed glass vial that was rinsed with filtered (Whatman nylon membrane, 0.2 μm), deionized water prior to the addition of suspension. Stock solutions of NaCl, MgCl2, CaCl2, and FeCl2 were prepared using reagent grade salts and deaerated, deionized water. The solutions were double filtered with 0.1 μm Whatman nylon membrane and Anodisc membrane filters. To determine the effect of each electrolyte on magnetite cluster aggregation, known volumes of salt solution, corresponding to the desired salt concentration, were added to the pre-sonicated suspensions. All vials were vortex mixed for approximately five seconds upon salt addition to ensure adequate mixing.
Determination of magnetite cluster sedimentation rates
Magnetite cluster sedimentation was monitored using a Varian Cary 5000 UV-vis-NIR spectrophotometer. Magnetite suspensions with concentrations ranging from 0.22–22 mM (50–500 mg L−1) were prepared inside the anaerobic glovebox by diluting a sonicated (FS204 Sonicator Bath, Fisher Scientific) magnetite stock. The dilute suspension was then sonicated for an additional 3 minutes prior to transferring a 3 mL aliquot to a quartz cuvette sealed with a rubber septum. Outside the glovebox, a syringe was used to add a given volume of deaerated 0.1 M NaCl to the magnetite suspension to vary ionic strength and induce sedimentation. UV-vis-NIR spectra were periodically obtained between 200 and 1350 nm for periods up to 60 minutes. In some experiments, measurements at 15 second intervals were obtained at a fixed wavelength of 508 nm for periods up to 60 minutes. Baseline corrections employing distilled deionized water were performed prior to sample analysis.Results and discussion
Magnetite primary particle characterization
As shown in Fig. S1† and as described previously,14 analysis of TEM images indicated that NaOH-magnetite has a particle radius of 5.0 ± 0.8 nm, while TMAOH-magnetite is smaller with a particle radius of 4.0 ± 0.7 nm. XRD, FTIR, and Raman measurements confirmed that the particles consist of magnetite/maghemite, and Scherer analyses of the collected X-ray diffractograms were consistent with the relative sizes determined via TEM. FTIR measurements for TMAOH-magnetite indicate that a layer of adsorbed tetramethyl ammonium (TMA+) cations exists at the surface of this nanomaterial. TEM images for NaOH-magnetite (Fig. 1a) and TMAOH-magnetite (Fig. 1b) illustrate the smaller size of TMAOH-magnetite. Furthermore, as shown by the lattice fringing in Fig. 1c, magnetite produced by these procedures is highly crystalline.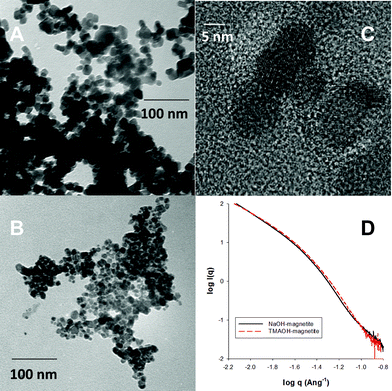 | ||
| Fig. 1 A and B) TEM images of NaOH-magnetite and TMAOH-magnetite, respectively. C) HRTEM image of TMAOH magnetite, D) SAXS characterization of NaOH- and TMAOH-magnetite. | ||
SAXS measurements were conducted to further characterize the primary nanoparticle size. As shown in Fig. 1d, the point at which there is an inflection in the Porod regime indicates a primary particle radius of 2.2 nm for NaOH-magnetite and 2.1 nm for TMAOH-magnetite. These values are smaller than the TEM determined size and we attribute this fact to the presence of small (<3 nm) nanoparticles that are detectable by SAXS, but are at the lower limit of our TEM imaging.
Magnetite cluster characterization
In both the NaOH-magnetite and TMAOH-magnetite suspensions, magnetite is present in the form of clusters of nanoparticles with DLS determined hydrodynamic radii varying from 100–200 to <30 nm, respectively (results not shown). These clusters, which presumably formed during nanomaterial synthesis, were highly resistant to disaggregation via bath sonication or solution agitation. Although the nucleation events leading to nanoparticle formation were rapid enough to ensure a small particle size,30 the high-salt concentration conditions used during synthesis were such that electrical double layer repulsion was minimal and the particles immediately aggregated. Many existing references describing nanoparticle syntheses report cluster sizes that are considerably larger than the nascent nanoparticle size.35The smaller cluster size of TMAOH-magnetite is attributed to the presence of the TMA+ cation at the nanoparticle surface. This surface associated cation electrosterically restricts particle–particle interactions and facilitates nanoparticle dispersion.36 The persistence of the adhered TMA+ layer was found to be a function of the number of wash cycles employed to clean the nanoparticles following synthesis. Sequential wash steps resulted in an increase in the measured hydrodynamic radius for TMAOH-magnetite. Immediately following synthesis, the measured hydrodynamic radius was 18 nm (≈4.5× larger than the TEM determined individual particle radius), but depletion of surface associated TMA+ following four additional wash cycles increased the measured radius to 30 nm (≈7.5× larger than the individual particle radius). As determined via ImageJ analysis of collected TEM images, these sequential washes did not statistically alter the intrinsic nanoparticle diameter (results not shown). In the experiments described herein, at least four wash steps were employed.
The surface charge of the nanomagnetite suspensions was determined as a function of the solution pH. The pHIEP – or the pH where the measured zeta potential of the nanoparticle clusters was zero – was 6.8 ± 0.3 for NaOH-magnetite and 6.6 ± 1.0 for TMAOH-magnetite (Fig. 2a). These values are not statistically different and are within the range of pHIEP values previously reported for magnetite.36,37 Below the pHIEP the surface is positively charged, while above the pHIEP the surface is negatively charged. The slightly lower (but not statistically significant) pHIEP for TMAOH-magnetite is consistent with the presence of adsorbed TMA+ cations at the iron oxide surface. The complexation of organic materials at an oxide surface generally results in a lowering of the measured pHIEP.37
Magnetite has a nondescript UV-vis-NIR spectrum consisting of overlapping absorption bands that are indicative of electronic transitions within the crystalline lattice. These transitions primarily result from 1) FeIII ligand field effects, 2) interactions between magnetically coupled FeIII ions, and 3) ligand (oxygen)–metal charge transfer excitations from the O(2p) non-bonding valence bands to the Fe(3d) ligand field orbitals or possibly between electron donor FeII and electron acceptor FeIII.38 The FeIII ligand field transitions within magnetite primarily result in absorbance between 290–380 nm, while charge transfer transitions are responsible for the majority of the absorption in the visible-region of the spectra.38 Magnetite also has an absorption maximum in the NIR region around 1500 nm due to electron hopping between octahedral FeII and FeIII (i.e., an intervalence charge transfer band [IVCT]).
Fig. 2b exhibits the UV-vis-NIR extinction (= absorption + scattering) spectra for NaOH-magnetite and TMAOH-magnetite. TMAOH-magnetite has higher extinction in the UV region than NaOH-magnetite, while in the near-IR it is lower. The former effect is attributed to the absorbance of the TMA+ cations (Fig. 2b inset), while the latter could be the result of the decreased particle size for TMAOH-magnetite or to its smaller cluster size. Each of these possibilities would result in less light extinction for a given mass of particles. Two extinction maxima in the magnetite spectrum exist over this wavelength range – one centered at 380 nm corresponding to FeIII ligand field transitions and another at λ > 1320 nm that corresponds to the IVCT band.39
During storage the magnetite stock suspensions, particularly NaOH-magnetite, aggregate significantly. To breakup these agglomerates and attain a stable initial cluster size the experimental solutions were bath sonicated prior to each experiment. As shown in Fig. S2 in the ESI,† the initial absorbance at 508 nm of a magnetite suspension varies with both the sonication time and the particle concentration. Based upon these results, a presonication period of three minutes was chosen for all experiments described herein.
Collected SAXS scattering curves were analyzed and fit to determine a df of 1.88 ± 0.10 for NaOH-magnetite and a df of 1.79 ± 0.09 for TMAOH-magnetite. The lower df for TMAOH-magnetite indicates that the TMAOH-magnetite clusters exhibit a less densely packed structure, while NaOH-magnetite is more tightly packed. Both values indicate that these clusters formed via DLCA.
Magnetite cluster–cluster aggregation
We evaluated the aggregation behavior of our magnetite clusters as dictated by solution pH and the presence of electrolytes. Cluster–cluster aggregation led to an increase in hydrodynamic radius that was quantified using DLS. | (3) |
 | (4) |
After applying eqn (4) to our collected DLS data we plotted the stability ratio for NaOH-magnetite and TMAOH-magnetite versus salt concentration for three different salts (NaCl, MgCl2, and CaCl2) in Fig. 4a. As shown, the calculated stability ratios decrease with an increase in salt concentration up to a limiting value of 1. At salt levels in excess of this concentration, aggregation is limited only by diffusion since the repulsive electrostatic energy barrier is diminished and further addition of salt no longer affects the aggregation rate. The salt concentration where this transition occurs is the critical coagulation concentration (CCC) and was experimentally determined by extrapolating the measured stability ratios at low salt concentrations to a value of 1. Using this approach, we determined approximate CCC values for our NaOH-magnetite clusters of: NaCl = 8 mM, MgCl2 = 0.3 mM, and CaCl2 = 0.2 mM. For the TMAOH-magnetite clusters the approximate CCC for NaCl was 5 mM. For NaOH-magnetite the difference between the results obtained with the monovalent and divalent cations is consistent with past reports and with the empirical Shulze–Hardy rule that predicts the CCC should scale with the sixth power of the valence.24 The difference in CCC values for CaCl2vs. MgCl2 is not statistically significant, but the data consistently show that NaOH-magnetite aggregates more rapidly in the presence of Ca2+ than at a comparable concentration of Mg2+. Stankus et al.43 recently reported that Ca2+ is more effective than Mg2+ at inducing aggregation of negatively charged AuNP, and they attributed this result to the fact that Ca2+ (electronegativity = 1.00 Pauling units) is slightly more electropositive than Mg2+ (1.31 Pauling units).
The most striking result presented in Fig. 4a is the lower observed CCC for TMAOH-magnetite than for NaOH-magnetite. Such a result is somewhat misleading, however, due to the smaller initial cluster size for TMAOH-magnetite than NaOH-magnetite. A smaller size cluster can be expected to aggregate more rapidly due to its higher overall rate of diffusion (which is inversely correlated to the cluster size). To illustrate the effects of salt on cluster size we present in Fig. 4b the measured cluster radius at t = 15 s (i.e., the first DLS measurement obtained after salt addition). As shown, the TMAOH clusters are consistently smaller than those for NaOH-magnetite at similar salt concentrations.
It is possible to define the minimum salt concentration required to initiate cluster growth. As shown, in Fig. 4b (t = 15 s) and Fig. S4† (for t = 60, 90, 120 s), for NaOH-magnetite this condition occurs at salt concentrations of 4 mM NaCl, 0.08 mM CaCl2, and 0.14 mM MgCl2. For TMAOH-magnetite no minimum salt concentration could be defined over the NaCl range investigated, thus suggesting that cluster growth occurs at values below 1 mM. As expected, the concentrations at which cluster growth occurs are consistently lower than the measured CCC values.
Magnetite cluster sedimentation
An inherent problem with DLS is that the method requires low particle concentrations to prevent multiple scattering events that lead to inaccurate light scattering measurements. Given this limitation, we examined the aggregation and sedimentation behavior of magnetite at higher nanoparticle concentrations by monitoring changes in optical absorbance as a function of time using UV-vis-NIR spectroscopy. Coagulation and sedimentation of the NaOH-magnetite and TMAOH-magnetite clusters was initiated by NaCl addition. Representative sets of sedimentation spectra are shown in Fig. 5. These spectra, obtained for NaOH-magnetite at a concentration of 0.864 mM (200 mg L−1), illustrate that NaCl addition initiates the aggregation and sedimentation of the magnetite clusters. To probe magnetite sedimentation in greater temporal detail than enabled by full spectral monitoring we conducted a comprehensive series of experiments in which we monitored changes in absorbance at 508 nm over time. We selected this value for consistency with the literature7 as well as the fact that the absorbance at this wavelength is not affected by the magnetite oxidation state. As documented previously, changes in oxidation state primarily affect the NIR portion of the UV-vis-NIR spectrum.39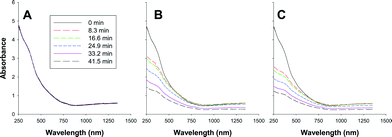 | ||
| Fig. 5 Collected sedimentation curves for 0.864 mM NaOH-magnetite. A) No salt addition, B) 10 mM NaCl, C) 20 mM NaCl. | ||
The addition of salt at concentrations ranging from 2 to 20 mM caused a measurable decrease in absorption at 508 nm for both NaOH-magnetite (Fig. 6a) and TMAOH-magnetite (Fig. 6b). The detrimental effect of salt addition on the colloidal stability of magnetite was expected since an increase in the ionic strength of the solution lowers the repulsive electrostatic barrier and enables rapid coagulation. Relative to the salt-free suspension, the observed sedimentation kinetics were enhanced upon addition of ≥2 mM salt; however, there was no discernable trend observed in the sedimentation curves for salt concentrations between 2 and 20 mM (data not shown). This effect was surprising since we previously had shown using DLS (Fig. 4a) that the NaCl CCC for NaOH-magnetite was 8 mM and thus we had anticipated that there would be differences in the sedimentation curves obtained below the CCC (RLCA conditions) relative to those obtained above the CCC (DLCA conditions). It is possible that the higher magnetite concentrations used in the sedimentation studies may have masked the salt effects due to the higher mass loading. It would be expected, however, that the CCC should be invariant with changes in the mass load since it is defined as the point where the salt concentration exceeds that required to eliminate electrostatic repulsion between two interacting objects.
The collected sedimentation curves can be subdivided into three regions that are demarcated by changes in slope (Fig. S6†).7 The first region (aggregation I) corresponds to the initial coagulation of the magnetite clusters. In this region, the clusters are coagulating, but have not reached the critical size needed to initiate rapid sedimentation. Once the critical size is reached, at time tcrit1, sedimentation occurs rapidly (sedimentation I). The kinetics of sedimentation are determined by calculating the slope of the collected results over this period. For some suspensions, particularly those with high salt and mass concentrations, a third region with a slower sedimentation rate can be observed (sedimentation II). This region, initiated at time tcrit2, has previously been interpreted as the sedimentation of clusters that failed to attain critical size.
As shown in Fig. 6 and summarized in Table S1,† changes in magnetite concentration systematically altered the measured rates of aggregation and sedimentation. Sedimentation experiments were performed using magnetite suspensions with concentrations ranging from 0.22–2.2 mM (50–500 mg L−1) and NaCl concentrations ranging from 0–30 mM. The apparent aggregation rates were obtained by determining the slope of the change in absorbance measured at 508 nm, over time up to tcrit1.
A direct relationship between particle concentration and aggregation rate is shown in Fig. 7a and b. As shown, the effect of particle concentration was significant for each tested salt concentration and, as noted previously, there was little difference in the aggregation kinetics measured for 10–30 mM NaCl.
At the lowest mass concentrations tested (0.22 and 0.43 mM), TMAOH-magnetite clusters aggregate more rapidly than NaOH-magnetite, as evinced by their relative kagg values, while at the higher mass concentrations (0.86 and 1.3 mM), the opposite is true. The former result is consistent with the DLS results presented in Fig. 4a that suggested that TMAOH-magnetite aggregates more rapidly, while the latter result is inconsistent with the DLS results. For low magnetite concentrations the TMAOH-magnetite clusters aggregate more quickly and reach the critical size required to initiate settling more rapidly. To illustrate this effect, we plotted the variation in tcrit1 as a function of the magnetite concentration (Fig. S7†). As illustrated, TMAOH-magnetite consistently has a lower tcrit1 value than NaOH-magnetite. Furthermore, for both NaOH-magnetite and TMAOH-magnetite higher initial concentrations require increasingly shorter aggregation times to reach the critical size required for settling. The tcrit1 values appear to plateau at high magnetite concentrations, thereby suggesting that above a certain mass concentration, cluster sedimentation is initiated at a fixed point in time. As shown in Fig. S7,† such a plateau is consistent with the experimental results of Phenrat et al.7
For a given mass concentration, the measured rate constants (kSED1) for the settling of TMAOH-magnetite during the sedimentation I period are generally higher than those for NaOH-magnetite. Such a result, and the observed trends in the aggregation rates, are consistent with the lower fractal dimension of the TMAOH-magnetite clusters. In the following section we examine how the different df values for NaOH-magnetite and TMAOH-magnetite alter their respective sedimentation rates.
Mathematical evaluation of cluster sedimentation
Based upon the fractal dimension it is possible to estimate the expected settling velocity (u*) for a fractal cluster. This can be done using a modified form of Stokes law:22,48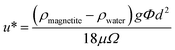 | (5) |
 | (6) |
 | (7) |
For this effort, we estimated the cluster permeability (K) using the Happel cell model:
 | (8) |
 | (9) |
We note that the simple model defined by eqn (5)–(9) provides insight into how the fractal dimension of a nanoparticle cluster affects its settling rate, but does not consider the complicating effects of cluster restructuring48 that are expected to occur during aggregation and/or sedimentation. Such restructuring would alter the fractal dimension and thus the dynamics of nanoparticle cluster settling may be considerably more complex than illustrated herein. Therefore for this reason, we refrain from making direct comparison of our experimental and model results. Collectively, however, the experimental and model results shown here clearly indicate the important, yet often overlooked role of fractal dimension in nanoparticle aggregation and settling.
Conclusions
Following salt addition, and in the absence of stabilizers, magnetite clusters aggregate and readily settle out of suspension. The rates of aggregation and sedimentation are dependent on particle concentration and aqueous conditions such as pH and ionic strength. These factors have historically been considered to be the primary ones that dictate the fate of magnetite and other nanoparticles in natural and engineered systems. As documented, herein, however the fractal dimension of the aggregating and sedimenting clusters must also be considered. As shown, simple measurements of nanoparticle aggregation are insufficient to predict removal rates for suspended nanoparticles. A combination of aggregation, sedimentation, and fractal dimension measurements are collectively required to enable accurate predictions of nanoparticle fate.Acknowledgements
This material is based upon work supported by the National Science Foundation (NSF) and the Environmental Protection Agency (EPA) under NSF Cooperative Agreement EF-0830093, Center of the Environmental Implications of NanoTechnology (CEINT). Any opinions, findings, conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the NSF or the EPA. This work has not been subjected to EPA review and no official endorsement should be inferred. Additional funding was provided by the National Science Foundation (CBET-0537117) and the Labex Serenade (no ANR-11-LABX-0064) funded by the “Investissements d'Avenir” French Government program of the French National Research Agency (ANR) through the A*MIDEX project (no ANR-11-\-02).References
- A. F. White, M. L. Peterson and M. F. Hochella, Electrochemistry and dissolution kinetics of magnetite and ilmenite, Geochim. Cosmochim. Acta, 1994, 58(8), 1859–1875 CrossRef CAS.
- A. F. White and M. L. Peterson, Reduction of aqueous transition metal species on the surfaces of Fe(II)-containing oxides, Geochim. Cosmochim. Acta, 1996, 60(20), 3799–3814 CrossRef CAS.
- T. Kohn, K. J. T. Livi, A. L. Roberts and P. J. Vikesland, Longevity of granular iron in groundwater treatment processes: Corrosion product development, Environ. Sci. Technol., 2005, 39(8), 2867–2879 CrossRef CAS PubMed.
- S. Glasauer, S. Langley and T. J. Beveridge, Intracellular iron minerals in a dissimilatory iron-reducing bacterium, Science, 2002, 295(5552), 117–119 CrossRef CAS PubMed.
- D. R. Lovley and E. J. P. Phillips, Novel mode of microbial energy metabolism - organic-carbon oxidation coupled to dissimilatory reduction of iron or manganese, Appl. Environ. Microbiol., 1988, 54(6), 1472–1480 CAS.
- I. Medvedeva, Y. Bakhteeva, S. Zhakov, A. Revvo, I. Byzov, M. Uimin, A. Yermakov and A. Mysik, Sedimentation and aggregation of magnetite nanoparticles in water by a gradient magnetic field, J. Nanopart. Res., 2013, 15(11) DOI:10.1007/s11051-013-2054-y.
- T. Phenrat, N. Saleh, K. Sirk, R. D. Tilton and G. V. Lowry, Aggregation and sedimentation of aqueous nanoscale zerovalent iron dispersions, Environ. Sci. Technol., 2007, 41(1), 284–290 CrossRef CAS PubMed.
- N. Savage and M. S. Diallo, Nanomaterials and water purification: Opportunities and challenges, J. Nanopart. Res., 2005, 7(4–5), 331–342 CrossRef CAS.
- S. C. N. Tang and I. M. C. Lo, Magnetic nanoparticles: Essential factors for sustainable environmental applications, Water Res., 2013, 47(8), 2613–2632 CrossRef CAS PubMed.
- P. J. Vikesland, A. M. Heathcock, R. L. Rebodos and K. E. Makus, Particle size and aggregation effects on magnetite reactivity toward carbon tetrachloride, Environ. Sci. Technol., 2007, 41(15), 5277–5283 CrossRef CAS PubMed.
- W. Yantasee, C. L. Warner, T. Sangvanich, R. S. Addleman, T. G. Carter, R. J. Wiacek, G. E. Fryxell, C. Timchalk and M. G. Warner, Removal of heavy metals from aqueous systems with thiol functionalized superparamagnetic nanoparticles, Environ. Sci. Technol., 2007, 41(14), 5114–5119 CrossRef CAS PubMed.
- C. T. Yavuz, J. T. Mayo, W. W. Yu, A. Prakash, J. C. Falkner, S. Yean, L. Cong, H. J. Shipley, A. Kan, M. Tomson, D. Natelson and V. L. Colvin, Low-field magnetic separation of monodisperse Fe3O4 nanocrystals, Science, 2006, 314(5801), 964–967 CrossRef PubMed.
- M. L. McCormick, E. J. Bouwer and P. Adriaens, Carbon tetrachloride transformation in a model iron-reducing culture: Relative kinetics of biotic and abiotic reactions, Environ. Sci. Technol., 2002, 36(3), 403–410 CrossRef CAS PubMed.
- R. L. Rebodos and P. J. Vikesland, Effects of oxidation on the magnetization of nanoparticulate magnetite, Langmuir, 2010, 26(22), 16745–16753 CrossRef CAS PubMed.
- Y. Lu, Y. D. Yin, B. T. Mayers and Y. N. Xia, Modifying the surface properties of superparamagnetic iron oxide nanoparticles through a sol–gel approach, Nano Lett., 2002, 2(3), 183–186 CrossRef CAS.
- L. A. Harris, J. D. Goff, A. Y. Carmichael, J. S. Riffle, J. J. Harburn, T. G. St Pierre and M. Saunders, Magnetite nanoparticle dispersions stabilized with triblock copolymers, Chem. Mater., 2003, 15(6), 1367–1377 CrossRef CAS.
- C. T. Yavuz, J. T. Mayo, S. Yean, L. Cong, W. Yu, J. Falkner, A. Kan, M. Tomson and V. L. Colvin, in Particle size dependence of nano-magnetite in arsenic removal, ed. F. Kongoli and R. G. Reddy, Sohn International Symposium on Advanced Processing of Metals and Materials, San Diego, CA, Aug 27–31, 2006 Search PubMed; C. T. Yavuz, J. T. Mayo, S. Yean, L. Cong, W. Yu, J. Falkner, A. Kan, M. Tomson and V. L. Colvin, in Particle size dependence of nano-magnetite in arsenic removal, ed. F. Kongoli and R. G. Reddy, Minerals, Metals & Materials Soc, San Diego, CA, 2006, pp. 221–228 Search PubMed.
- G. Rubasinghege, R. W. Lentz, H. Park, M. M. Scherer and V. H. Grassian, Nanorod dissolution quenched in the aggregated state, Langmuir, 2010, 26(3), 1524–1527 CrossRef CAS PubMed.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Universality in colloid aggregation, Nature, 1989, 339(6223), 360–362 CrossRef CAS.
- G. Nichols, S. Byard, M. J. Bloxham, J. Botterill, N. J. Dawson, A. Dennis, V. Diart, N. C. North and J. D. Sherwood, A review of the terms agglomerate and aggregate with a recommendation for nomenclature used in powder and particle characterization, J. Pharm. Sci., 2002, 91(10), 2103–2109 CrossRef CAS PubMed.
- B. E. Logan and J. R. Kilps, Fractal dimensions of aggregates formed in different fluid mechanical environments, Water Res., 1995, 29(2), 443–453 CrossRef CAS.
- X. Y. Li and B. E. Logan, Collision frequencies of fractal aggregates with small particles by differential sedimentation, Environ. Sci. Technol., 1997, 31(4), 1229–1236 CrossRef CAS.
- P. Meakin, Fractal aggregates, Adv. Colloid Interface Sci., 1987, 28, 249–331 CrossRef.
- P. C. Hiemenz, Principles of colloid and surface chemistry, Marcel Dekker Inc., New York, New York, 3rd edn, 1997 Search PubMed.
- P. Sandkuhler, M. Lattuada, H. Wu, J. Sefcik and M. Morbidelli, Further insights into the universality of colloidal aggregation, Adv. Colloid Interface Sci., 2005, 113(2–3), 65–83 CrossRef PubMed.
- M. Berka and J. A. Rice, Relation between aggregation kinetics and the structure of kaolinite aggregates, Langmuir, 2005, 21(4), 1223–1229 CrossRef CAS PubMed.
- S. E. Mylon, K. L. Chen and M. Elimelech, Influence of natural organic matter and ionic composition on the kinetics and structure of hematite colloid aggregation: Implications to iron depletion in estuaries, Langmuir, 2004, 20(21), 9000–9006 CrossRef CAS PubMed.
- B. A. Chambers, A. Afrooz, S. Bae, N. Aich, L. Katz, N. B. Saleh and M. J. Kirisits, Effects of chloride and ionic strength on physical morphology, dissolution, and bacterial toxicity of silver nanoparticles, Environ. Sci. Technol., 2014, 48(1), 761–769 CrossRef CAS PubMed.
- R. Pamies, J. G. H. Cifre, V. F. Espin, M. Collado-Gonzalez, F. G. D. Banos and J. G. de la Torre, Aggregation behaviour of gold nanoparticles in saline aqueous media, J. Nanopart. Res., 2014, 16(4) DOI:10.1007/s11051-014-2376-4.
- L. Vayssières, C. Chaneac, E. Tronc and J. P. Jolivet, Size tailoring of magnetite particles formed by aqueous precipitation: An example of thermodynamic stability of nanometric oxide particles, J. Colloid Interface Sci., 1998, 205(2), 205–212 CrossRef PubMed.
- A. Masion, D. Tchoubar, J. Y. Bottero, F. Thomas and F. Villieras, Chemistry and structure of Al(OH)/organic precipitates - a small-angle x-ray-scattering study. 1. Numerical procedure for speciation from scattering curves, Langmuir, 1994, 10(11), 4344–4348 CrossRef CAS.
- A. Masion, J. Y. Bottero, F. Thomas and D. Tchoubar, Chemistry and structure of Al(OH)/organic precipitates - a small-angle x-ray-scattering study. 2. Speciation and structure of the aggregates, Langmuir, 1994, 10(11), 4349–4352 CrossRef CAS.
- A. Afrooz, I. A. Khan, S. M. Hussain and N. B. Saleh, Mechanistic heteroaggregation of gold nanoparticles in a wide range of solution chemistry, Environ. Sci. Technol., 2013, 47(4), 1853–1860 CrossRef CAS PubMed.
- I. A. Khan, A. Afrooz, J. R. V. Flora, P. A. Schierz, P. L. Ferguson, T. Sabo-Attwood and N. B. Saleh, Chirality affects aggregation kinetics of single-walled carbon nanotubes, Environ. Sci. Technol., 2013, 47(4), 1844–1852 CrossRef CAS PubMed.
- A. R. Petosa, D. P. Jaisi, I. R. Quevedo, M. Elimelech and N. Tufenkji, Aggregation and deposition of engineered nanomaterials in aquatic environments: Role of physicochemical interactions, Environ. Sci. Technol., 2010, 44(17), 6532–6549 CrossRef CAS PubMed.
- S. C. Pang, S. F. Chin and M. A. Anderson, Redox equilibria of iron oxides in aqueous-based magnetite dispersions: Effect of pH and redox potential, J. Colloid Interface Sci., 2007, 311(1), 94–101 CrossRef CAS PubMed.
- U. Schwertmann and R. M. Cornell,in The iron oxides: Structure, properties, reactions, occurrence and uses, VCH, Weinheim, Germany, 1996 Search PubMed.
- R. M. Cornell and U. S. Schwertmann, The iron oxides structure, properties, reactions, occurrences and uses, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2nd edn, 2003, p. 664 Search PubMed.
- J. Tang, M. Myers, K. A. Bosnick and L. E. Brus, Magnetite Fe3O4 nanocrystals: Spectroscopic observation of aqueous oxidation kinetics, J. Phys. Chem. B, 2003, 107(30), 7501–7506 CrossRef CAS.
- K. L. Chen, S. E. Mylon and M. Elimelech, Enhanced aggregation of alginate-coated iron oxide (hematite) nanoparticles in the presence of calcium, strontium, and barium cations, Langmuir, 2007, 23(11), 5920–5928 CrossRef CAS PubMed.
- R. A. French, A. R. Jacobson, B. Kim, S. L. Isley, R. L. Penn and P. C. Baveye, Influence of ionic strength, pH, and cation valence on aggregation kinetics of titanium dioxide nanoparticles, Environ. Sci. Technol., 2009, 43(5), 1354–1359 CrossRef CAS PubMed.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Particle deposition and aggregation: Measurment, modelling and simulation, Butterworth-Heinemann, Woburn, MA, 1995 Search PubMed.
- D. Stankus, S. Lohse, J. Hutchison and J. Nason, Interactions between natural organic matter and gold nanoparticles stabilized with different organic capping agents, Environ. Sci. Technol., 2010, 45, 3238–3244 CrossRef PubMed.
- C. A. Gorski, J. T. Nurmi, P. G. Tratnyek, T. B. Hofstetter and M. M. Scherer, Redox behavior of magnetite: Implications for contaminant reduction, Environ. Sci. Technol., 2010, 44(1), 55–60 CrossRef CAS PubMed.
- C. A. Gorski and M. M. Scherer, Influence of magnetite stoichiometry on fe-ii uptake and nitrobenzene reduction, Environ. Sci. Technol., 2009, 43(10), 3675–3680 CrossRef CAS PubMed.
- D. E. Latta, C. A. Gorski, M. I. Boyanov, E. J. O'Loughlin, K. M. Kemner and M. M. Scherer, Influence of magnetite stoichiometry on UVI reduction, Environ. Sci. Technol., 2012, 46(2), 778–786 CrossRef CAS PubMed.
- T. S. Pasakarnis, M. I. Boyanov, K. M. Kemner, B. Mishra, E. J. O'Loughlin, G. Parkin and M. M. Scherer, Influence of chloride and Fe(II) content on the reduction of Hg(II) by magnetite, Environ. Sci. Technol., 2013, 47(13), 6987–6994 CrossRef CAS PubMed.
- A. Thill, S. Moustier, J. Aziz, M. R. Wiesner and J. Y. Bottero, Flocs restructuring during aggregation: Experimental evidence and numerical simulation, J. Colloid Interface Sci., 2001, 243(1), 171–182 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. Nanoparticle concentration calculations; additional figures and summary tables. See DOI: 10.1039/c5en00155b |
| This journal is © The Royal Society of Chemistry 2016 |






