Economically sustainable scaling of photovoltaics to meet climate targets

Abstract

To meet climate targets, power generation capacity from photovoltaics (PV) in 2030 will have to be much greater than is predicted from either steady state growth using today's manufacturing capacity or industry roadmaps. Analysis of whether current technology can scale, in an economically sustainable way, to sufficient levels to meet these targets has not yet been undertaken, nor have tools to perform this analysis been presented. Here, we use bottom-up cost modeling to predict cumulative capacity as a function of technological and economic variables. We find that today’s technology falls short in two ways: profits are too small relative to upfront factory costs to grow manufacturing capacity rapidly enough to meet climate targets, and costs are too high to generate enough demand to meet climate targets. We show that decreasing the capital intensity (capex) of PV manufacturing to increase manufacturing capacity and effectively reducing cost (e.g., through higher efficiency) to increase demand are the most effective and least risky ways to address these barriers to scale. We also assess the effects of variations in demand due to hard-to-predict factors, like public policy, on the necessary reductions in cost. Finally, we review examples of redundant technology pathways for crystalline silicon PV to achieve the necessary innovations in capex, performance, and price.

---

Broader context

To reduce CO₂ emissions enough over the next fifteen years and avoid the worst effects of climate change will require dramatic increases in the deployment of renewable energy, photovoltaics (PV) in particular. Climate action plans call for 2–10 terawatts (TW) of PV by 2030. Current manufacturing capacity could supply enough for 1 TW of cumulative installations at the end of this period, implying that growth in manufacturing capacity is necessary. Industry roadmaps project up to 2.6 TW but largely fail to assess whether these targets are economically feasible with today’s PV module technology. Addressing the question of what technological innovations, if any, would enable rapid manufacturing scale-up requires a conceptual advance in modeling methodology. We address this challenge by coupling three industry-validated models: a bottom-up cost model, an economically sustainable growth-rate calculator, and a constraining demand curve. This approach enables us to determine the sensitivity of PV industry growth to specific technological and economic variables, considering both their effect on the ratio of up-front factory costs to revenue and demand as a function of PV module price. Shifting the demand curve enables us to consider the effects of different policy decisions, like a carbon tax or deployment subsidies.

1. Climate-driven deployment targets for photovoltaics

Recent studies show that carbon dioxide (CO₂) emissions must peak in the next fifteen years to ensure a high probability of limiting average global warming to less than 1.5–2 °C above pre-industrial levels^1–5 and thereby avoid the worst effects of climate change. As global energy demand is expected to rise significantly over the same period,^1–2,6 achieving this goal will require the deployment of terawatts of new low-carbon energy generation, compared with less than 1 TW of non-hydro renewables today.

Photovoltaics (PV) have several advantages compared with other low-carbon technologies: the vast size of the solar resource,^6,7 the proven track record of reliability^8–10 and bankability¹¹ of PV installations, the rapidity with which new manufacturing capacity can be brought online and projects developed and built,¹² and their modular nature, which allows deployment in areas that may lack electric grid infrastructure. Concordantly, aggressive PV deployment targets, ranging from 2–10 TW by 2030, are widely viewed as vital to mitigate climate change (Fig. 1, green symbols/line).^1,2,13–15 We consider a range of climate and CO₂ reduction scenarios, which results in a range of PV deployment targets. The high end provides the lowest risk to the climate.

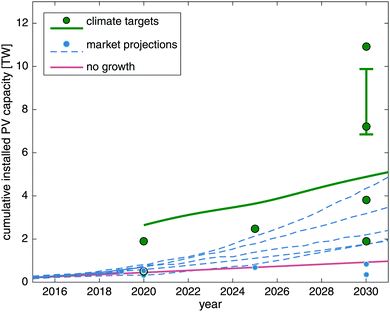Fig. 1 PV deployment targets consistent with average warming less than 2 °C above pre-industrial levels (green symbols and line), industry projections of PV deployment (blue symbols and lines), and upper bound of future installations with no additional manufacturing capacity (pink line). If data was represented as lines in the source, it is represented as lines here. If it was reported as individual data points in the source, it is represented by symbols here. Sources for specific data can be found in ESI,† Fig. S1.

Future deployment of PV depends on a number of factors. We will focus this discussion on the upper bound imposed by one technical constraint, the annual manufacturing capacity for PV modules, and one market constraint, total demand for PV. Manufacturing capacity limits annual installed capacity, which in turn limits cumulative installed capacity each year. Demand for PV modules has a strong dependence on public policy and the cost of competing (e.g., fossil fuel) and supporting (e.g., balance-of-systems, energy storage) technologies. However, under a given set of assumptions about the economic and technology environment, total demand can be given as a function of PV module price. This relationship is called a demand curve.

As shown by the pink curve in Fig. 1, current PV manufacturing capacity¹⁶ is sufficient to produce just under 1 TW in the next 15 years. Thus, growth in manufacturing capacity‡ is needed to meet climate-driven deployment targets. According to market research,¹⁶ under the current cost structure for PV modules, total demand would be less than 1 TW even if their price was equal to their variable cost of production.

Several PV industry projections^15,17–26 (Fig. 1, blue symbols/lines) predict deployment comparable to some climate-driven targets. The most aggressive projections fall well short of targets that minimize climate risks, but even these projections imply significant growth in manufacturing capacity and easing of demand constraints. However, most publicly available projections do not establish whether current technology can reach these targets and fail to identify effective pathways to achieve the necessary manufacturing capacity and demand.

In this work, we use bottom-up cost modeling to determine (1) if current crystalline silicon PV module technology can achieve growth rates commensurate with climate targets without external financial support and (2) what innovation-driven cost reductions are needed for sufficient demand to achieve these targets. We find that dramatic reductions in the capital intensity and cost of PV module manufacturing are needed. The technology pathways we identify to achieve these goals are also likely to greatly reduce the energy and CO₂ payback times for PV modules.²⁷

2. PV manufacturing cost and growth models

Our cost model,§ ^28,29 presented schematically in Fig. 2, produces a discounted cash flow for a hypothetical PV manufacturer by summing the individual cost components of the manufacturing process and subtracting these from revenues and financing. In simple terms, the “cash in” variables are (1) net revenues from PV module sales, expressed per unit as operating margin (margin), and (2) debt financing. Because debt typically leverages equity within the company, we use the variable debt/equity ratio, which we hold constant over time.

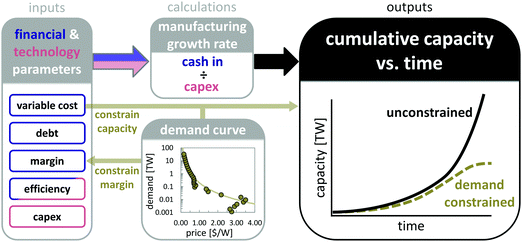Fig. 2 Schematic of our model to calculate economically sustainable growth rate, constrained by power law fit to a market-driven demand curve,¹⁶ to predict cumulative capacity.

The “cash out” variables (before taxes and interest on debt are paid) are the fixed costs of new factories and equipment (expressed as capex) and the variable costs of production. Because we are interested in the cost per unit power, not per panel, we divide both fixed and variable costs by the power produced by the module. We use efficiency as a proxy variable for module power, dollars per watt as the unit of cost, and dollars per watt of installed annual capacity as the unit of capex.^28,70 To estimate an upper bound for manufacturing capacity growth rate, we assume that no dividends are paid and all profits (after taxes and interest on debt) are reinvested in expansion.²⁸

The ratio of “cash in” (margin and debt) to capex determines how quickly new factories can be built and therefore how quickly PV manufacturing capacity can grow. Thus, increases in “cash in” or decreases in capex increase growth rate. To set an upper bound on cumulative installed capacity, we assume 100% utilization of manufacturing capacity. Because we consider a 15-year time horizon while PV panels typically last at least 20 years, we further assume no replacement. Therefore, cumulative installed capacity is just the sum of the previous year’s cumulative capacity and the manufacturing capacity in the current year. Manufacturing capacity in the current year is manufacturing capacity in the previous year times one plus the growth rate.

The growth rate calculator begins by assuming a constant margin. The product of this margin and the sum of fixed and variable costs sets a selling price. If cumulative capacity exceeds demand at this price, the calculator takes the price corresponding to this capacity on the demand curve, and uses the (lower) margin implied by this price. This reduced margin limits growth. If price falls below variable cost, production ceases altogether. For this work, we use a power law fit to a demand curve from ref. 16 containing historical data on PV module sales and projected demand as a function of price (see Fig. 2). We fit the data because the historical data is not single-valued. For more details on these variables, calculations, and the demand curve, see ESI† and ref. 29.

We perform a sensitivity analysis on each of the variables in our cash flow to discern which have the greatest potential to increase growth rate and ease the demand constraint. For our baseline calculation, around which we vary these parameters, we use current industry data for variable costs, capex, and efficiency, set margin such that the net profit is equal to the cost of capital,³⁰ and use a debt/equity ratio of 1 : 1. These baseline parameters are listed in Table S1 in the ESI,† and details of how they were selected are in ESI† and ref. 28 and 29.

We model crystalline silicon because it represents over 90% of the PV market,³¹ has dominated for decades,³² has a large existing manufacturing base, is sufficiently abundant to scale to tens of terawatts,³³ and reliable cost data is available. However, our sustainable growth modeling methodology, and therefore the capex and cost implications, could apply to any technology. This includes commercially available thin-film technologies like cadmium telluride and copper (indium, gallium) diselenide, if they are not limited by the availability of Te and In.^14,34,35 Given the aggressive capex, variable cost, and efficiency improvements demanded by the advanced scenario, non-silicon technologies have the challenge of scaling from a lower baseline, but an opportunity to gain market share through significantly higher margins and lower capex; further discussion is provided in ESI.†

3. Sensitivity analysis of cost and growth model variables

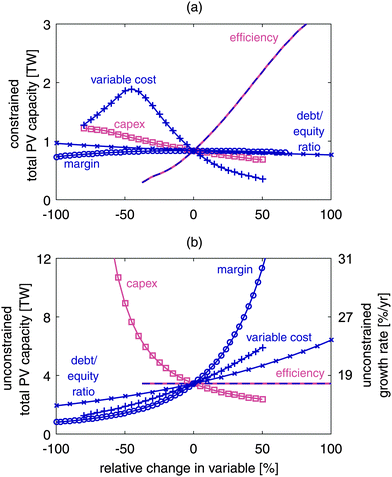
Results from the baseline scenario (the point of intersection of the curves in Fig. 3) show that growth rate must be increased while costs are decreased to reach aggressive deployment targets. As stated above, the baseline scenario is limited by demand to less than 1 TW in 2030 (Fig. 3a), but even without demand constraints, manufacturing growth would limit cumulative installed capacity to 3.4 TW (Fig. 3b).

Fig. 3 (a) Demand-constrained cumulative installed capacity in 2030 as a function of capex, module efficiency, margin, variable costs, and debt/equity ratio. (b) Unconstrained cumulative installed capacity in 2030 as a function of the same variables. This capacity depends only on growth rate (right axis). Each parameter is varied independently and reported as a fractional increase or decrease from the baseline scenario.

Fig. 3a shows the demand-constrained cumulative installed capacity in 2030 for a range of values, varying each parameter independently. The left axis in Fig. 3b shows the unconstrained installed PV capacity in 2030, which depends only on the growth rate. The right axis in Fig. 3b shows the corresponding growth rates.

This sensitivity analysis shows that three of our variables (margin, debt/equity ratio, and capex) can increase growth rate but have little potential to reduce cost and increase demand, while the other two (variable costs and efficiency) can reduce cost but have little potential to increase growth rate.

Increasing margin increases growth rate by increasing revenue from sales (a major component of “cash in”). However, PV modules have become a commodity with little product differentiation. Module manufacturers are therefore price-takers with little ability to impact margin,^36,37 and we see little practical opportunity to increase growth rate by increasing margins.

Increased debt without significant reductions in cost will increase growth temporarily. Ultimately, however, once the demand ceiling is reached, margin will be eroded, leading to reduced revenue, reduced growth and lower total installed capacity. The increased debt approach is therefore risky for manufacturers. Increased debt is also a weaker lever on growth than reducing capex, which reduces the cost for a new factory. Assuming constant “cash in,” reduced capex increases the rate at which new factories can be built and manufacturing capacity added.

In our growth model, the only positive effect reducing variable cost has on installed capacity is triggering a reduction of price due to the assumption of constant margin. We assume margins are constant because technology diffusion and the treatment of PV modules as a commodity by consumers and installers drive down prices in response to reduced variable costs. Lower prices mean lower revenue (“cash in”). At constant capex, that means slower growth. Therefore, while reducing variable costs eases the demand constraint on total installed PV capacity, it reduces growth rate as well. This trade-off leads to the maximum in the variable costs curve in Fig. 3a.

Increasing efficiency, on the other hand, reduces both fixed and variable costs (per unit power). Assuming efficiency increases while capex and variable costs per module remain constant, higher efficiency can ease the demand constraint while maintaining a constant growth rate. This constant growth rate is indicated by the flat efficiency curve in Fig. 3b.

In certain instances, the financial incentives experienced by an individual company can oppose the goal of maximizing PV deployment. For example, to maximize short-term revenue, a company is motivated to reduce costs, striving for first-mover advantage or struggling to keep up with competitors. However, once a cost-reducing innovation spreads throughout the entire industry and prices are reduced across the board, lower prices decrease margins in absolute dollars.³⁸ Thus, the so-called “race to the bottom” generally results in decreased sustainable manufacturing growth rates, except for the first movers. In contrast, across-the-board increases in sustainable manufacturing growth rates can be achieved by reducing capex. Note that even if the entire industry lowers capex, the sustainable growth rate will increase for all companies, as new factories cost less money to build. However, the longer-term investment in capex reduction does not have as strong an impact on short-term revenue as other cost-reduction measures; thus, capex reduction is often not prioritized in industry roadmaps. Other trade-offs between the techno-economic inputs shown in Fig. 3 are analyzed in Fig. S3 in the ESI.†

4. PV deployment scenarios

To quantify the efficacy of various capex- and cost-reduction approaches, Fig. 4 shows the cumulative installed capacity as a function of time¶ for several representative scenarios: our baseline scenario with today’s technology (light blue), line-of-sight technology improvements from industry roadmaps (red), two advanced technology scenarios (dark blue and green), and line-of-sight technology with an increased debt/equity ratio (tan). Key input parameters for each scenario are in the ESI,† Table S1. The colored lines are constrained by our baseline assumptions for demand as a function of module price. The shaded area indicates the range of installed capacity when demand is increased or decreased from this baseline, as described in the ESI.† When the colored line is on the top boundary of the shaded area, it indicates that installed capacity is growth-constrained rather than demand-constrained for that scenario with our baseline demand assumptions. Climate targets are also include for reference (gray).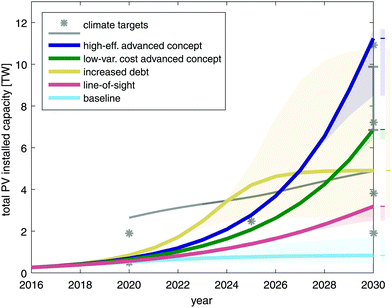

Fig. 4 Climate targets (gray line and symbols) along with our projections for: baseline technology (light blue), line-of-sight technology improvements (red), an advanced technology concept focused on increased efficiency (dark blue), an advanced technology concept focused on reduced variable costs (green), and line-of-sight technology improvements with a debt/equity ratio of 5 : 1 (tan). The shaded area indicates the range obtained with increased and decreased demand. Colored lines indicate projection for power law fit to projected demand curve from ref. 16. Shaded bars to the right of the plot indicate the range of capacities in 2030 with increased and decreased demand. Dark lines on these bars indicate capacity obtained with the power law fit to the demand curve in ref. 16. For details on fitting and shifting the demand curve, see ESI.†

Line-of-sight technology reduces wafer thickness from 180 μm with 130 μm of kerf (sawdust) to 120 μm with 130 μm of kerf. Additional modest reductions in capex and variable costs and an increase in efficiency are included as well. In this scenario, a total installed capacity of 3.2 TW is achievable by 2030. Gains in growth rate due to reduced capex are offset by reductions in revenue due to reduced variable costs, so the line-of-sight technology actually has a slightly lower unconstrained growth rate than baseline. Total installed capacity is limited by both price (3.2 TW) and growth rate (3.3 TW) for line-of-sight technology, indicating a need to reduce both capex and cost further.

We therefore consider scenarios for two advanced PV technology concepts. In both scenarios, wafer thickness and kerf are reduced to 20 μm each (the equivalent of 40 μm-thick kerfless wafers), which significantly reduces both capex and variable costs. Further deep reductions in capex are then coupled to either (1) a further large reduction of variable cost and the same increase in efficiency as in the line-of-sight scenario, or (2) a modest further reduction of variable costs and a large increase in efficiency (which further reduces both capex and variable costs). Scenario 1 represents direct reduction of variable costs by reducing the cost of inputs to production like electricity and silver, either through price reductions, quantity reductions, or replacement. This approach results in reduced revenue, which limits growth rate, and a cumulative installed capacity in 2030 of 6.9 TW. Scenario 2, which drives cost reduction primarily by increasing efficiency, results in faster growth and a cumulative installed capacity in 2030 of 11.2 TW.

There are clear and redundant pathways to achieve the reductions in capex and variable costs, as well as the improvements in efficiency described in the advanced scenarios. Over 30% of the capex in PV module manufacturing is in the production of polysilicon. Therefore, reduction of the silicon wafer thickness from its current value of about 180 μm to 10–20 μm (with equivalent reductions in kerf loss, or 30–50 μm with no kerf loss) would eliminate 90% of this capex. Multiple technologies exist, some of which have already demonstrated high efficiency on wafers as thin as 35 μm, including silicon grown epitaxially directly from vapor sources,³⁹ silicon wafers produced directly from molten silicon without casting and wire-sawing,⁴⁰ and thinner wire saws.^41–43 Thinner wafers also contribute to higher throughput processing, further reducing capex. Specifically, the throughput of crystal growth, ingot cropping, wire sawing, and wet chemical steps are increased by having thinner wafers.

Czochralski growth of monocrystalline silicon is very capital-intensive, representing over 15% of the capex in a monocrystalline silicon PV module.²⁹ Directional solidification of multicrystalline silicon is relatively low capex, and recent results on “high-performance” multicrystalline silicon offer promising routes to high efficiency.^39,44 The capex associated with multicrystalline silicon could be reduced by planned moves to larger ingots^31,45 (further increasing throughput). Czochralski growth could be replaced by multicrystalline silicon, one of the growth techniques mentioned above, or another technique like kyropolis growth, which has demonstrated good material quality with potentially low capex.⁴⁶

Further capex reductions are available through a variety of process modifications. Some examples follow. Replacing slurry wire sawing with structured or diamond wire eliminates equipment for slurry collection and increases throughput.⁴¹ Kerfless wafering would also eliminate this equipment and the equipment used to recondition scrap silicon. The throughput of emitter formation can be increased in the case of batch processing with a gas dopant source (e.g., POCl₃) by depositing at lower pressure.⁴⁷ This process can also be completely replaced by ion implantation^48,49 or chemical vapor deposition (CVD) either of a dopant source,⁵⁰ a doped epitaxial silicon layer,⁵¹ or a polysilicon layer.⁵² CVD and implant emitter formation also obviate the need for edge isolation because they are single-sided processes. The capex associated with contact firing can be reduced for a traditional belt furnace process by increasing the throughput of the entire manufacturing process (the throughput of a belt furnace is just determined by the belt length). Belt furnace firing can also be replaced by laser-firing^53–55 or another more efficient furnace.^56,57 On the module level, capex can be reduced by eliminating the aluminum frame^27,58,59 and simplified tabbing and stringing of cells together.⁶⁰

Combined, the processes mentioned above represent over 75% of the capex of producing a monocrystalline PV module.²⁹ As discussed in the main text, increasing efficiency also proportionally reduces capex (in dollars per watt). Additionally, the processes mentioned above represent over 70% of the embedded energy and CO₂ of a PV module,^61,62 and efficiency is inversely proportional to energy payback time. Thus, the advanced concepts described would drastically reduce PV systems’ embedded CO₂ and energy payback times,^27,63 mitigating the risk of substantial added electrical loads for PV system production at elevated manufacturing capacities;⁶⁴ see further discussion in ESI.† Variable cost reductions up to 40% are on industry roadmaps as described in detail in ref. 28 and 31.

Multiple technologies, including passivated emitter and rear local contacts, heterojunctions, interdigitated back contact designs, and fully passivated contacts, have demonstrated efficiencies over 25%,³⁹ and roadmaps exist up to 26–29%.^31,65,66 There is also promising work to reduce cell-to-module losses.^67–69

The price constraint on installed capacity depends strongly on the demand curve for PV. The demand curve in turn depends on a multitude of factors unrelated to PV module technology.|| To capture the uncertainty in these factors over a period of decades, we shift the demand curve to simulate increased and decreased demand at a given PV module price (see ESI† for details) and recalculate installations over time for each of our technology scenarios. As stated above, the range of installed capacity with increased and decreased demand is indicated by the shaded areas in Fig. 4. These results show that relatively small changes in demand can have dramatic impacts on installed capacity. For the high-efficiency advanced technology concept, a 25% (rel.) change in the price at which a given capacity is demanded can increase installed capacity to 11.5 TW or reduce it to 8.5 TW.

Debt can also be used to increase growth rate. However, it must come with significant reductions in cost to reach high installed capacity. To illustrate this point, a scenario with line-of-sight technology improvements and a debt/equity ratio of 5 : 1 is also shown in Fig. 4. As with the line-of-sight scenario with a debt/equity ratio of 1 : 1, installed capacity is limited to less than 5 TW. In addition, the demand curve has a much stronger effect on this scenario than on technology innovations, with the high demand case yielding 11 TW of PV but the low demand case less than 3 TW. This leads to a large range in the total amount of debt that would have to be sourced in such a scenario, ranging from $0.9 trillion to $3.7 trillion with baseline projected demand requiring $1.6 trillion. Finally, the interest rate on debt also has a significant impact on the installed capacity in the increased debt scenario. An increase from 5% (baseline assumption) to 10% reduces installed capacity in the high-demand case from 11 to 7 TW. This data is shown in Fig. S5 of the ESI.†

5. Conclusions

In summary, we find that further innovation is necessary to reach cumulative installed PV capacities commensurate with targets for keeping average global temperatures below 1.5–2 °C above pre-industrial levels without external subsidies. Line-of-sight technology improvements are insufficient to reach aggressive targets, which give the highest likelihood of preventing catastrophic climate change. To meet these targets will require dramatic reductions in capex along with significant increases in efficiency and/or hefty reductions in variable costs. Because reductions in variable costs also reduce growth rate under the assumption of fixed operating margins, we find that increased efficiency is preferred.

Finally, demand for PV, which limits total deployment at a given price, is strongly dependent on policy decisions. Installers price PV and consumers demand PV as an alternative to existing electricity options. Many policy decisions affect the relative prices of PV and fossil fuel alternatives, including utility tariff structures, ancillary services markets, electric grid technology, carbon pricing, renewable portfolio standards, fossil fuel subsidies, supply- and demand-side PV subsidies like feed-in-tariffs, investment tax credits, low and zero-interest loans, and subsidized land and equipment. Decisions about these policies will either increase or decrease dramatically the innovation and R&D investment required to achieve climate-driven PV deployment targets.

Acknowledgements

We thank P. Mints (SPV Market Research), R. Fu, M. Woodhouse, and K. Horowitz (NREL), D. Weiss and R. Garabedian (First Solar), BJ Stanbery (Siva Power), and L. Sekaric (U.S. DOE) for fruitful discussions, J. D. Jenkins (MIT), W. Tumas, N. M. Haegel, P. A. Basore, and S. Kurtz (NREL), and G. R. Sherman (PACE Financial Services) for critical reading of the manuscript, and F. Frankel (MIT) for advice regarding formatting of the figures. This material is based upon work supported by the Engineering Research Center Program of the National Science Foundation and the Office of Energy Efficiency and Renewable Energy of the Department of Energy (DOE) under NSF Cooperative Agreement No. EEC-1041895. D. Berney Needleman acknowledges the support of the Department of Defense (DoD) through the National Defense Science & Engineering Graduate (NDSEG) Fellowship program.

References

1. IPCC Core Writing Team, Climate Change 2014, Synthesis Report, Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Geneva, Switzerland, IPCC, 2014.
2. International Energy Agency, Energy and Climate Change: World Energy Outlook Special Report, 2015.
3. P. Friedlingstein, R. M. Andrew, J. Rogelj, G. P. Peters, J. G. Canadell and R. Knutti, et al. Persistent growth of CO₂ emissions and implications for reaching climate targets, Nat. Geosci., 2014, 7, 709–715.
4. J. Rogelj, W. Hare, J. Lowe, D. P. van Vuuren, K. Riahi and B. Matthews, et al. Emission pathways consistent with a 2 °C global temperature limit, Nat. Clim. Change, 2011, 1, 413–418.
5. UNFCCC, Conference of the Parties (COP), Adoption of the Paris Agreement, Proposal by the President [Internet], Paris, France, 2015 [cited 2015 Dec 18], available from: http://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf.
6. P. Moriarty and D. Honnery, What is the global potential for renewable energy?, Renewable Sustainable Energy Rev., 2012, 16, 244–252.
7. M. Z. Jacobson and M. A. Delucchi, A Path to Sustainable Energy by 2030, Sci. Am., 2009, 301, 58–65.
8. M. D. Kempe, Ultraviolet light test and evaluation methods for encapsulants of photovoltaic modules, Sol. Energy Mater. Sol. Cells, 2010, 94, 246–253.
9. E. Hasselbrink, M. Anderson, Z. Defreitas, M. Mikofski, Y.-C. Shen and S. Caldwell, et al. Validation of the PVLife model using 3 million module-years of live site data [Internet], in: Photovoltaic Specialists Conference (PVSC), 2013 IEEE 39th. IEEE, 2013 [cited 2016 Jan 9], page 0007–12, available from: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6744087.
10. D. C. Jordan and S. R. Kurtz, Reliability and Geographic Trends of 50 000 Photovoltaic Systems in the USA [Internet], in: 29th European PV Solar Energy Conference and Exhibition, 2014 [cited 2016 Jan 9], available from: http://www.nrel.gov/docs/fy14osti/62801.pdf.
11. W. Hoffmann, PV solar electricity industry, Market growth and perspective, Sol. Energy Mater. Sol. Cells, 2006, 90, 3285–3311.
12. U.S. Energy Information Admistration, Annual Energy Outlook 2015 [Internet], 2015 [cited 2015 Dec 18], available from: http://www.eia.gov/forecasts/aeo.
13. M. Z. Jacobson and M. A. Delucchi, Providing all global energy with wind, water, and solar power, Part I: Technologies, energy resources, quantities and areas of infrastructure, and materials, Energy Policy, 2011, 39, 1154–1169.
14. A. Feltrin and A. Freundlich, Material considerations for terawatt level deployment of photovoltaics, J. Renewable Energy, 2008, 33, 180–185.
15. R. C. Pietzcker, D. Stetter, S. Manger and G. Luderer, Using the sun to decarbonize the power sector: The economic potential of photovoltaics and concentrating solar power, Appl. Energy, 2014, 135, 704–720.
16. P. Mints, Price Point and other Ecomomic Levers Required for Over 1-TWp of PV, SPV Market Research, 2015.
17. J. Mayer, S. Philipps, N. S. Hussein, T. Schlegl and C. Senkpiel, Current and Future Cost of Photovoltaics: Long-term Scenarios for Market Development, System Prices and LCOE of Utility-Scale PV Systems, Fraunhofer ISE, Freiburg, Germany, 2015.
18. S. Henbest, New Energy Outlook 2015, Bloomberg Finance LP, 2015.
19. Solar PV Module Value Chain – Market Size, Average Price, Market Share and Key Country Analysis to 2020, GlobalData, 2014.
20. S. Wilkinson, J. Berg and S. von Aichberger, Marketbuzz, IHS Technology, 2015.
21. A. Metz, G. Demenik, A. Richter, T. Vlasenko, I. Buchovskaya, M. Zwegers, H. Xu, A. Luan, R. Wertz, A. Stassen, H. Forstner, W. Jooss, J. Haase, E. Dornberger, S. Raithel, J. Szlufcik, G. Coletti, W. Sinke, P. Wyers, J. Zhu, S. Zhang, A. Guo, L. Maosheng, J. Xia, Z. Yujun, J. Dong, C. Jian, S. Li, J. Yunpeng, X. Aimin, G. Xing, M. Fischer, P. Engelhardt, A. Gerlach, K. Petter, T. Spieß, A. Mette, M. Mette, K. Wang, C.-C. Li, Y. Wan, G. Li, K. C. Lin, L. Yong, S. Julsrud, Technology Roadmap: Solar Photovoltaic Energy, International Energy Agency, Paris, France, 2014.
22. M. Rekinger and F. Thies, Global Market Outlook for Solar Power 2015–2019, SolarPower Europe.
23. A. James, Global PV Demand Outlook 2015–2020, Exploring Risk in Downstream Solar Markets, GTM Research.
24. P. Gunjan, Global Solar Power Market, Frost & Sullivan, 2014.
25. Solar PV Market Analysis And Segment Forecasts to 2020, San Francisco, CA, Grand View Research, 2014.
26. PV Market Alliance, Global PV Market Report, 2015.
27. S. A. Mann, M. J. de Wild-Scholten, V. M. Fthenakis, W. G. J. H. M. van Sark and W. C. Sinke, The energy payback time of advanced crystalline silicon PV modules in 2020: a prospective study, Prog. Photovoltaics, 2014, 22, 1180–1194.
28. D. M. Powell, M. T. Winkler, A. Goodrich and T. Buonassisi, Modeling the Cost and Minimum Sustainable Price of Crystalline Silicon Photovoltaic Manufacturing in the United States, IEEE J. Photovolt., 2013, 3, 662–668.
29. D. M. Powell, R. Fu, K. Horowitz, P. A. Basore, M. Woodhouse and T. Buonassisi, The capital intensity of photovoltaics manufacturing: barrier to scale and opportunity for innovation, Energy Environ. Sci., 2015 [cited 2015 Sep 16], available from: http://pubs.rsc.org/en/Content/ArticleLanding/2015/EE/C5EE01509J.
30. R. Fu, T. L. James and M. Woodhouse, Economic Measurements of Polysilicon for the Photovoltaic Industry: Market Competition and Manufacturing Competitiveness, IEEE J. Photovolt., 2015, 5, 515–524.
31. ITRPV Working Group, International Technology Roadmap for Photovoltaic (ITRPV), 2014 Results [Internet], SEMI PV Group, 2015, available from: http://itrpv.net/.cm4all/iproc.php/Reports%20downloads/ITRPV_2015_Roadmap_Results_2014_150428.pdf?cdp=a.
32. B. Burger, K. Kiefer, C. Kost, S. Nold, S. Philipps and R. Preu, et al. Photovoltaics Report [Internet], Freiburg, Germany, Fraunhofer Institute for Solar Energy Systems, 2015 [cited 2016 Jan 14], available from: http://https://www.ise.fraunhofer.de/en/downloads-englisch/pdf-files-englisch/photovoltaics-report-slides.pdf.
33. C. Wadia, A. P. Alivisatos and D. M. Kammen, Materials Availability Expands the Opportunity for Large-Scale Photovoltaics Deployment, Environ. Sci. Technol., 2009, 43, 2072–2077.
34. M. A. Green, Estimates of Te and In prices from direct mining of known ores, Prog. Photovoltaics, 2009, 17, 347–359.
35. M. Woodhouse, A. Goodrich, R. Margolis, T. James, R. Dhere and T. Gessert, et al. Perspectives on the pathways for cadmium telluride photovoltaic module manufacturers to address expected increases in the price for tellurium, Sol. Energy Mater. Sol. Cells, 2013, 115, 199–212.
36. C. Zheng and D. M. Kammen, An innovation-focused roadmap for a sustainable global photovoltaic industry, Energy Policy, 2014, 67, 159–169.
37. T. Voituriez and X. Wang, Real challenges behind the EU–China PV trade dispute settlement, Clim. Policy, 2015, 15, 670–677.
38. M. Bazilian, I. Onyeji, M. Liebreich, I. MacGill, J. Chase and J. Shah, et al. Re-considering the economics of photovoltaic power, J. Renewable Energy, 2013, 53, 329–338.
39. M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Solar cell efficiency tables (version 47), Prog. Photovoltaics, 2016, 24, 3–11.
40. Hanwha Q CELLS confirms 19.1% cell efficiencies with 1366’s “Direct Wafer” technology [Internet], PV-Tech2015 [cited 2015 Nov 8], available from: http://www.pv-tech.org/news/hanwha_q_cells_confirms_19.1_cell_efficiencies_with_1366s_direct_wafer_tech.
41. A. Goodrich, P. Hacke, Q. Wang, B. Sopori, R. Margolis and T. L. James, et al. A wafer-based monocrystalline silicon photovoltaics road map: Utilizing known technology improvement opportunities for further reductions in manufacturing costs, Sol. Energy Mater. Sol. Cells, 2013, 114, 110–135.
42. B. Terheiden, T. Ballmann, R. Horbelt, Y. Schiele, S. Seren and J. Ebser, et al. Manufacturing 100-μm-thick silicon solar cells with efficiencies greater than 20% in a pilot production line: Manufacturing 100-μm-thick Si solar cells with efficiencies greater than 20%, Phys. Status Solidi A, 2015, 212(1), 13–24.
43. C. Gay, Significant research and technical paths for silicon: beyond DOE Sunshot goals, 2015.
44. F. Schindler, B. Michl, A. Kleiber, H. Steinkemper, J. Schon and W. Kwapil, et al. Potential Gain in Multicrystalline Silicon Solar Cell Efficiency by n-Type Doping, IEEE J. Photovolt., 2015, 5, 499–506.
45. G. Fisher, M. R. Seacrist and R. W. Standley, Silicon Crystal Growth and Wafer Technologies, Proc. IEEE, 2012, 100, 1454–1474.
46. M. Kivambe, D. M. Powell, S. Castellanos, M. Ann Jensen, A. E. Morishige and K. Nakajima, et al. Minority-carrier lifetime and defect content of n-type silicon grown by the noncontact crucible method, J. Cryst. Growth, 2014, 407, 31–36.
47. M. Muhlbauer, A. Piechulla, C. Voyer, M. Citro, R. Dahl and P. Fath, Industrial low-pressure phosphorus diffusion for high performance and excellent uniformity, in: 26th European International Conference on Photovoltaic Solar Energy, 5–9 Sept. 2011, WIP – Renewable Energies, 2011, 2028–2030.
48. M. Sheoran, M. Emsley, M. Yuan, D. Ramappa and P. Sullivan, Ion-implant doped large-area n-type Czochralski high-efficiency industrial solar cells, in: 2012 38th IEEE Photovoltaic Specialists Conference (PVSC), 2012, 0022547.
49. E. Cho, Y. Ok, K. Ryu, B. Rounsaville, A. D. Upadhyaya and V. Upadhyaya, et al. Comparison of POCl₃ diffusion with phosphorus ion implantation for Czochralski and Quasi-mono silicon solar cells, in: Photovoltaic Specialist Conference (PVSC), 2014 IEEE 40th, 2014, 2966–2968.
50. J. Engelhardt, A. Frey, S. Gloger, G. Hahn and B. Terheiden, Passivating boron silicate glasses for co-diffused high-efficiency n-type silicon solar cell application, Appl. Phys. Lett., 2015, 107(4), 042102.
51. T. Rachow, N. Milenkovic, B. Steinhauser, J. Benick, S. Janz and M. Hermle, et al. Solar Cells with Epitaxial or Gas Phase Diffused Emitters above 21% Efficiency, in: 5th International Conference on Silicon Photovoltaics, SiliconPV 2015, March 25, 2015 – March 27, 2015, Elsevier Ltd, 2015, 540–545.
52. P. G. Borden, L. Xu, B. McDougall, C. P. Chang, D. Pysch and P. Voisin, et al. Polysilicon tunnel junctions as alternates to diffused junctions, in: Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 2008.
53. E. Schneiderlöchner, R. Preu, R. Lüdemann and S. W. Glunz, Laser-fired rear contacts for crystalline silicon solar cells, Prog. Photovoltaics, 2002, 10, 29–34.
54. J. He, S. Hegedus, U. Das, Z. Shu, M. Bennett and L. Zhang, et al. Laser-fired contact for n-type crystalline Si solar cells: Laser-fired contact for Si solar cells, Prog. Photovoltaics, 2015, 23, 1091–1099.
55. M. Graf, J. Nekarda, F. L. Togny, A. Streek, R. Bohme and R. Preu, Comprehensive Simulation and Acceleration of the Foil-metallization Laser Process, Energy Procedia, 2015, 77, 694–700.
56. S. Peters, Rapid Thermal Processing of Crystalline Silicon Materials and Solar Cells, 2004.
57. Breakthrough Furnace can Cut Solar Industry Costs [Internet], Golden, CO, USA, National Renewable Energy Laborartory, 2013, available from: http://www.nrel.gov/docs/fy13osti/59012.pdf.
58. Plug and Play: Purchase, Install, and Connect Residential Solar Power in Hours [Internet], Energy.gov [cited 2016 Jan 26], available from: http://energy.gov/eere/success-stories/articles/plug-and-play-purchase-install-and-connect-residential-solar-power.
59. DUOMAX Series Dual Glass Module | Trina Solar USA [Internet], [cited 2016 Jan 26], available from: http://www.trinasolar.com/us/product/PDG5.html.
60. T. Buck, R. Kopecek, J. Libal, R. Petres, K. Peter and I. Rover, et al. Large Area Screen Printed N-Type MC-SI Solar cells With B-Emitter: Efficiencies Close to 15% and Innovative Module Interconnection, in: Conference Record of the 2006 IEEE 4th World Conference on Photovoltaic Energy Conversion, 2006, 1060–1063.
61. T. Wetzel and F. Feuerstein, Update of energy payback time data for crystalline silicon PV modules, in: Proceedings of the 26th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 2011.
62. V. M. Fthenakis and H. C. Kim, Photovoltaics: Life-cycle analyses, Sol. Energy, 2011, 85, 1609–1628.
63. V. Fthenakis, How long does it take for photovoltaics to produce the energy used?, Natl Assoc Prof Eng Mag, 2012, 16–17.
64. S. B. Darling and F. You, The case for organic photovoltaics, RSC Adv., 2013, 3, 17633–17648.
65. R. M. Swanson, Approaching the 29% limit efficiency of silicon solar cells, in: Conference Record of the Thirty-first IEEE Photovoltaic Specialists Conference, 2005, 889–894.
66. Energy Department Announces $12 Million to Accelerate Record-Breaking Solar Cell Efficiency [Internet], [cited 2015 Dec 29], available from: http://apps1.eere.energy.gov/news/progress_alerts.cfm/news_id=20465.
67. I. Haedrich, M. Wiese, B. Thaidigsman, D. Eberlein, F. Clement and U. Eitner, et al. Minimizing the Optical Cell-to-module Losses for MWT-modules, Energy Procedia, 2013, 38, 355–361.
68. I. Haedrich, U. Eitner, M. Wiese and H. Wirth, Unified methodology for determining CTM ratios: Systematic prediction of module power, Sol. Energy Mater. Sol. Cells, 2014, 131, 14–23.
69. J. Muller, D. Hinken, S. Blankemeyer, H. Kohlenberg, U. Sonntag and K. Bothe, et al. Resistive Power Loss Analysis of PV Modules Made From Halved 15.6 × 15.6 cm² Silicon PERC Solar Cells With Efficiencies up to 20.0%, IEEE J. Photovolt., 2015, 5, 189–194.
70. P. A. Basore, Paths to future growth in photovoltaics manufacturing, Prog. Photovoltaics, 2016 DOI:10.1002/pip.2761.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ee00484a

‡ The growth rate of cumulative installed capacity is often quoted for the PV industry. In this paper, we will use “growth” and “growth rate” to refer only to growth of manufacturing capacity (i.e. annual, not cumulative, installations).

§ The cost model is available for download as an Excel file in the ESI,† as are the Matlab scripts used to calculate manufacturing growth rate and thereby annual and cumulative installations over time.

¶ For scenarios that require technological innovation (efficiency increases, capex reduction), our simulations assume that all innovations are available starting in 2016. While clearly optimistic, it represents an upper bound for the impact of innovation. The final cumulative installed PV capacity is highly dependent upon the precise transition date to the advanced technology, but they cannot exceed the scenarios presented here. Installed capacity as a function of time for deployment of new technology in different years is shown in Fig. S4 of the ESI.†

|| Some example of these factors are: grid constraints and electricity markets, including utility tariff structures, ancillary services markets, and electric grid technology; energy and climate policy, including carbon pricing, fossil fuel subsidies, and supply- and demand-side PV subsidies like feed-in-tariffs, investment tax credits, renewable portfolio standards, low/zero-interest loans, subsidized land and equipment and the cost of supporting or competing technologies like fossil fuels, energy storage, PV balance-of-systems, and labor for manufacturing and installation.

---