Interactions between 2,4-bis-pteridine-1,5-benzodiazepine and group 12 dihalides: synthesis, spectral and XRD structural studies and theoretical calculations

Abstract

2,4-Bis(1,3,7-trimethyl-pteridine-2,4(1H,3H)-dione-6-yl)-2,3-dihydro-2-methyl-1H-1,5-benzodiazepine (DLMBZD) has been prepared and its molecular and crystal structures have been determined from spectral and XRD data. The benzodiazepine ligand was reacted with zinc(II), cadmium(II) and mercury(II) chloride, bromide and iodide to give complexes with general formula [M(DLMBZD)X₂]. The complexes have been synthesized and characterized by IR, NMR and elemental analysis. The structure of seven complexes has been obtained by single crystal X-ray diffraction. In all the cases, the metal is (2 + 2 + 1)-five-coordinated by two halide ligands, two nitrogen atoms from pyrazine and diazepine rings and a carbonyl oxygen from a pteridine ring. The coordinated-metal environment is a square-based pyramid, with increasing trigonality from Hg(II) to Zn(II) complexes. To coordinate the metals, the ligand folds itself, establishing four intramolecular σ–π interactions with the pyrimidine and pyrazine rings. A topological analysis of the electron density using the Quantum Theory of Atoms in Molecules and the complexes stability has been performed.

---

Introduction

Benzodiazepines (BZDs) are psychoactive drugs whose core chemical structure is the fusion of a benzene ring and a diazepine ring. The first benzodiazepine, chlordiazepoxide (Librium), was discovered accidentally by Leo Sternbach in 1955 and made available in 1960 by Hoffmann La Roche, which has also marketed diazepam (Valium) since 1963.¹ The medicinal and pharmacological relevance of the benzodiazepine family explains the interest in exploring their activity such as anticonvulsant, antianxiety, analgesic, hypnotic, anti-inflammatory, anti-depressive, anti-ulcerative, anti-allergic, antihistaminic, and antipyretic activities^2–4 and are considered as “privileged scaffolds” in medicinal chemistry.⁵

Benzodiazepine has a traditional place in antiepileptic therapies. The clinical use of BZDs can be divided into two categories. First, they are useful in the acute treatment of seizures as drugs of choice in status epilepticus and also in some febrile seizures. Second, the BZDs are useful in long-term therapy of certain seizures, primarily in the pediatric population.⁶

However, the biological activity is highly dependent on the nature of the BZD scaffold including the conformation of the 1,4-diazepine ring and its substituents, the propensity of the hydrogen bond donor and acceptor, and the electrostatic profile.⁷ Consequently, the development of expedient synthetic approaches to access new BZD scaffolds has attracted considerable attention in the discovery of biologically active compounds.⁸

The compounds with a 1,5-benzodiazepine scaffold have recently received growing attention because of their pharmacological properties.^9,10 There are some differences between the effects of 1,5- and 1,4-benzodiazepines. A greater therapeutic potential and lower incidence of side effects were described for 1,5-BZDs when compared to 1,4-BZDs. 1,5-Benzodiazepines exert a biological activity similar to well-known 1,4-derivatives¹¹ and their ring system has demonstrated wide utility not only in central nervous system (CNS)-drug design, but also as peptidomimetic scaffolds and key intermediates for the preparation of other fused ring compounds.¹² Beside this, 1,5-benzodiazepines show antimicrobial,¹³ antifeedant,¹⁴ anti-inflammatory and analgesic,¹⁵ and anticonvulsant activities.¹⁶

Several representative medicinal candidates containing a 1,5-benzodiazepine scaffold are exemplified in Scheme 1 including compounds a and b,¹⁷ two drugs for the treatment of schizophrenia, and compound c,¹⁸ an inhibitor of HIV-1 capsid assembly.

Scheme 1 Representative medicinal candidates containing the 1,5-benzodiazepine scaffold.

However, interactions between these drugs and metal ions have been scarcely investigated.¹⁹ Thus, a survey through the Cambridge Structural Database (webCSD service, updated Jun 2016) led us to only seven examples in which the 1,5-diazepine moiety is coordinated to a metal,²⁰ usually as a monodentate N-ligand,^20d,e,f,g sometimes behaving as a bridging ligand,^20a,b and only one example of N,N′-bidentate behaviour.^20c The changes induced in a benzodiazepine molecule by complexation may actually be reflected in the pharmacological properties of the substance and therefore such studies might help in elucidating the relationship between the chemical and pharmacological properties of these drugs. Nonetheless, to date, very few complexes of benzodiazepines have been characterized unambiguously.²¹

In this way, our efforts are focused on the design of potential bifunctional chelator ligand systems for use as potential drugs. So, we have recently started to study the interactions between benzodiazepines and metals mainly with reference to the synthesis and stereochemistry of the metallated species. Thus, in this work, the interactions of several zinc(II), cadmium(II) and mercury(II) halides with a new 1,5-benzodiazepine, in particular, with 2,4-bis(1,3,7-trimethyl-pteridine-2,4(1H,3H)-dione-6-yl)-2,3-dihydro-2-methyl-1H-1,5-benzodiazepine (Scheme 2) have been reported. Both the ligand and complexes were characterized using elemental analysis, FT-IR, solution ¹H, and ¹³C{1H} NMR spectroscopies, and single-crystal X-ray crystallography. The second part of this work has been devoted to the theoretical characterization of the nature of the metal–ligand interactions, also including those responsible for the stereochemical changes of the BZD moiety on coordination.

Scheme 2 Structure of 2,4-bis(1,3,7-trimethyl-pteridine-2,4(1H,3H)-dione-6-yl)-2,3-dihydro-2-methyl-1H-1,5-benzodiazepine (DLMBZD).

Results and discussion

Synthesis and structure of the ligand

The new ligand 2,4-bis(1,3,7-trimethyl-pteridine-2,4(1H,3H)-dione-6-yl)-2,3-dihydro-2-methyl-1H-1,5-benzodiazepine, hereafter denoted as DLMBZD (Scheme 2), has been synthesized in two steps starting with the synthesis of the proligand 6-acetyl-1,3,7-trimethyllumazine (DLMAceM) following a well-known procedure.²² The available 6-acetyl group allows for a classic condensation to isolate new multifunctional ligands containing the azomethine C=N bond. Benzodiazepines are generally synthesized by the condensation of o-phenylenediamine (OPDA) with α,β-unsaturated carbonyl compounds, β-haloketones, or with ketones using acidic catalysts which are critical to enhance the condensation process.²³

Herein, the benzodiazepine-derived ligand was obtained by refluxing in DLMAceM and o-phenylendiamine (2 : 1) in absolute ethanol for 24 h with addition of a small amount of acetic acid as a catalyst (yield ca. 70%). In the second step, a red solid, identified as 6-[N-(2-aminophenyl)ethanimidoyl]-1,3,7-trimethylpteridine-2,4(1H,3H)-dione (DLMOfen), was obtained. The identification and characterization of the title ligand DLMBZD was carried out using elemental and thermal analyses, and spectroscopic methods such as IR, ¹H, and ¹³C NMR spectroscopy (including HMBC and HMQC experiments). Recrystallizing the compound DLMBZD in acetonitrile led us to obtain crystals suitable for X-ray diffraction.

The single crystal XRD measurements indicate the presence of a racemate because of the centrosymmetric space group, but the asymmetric residual unit (ARU) also contains two different DLMBZD molecules with opposite chirality, although they are not enantiomers; thus, there are two slightly different R–S pairs. A view of the molecular structure of the S-molecule is depicted in Fig. 1.

Fig. 1 ORTEP drawing for the free ligand with ellipsoids at 50% probability. Another molecule in the ARU is labelled as C/D (pteridines) and G (benzodiazepine).

Both molecules in the ARU are very similar, showing no noteworthy geometrical features. In the pteridine moieties, the pyrimidine and pyrazine rings are roughly coplanar with dihedral angles ranging from 1.9(2) to 5.5(2)° and both pteridine mean planes are angled by 166.8(4) and 153.9(4)°. The diazepine rings are in a boat conformation (ca. 7% chair) with the C62 atom at the prow and the C1F/G–C2F/G bond at the poop.²⁴ The successive refinement cycles allowed us to locate the H atoms bound to nitrogen in the atoms N2F and N2G, being involved in an intramolecular N2–H⋯N5 H-bond (see Table S-01†). Moreover, the distances of C–N on both benzodiazepine nitrogen atoms clearly support the corresponding sp² (N1F/G) and sp³ (N2F/G) hybridizations: N1F–C1F, 1.409(4); N1G–C1G, 1.391(4); N1F–C61B, 1.286(4); N1G–C61D, 1.291(4); N2F–C2F, 1.402(4); N2G–C2G, 1.416(4); N2F–C61A, 1.474(4); N2G–C61C, 1.469(4) Å.

In the crystal structure, despite the fact that the water molecule was refined into three different positions (site occupation factors 55, 35 and 10%), very high thermal parameters indicating a high disorder were found. Also, PLATON found a number of short π–π ring and two σ–π carbonyl–pyrazine intermolecular interactions, as given in the ESI (Table S-01†).²⁵

The FT-IR spectrum exhibits a medium absorption band at ca. 3317 cm⁻¹ assignable to the N–H stretching vibration of the diazepine group. The characteristic bands of the lumazine skeleton are: the carbonyl groups of both lumazines can be seen by two medium bands at 1723 and 1695 cm⁻¹ and two strong bands at 1678 and 1670 cm⁻¹. The higher is mainly due to ν(C2=O) and the other one may be assigned to ν(C4=O). The band at 1555 cm⁻¹ is attributed to ν(C=N) of the pyrazine ring and the two bands at 1455 and 1288 cm⁻¹ could be assignable to ν(C=C) + ν(C–N) vibrations.²⁶

The assignment of NMR resonances was made using previously reported data²⁷ and the combination of HMBC and HMQC experiments allowed the unequivocal assignment of every carbon signal. The ¹H NMR spectrum of the DLMBZD in DMSO-d₆ showed δ 7.10 (m, C3F/C4F/C6F); 7.07 (s, N2F–H), 6.67 (m, C5F), 4.27, 2.93 (dd, C62B), 1.76 (s, C62A) and three couples of signals at 3.57/3.42, 3.35/3.14 and 2.79/2.41 ppm are assigned to the hydrogens of the methyl groups C3, C1 and C71 present in both lumazine moieties, respectively.

Crystal structure and spectral studies of the complexes

The coordination chemistry of the ligand towards several zinc(II), cadmium(II) and mercury(II) perchlorate and dihalide salts was studied. The reactions of the DLMBZD ligand with one equivalent of the corresponding salt in acetonitrile, ethanol or dichloromethane at different temperatures afforded cleanly the [MLX₂] complexes. These compounds were isolated in good yields and were characterized by elemental analysis, NMR spectroscopy, luminescence measurements and single-crystal X-ray diffraction. It must be pointed out that, in order to fulfill the coordinative capacity of the ligand, syntheses with a higher excess of metal (M/L = 2/1) were carried out but no different products than those reported here were found.

The structures of [MX₂(DLMBZD)] compounds, where MX₂ = ZnCl₂ (2), ZnBr₂ (3), ZnI₂ (4), CdCl₂ (5), CdI₂ (7), and HgI₂ (10) and the adduct 2[HgI₂(DLMBZD)]·HgI₂·2CH₃CN (11) were solved by means of XRD methods. A view of the HgI₂(DLMBZD) portion (10), similar to the other complexes, is shown in Fig. 2.

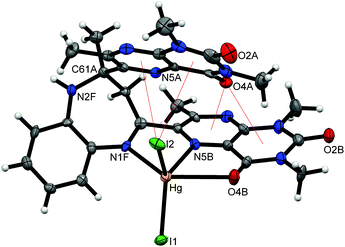Fig. 2 ORTEP drawing for [HgI₂(DLMBZD)] compound (10) (ellipsoids at 50% probability), showing the intramolecular σ–π interactions (red thin lines). Atom labels as shown in Fig. 1 (for clarity, only a few atoms have been labelled).

The geometrical features of the coordination sphere around the metal are given in Table 1. In all cases, the metal is (2 + 2 + 1)-five-coordinated by two halide ligands, two nitrogen atoms from pyrazine (N5B) and diazepine (N1F) rings and a carbonyl oxygen (O4A) from a pteridine ring. The most important feature is the difference between M–N and M–O bonds; M–N bond lengths range between 2.0–2.6 Å. The M–N1 (diazepine) bonds are 5–10% longer than those involving the pyrazine N5 nitrogen. On the other hand, O4 atoms are semi-coordinated to metals at distances 15–30% lengthened when compared with the M–N5 bond, which agrees with the most commonly reported coordinative behaviour of lumazine derivatives.²⁷ The increasing size from Zn to Hg may explain the different shapes of the coordination polyhedra, as measured by the Addison's τ (see Table 1).²⁸ Thus, these can be described as a square-based pyramid with decreasing trigonality from Zn (near 40% TBP) to Hg (only <5% TBP), passing through Cd (20% TBP).

Table 1 Distances (Å) and angles (°) in the coordination sphere of [ZnCl₂(DLMBZD)]·CH₂Cl₂·H₂O (2), [ZnBr₂(DLMBZD)]·CH₂Cl₂ (3), [ZnI₂(DLMBZD)]·CH₃CN (4), [CdCl₂(DLMBZD)] (5), [CdI₂(DLMBZD)] (7), [HgI₂(DLMBZD)] (10) and 2[HgI₂(DLMBZD)]·HgI₂·2CH₃CN (11)

	2	3	4	5	7	10	11
a In the free HgI2 molecule.
M–X1	2.221(2)	2.3268(8)	2.5153(9)	2.410(2)	2.685(1)	2.651(1)	2.6888(6)
							2.5828(7)^a
M–X2	2.211(1)	2.3171(7)	2.5186(8)	2.417(2)	2.701(1)	2.657(1)	2.6448(6)
M–N1F	2.186(4)	2.160(3)	2.183(5)	2.485(8)	2.484(9)	2.593(9)	2.533(5)
M–N5B	2.048(4)	2.032(3)	2.057(5)	2.277(8)	2.282(8)	2.372(9)	2.392(6)
M–O4B	2.685(5)	2.683(3)	2.752(6)	2.560(7)	2.582(7)	2.728(7)	2.752(7)
X1–M–X2	123.60(6)	124.57(3)	121.56(3)	126.73(9)	125.88(4)	135.02(4)	130.15(2)
							180^a
X1–M–N1F	110.4(1)	110.6(1)	115.1(1)	102.7(2)	105.7(2)	103.3(2)	106.8(1)
X1–M–N5B	111.4(1)	110.9(1)	111.6(1)	115.0(2)	116.1(2)	112.1(2)	103.8(1)
X1–M–O4B	88.8(2)	88.6(1)	87.7(2)	93.4(2)	94.4(2)	96.1(2)	93.1(2)
X2–M–N1F	104.4(1)	104.6(1)	104.3(2)	105.0(2)	103.8(2)	103.0(2)	103.0(1)
X2–M–N5B	118.5(1)	117.3(1)	117.6(1)	117.1(2)	116.5(2)	111.6(2)	124.5(1)
X2–M–O4B	85.6(2)	84.4(2)	82.7(2)	94.9(2)	93.2(2)	92.4(2)	96.7(1)
N1F–M–N5B	77.8(1)	78.1(1)	78.3(2)	69.3(3)	69.0(3)	66.9(3)	66.7(2)
N5B–M–O4B	69.4(2)	69.2(2)	68.7(2)	69.1(2)	68.6(3)	65.5(3)	64.9(2)
O4B–M–N1F	146.4(2)	146.5(1)	145.2(2)	138.4(2)	137.6(3)	132.4(3)	130.7(2)
%TBP (τ)	38%	36%	39%	19%	20%	4%	2%

---

About the stereochemistry of the molecules, all crystals are racemates containing equimolecular quantities of molecules with R and S forms of the ligand because compounds 2, 3, 4, and 11 crystallize in the centrosymmetric Pbca space group, whereas compounds 5, 7 and 10 crystallize in the polar Pna2₁ group.

On coordinating MX₂ molecules, the free DLMBZD undergoes drastic steric changes. The dihedron N5B–C6B–C61B–N1F is closed from nearly 180° to 25–30° in the complexes and the dihedron N5A–C6A–C61A–N2F is opened from ca. 10° to 140°, the diazepine ring being flattened from a quasi-boat (∼93%) to an intermediate boat-chair arrangement (∼60% boat).²⁴ Therefore, the dihedral angle between both pteridine skeletons is closed from ca. 160° to 30–50° in the complexes, the ligand becomes folded to establish four intramolecular π–π interactions between both the halogen (X2) and carbonyl (C4A=O4A) groups and the π-cloud of the pyrimidine and pyrazine rings of both pteridine moieties, very important to stabilize the metal-containing molecule (see Fig. 2). Details on these interactions, calculated using PLATON, are given in Table S-02.† The MX₂(DLMBZD) molecules are linked to each other in a monodimensional arrangement along the a (comps. 2, 3 and 4) or c (comps. 5, 7 and 10) axes, by means of N2F–H⋯X2 H-bonds with N2F⋯X2 distances ranging from 3.4–3.8 Å (Fig. 3). Chains are packed through other intermolecular contacts, as given in the ESI (Table S-02†).

Fig. 3 Ball and stick view from the [1 −1 0] direction of the H-bonded chain-like structure of [CdI₂(DLMBZD)] (H atoms omitted for clarity).

The compound 2[HgI₂(DLMBZD)]·HgI₂·2CH₃CN (11) also shows a chain-like structure following the [1 0 0] direction, with N2F–H2F⋯O2A (1 + x, y, z) bonds (N2F⋯O2A, 3.278(9) Å) (see Table S-02†). The ligand-free HgI₂ molecules are linked to the crystal structure mainly through weak contacts Hg2⋯I11 (−1 + x,y,z) (3.6318(9) Å), a little bit longer than the sum of the corresponding van der Waals radii. Additional Hg1⋯Hg2 (1 + x, y, z) (4.9757(9) Å) contacts found by PLATON are quite long to be considered effective in order to contribute to the crystal packing.

In the IR spectra of the complexes, the presence of the diazepine –NH group is manifested by one band of sharp and strong intensity (3340–3380 cm⁻¹). In all complexes, a strong shift (ca. 20 cm⁻¹) is observed in the band at 1695 and 1678 cm⁻¹, with respect to their position in the IR spectrum of the free ligand, indicating that only one lumazine is involved in the coordination to the metal ion. The absorption band located at 1555 cm⁻¹, in the IR spectra of the free ligand, is shifted (ca. 5–10 cm⁻¹) in the complexes, indicating the involvement of the N5 atom in coordination to the metal ion.⁴¹¹H, ¹³C and ¹H-¹⁵N HMBC NMR experiments in DMSO-d₆ solution for the isolated complexes have also been performed. Within the experimental error, the spectra of the complexes are very similar to the free ligand's spectrum because the coordination through the nitrogen N5 and N1F atoms does not lead to electronic density changes strong enough to be reflected in the spectra; of course, the weak coordination through the carbonyl O4 oxygen does not either.²⁹

Luminescence properties

The d¹⁰ metal complexes have been investigated for luminescent properties and potential application as photoactive materials. Table 2 shows the absorption and emission data of the title compounds in CH₃CN solution (10⁻⁵ M) at room temperature. The ligand exhibits absorption bands at 240 nm and 330 nm due to π–π* transitions. The absorption spectra of the complexes and DLMBZD are almost identical. In Fig. 4, emission spectra of DLMBZD and complexes at λ_exc = 225 nm are shown. To establish the origin of the emission, we investigated the luminescent properties of the free ligand. It shows two emissions at 290 and 370 nm when excited at 225 nm. Another emission appears at 470 nm (λ_exc = 420 nm).

Fig. 4 Emission spectra of compounds 1–10 in CH₃CN solution at room temperature (λ_exc = 225 nm).

Table 2 Luminescence data for the ligand DLMBZD and the title complexes

Compound	UV-Vis (nm)	λ max excitation (nm)	λ max emission (nm)
a Low intensity.
DLMBZD 1	250, 330	225, 420	290, 370, 470
2	245, 330	225, 380	290, 350, 450^a
3	245, 330	225	290, 350
4	245, 330	225, 375	330, 470
5	245, 330	225, 380	290, 450^a
6	245, 330	228	290^a
7	245, 330	225, 380	290, 355,^a 450^a
8	245, 330, 400	225	No emission
9	245, 330, 400	225, 375	290, 460
10	245, 325, 400	225, 380	290, 470

---

In general, the emission bands of complexes resemble those of the free organic precursor indicating that they are all ligand-based emissions.³⁰ The behavior observed in the intensity and energy of emissions can be probably due to the differences of anions and coordination environments around metal ions because luminescence is closely associated with the local environments around metal ions. The intensity of emissions is found to be weak suggesting that the metal ion partially quenches the emissions from the ligand except for compound 2 in which the luminescence found at 290 nm is enhanced.³¹ Such an effect is the highest in mercury(II) compounds as a consequence of the heavy-atom effect.

Computational chemistry

Assessment of theoretical approaches. In order to assess the performance of the density functionals used in this research a two-fold strategy has been used. Thus, in the first stage, the theoretical geometries of the complexes have been compared to the experimental XRD data when available, i.e., for ZnCl₂L, ZnBr₂L, ZnI₂L, CdCl₂L, CdI₂L and HgI₂L (for simplicity, hereafter the DLMBZD ligand will be denoted as L). The parameter used for such a comparison has been the root mean square deviation (RMS) of the theoretical data with respect to the experimental ones. The RMS has been calculated per type of internal coordinate, namely, bond lengths, bond angles and torsion angles.

In addition, two moieties are considered, the ligand L itself and the coordination sphere. The reason for that separation is the structure of those moieties is estimated with a significant difference of accuracy both experimentally and theoretically. Hence, those geometrical parameters characterizing the coordination sphere, which involved the transition metals as well as the halogen atoms (Table 3, lower limit of the experimental error interval), are determined with the highest accuracy with the XRD technique since the X-rays interact with the electrons, so the higher the electron density the higher the accuracy. Conversely, those atoms with the highest electron density are the most complicated to simulate at the theoretical level, then the accuracy for the calculated parameters of the coordination sphere is the lowest. The contrary occurs for the intraligand geometrical data since only second period atoms are involved, so the experimental error is higher than that for the coordination sphere and the theoretical one lower since there are less layers of electrons to simulate.

Table 3 Experimental error for XRD-data and theoretical RMS for bond lengths (Å) and bond angles (°) in the coordination sphere

System	Exp. error, 3σ	SOGGA11X	CAM-B3LYP	B3LYP	B3LYP-D3	ωB97XD
RMS bond lengths (Å)
ZnCl2L	0.006–0.030	0.142	0.145	0.152	0.130	0.126
ZnBr2L	0.002–0.018	0.158	0.162	0.175	0.149	0.139
ZnI2L	0.003–0.045	0.163	0.170	0.180	0.148	0.141
CdCl2L	0.006–0.030	0.069	0.070	0.089	0.082	0.056
CdI2L	0.002–0.036	0.091	0.094	0.120	0.103	0.075
HgI2L	0.021–0.045	0.140	0.138	0.176	0.145	0.122
RMS bond angles (°)
ZnCl2L	0.6–2.7	5.6	5.6	5.4	5.7	5.8
ZnBr2L	0.3–1.2	6.4	6.0	5.5	6.8	6.8
ZnI2L	0.6–3.0	9.1	8.4	7.9	9.7	9.5
CdCl2L	0.6–2.1	4.6	4.6	4.4	4.9	5.3
CdI2L	0.6–2.4	7.8	7.7	7.1	10.6	11.2
HgI2L	0.6–3.0	6.2	6.0	5.7	11.8	11.7

---

Therefore, Fig. 5 shows the RMS as well as the experimental error for intraligand bond lengths (up) and angles (down). It can be observed that the RMSs are always lower than the experimental error regardless of the theoretical approach except for the bond lengths of ZnBr₂L which shows a rather low experimental error for this internal coordinate with respect to the other complexes. Thus, as far as the bond lengths and bond angles of the ligand are concerned the theoretical methods simulate them within the experimental error. The torsion angles of these complexes are estimated in general, out of the experimental error irrespective of the moiety considered.

Fig. 5 Comparison between the experimental error and the theoretical RMS for intraligand bond lengths (Å, up) and angles (°, down). Symbols: black points, ligand; circles, ZnCl₂L; diamonds, ZnBr₂L; squares, ZnI₂L; crosses, CdCl₂L; triangles, CdI₂L; stars, HgI₂L. Experimental error 3σ (Å, up): hyphen-double dots, ZnI₂L/HgI₂L; hyphen-dots, CdI₂L; dots, ZnCl₂L/CdCl₂L; hyphens, ZnBr₂L; solid line, free ligand. Experimental error 3σ (°, down): hyphen-double dots, ZnI₂L/HgI₂L; hyphens, ZnCl₂L; hyphen-dots CdI₂L; dots CdCl₂L; solid line, ligand/ZnBr₂L.

Other interesting observations are that all the density functionals follow a similar pattern for the different RMSs of the intraligand bond lengths and bond angles. Hence, for bond lengths the order of the RMSs is ‘HgI₂L > ZnBr₂L > CdCl₂L > CdI₂L ≈ ZnI₂L ≈ ZnCl₂L > Ligand’ for all the theoretical approaches but for B3LYP and B3LYP-D3 for which ZnBr₂L > HgI₂L. As regards the bond angles the order is ‘HgI₂L > ZnI₂L > ZnBr₂L ≈ ZnCl₂L > CdI₂L > CdCl₂L > Ligand’ but with some minor exceptions.

As for the coordination sphere, the RMS data reported in Table 3 show values one or two orders of magnitude higher than the experimental error irrespective of the density functional. In addition, it can be observed that ωB97XD/B3LYP is the density functional that yields the lowest/highest RMSs for bond lengths irrespective of the complex. Conversely, for the bond angles almost the opposite behavior is observed. Since one of the aims of this research is to characterize the bonding pattern within the coordination sphere, this lack of accuracy in the estimation of its theoretical geometry makes it necessary to conduct further tests to determine the performance of the density functionals. Therefore, the second stage of assessment has been carried out by using some calculated parameters concerning the coordination sphere, namely, atomic charges and magnitudes of the electron density surface obtained under the Atoms in Molecules (AIM) theory; for instance, the electron density (ρ) of the Bond Critical Points (BCPs) as well as their Laplacian (∇²ρ). These parameters have been worked out for both the experimental geometries and the theoretical ones; provided similar patterns of behavior for these parameters were obtained for both types of structures, similar conclusions could be drawn for the bonding inside the coordination sphere (almost) irrespective of the quality of the geometry.

In this way, Table 4 reports the atomic charges obtained within both NBO and AIM frames for the experimental and theoretical structures of the target moiety, estimated with the approach CAM-B3LYP/DZP-DKH//CAM-B3LYP/LANL2DZ (it should be noted that all the theoretical approximations yield similar values for the atomic charges, Table S-03†). Thus, only small differences arise for the geometries that have been considered, the maximum amounting to ∼7% for the O4B atom. Furthermore, the absolute values of the charges for the atoms involved in the coordination sphere follow similar patterns regardless of the geometry. For example, the order observed for this parameter in ZnCl₂L is q(Zn) > q(Cl1,Cl2) > q(N5B,N1F,O4B) within the NBO scheme and ZnCl₂L is q(Zn) > q(N5B,N1F,O4B) > q(Cl1,Cl2)> for the AIM one independent of the used geometry.

Table 4 NBO and AIM atomic charges (a.u.) for both the experimental and theoretical optimized geometries

System	Atom	CAM-B3LYP				System	Atom	CAM-B3LYP				System	Atom	CAM-B3LYP
		Exp. Geometry		Theor. geometry				Exp. geometry		Theor. geometry				Exp. geometry		Theor. geometry
		NBO	AIM	NBO	AIM			NBO	AIM	NBO	AIM			NBO	AIM	NBO	AIM
ZnCl2L	Zn	1.05	1.14	1.09	1.15	CdCl2L	Cd	1.21	1.04	1.22	1.06	HgCl2L	Hg			1.10	0.94
	Cl2	−0.64	−0.79	−0.66	−0.79		Cl2	−0.69	−0.79	−0.71	−0.80		Cl2			−0.64	−0.64
	Cl1	−0.63	−0.78	−0.65	−0.78		Cl1	−0.69	−0.77	−0.69	−0.77		Cl1			−0.60	−0.61
	N5B	−0.52	−1.06	−0.52	−1.07		N5B	−0.51	−1.04	−0.51	−1.03		N5B			−0.48	−1.02
	N1F	−0.57	−1.13	−0.54	−1.10		N1F	−0.57	−1.12	−0.54	−1.11		N1F			−0.53	−1.07
	O4B	−0.57	−1.11	−0.61	−1.06		O4B	−0.60	−1.14	−0.64	−1.08		O4B			−0.64	−1.06
ZnBr2L	Zn	0.85	0.99	0.89	1.00	CdBr2L	Cd			1.01	0.91	HgBr2L	Hg			0.87	0.77
	Br2	−0.54	−0.72	−0.56	−0.74		Br2			−0.60	−0.78		Br2			−0.52	−0.65
	Br1	−0.53	−0.71	−0.55	−0.72		Br1			−0.58	−0.75		Br2			−0.49	−0.61
	N5B	−0.51	−1.08	−0.52	−1.08		N5B			−0.51	−1.03		N5B			−0.48	−1.03
	N1F	−0.57	−1.13	−0.54	−1.10		N1F			−0.54	−1.11		N1F			−0.53	−1.10
	O4B	−0.56	−1.12	−0.61	−1.05		O4B			−0.64	−1.06		O4B			−0.64	−1.07
Znl2L	Zn	0.74	1.05	0.79	1.06	Cdl2L	Cd	0.88	0.90	0.90	0.95	Hgl2L	Hg	0.79	0.71	0.77	0.71
	I2	−0.49	−0.76	−0.50	−0.77		I2	−0.54	−0.79	−0.55	−0.81		I3	−0.48	−0.63	−0.47	−0.64
	I1	−0.47	−0.74	−0.50	−0.77		I1	−0.53	−0.80	−0.54	−0.80		I2	−0.46	−0.62	−0.45	−0.65
	N5B	−0.52	−1.04	−0.52	−1.01		N5B	−0.51	−1.08	−0.50	−1.02		N5B	−0.49	−1.02	−0.47	−0.99
	N1F	−0.58	−1.06	−0.55	−1.08		N1F	−0.55	−1.11	−0.53	−1.10		N1F	−0.55	−1.10	−0.52	−1.11
	O4B	−0.56	−1.10	−0.60	−1.05		O4B	−0.61	−1.11	−0.64	−1.07		O4B	−0.61	−1.13	−0.64	−1.06

---

Moreover, Fig. 6 shows the values of the BCPs’ electron density (up) and their Laplacian (down) for the metal–halogen bonds (M–X) in the studied complexes with the two geometries being tested. Hence, it is observed for the series of Zn complexes as well as for the two components of the Cd one for which an experimental structure exist that both XRD (triangles and circles) and theoretical (squares and diamonds) geometries yield the same pattern of electron density and Laplacian decay, i.e., (ρ,∇²ρ)(ZnCl₂L) > (ρ,∇²ρ)(ZnBr₂L) > (ρ,∇²ρ)(ZnI₂L)/(ρ,∇²ρ)(CdCl₂L) > (ρ,∇²ρ)(CdI₂L). Likewise, the series of iodides shows the same pattern for both geometries, i.e., ρ(HgI₂L) ≈ ρ(ZnI₂L) > ρ(CdI₂L) and ∇²ρ(CdI₂L) > ∇²ρ(HgI₂L) ≈ ∇²ρ(ZnI₂L). It must be added that all the theoretical approximations produce similar values and patterns of behavior for the AIM data (Table S-04†).

Fig. 6 Electron density (up) and Laplacian of the electron density (down) for the metal–halogen bonds (CAM-B3LYP). Theoretical data: circles, M–X1; diamonds, M–X2. Experimental data: triangles, M–X1; squares, M–X2 (M–X, M: Zn, Cd, Hg; X: Cl, Br, I).

As a conclusion, it can be set forth that despite their low accuracy simulating the geometry of the coordination sphere, our theoretical models are still useful to analyze its bonding scheme.

Topology of the electron density: AIM analysis. Fig. 7, S-01 and S-02† show the topology of the electron density surface of the metal cation and the atoms linked to it for three examples of the target complexes, i.e., ZnBr₂L, CdCl₂L and HgI₂L, and the remaining compounds exhibit a similar appearance. As expected, the topology is correct, the BCPs exist between the transition metal and the atoms bonded to it; the BCPs and the atoms are joined by a Bond Path (BP) and an Interatomic Surface (IAS) (pseudo)perpendicular to the different BPs is found.

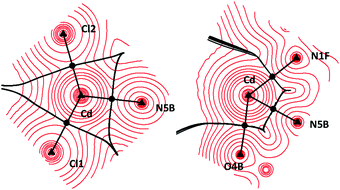Fig. 7 Topology of the CdCl₂L electron density surface. Triangles: atoms. Circles: bond critical points.

Fig. 6 along with the data reported in Table S-04† for all the theoretical approaches reveal the positive values of the BCPs’ Laplacian which means that they are minima of the electron density surface and consequently, the electron charge is shifted towards the bonded atoms, i.e., the interaction between the metal cation and the remaining atoms of the coordination sphere has a non-covalent nature irrespective of the transition metal and halogen atoms.

The previous feature is further confirmed by an analysis of the Molecular Orbitals (MOs) for the title compounds. Thus, Tables 5 and S-05,† reporting the composition of the MOs as a function of the atomic orbitals (only contributions ≥0.05, i.e. ≥5% are considered), show only a few MOs involving both the transition metal and the atoms bonded to it. In addition, those contributions are smaller than 0.15 (15%) for either the transition metal and/or the different atoms coordinated to it. This feature suggests that the covalent component of the bonding scheme for the coordination sphere is low. Furthermore, the presence of neat electron charges both on the transition metal and the atomic species surrounding it suggests that the bonding within the coordination sphere is of ionic nature (Tables 4 and S-03,† see the Population analysis section for further explanation).

Table 5 Molecular orbitals for the coordination sphere of Zn(II) and Cd(II) complexes (CAM-B3LYP/DZP-DKH)

System	MO	Description	System	MO	Description
ZnCl2L	HOMO−8	Cl1 p = 0.48; Cl2 p = 0.28; Zn p = 0.07	CdCl2L	HOMO−9	Cl2 p = 0.55; Cl1 p = 0.12; Cd p = 0.05
	HOMO−62	Zn d = 0.25; N1F p = 0.06		HOMO−62	Cd d = 0.29; N1F p = 0.06
	HOMO−65	O4B p = 0.26; Zn d = 0.12; O4B s = 0.08		HOMO−67	O4B p = 0.27; Cd d = 0.18; O4B s = 0.07
ZnBr2L	HOMO−7	Br1 p = 0.37; Br2 p = 0.35; Zn p = 0.08	CdBr2L	HOMO−7	Br1 p = 0.48; Br2 p = 0.30; Cd p = 0.07
	HOMO−8	Br2 p = 0.41; Br1 p = 0.17; Zn p = 0.06; Zn s = 0.06		HOMO−8	Br2 p = 0.52; Br1 p = 0.12; Cd p = 0.06; Cd s = 0.06
	HOMO−62	Zn d = 0.20; N1F p = 0.05		HOMO−62	Cd d = 0.38; N1F p = 0.07
	HOMO−65	O4B p = 0.25; Zn d = 0.13; O4B s = 0.08		HOMO−67	O4B p = 0.28; Cd d = 0.21; O4B s = 0.07
ZnI2L	HOMO−5	I1 p = 0.49; I2 p = 0.35; Zn p = 0.10	CdI2L	HOMO−5	I1 p = 0.56; I2 p = 0.26; Cd p = 0.10
	HOMO−8	I2 p = 0.21; I1 p = 0.12; Zn s = 0.05		HOMO−7	I2 p = 0.42; I1 p = 0.10; Cd s = 0.07; Cd p = 0.07
	HOMO−65	O4B p = 0.23; Zn d = 0.17; O4B s = 0.07		HOMO−62	Cd d = 0.35; N1F p = 0.07
				HOMO−67	O4B p = 0.27; Cd d = 0.22; O4B s = 0.07

---

Population analysis: NBO and AIM. As it can be observed in Tables 5 and S-03,† both schemes, NBO and AIM, are coincident, with all the theoretical approaches, allocating a positive charge ca. +1 (a.u.) or lower on the transition metals and negative charge on the atoms surrounding it. Likewise, it is observed that those negative charges are overestimated in AIM with respect to NBO ones. These observations along with those written down in the previous section lead to the conclusion that the bonding within the coordination sphere has a strong ionic nature.

Anyway, further and throughout the analysis of the charge allocated on the different atoms allows us to obtain some interesting details about the already commented bonding pattern. Hence, focusing on the charge placed on the transition metals and the halogen atoms, NBO and AIM produce a somewhat complementary view of the charge distribution. For the series MCl₂L/MBr₂L/MI₂L (M = Zn, Cd, Hg), it is observed in Tables 5 and S-03† that the absolute values of the NBO charges on the transition metal and the halogen atoms decrease in the order MCl₂L > MBr₂L > MI₂L. The previous behavior has been already observed for the positive value of the Laplacian at the BCPs (Fig. 6), which determines the non-covalent character of the studied complexes.

Therefore, within the frame of Pearson's Hard-Soft Acid–Base (HSAB) theory, it can be argued that the ionic character of the M–Halogen bonds decreases as the softness of the halogen atoms (bases) increases, and makes sense. AIM charges fail to reproduce this behavior, since the values of the negative charges on the halogen atoms are less sensitive to their softness and the change for the metal charge follows the order MCl₂L > MI₂L > MBr₂L.

On its side, AIM describes a decrease of the positive charge on the metals for the series ZnX₂L/CdX₂L/HgX₂L (X = Cl, Br, I) as their softness increases, i.e., ZnX₂L > CdX₂L > HgX₂L, which can be interpreted in the same terms commented on previously, and the ionic character of the complexes decreases as the metal softness increases. However, the explanations for the evolution of the halogen AIM charges are less simple since their negative values slightly increase from ZnX₂L to CdX₂L and then decreases to HgX₂L.

With regard to the atoms of the ligand (L) bonded to the metals, N5B, N1F and O4B, it is observed (Tables 5 and S-03†) that both methods exhibit a similar behavior with all the density functionals, and almost no dependence of the negative charge of these atomic species is observed as a function of the halogen atom for each transition metal. In addition, only a very slight dependence with the transition metal is observed which suggests that the main contribution to the charge of these atoms can be due to the chemical environment of the ligand itself.

Finally, an interesting point to comment consists of the fact that despite the fact that bivalent cations (Zn²⁺, Cd²⁺ and Hg²⁺) were used to synthesize the target compounds, the charge allocated on them is ca. +1 (a.u.) or lower, so it implies electron donation from the ligand atoms bonded to them as well as from the halogens. This feature can be analyzed through the NBO scheme by using the second order elements of the Fock matrix. Therefore, it can be observed in Table 6 that, as expected, the donor natural orbitals correspond to lone pairs of the atoms linked to the transition metal. Likewise, it is checked that the main contributions to the stabilization of the coordination sphere are due to the donations coming from the halogen atoms for chlorides and bromides as well. However, for the iodides, NBO shows a discrepancy with respect to the general picture here depicted that consist of NBO yielding a covalent bond among the transition metals and the iodine atoms. This is the reason for the lack of contributions from the iodine atoms to the central cation (Table 6). Anyway, considering the positive values of the Laplacian on the BCPs for the metal–halogen bonds (Fig. 6) joined to the low occurrence of MOs with a significant participation of the involved atomic species, our opinion is that NBO exaggerates the covalent character of these bonds for the target complexes. Also, this situation can be interpreted as a borderline case that supports the decrease of the ionic character of the metal–halogen bonding as a function of the halogen atom softness.

Table 6 NBO analysis. second order contributions to the Fock matrix (kcal mol⁻¹). ωB97XD/DZP-DKH

Donor^a	Acceptor^b	ZnCl2L	ZnBr2L	ZnI2L^c	CdCl2L	CdBr2L	CdI2L^c	HgCl2L	HgBr2L	HgI2L^c
a LP: occupied lone pair orbital. X: Cl, Br, I. b LP*: virtual lone pair orbital. M: Zn, Cd, Hg. c Since NBO yields covalent bonding between the metals and the iodide anions, the second order contributions for M⋯X1 and M⋯X2 have not been considered in this analysis due to their low significance.
LP(1)X1	→LP*(7)M	25.9	39.1		20.5	30.7		28.1	38.1
LP(4)X1	→LP*(6)M	88.0	104.4		71.2	89.6		127.7	171.3
LP(4)X1	→LP*(7)M	73.0	88.4		60.5	76.9		18.5	23.1
LP(1)X2	→LP*(7)M	21.1	35.3		15.6	27.5		23.8	15.0	11.2
LP(3)X2	→LP*(7)M	13.6	12.2	13.0	10.5	11.3	11.8		32.0
LP(4)X2	→LP*(6)M	83.6	98.9		62.7	80.7		113.9	158.7
LP(4)X2	→LP*(7)M	68.7	84.2		58.6	75.6		16.9	21.6
LP(1)O4B	→LP*(9)M	13.6	19.3	20.8	17.2	17.7	18.5	12.4	12.7	13.6
LP(2)O4B	→LP*(9)M	10.4	14.0	14.0	12.8	13.7	14.9	11.0	10.9
LP(1)N1F	→LP*(6)M	21.1	21.9	12.4	12.9	13.0	10.4	13.8	13.6
LP(1)N1F	→LP*(8)M	23.5	13.3	18.3	12.6	14.1	15.6
LP(1)N5B	→LP*(6)M	29.0	26.8	39.0	16.8	15.4	39.4	23.6	22.3	14.5
LP(1)N5B	→LP*(8)M	27.1	26.4		26.3	30.4			11.4

---

Analysis of the complexes stability. The interactions that contribute to the stability of the studied compounds can be divided into two groups. Of course, the main one consists of both interactions metal–ligand (M⋯L) and metal–halide (M⋯X). The second one is formed for those interactions of the type halide-ligand and intraligand. Thus, three of them have been considered in this study, two of the halide-ligand type X1⋯H6F–C6F and X2⋯C8AA=N8A (σ–π) and one of the intraligand type O4A⋯C4AB=N5B (σ–π).

In this context and within the NBO frame, Table 7 supports the summations of the second order contributions to the Fock matrix for each type of interaction, which allows us to do an analysis of its relative contribution to the stability of the complexes. As expected, the main contributions are due to the metal–halide as well as metal–ligand interactions. The highest values are obtained for M⋯X components which are comprised in the range of 140–250 kcal mol⁻¹ being stronger for M⋯Br than for M⋯Cl irrespective of the metal cation. Then, the metal–ligand links are one order of magnitude lower in energy than M⋯X ones with values that are included in the interval 10–60 kcal mol⁻¹ (an exception is the Hg⋯N1F for which no data have been recorded). Finally, the weakest contributions to the stability of the target complexes are those of the types, halide-ligand and intraligand, and their energy range is around 0–4 kcal mol⁻¹. A rough estimation of the relative contribution of all those interactions to the stability of the target compounds on the basis of the NBO data yields that M⋯X interactions contribute ∼70–85% of the stabilization energy, M⋯L ones contribute ∼10–25% and halide-ligand/intraligand ones contribute ∼0.5–2%.

Table 7 ωB97XD second order contributions to the Fock matrix for interaction type (kcal mol⁻¹)

Interactions	ZnCl2L	ZnBr2L	Znl2L^a	CdCl2L	CdBr2L	Cdl2L^a	HgCl2L	HgBr2L	Hgl2L^a
a Since NBO yields covalent bonding between the metals and the iodide anions, the second order contributions for M⋯X1 and M⋯X2 have not been considered in this analysis due to their low significance.
M⋯X2	186.9	242.9		147.4	195.2		154.6	227.2
M⋯X1	197.8	231.9		152.2	197.2		174.3	232.4
M⋯N5B	56.1	53.2	39.0	43.1	45.8	39.4	23.6	33.7	13.6
M⋯N1F	44.6	35.2	30.8	25.5	34.5	26.0	13.8	13.6	0.0
M⋯O4B	24.0	43.9	34.8	39.8	41.4	33.4	23.4	23.6	14.5
X2⋯C8AA=N8A	3.37	2.89	1.54	3.55	3.41	1.32	1.70	0.84	0.21
X1⋯H6F–C6F	2.62	2.02	2.29	2.70	1.82	1.84	1.83	0.90	0.97
O4A⋯C4AB=N5B	1.36	1.42	1.31	1.38	1.28	1.15	1.21	0.99	0.98

---

Atoms in Molecules theory support the previous analysis of the relative strength of the two groups of interactions. Thus, comparing the data appearing in Table S-04† for the main interactions, M⋯X/M⋯L, with those of Table S-06† for the halide-ligand/intraligand contact, it is observed for the electronic density (ρ) of the BCPs that the values for the main interactions are at least twice or three times higher than those for the weakest contributions. In addition, the ellipticity of the considered BCPs for the former interactions is lower than that of the latter interactions, which implies that the electronic charge is more dispersed in the latter and so it points out to their weak conditions too.

Experimental

Materials and instrumentation

All starting materials were purchased from standard commercial sources and used without further purification. Solvents were reagent-grade commercial materials and were used as received. Elemental analyses were performed on a Thermo Finnigan Flash 1112 Series CHNS-O microanalyser. IR spectra were measured over the range of 4000–400 cm⁻¹ on a Bruker FT-IR Tensor-27 with samples prepared as KBr pellets. ¹H and ¹³C-NMR spectra were recorded in DMSO-d₆ solutions on a Bruker AVANCE 400 spectrometer. Fluorescence excitation and emission spectra were recorded with a Cary Elipse fluorescence spectrophotometer in CH₃CN at room temperature.

Synthesis

All manipulations were performed under aerobic conditions using reagents (mainly from ALFA-AESAR) and solvents as received. The proligand 6-acetyl-1,3,7-trimethyllumazine (DLMAceM) was synthesized from 6-amino-1,3-dimethyl-5-nitrosouracil and acetylacetone following a reported method.²² Characterization data (elemental analysis, MS, IR and NMR) fit well with the proposed formulae and structures; for more information, see the ESI.†

Synthesis of the ligand 2,4-bis-(1,3,7-trimethyl-pteridine-2,4(1H,3H)-dione-6-yl)-2,3-dihydro-2-methyl-1H-1,5-benzodiazepine DLMBZD·½H₂O (1). The preparation was carried out by reacting o-phenylendiamine (1.08 g, 10 mmol) with the lumazine derivative (DLMAceM) (4.96 g, 20 mmol) in ethanol (50 mL). Acetic acid was used as a catalyst (ca. 1 mL). The mixture was refluxed for 25 h. The ligand was filtered off and isolated in a high yield (71%). After the main portion of DLMBZD was isolated, a red solid, identified as 6-[N-(2-aminophenyl)ethanimidoyl]-1,3,7-trimethylpteridine-2,4(1H,3H)-dione (DLMOfen), was obtained (yield ca. 12%).

Synthesis of [ZnCl₂(DLMBZD)]·CH₂Cl₂·H₂O (2). A solution of DLMBZD·½H₂O (57.8 mg, 0.1 mmol) and ZnCl₂ (13.6 mg, 0.1 mmol) in dichloromethane (40 mL) was stirred for 45 min and cooled to room temperature. The mixture was then filtered, and the final product was obtained as an orange solid (yield, 61%). Red crystals were formed after several days in a closed container with the solution placed in a refrigerator.

Synthesis of [ZnBr₂(DLMBZD)]·CH₂Cl₂ (3). This complex was obtained via an analogous procedure to that described for 2, but using zinc(II) bromide instead of ZnCl₂ (yield, 82%). After several days, X-ray quality red crystals were obtained from the mother liquor.

Synthesis of [ZnI₂(DLMBZD)]·CH₃CN (4). A mixture of ZnI₂ (63.8 mg, 0.2 mmol) and DLMBZD·½H₂O (115.5 mg, 0.2 mmol) in acetonitrile (30 mL) was refluxed for 14 h. The red reaction mixture was cooled and then filtered. Red crystals of the product slowly grew over a period of 5 days. The crystals were collected by filtration and dried in air (yield, 64%).

Synthesis of [CdCl₂(DLMBZD)] (5). To 0.2 mmol of the ligand dissolved in CH₃CN, ethanol or dichloromethane (30 mL), was added 0.2 mmol of the corresponding halide. The mixture was stirred for 1 h. The reaction mixture was filtered off to remove the precipitate. The formed solid was washed with ethanol, and air-dried (yield, 83%). From the clear liquor, crystals suitable for XRD were isolated.

[CdBr₂(DLMBZD)]·½CH₂Cl₂·H₂O (6). Using the same method as used for compound 5, an orange solid was isolated (yield, 85%).

[CdI₂(DLMBZD)] (7). Using the same method as used for compounds 5 and 6, orange crystals suitable for XRD were isolated (yield, 66%).

[HgCl₂(DLMBZD)]·H₂O (8). HgCl₂ (108.6 mg, 0.4 mmol) and DLMBZD·½H₂O (115.5 mg, 0.2 mmol) were added to 30 mL of CH₂Cl₂/EtOH (3 : 1) and the resulting orange solution was stirred for 50 min and cooled to room temperature. An orange solid was obtained from the mother liquor, it was filtered off, washed with ethanol and air-dried (yield, 82%).

[HgBr₂(DLMBZD)]·CH₂Cl₂ (9). To a stirred solution of DLMBZD·½H₂O (115.5 mg, 0.2 mmol) in a mixed CH₂Cl₂ : EtOH solution (15 : 5 mL) a solution of mercury(II) bromide (144.2 mg, 0.4 mmol) in CH₂Cl₂ (10 mL) was added. The resulting orange solution was stirred for 45 min and cooled to room temperature. An orange solid was obtained from the mother liquor, it was filtered off, washed with ethanol and air-dried (yield, 52%).

[HgI₂(DLMBZD)] (10). Mercury(II) iodide (90.9 mg, 0.2 mmol) was added to a solution of DLMBZD·½H₂O (115.5 mg, 0.2 mmol) in 30 mL of CH₃CN and stirred at ambient temperature for 5 h. Dark orange crystals suitable for X-ray diffraction were obtained several days later which were filtered off and air dried (yield, 72%). A few orange crystals with formula [HgI₂(DLMBZD)]₂[HgI₂]·2CH₃CN (11) were formed in a closed container with the solution placed in a refrigerator after several days.

Crystallography

Details of the crystallographic data collection and refinement parameters are given in Table 8. The structures were solved by direct methods and refined using SHELXL-2014/7 ³² employing full-matrix least-squares methods on F². Lorentz, polarization, and multiscan absorption corrections were applied with SADABS.³³ All non-hydrogen atoms were refined with anisotropic thermal parameters by full matrix least-squares procedures on F². In the structure of the free ligand, the hydrogen N–H atom from the benzodiazepine ring was located and refined isotropically; other hydrogen N–H and C–H atoms in the free ligand and complexes were also placed in idealized positions, and treated using riding models; O–H hydrogens were not found. All calculations and graphics were made with PLATON and MERCURY.³⁴

Table 8 Crystallographic and refinement data for DLMBZD (1), [ZnCl₂(DLMBZD)]·CH₂Cl₂·H₂O (2), [ZnBr₂(DLMBZD)]·CH₂Cl₂ (3), [ZnI₂(DLMBZD)]·CH₃CN (4), [CdCl₂(DLMBZD)] (5), [CdI₂(DLMBZD)] (7), [HgI₂(DLMBZD)] (10) and 2[HgI₂(DLMBZD)]·HgI₂·2CH₃CN (11)

Compound	1	2	3	4	5	7	10	11
CCDC number	988017	988018	988019	988020	991525	988021	988022	988023
Formula	C28H28N10O4·⅓H2O	C28H28Cl2N10O4Zn·½CH2Cl2·1½H2O	C28H28Br2N10O4Zn·CH2Cl2	C28H28I2N10O4Zn·1½CH3CN	C28H28Cl2N10O4Cd	C28H28I2N10O4Cd	C28H28I2N10O4Hg	C28H28I2N10O4Hg·½HgI2·CH3CN
FW (g mol^−1)	577.61	774.36	878.72	949.35	751.90	934.80	1022.99	1291.24
Color. habit	Colorless prism	Red prism	Red prism	Red prism	Red prism	Red prism	Orange prism	Orange prism
Crystal size (mm^3)	0.22 × 0.20 × 0.08	0.30 × 0.23 × 0.06	0.35 × 0.26 × 0.16	0.36 × 0.26 × 0.10	0.32 × 0.14 × 0.10	0.30 × 0.20 × 0.18	0.53 × 0.23 × 0.08	0.33 × 0.31 × 0.20
Crystal system	Triclinic	Orthorhombic	Orthorhombic	Orthorhombic	Orthorhombic	Orthorhombic	Orthorhombic	Monoclinic
Space group	P1̄	Pbca	Pbca	Pbca	Pna21	Pna21	Pna21	P21/c
Unit cell dimens. a (Å)	11.214(2)	13.269(5)	13.226(1)	13.574(1)	14.898(2)	14.988(1)	15.031(5)	11.257(2)
b (Å)	13.319(1)	17.848(4)	17.912(3)	18.296(3)	15.081(3)	15.329(4)	15.388(5)	16.968(2)
c (Å)	18.141(3)	28.167(9)	28.272(3)	28.833(5)	13.166(3)	14.063(2)	14.032(5)	19.592(2)
α (°)	93.53(1)	90	90	90	90	90	90	90
β (°)	90.17(1)	90	90	90	90	90	90	101.889(9)
γ (°)	102.74(1)	90	90	90	90	90	90	90
Volume (Å^3)	2637.5(7)	6671(4)	6698(1)	7161(2)	2958(1)	3231.2(9)	3246(1)	3661.8(9)
Z	4	8	8	8	4	4	4	4
Density (calc. Mg m^−3)	1.455	1.542	1.743	1.761	1.688	1.922	2.094	2.342
μ (mm^−1)	0.103	1.033	3.332	2.464	0.974	2.637	6.695	8.870
F (000)	1212	3184	3520	3736	1520	1808	1936	2396
Diffractometer	Bruker Nonius Kappa CCD
Radiation	Graphite-monochromated MoKα (λ = 0.71073 Å)
Temperature (K)	120(2)
θ range (°)	3.07–27.5	2.11–27.51	5.02–27.5	3.03–27.51	3.05–27.51	3.80–27.53	3.93–27.51	3.32–27.51
Index ranges	−14 < h < 14	−17 < h < 17	−17 < h < 17	−15 < h < 17	−19 < h < 19	−19 < h < 17	−19 < h < 19	−14 < h < 14
	−17 < k < 17	−23 < k < 23	−15 < k < 23	−23 < k < 23	−19 < k < 19	−17 < k < 18	−17 < k < 19	−22 < k < 22
	−23 < l < 23	−36 < l < 36	−36 < l < 36	−37 < l < 37	−17 < l < 17	−18 < l < 18	−17 < l < 18	−25 < l < 25
Reflecs collected	67 937	161 999	66 668	67 480	28 953	29 719	23 670	55 643
Indep./I > 2σ(I)	12 105/5758	7678/4755	7649/5563	8219/5877	6722/4981	7371/6111	7257/6089	8404/6299
R int	0.0874	0.1459	0.0718	0.0759	0.1050	0.0604	0.0621	0.0638
Weighting scheme w^−1 = σ^2(Fo^2) + (xP)^2 + yP (P = (Fo^2 + 2Fc^2)/3)
x/y	0.1700/0.0500	0.1000/20.0000	0.0370/36.0000	0.1035/40.1806	0.0700/0.0000	0.0755/0.0000	0.0500/2.0000	0.0400/16.0000
Data/param. Ratio	15.4	16.8	17.7	18.8	16.5	18.1	17.9	18.8
Goodness-of-fit on F^2	1.006	1.020	1.042	1.058	0.994	0.996	0.916	1.150
R 1/wR2 [I > 2σ(I)]	0.0830/0.2153	0.0688/0.1684	0.0527/0.1063	0.0524/0.1244	0.0487/0.1111	0.0404/0.0995	0.0352/0.0835	0.0376/0.0854
R 1/wR2 (all data)	0.1820/0.2867	0.1267/0.2034	0.0863/0.1196	0.0856/0.1404	0.0832/0.1288	0.0594/0.1149	0.0509/0.0936	0.0664/0.0972
Flack parameter	—	—	—	—	0.01(4)	0.03(3)	0.039(7)	—

---

Computational details

The geometry optimization as well as the vibrational spectrum calculation of the ligand and transition metal complexes were conducted by using the same series of density functionals, namely SOGGA11X,³⁵ ωB97XD,³⁶ CAM-B3LYP,³⁷ B3LYP³⁸ and B3LYP implementing Grimme's D3 dispersion correction scheme with the original damping function³⁹ (B3LYP-D3) through empirical dispersion = gd3 command. An all electron-DZP basis set⁴⁰ was used on all atoms for calculations involving the ligand. Moreover, the LANL2DZ-ECP basis set⁴¹ was used on all atoms for transition metal complex calculations. As for the complexes, single point relativistic calculations were performed in order to produce Natural Bond Analysis⁴² (NBO) data and a wave function to be used in an analysis of the electronic density. Those calculations were accomplished with the same series of density functionals commented previously within the second order Douglas–Kress–Hall scheme.⁴³ In addition, the DZP–DKH basis set⁴⁴ was used which is optimized for relativistic calculations. Finally, the electron density analysis was accomplished by using the Atoms in Molecules theory⁴⁵ implemented in the AIM2000 code.⁴⁶

Conclusions

The zinc, cadmium and mercury complexes containing a 1,5-benzodiazepine derived from 6-acetyl-1,3,7-trimethyllumazine as a ligand and perchlorate, chloride, bromide and iodide counter anions have been isolated. Metals are (2 + 2 + 1)-coordinated as a square-based pyramid with increasing trigonality from Hg to Zn. The benzodiazepine ligand acts as a N,N,(O)-tridentate chelator through nitrogen atoms from the diazepine and pyrazine moieties and also, semi-coordination of an exocyclic carbonylic oxygen can be found. To coordinate the metal, the ligand undergoes drastic stereochemical changes, because it has to be folded due to the interactions established between the electronic density of pyrimidine and pyrazine rings from the pteridine moieties with a coordinated halide and a carbonyl group.

The analysis of the topology of the electron density surface within the Atoms In Molecules (AIM) frame along with an analysis of the atomic charge distribution and the second order contributions to the Fock matrix within the Natural Bond Orbitals (NBO) scheme lead to the conclusion that the bonding for the coordination sphere of the series of complexes under study has mainly an ionic nature that decreases as the softness of both the group 12 transition metals and the halogen atoms bonded to them increase, which makes sense in view of Pearson's Hard-Soft Acid–Base (HSAB) theory. In addition, the analysis of the Molecular Orbitals (MO) for the target moiety supports the previous conclusions. All the density functionals used in this research (SOGGA11X, ωB97XD, CAM-B3LYP, B3LYP, and B3LYP with Grimme's D3 dispersion correction) yield similar results and patterns of behavior for most of the analyzed data. A rough estimation of the relative contribution of all those interactions to the stability of the target compounds on the basis of the NBO data yields that M⋯Y interactions contribute ∼70–85% of the stabilization energy, M⋯L ones contribute ∼10–25% and halide-ligand/intraligand ones contribute ∼0.5–2%.

Acknowledgements

Supported by the University of Jaén (Plan de Apoyo a la Investigación, al Desarrollo Tecnológico y a la Innovación), Junta de Andalucía (PAIDI groups FQM195, FQM273 and FQM337) and the State Secretariat for Research, Development and Innovation of Spanish Ministry of Economy and Competitivity (Project “Red de Excelencia MetalBio”, CTQ2015-71211-REDT). Computational resources supplied by the Centro de Servicios de Informática y Redes de Comunicaciones (CSIRC-University of Granada, Spain) are acknowledged.

Notes and references

1. M. J. Kukla and H. J. Berslin, J. Med. Chem., 1991, 34, 746.
2. L. O. Rundall and B. Kiappel, in Benzodiazepines, ed. S. Garattini, E. Mussini and L. O. Randall, Raven Press, New York, 1973, p. 27.
3. (a) C. S. Radatz, R. B. Silva, G. Perin, E. J. Lenardao, R. G. Jacob and D. Alves, Tetrahedron Lett., 2011, 52, 4132; (b) M. Abdollahi-Alibeik, I. Mohammadpoor-Baltork, Z. Zaghaghi and B. Yousefi, Catal. Commun., 2008, 9, 2496; (c) K. S. Atwal, J. L. Bergey, A. Hedberg and S. Moreland, J. Med. Chem., 1987, 30, 635; (d) M. D. Braccio, G. Grossi, G. Roma, L. Vargiu, M. Mura and M. E. Marongiu, Eur. J. Med. Chem., 2001, 36, 935.
4. H. Nakano, T. Inoue, N. Kawasaki, H. Miyataka, H. Matsumoto, T. Taguchi, N. Inagaki, H. Nagai and T. Satoh, Bioorg. Med. Chem., 2000, 8, 373.
5. (a) B. E. Evans, K. E. Rittle, M. G. Bock, R. M. DiPardo, R. M. Freidinger, W. L. Whitter, G. F. Lundell, D. F. Veber, P. S. Anderson, R. S. L. Chang, V. J. Lotti, D. J. Cerino, T. B. Chen, P. J. Kling, K. A. Kunkel, J. P. Springer and J. Hirshfield, J. Med. Chem., 1988, 31, 2235; (b) H. Schutz, Benzodiazepines, Springer, Heidelberg, 1982; (c) D. A. Horton, G. T. Boume and M. L. Smythe, Chem. Rev., 2003, 103, 893; (d) R. R. Nadendla, Principles of Organic Medicinal Chemistry, New Age International Ltd, New Delhi, 2005, pp. 74, 83, 111.
6. M. A. Rogawski and R. J. Porter, Pharm. Rev., 1990, 42, 223.
7. G. H. Loew, J. R. Nienow and M. Poulsen, Mol. Pharmacol., 1984, 26, 19.
8. J. Spencer, R. P. Rathnam and B. Z. Chowdhry, Future Med. Chem., 2010, 2, 1441.
9. (a) K. S. Atwal, J. L. Bergey, A. Hedberg and S. Moreland, J. Med. Chem., 1987, 30, 635; (b) V. J. Merluzzi, K. D. Hargrave, M. Labadia, K. Grozinger, M. Skoog, J. C. Wu, C. K. Shih, K. Eckner, S. Hattox, J. Adams, A. S. Rosenthal, R. Faanes, R. J. Eckner, R. A. Koup and J. L. Sullivan, Science, 1990, 250, 1411; (c) A. Ursini, A. Capelli, R. A. E. Carr, P. Cassar, M. Corsi, O. Curcuruto, G. Curotto, M. D. Cin, S. Davalli, D. Donati, A. Feriani, H. Finch, G. Finizia, G. Gaviraghi, M. Marien, G. Pentassuglia, S. Polinelli, E. Ratti, A. Reggiani, G. Tarzia, G. Tedesco, M. E. Tranquillini, D. G. Trist and F. T. M. Van Amsterdam, J. Med. Chem., 2000, 43, 3596; (d) G. Grossi, M. D. Braccio, G. Roma, V. Ballabeni, M. Tognolini, F. Calcina and E. Barocelli, Eur. J. Med. Chem., 2002, 37, 933; (e) W. Nawrocka, B. Sztubab, A. Opolskic, J. Wietrzykc, M. W. Kowalskad and T. Glowiakd, Arch. Pharm. Pharm. Med. Chem., 2001, 334, 3; (f) Y. Ohtake and Y. Fukaya, Eur. Patent1820799A1, 2007.
10. (a) M. Froimowitz and V. Cody, J. Med. Chem., 1993, 36, 2219; (b) D. J. Lauffer and M. D. Mullican, Bioorg. Med. Chem. Lett., 2002, 12, 1225; (c) O. Nyanguile, F. Pauwels, W. Van den Broeck, C. W. Boutton, L. Quirynen, T. Ivens, L. Van der Helm, G. Vandercruyssen, W. Mostmans, F. Delouvroy, P. Dehertogh, M. D. Cummings, J. F. Bonfanti, K. A. Simmen and P. Raboisson, Antimicrob. Agents Chemother., 2008, 52, 4420; (d) K. Vandyck, M. D. Cummings, O. Nyanguile, C. W. Boutton, S. Vendeville, D. McGowan, B. Devogelaere, K. Amssoms, S. Last, K. Rombauts, A. Tahri, P. Lory, L. Hu, D. A. Beauchamp, K. Simmen and P. Raboisson, J. Med. Chem., 2009, 52, 4099.
11. (a) M. C. Aversa, A. Ferlazzo, P. Gionnetto and F. H. Kohnke, Synthesis, 1986, 230; (b) M. Essaber, A. Baouid, A. Hasnaoui, A. Benharref and J. P. Lavergne, Synth. Commun., 1998, 28, 4097; (c) J. X. Xu, H. T. Wu and S. Jin, Chin. J. Chem., 1999, 17, 84; (d) J. X. Xu, H. T. Wu and S. Jin, Chin. J. Chem., 1999, 17, 404; (e) K. V. V. Reddy, P. S. Rao and D. Ashok, Synth. Commun., 2000, 30, 1825; (f) A. M. El-Sayed, H. Abdel-Ghany and A. M. M. El-Saghier, Synth. Commun., 1999, 29, 3561; (g) W. Ried and E. Torinus, Chem. Ber., 1959, 92, 2902; (h) J. A. L. Herbert and H. Suschitzky, J. Chem. Soc., Perkin Trans. 1, 1974, 2657; (i) G. Papori and D. Babulal, Synth. Commun., 2010, 40, 1685; (j) K. Chun-Wei, W. Chun-Chao, K. Veerababurao and Y. Ching-Fa, Molecules, 2008, 13, 2313; (k) P. Xiang-Qiang, Z. Jian-Ping, H. Zhi-Hao and Z. Wei, Tetrahedron Lett., 2008, 49, 5302; (l) P. Aastha, K. Navneet, A. Anshu, S. Pratima and K. Dharma, Res. J. Chem. Sci., 2013, 3, 90.
12. (a) J. Gante, Angew. Chem., Int. Ed. Engl., 1994, 33, 1699; (b) C. D. Gutiérrez, A. Termin, P. Joshi, S. Hadida, D. Bergeron, S. Yoo and J. Cao, WO2008011190, 2004; (c) S. W. Goldstein, K. P. Longo, A. A. Nagel and J. A. Lowe, IIIUS6319915, 2000; (d) J. Jaquith, WO2007101347, 2007; (e) J. M. C. Golec, D. J. Lauffer, D. J. Livingston, M. D. Mullican, P. L. Nyce, A. L. C. Robidoux and M. W. Wannamaker, WO9824804, 1998; (f) M. Amblard, I. Daffix, P. Bedos, D. Pruneau, J. L. Paquet, J. M. Luccarini, P. Dodey and J. Martínez, J. Med. Chem., 1999, 42, 4185; (g) J. Gan and D. Ma, Org. Lett., 2009, 11, 2788; (h) G. M. Zats, M. Kovaliov, A. Albecka and S. Shatzmillerb, J. Pept. Sci., 2015, 21, 512.
13. (a) K. P. Jadhav and D. B. Ingled, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 1983, 22, 180; (b) L. Wang, X. Li and Y. An, Org. Biomol. Chem., 2015, 13, 5497; (c) Y. An, Z. Hao, Z. Zhang and L. Wang, Chem. Biol. Drug Des., 2016, 1.
14. R. J. Reddy, D. Ashok and P. N. Sharma, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 1993, 32, 404–406.
15. K. Satyanarayana and M. N. A. Rao, Indian J. Pharm. Sci., 1993, 55, 230.
16. G. Dessarro, A. Chimirri, A. Dessaro and R. Gitto, Chem. Abstr., 1995, 106, 11222g.
17. A. Leyva-Pérez, J. R. Cabrero-Antonino and A. Corma, Tetrahedron, 2010, 66, 8203 and references therein.
18. L. D. Fader, R. Bethell, P. Bonneau, M. Bös, Y. Bousquet, M. G. Coordingley, R. Coulombe, P. Deroy, A. M. Faucher, A. Gagnon, N. Goudreau, C. Grand-Maître, I. Guse, O. Hucke, S. H. Kawai, J. E. Lacoste, S. Landry, C. T. Lemke, E. Malenfant, S. Mason, S. Morin, J. O'Meara, B. Simoneau, S. Titolo and C. Yoakim, Bioorg. Med. Chem. Lett., 2011, 21, 398.
19. (a) C. Preti and G. Tosi, J. Coord. Chem., 1976, 6, 81; (b) C. Preti and G. Tosi, J. Inorg. Nucl. Chem., 1979, 41, 263; (c) C. Preti and G. Tosi, J. Coord. Chem., 1979, 8, 223.
20. (a) S. Zhang, I. Vystorop, Z. H. Tang and W. H. Sun, Organometallics, 2007, 26, 2456; (b) S. Zhang, W. H. Sun, X. F. Kuang, I. Vystorop and J. J. Yi, J. Organomet. Chem., 2007, 692, 5307; (c) S. G. Kang, J. S. Choi, K. H. Nam, H. P. Chun and K. M. Kim, Inorg. Chim. Acta, 2004, 357, 2783; (d) M. B. Hursthouse, S. J. Coles and M. B. Smith, Cambridge Structural Database Priv. Comm., XADYIL (CCDC ref. 216599), 2003; (e) M. B. Hursthouse, M. E. Light and M. B. Smith, Cambridge Structural Database Priv. Comm., IKEJIR (CCDC ref. 217986), 2003; (f) M. C. Aversa, P. Giannetto, G. Bruno, M. Cusumano, A. Giannetto and S. Geremia, J. Chem. Soc., Dalton Trans., 1990, 2433; (g) Z. Szeverenyi, V. Fulop, A. Kalman and L. I. Simandi, Inorg. Chim. Acta, 1988, 147, 135.
21. G. S. Bayes, S. S. Raut, V. R. Patil and R. S. Lokhande, J. Solution Chem., 2012, 41, 241–248.
22. Y. Kim, J. Kim and Y. Kang, J. Korean Chem. Soc., 1999, 43, 535.
23. P. S. Salve and D. S. Mali, Int. J. Pharma Bio Sci., 2013, 4, 345.
24. D. Cremer, B. Dick and B. Christeu, J. Mol. Struct.: THEOCHEM, 1984, 110, 277.
25. C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885.
26. (a) E. R. Acuña-Cueva, R. Faure, N. A. Illán-Cabeza, S. B. Jiménez-Pulido, M. N. Moreno-Carretero and M. Quirós-Olozábal, Polyhedron, 2003, 22, 483; (b) E. R. Acuña-Cueva, S. B. Jiménez-Pulido, M. N. Moreno-Carretero and M. Quirós-Olozábal, Struct. Chem., 2004, 15, 159; (c) D. Lin-Vien, N. B. Colthup, W. G. Fateley and J. G. Graselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, Academic Press, 1991.
27. (a) E. R. Acuña-Cueva, R. Faure, N. A. Illán-Cabeza, S. B. Jiménez-Pulido, M. N. Moreno-Carretero and M. Quirós-Olozábal, Inorg. Chim. Acta, 2003, 351, 356; (b) E. R. Acuña-Cueva, R. Faure, N. A. Illán-Cabeza, S. B. Jiménez-Pulido, M. N. Moreno-Carretero and M. Quirós-Olozábal, Inorg. Chim. Acta, 2003, 342, 209; (c) E. R. Acuña-Cueva, R. Faure, N. A. Illán-Cabeza, S. B. Jiménez-Pulido and M. N. Moreno-Carretero, Polyhedron, 2002, 21, 1961.
28. A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349.
29. (a) J. C. Jin, Y. Y. Wang, W. H. Zhang, A. S. Lermontov, E. K. Lermontova and Q. Z. Shi, Dalton Trans., 2009, 10181; (b) W. P. Wu, Y. Y. Wang, C. J. Wang, Y. P. Wu, P. Liu and Q. Z. Shi, Inorg. Chem. Commun., 2006, 9, 645.
30. C. Ren, P. Liu, Y. Y. Wang, W. H. Huang and Q. Z. Shi, Eur. J. Inorg. Chem., 2010, 5545.
31. R. S. Drago, Physical Methods in Chemistry, Saunders, Philadelphia, 1977.
32. (a) G. M. Sheldrick, SHELXL-2014/7, University of Göttingen, Germany, 2014; (b) L. J. Farrugia, WinGX 2014.1, University of Glasgow, Scotland, 1997–2014.
33. G. M. Sheldrick, SADABS 2.10, University of Göttingen, Germany, 2003.
34. (a) A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 2003; (b) Cambridge Crystallographic Data Centre MERCURY 3.8. Cambridge, England, 2001–2016.
35. R. Peverati and D. G. Truhlar, J. Chem. Phys., 2011, 135, 191102.
36. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
37. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51.
38. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
39. S. Grimme, J. Anthony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
40. (a) A. Canal-Neto, E. P. Muniz, R. Centoducatte and F. E. Jorge, J. Mol. Struct.: THEOCHEM, 2005, 718, 219; (b) G. G. Camiletti, S. F. Machado and F. E. Jorge, J. Comput. Chem., 2008, 29, 2434; (c) C. L. Barros, P. J. P. de Oliveira, F. E. Jorge, A. Canal-Neto and M. Campos, Mol. Phys., 2010, 108, 1965.
41. (a) T. H. Dunning Jr. and P. J. Hay, Methods of Electronic Structure Theory, ed. H. F. Schaefer III, Plenum Press, 1977, vol. 2; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 284; (d) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
42. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
43. (a) M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89; (b) B. A. Hess, Phys. Rev. A, 1985, 32, 756.
44. (a) F. E. Jorge, A. Canal-Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108; (b) A. Canal-Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158; (c) C. L. Barros, P. J. P. de Oliveira, F. E. Jorge, A. Canal Neto and M. Campos, Mol. Phys., 2010, 108, 1965.
45. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990.
46. F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545.

---

Footnote

† Electronic supplementary information (ESI) available: Characterization data (elemental analysis, IR and NMR), Fig. S-01 and S-02 (topology of ZnBr₂L and HgI₂L electron density surfaces) and Tables S-01 to S-06 (weak interactions in the crystal structure of free DLMBZD, packing interactions in the crystal structure of the complexes, NBO and AIM atomic charges for the theoretical optimized geometries, topology data for the electron density surface of the coordination sphere, molecular orbitals for the coordination sphere of Hg(II) complexes and topology data for the electron density surface of the halide-ligand/intraligand). CCDC 988017–988023 and 991525 for compounds DLMBZD (1), [ZnCl₂(DLMBZD)]·CH₂Cl₂·H₂O (2), [ZnBr₂(DLMBZD)]·CH₂Cl₂ (3), [ZnI₂(DLMBZD)]·CH₃CN (4), [CdI₂(DLMBZD)] (7), [HgI₂(DLMBZD)] (10) and 2[HgI₂(DLMBZD)]·HgI₂·2CH₃CN (11) and [CdCl₂(DLMBZD)] (5). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt03583c

---