Open Access Article
Open Access ArticleSolvent-induced structural diversity in tetranuclear Ni(II) Schiff-base complexes: the first Ni4 single-molecule magnet with a defective dicubane-like topology†
Radovan
Herchel
 ,
Ivan
Nemec
,
Ivan
Nemec
 ,
Marek
Machata
and
Zdeněk
Trávníček
*
,
Marek
Machata
and
Zdeněk
Trávníček
*
Department of Inorganic Chemistry, Regional Centre of Advanced Technologies and Materials, Faculty of Science, Palacký University, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic. E-mail: zdenek.travnicek@upol.cz
First published on 25th October 2016
Abstract
Two tetranuclear NiII complexes, namely [Ni4(L)4(CH3OH)3(H2O)]·CH3OH (1) and (Pr3NH)2[Ni4(L)4(CH3COO)2] (2, Pr3N = tripropylamine), were synthesized from a tridentate Schiff base ligand H2L (2-[(E)-(2-hydroxybenzylidene)amino]phenol) and Ni(CH3COO)2·4H2O, using different solvents and their ratios (CH3OH and/or CH2Cl2). The prepared Ni4 complexes are of different structural types, involving an Ni4O4 cubane-like core (1) and Ni4O6 defective dicubane-like core (2), with all the Ni atoms hexacoordinated. The complexes were characterized by elemental analysis, FT-IR spectroscopy, variable temperature and field magnetic measurements, and single crystal X-ray analysis. The DFT and CASSCF/NEVPT2 theoretical calculations were utilized to reveal information about the isotropic exchange parameters (Jij) and single-ion zero-field splitting parameters (Di, Ei). The variable temperature magnetic data suggested the competition of the antiferromagnetic and ferromagnetic intracluster interactions in compound 1, which is in contrast to compound 2, where all intracluster interactions are ferromagnetic resulting in the ground spin state S = 4 with an easy-axis type of anisotropy quantified by the axial zero-field splitting parameter D = −0.81 cm−1. This resulted in the observation of a field-induced slow-relaxation of magnetization (U = 3.3–6.7 K), which means that the complex 2 represents the first Ni4 single-molecule magnet with the defective dicubane-like topology.
Introduction
Polynuclear coordination compounds with paramagnetic metal centers have attracted much attention over the last few decades due to their potential application as a new type of magnetic material. Such molecular compounds may exhibit slow-relaxation of magnetization of the molecular origin and thus they can behave as single-molecule magnets (SMMs).1 Interesting quantum phenomena such as quantum tunneling of magnetization (QTM),1b quantum coherence1g and quantum interference1i have been found in such compounds. SMMs have the potential to be utilized in ultra-high density data storage devices,1a,j quantum computing1c or molecular spintronics.1h Despite the recent achievements in the research of SMMs with one paramagnetic metal center (so called single-ion magnets),2 in order to obtain SMMs, the synthesis of high-spin polynuclear metal complexes is the most used approach at all.3 For obtaining such compounds it is essential to modulate molecular properties so that the coupling between neighboring metal centers results in the non-zero ground spin state with S > 1/2, and most importantly, the metal centers should have non-negligible magnetic anisotropy.In designing SMMs, coordination compounds involving NiII metal centers are particularly attractive because they can possess large magnetic anisotropy on their central atoms.4 Furthermore, it is of interest that multiple polynuclear NiII compounds have often been shown to exhibit slow-relaxation of magnetization.5,6 Among such polynuclear NiII complexes, compounds belonging to the class containing a tetranuclear Ni–O–Ni bridged cubane-like core have been intensively studied for the last few decades.6k,7–11 For this type of compound a correlation between the sign and value of the magnetic exchange constant (J) and structural properties has been established.8 According to these studies the Ni–O–Ni angle has been recognized as the most important parameter.8a The magnetic exchange is expected to be ferromagnetic, when the bond angle is close to 90°, while as the Ni–O–Ni angle increases, the value of J decreases following a linear relationship. When the angle is close to 99° the magnetic coupling between the NiII atoms becomes antiferromagnetic. In some of the cases, the absolute value of |J| can exceed 20 cm−1.7 However, some examples can be found which do not follow the above-mentioned relationship.12,17b This can be explained by additional structural factors influencing exchange interactions such as the Ni–O bond distance, the dihedral angle within the Ni2O2 unit and the Ni–O–R angle (R = substituent covalently bound to the bridging oxygen atom) or the presence of an additional bridging group which may also affect the character and strength of the exchange coupling.11,17b
While numerous studies have recently investigated cubane-like NiII complexes,5f,8,9,10 which in some cases showed slow-relaxation of magnetization,5 only a few studies have focused on NiII complexes with a defective dicubane-like Ni4O6 core with one shared face and one vertex missing from each cube (Fig. 1).8e,13 Interestingly, both mentioned types of NiII complexes can be advantageously obtained by the reaction of a NiII salt and polydentate ligands such as Schiff bases, in which oxygen atoms of phenoxo, alkoxo or hydroxo groups can act as μ2 or μ3 bridging atoms incorporated in the cubane/defective dicubane core.5d,8d,e,10 Furthermore, minor ligand changes can significantly affect the Ni–O–Ni bond angles and Ni⋯Ni distances across the faces of the distorted cube significantly and thus, they can change the magnetic properties of the prepared complexes considerably.8c,16d In this context, polydentate Schiff base ligands derived from salicylaldehyde and its derivatives are good candidates to be used for the synthesis of novel cubane-like NiII complexes,14,15b,17d and also, for the study of not so well explored defective dicubane-like NiII complexes.13c,d The assembly process is also dependent upon the crystallization conditions, such as temperature, solvent, pH and concentration of reagents.8c,e,13c,d All these factors can also significantly influence both the structure and magnetic properties of the resulting compounds. For example, Meyer and co-workers showed how the incorporation of different solvent molecules in the coordination sphere of NiII atoms within a distorted cubane core resulted in the switching paramagnetic S = 4 ground state into the diamagnetic S = 0 ground state.8c
Herein, we report the preparation, structural and magnetic properties of two tetranuclear NiII complexes with different topologies depending on different preparation conditions (solvents’ ratio, Fig. 1): a cubane-like complex [Ni4(L)4(CH3OH)3(H2O)] (1, CH2Cl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3OH = 3
CH3OH = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and a defective dicubane-like complex (Pr3NH)2[Ni4(L)4(CH3COO)2] (2, Pr3NH+ = tripropylammonium cation, CH2Cl2 only). As a ligand the Schiff base H2L (2-[(E)-(2-hydroxybenzylidene)amino]phenol) with the {NO2} donor set was used.
1) and a defective dicubane-like complex (Pr3NH)2[Ni4(L)4(CH3COO)2] (2, Pr3NH+ = tripropylammonium cation, CH2Cl2 only). As a ligand the Schiff base H2L (2-[(E)-(2-hydroxybenzylidene)amino]phenol) with the {NO2} donor set was used.
Results and discussion
Synthesis
Two different tetranuclear Ni4 complexes were successfully synthesized by the reaction of a tridentate Schiff base ligand H2L and Ni(CH3COO)2·4H2O in the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the presence of Pr3N as a base using distinct reaction media (Fig. 1): a cubane complex 1 (CH3OH–CH2Cl2 in the volume ratio 1
1 in the presence of Pr3N as a base using distinct reaction media (Fig. 1): a cubane complex 1 (CH3OH–CH2Cl2 in the volume ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and a defective dicubane complex 2 (CH2Cl2 only). The fact that the reactions in different solvents resulted in the formation of different complexes can be reasonably explained on the basis of their crystal structures. In particular, the way how the solvent molecule is involved (or not involved) in the molecular structure of each compound affects the resulting composition significantly (vide infra).
3) and a defective dicubane complex 2 (CH2Cl2 only). The fact that the reactions in different solvents resulted in the formation of different complexes can be reasonably explained on the basis of their crystal structures. In particular, the way how the solvent molecule is involved (or not involved) in the molecular structure of each compound affects the resulting composition significantly (vide infra).
Description of structures
The ligands are asymmetric and can be divided into the salicylaldehydic and aminophenolic parts respective to the reactants they originate from. The ligand asymmetry is apparent when inspecting the bridging function of the oxygen atoms. For example, previously reported FeIII complexes involve both types of the oxygen atoms in their structure (OSal in the salicylaldehydic part, OA in the aminophenolic part) as donor atoms, but only the OA atoms serve as the bridging ones.15a–g However, the further examples involving NiII4,15k NiII2LnIII215h and FeIII2LnIII (ref. 15i,m) complexes (where Ln = Gd, Tb, Dy) with L2− or 3m-L2− ligands (H2-3m-L = (2-[(E)-(2-hydroxy-3-methoxy-benzylidene)amino]phenol)) possessed the OSal atoms also in a bridging function. In both compounds (1–2), the complex moieties contain four NiII atoms and four doubly deprotonated Schiff base ligands L2−. Basic differences between the crystal structures of 1 and 2 can be summarized into several points. Firstly, a cubane-like core can be found in 1, whereas compound 2 contains a defective dicubane core. Secondly, despite the same reactants used in the preparation of 1 and 2 their composition differs significantly. In 1, methanol molecules are incorporated both into the complex molecule as ligands and into the crystal structure as lattice solvent molecules, with important consequences for crystal packing (vide infra). In 2, two CH3COO− anions are incorporated in the molecular structure. Finally, it can be seen that the metal centers in both 1 and 2 are hexacoordinated with the {NiNO5} chromophores (Fig. 1 and 3).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table S1†). The asymmetric unit comprises one electroneutral tetranuclear [Ni4(L)4(CH3OH)3(H2O)] molecule (Fig. 3a) and one lattice CH3OH molecule. The [Ni4(μ3-OA)4] cubane core (Fig. 3b) consists of the OA atoms of the Schiff base ligand and the NiII atoms occupying the alternating vertices of the distorted cube, similarly to other Schiff base NiII cubane-like core compounds.8d,e,16,17 Each hexacoordinated NiII atom in the complex molecule of 1 involves the same coordination environment with similar bond lengths. The axial positions in the coordination polyhedron are occupied by the oxygen atoms from the coordinated solvent molecules (OSolv) and by the μ3-OA atoms from the adjacent L2− ligands.
(Table S1†). The asymmetric unit comprises one electroneutral tetranuclear [Ni4(L)4(CH3OH)3(H2O)] molecule (Fig. 3a) and one lattice CH3OH molecule. The [Ni4(μ3-OA)4] cubane core (Fig. 3b) consists of the OA atoms of the Schiff base ligand and the NiII atoms occupying the alternating vertices of the distorted cube, similarly to other Schiff base NiII cubane-like core compounds.8d,e,16,17 Each hexacoordinated NiII atom in the complex molecule of 1 involves the same coordination environment with similar bond lengths. The axial positions in the coordination polyhedron are occupied by the oxygen atoms from the coordinated solvent molecules (OSolv) and by the μ3-OA atoms from the adjacent L2− ligands.
In three cases, the OSolv atoms originate from the CH3OH molecules (d(Ni–OSolv) = from 2.10 to 2.11 Å) and in one case from H2O molecules (d(Ni–OSolv) = 2.085(3) Å). The axial Ni–OA bonds are the longest with bond distances ranging from 2.22 to 2.28 Å. Each Ni atom in 1 has the equatorial positions occupied by three donor atoms from chelating ligand L2− (μ3-OA, OSal and NIm atoms) and the fourth position is occupied by the μ3-OA atom from the adjacent L2− ligand. The Ni–NIm bonds adopt the shortest lengths: d(Ni–NIm) = 1.97–1.98 Å. The Ni–OA bonds within the chelate ring of the L2− ligand are significantly longer (from 2.04 to 2.07 Å) than the Ni–OSal bonds (from 1.95 to 1.97 Å).
The coordinated solvent molecules are involved in the stabilization of the cubane core as it was observed previously in other cubane-based NiII compounds.5d,8a,c,e,16,18 The hydrogen bonds between the solvent molecules (CH3OH, H2O as hydrogen bonding donors) and the adjacent OSal atoms are of significant strength with donor⋯acceptor distances from a very narrow range (from 2.63 to 2.69 Å). This fact has a crucial influence on the deformation of the cubane core; the Ni⋯Ni distances are significantly shorter between the atoms lying within the hydrogen bond bridged faces (3.06–3.10 Å) than those without such intramolecular interaction (3.36 and 3.38 Å). The shorter Ni⋯Ni separations resulted in smaller Ni–OA–Ni bond angles: 90.7–98.7° vs. 102.6–104.0 Å. Such a structural relationship between the intramolecular hydrogen bonding and Ni⋯Ni distances was also found in previously reported Ni4 cubane compounds.16
The intermolecular contacts in 1 are mediated mainly by two hydrogen bonds between the coordinated H2O molecule and non-coordinated CH3OH molecule (d(O⋯O) = 2.731(4) Å) and between the non-coordinated CH3OH molecule and the OSal atom from the complex molecule (d(O⋯O) = 2.887(4) Å). These two hydrogen bonds form linear supramolecular 1D chains along the crystallographic axis a (Fig. S1†).
The complex anion in 2 can be also viewed as two parallel and almost planar dinuclear {Ni2(L)2} subunits symmetrically related to an inversion center. Both subunits are slightly shifted with respect to each other, so the metal atoms are in a rhomb-like arrangement (Fig. 3c). The acetato ligand is bridging the Ni1 and Ni2 atoms (by the oxygen atoms, OAc) in a syn–syn manner (Fig. 3c). The OAc atoms occupy one of the axial positions in the coordination polyhedra of the Ni1 and Ni2 atoms (d(Ni–OAc) = 2.1050(16) and 2.0534(16) Å). The remaining axial positions are occupied by the μ-OA atoms (in the case of Ni1, d(Ni1–OA) = 2.1810(16) Å) or μ3-OA atoms (Ni2, d(Ni2–OA) = 2.1396(10) Å) from the symmetry related dinuclear subunit. The equatorial planes within the coordination polyhedra of the Ni1 and Ni2 atoms are formed by three donor atoms from the chelating ligand L2− (OA, OSal and NIm atoms) and by one bridging OSal (in the case of Ni1, d(Ni1–OSal) = 2.0387(15) Å) or OA (Ni2, d(Ni1–OA) = 2.0549(16) Å) atom from the adjacent L2− ligand within the dinuclear subunit.
The Ni⋯Ni separations in 2 are in all cases shorter than the sum of van der Waals radii (rvdW(Ni) = 1.63 Å). They are shorter within the {Ni2(L)2} subunit (d(Ni1⋯Ni2) = 3.0030(4) Å) than between the NiII atoms which belong to different dimers (d(Ni2⋯Ni2i) = 3.1662(2) Å and d(Ni1⋯Ni2i) = 3.1971(6) Å, symmetry code: (i) −x, 1 − y, 1 − z). The Ni–O–Ni angles are (94.12(7) and 96.10(7)°) within the {Ni2(L)2} subunit smaller than those between the symmetry related Ni atoms in the complex molecule (97.87(7), 97.99(7) and 99.54(7)°).
In the crystal structure of 2, only one type of significant intermolecular interaction is present: the N–H⋯O hydrogen bond between the Pr3NH+ cation and the OSal atom from the complex anion with the donor⋯acceptor distance 2.820(3) Å.
Theoretical calculations of magnetic parameters
The ab initio calculations have become an integral part of the deep-aimed studies of various physical properties of transition metal complexes. Recently, we demonstrated that ab initio methods can be successfully used in the predictive role in magnetochemistry, thus helping in postulating trustworthy spin Hamiltonians and guide the theoretical analysis of the experimental magnetic data.19 Herein, we used the freely available computational package ORCA20 to predict the dominant terms defining the magnetism of compounds 1 and 2, that is the magnetic exchange among nickel atoms and also their single-ion contributions to magnetic anisotropy. | (1) |
 | (2) |
| J(cm−1) = 171(1) − 1.72(4)·α(Ni–O–Ni) | (3) |
 | ||
| Fig. 4 The DFT derived J-parameters for compounds 1 and 2 (full points). The full line corresponds to eqn (3). | ||
In compound 2, there are two symmetrically independent nickel atoms and three different superexchange pathways. Therefore, this spin Hamiltonian:
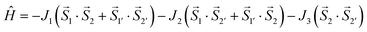 | (4) |
 | (5) |
We used the fact that only one L2− ligand binds in a tridentate fashion to the Ni1 atom, so in the molecular fragments (c) and (d) the monodentate ligands L were replaced either by PhO− or CH3O− moieties (Fig. S3, ESI†). Reducing the number of atoms involved in the molecular fragments of 2 resulted in speeding up the CASSCF/NEVPT2 calculations in the following order (a) < (b) < (c) < (d). The effect of reducing the size of the molecular fragment on the calculations of the D-tensor parameters D and E is documented as: D = +9.62 cm−1, E/D = 0.18 for (a), D = +9.43 cm−1, E/D = 0.21 for (b), D = +9.58 cm−1, E/D = 0.21 for (c) and D = +8.02 cm−1, E/D = 0.19 for (d). Thus, the calculations proved that the approaches (a–c) resulted in almost the same ZFS parameters, only in the case of (d) the D-parameter is slightly lower, which can be explained by the difference in the electronic properties of phenyl/methyl groups (−I/+I inductive effect), hence different electron densities on the oxygen donor atom. Therefore, the justified approach (c) based on using mononuclear fragments where monodentate ligands L2− are replaced by phenolato ligands was used to calculate the ZFS parameters for all the nickel atoms in compounds 1 and 2 and the results are summarized in Table 1.
| Atom | D (cm−1) | E/D | g 1 | g 2 | g 3 | |
|---|---|---|---|---|---|---|
| 1 | Ni1 | +12.4 | 0.194 | 2.185 | 2.265 | 2.297 |
| Ni2 | +12.3 | 0.315 | 2.177 | 2.245 | 2.298 | |
| Ni3 | +13.5 | 0.189 | 2.176 | 2.263 | 2.298 | |
| Ni4 | +12.5 | 0.197 | 2.181 | 2.260 | 2.294 | |
| 2 | Ni1 | +9.58 | 0.209 | 2.206 | 2.264 | 2.292 |
| Ni2 | −8.45 | 0.309 | 2.199 | 2.236 | 2.279 |
The absolute value of the axial single-ion parameter |D| varies between 8.5 and 13.5 cm−1 and also considerable rhombicity (E/D) was found for all the nickel atoms in the studied compounds 1 and 2 (Table 1). The calculated g-parameters are in a narrow interval, g = 2.18–2.30. The individual g-tensor and D-tensor axes are visualized in Fig. S4.† In all the molecular fragments, the g-tensor axes coincide with the D-tensor axes, and under conditions that the ZFS-tensor defines the coordination axes X, Y and Z, the following relationships hold true for the g-components: gx = g2, gy = g3, gz = g1 for D > 0, and gx = g2, gy = g1, gz = g3 for D < 0. This is in agreement with the simplified relationships (eqn (6)) derived from ligand field theory using second-order perturbation theory and so called Λ-tensor22
 | (6) |
Next, we need to discuss thoroughly the D-tensor orientations in each studied compound, because within the spin Hamiltonian formalism, the co-linearity of the local D-tensors is generally assumed. The inspection of the local D-tensor axes labelled as DX, DY and DZ in 1 (Fig. S4†) showed that for all four nickel atoms (Ni1⋯Ni4), the DX axis coincides with OL–Ni–OL, the DY axis coincides with NIm–Ni–OPh and the DZ axis coincides with OPh–Ni–OSolv, where OL is the oxygen donor atom from the L2− ligand bound in the terminal tridentate fashion to the nickel atom, OPh is the oxygen donor atom from the L2− ligand bound in the bridging monodentate fashion to the nickel atom and OSolv is the oxygen donor atom from the CH3OH/H2O ligand. If we assume idealized S4 symmetry of the Ni4 molecular fragment of 1, then we can schematically visualize in Fig. 5a the orientation of the local axes of all the nickel atoms. Under this assumption holds D1 ≡ D3 and D2 ≡ D4. If the molecular axes are made identical to D1 (or D3), then the local axes of D2 are transformed into the molecular coordinate system (D′2) using C4(y) operation of the symmetry as
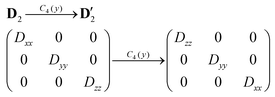 | (7) |
 | (8) |
 | (9) |
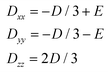 | (10) |
 | (11) |
Now, the local D and E ZFS parameters for the Ni2 atom are transformed into the molecular coordination system as
 | (12) |
As the operation of inversion has no effect on the D-tensor, the local D-tensors of Ni1i and Ni2i atoms have the same properties as for Ni1 and Ni2 atoms.
The analysis of the magnetic data for compound 1 is based on the following spin Hamiltonian (Fig. 5b)
 | (13) |
| J(cm−1) = a − b·α(Ni–O–Ni) | (14) |
Furthermore, the CASSCF/NEVPT2 calculations showed that the local ZFS parameters are very similar for all four symmetrically independent nickel atoms (Table 1), so the following restriction was applied: D1 = D2 = D3 = D4 = Dloc and E1 = E2 = E3 = E4 = Eloc. Also, the local ZFS parameters of D2 and D4 were transformed according to eqn (9) in the spin Hamiltonian (eqn (13)). Moreover, only the isotropic g-value was assumed, because the ab initio calculated g-parameters do not possess large anisotropy. Thus, we are left with only five independent parameters for the fitting procedure, in which simultaneously both temperature and field dependent data were analyzed. As a result, the best-fitted parameters were obtained: a = 171.0, b = −1.721, g = 2.147, Dloc = +14.5 cm−1, Eloc/Dloc = 0.267 and χTIP = 12.9 × 10−9 m3 mol−1 (Fig. 5c), where χTIP stands for temperature-independent paramagnetism (note: the estimation of the standard deviations resulted in: a = 171(9), b = −1.72(9), g = 2.147(4), Dloc = +14.5(3) cm−1, Eloc = 3.9(2) cm−1).23 Then, the individual J-values were calculated as J12 = +8.05 cm−1, J13 = −6.48 cm−1, J14 = +8.91 cm−1, J23 = +9.93 cm−1, J24 = −6.74 cm−1 and J34 = +9.32 cm−1. All the fitted parameters are in very good concordance with the theoretical ones showing the power of ab initio theoretical calculations in the analyses of such complicated systems.
The analysis of the magnetic data for compound 2 is based on the slightly modified spin Hamiltonian (Fig. 5e)
 | (15) |
The situation in this complex is more complicated by the fact that there is no magneto-structural correlation for the J-parameters. From the DFT calculations of the J-values, we can conclude that J1 and J3 are almost equal, so we can apply the restriction that J1 = J3, and that J2 is four-times larger than J1 or J3, so we also applied the restriction that J2 = 4J1. In order to further reduce the number of free parameters, the CASSCF/NEVPT2 calculations were also utilized in such a way that based on the opposite values of the local D1 and D2 parameters, these simplifications were used: D1 = D1′ = Dloc, D2 = D2′ = −Dloc and analogously E1 = E1′ = Eloc, E2 = E2′ = −Eloc. Then, the transformation of D2 and D2′ tensors was applied using eqn (12) similarly as in the case of 1. The fitting procedure resulted in J1 = J3 = +2.61 cm−1, J2 = +10.5 cm−1, Dloc = +8.60 cm−1, Eloc/Dloc = 0.277 and g = 2.309 (Fig. 5f) (note: the estimation of the standard deviations resulted in: J1 = J3 = +2.61(4) cm−1, Dloc = +9(3) cm−1, Eloc = 2(3) cm−1 and g = 2.309(3)).22 These derived parameters are in good conformity with the theoretically predicted values, however, the estimated standard deviations of ZFS parameters Dloc and Eloc are rather large showing smaller sensitivity of the experimental magnetic data to the variation of these parameters. Nevertheless, such uncertainty of the fitted ZFS parameters underlines the importance of ab initio methods in the theoretical analysis of the magnetic properties of polynuclear species.
It is evident from the magnetic analysis that the structural variations found in compounds 1 and 2 led to enhanced differences in their magnetic behavior despite a very similar chemical composition. In order to better understand the interplay between the ferromagnetic and antiferromagnetic exchange interactions within these compounds, the energy levels were plotted as a function of the final spin S under the condition that the spin Hamiltonian is isotropic (all ZFS parameters are zero) – Fig. 6.
 | ||
| Fig. 6 The energy patterns for compounds 1 and 2 calculated within the isotropic exchange limit with the Jij-parameters listed in the text and setting all D and E parameters to zero. | ||
From this plot it is obvious that the ground state for compound 1 is S = 0 and there are close-lying states (<5 cm−1) with S = 4 and S = 2. In contrast, ferromagnetic interactions in compound 2 led to the ground state with the maximum spin, S = 4, and the first excited state with S = 3 is separated by energy difference ΔE = 7.4 cm−1 (10.7 K). Furthermore, we have depicted a three-dimensional plot of the molar magnetization for 2 (Fig. 7a) from which is evident that there is an axial type of the magnetic anisotropy with a small rhombicity. Therefore, it seems appropriate to utilize giant spin approximation and fit the isothermal magnetization data for 2 with the spin Hamiltonian for the ground spin state S = 4 in order to alternatively determine the magnetic anisotropy of the ground spin state with eqn (16)
 | (16) |
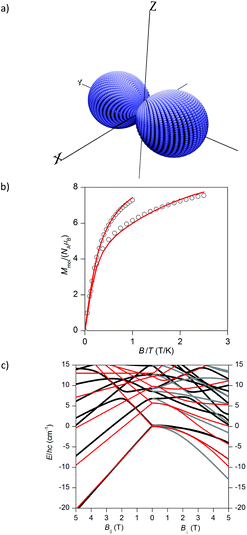 | ||
| Fig. 7 (a) The 3D plot of the molar magnetization calculated for 2 with multi-spin Hamiltonian in eqn (15) for B = 0.5 T at T = 2 K. (b) The reduced isothermal magnetization data for 2 measured at T = 2 and 5 K fitted with the single-ion zero-field splitting spin Hamiltonian for S = 4 (eqn (16)). Empty circles – experimental data, full lines – calculated data with D = −0.81 cm−1 and g = 2.17. (c) The comparison of the lowest energy levels of 2 calculated with multi-spin Hamiltonian in eqn (15) (black and grey lines) and with giant spin approximation Hamiltonian in eqn (16) (red lines). The B‖ indicates the direction of the magnetic field parallel to the easy axis, whereas B⊥ indicates the direction of the magnetic field perpendicular to the easy axis of the system. | ||
The results of the analysis are shown in Fig. 7b and the obtained parameters are D = −0.81 cm−1 and g = 2.17 (note: the estimation of the standard deviation resulted in: D = −0.81(3) cm−1 and g = 2.17(1)).22 These values are comparable to the previously reported Ni4 SMMs as outlined in Table 2. However, such large D-values result in ZFS of the S = 4 spin state into |4,0〉, |4,±1〉, |4,±2〉, |4,±3〉 and |4,±4〉 states with the energy separations equal to 0, D, 4D, 9D, and 16D, respectively. Thus, the ground state |4,±4〉 is separated from the highest excited state |4,0〉 by energy equal to 16D = 13.0 cm−1 and this value is larger than calculated separation 7.4 cm−1 between S = 4 and S = 3 states in the isotropic limit (Fig. 6). Indeed, the detailed inspection of the low-lying energy levels resulting from full multi-spin Hamiltonian in eqn (15) and from giant spin approximation Hamiltonian in eqn (16) shows that only the lowest energy levels are well recovered by the latter model (Fig. 7c). Moreover, it is evident that there is a strong mixing of different spin levels due to ZFS terms, so called S-mixing,24 and therefore the giant spin approximation would require inclusion of the higher order Steven's operators for ZFS to achieve even better description of low-lying states, which was also discussed for another Ni4 compound, [Ni4(hmp)4(dmb)4Cl4].25 To conclude, both the analyses showed that there is the axial type of the magnetic anisotropy in 2, however the utilization of the giant spin approximation is on the edge due to large mixing of the ground state S = 4 with the excited state S = 3 induced by ZFS.
| Compound | D (cm−1) | U eff (cm−1) | τ 0 (s) | Ref. |
|---|---|---|---|---|
| a SMM behavior confirmed by magnetic hysteresis measurement, AC susceptibility data not available. b Hhmp = (pyridin-2-yl)methanol; dmb = 3,3-dimethylbutan-1-ol; dmp = 2,2-dimethylpropan-1-ol; dmp = 3-cyclohexylpropan-1-ol; HtBuhmp = (4-tert-butylpyridine-2-yl)methanol; H3thme = 2-(hydroxymethyl)-2-methylpropane-1,3-diol; H2idm = iminodimethanol; Hpthtp = 4-(pyridin-2-yl)tetrahydro-2H-thiopyran-4-ol; Hmpp = 2-methyl-1-(pyridin-2-yl)propan-2-ol; Hmpzph = 2-(5-methyl-1H-pyrazol-3-yl)phenol. | ||||
| [Ni4(hmp)4(CH3OH)4Cl4]b | −0.60 | 5a | ||
| [Ni4(hmp)4(CH3CH2OH)4Cl4] | −0.60 | 5.00 | 9.5 × 10−8 | 5a and 6g |
| [Ni4(hmp)4(dmb)4Cl4] | −0.61 | 1.39 | 6.3 × 10−3 | 5a,d |
| [Ni4(hmp)4(dmp)4Cl4]b | −0.61 | 5f | ||
| [Ni4(hmp)4(chp)4Cl4]b | −0.59 | 5d | ||
| [Ni4(hmp)4(dmb)4Br4]b | −0.56 | 5d | ||
| [Ni4(tBuhmp)4(dmb)4Cl4]b | −0.68 | 5d | ||
[Ni4(H2thme)4(CH3CN)4](NO3)4·1.33NaNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−0.43 | 5b | ||
| [Ni4(Hidm)4Cl4]b | −0.75 | 5e | ||
| [Ni4(Hpthtp)4Cl8] | −0.44 | 20.1 | 1.64 × 10−9 | 6k |
| [Ni4(Hmpp)4Cl8]b | −0.88 | 6j | ||
| [Ni4(Hmpp)4OH4Cl4]b | −0.63 | 6j | ||
| [Ni4(mpzph)4(OH)(CH3O)3(CH3OH)3](CH3OH)b | −0.26 | 1.50 × 10−6 | 17a | |
| (Pr3NH)2[Ni4(L)4(CH3COO)2] (2) | −0.81 | 2.3–4.7 | 79.7–0.261 × 10−6 | This work |
|
||||
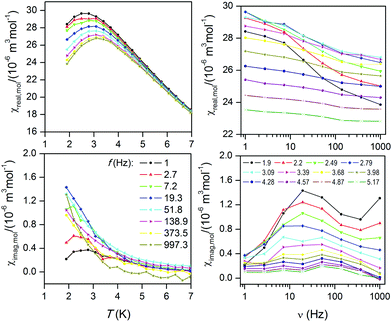
The above discussed analysis of the static magnetic properties of 1–2, encouraged us to measure also AC susceptibility data for compound 2, but there was no out-of-phase signal in zero static magnetic field. However, the field dependent measurement performed at T = 1.9 K confirmed a slow-relaxation of magnetization only in 2 (Fig. S5, ESI†) and for that reason, AC susceptibility was acquired in the non-zero static field, Bdc = 0.5 T at low temperatures as shown in Fig. 8. Note: AC susceptibility data were also taken for compound 1 in zero and non-zero static fields, but no out-of-phase signal was detected, which indirectly confirmed our outcomes from magnetic analysis.
Unfortunately, we did not observe clear maxima on out-of-phase susceptibilities for 2 down to 1.9 K, so the standard procedure for constructing the Argand (Cole–Cole) diagram was not applicable. However, at least the approximate relationship26
| ln(χ′′/χ′) = ln(2πfτ0) + U/kT | (17) |
Conclusions
To conclude, the utilization of the tridentate Schiff base ligand H2L (2-hydroxy-phenylsalicylaldimine) and Ni(CH3COO)2·4H2O, in different reaction solvent ratios, led to the synthesis of two structurally different tetranuclear complexes 1 and 2. Single-crystal X-ray structural analysis revealed that compound 1 contains a cubane-like [Ni4O4] core (a mixture of CH3OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 in vol. ratio 1
CH2Cl2 in vol. ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 was used), while compound 2 involves a defective dicubane-like [Ni4O6] core (CH2Cl2 only). Consequently, the solvent molecules were incorporated in the structure of compound 1 and they are involved in mediation of intra and intermolecular hydrogen bonds. Compound 2 represents the very first example of tetranuclear NiII complex with a defective dicubane core and with all the NiII atoms being hexacoordinate.
3 was used), while compound 2 involves a defective dicubane-like [Ni4O6] core (CH2Cl2 only). Consequently, the solvent molecules were incorporated in the structure of compound 1 and they are involved in mediation of intra and intermolecular hydrogen bonds. Compound 2 represents the very first example of tetranuclear NiII complex with a defective dicubane core and with all the NiII atoms being hexacoordinate.
The variable temperature magnetic data suggested the presence of prevailing intracluster ferromagnetic coupling (1 and 2). However, more thorough analysis revealed the competition between the antiferromagnetic and ferromagnetic intracluster interactions in compound 1 which resulted in the S = 0 ground spin state. This is in stark contrast to 2 with its S = 4 ground spin state due to solely ferromagnetic coupling. Furthermore, the energy states in both compounds are affected by significant magnetic anisotropy of the metal atoms, which reflects the structural variations in 1 and 2. The ab initio CASSCF/NEVPT2 calculations of the isotropic exchange parameters (Jij) using the DFT and single-ion zero-field splitting parameters (Di, Ei) played the key role in the advanced magnetic analysis of these compounds, which resulted in the trustworthy parameter set. This was also achieved by simultaneous fitting of temperature and field dependent magnetic data.
This work clearly shows the difficulty in the rational design of highly anisotropic polynuclear complexes as candidates for SMMs. Nevertheless, the field induced SMM behavior found in compound 2 opens a new perspective for the preparation of tetranuclear compounds with a defective dicubane-like topology and ferromagnetic exchange interactions acting as nanomagnets.
Experimental section
Synthesis
All used chemicals and solvents were purchased from commercial sources and used without any further purification.Equipment, measurements and software
Elemental analysis was performed on a Thermo Scientific FLASH 2000 CHNS-O Analyser. Infrared spectra of the compounds were recorded with a ThermoNicolet Nexus 670 FT-IR spectrometer using the ATR technique on the diamond plate in the region 4000–400 cm−1. Temperature dependent (T = 1.9–300 K, B = 0.1 T) and field dependent (B = 0–7 T, T = 2 and 5 K) magnetic measurements were carried out on an SQUID magnetometer (MPMS, Quantum Design) on polycrystalline samples. The data were corrected for the diamagnetism of the constituents.X-ray diffraction analysis
Single crystal X-ray diffraction data are listed in Table S1.† The data were recorded on an Oxford diffraction Xcalibur 2 CCD diffractometer with a Sapphire CCD detector, sealed tube (Mo Kα radiation, Kα = 0.71073 Å) and equipped with an Oxford Cryosystems nitrogen gas-flow apparatus. The CrysAlis program package (version 1.171.33.52, Oxford Diffraction) was used for data collection and reduction.27 The molecular structures were solved by direct methods SHELX-2014 and all non-hydrogen atoms were refined anisotropically on F2 using the full-matrix least-squares procedure SHELXL-97.28 All the hydrogen atoms were found in differential Fourier maps and their parameters were refined using a riding model with Uiso(H) = 1.2 (CH, CH2, OH) or 1.5Ueq (CH3).Theoretical methods
Ab initio theoretical calculations were performed with the ORCA 3.0.3 computational package.29 Single point DFT energy calculations based on X-ray geometries were done using the B3LYP functional.30 The isotropic exchange constants J were calculated by comparing the energies of high-spin (HS) and broken-symmetry (BS) spin states using Ruiz's approach.31 Calculations of the ZFS parameters were performed using the state average complete active space self-consistent field (SA-CASSCF)32 wave functions complemented by the N-electron valence second order perturbation theory (NEVPT2).33 The active spaces of the CASSCF calculations comprises five metal-based d-orbitals and eight electrons, CAS(8,5). In the state averaged approach all multiplets for the given electron configuration were equally weighted, which means 10 triplet and 15 singlet states. The ZFS parameters, based on dominant spin–orbit coupling contributions from excited states, were calculated through the quasi-degenerate perturbation theory (QDPT),34 in which approximations to the Breit–Pauli form of the spin-orbit coupling operator (SOMF approximation)35 and the effective Hamiltonian theory36 were utilized. In all calculations, the polarized triple-ζ quality basis set (def2-TZVP(-f)) proposed by Ahlrichs and co-workers was used for all atoms.37 We also used the RI approximation with the decontracted auxiliary def2-TZV/J or def2-TZV/C Coulomb fitting basis sets and the chain-of-spheres approximation to exact exchange.38 Increased integration grids (Grid5 in ORCA convention) and tight SCF convergence criteria were used in all calculations.Acknowledgements
We acknowledge the financial support from the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic, and from Palacký University in Olomouc (PrF_2015_019 and PrF_2016_007). I.N would like to acknowledge the Grant Agency of the Czech Republic (GAČR 13-27355P) for financial support.Notes and references
- (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nat., 1993, 365, 141 CrossRef CAS; (b) L. Thomas, F. Lionti, R. Ballou, D. Gatteschi, R. Sessoli and B. Barbara, Nat., 1996, 383, 145 CrossRef CAS; (c) M. N. Leuenberger and D. Loss, Nat., 2001, 410, 789 CrossRef CAS PubMed; (d) S. Wang, J. L. Zuo, H. C. Zhou, H. J. Choi, Y. X. Ke, J. R. Long and X. Z. You, Angew. Chem., Int. Ed., 2004, 43, 5940 CrossRef CAS PubMed; (e) M. H. Zeng, M. X. Yao, H. Liang, W. X. Zhang and X. M. Chen, Angew. Chem., Int. Ed., 2007, 46, 1832 CrossRef CAS PubMed; (f) C. J. Milios, A. Vinslava, P. A. Wood, S. Parsons, W. Wernsdorfer, G. Christou, S. P. Perlepes and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 8 CrossRef CAS PubMed; (g) S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Müller and B. Barbara, Nat., 2008, 453, 203 CrossRef CAS PubMed; (h) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talariano, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194 CrossRef CAS PubMed; (i) O. Waldmann, T. C. Stamatatos, G. Christou, H. U. Güdel, I. Sheikin and H. Mutka, Phys. Rev. Lett., 2009, 102, 157202 CrossRef CAS PubMed; (j) M. Affronte, J. Mater. Chem., 2009, 19, 1731 RSC; (k) T. Taguchi, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2010, 49, 199 CrossRef CAS PubMed; (l) S. N. Wang, L. Q. Kong, H. Yang, Z. T. He, Z. Jiang, D. C. Li, S. Y. Zheng, M. J. Niu, Y. Song and J. M. Dou, Inorg. Chem., 2011, 50, 2705 CrossRef CAS PubMed; (m) G. P. Guedes, S. Soriano, N. M. Comerlato, N. L. Speziali, M. A. Novak and M. G. F. Vaz, Inorg. Chem. Commun., 2013, 37, 101 CrossRef CAS; (n) F. J. Kettles, V. A. Milway, F. Tuna, R. Valiente, L. H. Thomas, W. Wernsdorfer, S. T. Ochsenbein and M. Murrie, Inorg. Chem., 2014, 53, 8970 CrossRef CAS PubMed; (o) S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655 RSC.
- (a) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 RSC; (b) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289-290, 379 CrossRef.
- (a) D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804 CrossRef; (b) T. C. Stamatatos, V. Nastopoulos, A. J. Tasiopoulos, E. E. Moushi, W. Wernsdorfer, G. Christou and S. P. Perlepes, Inorg. Chem., 2008, 47, 10081 CrossRef CAS PubMed; (c) J. Martínez-Lillo, A.-R. Tomsa, Y. Li, L.-M. Chamoreau, E. Cremades, E. Ruiz, A.-L. Barra, A. Proust, M. Verdaguer and P. Gouzerh, Dalton Trans., 2012, 41, 13668 RSC; (d) A. E. Thuijs, P. King, K. A. Abboud and G. Christou, Inorg. Chem., 2015, 54, 9127 CrossRef CAS PubMed.
- S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Inorg. Chem., 2014, 53, 676 CrossRef PubMed.
- (a) E.-C. Yang, W. Wernsdorfer, S. Hill, R. S. Edwards, M. Nakano, S. Maccagnano, L. N. Zakharov, A. L. Rheingold, G. Christou and D. N. Hendrickson, Polyhedron, 2003, 22, 1727 CrossRef CAS; (b) M. Moragues-Cánovas, M. Helliwell, L. Ricard, É. Rivière, W. Wernsdorfer, E. Brechin and T. Mallah, Eur. J. Inorg. Chem., 2004, 11, 2219 CrossRef; (c) D. N. Hendrickson, E. C. Yang, R. M. Isidro, C. Kirman, J. Lawrence, R. S. Edwards, S. Hill, A. Yamaguchi, H. Ishimoto, W. Wernsdorfer, C. Ramsey, N. Dalal and M. M. Olmstead, Polyhedron, 2005, 24, 2280 CrossRef CAS; (d) E. C. Yang, W. Wernsdorfer, L. N. Zakharov, Y. Karaki, A. Yamaguchi, R. M. Isidro, G. Di Lu, S. A. Wilson, A. L. Rheingold, H. Ishimoto and D. N. Hendrickson, Inorg. Chem., 2006, 45, 529 CrossRef CAS PubMed; (e) A. Ferguson, J. Lawrence, A. Parkin, J. Sanchez-Benitez, K. V. Kamenev, E. K. Brechin, W. Wernsdorfer, S. Hill and M. Murrie, Dalton Trans., 2008, 37, 6409 RSC; (f) F. Moro, F. Piga, I. Krivokapic, A. Burgess, W. Lewis, J. McMaster and J. Van Slageren, Inorg. Chim. Acta, 2010, 363, 4329 CrossRef CAS; (g) S. Hameury, L. Kayser, R. Pattacini, G. Rogez, W. Wernsdorfer and P. Braunstein, Dalton Trans., 2013, 42, 5013 RSC.
- (a) C. Cadiou, M. Murrie, C. Paulsen, V. Villar, W. Wernsdorfer and R. E. P. Winpenny, Chem. Commun., 2001, 24, 2666 RSC; (b) H. Andres, R. Basler, A. J. Blake, C. Cadiou, G. Chaboussant, C. M. Grant, G. Hans-Ulrich, M. Murrie, S. Parsons, C. Paulsen, F. Semadini, V. Villar, W. Wernsdorfer and R. E. P. Winpenny, Chem. Eur. J., 2002, 8, 4867 Search PubMed; (c) S. T. Ochsenbein, M. Murrie, E. Rusanov, H. Stoeckli-Evans, C. Sekine and H. U. Güdel, Inorg. Chem., 2002, 41, 5133 CrossRef CAS PubMed; (d) A. Bell, G. Aromí, S. J. Teat, W. Wernsdorfer and R. E. P. Winpenny, Chem. Commun., 2005, 22, 2808 RSC; (e) G. Aromí, S. Parsons, W. Wernsdorfer, E. K. Brechin and E. J. L. McInnes, Chem. Commun., 2005, 40, 5038 RSC; (f) E. Pardo, P. Burguete, R. Ruiz-García, M. Julve, D. Beltrán, Y. Journaux, P. Amorós and F. Lloret, J. Mater. Chem., 2006, 16, 2702 RSC; (g) Y.-R. Li, H.-Q. Liu, Y. Liu, S.-K. Su and Y.-P. Wang, Chin. Phys. Lett., 2009, 26, 077504 CrossRef; (h) R. T. W. Scott, L. F. Jones, I. S. Tidmarsh, B. Breeze, R. H. Laye, J. Wolowska, D. J. Stone, A. Collins, S. Parsons, W. Wernsdorfer, G. Aromí, E. J. L. McInnes and E. K. Brechin, Chem. – Eur. J., 2009, 15, 12389 CrossRef CAS PubMed; (i) S. Petit, P. Neugebauer, G. Pilet, G. Chastanet, A. L. Barra, A. B. Antunes, W. Wernsdorfer and D. Luneau, Inorg. Chem., 2012, 51, 6645 CrossRef CAS PubMed; (j) S. Hameury, L. Kayser, R. Pattacini, G. Rogez, W. Wernsdorfer and P. Braunstein, Dalton Trans., 2013, 42, 5013 RSC; (k) A. Ghisolfi, K. Y. Monakhov, R. Pattacini, P. Braunstein, X. López, C. de Graaf, M. Speldrich, J. van Leusen, H. Schilder and P. Kögerler, Dalton Trans., 2014, 43, 7847 RSC.
- L. Ballester, E. Coronado, A. Guti, A. Mange, M. F. Perpifitin, E. Pinilla and T. Ricot, Inorg. Chem., 1992, 31, 2053 CrossRef CAS.
- (a) M. A. Halcrow, J. Sun, J. C. Huffman and G. Christou, Inorg. Chem., 1995, 34, 4167 CrossRef CAS; (b) C. N. Complex, J. M. Clemente-juan, B. Donnadieu, J. Tuchagues and R. V. May, Inorg. Chem., 2000, 4, 5515 Search PubMed; (c) A. Das, F. J. Klinke, S. Demeshko, S. Meyer, S. Dechert and F. Meyer, Inorg. Chem., 2012, 51, 8141 CrossRef CAS PubMed; (d) S. Karmakar and S. Khanra, CrystEngComm, 2014, 16, 2371 RSC; (e) P. S. Perlepe, A. A. Athanasopoulou, K. I. Alexopoulou, C. P. Raptopoulou, V. Psycharis, A. Escuer, S. P. Perlepes and T. C. Stamatatos, Dalton Trans., 2014, 43, 16605 RSC.
- (a) Y. M. Li, J. J. Zhang, R. B. Fu, S. C. Xiang, T. L. Sheng, D. Q. Yuan, X. H. Huang and X. T. Wu, Polyhedron, 2006, 25, 1618 CrossRef CAS; (b) K. G. Alley, R. Bircher, H. U. Güdel, B. Moubaraki, K. S. Murray, B. F. Abrahams and C. Boskovic, Polyhedron, 2007, 26, 369 CrossRef CAS; (c) D. Mandal, C. S. Hong, H. C. Kim, H. K. Fun and D. Ray, Polyhedron, 2008, 27, 2372 CrossRef CAS; (d) Y. Xie, J. Ni, F. Zheng, Y. Cui, Q. Wang, S. W. Ng and W. Zhu, Cryst. Growth Des., 2009, 9, 118 CrossRef CAS; (e) C. G. Efthymiou, C. Papatriantafyllopoulou, G. Aromi, S. J. Teat, G. Christou and S. P. Perlepes, Polyhedron, 2011, 30, 3022 CrossRef CAS; (f) R. Touzani, M. Haibach, A. J. Nawara-Hultzsch, S. El Kadiri, T. J. Emge and A. S. Goldman, Polyhedron, 2011, 30, 2530 CrossRef CAS; (g) G. M. Yu, L. Zhao, L. F. Zou, Y. N. Guo, G. F. Xu, Y. H. Li and J. Tang, J. Chem. Crystallogr., 2011, 41, 606 CrossRef CAS; (h) J.-P. Costes, G. Novitchi, L. Vendier, G. Pilet and D. Luneau, C. R. Chim., 2012, 15, 849 CrossRef CAS; (i) S. T. Meally, S. M. Taylor, E. K. Brechin, S. Piligkos and L. F. Jones, Dalton Trans., 2013, 42, 10315 RSC; (j) H. S. Wang and Y. Song, Inorg. Chem. Commun., 2013, 35, 86 CrossRef CAS.
- (a) S. Mukherjee, T. Weyhermüller, E. Bothe, K. Wieghardt and P. Chaudhuri, Eur. J. Inorg. Chem., 2003, 5, 863 CrossRef; (b) M. Koikawa, M. Ohba and T. Tokii, Polyhedron, 2005, 24, 2257 CrossRef CAS; (c) A. K. Ghosh, M. Shatruk, V. Bertolasi, K. Pramanik and D. Ray, Inorg. Chem., 2013, 52, 13894 CrossRef CAS PubMed; (d) M. S. Jana, J. L. Priego, R. Jiménez-Aparicio and T. K. Mondal, Spectrochim. Acta, Part A, 2014, 133, 714 CrossRef CAS PubMed; (e) M. Pait, A. Bauzá, A. Frontera, E. Colacio and D. Ray, Inorg. Chem., 2015, 54, 4709 CrossRef CAS PubMed.
- K. S. Murray, in Advances in Inorganic Chemistry, ed. A. G. Sykes, Academic Press, 1995, vol. 43, p. 261 Search PubMed.
- G. Aromí, A. S. Batsanov, P. Christian, M. Helliwell, O. Roubeau, G. A. Timco and R. E. P. Winpenny, Dalton Trans., 2003, 32, 4466 RSC.
- (a) P. King, R. Clerac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Dalton Trans., 2004, 977, 2670 RSC; (b) C. G. Efthymiou, C. P. Raptopoulou, A. Terzis, R. Boča, M. Korabic, J. Mrozinski, S. P. Perlepes and E. G. Bakalbassis, Eur. J. Inorg. Chem., 2006, 11, 2236 CrossRef; (c) S. Banerjee, M. Nandy, S. Sen, S. Mandal, G. M. Rosair, A. M. Z. Slawin, C. J. Gómez García, J. M. Clemente-Juan, E. Zangrando, N. Guidolin and S. Mitra, Dalton Trans., 2011, 40, 1652 RSC; (d) S. Liu, S. Wang, F. Cao, H. Fu, D. Li and J. Dou, RSC Adv., 2012, 2, 1310 RSC; (e) V. Psycharis, B. A. Terzis and B. V. Tangoulis, Aust. J. Chem., 2012, 65, 1608 CrossRef.
- (a) S. Hazra, R. Koner, P. Lemoine, E. Carolina Sañudo and S. Mohanta, Eur. J. Inorg. Chem., 2009, 23, 3458 CrossRef; (b) Y. Zhang, X. M. Zhang, T. F. Liu and W. G. Xu, Transition Met. Chem., 2010, 35, 851 CrossRef CAS; (c) S. Shit, M. Nandy, G. Rosair, C. J. Gómez-García, J. J. B. Almenar and S. Mitra, Polyhedron, 2013, 61, 73 CrossRef CAS.
- (a) A. Elmali, O. Atakol, I. Svoboda and H. Fuess, Z. Kristallogr., 1992, 202, 323 CAS; (b) A. Elmali, Y. Elerman, I. Svoboda and H. Fuess, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 965 CrossRef; (c) A. Elmali, Y. Elerman, I. Svoboda, H. Fuess, K. Griesar and W. Haase, Z. Naturforsch., B: Chem. Sci., 1994, 49, 1239 CAS; (d) A. Elmali, Y. Elerman, I. Svoboda, H. Fuess, K. Griesar and W. Hasse, Z. Naturforsch., B: Chem. Sci., 1994, 49, 365 CAS; (e) A. Elmali, Y. Elerman, I. Svoboda and H. Fuess, J. Mol. Struct., 2000, 516, 43 CrossRef CAS; (f) A. Elmali, Y. Elerman and I. Svoboda, Z. Naturforsch., B: Chem. Sci., 2001, 56, 897 CAS; (g) A. Elmali, Y. Elerman, C. T. Zeyrek and I. Svoboda, Z. Naturforsch., B: Chem. Sci., 2003, 58, 433 CAS; (h) K. C. Mondal, G. E. Kostakis, Y. Lan, W. Wernsdorfer, C. A. Anson and A. K. Powell, Inorg. Chem., 2011, 50, 11604 CrossRef CAS PubMed; (i) I. Nemec, M. Machata, R. Herchel, R. Boča and Z. Trávníček, Dalton Trans., 2012, 41, 14603 RSC; (j) P. Bag, J. Goura, V. Mereacre, G. Novitchi, A. K. Powell and V. Chandrasekhar, Dalton Trans., 2014, 43, 16366 RSC; (k) S. Saha, S. Pal, C. J. Gómez-García, J. M. Clemente-Juan, K. Harms and H. P. Nayek, Polyhedron, 2014, 74, 1 CrossRef CAS; (l) N. C. Anastasiadis, D. A. Kalofolias, A. Philippidis, S. Tzani, C. Raptopoulou, V. Psycharis, C. J. Milios, A. Escuer and S. P. Perlepes, Dalton Trans., 2015, 44, 10200 RSC; (m) W.-W. Kuang, C.-Y. Shao and P.-P. Yang, J. Coord. Chem., 2015, 68, 1412 CrossRef CAS.
- (a) J. W. Ran, S. Y. Zhang, B. Xu, Y. Xia, D. Guo, J. Y. Zhang and Y. Li, Inorg. Chem. Commun., 2008, 11, 73 CrossRef CAS; (b) Q. Liang, R. Huang, X. Chen, Z. Li, X. Zhang and B. Sun, Inorg. Chem. Commun., 2010, 13, 1134 CrossRef CAS; (c) S. Y. Zhang, W. Q. Chen, B. Hu, Y. M. Chen, W. Li and Y. Li, Inorg. Chem. Commun., 2012, 16, 74 CrossRef CAS; (d) S. Nayak, G. Novitchi, S. Muche, D. Luneau and S. Dehnen, Z. Anorg. Allg. Chem., 2012, 638, 1127 CrossRef CAS.
- (a) C. Boskovic, E. Rusanov, H. Stoeckli-Evans and H. U. Güdel, Inorg. Chem. Commun., 2002, 5, 881 CrossRef CAS; (b) A. Sieber, C. Boskovic, R. Bircher, O. Waldmann, S. T. Ochsenbein, G. Chaboussant, H. U. Güdel, N. Kirchner, J. van Slageren, W. Wernsdorfer, A. Neels, H. Stoeckli-Evans, S. Janssen, F. Juranyi and H. Mutka, Inorg. Chem., 2005, 44, 4315 CrossRef CAS PubMed; (c) S.-S. Qian, Y. Zhao, M.-M. Zhen, C.-L. Zhang, Z.-L. You and H.-L. Zhu, Transition Met. Chem., 2013, 38, 63 CrossRef CAS; (d) Z. Lu, T. Fan, W. Guo, J. Lu and C. Fan, Inorg. Chim. Acta, 2013, 400, 191 CrossRef CAS.
- (a) G. Aromí, E. Bouwman, E. Burzurí, C. Carbonera, J. Krzystek, F. Luis, C. Schlegel, J. Van Slageren, S. Tanase and S. J. Teat, Chem. – Eur. J., 2008, 14, 11158 CrossRef PubMed; (b) C. G. Efthymiou, C. Papatriantafyllopoulou, N. I. Alexopoulou, C. P. Raptopoulou, R. Boča, J. Mrozinski, E. G. Bakalbassis and S. P. Perlepes, Polyhedron, 2009, 28, 3373 CrossRef CAS; (c) W.-H. Zhang, N. B. Sulaiman, P. X. S. Tio and T. S. A. Hor, CrystEngComm, 2011, 13, 2915 RSC; (d) S.-H. Zhang, N. Li, C.-M. Ge, C. Feng and L.-F. Ma, Dalton Trans., 2011, 40, 3000 RSC; (e) J. P. Sun, L. C. Li and X. J. Zheng, Inorg. Chem. Commun., 2011, 14, 877 CrossRef CAS; (f) A. B. Canaj, D. I. Tzimopoulos, A. Philippidis, G. E. Kostakis and C. J. Milios, Inorg. Chem., 2012, 51, 10461 CrossRef CAS PubMed; (g) F. Habib, C. Cook, I. Korobkov and M. Murugesu, Inorg. Chim. Acta, 2012, 380, 378 CrossRef CAS; (h) C. Ding, C. Gao, S. Ng, B. Wang and Y. Xie, Chem. – Eur. J., 2013, 19, 9961 CrossRef CAS PubMed; (i) S. H. Zhang, Y. D. Zhang, H. H. Zou, J. J. Guo, H. P. Li, Y. Song and H. Liang, Inorg. Chim. Acta, 2013, 396, 119 CrossRef CAS.
- R. Herchel, I. Nemec, M. Machata and Z. Trávníček, Inorg. Chem., 2015, 54, 8625 CrossRef CAS PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- (a) R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896 CrossRef CAS PubMed; (b) B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2015, 54, 3352 CrossRef PubMed; (c) K. Matelková, R. Boča, Ľ. Dlháň, R. Herchel, J. Moncol, I. Svoboda and A. Mašlejová, Polyhedron, 2015, 95, 45 CrossRef; (d) I. Nemec, R. Herchel, I. Svoboda, R. Boča and Z. Trávníček, Dalton Trans., 2015, 44, 9551 RSC.
- R. Boča, Ľ. Dlháň, W. Haase, R. Herchel, A. Mašlejová and B. Papánková, Chem. Phys. Lett., 2003, 373, 402 CrossRef.
- The standard deviations were calculated as σi = (P–1ij·S/(N – k))–1/2, where Pij = ∑(δμn/δai·δμn/δaj) and S = ∑(μn – μexpn)2 with n = 1 to N; ai and aj are the fitted parameters, N is the number of the experimental points (sum of temperature and field dependent data), μn and μexpn are the calculated and experimental effective magnetic moments for the given temperature and magnetic field.
- (a) E. Liviotti, S. Carretta and G. Amoretti, J. Chem. Phys., 2002, 117, 3361 CrossRef CAS; (b) S. Carretta, E. Liviotti, N. Magnani, P. Santini and G. Amoretti, Phys. Rev. Lett., 2004, 92, 207205 CrossRef CAS PubMed.
- A. Wilson, E.-C. Yang, D. N. Hendrickson and S. Hill, Polyhedron, 2007, 26, 2065 CrossRef CAS.
- (a) J. Bartolomé, G. FIloti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter, 2009, 80, 014430 CrossRef; (b) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300 CrossRef CAS PubMed.
- CrysAlis software package, Version 1.171.33.52, Agilent, Technologies, Yarnton, England Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3 CrossRef PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- (a) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS; (b) E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982 CrossRef CAS PubMed.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS; (b) C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS; (d) C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043 CrossRef CAS PubMed; (e) C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977 CrossRef CAS PubMed.
- (a) A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef; (b) A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef; (c) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- (a) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98 CrossRef CAS; (b) R. Izsak and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional X-ray data, magnetic data and analysis, and details of theoretical calculations. CCDC 1443519–1443520. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt03520e |
| This journal is © The Royal Society of Chemistry 2016 |