Synthesis, reactivity, structures, and dynamic properties of gyroscope like iron complexes with dibridgehead diphosphine cages: pre- vs. post-metathesis substitutions as routes to adducts with neutral dipolar Fe(CO)(NO)(X) rotors

Abstract

Three routes are explored to the title halide/cyanide complexes trans-Fe(CO)(NO)(X)(P((CH₂)₁₄)₃P) (9c-X; X = Cl/Br/I/CN), the Fe(CO)(NO)(X) moieties of which can rotate within the diphosphine cages (ΔH^‡/ΔS^‡ (kcal mol⁻¹/eu⁻¹) 5.9/−20.4 and 7.4/−23.9 for 9c-Cl and 9c-I from variable temperature ¹³C NMR spectra). First, reactions of the known cationic complex trans-[Fe(CO)₂(NO)(P((CH₂)₁₄)₃P)]⁺ BF₄⁻ and Bu₄N⁺ X⁻ give 9c-Cl/-Br/-I/-CN (75–83%). Second, reactions of the acyclic complexes trans-Fe(CO)(NO)(X)(P((CH₂)_mCH=CH₂)₃)₂ and Grubbs’ catalyst afford the tris(cycloalkenes) trans-Fe(CO)(NO)(X)(P((CH₂)_mCH=CH(CH₂)_m)₃P) (m/X = 6/Cl,Br,I,CN, 7/Cl,Br, 8/Cl,Br) as mixtures of Z/E isomers (24–41%). Third, similar reactions of trans-[Fe(CO)₂(NO)(P((CH₂)_mCH=CH₂)₃)₂]⁺ BF₄⁻ and Grubbs’ catalyst afford crude trans-[Fe(CO)₂(NO)P((CH₂)_mCH=CH(CH₂)_m)₃P)]⁺ BF₄⁻ (m = 6, 8). However, the C=C hydrogenations required to consummate routes 2 and 3 are problematic. Crystal structures of 9c-Cl/-Br/-CN are determined. Although the CO/NO/X ligands are disordered, the void space within the diphosphine cages is analyzed in terms of horizontal and vertical constraints upon Fe(CO)(NO)(X) rotation and the NMR data. The molecules pack in identical motifs with parallel P–Fe–P axes, and without intermolecular impediments to rotation in the solid state.

---

Introduction

As has been extensively documented¹ and surveyed in previous papers in this series,^2–9 gyroscopes are utilized in a multitude of technologies. Older readers may recall the Sperry Rand Corporation, which ceased to exist following a hostile merger that resulted in Unisys (1986),¹⁰ had an earlier incarnation as the Sperry Gyroscope Company.¹¹ The latter was founded in 1910 and for some time supplied most of the world's torpedo warhead and gyrocompass guidance systems. These days, dedicated “gyroscope companies” appear to be extinct, but their spirit lives on in a small cadre of research groups that seek to realize such devices at a molecular level.^12–15 Representative applications for which miniaturization is especially important include drones, virtual reality headsets, mobile phone displays, and flying suits as popularized by Iron Man.¹⁶

Some candidates for molecular gyroscopes that have been under study in the authors’ laboratory are represented by II and IV in Scheme 1.^2–8a These consist of a P–M–P axis about which the metal based ancillary ligands (L_y) can rotate; the ML_y moiety is termed the “rotator”. Steric shielding is provided by a cage like trans spanning dibridgehead diphosphine or “stator”. This is assembled via three fold intramolecular ring closing alkene metathesis. Interestingly, a variety of substitution reactions can subsequently be effected (II → IV), despite the steric shielding of the metal core.

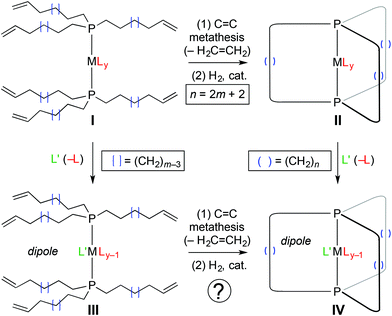Scheme 1 General synthetic approaches to gyroscope like complexes with different ligands on the rotator.

Importantly, all of the physics that underlies the classical mechanical gyroscope¹⁷ – most fundamentally, the conservation of angular momentum – holds at the molecular level.¹⁸ One essential requirement is unidirectional rotation. In contrast, rotations about bonds in molecules are, in accord with microscopic reversibility, bidirectional or Brownian. Hence, this problem must be solved in order to attain molecular gyroscopes. Of several approaches that have been considered,¹⁸ the most easily conceptualized utilizes electric fields.¹⁹ Electric fields interact with dipoles, and it is a simple matter to prepare gyroscope like complexes in which the rotator possesses a dipole moment (e.g., IV). Application of a static electric field will orient the dipoles in the sample. The net result is, as termed by Garcia-Garibay, a “molecular compass”.²⁰

The next level of function would be achieved with a rotating electric field, which could drive the dipole unidirectionally. Indeed, the optimal rotational frequency has already been computed for various rotational barriers.¹⁸ Importantly, if the field rotates too fast, the dipole of the rotator cannot “keep up”. For some readers, it may be easier to envision this experiment with some type of “ordered array”, such as an ensemble of surface mounted species, or a suitable crystal. Regardless, neutral compounds are preferable to ionic compounds, as any counter ions will interact with the dipoles, and invariably increase the rotational barrier. In fluid environments, counter ions would seek to “follow” the dipole, and in the solid state, the electrostatic potential would increase the energies of selected maxima and/or decrease the energies of selected minima.

We have reported iron complexes of the types II or IV with Fe(CO)₃, Fe(CO)₂(NO)⁺ and Fe(CO)₃(H)⁺ rotators and chains of ten to eighteen methylene carbon atoms.² The Fe(CO)₃ rotators of course lack dipole moments. The others feature dipoles, but are accompanied by counter anions. Accordingly, we sought to address two major objectives in this study. First, could the Fe(CO)₂(NO)⁺ systems be elaborated with anionic (pseudo)halide nucleophiles to neutral Fe(CO)(NO)(X) species? As reported earlier, the acyclic (pseudo)halide complexes trans-Fe(CO)(NO)(X)(P((CH₂)_mCH=CH₂)₃)₂ ²¹ and related bis(phosphine) adducts^22–25 are easily accessed from Fe(CO)₂(NO)⁺ precursors. Second, would the ring closing metatheses to give dibridgehead diphosphine ligands best be carried out before, during, or after the substitution sequences?

In this paper, we report a detailed investigation of the aforementioned possibilities, which are embodied in Scheme 2 by routes I (1 → 2 → 3 → 4⁺ BF₄⁻ → 9-X), II (1 → 5⁺ BF₄⁻ → 6-X → 7-X → 9-X), and III (1 → 5⁺ BF₄⁻ → 8⁺ BF₄⁻ → 4⁺ BF₄⁻ → 9-X). In the course of these efforts, barriers to Fe(CO)(NO)(X) rotation for some of the new gyroscope like complexes could be determined, as well as three crystal structures. These reveal a number of auspicious attributes, which suggest that with continued optimization, it may be possible to realize functional molecular gyroscopes with related iron complexes.

Scheme 2 Three possible synthetic routes to the title complexes 9-X: a, alkene metathesis; b, hydrogenation.

Results

Syntheses of title complexes

The first route to the title complexes trans-Fe(CO)(NO)(X)(P((CH₂)_n)₃P) (9-X) in Scheme 2 begins with three efficient steps described in previous papers (a, b, c).² Then a carbonyl ligand of the cationic dicarbonyl nitrosyl complex trans-[Fe(CO)₂(NO)(P((CH₂)_n)₃P)]⁺ BF₄⁻ (4⁺ BF₄⁻) must be displaced by a halide or pseudohalide ion of a suitable salt.

As shown in Scheme 3, solutions of trans-[Fe(CO)₂(NO)(P((CH₂)₁₄)₃P)]⁺ BF₄⁻ (4c⁺ BF₄⁻),² which features three seventeen membered macrocycles, and the ammonium salts Bu₄N⁺ X⁻ (X = Cl, Br, I, or CN; 1–2 equiv.) were combined. Workups gave the target halide or cyanide complexes trans-Fe(CO)(NO)(X)(P((CH₂)₁₄)₃P) (9c-Cl, -Br, -I, -CN) as pale orange solids in 75–83% yields. These were always handled under inert atmospheres, but their high thermal stabilities were reflected by melting points (no decomposition) of at least 140 °C.

Scheme 3 Route I to the title complexes; substitution of the carbonyl ligand by (pseudo)halide nucleophiles following the alkene metathesis/hydrogenation/nitrosylation sequence.

As summarized in Table 1 and the Experimental section, the new complexes were characterized by IR and NMR (¹H, ¹³C{¹H}, ³¹P{¹H}) spectroscopy, microanalyses, and mass spectrometry. The IR spectra of 9c-Cl, -Br, -I, -CN (Table 1) exhibited strong ν_CO (1905–1917 cm⁻¹) and ν_NO (1678–1703 cm⁻¹) bands; that of 9c-CN furthermore showed a weak ν_CN band (2098 cm⁻¹). Consistent with related compounds,^22–25 the frequencies were lower than those of the cationic precursor 4c⁺ BF₄⁻, and increased in the order X = Cl/Br/I/CN.

Table 1 Key IR and NMR data for gyroscope like iron carbonyl complexes

Complex	IR^a [cm^−1]			^31P{^1H} (δ/ppm)^b	^13C{^1H} (δ/ppm)^b^,^c
	ν CO (s)	ν NO (s)	ν CN (w)		C O	C N	PCH2	PCH2CH2	PCH2CH2CH2
					[^2JCP Hz]	[^2JCP Hz]	[^1JCP Hz]		[^3JCP Hz]
a Powder film (s = strong, w = weak). b Spectra were recorded in CDCl3 at ambient probe temperature. c All signals for which J values are given correspond to a triplet or a virtual triplet. d The spectrum of 9c-I exhibits three sets of P(CH2)n/2 signals at ambient probe temperatures. These coalesce at higher temperatures as exemplified in Fig. 5. The PCH2 signals overlap with other CH2 signals and could not be assigned.
3c	1861	—	—	66.9	215.6 [29.0]	—	31.6 [15.1]	24.0	31.0 [6.6]
4c ^+ BF4^–	1965	1764	—	56.8	208.2 [25.3]	—	28.7 [15.4]	24.6	30.7 [7.6]
9c-Cl	1905	1678	—	48.7	218.9 [37.4]	—	26.8 [12.9]	23.5	30.6 [6.5]
9c-Br	1907	1683	—	45.2	218.7 [36.7]	—	26.5 [12.9]	23.2	30.6 [6.1]
9c-I	1911	1691	—	41.7	218.7 [35.5]	—		24.1/23.8/23.5^d	30.5/30.2/29.9^d
9c-CN	1917	1703	2098	58.2	218.3 [30.1]	140.7 [40.6]	29.3 [13.5]	23.8	30.7 [6.9]

---

In each ¹³C{¹H} NMR spectrum, the CO signal was coupled to both phosphorus atoms (t, 218.9–218.3 ppm), with the ²J_CP values (37.4–30.1 Hz) decreasing in the series X = Cl/Br/I/CN. These were downfield from that of 4c⁺ BF₄⁻ (208.2 ppm), which showed a lower ²J_CP value (25.3 Hz). The CN signal of 9c-CN (140.7 ppm) was similarly coupled to phosphorus (t, ²J_CP = 40.6 Hz). The ¹³C{¹H} NMR spectra of 9c-Cl, -Br, -CN gave one set of P(CH₂)_n/2 signals. The PCH₂CH₂CH₂ resonances were assigned according to chemical shift and coupling trends established earlier for related complexes using 2D NMR experiments.² The PCH₂ and PCH₂CH₂CH₂ peaks were apparent triplets due to virtual coupling (J_CP 12.9–13.5 and 6.1–6.9 Hz).²⁶ However, the spectrum of 9c-I was more complicated, showing three sets of P(CH₂)_n/2 signals. This difference is further analyzed in connection with variable temperature NMR data below.

As sketched in Scheme 2, route II to 9-X involves ring closing metatheses about the dipolar rotators of the previously reported adducts trans-Fe(CO)(NO)(X)(P((CH₂)₆CH=CH₂)₃)₂ (6c-X),²¹ followed by hydrogenations of the C=C linkages (steps a′, b′). Many gyroscope like complexes with halide ligands have been similarly accessed.^3,5,6,8a Accordingly, as shown in Scheme 4, dilute CH₂Cl₂ solutions of 6c-Cl, -Br, -I, -CN (0.0020 M) and Grubbs’ catalyst (first generation; 18 mol% or 6 mol%/new C=C linkage) were refluxed. After 24 h, aliquots were analyzed by ¹H NMR (CDCl₃). Except in the case of 6c-I, the terminal alkene signals (5.87–5.73/5.09–4.96 ppm, =CH/=CH₂) were no longer detected. For 6c-I, additional catalyst was required for complete conversion as described in the Experimental section.

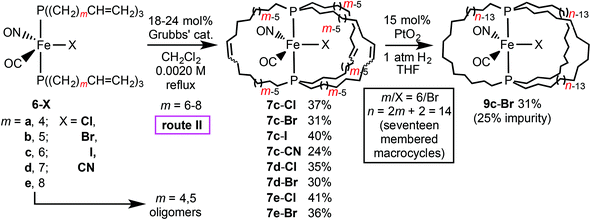Scheme 4 Route II to the title complexes; alkene metathesis after completion of the substitution sequence.

Chromatographic workups afforded trans-Fe(CO)(NO)(X)(P((CH₂)₆CH=CH(CH₂)₆)₃P) (7c-Cl, Br, I, CN), which feature three unsaturated seventeen membered macrocycles, as air sensitive red-brown waxy solids in 24–40% yields. Both ¹H and ³¹P{¹H} NMR spectra indicated mixtures of E/Z C=C isomers. The synthesis of 6c-I was found to be poorly reproducible and the yield of 7c-CN was consistently low. Hence, studies of substrates with shorter (a,b) or longer (d,e) methylene segments were limited to bromide and chloride complexes.

In the cases of 6d,e-Cl and 6d,e-Br, workups gave the larger nineteen and twenty-one membered macrocycles trans-Fe(CO)(NO)(X)(P((CH₂)_mCH=CH(CH₂)_m)₃P) (7d,e-Cl or 7d,e-Br) in 30–41% yields. However, conversions of 6a,b-Cl and 6a,b-Br to the smaller macrocycles 7a,b-Cl and 7a,b-Br could not be verified, even though yields were high for the Fe(CO)₃ analogs.² The ¹H NMR spectra always showed residual CH=CH₂ signals, and although CH=CH signals were apparent these could equally well arise from oligomers.²⁷

As illustrated in Schemes 2 and 4, route II would conclude with a three fold C=C hydrogenation to give 9-X. This proved challenging. The hydrogenation catalyst used in route 1, ClRh(PPh₃)₃, gave only partial conversions, despite extensive optimization efforts. Crabtree's catalyst and Pd/C also proved problematic. Adams’ catalyst, PtO₂, has been successfully employed with other families of gyroscope like complexes.^3–6,8 Indeed, complete conversion of 7c-Br could be effected with 15 mol% under 1 atm of H₂ at room temperature. A chromatographic workup gave trans-Fe(CO)(NO)(Br)(P((CH₂)₁₄)₃P) (9c-Br) in 31% yield. However, the ³¹P{¹H} NMR spectrum exhibited two signals (45.1, 48.2 ppm; 75 : 25 area ratio). The chemical shift of the major peak agreed with that of 9c-Br from route I, and a mass spectrum showed an abundant ion of the correct mass (and no ions of higher masses). However, efforts to separate the byproduct were unsuccessful. Considering the moderate yields of the ring closing metatheses in Scheme 4, and the 43–64% yield range for the conversion of 1 to 6-X (Scheme 2) as described earlier,²¹ route II falls far short of route I in terms of overall yields.

As depicted in Schemes 2 and 5, route III to 9-X involves ring closing metathesis after the first but before the second ligand substitution at iron – i.e., at the stage of the cationic dicarbonyl nitrosyl complex 5⁺ BF₄⁻. As shown in Scheme 5, a 0.0020 M CH₂Cl₂ solution of trans-[Fe(CO)₂(NO)(P((CH₂)₆CH=CH₂)₃)₂]⁺ BF₄⁻ (5c⁺ BF₄⁻) was refluxed with Grubbs’ catalyst. Workup afforded trans-[Fe(CO)₂(NO)(P((CH₂)₆CH=CH(CH₂)₆)₃P)]⁺ BF₄⁻ (8c⁺ BF₄⁻) in 57% yield. The ³¹P{¹H} spectrum exhibited two signals (60.9, 60.1 ppm; 82 : 18 area ratio), consistent with Z/E C=C isomers. A similar reaction of 5e⁺ BF₄⁻ afforded the crude higher homolog 8e⁺ BF₄⁻, which was not further analyzed.

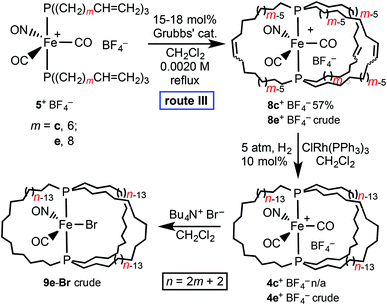Scheme 5 Route III to the title complexes; alkene metathesis during the course of the substitution sequence.

Hydrogenations of 8c,e⁺ BF₄⁻ under the conditions employed for other metathesis products above gave variable results. With 8c⁺ BF₄⁻, substantial amounts of starting material were always recovered under a variety of conditions. In contrast, when 8e⁺ BF₄⁻ and H₂ (5 atm) were combined in the presence of ClRh(PPh₃)₃, a ¹H spectrum of an aliquot showed no residual CH=CH signals. However, a ³¹P{¹H} NMR spectrum of the crude trans-[Fe(CO)₂(NO)(P((CH₂)₁₈)₃P)]⁺ BF₄⁻ (4e⁺ BF₄⁻) indicated a purity of only 80%. Nevertheless, it was further reacted with Bu₄N⁺ Br⁻. A chromatographic workup gave crude trans-Fe(CO)(NO)(Br)(P((CH₂)₁₈)₃P) (9e-Br), which exhibited ³¹P{¹H} NMR signals at 45.4, 45.0, and 44.8 ppm (5 : 80 : 15 area ratio). The major peak agrees well with what would be expected based upon the chemical shift of the lower homolog 9c-Br (45.2 ppm). The mass spectrum showed a molecular ion and fragmentation pattern consistent with the presence of 9e-Br. Nonetheless, although the starting materials in Scheme 5 (5c,e⁺ BF₄⁻) are available in 96% yields from 1 (Scheme 2), it is clear that route III to the title complexes is not competitive with route I.

Molecular and lattice structures

Structural data were sought for as many gyroscope like complexes as possible. Single crystals of 9c-Cl, -Br, -CN could be grown. X-ray data were collected, and the structures were solved as summarized in the Experimental section and Table 2. Key metrical parameters are given in Table 3.

Table 2 Summary of crystallographic data^a

Complex	9c-Cl	9c-Br	9c-CN
a Data common to all structures: T = 173(2) K; λ = 0.71073 Å.
Empirical formula	C43H84ClFeNO2P2	C43H84BrFeNO2P2	C44H84FeN2O2P2
Formula weight	800.35	844.81	790.92
Crystal system	Monoclinic	Monoclinic	Monoclinic
Space group	C2/c	C2/c	C2/c
Unit cell dimensions
a [Å]	21.4367(4)	21.2190(8)	21.4114(6)
b [Å]	13.8586(4)	13.9660(8)	13.9998(2)
c [Å]	18.3518(5)	18.1727(2)	18.2960(5)
α [°]	90	90	90
β [°]	122.459(1)	121.002(4)	122.681(9)
γ [°]	90	90	90
Volume [Å^3]	4600.3(2)	4616.1(3)	4616.1(3)
Z	4	4	4
ρ calcd [Mg m^−3]	1.1560.489	1.2160.489	1.1380.489
μ [mm^−1]	0.489	1.295	0.431
F(000)	1752	1824	1736
Crystal size [mm^3]	0.35 × 0.30 × 0.20	0.30 × 0.30 × 0.30	0.35 × 0.20 × 0.20
Range for data collection	2.37 to 27.44	2.92 to 27.57	2.26 to 27.50
Index ranges	–27 ≤ h ≤ 27	–27 ≤ h ≤ 27	–27 ≤ h ≤ 27
	–17 ≤ k ≤ 17	–18 ≤ k ≤ 18	–18 ≤ k ≤ 17
	–23 ≤ l ≤ 23	–23 ≤ l ≤ 23	–23 ≤ l ≤ 23
Reflections collected	9763	39 777	9935
Independent reflections	5244	5278	5286
Data/restraints/parameters	5244/3/234	5278/0/230	5286/0/232
Goodness-of-fit on F^2	1.062	1.026	0.984
Final R indices [I > 2σ(I)]	R 1 = 0.0503, wR2 = 0.1496	R 1 = 0.0613, wR2 = 0.1595	R 1 = 0.0346, wR2 = 0.0900
R indices (all data)	R 1 = 0.0648, wR2 = 0.1612	R 1 = 0.0857, wR2 = 0.1774	R 1 = 0.0464, wR2 = 0.0960
Largest diff. peak & hole [e Å^−3]	0.975/−1.014	2.200/−2.197	0.219/−0.772

---

Table 3 Key intramolecular and intermolecular distances in crystallographically characterized gyroscope like complexes (Å), and selected bond and torsion angles (°)

Complex	9c-Cl	9c-Br	9c-CN
a These values have considerable uncertainty given the disorder and refinement constraints described in the Experimental section; at the same time, it is unlikely that they lead to an overestimation of the rotator radius. b The longest of the F̲e̲CO̲, F̲e̲NO̲, or F̲e̲CN̲ distances, plus the van der Waals radius of the terminal atom (oxygen, 1.52 Å). c The distance from iron to the two remote carbon atoms of the three macrocycles (a, b, c; the first contains the idealized C2 axis) that are closest to the plane of the rotator (Fe–Cdistal). d The shortest of the previous six distances, minus the van der Waals radius of the carbon atom (1.70 Å). e The longest of the previous six distances, minus the van der Waals radius of the carbon atom. f The distance from iron to the nearest carbon atom of a neighboring gyroscope like molecule. g The previous entry minus the van der Waals radius of the carbon atom. h The distance between planes defined by the three carbon atoms attached to each phosphorus atom, taken at the centroid of the three carbon atoms. i The previous value minus the van der Waals radii of two carbon atoms. j The distance between the PC̲H2 carbon atoms of each macrocycle. k The C–P–P–C torsion angle within the three macrocycles (a, b, c).
Fe–P	2.2527(6)	2.2705(8)	2.2310(3)
F̲e̲CO̲	2.90^a	2.70^a	2.99^a
F̲e̲NO̲	2.75^a	3.00^a	2.99^a
F̲e̲X̲	2.363(4)	2.5280(19)	2.88^a
Radius of rotator^b	4.42	4.52	4.51
Fe–Ca ^c	7.89	7.91	7.93
Fe–C′a ^c	7.89	7.91	7.93
Fe–Cb ^c	6.65	6.73	6.62
Fe–C′b ^c	7.46	7.37	7.43
Fe–Cc ^c	7.46	7.37	7.43
Fe–C′c ^c	6.65	6.73	6.62
Fe–Cdistal–vdW^d	4.95	5.03	4.92
Fe–Cdistal′–vdW^e	6.19	6.21	6.23
Fe–Cneighbor ^f	5.99	6.06	6.04
Fe–Cneighbor–vdW^g	4.29	4.36	4.34
∠P–Fe–P	177.9	178.2	176.1
P(C̲H2)3/P(C̲H2)3 ^h	6.02	6.08	5.98
P(C̲H2)3/P(C̲H2)3–2vdW^i	2.62	2.68	2.58
C̲ aP–Fe–PC̲a ^j	6.04	6.12	5.98
C̲ bP–Fe–PC̲b	6.16	6.20	6.12
C̲ cP–Fe–PC̲c	6.16	6.20	6.12
Ca–P–P–Ca ^k	38.4	38.2	38.5
Cb–P–P–Cb	37.9	37.5	38.2
Cc–P–P–Cc	37.9	37.5	38.2

---

Thermal ellipsoid representations of 9c-Cl, -Br, -CN are provided in Fig. 1. In all three structures, the CO/NO/X ligands were disordered over three positions. In the case of 9c-Cl, the ligands could nonetheless be distinguished (33% occupancy, each position); for refinement, the CO and NO positions were arbitrarily assigned in accord with the overall symmetry. With 9c-Br, the bromide ligand exhibited 33% occupancy at each position, but the CO and NO ligands could not be distinguished. For refinement, they were assigned equal occupancies in each position. In the case of 9c-CN, none of the ligands could be distinguished and were presumed to be equally disordered over three positions. Refinement was carried out with fixed occupancy factors as described in the Experimental section.

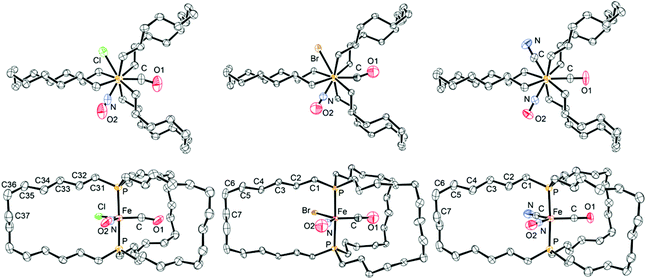Fig. 1 Thermal ellipsoid plots (50% probability) of the molecular structures of 9c-Cl, 9c-Br, and 9c-CN (left to right; all Fe(CO)(NO)(X) moieties are disordered).

As a result, the positions of the Fe(CO)(NO)(X) ligands in Fig. 1 are arbitrary, and their bond lengths must be cautiously interpreted. In each structure, the dibridgehead diphosphine ligand exhibits a crystallographic C₂ axis coincident with the F̲e̲–C̲O linkage (the numbered carbon atoms in Fig. 1 thereby exchange between the upper and lower hemispheres). In all complexes, the CH₂/(CO)(NO)(X)/CH₂ substituents along the P–Fe–P axes adopt staggered conformations (Fig. 1, top). The crystal structure of the tricarbonyl complex 3c (Scheme 2), which has been analyzed in previous papers,² exhibits an analogous symmetry axis and diphosphine and P–Fe–P conformations.

In all three structures, the lattice packing is analogous to that in 3c (monoclinic, C2/c, Z = 4).² A representative example (9c-Br) is shown in Fig. 2. The molecules align in well defined layers in which all P–Fe–P axes are parallel (Fig. 2, left). Within each layer the individual molecules alternate between two different orientations (Fig. 2, right). As would be expected, the unit cell dimensions are virtually identical (Table 2), with the volumes spanning the narrow range of 4600.3 to 4616.1 ų (3c: 4633.5 ų).²

Fig. 2 The crystal lattice of 9c-Br as viewed along (left) and perpendicular (right) to the b axis (the Fe(CO)(NO)(Br) moieties are disordered).

A model for approximating the void space available to the rotator within the dibridgehead diphosphine cages has been developed in several papers.^2b,3b,8a,9Fig. 3 applies this paradigm to 9c-X. The first step is to determine the rotator radius. Towards this end, one takes the distance from the metal to the most remote atom of each ligand on the rotator (e.g., F̲e̲CO̲, F̲e̲NO̲, F̲e̲CN̲ for the diatomic ligands). Then the van der Waals radius of the remote atom is added (oxygen, 1.52 Å; nitrogen, 1.55 Å; chloride, 1.75 Å; bromide, 1.85 Å; iodide, 1.98 Å).²⁸ The ligand that yields the greatest value can be termed “radius determining”.

Fig. 3 Spatial relationships involving the iron atom, rotator, and (CH₂)₁₄ bridges in 9c-X; see text and Table 3 (vdW = van der Waals; A/B/C refer to the macrocycle labels in Table 3).

Given the complexities introduced by the crystallographic disorder, boxes are presented for each complex of interest in Fig. 3. These summarize the radii associated with each ligand based upon either the data in Table 3 or model complexes in the literature.²⁹ The radius determining values are denoted in red, and in three cases correspond to FeCO or FeNO ligands (4.42–4.52 Å). For 9c-I, which could not be structurally characterized, the iodide ligand should be radius determining (4.68 Å).²⁹ Regardless, it can be confidently concluded that all rotator radii fall into the relatively narrow range of 4.42–4.68 Å.

The “horizontal clearance” within the diphosphine cage is then estimated. First, the distances from iron to the distal carbon atoms of all three methylene chains are determined (per Table 3 and Fig. 3, the chains are labeled a/b/c). Since the P(CH₂)₁₄P linkages are roughly symmetric with respect to the rotator plane, these should normally be C7 and C8. The van der Waals radius of a carbon atom (1.70 Å)²⁸ is then subtracted, giving six values as summarized in Table 3.³⁰ In order to reflect the minimum clearance available, the shortest is normally used for analysis (Fe–C_distal–vdW, Table 3), although other approaches have been considered.^2,9,31 In any case, the horizontal clearances for 9c-Cl, -Br, -CN fall in the range of 4.92–5.03 Å, as highlighted in Fig. 3 (red), and a similar value would be expected for crystalline 9c-I. Hence, the clearances are significantly greater than the radii of the four rotators. Implications regarding the NMR data presented above or below are analyzed in the Discussion section.

Another issue concerns the feasibility of rotator rotation in the crystal lattice. Here, there is the additional consideration of interference from neighboring molecules. Of special interest are cases where the distances from the metal atom of one complex to the nearest non-hydrogen atoms of a neighboring complex are greater than the radius of the rotator, after adjusting for the van der Waals radius of the non-hydrogen atom.³⁰ In this limit, sufficient steric spacing is assured.

Data are obtained from the crystal structures as exemplified for 9c-Cl in Fig. 4 and summarized in Table 3. The intermolecular distances are quite similar for all three complexes (5.99–6.06 Å; “Fe–C_neighbor”), giving 4.29–4.36 Å (“Fe–C_neighbor–vdW”) after the van der Waals correction.³⁰ These values are comparable to the rotator radii (4.42–4.52 Å). Furthermore, the atom of the neighboring molecule that exhibits the shortest distance (C23 in Fig. 4) is markedly removed from the plane of the rotator, attenuating the degree of interaction. The next nearest atom, which is barely removed from the rotator plane (C18 in Fig. 4), allows for more clearance (4.44 Å, 4.48 Å, and 4.55 Å in 9c-Cl, -Br, -CN after van der Waals corrections). In any case, any impediment to rotator rotation imposed by the crystal lattice is not likely to be significantly greater than that imposed by the horizontal dimension of the diphosphine cage.

Fig. 4 Distances from the iron atom of crystalline 9c-Cl to the six nearest non-hydrogen atoms of a neighboring molecule.

Variable temperature NMR data

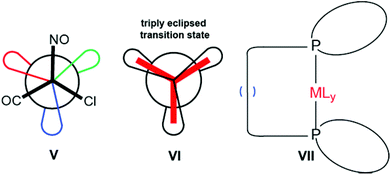
¹³C{¹H} NMR spectra of 9c-Cl were recorded in CD₂Cl₂ at temperatures ranging from 25 to −85 °C. The chemical shifts of the PCH₂CH₂CH₂ carbon atoms varied moderately (Δδ 0.3–0.6 ppm) as they broadened and ultimately decoalesced into three peaks, as exemplified for the PCH₂CH₂ signal in Fig. 5 (left). This corresponds to Fe(CO)(NO)(Cl) rotation becoming slow on the NMR time scale, leading to three symmetry inequivalent macrocycles with different sets of NMR chemical shifts, as represented in V (Fig. 6). In order for a methylene group to sample all environments in V, the Fe(CO)(NO)(Cl) moiety must rotate by 240° through transition states of the type VI. Alternative processes that might render the methylene signals equivalent, such as mechanisms involving CO or phosphine dissociation (or with 9c-CN, cyanide dissociation) can be excluded due to coupling constants that are maintained at the high temperature limit (J_CP, Table 1).

Fig. 5 Partial ¹³C NMR spectra (PCH₂CH₂ signals) of 9c-Cl (CD₂Cl₂, left), and 9c-I (C₆D₅Cl, right) as a function of temperature. Each spectrum is paired with simulated line shapes (red).

Fig. 6 Additional relevant structures.

The spectra of 9c-Cl were simulated using gNMR (Fig. 5, red traces),³² which afforded the rate constant at each temperature. An Eyring plot (Fig. s1, ESI†) gave ΔH^‡ and ΔS^‡ values of 5.9 kcal mol⁻¹ and −20.1 eu for the 240° rotation of the Fe(CO)(NO)(Cl) moiety. Other examples have been reported where three identical groups similarly exchange between three distinct environments and the rate constants determined by line shape analysis.³³

Next, ¹³C NMR spectra of 9c-I were recorded in C₆D₅Cl between −20 and 100 °C (Fig. 5, right). As noted in connection with Table 1, Fe(CO)(NO)(I) rotation was slow on the NMR time scale at room temperature, as evidenced by three peaks of equal area for the PCH₂CH₂ and other methylene signals. However, a well defined three fold coalescence was observed near 55 °C. The data were treated as for 9c-Cl, giving ΔH^‡ and ΔS^‡ values of 7.6 kcal mol⁻¹ and −23.9 eu. This yields a ΔG^‡_{298 K} value (14.7 kcal mol⁻¹) that is as expected higher than that of 9c-Cl (11.9 kcal mol⁻¹). The activation parameters are summarized in Table 4, together with those of other trigonal bipyramidal iron gyroscope like complexes.^2,9 Additional aspects of these data are analyzed in the Discussion section.

Table 4 Activation parameters for Fe(CO)(NO)(X) rotation within E((CH₂)_n)₃E cages as determined by variable temperature ¹³C{¹H} NMR in solution

Compound	X/E/n/z	ΔH^‡ (kcal mol^−1)	ΔS^‡ (eu)^a	ΔG^‡298 K (kcal mol^−1)	ΔG^‡383 K (kcal mol^−1)
a cal mol^−1 K^−1. b Spectra were recorded in CD2Cl2. c Spectra were recorded in C6D5Cl. d Data are from ref. 2. e Spectra were recorded in CDFCl2. f Diarsenic analog of 4a^+ BF4^− or 4b^+ BF4^−; data are from ref. 9.
9c-Cl	Cl/P/14/0	5.9	−20.4	11.9	13.6
9c-I	I/P/14/0	7.6	−23.9	14.7	16.8
4b^+ BF4^–^c^,^d	CO/P/12/1	8.3	−28.4	16.7	19.2
4c^+ BF4^–^d^,^e	CO/P/14/1	9.5	−6.5	11.4	11.9
4a-As2^+ BF4^−^c^,^f	CO/As/10/1	—	—	—	>19.4
4b-As2^+ BF4^−^b^,^f	CO/As/12/1	7.7	−22.1	14.2	16.2

---

Discussion

Synthetic strategies and cage effects

The major objective of this study was to efficiently access gyroscope like complexes based upon cage like dibridgehead diphosphines that contain neutral dipolar Fe(CO)(NO)(X) rotators (9-X).³⁴ A companion objective was to determine whether the ring closing metatheses that afford the diphosphine cages are best carried out before (route I), after (route II), or during (route III) substitution sequences involving various Fe(CO)₃ precursors. As shown in Schemes 3–5, route I proved to be unequivocally superior. Routes II and III suffered from lower yields in both the metathesis and C=C hydrogenation steps. Thus, perhaps counterintuitively, it proves best to effect substitution of the rotator in the most sterically shielded adduct.

With additional experimentation, an effective hydrogenation catalyst might have been found for routes II and III. However, conditions successfully employed with other types of gyroscope like complexes gave mediocre results. In the metathesis step, an alternative cyclization mode is possible involving a combination of interligand and intraligand coupling. After hydrogenation, species of the type VII would result (Fig. 6). These are routinely encountered as byproducts in metatheses of related octahedral complexes (as well as a few square planar complexes),^2b,8a and exhibit distinctive NMR properties. However, they have not yet been detected in any reactions of trigonal bipyramidal precursors, which as analyzed in previous papers can be viewed as conformationally pre-organized for three fold interligand metatheses.^2,9

With the ready availability of 9c-X (Scheme 3), there is an opportunity to probe for “cage effects” relative to the acyclic analogs 6c-X (Scheme 2).²¹ However, any perturbations on spectroscopic properties appear to be modest. The ³¹P{¹H} NMR signals of 9c-Cl, -Br, -I, -CN (Table 1) are generally 2–3 ppm downfield of those of 6c-Cl, -Br, -I, -CN. In contrast, the CO ¹³C{¹H} signals of 9c-Cl, -Br, -I, -CN are always ∼2 ppm upfield. The IR ν_CO and ν_NO values are greater for 9c-Cl, -Br, -I, -CN; the trend is most pronounced for 9c-Ivs. 6c-I (1911 and 1691 cm⁻¹vs. 1905 and 1681 cm⁻¹). A more interesting type of cage effect would involve possible changes in the mechanisms of substitution of 5⁺ BF₄⁻vs. 4⁺ BF₄⁻ (Scheme 2), and conditions for monitoring these rates are currently being optimized.

Structures and dynamic properties

Apart from the disorder of the rotators, the homology exhibited by the molecular structures and crystal lattices of the gyroscope like complexes 9c-Cl, -Br, -CN (Fig. 1 and 2) is striking. Considering that the tricarbonyl complex 3c exhibits analogous structural features,² it seems that – at least for species with seventeen membered macrocycles – all neutral iron adducts with rotators comprised of three small ligands (e.g., H, F, CS, C≡CH, CH₃, etc.) should crystallize similarly. This is supported by the closely comparable structures of the corresponding dibridgehead diarsine⁹ and Os(CO)₃ complexes.^8a Thus, a diverse parameter space has been defined by which various properties of trigonal bipyramidal molecular gyroscopes can be optimized while maintaining homologous solid state structures.

The activation parameters for Fe(CO)(NO)(X) rotation in 9c-Cl, -I can be compared to those reported earlier for Fe(CO)₂(NO)⁺ rotation in 4c⁺ BF₄⁻ (Table 4).² At first glance, the ΔG^‡_{298 K} values for 9c-Cl, -I follow the trend expected based upon the relative sizes of the chloride and iodide ligands (11.9 and 14.7 kcal mol⁻¹). However, in some ways this is a misleading comparison, as Fig. 3 shows that the carbonyl ligand – not chloride – is radius determining in the former (4.42 vs. 4.11 Å). Importantly, the carbonyl ligand is also radius determining in 4c⁺ BF₄⁻, as gauged by the crystal structure of the tricarbonyl complex 3c (4.45 Å)² or the diarsine analog of the lower homolog 4b⁺ BF₄⁻ (4.42 Å; 4b-As₂⁺ BF₄⁻).⁹ Accordingly, 9c-Cl and 4c⁺ BF₄⁻ exhibit very similar ΔG^‡_{298 K} values (11.9 and 11.4 kcal mol⁻¹). One also sees in Table 4 that the ΔG^‡_{298 K} value for 4c⁺ BF₄⁻ is much lower than that for 4b⁺ BF₄⁻ (11.4 vs. 16.7 kcal mol⁻¹). The latter features smaller fifteen membered macrocycles and diminished horizontal clearance.

As illustrated by 4b⁺ BF₄⁻ and 4b-As₂⁺ BF₄⁻ in Table 4, ΔG^‡_{298 K} values significantly decrease when the bridgehead phosphorus atoms are replaced by arsenic atoms (16.7 vs. 14.2 kcal mol⁻¹). This has been interpreted in terms of increased “vertical clearance” provided by the iron arsenic bonds, which are typically 3–4% longer than iron phosphorus bonds. Since, in principle, there is sufficient horizontal clearance to accommodate the iodide ligand of 9c-I within the diphosphine cage (Fig. 3), we suggest that the increased ΔG^‡_{298 K} value vs. that of 9c-Cl is largely derived from steric interactions in the vertical dimension. This can be analyzed as exemplified in Fig. 7, which focuses on the spatial relationships between the rotator ligands and the C–P–Fe–P–C linkages of 9c-Cl.

Fig. 7 Steric relationships between atoms in 9c-Cl relevant to “vertical clearance” of the rotator. VIII: separation of planes defined by the PCH₂ carbon atoms. IX: rotated 90° from VIII so that the chlorine atom points at the reader, and with the iron, phosphorus, chlorine, and PCH₂ carbon atoms that most closely flank the chlorine ligand (which are from different macrocycles) at van der Waals radii. X: relationship of the two PCH₂ carbon atoms within a macrocycle.

First, all of the ligands on the rotator must “squeeze” between the upper and lower PCH₂ groups as they sweep through any arc of ≥120°. In the transition states (VI, Fig. 6), these will be PCH₂ groups from the same macrocycle. In the ground states sampled by the crystal structures, the PCH₂ groups nearest to a given ligand will be from different macrocycles (Fig. 1, top). In any case, planes may be defined by the three upper and three lower PCH₂ groups, as shown in VIII in Fig. 7. Given the crystallographic C₂ axes of the diphosphine ligands, these will be parallel. As summarized in Table 3, the plane/plane distances range from 5.98 to 6.08 Å for 9-Cl, -Br, -CN. When the van der Waals radii of two PCH₂ carbon atoms are subtracted (3.40 Å),²⁸ vertical clearances of 2.58 to 2.68 Å are obtained.³⁰

Another measure of vertical clearance is provided by the distance between the PCH₂ carbon atoms on each macrocycle, as illustrated in X. For 9c-Cl these distances range from 6.04 to 6.16 Å, as summarized in Table 3. For 9c-Br, -CN, the corresponding ranges are 6.08–6.20 Å and 5.98–6.12 Å. When the van der Waals radii of the two PCH₂ carbon atoms are subtracted, vertical clearances of 2.64–2.76 Å (9c-Cl), 2.68–2.80 Å (9c-Br), and 2.58–2.72 Å (9c-CN) are obtained. These distances are slightly longer than the plane/plane distances or clearances in VIII as the vector between the two PCH₂ atoms is not perpendicular to the plane.

In the vertical dimension, what counts is not the radius defined by a given ligand but its “fatness”. This would be approximated by the van der Waals diameter. Every polyatomic ligand is characterized by a fatness determining atom, and every rotator by a fatness determining ligand. The diameters of the ligands in Fig. 3 increase from NO (3.10 Å), CO and CN (3.40 Å), Cl (3.50 Å), Br (3.70 Å), to I (3.96 Å).²⁶ Hence, for the rotors of the halide complexes, the halide ligands are fatness determining, and for the cyanide complex the slightly more svelte CO and CN ligands are fatness determining. However, there is not much difference between the fatness of the Cl, CN, and CO ligands.

Regardless, all of the preceding values are somewhat greater than the vertical clearances represented in VIII, X, or the analogous structures for 9c-Br, -CN. This is particularly evident in IX, which is simply a partial view of the crystal structure with selected atoms at van der Waals radii. In solution, the tightness of the “squeeze” associated with the transition state VI (Fig. 6) can be ameliorated by simultaneous conformational changes within the macrocycles, as previously discussed.^2b However, we suggest that the residual steric interactions are responsible for the major part of the activation barriers – more than any interactions connected with horizontal clearance in seventeen membered macrocycles. Thus, the introduction of the larger iodide ligand in 9c-I leads to top/bottom steric interactions that no longer allow Fe(CO)(NO)(X) rotation to be rapid on the NMR time scale at room temperature.

A final point concerns the negative ΔS^‡ values in Table 4. These are consistent with the loss of entropy that would be anticipated from the three fold eclipsing interaction in transition state VI. Furthermore, this interaction would presumably be accompanied by correlated changes in the macrocycle conformations, which as noted above could attenuate van der Waals contacts originating from the tight vertical clearances.

Towards molecular gyroscopes

In the introduction, the use of external electric fields to orient dipolar rotators or compel unidirectional motion¹⁹ was discussed. This study, coupled with earlier installments,^2,9 has provided a clear road map for approaching these objectives. First, facile routes to neutral gyroscope like iron complexes with dipolar rotors and cage like dibridgehead diphosphine stators have been developed. Second, these complexes can easily be expanded in the vertical dimension by switching from phosphorus to arsenic donor atoms,⁹ and very likely to antimony and bismuth donor atoms. The iron bismuth bond length in Fe(CO)₄(Bit-Bu₃) is 2.6269(9) Å,³⁵ as compared to a range of 2.2310(3) to 2.2705(8) Å for the iron phosphorus bonds in Table 3. This 14–18% increase should greatly attenuate the types of steric interactions analyzed in Fig. 7. Metal fragments that give longer metal/donor atom bonds, such as Os(CO)₃, can also be bought into play.^8a Both the radius and fatness of the rotator can be decreased by introducing still smaller ligands such as hydride and fluoride. All of these strategies, and a number of others,^2,9 hold great promise for achieving very low rotational barriers, analogous to the idealized frictionless limit for flywheels of classical mechanical gyroscopes.

The reliably reproducible solid state properties of gyroscope like complexes based upon trigonal planar rotators and dibridgehead bis(donor atom) stators that define three seventeen membered macrocycles constitute another bonus. Since there are no substantial intermolecular impediments to M(L)(L′)(L′′) (Fe(CO)(NO)(X)) rotation in the crystal lattices, and all E–M–E (P–Fe–P, As–Fe–As, P–Os–P, etc.) axes are parallel, it is easy to envision how applying a rotating electric field to a properly oriented crystal could simultaneously transform 10¹⁷ molecules (ca. 1 μmol) into an array of functioning gyroscopes. Indeed, solid state ¹³C NMR studies of the tricarbonyl complex 3c have established rapid rotation between −60 and 95 °C.^2b,36 Furthermore, this substrate is, in view of the insights gleamed from this and previous papers, by no means optimized for a low rotational barrier.

Promising leads for molecular gyroscopes have also been developed with other metal coordination geometries,^3,5,8 other types of expanded and/or conformationally restricted stators,⁴ and organic or organosilicon systems under study by Garcia-Garibay¹² and Setaka.¹³ However, variations on the trigonal bipyramidal complexes described herein are viewed as having particular potential, and further studies will be reported in due course.

Experimental section

General data

All reactions were conducted under N₂ or H₂ atmospheres. Chemicals were treated as follows: CH₂Cl₂, ether, and hexanes, dried and degassed using a Glass Contour solvent purification system; CDCl₃, C₆D₆, (2 × Cambridge Isotope Laboratories), Bu₄N⁺ X⁻ (X = Cl or CN, Aldrich, 95–97%; Br, TCI, 99%; I, Alfa Aesar, 98%), Grubbs’ catalyst (Ru(=CHPh)(PCy₃)₂(Cl)₂; Strem), SiO₂ (Silicycle, 40–63 μm, 230–400 mesh), neutral Al₂O₃ (Macherey-Nagel), Celite (EMD), used as received.

NMR spectra were recorded on standard 400 or 500 MHz spectrometers at ambient probe temperatures and referenced as follows (δ, ppm): ¹H, residual internal C₆D₅H (7.15) or CHCl₃ (7.26); ¹³C, internal C₆D₆ (128.0) or CDCl₃ (77.0); ³¹P, external H₃PO₄ (0.00). IR spectra were recorded using a Shimadzu IRAffinity-1 spectrometer with a Pike MIRacle ATR system (diamond/ZnSe crystal). Mass spectra and melting points were determined per earlier papers.^2b,9 Microanalyses were conducted on a Carlo Erba EA1110 instrument or by Atlantic Microlab.

trans-Fe(CO)(NO)(Cl)(P((CH₂)₁₄)₃P) (9c-Cl). A Schlenk flask was charged with trans-[Fe(CO)₂(NO)(P((CH₂)₁₄)₃P)]⁺ BF₄⁻ (4c⁺ BF₄⁻;² 0.060 g, 0.068 mmol) and CH₂Cl₂ (15 mL), and Bu₄N⁺ Cl⁻ (0.028 g, 0.102 mmol) was added with stirring. After 18 h, the solvent was removed by oil pump vacuum. Then CH₂Cl₂ (10 mL) was added and the mixture was filtered through silica (2.5 × 5.0 cm) with CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum to give 9c-Cl as a pale orange solid (0.044 g, 0.055 mmol, 81%), mp 139–141 °C (capillary). Anal. Calcd for C₄₃H₈₄ClFeNO₂P₂ (799.50): C 64.53, H 10.58; found: C 64.18, H 10.63.

NMR (CDCl₃, δ in ppm): ¹H NMR (500 MHz): 1.98–1.86 (m, 12H, CH₂), 1.66–1.48 (m, 12H, CH₂), 1.44–1.37 (m, 12H, CH₂), 1.36–1.27 (m, 48H, CH₂); ¹³C{¹H} NMR (126 MHz) 218.9 (t, ²J_CP = 37.4 Hz, CO), 30.6 (virtual t, ³J_CP, ⁵J_CP′ = 6.5 Hz,²⁶ PCH₂CH₂CH₂), 27.9 (s, CH₂), 27.6 (s, CH₂), 26.9 (s, CH₂), 26.80 (s, CH₂), 26.75 (virtual t, ¹J_CP, ³J_CP′ = 12.9 Hz,²⁶ PCH₂), 23.5 (s, CH₂); ³¹P{¹H} NMR (202 MHz): 48.7 (s).

IR (powder film, cm⁻¹): 2926 (w), 2856 (w), 1905 (s, ν_CO), 1678 (s, ν_NO), 1458 (w), 1409 (w), 1087 (w), 803 (w), 760 (w), 719 (w). MS:³⁷ 801 (9c-Cl⁺, 5%), 771 ([9c-Cl − CO]⁺, 30%), 741 ([9c-Cl − CO − NO]⁺, 100%), 738 ([9c-Cl − NO − Cl]⁺, 65%), 684 ([9c-Cl − CO − NO − Cl − Fe + 2O]⁺, 65%), 668 ([9c-Cl − CO − NO − Cl − Fe + O]⁺, 40%), 652 ([9c-Cl − CO − NO − Cl − Fe]⁺, 20%).

trans-Fe(CO)(NO)(Br)(P((CH₂)₁₄)₃P) (9c-Br). Route I. Complex 4c⁺ BF₄⁻ (0.107 g, 0.122 mmol), CH₂Cl₂ (20 mL), and Bu₄N⁺ Br⁻ (0.079 g, 0.244 mmol) were combined in a procedure analogous to that for 9c-Cl. An identical workup gave 9c-Br as a pale orange solid (0.082 g, 0.097 mmol, 79%), mp 150–152 °C (capillary). Anal. Calcd for C₄₃H₈₄BrFeNO₂P₂ (843.45): C 61.13, H 10.02; found: C 61.42, H 10.07. Route II. A Fischer-Porter bottle was charged with 7c-Br (0.158 g, 0.198 mmol), PtO₂ (0.007 g, 0.030 mmol, 15 mol%), THF (20 mL), and H₂ (1 atm). The solution was stirred at 23 °C. After 48 h, the solvent was removed by oil pump vacuum. The residue was filtered through neutral alumina (2.5 × 5.0 cm) with THF. The solvent was removed from the filtrate by oil pump vacuum to give 9c-Br as a red-brown solid (0.049 g, 0.061 mmol, 31%) that was ca. 75% pure by ³¹P NMR.

NMR (CDCl₃, δ in ppm): ¹H NMR (500 MHz): 2.17–1.80 (m, 12H, CH₂), 1.68–1.47 (m, 12H, CH₂), 1.44–1.36 (m, 12H, CH₂), 1.36–1.18 (m, 48H, CH₂); ¹³C{¹H} NMR (100 MHz): 218.6 (t, ²J_CP = 36.5 Hz, CO), 30.3 (virtual t, ³J_CP, ⁵J_CP′ = 7.8 Hz,²⁶ PCH₂CH₂CH₂), 27.7 (s, CH₂), 27.3 (s, CH₂), 26.8 (s, CH₂), 26.6 (s, CH₂), 26.5 (virtual t, ¹J_CP, ³J_CP′ = 12.9 Hz,²⁶ PCH₂), 23.2 (s, CH₂); ³¹P{¹H} NMR (202 MHz): 45.2 (s); for sample from route II (162 MHz) 48.2 (s, 25% impurity), 45.1 (s, 75%).

IR (powder film, cm⁻¹): 2926 (w), 2853 (w), 1907 (s, ν_CO), 1683 (s, ν_NO), 1456 (w), 1409 (w), 1234 (w), 1087 (w), 791 (w), 758 (w), 718 (w). MS:³⁷ 815 ([9c-Br − CO]⁺, 20%), 785 ([9c-Br − CO − NO]⁺, 100%), 736 ([9c-Br − CO − Br]⁺, 35%), 734 ([9c-Br − NO − Br]⁺, 40%), 704 ([9c-Br − CO − NO − Br]⁺, 5%), 664 ([9c-Br − CO − NO − Br − Fe + O]⁺, 10%), 648 ([9c-Br − CO − NO − Br − Fe]⁺, 25%).

trans-Fe(CO)(NO)(I)(P((CH₂)₁₄)₃P) (9c-I). Complex 4c⁺ BF₄⁻ (0.090 g, 0.102 mmol), CH₂Cl₂ (20 mL), and Bu₄N⁺ I⁻ (0.030 g, 0.114 mmol) were combined in a procedure analogous to that for 9c-Cl. An identical workup gave 9c-I as a pale orange solid (0.069 g, 0.077 mmol, 75%), mp 162–164 °C (capillary; dec). Anal. Calcd for C₄₃H₈₄FeINO₂P₂ (891.44): C 57.91, H 9.49; found: C 57.77, H 9.60.

NMR (CDCl₃, δ in ppm): ¹H NMR (500 MHz): 2.34–1.89 (m, 24H, CH₂), 1.78–1.58 (m, 24H, CH₂), 1.52–1.46 (m, 12H, CH₂), 1.46–1.39 (m, 12H, CH₂), 1.39–1.30 (m, 12H, CH₂); ¹³C{¹H} NMR (125 MHz): 218.7 (t, ²J_CP = 35.5 Hz, CO), 30.5, 30.2, 29.9 (overlapping multiplets, 3PCH₂CH₂CH₂), 28.0–26.8 (overlapping signals, CH₂), 24.1, 23.7, 23.5 (overlapping multiplets, 3PCH₂CH₂); ³¹P{¹H} NMR (202 MHz): 41.6 (s).

IR (powder film, cm⁻¹): 3076 (w), 2926 (w), 2853 (w), 1911 (s, ν_CO), 1691 (s, ν_NO), 1459 (w), 1409 (w), 1262 (w), 1089 (w), 1019 (w), 799 (w), 756 (w), 718 (w). MS:³⁷ 892 (9c-I⁺, 5%), 864 ([9c-I − CO]⁺, 25%), 834 ([9c-I − CO − NO]⁺, 100%), 767 ([9c-I − I]⁺, 5%), 737 ([9c-I − NO − I]⁺, 25%), 684 ([9c-I − CO − NO − I − Fe + 2O]⁺, 100%), 668 ([9c-I − CO − NO − I − Fe + O]⁺, 15%), 652 ([9c-I − CO − NO − I − Fe]⁺, 10%).

trans-Fe(CO)(NO)(CN)(P((CH₂)₁₄)₃P) (9c-CN). Complex 4c⁺ BF₄⁻ (0.050 g, 0.056 mmol), CH₂Cl₂ (15 mL), and Bu₄N⁺ CN⁻ (0.030 g, 0.114 mmol) were combined in a procedure analogous to that for 9c-Cl. An identical workup gave 9c-CN as a pale orange solid (0.036 g, 0.046 mmol, 83%), mp 141–143 °C (capillary; dec). Anal. Calcd for C₄₄H₈₄FeN₂O₂P₂ (790.54): C 63.95, H 10.25; found: C 64.01, H 10.22.

NMR (CDCl₃, δ in ppm): ¹H NMR (500 MHz): 2.11–1.97 (m, 12H, CH₂), 1.86–1.74 (m, 12H, CH₂), 1.61–1.48 (m, 60H, CH₂); ¹³C{¹H} NMR (126 MHz): 218.3 (t, ²J_CP = 30.1 Hz, CO), 140.7 (t, ²J_CP = 40.6 Hz, CN), 30.7 (virtual t, ³J_CP, ⁵J_CP′ = 6.9 Hz,²⁶ PCH₂CH₂CH₂), 29.3 (virtual t, ¹J_CP, ³J_CP′ = 13.5 Hz,²⁶ PCH₂), 27.9 (s, CH₂), 27.8 (s, CH₂), 27.0 (s, CH₂), 26.7 (s, CH₂), 23.8 (s, CH₂); ³¹P{¹H} NMR (202 MHz): 58.2 (s).

IR (powder film, cm⁻¹): 2924 (w), 2852 (w), 2098 (w, ν_CN), 1917 (s, ν_CO), 1703 (s, ν_NO), 1458 (w), 1307 (w), 1238 (w), 1089 (w), 985 (w), 759 (w), 736 (w), 721 (w), 619 (s). MS:³⁷ 791 (9c-CN⁺, 15%), 762 ([9c-CN − CO]⁺, 55%), 737 ([9c-CN − CO − CN]⁺, 35%), 732 ([9c-CN − NO − CO]⁺, 100%), 704 ([9c-CN − CO − NO − CN ]⁺, 5%).

trans-Fe(CO)(NO)(Cl)(P((CH₂)₆CH=CH(CH₂)₆)₃P) (7c-Cl). A Schlenk flask was charged with trans-Fe(CO)(NO)(Cl)(P((CH₂)₆CH=CH₂)₃)₂, (6c-Cl;²¹ 0.127 g, 0.145 mmol), CH₂Cl₂ (75 mL; the resulting solution is 0.0020 M in 6c-Cl), and Grubbs’ catalyst (0.022 g, 0.026 mmol, 18 mol%), and fitted with a condenser. The solution was refluxed. After 48 h, the solvent was removed by oil pump vacuum. The residue was filtered through neutral alumina (2.5 × 2.5 cm) using 2 : 1 v/v hexane/CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum to give 7c-Cl as a red-brown waxy solid (0.046 g, 0.054 mmol, 37%, mixture of E/Z isomers).

NMR (CDCl₃, δ in ppm): ¹H (500 MHz) 5.48–5.20 (m, 6H, CH=), 2.04–1.93 (m, 12H, CH₂), 1.88–1.64 (m, 12H, CH₂), 1.62–1.47 (m, 12H, CH₂), 1.41–1.28 (m, 36H, CH₂); ³¹P{¹H} (202 MHz) 50.4 (s, 77%), 49.8 (s, 23%).

trans-Fe(CO)(NO)(Br)(P((CH₂)₆CH=CH(CH₂)₆)₃P) (7c-Br). A Schlenk flask was charged with trans-Fe(CO)(NO)(Br)(P((CH₂)₆CH=CH₂)₃)₂, (6c-Br;²¹ 0.157 g, 0.170 mmol), CH₂Cl₂ (85 mL; the resulting solution is 0.0020 M in 6c-Br), and Grubbs’ catalyst (0.025 g, 0.031 mmol, 18 mol%), and fitted with a condenser. The solution was refluxed. After 48 h, the solvent was removed by oil pump vacuum. The residue was filtered through neutral alumina (2.5 × 2.5 cm) using 1 : 1 v/v hexane/CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum to give 7c-Br as a red-brown waxy solid (0.047 g, 0.053 mmol, 31%, mixture of E/Z isomers).

NMR (CDCl₃, δ in ppm): ¹H (500 MHz) 5.43–5.15 (m, 6H, CH=), 2.10–1.90 (m, 12H, CH₂), 1.91–1.66 (m, 12H, CH₂), 1.64–1.45 (m, 12H, CH₂), 1.42–1.27 (m, 36H, CH₂); ³¹P{¹H} (202 MHz) 50.4 (s, 63%), 49.8 (s, 15%), 47.8 (s, 22%).

trans-Fe(CO)(NO)(I)(P((CH₂)₆CH=CH(CH₂)₆)₃P) (7c-I). A Schlenk flask was charged with trans-Fe(CO)(NO)(I)(P((CH₂)₆CH=CH₂)₃)₂, (6c-I;²¹ 0.232 g, 0.239 mmol), CH₂Cl₂ (120 mL; the resulting solution is 0.0020 M in 6c-I), and Grubbs’ catalyst (0.035 g, 0.043 mmol, 18 mol%), and fitted with a condenser. The solution was refluxed. After 19 h, additional catalyst was added (0.012 g, 0.014 mmol, 6 mol%). After another 24 h, the solvent was removed by oil pump vacuum. The residue was filtered through neutral alumina (2.5 × 2.5 cm) using CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum to give 7c-I as red-brown waxy solid (0.091 g, 0.096 mmol, 40%, mixture of E/Z isomers).

NMR (CDCl₃, δ in ppm): ¹H (500 MHz) 5.47–5.20 (m, 6H, CH=), 2.12–1.47 (m, 36H, CH₂), 1.46–1.28 (m, 36H, CH₂); ³¹P{¹H} (202 MHz) 44.9 (s, 63%), 42.0 (s, 15%).

trans-Fe(CO)(NO)(CN)(P((CH₂)₆CH=CH(CH₂)₆)₃P) (7c-CN). A Schlenk flask was charged with trans-Fe(CO)(NO)(CN)(P((CH₂)₆CH=CH₂)₃)₂, (6c-CN;²¹ 0.162 g, 0.187 mmol), CH₂Cl₂ (95 mL; the resulting solution is 0.0020 M in 6c-CN), and Grubbs’ catalyst (0.028 g, 0.034 mmol, 18 mol%), and fitted with a condenser. The solution was refluxed. After 48 h, the solvent was removed by oil pump vacuum. The residue was filtered through neutral alumina (2.5 × 2.5 cm) with CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum to give 7c-CN as a red-brown waxy solid (0.038 g, 0.045 mmol, 24%, mixture of E/Z isomers).

NMR (CDCl₃, δ in ppm): ¹H (500 MHz) 5.41–5.17 (m, 6H, CH=), 2.08–1.90 (m, 12H, CH₂), 1.89–1.60 (m, 12H, CH₂), 1.61–1.46 (m, 12H, CH₂) 1.46–1.26 (m, 36H, CH₂); ³¹P{¹H} (202 MHz) 60.2 (s, 75%), 59.6 (s, 15%), 59.4 (s, 22%).

trans-[Fe(CO)₂(NO)(P((CH₂)₆CH=CH(CH₂)₆)₃P)]⁺ BF₄⁻ (8c⁺ BF₄⁻). A Schlenk flask was charged with trans-[Fe(CO)₂(NO)(P((CH₂)₆CH=CH₂)₃)₂]⁺ BF₄⁻ (5c⁺ BF₄⁻;²¹ 0.151 g, 0.159 mmol), CH₂Cl₂ (80 mL; the resulting solution is 0.0020 M in 5c⁺ BF₄⁻), and Grubbs’ catalyst (0.024 g, 0.029 mmol, 18 mol%), and fitted with a condenser. The solution was refluxed. After 48 h, the solvent was removed by oil pump vacuum. The residue was filtered through celite (2.5 × 2.5 cm) with CH₂Cl₂. The solvent was removed from the filtrate by oil pump vacuum and the residue was triturated under ether. The ether was decanted and the residue dried by oil pump vacuum to give 8c⁺ BF₄⁻ as a red-brown waxy solid (0.083 g, 0.091 mmol, 57%, mixture of E/Z isomers).

NMR (CDCl₃, δ in ppm): ¹H (500 MHz) 5.48–5.11 (m, 6H, CH=), 2.36–2.13 (m, 12H, CH₂), 2.09–1.80 (m, 12H, CH₂), 1.70–1.25 (m, 48H, CH₂); ³¹P{¹H} (202 MHz) 60.9 (s, 82%), 60.1 (s, 18%).

Crystallography

A concentrated CH₂Cl₂ solution of 9c-Cl was layered with MeOH and kept at room temperature. After 4 d, data were collected on one of the orange prisms as outlined in Table 2. Analogous procedures gave deep red prisms of 9c-Br and pale orange prisms of 9c-CN, which were similarly analyzed.

Cell parameters were obtained from 10 frames using a 10° scan and refined with the following numbers of reflections: 9c-Cl, 5268; 9c-Br, 280; 9c-CN, 5177. Lorentz, polarization, and absorption corrections were applied.³⁸ Space groups were determined from systematic absences and subsequent least-squares refinement. The structures were solved by direct methods. The parameters were refined with all data by full-matrix-least-squares on F² using SHELXL-97.³⁹ Non-hydrogen atoms were refined with anisotropic thermal parameters. The hydrogen atoms were fixed in idealized positions using a riding model. Scattering factors were taken from the literature.⁴⁰ In the structure of 9c-Cl, the Cl, NO, and CO ligands were disordered over three positions (33% occupancy). For refinement, the CO and NO positions were arbitrarily assigned in accord with the overall symmetry. In the structure of 9c-Br, the bromine atom was disordered over three positions (33% occupancy). The NO and CO ligands were also disordered over three positions, and furthermore could not be distinguished. For refinement, they were assigned 50% occupancy within each of the three conformations. In the structure of 9c-CN, the CN, NO, and CO ligands were equally disordered over three positions. Refinements were carried out with fixed occupancy factors for each position (2/3 C + 1/3 N for the ligating atom and 2/3 O + 1/3 N for the non-ligating atom).

Acknowledgements

The authors thank the US National Science Foundation (CHE-0719267, CHE-1153085, CHE-156601) and Deutsche Forschungsgemeinschaft (DFG, GL 300/9-1) for support, and Mr. Andreas Ehnbom for preliminary dipole moment computations.

Notes and references

1. See http://www.gyroscopes.org/uses.asp. The authors are unaware of any books or peer reviewed articles that match the diversity of examples on the gyroscope.org web site, which is maintained by G. Turner.
2. (a) T. Shima, F. Hampel and J. A. Gladysz, Angew. Chem., Int. Ed., 2004, 43, 5537–5540 ( Angew. Chem. , 2004 , 116 , 5653–5656 ); (b) G. M. Lang, T. Shima, L. Wang, K. J. Cluff, F. Hampel, J. Blumel and J. A. Gladysz, J. Am. Chem. Soc., 2016, 138, 7649–7663.
3. (a) A. J. Nawara, T. Shima, F. Hampel and J. A. Gladysz, J. Am. Chem. Soc., 2006, 128, 4962–4963; (b) A. J. Nawara-Hultzsch, M. Stollenz, M. Barbasiewicz, S. Szafert, T. Lis, F. Hampel, N. Bhuvanesh and J. A. Gladysz, Chem. – Eur. J., 2014, 20, 4617–4637; (c) D. Taher, A. J. Nawara-Hultzsch, N. Bhuvanesh, F. Hampel and J. A. Gladysz, J. Organomet. Chem., 2016 DOI:10.1016/j.jorganchem.2016.03.022 , in press (available on the web).
4. L. Wang, F. Hampel and J. A. Gladysz, Angew. Chem., Int. Ed., 2006, 45, 4372–4375 ( Angew. Chem. , 2006 , 118 , 4479–4482 ).
5. (a) L. Wang, T. Shima, F. Hampel and J. A. Gladysz, Chem. Commun., 2006, 4075–4077; (b) A. L. Estrada, T. Jia, N. Bhuvanesh, J. Blümel and J. A. Gladysz, Eur. J. Inorg. Chem., 2015, 5318–5321.
6. G. D. Heß, F. Hampel and J. A. Gladysz, Organometallics, 2007, 26, 5129–5131.
7. K. Skopek and J. A. Gladysz, J. Organomet. Chem., 2008, 693, 857–866.
8. (a) T. Fiedler, N. Bhuvanesh, F. Hampel, J. H. Reibenspies and J. A. Gladysz, Dalton Trans., 2016, 45, 7131–7147; (b) T. Fiedler, L. Chen, N. D. Wagner, D. R. Russell and J. A. Gladysz, Organometallics, 2016, 35, 2071–2075.
9. G. M. Lang, N. Bhuvanesh, J. H. Reibenspies and J. A. Gladysz, Organometallics, 2016, 35, 2873–2889.
10. http://www.unisys.com/about-us/company-history .
11. http://findingaids.hagley.org/xtf/view?docId=ead/1915.xml .
12. (a) T.-A. V. Khuong, J. E. Nuñez, C. E. Godinez and M. A. Garcia-Garibay, Acc. Chem. Res., 2006, 39, 413–422; (b) C. S. Vogelsberg and M. A. Garcia-Garibay, Chem. Soc. Rev., 2012, 41, 1892–1910; (c) S. Pérez-Estrada, B. Rodríguez-Molina, L. Xiao, R. Santillan, G. Jiménez-Osés, K. N. Houk and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2015, 137, 2175–2178; (d) R. Acros-Ramos, B. Rodríguez-Molina, E. Gonzalez-Rodriguez, P. I. Ramirez-Montes, M. E. Ochoa, R. Santillan, N. Farfán and M. A. Garcia-Garibay, RSC Adv., 2015, 5, 55201–55208; (e) X. Jiang, Z. J. O'Brien, S. Yang, L. H. Lai, J. Buenaflor, C. Tan, S. Khan, K. N. Houk and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2016, 138, 4650–4656.
13. (a) W. Setaka and K. Yamaguchi, J. Am. Chem. Soc., 2013, 135, 14560–14563 and earlier work cited therein. (b) W. Setaka, K. Inoue, S. Higa, S. Yoshigai, H. Kono and K. Yamaguchi, J. Org. Chem., 2014, 79, 8288–8295; (c) H. Shionari, Y. Inagaki, K. Yamaguchi and W. Setaka, Org. Biomol. Chem., 2015, 13, 10511–10516; (d) Y. Nishiyama, Y. Inagaki, K. Yamaguchi and W. Setaka, J. Org. Chem., 2015, 80, 9959–9966.
14. T. Fiedler and J. A. Gladysz, Multifold Ring Closing Olefin Metatheses in Syntheses of Organometallic Molecules with Unusual Connectivities, in Olefin Metathesis: Theory and Practice, ed. K. Grela, Wiley/VCH, Weinheim, 2013, pp. 311–328.
15. See also: E. Prack, C. A. O'Keefe, J. K. Moore, A. Lai, A. J. Lough, P. M. Macdonald, M. S. Conradi, R. W. Schurko and U. Fekl, J. Am. Chem. Soc., 2015, 137, 13464–13467.
16. Since fictional characters can often be useful in outreach lectures, we note that the presence of gyro stabilizers in Iron Man's flying suit was first described in Iron Man, April 1976, Vol. 1, #85 (see https://www.quora.com/How-do-Tony-Starks-Iron-Man-suits-generate-lift-for-horizontal-flight). Were Tony Stark a real person, he would have assuredly wanted his gyroscopes to be molecular and based upon iron.
17. (a) E. Butikov, Eur. J. Phys., 2006, 27, 1071–1081; (b) D. Kleppner and R. J. Kolenkow, An Introduction to Mechanics, Cambridge University Press, Cambridge, 2010, ch. 7.3–7.5.
18. G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Chem. Rev., 2005, 105, 1281–1376.
19. (a) V. Bermudez, N. Capron, T. Gase, F. G. Gatti, F. Kajzar, D. A. Leigh, F. Zerbetto and S. Zhang, Nature, 2000, 406, 608–611; (b) R. D. Horansky, L. I. Clarke, J. C. Price, T.-A. V. Khuong, P. D. Jarowski and M. A. Garcia-Garibay, Phys. Rev. B: Condens. Matter, 2005, 72, 014302; (c) R. D. Horansky, L. I. Clarke, E. B. Winston, J. C. Price, S. D. Karlen, P. D. Jarowski, R. Santillan and M. A. Garcia-Garibay, Phys. Rev. B: Condens. Matter, 2006, 74, 054306; (d) P. Dhar, C. D. Swayne, T. M. Fischer, T. Kline and A. Sen, Nano Lett., 2007, 7, 1010–1012; (e) J. J. Arcenegui, P. García-Sánchez, H. Morgan and A. Ramos, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2013, 88, 033025-1–033025-8; (f) I. Neumann, K. E. Gottschalk and R. D. Astumian, ACS Nano, 2012, 6, 5242–5248.
20. (a) Z. Dominguez, T.-A. Khuong, H. Dang, C. N. Sanrame, J. E. Nuñez and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2003, 125, 8827–8837; (b) T.-A. Khuong, G. Zepeda, R. Ruiz, S. I. Khan and M. A. Garcia-Garibay, Cryst. Growth Des., 2004, 4, 15–18; (c) B. Rodriguez-Molina, M. E. Ochoa, N. Farfán, R. Santillan and M. A. Garcia-Garibay, J. Org. Chem., 2009, 74, 8554–8565.
21. G. M. Lang, D. Skaper, T. Shima, M. Otto, L. Wang and J. A. Gladysz, Aust. J. Chem., 2015, 68, 1342–1351.
22. G. Dolcetti, L. Busetto and A. Palazzi, Inorg. Chem., 1974, 13, 222–225.
23. W. E. Carroll, A. F. Deeney and F. J. Lalor, J. Chem. Soc., Dalton Trans., 1974, 1430–1433.
24. (a) M. Jänicke, H.-U. Hund and H. Berke, Chem. Ber., 1991, 124, 719–723; (b) In Tables 3 and 4 in this paper, the labels a and c (denoting the phosphorus donor ligand) for compounds 5 and 7 are reversed.
25. See also: J. L. A. Roustan, J. Y. Merour and A. Forgues, J. Organomet. Chem., 1980, 186, C23–C26.
26. W. H. Hersh, J. Chem. Educ., 1997, 74, 1485–1488 . The J values given represent the apparent coupling between adjacent peaks of the triplet.
27. Selected spectra are provided elsewhere: G. M. Lang, Doctoral thesis, Texas A&M University, 2016, ch. 5.
28. (a) B. Cordero, V. Gómez, A. E. Platero-Prats, M. Réves, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832; (b) A. Bondi, J. Phys. Chem., 1964, 68, 441–451; (c) M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812.
29. (a) Fe(CO)₂(I)(PEt₃)₂: Fe–I 2.610(1) Å. H. Kandler, C. Gauss, W. Bidell, S. Rosenberger, T. Bürgi, I. L. Eremenko, D. Veghini, O. Orama, P. Burger and H. Berke, Chem. – Eur. J., 1995, 1, 541–548; (b) Fe(CO)₂(I)(Me)(P(Me)₃)₂: Fe–I 2.695(1) Å. G. Bellachioma, G. Cardaci, A. Macchioni, G. Reichenbach, E. Foresti and P. Sabatino, J. Organomet. Chem., 1997, 531, 227–235; (c) Fe(CO)₂(I)(Ph)(P(Me)₃)₂: Fe–I 2.61(3) Å. C. Venturi, G. Bellachioma, G. Cardaci and A. Macchioni, Inorg. Chim. Acta, 2004, 357, 3712–3720; (d) The average of all of the FeCO distances in the preceding compounds is 4.43 Å.
30. In evaluating the viability of dynamic processes in organic molecules from space filling models, it is generally found that the spatial contributions of the hydrogen atoms can be neglected.
31. Given the fluxionality of the methylene chains in solution, another approximation would be to take the average of the six distances.
32. P. H. M. Budzelaar, gNMR: NMR Simulation Program, Version 5.0.6.0, Adept Scientific, Luton, UK, 2006.
33. B. L. Hawkins, W. Bremser, S. Borcić and J. D. Roberts, J. Am. Chem. Soc., 1971, 93, 4472–4479.
34. A reviewer has inquired about the magnitude of the dipole moments, and interactions in the solid state. First, preliminary DFT calculations on the model compounds trans-Fe(CO)(NO)(X)(PMe₃)₂, indicate values of 1.38, 2.00, and 2.68 D for X = Cl, Br, and CN, respectively. The dipoles approximately bisect the OC–Fe–NO angles, with the negative ends extending between the two oxygen atoms. Second, there is an extensive literature regarding dipolar interactions between rotators in crystals and ordered arrays.¹⁸ For another lead reference, see: J. J. de Jonge, M. A. Ratner and S. W. de Leeuw, J. Phys. Chem. C, 2007, 111, 3770–3777.
35. H. J. Breunig, T. Borrmann, E. Lork, O. Moldovan, C. I. Rat and R. P. Wagner, J. Organomet. Chem., 2009, 694, 427–432.
36. A reviewer has inquired whether the activation parameters determined for rotation of trivalent iron rotators in solution (Table 4) have any relationship to those in the crystal lattice. Naturally, different values would be expected. However, considering the homology of many of the crystal structures, it is possible that they might scale in a linear relationship.
37. FAB, 3-NBA, m/z (relative intensity, %); the most intense peak of the isotope envelope is given.
38. (a) B. V. Nonius, Collect, data collection software, 1998; (b) Z. Otwinowski and W. Minor, Scalepack, data processing software, Methods Enzymol., 1997, 276, 307 (Macromolecular Crystallography, Part A).
39. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
40. D. T. Cromer and J. T. Waber, in International Tables for X-ray Crystallography, ed. J. A. Ibers and W. C. Hamilton, Kynoch, Birmingham, England, 1974.

---

Footnote

† Electronic supplementary information (ESI) available: Additional synthetic procedures, NMR data and Eyring plots. CCDC 1499242–1499244. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt03258c

---