Muffin-like lanthanide complexes with an N₅O₂-donor macrocyclic ligand showing field-induced single-molecule magnet behaviour

Abstract

Three mononuclear lanthanide complexes of a 2-pyridylmethyl pendant-armed 15-membered ligand {(3,12-bis(2-pyridylmethyl)-3,12,18-triaza-6,9-dioxabicyclo-[12.3.1]octadeca-1,14,16-triene); L} with general formula [Ln(L)(H₂O)(NO₃)](NO₃)₂ (Ln = Tb (1), Dy (2), and Er (3)) are reported. Based on X-ray diffraction analysis of 1 and 2, the central lanthanide atoms are nine-coordinated with the N₅O₄ donor set originating from the ligand L and one coordinated water molecule and one monodentate-bonded nitrato ligand. The coordination geometry of the [LnN₅O₄] cores can be described as a muffin-like shape. Magnetic measurements revealed that all three compounds show field-induced single-molecule magnet behaviour, with estimated energy barriers U ≈ 44–82 K. The experimental study was complemented by CASSCF calculations showing a trend of an increasing first excited energy gap (Tb → Dy → Er) within the muffin-like geometry with the lowest magnetization tunnelling probability for the Dy^III complex 2.

---

Introduction

Lanthanide ions reveal many unique physical and photophysical properties, such as large magnetic moments and magnetic anisotropy as well as long-life luminescence with sharp emission lines.¹ Therefore, their complexes have found many applications in luminescent sensors,² MRI contrast agents,³ radionuclide therapy,^4,5 and magnetically active liquid crystals.⁶ In the past few decades, more attention has been devoted to the magnetic properties of lanthanide complexes, because they were found as ideal candidates for single molecular magnets (SMMs)^7,8 or single ion magnets (SIMs)^9–11 due to their large magnetic moments and high magnetic anisotropy, and because of their potential applications in quantum computing,¹² high-density memory storage devices and molecule spintronics¹³ and single molecule transistors.¹⁴

Many complexes of lanthanides with pthalocyanines,¹⁵ Schiff bases,¹⁶ β-diketones,¹⁷ and polyoxometalates¹⁸ show a high effective spin-reversal energy barrier (U_eff) and blocking temperature (T_B), i.e. parameters usually characterizing the SMM/SIM properties.^7–11 An attractive alternative to the above-mentioned ligands may be macrocycles with a variable cavity size and donor atom set favouring the desired types/sizes of metal ions.

In the past, only a few complexes of lanthanides with 2-pyridylmethyl pendant armed polyaza- or polyoxa-aza macrocyclic ligands were prepared and studied (Scheme 1). The tetrakis(2-pyridylmethyl) derivative of cyclen L1 was studied in complexes with select lanthanides (La, Pr, Nd, Eu, Gd, Tb, Er, and Yb),^19,20 which were nine-coordinated with approximately monocapped square-antiprismatic geometry (twisted for Pr, Nd and Eu). The complex cations were chiral and they crystallized as racemic compounds.^19,20 An extended 18-membered hexaaza macrocyclic ligand with four 2-pyridylmethyl pendant arms (L2) and its complexes with general formula Ln[Ln(L2)](NO₃)₆·nH₂O, where n = 2–4, Ln = La, Ce, Pr, Gd, Tb, Er and Tm, were studied.²¹ Lanthanide atoms in [Ln(L2)]³⁺ were ten-coordinated and showed a distorted bicapped square antiprismatic geometry. The 18-membered tetraoxa-diaza macrocyclic ligand L3 was studied only in its La³⁺ complex and only in solution.²² Surprisingly, no magnetic or luminescence properties of the above-mentioned complexes have been investigated in detail to date. On the other hand, our attention was more devoted to rather unusual seven-coordinate lanthanide complexes, because they may represent a very promising geometry for optimal/effective preparation of lanthanide-based SMMs/SIMs. As it was published recently, the highest magnetization reversal barrier, even higher than 1000 K (U_eff = 708 or 1025 K), was observed in seven-coordinate Dy^III complexes [Dy(L4)X],²³ where X = Cl⁻ or Br⁻, with a pentagonal bipyramidal coordination sphere confirmed by X-ray analysis. Among these seven-coordinate complexes, to the best of our knowledge, there are only three studies dealing with lanthanide complexes of 15-membered macrocyclic ligands (L5,²⁴ and L6)^25,26 and lanthanides (Dy^III,^24–26 Er^III, Tm^III, Lu^III),²⁴ in which the central atom should adopt the pentagonal bipyramidal geometry, which unfortunately have not been confirmed by X-ray analysis yet. Nevertheless, the Dy^III complexes [Dy(L5)Cl₂]Cl·6H₂O,^25,26 and [Dy(L6)Cl₂]Cl·4H₂O²⁵ revealed large magnetic anisotropy which was reflected in their SMM/SIM behavior (U_eff = 7.75 and 23.7 K; τ₀ = 7.52 × 10⁻⁷ and 6.4 × 10⁻⁶ s, respectively).²⁶ In this perspective, herein, we report the syntheses, X-ray crystal structures and magnetic properties of three mononuclear lanthanide complexes (Tb^III, Dy^III, and Er^III) with the 2-pyridylmethyl pendant-armed 15-membered macrocyclic ligand (L), which was recently synthesized and proved to provide seven-coordinate late first-row transition metal complexes, and even a Co(II) mononuclear SMM.²⁷ In this work, we tested the coordination mode of L in lanthanide complexes and their magnetic properties.

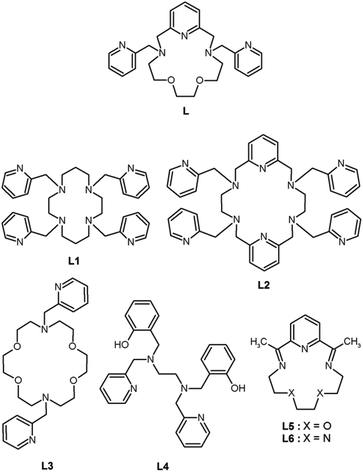Scheme 1 The structural formulae of the ligand L (this work) and other ligands L1–L6 mentioned within the text.

Experimental section

Materials and methods

3,12-Bis(2-pyridylmethyl)-3,12,18-triaza-6,9-dioxabicyclo-[12.3.1]octadeca-1,14,16-triene (L) was prepared according to the literature.²⁷ Other chemicals were purchased from commercial sources and used without further purification. Elemental analysis (C, H, N) was performed on a Flash 2000 CHNO-S Analyzer (Thermo Scientific, Waltham, MA, USA). Infrared spectra (IR) were recorded on a Thermo Nicolet NEXUS 670 FT-IR spectrometer (Thermo Nicolet, Waltham, MA, USA) employing the ATR technique on a diamond plate in the range of 200–4000 cm⁻¹. The mass spectra (MS) were collected on a LCQ Fleet Ion Mass Trap mass spectrometer (Thermo Scientific, Waltham, MA, USA) equipped with an electrospray ion source and a three-dimensional ion-trap detector in the positive mode. The temperature dependent (T = 1.9–300 K, B = 0.1 T) and field dependent (B = 0–9 T, T = 2, 5, and 10 K) magnetization measurements were performed on a PPMS Dynacool (Quantum Design Inc., San Diego, CA, USA). Dynamic magnetic properties were studied by measuring ac susceptibility on a MPMS XL-7 SQUID magnetometer (Quantum Design Inc., San Diego, CA, USA). Powder XRD patterns were recorded with a MiniFlex600 (Rigaku) using Cu Kα radiation (λ = 1.5418 Å). Emission spectra were recorded in an acetonitrile/methanol mixture (V/V = 1 : 1) at room temperature using an AvaSpec-HS1024×122TE spectrometer. The excitation source was a deuterium arc lamp.

Synthesis of [Tb(L)(NO₃)(H₂O)](NO₃)₂ (1)

To a stirred solution of L (71.0 mg, 0.16 mmol) in 10 mL of acetonitrile, Tb(NO₃)₃·5H₂O (71.2 mg, 0.16 mmol) was added. The resulting solution was refluxed under stirring for 2 h. The obtained clear colourless solution was allowed to crystallize by diffusion of diethyl ether vapour at room temperature. After 3 days, colourless crystals (66 mg, yield 52%) were isolated by filtration on a glass frit, washed with cold diethyl ether (2 × 1 mL) and dried under vacuum over NaOH for the next 2 days. Anal. Calcd for C₂₅H₃₃N₈O₁₂Tb₁: C, 37.70; H, 4.18; N, 14.07%. Found: C, 37.81; H, 4.22; N, 13.88%. MS, m/z (+): 434.28 [L + H]⁺ (I_rel = 100%); 456.29 [L + Na]⁺ (I_rel = 61%); 653.08 [(TbL(NO₃)₂)−4O + H]⁺ (I_rel = 53%); 685.06 [(TbL(NO₃)₂)−2O + H]⁺ (I_rel = 32%); 716.08 [TbL(NO₃)₂]⁺ (I_rel = 39%). IR (ATR, cm⁻¹): 831 (m), 950 (m), 1011 (m), 1033 (s), 1057 (m), 1082 (m), 1283 (s), 1296 (s), 1322 (s), 1370 (s), 1445 (m), 1605 (m), 2893 (s), 2909 (s), 2952 (s).

Synthesis of [Dy(L)(NO₃)(H₂O)](NO₃)₂ (2)

The synthesis follows the same procedure as described for 1 except that Dy(NO₃)₃·6H₂O was used as the starting material instead of Tb(NO₃)₃·5H₂O. Colourless crystals were isolated after 1 day (121 mg, yield 84%). Anal. Calcd for C₂₅H₃₃N₈O₁₂Dy₁: C, 37.53; H, 4.15; N, 14.01%. Found: C, 37.64; H, 4.19; N, 13.89%. MS, m/z (+): 434.28 [L + H]⁺ (I_rel = 100%); 456.28 [L + Na]⁺ (I_rel = 67%); 658.08 [(DyL(NO₃)₂)−4O + H]⁺(I_rel = 16%); 690.07 [(DyL(NO₃)₂)−2O + H]⁺(I_rel = 11%); 721.08 [DyL(NO₃)₂]⁺ (I_rel = 12%). IR (ATR, cm⁻¹): 832 (m), 950 (m), 1011 (m), 1032 (s), 1057 (m), 1082 (m), 1281 (s), 1296 (s), 1323 (s), 1370 (s), 1446 (m), 1605 (m), 2894 (s), 2909 (s), 2954 (s).

Synthesis of [Er(L)(NO₃)(H₂O)](NO₃)₂ (3)

The synthesis follows the same procedure as described for 1 except that Er(NO₃)₃·5H₂O was used as the starting material instead of Tb(NO₃)₃·5H₂O. Light pink crystals were isolated after 3 days (92 mg, yield 67%). Anal. Calcd for C₂₅H₃₃N₈O₁₂Er₁: C, 37.31; H, 4.13; N, 13.92%. Found: C, 37.29; H, 4.27; N, 13.78%. MS, m/z (+): 434.27 [L + H]⁺ (I_rel = 100%); 456.28 [L + Na]⁺ (I_rel = 77%); 662.07 [(ErL(NO₃)₂)−4O + H]⁺(I_rel = 15%); 694.04 [(ErL(NO₃)₂)−2O + H]⁺ (I_rel = 10%); 725.06 [ErL(NO₃)₂]⁺ (I_rel = 10%). IR (ATR, cm⁻¹): 833 (m), 951 (m), 1012 (m), 1033 (s), 1058 (m), 1082 (m), 1282 (s), 1296 (s), 1324 (s), 1369 (s), 1446 (m), 1606 (m), 2869 (s), 2910 (s), 2956 (s).

X-ray structure analysis

Single crystals of 1 and 2 suitable for X-ray diffraction analysis were prepared by slow diffusion of diethyl ether vapour into the acetonitrile solutions of the appropriate complex at room temperature. Crystallographic data were collected at 120 K on a Bruker D8 QUEST diffractometer equipped with a PHOTON 100 CMOS detector using Mo-Kα radiation (λ = 0.71073 Å). The APEX3 software package²⁸ was used for data collection and reduction. The molecular structures were solved by direct methods (SHELXS) and refined by full-matrix least-squares procedure SHELXL (version 2014/7),²⁹ and using XShell software package.²⁸ Hydrogen atoms of both structures were found in the difference Fourier maps and refined using a rigid model, except for O-attached hydrogens whose positions were refined freely, with C–H = 0.95 (CH)_ar and C–H = 0.99 Å (CH₂), and with U_iso(H) = 1.2U_eq(OH, CH, CH₂). The molecular and crystal structures of the studied compounds, depicted in Fig. 1 and Fig. S2,† were drawn using Diamond software.³⁰

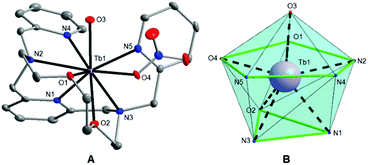Fig. 1 (A) Molecular structure of the [Tb(L)(H₂O)(NO₃)]²⁺ complex cation in 1. The thermal ellipsoids are drawn with the 50% probability level. The hydrogen atoms are omitted for clarity. (B) The muffin-like coordination geometry of the [TbN₅O₄] core in 1.

Theoretical calculations

The post-Hartree–Fock calculations performed on the [Ln(L)(NO₃)(H₂O)](NO₃)₂ complexes 1–3 using the geometries experimentally determined by X-ray analysis were done with the MOLCAS 8.0 program package.³¹ The active space of the CASSCF calculations³² comprised of eight, nine and eleven electrons in seven metal-based f-orbitals for 1, 2, and 3, respectively. The Restricted Active Space Self-Consistent Field (RASSCF) method was employed in CASSCF calculations with the following numbers of multiplets: 7 septets, 140 quintets, 306 triplets and 245 singlets for Tb^III, 21 sextets, 224 quartets and 490 doublets for Dy^III, 35 quartets and 112 doublets for Er^III. The spin–orbit coupling based on atomic mean field approximation (AMFI)³³ was taken into account using RASSI-SO with the following numbers of multiplets: 7 septets, 110 quintets, 180 triplets and 180 singlets for Tb^III, 21 sextets, 128 quartets and 130 doublets for Dy^III, 35 quartets and 112 doublets for Er^III. The relativistic effects were treated with the Douglas–Kroll Hamiltonian.³⁴ The following basis sets were employed: Ln·ANO-RCC-VQZP (Ln = Tb, Dy and Er for 1–3), O·ANO-RCC-VDZP, N·ANO-RCC-VDZP, C·ANO-RCC-VDZ and H·ANO-RCC-VDZ.³⁵ Then, the SINGLE_ANISO module³⁶ was used to calculate all relevant information and magnetic data.

Results and discussion

Description of crystal structures

Single-crystal X-ray diffraction analysis (for 1 and 2) and powder diffraction analysis (for 3) revealed that all the three compounds are isostructural (Fig. S1†), and crystallize in the tetragonal non-centrosymmetric P4₁ space group. The crystallographic data and structure refinements for complexes 1 and 2 are given in Table 1, and the selected bond lengths and angles are listed in Table 2. The asymmetric units of 1 and 2 contain one [Ln(L)(H₂O)(NO₃)]²⁺ complex cation and two nitrate anions. The central Ln^III atom is coordinated by the heptadentate ligand (L) with the N₅O₂ donor set, which is twisted due to its high flexibility and because the large size of the Ln³⁺ ion does not fit into the small macrocyclic cavity, and by one oxygen atom from the water molecule (O3), and one oxygen atom from the nitrato ligand (O4) (Fig. 1A and S2A†). Thus, the coordination number of the Ln^III atom in both complexes is nine. The geometries of the coordination polyhedra of lanthanide ions in 1 and 2 were analysed by the program Shape 2.1.³⁷ The lowest value of deviation was found for a muffin shape (Table S1†), with the basal trigonal plane formed by O2, N1, and N3 atoms in 1 (O1, N1, and N2 in 2), the equatorial pentagonal plane (O1, O4, N2, N4, and N5 in 1; O2, O4, N3, N4, and N5 in 2), and an O3 atom at the vertex of the muffin (Fig. 1B and S2B†).

Table 1 Crystal data and structure refinements for the complexes 1 and 2

Compound	1	2
Formula	C25H33N8O12Tb1	C25H33N8O12Dy1
M r	796.50	800.08
Color	Colorless	Colorless
Crystal system	Tetragonal	Tetragonal
Space group (no.)	P41 (76)	P41 (76)
a (Å)	11.4208(4)	11.4177(4)
b (Å)	11.4208(4)	11.4177(4)
c (Å)	22.4435(11)	22.4321(11)
α (°)	90	90
β (°)	90	90
γ (°)	90	90
U (Å^3)	2927.4(3)	2924.3(3)
Z	4	4
λ (Å), Mo Kα	0.71073	0.71073
T (K)	120	120
D calc (g cm^−3)	1.807	1.817
μ (mm^−1)	2.494	2.634
F (000)	1600	1604
Reflections collected	125 618	98 029
Independent reflections	6717 [R(int) = 0.0351]	6670 [R(int) = 0.0285]
Data/restraints/parameters	6717, 3, 421	6670, 3, 421
Goodness-of-fit on F^2	1.110	1.126
R 1, wR2 (I > 2σ(I))	0.0127, 0.0311	0.0151, 0.0361
R 1, wR2 (all data)	0.0138, 0.0315	0.0161, 0.0365
Largest diff. peak and hole, A^−3	0.184, –0.632	0.581, –0.768
CCDC number	1487176	1487175

---

Table 2 Selected interatomic distances (Å) and angles (°) in complexes 1 and 2

Distances	1	2
Ln–N1	2.510(2)	2.500(3)
Ln–N2	2.599(2)	2.567(2)
Ln–N3	2.579(2)	2.591(3)
Ln–N4	2.671(2)	2.522(3)
Ln–N5	2.528(2)	2.659(3)
Ln–O1	2.4847(18)	2.489(2)
Ln–O2	2.4961(18)	2.479(2)
Ln–O3	2.3468(19)	2.331(2)
Ln–O4	2.3611(19)	2.348(2)
Angles
O3–Ln–N1	135.01(7)	135.08(9)
O3–Ln–N2	77.87(7)	146.84(9)
O3–Ln–N3	146.96(8)	77.74(9)
O3–Ln–N4	75.74(7)	81.08(9)
O3–Ln–N5	81.35(7)	75.89(8)
O3–Ln–O1	73.90(6)	132.74(8)
O3–Ln–O2	132.85(6)	73.68(8)
O3–Ln–O4	81.97(7)	81.82(8)

---

The Tb–N bond lengths are in the range of 2.510(2) to 2.671(2) Å and Tb–O bonds vary from 2.347(2) to 2.496(2) Å in 1. The Dy–N bond lengths are in the range of 2.500(3) to 2.659(3) Å, while the Dy–O bonds vary from 2.331(2) to 2.489(2) Å.

Crystal structures of 1 and 2 are stabilized by networks of strong O–H⋯O hydrogen bonds and weak non-covalent C–H⋯O and C–H⋯N interactions. The O–H⋯O hydrogen bonds connect the coordinated water molecules and non-coordinated nitrate anions, with the O⋯O separations of 2.746(3) and 2.660(3) Å for 1. Selected non-covalent contacts are summarized in Table S2 (ESI†).

Photoluminescence properties

While many lanthanide complexes show interesting luminescence properties, the luminescence spectra of all the complexes 1–3 were measured. In accordance with the literature³⁸ a reasonable signal was obtained only in the case of complex 1. Its photoluminescence spectrum in the acetonitrile/methanol mixture (c = 1 × 10⁻³ mol dm⁻³) recorded at room temperature exhibited a broad minor peak at 306 nm assignable to the π → π* transition and intensive peaks with the maxima at 492, 547, 587 and 622 nm, attributable to the ⁵D₄ → ⁷F₆, ⁵D₄ → ⁷F₅, ⁵D₄ → ⁷F₄, and ⁵D₄ → ⁷F₃ transitions, which are typically observed in spectra of Tb^III complexes.³⁸ In order to investigate an “antenna effect” of the 2-pyridylmethyl pendant arms in L, a comparison of 1 with the Tb^III complex with a parent macrocycle 15-pyN₃O₂³⁹ without pendant arms was performed. As is shown in Fig. S3,† complex 1 exhibits a strong characteristic emission in the visible region. This observation is in accordance with the fact that the pyridine moiety is well known for sensing of lanthanide emission.^38,40

Magnetic properties

Static magnetic properties. The temperature and field dependent static magnetic data were acquired on polycrystalline samples of 1–3 as shown in Fig. 2. The value of μ_eff/μ_B at room temperature is 9.68 for 1, 10.39 for 2, and 9.16 for 3, and is close to the expected paramagnetic value of 9.72 (Tb^III, ⁷F₆), 10.65 (Dy^III, ⁶H_15/2), and 9.58 (Er^III, ⁴I_13/2). There is a gradual decrease of μ_eff/μ_B upon cooling the samples to 1.9 K for all compounds 1–3, which is due to depopulation of ligand field multiplets arising from ground atomic terms effected by spin–orbit coupling and a ligand field of the chromophores. There are no maxima on susceptibility, which excludes the existence of significant intermolecular contacts of the antiferromagnetic nature. The reciprocal susceptibilities were analysed using the Curie–Weiss law in the temperature range of 25–300 K (Fig. S4†), which resulted in C = 1.49 × 10⁻⁴ m³ mol⁻¹ K, Θ = –4.9 K and g = 1.50 for 1, C = 1.73 × 10⁻⁴ m³ mol⁻¹ K, Θ = –7.9 K and g = 1.31 for 2, C = 1.38 × 10⁻⁴ m³ mol⁻¹ K, Θ = –16.3 K and g = 1.17 for 3. All the Weiss constants are of negative values and g-factors are close to theoretical Landé g-factors, i.e. 1.50, 1.33, and 1.20 for Tb^III, Dy^III, and Er^III, respectively. The isothermal magnetization data, M_mol/N_Aμ_B, measured at T = 2 K saturate to 5.1 for 1, 5.6 for 2 and 4.6 for 3 and these values are well below theoretically predicted values based on J and Landé g-factors, which are 9.0 for Tb^III, 10.0 for Dy^III and 9.0 for Er^III. This points out to large magnetic anisotropy of these complexes.

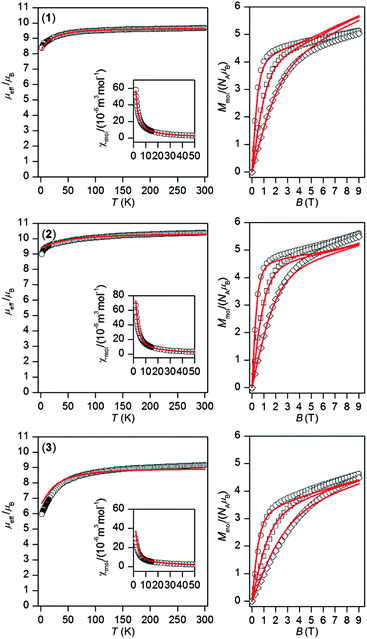Fig. 2 Magnetic data of complexes 1–3. Temperature dependence of the effective magnetic moment (left) and the isothermal molar magnetizations measured at 2 (○), 5 (□) and 10 (◊) K (right). The full lines correspond to ab initio CASSCF calculations done with MOLCAS/SINGLE_ANISO, and were scaled by the factors: f = 0.990 for 1, f = 0.947 for 2 and f = 0.877 for 3.

Dynamic magnetic properties

In order to examine the possible SMM properties of the herein studied coordination compounds 1–3, the ac susceptibility measurements were performed first in zero and nonzero static magnetic fields as depicted in Fig. S5.† None of the compounds showed a nonzero out-of-phase signal of ac susceptibility at zero static magnetic field, but evidently, a small magnetic field must be applied to observe slow relaxation of magnetization and suppression of the tunneling effect. Therefore, the temperature dependence of ac susceptibility was measured at B_DC = 0.1 T for frequencies of 1–1500 Hz as shown in Fig. 3. Only in the case of the Dy^III compound 2, we observed clearly maxima of out-of-phase susceptibility dependent of the applied frequency and these data were then analysed with the one-component Debye model

χ(ϖ) = χ_S + (χ_T − χ_S)/|1 + (iϖτ)^1−α| (1)

which resulted in isothermal (χ_T) and adiabatic (χ_S) susceptibilities, relaxation times (τ) and distribution parameters (α) (Table S3†) and construction of the Argand (Cole–Cole) plot (Fig. S6†). Then, the Arrhenius equation was applied to the temperature dependence of the relaxation times, which resulted in the relaxation time τ₀ = 2.63 × 10⁻⁸ s and the effective magnetization reversal barrier U = 24.4 K (16.9 cm⁻¹) – Fig. S6.† The ac susceptibility data for 1 and 3 cannot be analysed with eqn (1) due to the absence of maxima on imaginary susceptibility. Therefore, we used a simplified model⁴¹ according to eqn. (2)

ln(χ′′/χ′) = ln(2πfτ₀) + U/kT (2)

where higher temperature ac data for higher applied frequencies were included as shown in Fig. S7.† The linear regression analysis resulted in sets of parameters listed in Table 3. The variations in the fitted parameters refer to the distributions of relaxation processes, which are reflected in eqn (1) by parameter α. Maximal U were found as U = 43.5 K for 1, U = 64.1 K for 2 and U = 82.2 K for 3. In the case of 2, U = 64.1 K is 2.7 times larger than U = 24.4 K derived from eqn (1), which can be explained by the fact that the analysis based on eqn (1) is limited only to ac susceptibility data having maxima in the Argand diagram, which means data measured between T = 1.9 and 2.8 K. However, a non-zero out-of-phase ac susceptibility is already observed below 4 K (Fig. 3) and especially high temperature data should correspond to the Orbach relaxation mechanism, thus eqn (2) could lead to a better estimate of the relaxation barrier.

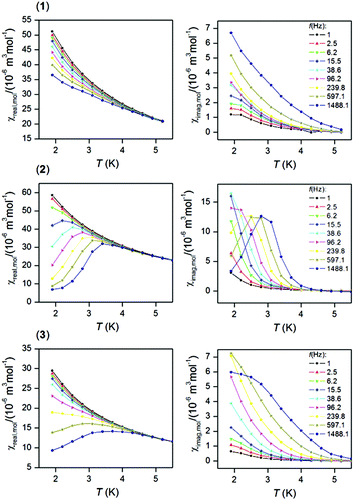Fig. 3 In-phase χ_real (left) and out-of-phase χ_imag (right) molar susceptibilities for 1–3 at the applied external field B_DC = 0.1 T. Lines serve as guides.

Table 3 The parameters resulting from the analysis of ac susceptibility data using eqn (2) for complexes 1–3

	f (Hz)	1488.1	597.1	239.8	96.2
1 (Tb)	τ 0 (10^−10 s)	2.33	2.68	20.1	38.6
	U (cm^−1)	30.2	29.2	23.9	24.0
	U (K)	43.5	42.0	34.4	34.6
2 (Dy)	τ 0 (10^−10 s)	0.00368	0.0204	17.9	434
	U (cm^−1)	44.6	39.4	22.0	16.3
	U (K)	64.1	56.7	31.6	23.5
3 (Er)	τ 0 (10^−10 s)	0.00288	0.340	4.45	58.1
	U (cm^−1)	57.1	39.3	31.3	23.6
	U (K)	82.2	56.5	45.0	34.0

---

Theoretical calculations

In order to better understand the magnetic properties of these compounds, the CASSCF calculations were performed using MOLCAS 8.0 together with the SINGLE_ANISO program on complexes [Ln(L)(NO₃)(H₂O)](NO₃)₂1–3 using geometries following from experimental X-ray data. The resulting wave functions and the energies of the molecular multiplets were used for the calculation of the magnetic properties, g tensors of the lowest Kramers doublet states (Tables S4–S6,† Fig. S8†). In the case of Tb^III compound 1, a priori there are no Kramers doublets arising from atomic multiplet ⁷F₆, however, the two lowest energy states are almost degenerate, and treating them as Kramers doublets with S_eff = 1/2 resulted in g_z = 16.7 and g_x = g_y ≈ 0.00 (Table S4†), which means that there is large axial magnetic anisotropy. In the case of Kramers doublet ions, Dy^III and Er^III, we were able to construct a scheme of the magnetization blocking barrier as shown in Fig. 4. The values displayed on each arrow are the mean absolute values for the corresponding matrix elements of the transition magnetic moment and for values larger than 0.1 an efficient relaxation mechanism is expected.⁹ Evidently, the tunnelling mechanism is probable in both compounds 2 and 3, and also thermal relaxation through the first excited state. The coefficients are slightly lower in the case of 2, which probably explains slower relaxation of the magnetization in the case of the Dy^III compound in spite of the larger U in the Er^III compound. The maximal U values extracted from ac susceptibility data with eqn (2), U = 43.5 K for 1, U = 64.1 K for 2 and U = 82.2 K for 3, follow the trend from the calculated energies of the first excited state within this series by CASSCF, 33.3 K for 1, 55.0 K for 2 and 69.0 K for 3 (Tables S4–S6†). Also, the magnetic properties were calculated with the SINGLE_ANISO module, and are compared to the experimental ones in Fig. 2.

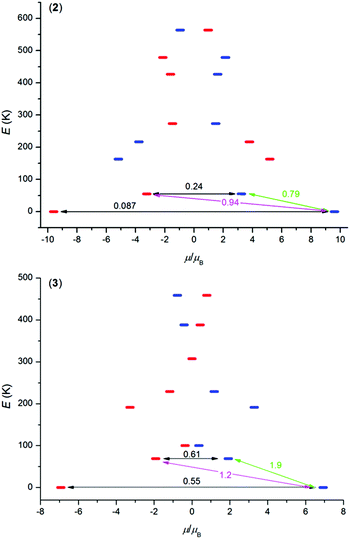Fig. 4 The ab initio computed magnetization blocking barrier for complexes 2 and 3. The thick blue/red bars indicate the Kramer's doublets (KDs) as a function of magnetic moment. Green lines indicate the magnetization reversal mechanism. The magenta lines show the possible pathway of the Orbach process. The black lines represent the presence of QTM/TA-QTM between the connecting pairs.

Conclusions

In summary, we have successfully prepared three mononuclear lanthanide complexes (Tb^III1, Dy^III2, and Er^III3) with a macrocyclic ligand {(3,12-bis(2-pyridylmethyl)-3,12,18-triaza-6,9-dioxabicyclo-[12.3.1]octadeca-1,14,16-triene; L} containing two 2-pyridylmethyl pendant arms, and these complexes were characterized structurally and magnetically. In all the cases, a central lanthanide(III) atom was coordinated by a N₅O₂-donor set of L, but due to the high ligand flexibility, the coordination sphere was completed by one water molecule and one nitrato ligand. Thus, the lanthanide(III) atom revealed a coordination number of nine with the N₅O₄-donor set, with a muffin-like geometry. The ac susceptibility measurements showed that all three compounds behave as field-induced single-molecule magnets with the estimated energy barriers U ≈ 44–82 K. The CASSCF calculations analysed with the SINGLE_ANISO module were helpful in understanding this behaviour, and the reasons for that are as follows: (i) the same increasing trend (Tb → Dy → Er) for the first excited state energy gap was found as resulted from the analysis of ac susceptibility; (ii) the lowest transition probabilities for the relaxation of the magnetization were found for 2, for which several maxima out-of-phase ac susceptibilities were already observed; (iii) a relatively small energy splitting and large non-colinearity of the easy axes explain why this series of SMMs shows fast relaxation of magnetization. To summarize, the herein reported compounds 1–3 are the first lanthanide-based SMMs comprising a 2-pyridylmethyl pendant-armed macrocyclic ligand. Nevertheless, the herein reported 15-membered macrocyclic ligand L was proved to be prospective for the synthesis of magnetically interesting coordination compounds, and the investigation of alternative arm-groups is underway.

Acknowledgements

The authors are grateful for the financial support from the National Program of Sustainability (NPU LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic.

Notes and references

1. S. Cotton, Lanthanide and Actinide Chemistry, Wiley, Chippenham, 2006.
2. (a) A. De Bettencourt-Dias, Luminescence of Lanthanide Ions in Coordination Compounds and Nanomaterials, John Wiley & Sons, Chichester, United Kingdom, 2014; (b) P. Vaněk, P. Lubal, P. Hermann and P. Anzenbacher Jr., J. Fluoresc., 2013, 23, 57–69.
3. (a) A. Merbach, L. Helm and É. Tóth, The Chemistry of Contrast Agents in Medicinal Magnetic Resonance Imaging, John Wiley & Sons, Chichester, United Kingdom, 2013; (b) A. J. Amoroso and S. J. A. Pope, Chem. Soc. Rev., 2015, 44, 4723–4742.
4. (a) R. D. Teo, J. Termini and H. B. Gray, J. Med. Chem., 2016, 59, 6012–6024; (b) A. Majkowska and A. Bilewicz, J. Inorg. Biochem., 2011, 105, 313–320.
5. T. W. Speer, Targeted Radionuclide Therapy, Lippincott Williams & Wilkins, Philadelphia, USA, 2010.
6. (a) K. Binnemans, Y. G. Galyametdinov, R. Van Deun, D. W. Bruce, S. R. Collinson, A. P. Polishchuk, I. Bikchantaev, W. Haase, A. V. Prosvirin, L. Tinchurina, I. Litvinov, A. Gubajdullin, A. Rakhmatullin, K. Uytterhoeven and L. Van Meervelt, J. Am. Chem. Soc., 2000, 122, 4335–4344; (b) Ch. Lu, S. Das, N. Siraj, P. K. S. Magut, M. Li and I. Warner, J. Phys. Chem. A, 2015, 119, 4780–4786.
7. (a) H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33.
8. (a) J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer, Berlin, Germany, 2015; (b) C. Benelli and D. Gatteschi, Introduction to Molecular Magnetism, Wiley-VCH, Weinheim, Germany, 2015; (c) R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH, Weinheim, Germany, 2015.
9. S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289, 379–392.
10. A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380.
11. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
12. A. Dei and D. Gatteschi, Angew. Chem., Int. Ed., 2011, 50, 11852–11858.
13. S.-Y. Lin, C. Wang, L. Zhao, J. Wu and J. Tang, Dalton Trans., 2015, 44, 223–229.
14. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360.
15. (a) S. Takamatsu and N. Ishikawa, Polyhedron, 2007, 26, 1859–1862; (b) H. Wang, B.-W. Wang, Y. Bian, S. Gao and J. Jiang, Coord. Chem. Rev., 2016, 306, 195–216.
16. (a) M.-X. Yao, Z. Qi, F. Gao, Y.-Z. Li, Y. Song and J.-L. Zuo, Dalton Trans., 2012, 41, 13682–13690; (b) H. L. C. Feltham, F. Klöwer, S. A. Cameron, D. S. Larsen, Y. Lan, M. Tropiano, S. Faulkner, A. K. Powell and S. Brooker, Dalton Trans., 2011, 40, 11425–11432.
17. (a) N. F. Chilton, S. K. Langley, B. Moubaraki, A. Soncini, S. R. Batten and K. S. Murray, Chem. Sci., 2013, 4, 1719–1730; (b) G.-J. Chen, Y.-N. Guo, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, P. Cheng and D.-Z. Liao, Chem. – Eur. J., 2012, 18, 2484–2487.
18. (a) M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875; (b) M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita- Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479.
19. L. S. Natrajan, N. M. Khoabane, B. L. Dadds, C. A. Muryn, R. G. Pritchard, S. L. Heath, A. M. Kenwright, I. Kuprov and S. Faulkner, Inorg. Chem., 2010, 49, 7700–7709.
20. J. J. Wilson, E. R. Birnbaum, E. R. Batista, R. L. Martin and K. D. John, Inorg. Chem., 2015, 54, 97–109.
21. M. del, C. Fernández-Férnández, R. Bastida, A. Macías, P. Pérez-Lourido, C. Platas-Iglesias and L. Valencia, Inorg. Chem., 2006, 45, 4484–4496.
22. K. V. Damu, M. S. Shaikjee, J. P. Michael, A. S. Howard and R. D. Hancock, Inorg. Chem., 1986, 25, 3879–3883.
23. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450.
24. V. Patroniak-Krzyminiewska and W. Radecka-Paryzek, Collect. Czech. Chem. Commun., 1998, 63, 363–370.
25. E. L. Gravey, Y. Beldjoudi, J. M. Rawson, T. C. Stamatatos and M. Pilkington, Chem. Commun., 2014, 50, 3741–3743.
26. E. L. Gravey and M. Pilkington, Polyhedron, 2016, 108, 122–130.
27. P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2016, 55, 5957–5972.
28. Bruker. APEX3, Bruker AXS Inc., Madison, Wisconsin, USA, 2015.
29. G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8.
30. K. Brandenburg, DIAMOND, Release 3.2k, Crystal Impact GbR, Bonn, Germany, 2004.
31. (a) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247; (b) J. A. Duncan, J. Am. Chem. Soc., 2009, 131, 2416; (c) G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrády and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239; (d) V. Veryazov, P.-O. Widmark, L. Serrano-Andres, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635.
32. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
33. (a) B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371; (b) B. Schimmelpfennig, AMFI, an atomic mean-field spin-orbit integral program, Stockholm University, 1996.
34. (a) N. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155; (b) B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
35. (a) B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2008, 112, 11431–11435; (b) B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P.-O. Widmark, Chem. Phys. Lett., 2005, 409, 295–299.
36. (a) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129; (b) L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pillet and D. Luneau, J. Am. Chem. Soc., 2008, 130, 12445–12455; (c) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112; (d) L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337.
37. (a) M. Llunell, D. Casanova, J. Cicera, P. Alemany and S. Alvarez, SHAPE, Version 2.1, Barcelona, Spain, 2013; (b) S. Alvarez, Dalton Trans., 2005, 2209–2233; (c) D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Chem. – Eur. J., 2003, 9, 1281–1295; (d) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Chem. – Eur. J., 2008, 14, 1291–1303; (e) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Dalton Trans., 2008, 2583–2591.
38. (a) M. Sobieray, J. Gode, C. Seidel, M. Poß, C. Feldmann and U. Ruschewitz, Dalton Trans., 2015, 44, 6249–6259; (b) T. Güden-Silber, K. Klein and M. Seitz, Dalton Trans., 2013, 42, 13882–13888; (c) S. V. Eliseeva, D. N. Pleshkov, K. A. Lyssenko, L. S. Lepnev, J.-C. G. Bünzli and N. Kuzmina, Inorg. Chem., 2011, 50, 5137–5144; (d) S. Pandya, J. Yu and D. Parker, Dalton Trans., 2006, 2757–2766; (e) A. de Bettencourt-Dias, P. S. Barber and S. Viswanthan, Coord. Chem. Rev., 2014, 273–274, 165–200.
39. B. Drahoš, J. Kotek, P. Hermann, I. Lukeš and É. Tóth, Inorg. Chem., 2010, 49, 3224–3238.
40. (a) L. Pellegatti, J. Zhang, B. Drahoš, S. Villette, F. Suzenet, G. Guillaumet, S. Petoud and É. Tóth, Chem. Commun., 2008, 6591–6593; (b) C. S. Bonnet, F. Buron, F. Caillé, C. M. Shade, B. Drahoš, L. Pellegatti, J. Zhang, S. Villette, L. Helm, C. Pichon, F. Suzenet, S. Petoud and É. Tóth, Chem. – Eur. J., 2012, 18, 1419–1431.
41. (a) J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter, 2009, 80, 014430; (b) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1487175 and 1487176. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt02537d

---