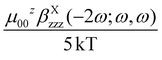Nonlinear optical properties of intriguing Ru σ-acetylide complexes and the use of a photocrosslinked polymer as a springboard to obtain SHG active thin films

Abstract

This work reports on the design, synthesis and photo-physical properties of two ruthenium σ-alkynyl complexes. It is shown that, despite similar optical absorption features recorded in solution, the introduction of a benzaldehyde moiety leads to an improved non-linear optical (NLO) response as measured by Electric Field Induced Second Harmonic (EFISH) generation and Third Harmonic Generation (THG) at 1.907 μm, both related to the second order hyperpolarizability. These structure–property relationships are rationalized based on few state modelling. Complex 2 is subsequently processed to afford composite films that demonstrate a χ² of 1.4 pm V⁻¹, quite remarkable given the ease of film processing implemented in this work.

---

Introduction

During the last two decades, transition metal compounds with high nonlinear optical properties (NLO) have been extensively investigated in view of the large opportunity for their applications, for example as molecular building blocks for optical communications, optical data processing and storage or electrooptical devices.¹ Remarkably, coordination complexes may offer additional flexibility when compared to organic NLO chromophores by introducing NLO active charge-transfer transitions between the metal and the ligands, tunable by virtue of the nature, oxidation state, and coordination sphere of the metal center.²

It is well known that typical second-order NLO chromophores are dipolar molecules bearing an electron donor and an electron acceptor group connected through a π-conjugated polarizable spacer.² Although the molecular structure–NLO activity relationships for third-order properties are less straightforward than for second-order properties, it has been established with organic compounds that the cubic nonlinearity can be increased by many factors such as: (i) increase in π-delocalization (e.g. progressing from small molecules to conjugated polymers), (ii) introduction of strong donor and acceptor functional groups, (iii) adequate chain orientation, packing density, and conformation, and (iv) increase of the dimensionality.³ Metal σ-acetylides, reported in the 1960s,⁴ represent a widely investigated class of active NLO chromophores, mainly developed by M. Humphrey et al.⁵ and W.-Y. Wong,⁶ where in general the metal acts as the donor group of a donor–acceptor system connected by a π-linker. The almost linear M–C≡C–R structure allows for good coupling between the d metal orbitals and the π* system of the σ-acetylide bridge affording a significant NLO response controlled by low-energy MLCT excitations. In general phosphine, and particularly diphosphine, electron donor ligands are particularly appreciated in NLO since they enrich the electronic content of the metal, while increasing at the same time the molecular stability. Of particular interest are ruthenium σ-alkynyl complexes, due to their simple high-yielding syntheses,⁷ enhanced NLO coefficients,⁸ easy preparation of multimetallic dendrimers,⁹ and reversible redox properties which afford the possibility of NLO switching.¹⁰

On the other hand, the possibility to reversibly photoisomerize azobenzene has made it one of the most ubiquitous light-sensitive molecular switches. Also donor–acceptor substituted azo dyes, which are molecules with easily polarizable electrons, show large second-order nonlinearities. The latter can be enhanced by either increasing the conjugation length (improving delocalization) or increasing the strength of the donor or acceptor groups (improving electron asymmetry).²

It was shown by some of us that the introduction of an azobenzene fragment in the same conjugated chain as the ruthenium-acetylide not only favors the trans–cis–trans photoisomerization of the azo unit, but also increases the rate of the thermal cis → trans back isomerization.¹¹ The resulting azobenzene-containing ruthenium(II) acetylides showed good processability, which allowed spin-coated uniform thin films to be prepared, and surface relief gratings to be studied.¹¹

These investigations prompted us to prepare two ruthenium σ-alkynyl complexes (1 and 2, Scheme 1) in order to study their NLO response by means of the EFISH (Electric-Field Induced Second Harmonic generation) and THG (Third Harmonic Generation) techniques.¹² The results were complemented by a theoretical investigation of both linear and NLO responses.

Scheme 1 Formulas of the two investigated complexes.

Then, due to the importance of second-order NLO active polymeric films for photonic applications,^2e compound 2 was dispersed and oriented by poling in polymethylmethacrylate (PMMA) and polystyrene (PS) matrices, affording composite films from which the second harmonic generation (SHG) was determined. Also, because in the case of host/guest PMMA or PS materials a fading of the NLO signal with time is often observed, due to the loss of orientation of the chromophores in the absence of poling, the use of an alternative polymeric photocrosslinked matrix was investigated so as to improve the temporal stability of the NLO response.

Results and discussion

Synthesis of dyes

Synthetic routes for complexes 1 and 2 are shown in Scheme 2. For the synthesis of the azo dyes, 3, 4a and 4b, 4-bromo aniline was first diazotized using sodium nitrite in the presence of concentrated sulfuric acid, which coupled with N-hydroxyethyl-N-ethylaniline to provide 3 in good yields. The alkynes were prepared via Sonogashira Pd/Cu cross-coupling protocols.¹³4a was desilylated in a conventional fashion (K₂CO₃/MeOH) to afford terminal acetylenes 4b. The structures of these azo organic precursors were confirmed by their spectral data. The azo-containing bifunctional ruthenium-acetylides 1 and 2 were then prepared according to previously published experimental procedures, as shown in Scheme 2.¹¹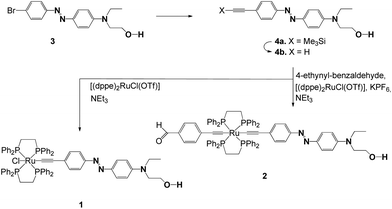

Scheme 2 Preparation of the trans-Ru−X(C≡CR)(dppe)₂ complexes 1 and 2 from [(dppe)₂RuCl(OTf)] via intermediate vinylidene complexes [RuCl(=C=CHR)(dppe)₂]PF₆.

Complex 1 was prepared in two steps from [(dppe)₂RuCl(OTf)] (dppe = 1,2-bis(diphenylphosphino)ethane).¹⁴ A vinylidene intermediate was first obtained by reaction in the presence of alkyne 4b. The completion of the reaction was monitored by ³¹P NMR. After removing the excess of 4b, subsequent deprotonation by triethylamine afforded 1 as a dark-red powder in 70% yield. Similarly, 2 was prepared in two steps.

A vinylidene intermediate was first prepared by reacting [(dppe)₂RuCl(OTf)]¹⁴ in the presence of 4-ethynylbenzaldehyde.¹⁵ The completion of the reaction was monitored by ³¹P NMR. After removing the excess of 4-ethynylbenzaldehyde, the addition of 4b, and subsequent deprotonation by triethylamine in the presence of KPF₆, afforded complex 2 as a red powder in 52% yield from [(dppe)₂RuCl(OTf)]. Compounds 1 and 2 were fully characterized by spectroscopic methods.

UV–vis spectra

The absorption spectra of dyes 1 and 2 were recorded in dichloromethane (DCM) at a concentration of 10⁻⁴–10⁻⁶ M in the wavelength range 300–700 nm (Fig. 1).

Fig. 1 UV-vis absorption spectra of compounds 1 and 2 in DCM (a) experimental spectra and (b) calculated spectra for a HWHM = 2000 cm⁻¹.

These spectra show broad absorption bands with λ_max at 491 nm (1) and 492 nm (2). In DCM, the corresponding half width at half maximum (HWHM) amounts to 2700 cm⁻¹ (1) and 3600 cm⁻¹ (2), with molar extinction coefficients of 1.58 × 10⁵ and 1.66 × 10⁵ L mol⁻¹ cm⁻¹, respectively.

The calculated absorption spectra, using standard DFT and TD-DFT computations (see Computational details), nicely agree with the experimental ones (Fig. 1) and allow assignment of the underlying electronic transition and redistribution. In fact, for both compounds, the two transitions have significant oscillator strengths between 350 and 600 nm (Fig. 2). The main calculated absorption band stems from the first excited state and corresponds to electronic transfer from the HOMO to the LUMO. The HOMO is delocalized over the whole molecular backbone and involves both the trans azobenzene unit and the alkynyl ruthenium fragment with comparable weight on the Ru atom for both compounds (weight percentages of Ru given in the caption of Fig. 2). Meanwhile, the LUMO is mainly based on the azobenzene-based ligand.¹⁶ The main difference between complexes 1 and 2 has to be related to a significantly larger transition dipole moment for 2 as a result of the benzaldehyde moiety (Table 1).¹⁷ Similarly, ground state dipole moments are also larger, with a more than two-fold increase, while the excited state dipole remains sizeable in 1 and almost vanishes in 2.

Fig. 2 Main molecular orbitals involved in the two lowest lying electronic transitions having a sizeable oscillator strength (f₀₁) for compounds 1′ and 2′ (models of 1 and 2, see Computational details). Corresponding wavelengths are also given. Both geometries and properties have been computed in the presence of a solvent (DCM). The weight on the Ru atom amounts to 17 and 19% respectively in the HOMO and HOMO−2 of compound 1′ and to 15 and 38% in the HOMO and HOMO−1 of compound 2′.

Table 1 Computed transition dipole moments and energies, state dipole moments as well as first and second order hyperpolarizabilities given according to the Taylor convention¹⁷

Cpd	ω 01 (eV)	μ ^z01 (D)	μ ^z00 (D)	μ ^z11 (D)	β ^Tzzz(−2ω; ω, ω) (10^−28 esu)	γ ^Tzzzz(−2ω; ω, ω, 0) (10^−33 esu)	γ ^Tzzzz(−3ω; ω, ω, 0) (10^−33 esu)	[small gamma, Greek, macron] ^Tav(−2ω; ω, ω, 0) (10^−33 esu)	[small gamma, Greek, macron] ^Tav(−3ω; ω, ω, 0) (10^−33 esu)
z is the ground state dipole moment axis. Geometries are optimized in the presence of solvent (DCM), and properties computed in the gas phase. The bright excited state of compound 2′ is the second one at this level of theory (see the ESI for data computed at other levels of theory).
1′	2.60	−10.2	3.2	−3.6	−1.69	−1.37	−3.33	−0.27	−0.67
2′	2.66	−13.7	8.9	0.7	−3.46	−6.23	−12.71	−1.25	−2.54

---

Besides, the more pronounced shoulder visible in the absorption spectrum of compound 2 near 400 nm, as compared to 1, is consistent with a second bright-excited state (i.e. having significant oscillator strength) lying closer to the first one and bearing a larger oscillator strength (Fig. 2). This is also in line with the significantly larger HWHM. Interestingly, the involved MOs in these excitations at a higher energy are very different for 1 and 2 (Fig. 2): the electron withdrawing character of the benzaldehyde moiety appears clearly, the LUMO+1 of 2 is mainly localized on the latter moiety, contrastingly to complex 1 which cannot exhibit a MO of this kind.

We also note the differences in the occupied MOs involved in this excitation: the metallic character of the HOMO−1 of complex 2 is much higher than the weight of the metal in HOMO−2 of 1 (38 vs. 19%). Consistently with earlier findings, this shoulder in the absorption spectrum of compound 2 near 400 nm can be attributed to the benzaldehyde based alkynyl ruthenium fragment.

C and H are depicted in grey, N, Cl, O, P and Ru are depicted in blue, green, red, orange and fuchsia, respectively.

Nonlinear optical properties in solution

The NLO properties of complexes 1 and 2 were investigated by the EFISH technique and THG experiments, working in CH₂Cl₂ solution (10⁻³ M) with a non-resonant incident wavelength of 1.907 μm, whose second and third harmonic (2ω = 0.953 μm; 3ω = 0.636 μm) lie in rather transparent regions of the absorption spectra of the investigated molecules, although there is a weak tail at ca. 630 nm that could cause a slight pre-resonance enhancement of the NLO response in our THG measurements (see Table S1†).

In the EFISH experiment, the incident beam was synchronized with a DC (Direct Current) field applied to the solution with the aim to break its intrinsic centrosymmetry. This technique gives γ_EFISH, which gathers a contribution stemming from the cubic term, γ(−2ω; ω, ω, 0), and one related to the orientational contribution of the quadratic term, β_λ(−2ω; ω, ω) = β_EFISH:^12a,18

μ₀₀ is the static ground state dipole moment and β_EFISH is the vectorial projection along the dipole moment direction of the tensorial first hyperpolarizability. In eqn (1), superscript X indicates the use of the phenomenological convention.^18b,c

In the case of push–pull molecules with a limited electronic polarizability, the γ(−2ω; ω, ω, 0) contribution, which is one among the third order polarizabilities at frequency ω of the incident light, is negligible allowing a straightforward determination of μβ_EFISH.² In most of the reported β_EFISH, including elongated chromophores, the third order term is usually ignored. However, as reported by Prasad and Williams,^1a for long π-electron conjugated molecules having donor–acceptor groups at the terminal ends, the cubic electronic contribution can be dramatically larger than the μβ_EFISH/5kT term and can no more be ignored. This prevents the determination of μβ_EFISH, as the accessible range of temperature is usually too limited to disentangle the two contributions using eqn (1).

As a matter of fact, it has been reported that the cubic contribution to γ_EFISH can be reasonably neglected only when the cubic γ_THG values are less than 5–20% of the γ_EFISH values.^12d Thus, for π-delocalized Ru acetylide complexes, known for their significant third order NLO responses, the third order term should not be excluded a priori. Indeed, within the two-state model the computed diagonal hyperpolarizabilities are in the same order of magnitude (Table 1). To further assess the respective contributions in complexes 1 and 2, we carried out EFISH as well as THG experiments. The latter provide the cubic hyperpolarizability γ_THG(−3ω; ω, ω, ω), since they are performed in the absence of a DC field contrastingly to γ_EFISH.

As evidenced in Table 2, complexes 1 and 2 are characterized by high γ_EFISH and γ_THG values, obtained through EFISH and THG experiments working in CH₂Cl₂ with an incident wavelength of 1.907 μm. As γ_THG and γ_EFISH values are of the same order of magnitude, it is unwise to determine μβ_EFISH by assuming a priori a negligibly small contribution of the third order term to eqn (1). The absolute magnitude of γ_EFISH is significantly larger for complex 2 than for complex 1 and both γ_EFISH and γ_THG are negative. Experimental γ_EFISH and γ_THG have similar magnitude in the case of complex 1, whereas, in the case of complex 2, γ_EFISH is significantly larger than γ_THG by a factor of 1.6.

Table 2 γ _EFISH and γ_THG measurements in 10⁻³ CH₂Cl₂ solution with an incident wavelength of 1.907 μm

Sample	γ EFISH (10^−33 esu)	γ THG (10^−33 esu)
	−2.07	−2.03
	−7.33	−4.64

---

These experimental data are in agreement with theoretical predictions (Table 3). Both signs and respective amplitudes of the NLO properties can be further rationalized within the two-state model (Tables 1, 3 and the ESI†). First, all first order hyperpolarisabilities are found to be negative. This is a clear indication that the difference in the state dipole moments, Δμ = μ^z₁₁ − μ^z₀₀, is negative.

Table 3 Computed contributions to γ^TOT,X_EFISH ^a

Sample		[small gamma, Greek, macron] ^XEFISH (10^−33 esu)	γ ^TOT,XEFISH (10^−33 esu)
a Geometries are optimized in the presence of a solvent (DCM), and properties computed in the gas phase (see the ESI for data computed at other levels of theory).
1′	−0.65	−0.07	−0.72
2′	−3.75	−0.31	−4.06

---

It is noteworthy that the cause of this negative sign is related to reversal signs between the ground and excited state dipole moments in complex 1, whereas it is induced by a dramatic decrease without sign inversion in complex 2 (Table 1 and the ESI†).¹⁷

The computed second order hyperpolarizabilities also reveal significant differences between the two compounds. The absolute magnitude of γ_EFISH is significantly smaller for complex 1 as compared to 2 (Table 1), and the related NLO properties (Tables 1 and 3) exhibit the same trend. But most importantly, the results of the few state model are indicative of a significantly larger contribution to γ^{TOT, X}_EFISH stemming from the first hyperpolarizability as compared to the third order contribution to [small gamma, Greek, macron]^X_EFISH (Table 3). As is often the case, our computed values are smaller than the experimental values,¹⁹ but we stress that it depends a lot on the level of theory in use (see Computational details and the ESI†).

SHG measurements on thin films

Although the NLO response of molecular systems is important, a step further is their molecular engineering in order to obtain organized molecular materials showing a temporally stable and high bulk second-order NLO response.²⁰ Applications of ruthenium σ-acetylide complexes to produce second-order bulk NLO materials or structured films are very limited.^2e In spite of their large molecular quadratic hyperpolarizabilities, they form crystalline materials which exhibit modest bulk SHG efficiency,^5c,16,21 due to the reluctance of acetylide complexes to crystallize in non-centrosymmetric structures. However, a film of a ruthenium oligothienylacetylide NLO chromophore, incorporated into a polymethylmethacrylate (PMMA) matrix, revealed an acoustically induced SHG signal with a good χ⁽²⁾ value (0.80 pm V⁻¹).¹⁶ Besides, a host/guest film based on a dinuclear Ru(II) alkynyl complex dispersed in PMMA exhibits good and stable SHG performances (χ⁽²⁾ = 3.28 pm V⁻¹),²² probably due to the relatively large size of the NLO chromophore which would hinder its mobility even in a host/guest film.

In addition, we have investigated the potential of complex 2 as a molecular building block for composite films with Second Harmonic Generation (SHG) properties,²² following the standard Maker fringe technique.²³ We produced a composite film of complex 2 in PMMA (6% weight of the chromophore with respect to PMMA, and 9% weight of PMMA with respect to CH₂Cl₂) and studied the SHG signal of the resulting poled host–guest system (see the Experimental section).

The corona-wire poling dynamic of the SHG behaviour of a PMMA film containing complex 2 is reported in Fig. 3. The SHG signal was negligible at room temperature, but it quickly increased when the temperature was increased up to 55 °C and a strong electric field of 9 kV was applied. On reaching a stable SHG signal, the sample was cooled at room temperature and the dry box was opened. The final switch off of the electric field caused a rapid downfall of the SHG signal to zero. A similar behaviour is observed when using polystyrene instead of PMMA in the host/guest system (see Fig. S1†).

Fig. 3 In situ corona-wire poling dynamic of a PMMA film containing complex 2, as a host/guest system.

In order to increase the SHG response stability, we used a novel approach to prepare a “host/guest” film with complex 2 and a polymer that under UV-A light and a nitrogen atmosphere allows a fast photocrosslinking of the film. To a dichloromethane solution of dipentaerythritol pentaacrylate – DiPEPA, complex 2 was added (4 wt% on DiPEPA) together with a liquid photoinitiator based on 2-hydroxy-2-methyl-1-phenyl-propan-1-one (3 wt%). The solution was deposited onto a glass substrate by spin-coating. The as-deposited wet film was irradiated with UV-A light for 60 s under a nitrogen atmosphere to allow for photocrosslinking of the film to occur (see the Experimental section for details).

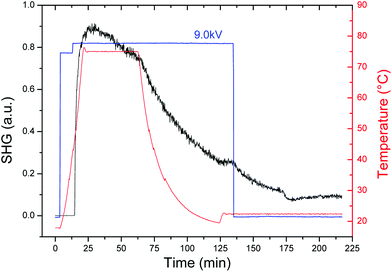
The corona-wire poling dynamics of the photocrosslinked film containing complex 2 is shown in Fig. 4, in which the optimized poling parameter temperature (75 °C) and electric field (9.0 kV) have permitted us to obtain a sufficiently high and stable SHG signal. Interestingly, whereas the SHG signal of the PMMA film drops to zero when the electric field is turned off, for the photocrosslinked film a fair SHG signal is maintained. The χ⁽²⁾₃₃ component of the second-order susceptibility tensor χ⁽²⁾ for the poled film (C_∞,v symmetry) was obtained by following the standard Maker fringe technique, as previously reported.²² The χ⁽²⁾₃₃ value of the composite film (thickness is 3.3 μm, measured with a profilometer) is 1.4 pm V⁻¹, which is a remarkable value for the easily prepared film made of complex 2. This is an important result that provides evidence of the potential of the photocrosslinking approach in order to increase both the response and stability of the NLO ruthenium acetylides and coordination compounds.

Fig. 4 In situ corona-wire poling dynamic of a photocrosslinked film containing complex 2.

Experimental section

Synthesis of 1 and 2

All manipulations were performed using Schlenk techniques under an Ar atmosphere. All commercially available starting materials were used as received. All solvents were dried and purified by standard procedures. The following compounds were prepared by literature procedures: [(dppe)₂RuCl(OTf)],¹⁴ 4-ethynylbenzaldehyde.¹⁵ The preparation procedures and characterization of compounds 3, 4a and 4b are described in the ESI.†

Synthesis of 1. In a Schlenk tube, 0.157 mmol, 170 mg of [(dppe)₂RuCl(OTf)]¹⁴ and 53 mg, 0.18 mmol of 4b were introduced under argon and dissolved in 10 ml of freshly distilled and degassed dichloromethane. The resulting mixture was stirred at r.t. overnight. The completion of the reaction was monitored by ³¹P NMR spectrometry (s, 39.1 ppm). The solvent was removed under reduced pressure and the solid residue was washed several times with diethyl ether. The product was dissolved in 10 ml of freshly distilled and degassed dichloromethane and deprotonated upon addition of NEt₃ (0.3 mL). Then the product was purified by silica gel column chromatography (eluent: diethyl ether/THF 100 : 0 to 80 : 20), compound 1 was afforded as a dark red solid (135 mg) with 70% yield. ¹H NMR (CDCl₃, 400 MHz, 297 K, δ ppm): 7.81 (d, ³J_HH = 8.8 Hz, 2H), 7.71 (d, ³J_HH = 7.9 Hz, 2H), 7.65–6.80 (m, 42H), 6.73 (d, ³J_HH = 8.9 Hz, 2H), 3.78 (t, ³J_HH = 7.8 Hz, 2H), 3.58 (t, ³J_HH = 7.8 Hz, 2H), 3.49 (t, ³J_HH = 7.0 Hz, 2H), 2.80 (m, 8H, CH₂ dppe), 1.03 (t, ³J_HH = 7.0 Hz, 3H). ¹³C NMR (CDCl₃, 125 MHz, 297 K, δ ppm): 150.7, 149.5, 143.6, 136.8 (qt, |¹J_P−C + ³J_P−C| = 11 Hz), 135.3 (qt, |¹J_P−C + ³J_P−C| = 10 Hz), 134.6, 134.4, 132.9, 132.5 (|²J_P−C | = 14.9 Hz), 131.0, 124.7, 122.8, 121.7, 115.9, 65.4, 48.0, 45.0, 30.7 (qt, |¹J_P−C–³J_P−C| = 23 Hz), 14.0. ³¹P {¹H} NMR (CDCl₃, 81 MHz, 297 K, δ ppm): 49.5 (s). Elemental analysis: C₇₀H₆₆ClN₃OP₄Ru calc. C, 68.59; H, 5.43; N, 3.43; found: C, 68.38; H, 5.32; N, 3.49.

Synthesis of 2. In a Schlenk tube, 0.138 mmol (150 mg) of [(dppe)₂RuCl(OTf)]¹⁵ and 20 mg (0.152 mmol) of 4-ethynylbenzaldehyde¹⁶ were introduced under argon and dissolved in 10 ml of freshly distilled and degassed dichloromethane. The resulting mixture was stirred at room temperature overnight. The completion of the reaction was monitored by ³¹P NMR spectrometry (s, 36.7). The solvent was removed under reduced pressure and the dried product was washed several times with diethyl ether to remove the excess of 4-ethynyl benzaldehyde. Then this residue was dissolved in 10 ml of dichloromethane. 4b (60 mg, 0.20 mmol) and KPF₆ (100 mg, 40.54 mmol) were successively added, followed by 0.24 mmol (34 μL) of triethylamine. The reaction mixture was stirred for 16 hours. The formation of the final product was monitored by ³¹P NMR. 2 was purified by silica gel column chromatography (eluent: diethyl ether/THF 100 : 0 to 70 : 30) and afforded as a red orange solid (95 mg) in 52% yield. ¹H NMR (CDCl₃, 400 MHz, 297 K, δ ppm): 9.92 (s, 1H), 7.85 (d, ³J_HH = 8.9 Hz, 2H), 7.8–6.8 (m, 50H), 3.78 (t, ³J_HH = 7.4 Hz, 2H), 3.60 (t, ³J_HH = 7.4 Hz, 2H), 3.48 (t, ³J_HH = 7.0 Hz, 2H), 2.4 (m, 8H), 1.04 (t, ³J_HH = 7.0 Hz, 3H). ¹³C NMR (CDCl₃, 125 MHz, 297 K, δ ppm): 191.3 (C₂₆), 150.0, 149.3, 148.3 (q, ²J_P−C = 18.7 Hz), 143.5, 136.8 (qt, |¹J_P−C + ³J_P−C| = 11 Hz), 136.7 (qt, |¹J_P−C + ³J_P−C| = 10 Hz), 134.2, 134.1, 137.0, 131.8, 131.1, 130.2, 129.5, 124.8, 122.1, 121.4, 119.2, 111.1, 110.4, 65.4, 47.9, 45.0, 31.4 (qt, |¹J_P−C–³J_P−C| = 24 Hz), 14.1. ³¹P{¹H} NMR (CDCl₃, 81 MHz, 297 K, δ ppm): 54.6 (s). Elemental analysis: C₇₉H₇₁N₃O₂P₄Ru: calc. C, 71.92; H, 5.42; N, 3.18; found: C 72.05, H 5.13, N 3.41.

Physical measurements and instrumentation

NMR spectra were recorded on AV 400 MHz or AV 500 MHz spectrometers. ¹H and ¹³C chemical shifts are given versus SiMe₄ and were determined with reference to residual ¹H and ¹³C solvent signals. High resolution mass spectra (HRMS) were recorded on a MS/MS ZABSpec TOF at the CRMPO (Centre de Mesures Physiques de l'Ouest) in Rennes. UV-vis absorption spectra were recorded using a UVIKON 9413 or Biotek Instruments XS spectrophotometer using quartz cuvettes of 1 cm path-length.

Preparation of host–guest films of complex 2 in PMMA and PS matrices

Composite films were produced by spin coating on ordinary non-pretreated glass substrates (thickness 1 mm) previously cleaned with water/acetone. The solution was obtained from 300 mg of the polymer, polymethylmethacrylate (PMMA) or polystyrene (PS) and 15 mg of 2 dissolved in dichloromethane (4.5 mL). Parameters of spinning (RPM, revolutions per minute) RPM1: 700; Ramp1: 1 s, Time1: 5 s; RPM2: 2000; Ramp2: 5 s, Time2: 45 s.

Preparation of the glass substrate (silanization)

To improve the adhesion of the polymeric films to the glass substrate, 25 mm × 25 mm × 1 mm microscope slides (Thermo Fisher) were subjected to successive ultrasonication in de-ionized water (20 min), acetone (20 min) and isopropyl alcohol (20 min). The substrates were then dried under a stream of nitrogen. Cleaned glass substrates were then immersed in a solution of vinyltrimethoxysilane (10 vol% in toluene) overnight. After that, the surface-modified glass slides were thoroughly rinsed with toluene and dried under a stream of nitrogen just before solution deposition.

Preparation of crosslinked polymer films containing complex 2

A solution of dipentaerythritol pentaacrylate – DiPEPA (SR399, Sartomer) in dichloromethane (20 wt%) was prepared under magnetic stirring. Once complete dissolution was achieved (after about 4 h), complex 2 was added (4 wt% on DiPEPA) together with a liquid photoinitiator based on 2-hydroxy-2-methyl-1-phenyl-propan-1-one (Darocur 1173, CIBA) (3 wt%) and the solution was maintained under magnetic stirring for about 1 h.

The solution was deposited onto pre-treated and pre-cleaned glass substrates by spin-coating (600 rpm, 40 s). The as-deposited wet film was irradiated with UV-A light for 60 s under a nitrogen atmosphere to allow for photocrosslinking of the film to occur. The film was ready for further analysis. (T_g is between 75 and 90 °C).

EFISH measurements

All EFISH measurements¹² were carried out at the Dipartimento di Chimica of the Università degli Studi di Milano, in CH₂Cl₂ solutions at a concentration of 1 × 10⁻³ M, working with a non-resonant incident wavelength of 1.907 μm, obtained by Raman-shifting the fundamental 1.064 μm wavelength produced by a Q-switched, mode-locked Nd³⁺:YAG laser manufactured by Atalaser. The apparatus for the EFISH measurements is a prototype made by SOPRA (France). The γ_EFISH and high γ_THG values reported are the mean values of 16 successive measurements performed on the same sample.

SHG measurements

Second Harmonic Generation (SHG) experiments were performed using a Q-switched Nd:YAG (Quanta System Giant G790-20) laser at 1.064 μm wavelength with a pulse of 7 ns and 20 Hz repetition rate. For poling measurements, the fundamental beam was attenuated to 0.57 mJ and was focused with a lens (f = 600 mm) on the sample, placed over the hot stage. The corona poling process was carried out inside a specially built dry box, in an N₂ atmosphere. The fundamental beam was polarized in the plane of incidence (p-polarized) with an angle of about 55° with respect to the sample in order to optimize the SHG signal. The hot stage temperature was controlled by a GEFRAN 800 controller, while the corona wire voltage (up to 10.0 kV across a 10 mm gap) was applied by using a TREK610E high-voltage-supply. After rejection of the fundamental beam by using an interference filter and a glass cut-off filter, the p-polarized SHG signal at 532 nm was detected with a UV-Vis photomultiplier (PT) Hamamatsu C3830.9-14.

Computational details

The DFT calculations reported in this work have been performed using the Gaussian09²⁴ program. The geometries of all the compounds have been optimized without symmetry constraints using the MPW1PW91 functional²⁵ and the LANL2DZ²⁶ basis set augmented with polarization functions on all the atoms, except hydrogen atoms. The solvent effects, in our case CH₂Cl₂, were taken into account by the means of the Polarizable Continuum Model (PCM).²⁷ Calculations were carried out for complexes 1′ and 2′ (models of 1 and 2) where ethyl and hydroxyethyl chains of 1 and 2 were both replaced with n-butyl chains. Then, the calculations of the frequencies of normal modes of vibration have been carried out to confirm the ground state character of the optimized geometries. Next, TD-DFT calculations have been performed at different levels of theory using the previously optimized geometries. Computed absorption spectra were plotted using GaussView,²⁸ taking a half-bandwidth for each Gaussian of 2000 cm⁻¹. For these model complexes we noticed substantial changes of calculated NLO properties either by varying the exchange correlation functional or by changing the solvation cavity model. Thus, we turned to few state models to rationalize NLO responses and used the two-state model with state and transition dipole moments as well as transition energies derived from our TD-DFT computations.

All calculated values were obtained in the dipole orientation for which the ground state dipole moment aligns along the z-axis. We limited the analysis to the main diagonal component of the hyperpolarizability tensors (β^X_zzz(−2ω; ω, ω), γ^X_zzzz(−2ω; ω, ω, 0), γ^X_zzzz(−3ω; ω, ω, 0)) using the expressions given by Willets et al.^18b For consistency with experimental data theoretical values (usually defined according to a Taylor expansion, (T)) are also given in the phenomenological convention (X).^18b,c We stress that implementation of a few state model allows for qualitative interpretation only. In fact, contributions from higher lying excited states are not considered and off-diagonal components may contribute to γ_THG as well. In addition, contributing factors such as those currently tackled to achieve accurate prediction of linear optical properties (band shape, amplitude and position) of solvated chromophores,¹⁷ are yet very computationally demanding but another source of inaccuracy. In particular, no state specific corrections,^17b explicit solvent molecules, counter-ions or vibronic contributions^17c have been taken into account. Therefore, in order to assess the overall trends, we have also performed calculations (i) with both geometry and properties computed in the gas phase and (ii) starting from the geometry optimized in CH₂Cl₂ (DCM) and performing the subsequent TD-DFT calculations in the gas phase. Last, no local field corrections have been considered as they are usually implemented in the experimental data processing that leads to the microscopic quantities.

Conclusions

In summary, we have synthesized two Ru acetylide complexes demonstrating sizeable nonlinear optical responses, as measured with the EFISH and THG techniques in solution. The introduction of an electron-withdrawing group such as para-benzaldehyde in complex 2, enhances both the ground state and transition dipole moment as compared to complex 1. Concomitantly, both measured γ_EFISH and γ_THG undergo a significant increase, as it is for computed values when considering the appropriate level of theory, namely non-equilibrium solvation conditions whenever the solvent is taken into account. This has been further rationalized thanks to few state modelling, revealing that despite large THG hyperpolarizabilities, γ_EFISH mainly stems from contributions related to the first order term. In addition, a composite film of complex 2 with a photocrosslinked polymer leads to a sizeable SHG response, χ² = 1.4 pm V⁻¹. The next step will be to covalently link the chromophores to a crosslinked matrix in order to further increase the response and the stability of the SHG signal.

Acknowledgements

A. A., A. B. and C. K. gratefully acknowledge the technical support provided by Rémi Marchal. This work was granted access to the HPC resources of CINES and IDRIS under the allocations 2015-[x2015080649] made by GENCI (Grand Equipement National de Calcul Intensif).

Notes and references

1. (a) N. P. Prasad and D. J. Williams, Introduction to Nonlinear Optical Effects in molecules and Polymers, Wiley, New York, 1991; (b) J. Zyss, Molecular Nonlinear Optics: Materials, Physics and Devices, Academic Press, Boston, 1994.
2. See for example (a) B. J. Coe, Comprehensive Coordination Chemistry II, Elsevier Pergamon, Oxford, UK, 2004, vol. 9; (b) O. Maury and H. Le Bozec, Acc. Chem. Res., 2005, 38, 691; (c) B. J. Coe, Acc. Chem. Res., 2006, 39, 383; (d) J. P. Morrall, G. T. Dalton, M. G. Humphrey and M. Samoc, Adv. Organomet. Chem., 2007, 55, 61; (e) S. Di Bella, C. Dragonetti, M. Pizzotti, D. Roberto, F. Tessore and R. Ugo, Topics in Organometallic Chemistry 28, Molecular Organometallic Materials for Optics, ed. H. Le Bozec and V. Guerchais, Springer, New York, 2010, vol. 28, pp. 1–55; (f) O. Maury and H. Le Bozec, Molecular Materials, ed. D. W. Bruce, D. O'Hare and R. I. Walton, Wiley, Chichester, 2010, pp. 1–59; (g) E. Lucenti, E. Cariati, C. Dragonetti, L. Manassero and F. Tessore, Organometallics, 2004, 23, 687; (h) J. Boixel, V. Guerchais, H. Le Bozec, D. Jacquemin, A. Amar, A. Boucekkine, A. Colombo, C. Dragonetti, D. Marinotto, D. Roberto, S. Righetto and R. De Angelis, J. Am. Chem. Soc., 2014, 136, 5367.
3. J. L. Bredas, C. Adant, P. Tackx and A. Persoons, Chem. Rev., 1994, 94, 243.
4. (a) R. Nast, Angew. Chem., Int. Ed., 1962, 1, 276; (b) R. Nast, Angew. Chem., Int. Ed., 1965, 4, 366.
5. (a) I. R. Whittall, M. G. Humphrey, M. Samoc, J. Swiatkiewicz and B. Luther-Davies, Organometallics, 1995, 14, 5493; (b) A. M. McDonagh, N. T. Lucas, M. P. Cifuentes, M. G. Humphrey, S. Houbrechts and A. Persoons, J. Organomet. Chem., 2000, 605, 184; (c) C. E. Powell and M. G. Humphrey, Coord. Chem. Rev., 2004, 248, 725; (d) M. G. Humphrey and M. Samoc, Adv. Organomet. Chem., 2008, 55, 61; (e) M. P. Cifuentes and M. G. Humphrey, J. Organomet. Chem., 2004, 689, 3968; (f) G. Guillaume, M. P. Cifuentes, F. Paul and M. G. Humphrey, J. Organomet. Chem., 2014, 751, 181.
6. (a) G.-J. Zhou and W.-Y. Wong, Chem. Soc. Rev., 2011, 40, 2541; (b) G.-J. Zhou, W.-Y. Wong, Z. Lin and C. Ye, Angew. Chem., Int. Ed., 2006, 45, 6189; (c) G.-J. Zhou, W.-Y. Wong, C. Ye and Z. Lin, Adv. Funct. Mater., 2007, 17, 963; (d) G. Zhou, W.-Y. Wong, S.-Y. Poon, C. Ye and Z. Lin, Adv. Funct. Mater., 2009, 19, 531; (e) G.-J. Zhou, W.-Y. Wong, D. Cui and C. Ye, Chem. Mater., 2005, 17, 5209.
7. (a) A. M. McDonagh, I. R. Whittall, M. G. Humphrey, D. C. R. Hockless, B. W. Skelton and A. H. White, J. Organomet. Chem., 1996, 523, 33; (b) A. M. McDonagh, M. P. Cifuentes, I. R. Whittall, M. G. Humphrey, M. Samoc, B. Luther-Davies and D. C. R. Hockless, J. Organomet. Chem., 1996, 526, 99.
8. (a) R. H. Naulty, A. M. McDonagh, I. R. Whittall, M. P. Cifuentes, M. G. Humphrey, S. Houbrechts, J. Maes, A. Persoons, G. A. Heath and D. C. R. Hockless, J. Organomet. Chem., 1998, 563, 137; (b) S. K. Hurst, M. G. Humphrey, J. P. Morrall, M. P. Cifuentes, M. Samoc, B. Luther-Davies, G. A. Heath and A. C. Willis, J. Organomet. Chem., 2003, 670, 56.
9. K. A. Green, M. P. Cifuentes, M. Samoc and M. G. Humphrey, Coord. Chem. Rev., 2011, 255, 2025.
10. K. A. Green, M. P. Cifuentes, M. Samoc and M. G. Humphrey, Coord. Chem. Rev., 2011, 255, 2530.
11. K. N. Gherab, R. Gatri, Z. Hank, B. Dick, R.-J. Kutta, R. Winter, J. Luc, B. Sahraoui and J.-L. Fillaut, J. Mater. Chem., 2010, 20, 2858.
12. (a) B. F. Levine and C. G. Bethea, Appl. Phys. Lett., 1974, 24, 445; (b) B. F. Levine and C. G. Bethea, J. Chem. Phys., 1975, 63, 2666; (c) I. Ledoux and J. Zyss, J. Chem. Phys., 1982, 73, 203; (d) A. Colombo, D. Locatelli, D. Roberto, F. Tessore, R. Ugo, M. Cavazzini, S. Quici, F. De Angelis, S. Fantacci, I. Ledoux-Rak, N. Tancrez and J. Zyss, Dalton Trans., 2012, 41, 6707.
13. S. Takahashi, Y. Kuroyama, K. Sonogashira and N. Hagihara, Synthesis, 1980, 630.
14. (a) N. Mantovani, M. Brugnati, L. Gonsalvi, E. Grigiotti, F. Laschi, L. Marvelli, M. Peruzzini, G. Reginato, R. Rossi and P. Zanello, Organometallics, 2005, 24, 405; (b) S. Rigaut, J. Perruchon, L. Le Pichon, D. Touchard and P. H. Dixneuf, J. Organomet. Chem., 2003, 670, 37.
15. W. B. Austin, N. Bilow, W. J. Kelleghan and K. S. Y. Lau, J. Org. Chem., 1981, 46, 2280.
16. J. L. Fillaut, J. Perruchon, P. Blanchard, J. Roncali, S. Golhen, M. Allain, A. Migalsaka-Zalas, I. V. Kityk and B. Sahraoui, Organometallics, 2005, 24, 687.
17. (a) D. Jacquemin and C. Adamo, Topics in Current Chemistry, in Computational Molecular Electronic Spectroscopy with TD-DFT, Springer, Berlin, Heidelberg, 2015, pp. 1–29; (b) C. Katan, P. Savel, B. M. Wong, T. Roisnel, V. Dorcet, J.-L. Fillaut and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 9064; (c) W. Liang, H. Ma, H. Zang and C. Ye, Int. J. Quantum Chem., 2015, 115, 550.
18. (a) S. K. Saha and G. K. Wong, Appl. Phys. Lett., 1979, 34, 423; (b) A. Willets, J. E. Rice, D. M. Burland and D. P. Shelton, J. Chem. Phys., 1992, 97, 7590; (c) H. Reis, J. Chem. Phys., 2006, 125, 014506.
19. M. Pizzotti, R. Ugo, E. Annoni, S. Quici, I. Ledoux-Rak, G. Zerbi, M. Del Zoppo, P. Fantucci and I. Invernizzi, Inorg. Chim. Acta, 2002, 340, 70–80.
20. As examples; (a) E. Cariati, R. Macchi, D. Roberto, R. Ugo, S. Galli, N. Masciocchi and A. Sironi, Chem. Mater., 2007, 19, 3704; (b) L. R. Dalton, P. A. Sullivan and D. H. Bale, Chem. Rev., 2010, 110, 25 , and references therein.
21. A. Migalska-Zalas, B. Sahraoui, I. V. Kityk, S. Tkaczyk, V. Yuvshenko, J. L. Fillaut, J. Perruchon and T. J. J. Muller, Phys. Rev. B: Condens. Matter, 2005, 71, 035119.
22. A. Colombo, F. Nisic, C. Dragonetti, D. Marinotto, I. P. Oliveri, S. Righetto, M. G. Lobello and F. De Angelis, Chem. Commun., 2014, 50, 7986.
23. (a) S. Proutiere, P. Ferruti, R. Ugo, A. Abbotto, R. Bozio, M. Cozzuol, C. Dragonetti, E. Emilitri, D. Locatelli, D. Marinotto, G. Pagani, D. Pedron and D. Roberto, Mater. Sci.Eng. B, 2008, 147, 293; (b) D. Marinotto, S. Proutiere, C. Dragonetti, A. Colombo, P. Ferruti, D. Pedron, M. C. Ubaldi and S. Pietralunga, J. Non-Cryst. Solids, 2011, 357, 2075; (c) D. Marinotto, R. Castagna, S. Righetto, C. Dragonetti, A. Colombo, C. Bertarelli, M. Garbugli and G. Lanzani, J. Phys. Chem. C, 2011, 115, 20425; (d) D. Roberto, A. Colombo, C. Dragonetti, D. Marinotto, S. Righetto, S. Tavazzi, M. Escadeillas, V. Guerchais, H. Le Bozec, A. Boucekkine and C. Latouche, Organometallics, 2013, 32, 3890; (e) C. Dragonetti, A. Colombo, D. Marinotto, S. Righetto, D. Roberto, A. Valore, M. Escadeillas, V. Guerchais, H. Le Bozec, A. Boucekkine and C. Latouche, J. Organomet. Chem., 2014, 751, 568; (f) C. Dragonetti, A. Colombo, M. Fontani, D. Marinotto, F. Nisic, S. Righetto, D. Roberto, F. Tintori and S. Fantacci, Organometallics, 2016, 35, 1015.
24. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian Inc., Pittsburgh, PA, 2009.
25. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664.
26. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
27. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
28. R. II Dennington, T. Keith, J. Millam, K. Eppinnett, W. L. Hovell and R. Gilliland, GaussView, Version 3.09, Semichem, Inc., Shawnee Mission, KS, 2003.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated electronic properties for complexes 1′ and 2′ at different levels of theory; in situ corona-wire poling dynamics of a PS film containing complex 2. See DOI: 10.1039/c6dt01762b

---