Ferromagnetic coupling mediated by Co⋯π non-covalent contacts in a pentacoordinate Co(II) compound showing field-induced slow relaxation of magnetization

Abstract

[Co^II(dpt)(NCS)₂], where dpt = bis(3-aminopropyl)amine, was identified as a pentacoordinate Co^II compound showing field-induced slow relaxation of magnetization. Furthermore, intermolecular ferromagnetic coupling mediated by Co⋯π non-covalent contacts, where π orbitals originate from the thiocyanato ligand, is reported for the first time.

---

Mononuclear pentacoordinate Co^II complexes represent a relatively wide group of compounds exhibiting slow-relaxation of magnetization of purely molecular origin (so called single molecule magnets, SMMs).¹ Pentacoordinate complexes can adopt geometries of the coordination polyhedron ranging from square pyramidal (SPY) to trigonal bipyramidal (TBY) (Note: both geometries can be described by the Addison parameter τ).² For both geometries of Co^II complexes a large ground state splitting into two Kramers doublets can be observed, but it must be emphasized that much larger values of splitting are expected for compounds approaching the ideal SPY geometry.³ Despite this fact, the largest spin reversal barriers (U_eff) for pentacoordinate Co^II compounds have been observed for compounds with the geometry close to TBY, such as [Co(NS₃^iPr)Cl]BPh₄ (U_eff = 32 cm⁻¹, NS₃^iPr = [2-(isopropylthio)ethyl]amine).⁴ Nevertheless, it is apparent that pentacoordinate Co^II compounds can exhibit very interesting magnetic properties in both geometries of the coordination polyhedron.¹ It is important to note that U_eff is equal to ground state splitting if one considers the Orbach relaxation process only.^1a The experimentally obtained U_eff values often decline from this theoretical prediction due to the presence of other relaxation processes (such as direct or Raman) and furthermore, the relaxation processes can be significantly affected by non-covalent interactions. This has been previously reported for the compound [Co(bpp)Cl₂], (bpp = 4-hept-1-ynyl-2,6-dipyrazol-1-ylpyridine), in which a weak ferromagnetic interaction mediated by π–π stacking of aromatic rings gave rise to a second relaxation process.⁵ Thus it is obvious that knowledge regarding the influence of weak non-covalent contacts on magnetic properties of SMMs is of crucial importance.

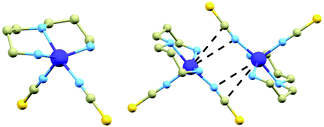
In this article we report on the magnetic properties of compound [Co(dpt)(NCS)₂], (1, dpt = bis(3-aminopropyl)amine), which was previously prepared and structurally characterized by J. Boeckmann et al.⁶ The molecular structure of this compound (Fig. 1, left) consists of the dpt ligand coordinated to the Co^II atom in a tridentate chelate manner and two NCS⁻ ligands bound in a monodentate way. The primary amine groups form two shorter Co–N bonds (2.076(1) and 2.082(1) Å), while the secondary amine group forms a longer Co–N bond: 2.197(2) Å. The isothiocyanato ligands coordinate to the Co^II atom with two distinct Co–N distances (2.004(1) and 2.120(2) Å). According to the Addison parameter, the chromophore geometry is almost directly in between the ideal SPY and TBY geometries (τ = 0.46).‡ The crystal structure of 1 is composed of [Co(dpt)(NCS)₂]₂ dimers which are held together by weak N–H⋯S hydrogen bonding (d(N⋯S) = 3.590(1) Å) between the hydrogen atoms of the secondary amine groups and thiocyanato ligands (the one with the longer Co–N distance, further abbreviated as L_NCS1). Furthermore, it is apparent that within the dimer there is a possible Co⋯N interaction (d(Co⋯N) = 3.541(1) Å) involving L_NCS1 (Fig. 1, right).

Fig. 1 Molecular structure of 1 (left). A perspective view on a centrosymmetric supramolecular dimer {Co(dpt)(NCS)₂}₂ (right) with the highlighted shortest Co⋯C and Co⋯N distances (black dashed lines). The hydrogen atoms were omitted for clarity.

However, since the nitrogen atom from the NCS⁻ ligand is essentially a sigma donor, it is doubtful to expect a direct Co⋯N interaction of such an already coordinated atom. Next, an important structural feature in 1 should be emphasized – the centroid of the N–C bond on L_NCS1 has also a very short distance from the Co^II atom: 3.550 Å. Also the Hirschfield surface analysis using a CrystalExplorer package⁷ indicates that the electron density located between the carbon and nitrogen atoms on L_NCS1 is involved in interaction with the Co^II atom (Fig. S1, ESI†). This indicates the Co⋯π type of interaction in which the NCS⁻ ligands act as a donor of π electrons. Generally, the thiocyanato(e) ligand/anion is known to behave as a very variable acceptor of hydrogen bonding able to accept non-covalent interactions from all directions,⁸ not only from the directions corresponding to the location of the lone pairs of the nitrogen and sulphur atoms. This is due to the delocalization of the electrons over the whole NCS⁻ ligand which can lead to the formation of relatively strong O/N–H⋯π non-covalent interactions.⁹ Such a type of hydrogen bonding is observed also in 1 where the primary amine groups together with NCS⁻ ligands are involved in N–H⋯π non-covalent interactions (Fig. S2 in the ESI†). The M⋯π (M = transition metal atoms) non-covalent interactions are well-known especially for the coordination compounds of heavy transition metal atoms, such as Pt^II, Pd^II, Au^I/III or Ag^I,¹⁰ but to the best of our knowledge, this type of Co⋯π interaction has not been reported in the literature to date.

The static magnetic data were measured as a temperature and field dependence of the magnetic moment. The temperature dependence of the effective magnetic moment (μ_eff) and the field dependence of the magnetization (M_mol) of 1 are shown in Fig. 2. The μ_eff value at 300 K is at 4.56μ_B which is significantly higher than the spin-only value for S = 3/2 and g = 2.0 (3.87μ_B). This implies a non-negligible contribution of the spin–orbit coupling and thus g > 2.0. The μ_eff value is almost constant down to 100 K where a gradual decrease of μ_eff starts. This is a fingerprint of large magnetic anisotropy arising from zero-field splitting (ZFS). At approximately 10 K the turnover in the course of μ_eff occurs and the increase of the μ_eff values from ca. 3.88 to 3.96μ_B is observed (Fig. 2, left). This is typical of weak ferromagnetic interactions between the molecules within the crystal lattice. The field dependent molar magnetization saturates to 2.0 at 5 T which, again, implies a large ZFS. Thus, the data were fitted using the spin Hamiltonian including the ZFS parameters D and E (rhombic) of magnetic anisotropy and the magnetic coupling was included by involving the isotropic exchange constant J:

Fig. 2 Left: the temperature dependence of the effective magnetic moment and molar magnetization measured at B = 0.1 T. Right: the reduced magnetization data measured at T = 2 and 5 K. Empty circles: experimental data. Red full lines: calculated data using eqn (1), with g = 2.34, D = −36.8 cm⁻¹, E/D = 0.22 and χ_TIP = 3.3 × 10⁻⁹ m³ mol⁻¹.

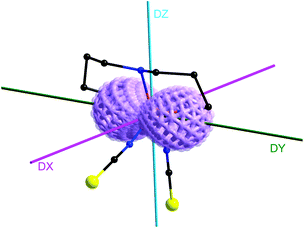
The simultaneous fitting of the temperature and field dependencies resulted in two sets of parameters: g = 2.34, D = 36.2 cm⁻¹, E/D = 0.33, J = +0.27 cm⁻¹ or g = 2.34, D = −36.8 cm⁻¹, E/D = 0.22, J = +0.25, where the fit for the negative D value is somewhat better (Fig. 2 and Fig. S4 in the ESI†), since the fit with the positive D value slightly overestimates the field dependence of molar magnetization. Apparently, the coupling constant J is almost of the same value in both fits. In order to support the results and conclusions theoretically, we performed CASSCF/NEVPT2 calculations using an ORCA 3.0 computational package.¹¹ The relativistic effects were included with a zero order regular approximation (ZORA) and the scalar relativistic contracted version of def2-TZVP(-f) basis functions. The spin Hamiltonian parameters were extracted with the help of effective Hamiltonian theory. These calculations were performed for a monomeric [Co(dpt)(NCS)₂] moiety and the results indicate a positive value of the axial ZFS parameter, D = 34.0 cm⁻¹, and strong rhombicity, E/D = 0.22, with the g-tensor for S = 3/2, g = 2.079, 2.362 and 2.497 – Fig. S5.† Such a large rhombicity even with the positive D parameter leads to an easy axis type of magnetic anisotropy, which is confirmed by the values of the g-tensor parameters (1.829, 3.076, 6.376) of the lowest Kramers doublet calculated for the effective spin S_eff = 1/2, and it is also evident from a 3D plot of magnetization overlaid on the molecular structure of 1 (Fig. 3).

Fig. 3 Molecular structures of 1 overlaid with a 3D plot of molar magnetization derived from the CASSCF/NEVPT2 energy levels with the corresponding x, y, and z axes of the D-tensor. The molar magnetizations were calculated for T = 2 K and B = 1 T. The hydrogen atoms were omitted for clarity.

Furthermore, the calculated D-value is very close to |D| derived from the analyses of the experimental magnetic data, and it must be also stated that in the case of large rhombicity, E/D → 1/3, the sign of the D parameter is indistinguishable by experimental techniques.¹² The large magnetic anisotropy was also confirmed by the additional X-band EPR spectra acquired at T = 110 K, where despite their low quality, two effective g-parameters at 2.85 and 5.90 were identified (Fig. S6†).

The DFT calculations based on the B3LYP functional were utilized to calculate the isotropic exchange parameter J using the broken symmetry approach for the dinuclear molecular motif [{Co(dpt)(NCS)₂}₂].

The resulting J = +0.22 cm⁻¹ calculated by the Yamaguchi formula is in good agreement with the experimental one. There are three magnetic orbitals responsible for the magnetic exchange between the cobalt atoms as shown in Fig. S7.† Evidently, the orbitals with the largest overlap are orthogonal and therefore responsible for the ferromagnetic exchange. These orbitals are involved in the Co⋯π interaction as described above, which is also apparent from the contour plot in Fig. 4, where the spin density in the Co–NCS⋯Co–NCS moiety is shown. Thus, the results of the calculations strongly support the occurrence of the superexchange pathway through the Co⋯π interactions.

Fig. 4 Spin density contour plot in the {Co–C–Co–C} plane of 1, where C belongs to the thiocyanate ligand calculated by B3LYP/ZORA/def2-TZVP(-f).

Next, an ac susceptibility measurement of 1 revealed non-zero imaginary susceptibility at low temperatures when a small static field was applied – Fig. 5. The maxima of imaginary susceptibility were found at low frequencies (Fig. 5, middle), and analysed with the one-component Debye's model

χ(ω) = χ_S + (χ_T − χ_S)/[1 + (iωτ)^1−α] (2)

which resulted in sets of isothermal (χ_T) and adiabatic (χ_S) susceptibilities, relaxation times (τ) and distribution parameters (α) (Table S1†). The τ was found in a 10⁻² s range, which points to the existence of a slower relaxation process than that typical of SMMs. A similar observation and course of the Argand diagram were reported in ferromagnetically non-covalently π⋯π coupled pentacoordinate Co^II single-molecule magnets.⁵

Fig. 5 In-phase χ_real and out-of-phase χ_imag molar susceptibilities for 1 measured at the applied external field B_dc = 0.3 T as a function of temperature (top) and frequency (middle). Lines serve as guides for the eye. Argand (Cole–Cole) plot and temperature dependence of relaxation times (bottom). Full lines are fitted data with eqn (2).

In order to more deeply elucidate the role of the Co⋯π interaction in the magnetism of 1, the zinc diluted sample 1-Zn (Co^II molar fraction of 0.14, for details see the ESI†) was prepared and its dc and ac magnetic data were measured. The static magnetic data of 1-Zn (Fig. S8†) confirmed that dilution with a diamagnetic transition metal is sufficient to eliminate ferromagnetically coupled Co^II complexes in the solid state. This is also reflected in the dynamic magnetic data, where the slower relaxation process was eliminated, but new faster relaxation process emerged and can be attributed to isolated mononuclear Co^II complexes (Fig. 6). A similar analysis of ac susceptibility data of 1-Zn was done using eqn (2) and the corresponding Argand plot is shown in Fig. 6 (bottom) and the parameters are listed in Table S2.† Subsequent analysis of the relaxation times with the Arrhenius equation ended with U_eff = 14 K and τ₀ = 6.17 × 10⁻⁶ s. Thus it is evident that a weak ferromagnetic exchange in 1 is responsible for ca. 100× slowing down of the magnetization relaxation (τ ≈ 10⁻⁴ s in 1-Zn → τ ≈ 10⁻² s in 1). In contrast, two relaxation processes were observed simultaneously for π⋯π coupled Co^II SMMs,⁵ a slower one with τ ≈ 10⁻¹ s and a faster one with τ ≈ 10⁻⁵–10⁻⁶ s. Thus, we can speculate that the different chemical nature of the non-covalent contacts (Co⋯π vs. π⋯π) resulting in different strengths of magnetic exchange couplings (J = 0.3 cm⁻¹vs. J = 1.4 cm⁻¹) is responsible for the variation of the relaxation processes in this unique class of SMMs.

Fig. 6 In-phase χ_real and out-of-phase χ_imag molar susceptibilities for 1-Zn measured at the applied external field B_dc = 0.3 T as a function of temperature (top) and frequency (middle). Lines serve as guides for the eye. Argand (Cole–Cole) plot with full lines fitted data with eqn (2) and temperature dependence of relaxation times fitted with Arrhenius law (bottom).

To conclude, the reported pentacoordinate Co^II complex was identified exhibiting a field-induced slow relaxation of magnetization and it was shown that its magnetic properties are influenced by ferromagnetic exchange coupling mediated by weak non-covalent contacts of the Co⋯π type. The magnetic coupling through such a non-covalent contact was identified for the first time and its deep impact on the magnetization relaxation phenomenon was scrutinized.

We acknowledge the financial support from the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic. We would like to thank Dr. Giorgio Zoppellaro for recording EPR spectra.

Notes and references

1. (a) J. M. Frost, K. L. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491; (b) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147; (c) D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297.
2. A. W. Addison, T. N. Rao, J. Reedijk, J. Vanrijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
3. (a) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392; (b) I. Nemec, H. Liu, R. Herchel, X. Zhang and Z. Trávníček, Synth. Met., 2016, 215, 158–163.
4. F. Shao, B. Cahier, N. Guihery, E. Riviere, R. Guillot, A.-L. Barra, Y. Lan, W. Wernsdorfer, V. E. Campbell and T. Mallah, Chem. Commun., 2015, 51, 16475–16478.
5. C. Rajnák, J. Titiš, O. Fuhr, M. Ruben and R. Boča, Inorg. Chem., 2014, 53, 8200–8202.
6. J. Boeckmann and C. Nather, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, m1025–m1026.
7. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2012.
8. G. Desiraju and T. Steiner, The weak hydrogen bond, International union of crystallography, Oxford Press, 1999.
9. (a) L. Tchertanov and C. Pascard, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 685–690; (b) J. P. M. Lommerse and J. C. Cole, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 316–319.
10. See e.g. (a) M. Panda, S. Das, G. Mostafa, A. Castineiras and S. Goswami, Dalton Trans., 2005, 1249–1255; (b) M. O. BaniKhaled, J. D. Becker, M. Koppang and H. Sun, Cryst. Growth Des., 2016, 16, 1869–1878; (c) E. R. T. Tiekink and J. Zukerman-Schpector, CrystEngComm, 2009, 11, 1176–1186; (d) O. Z. Yeşilel, G. Günay and O. Büyükgüngör, Polyhedron, 2011, 30, 364–371.
11. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78.
12. R. Boča, A Handbook of Magnetochemical Formulae, Elsevier, Amsterdam, 2012.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt01539e

‡ τ = 0 for ideal square pyramidal and 1 for ideal trigonal bipyramidal geometry.

---