Synergy between experimental and computational approaches to homogeneous photoredox catalysis

Abstract

In this Frontiers article, we highlight how state-of-the-art density functional theory calculations can contribute to the field of homogeneous photoredox catalysis. We discuss challenges in the fields and potential solutions to be found at the interface between theory and experiment. The exciting opportunities and insights that can arise through such an interdisciplinary approach are highlighted.

---

Taye B. Demissie

Taye B. Demissie received his Ph.D. from the Institute of Physical Chemistry of the Polish Academy of Sciences (Warsaw, 2014). Currently he is a postdoctoral researcher at the Centre for Theoretical and Computational Chemistry, Department of Chemistry, UiT The Arctic University of Norway, in the research groups of Prof. Kenneth Ruud and Assoc. Prof. Jørn H. Hansen. Taye is interested in computational studies of photocatalysis, reaction mechanisms, relativistic effects, molecular spectroscopy calculations and related chemical studies.

Jørn H. Hansen

Jørn H. Hansen received his Ph.D. from Emory University (Atlanta, GA) in 2010, followed by postdoctoral research at Princeton University, before joining UiT The Arctic University of Norway as an associate professor of chemistry in 2012. His research interests range from method development and applications of photocatalytic late-stage functionalization, chemical library design with bioactive and functional heterocycles, via computational mechanistic analysis to chemical education.

---

Introduction

Homogeneous photoredox catalysis has emerged as a powerful activation mode for chemical synthesis.^1–3 Although the underlying principles have been known for several decades, the current widespread applications in organic synthesis originated from a renaissance of the field in 2008.^4,5 These seminal works demonstrated how visible-light photoredox catalysis could enable elusive and selective transformations of high value for molecular construction. Since then, the field has virtually exploded and photoredox catalysis has proved its utility in complex molecule synthesis.^3,4,6–9 Most impressively, photoredox catalytic methods enable a highly attractive strategy for late-stage functionalization of complex molecules (Fig. 1).¹⁰

Fig. 1 Basic principles of photoredox catalysis in organic synthesis. The photocatalyst harvests photon energy and transforms it into chemical potential that can be exploited for selective complex molecule construction. Radicals can be generated in both the reductive and oxidative quenching cycles and can then undergo the desired functionalizations of complex molecules.

Density functional theory (DFT) is one of the most widely used theoretical methods for studying catalytic processes.^11–14 Its dependence on electron density allows DFT to be computationally efficient and affordable when compared to the most accurate coupled-cluster approaches.^15,16 Even though the latter are accurate in non-relativistic theory, their utility is limited for realistic systems because too many atoms are usually involved. In contrast, DFT can be used in calculations involving realistic molecular models with reasonable computational cost and accuracy.^15,16 There have also been improvements in DFT-techniques in recent years when it comes to solvent effects and relativistic corrections. Therefore, it remains a powerful computational approach for achieving reasonable theoretical results.

In this Frontiers article, we would like to highlight an area in which homogeneous photoredox catalysis can have considerable impact, namely late-stage functionalization, and what is needed to continue expanding utility and scope. We will indicate how density functional computations can be used as powerful tools to enable further discoveries and deepen understanding of this chemistry. Computational and experimental methods can be synergistically employed in prediction and design of reactions and catalysts, as well as reveal elusive mechanistic details.

Catalysts, mechanism and properties

Although widely used in transition metal catalysis,^17–19 DFT has not been employed actively in the field of homogeneous photoredox catalysis. This is surprising, since DFT can offer insights through estimations and modelling of a range of molecular properties and reaction parameters of relevance. Experimental mechanistic studies of visible-light photocatalyzed transformations have become the subject of intense efforts in several research groups.^{3,6,7,9,20–24} Although many experimental tools exist to investigate the mechanistic phenomena of such reactions, computational techniques can offer a range of supporting and complementary insights. DFT is particularly useful for studying mechanistic details unattainable by any other means.

A recent study showed how DFT can be employed to calculate ground and excited state redox potentials for a broad range of transition metal photoredox catalysts with good accuracy.²⁵ Obtaining experimental excited-state redox potentials is not straightforward, and the study demonstrates that DFT can be a powerful tool for property predictions and catalyst design in this area (Fig. 2). Such methods can potentially assist the ongoing efforts in designing new catalysts with considerably minimized costs. Moreover, DFT could suggest suitable substrate–catalyst and ligand–metal combinations when designing potent photocatalysts for given reaction systems. Furthermore, UV/Vis-absorption wavelength ranges for photocatalysts can be estimated using time-dependent (TD)-DFT, which would enable prediction of absorption properties as well. The approach has also been used to accurately calculate the electrochemical potentials of various organic molecules.^26,27 Overall, a range of interesting parameters can be computed using DFT, however, proper validation of such computations by comparison with experimental data is essential.

Fig. 2 Redox properties can be predicted with reasonable accuracy for a range of transition metal photocatalysts. The figure shows the correlation between experimental and predicted redox potentials for a range of common photocatalysts, adapted from ref. 25.

The photocatalytic cycle harvests photon energy to fuel the chemical reaction in question (Fig. 1). It does not directly involve bond-breaking and bond-forming events (as known to date). As such, it is of broad interest to develop multifunctional catalytic systems, capable of catalyzing bond-rearranging events in addition to the light harvesting process. A few examples exist of such catalytic systems and this field is growing rapidly.^28–34 This is also an area in which DFT could be utilized for design, studies of properties and development of predictive tools, particularly considering that preparation of complex catalyst systems could be highly resource and time consuming.

Late-stage functionalization

The purpose of late-stage functionalization can be two-fold. Either one wishes to (1) install a specific functional group in the desired position of a molecular scaffold if the objective is target synthesis or (2) install a variety of groups in different positions if the objective is chemical library diversification.³⁵ In both cases it would be advantageous to have at one's disposal diverse structural elements to introduce in a selective manner. As such, an important area within late-stage photocatalytic C–H functionalization will be to develop a broad range of versatile precursors capable of activation in a given catalytic system. A recent important example is the late-stage methylation of voriconazole (Scheme 1).¹⁰ The introduction of small alkyl groups in selected positions of drug candidates is of high interest in medicinal chemistry. Such groups can potentially fine-tune properties related to bioavailability and stability.¹⁰ New peroxide-based reagents were developed capable of selectively delivering small alkyl groups via photoredox catalysis. This was thoroughly demonstrated in site-selective methylation of several complex drug molecules. The specific catalyst needed was obtained through robotically assisted screening. Clearly, a multitude of interrelated problems must be considered when designing a desired functionalization strategy, including the stability, versatility and redox properties of the radical precursor and catalyst, in addition to understanding and predicting the site selectivity of the ensuing functionalization process.

Scheme 1 Site-specific introduction of given functional groups is a major challenge in synthesis. Photoredox catalysis enables selective late-stage C–H functionalization of complex molecules, here shown by methylation of the complex heterocyclic drug voriconazole.¹⁰

Although several examples now exist,¹ a major advance in photocatalytic late-stage functionalization chemistry was reported by Nicewicz and co-workers in 2015.³⁶ The team achieved selective aryl C–H amination with a range of N–H containing heterocycles using organic photoredox catalysis (Scheme 2). The work is remarkable considering the central role of such heterocycles in both medicinal development and organic materials chemistry. Moreover, since the transformation is achieved at a late-stage on a relatively inert C–H bond, it can enable rapid access to heterocycle-functionalized chemical libraries. This transformation, and future variants of this kind, are truly enabling chemical technologies and can have tremendous impact in many areas that rely on chemical library development in which heterocyclic structures play a major role.

Scheme 2 Nicewicz's site-selective C–H amination in which a biologically interesting pyrazole heterocycle has been introduced through late-stage functionalization.³⁶

Understanding mechanistic details in the type of transformation discussed above and being able to predict it would be a central goal for applications of DFT in homogeneous photoredox catalysis.^25,37–39 We have recently employed DFT calculations to support a proposed photocatalytic mechanism of the C–H functionalization of indoles based on predicted redox potentials and comparison of various possible mechanistic pathways (Scheme 3).²⁵ Another aspect of the mechanism so far not addressed concerns site-selectivity. Although it would be easy to predict for simple indoles by most chemists, it may not be straightforward in more complex molecules with multiple potential reaction sites. If one could reliably predict sites of late-stage C–H functionalization in complex molecules and suitable catalysts using DFT, this would be an invaluable tool for planning molecular construction and designing chemical libraries using this chemistry. A lot of experimental data is available on radical site selectivity and recent notable studies include those of Baran⁴⁰ and others.^41–43 DFT can be employed to correlate the extensive experimental observations in this area with computed parameters and properties to advance and simplify predictions.³⁷ This would be a highly desirable tool for synthetic planning with late-stage photocatalytic C–H functionalization.

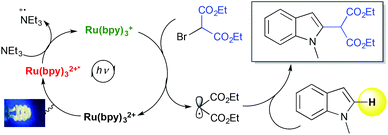Scheme 3 DFT has been employed to support a mechanism of the photocatalyzed C–H functionalization of indoles proposed by Stephenson et al. The mechanism involves photocatalyzed reduction of diethylbromomalonate with subsequent radical addition to the indole.^6,25

Computational challenges and possibilities

A range of challenges in computational methodologies must be addressed in order to enable accurate predictions and modelling of photochemical events. Considering solvent effects in theoretical studies of chemical reactions is one of the major challenges. Modelling the condensed phase of reactions is often crucial to get reasonable agreement with experiment and to successfully predict reaction mechanisms. There are a few theoretical implicit solvent models that are widely used to model condensed-phase reactions, such as the conductor-like screening model (COSMO),⁴⁴ the polarizable continuum model (PCM)⁴⁵ and the solvation model based on density (SMD).⁴⁶ Explicit solvent models that include discrete solvent molecules distributed around the solute, where specific solvent–solute interactions are taken into account, are other possibilities. The latter models are still too costly for DFT due to the number of solvent molecules needed for a good description. In this aspect, there are continuous efforts to refine and enhance models to incorporate better descriptions. Among these, the hybrid quantum mechanics/molecular mechanics (QM/MM) method,⁴⁷ which treats the core part of the realistic molecular model using QM and the outer region involving the explicit solvent molecules using MM, and the polarizable embedding (PE)^48,49 in which the classical region is represented by an electrostatic potential with up to octupole moments and induced point dipole moments are notable. These models maintain a very accurate description of the core molecule or reaction center, whilst influences from the larger solvation sphere are still included (Fig. 3).

Fig. 3 1-Methylindole surrounded by explicit water molecules. In the QM/MM description, the region inside the inner circle is treated using quantum mechanics (QM), whereas the outer region is treated using molecular mechanics (MM) calculations.

The most widely used catalysts in photocatalytic synthetic reactions are complexes of transition metals, although organic molecules with the appropriate redox properties are increasingly popular.³⁶ In the case of transition metal catalysis, modelling or designing effective catalysts for specific reactions using computational methods involves the treatment of relativistic effects. The computational program packages used to treat relativistic effects available to date are very limited. In many theoretical studies such effects are treated through effective core potentials (ECP), which allow implicit treatment of the core electrons of the metal atoms and include relativistic corrections through parameterization. However, if one aims for accuracy in the calculations involving heavy atoms the use of ECPs may not be enough. In such cases, the use of two-component (e.g. the spin–orbit zero-order-regular approximations (SO-ZORA),⁵⁰ the Douglas–Kroll–Hess (DKH)⁵¹ or the exact two-component (X2C)^52–54) and the four-component (Dirac-Coulomb)⁵⁵ relativistic Hamiltonians should be considered. In the latter case, the catalyst size and many other chemical species in the reaction medium limit its use. Tremendous improvements have been made during the last decade in optimizing the program packages based on the two-component relativistic Hamiltonians to be used for such calculations. One good example is the Amsterdam density functional (ADF)⁵⁶ which offers possibilities for ZORA calculations.

Theoretical studies of transition metal photocatalysts using relativistic approaches consider full geometry optimizations and vibrational frequency calculations in both ground and excited states. There are limitations in the latter type of calculations⁵⁷ as there are no implementations for TD-DFT analytical frequency calculations in the most commonly used program packages. However, there is a possibility of calculating the vibrational frequencies numerically. There is a hope that this will be solved very soon.^58,59 Besides the current limitations, DFT will continue to expand and define its central role as an attractive, state-of-the-art method enabling deep understanding and design of new experiments in catalytic chemistry.

Future outlook

As progress continues into an exciting era for homogeneous photoredox catalysis, there is a constant need for deeper understanding of catalyst properties, selectivity and reactivity to refine the chemical methods into enabling technologies. The power of deep understanding lies in its enabling potential as it allows us to predict and streamline chemical synthesis. In particular, a thorough understanding of principles involved in photocatalytic late-stage functionalization would be of paramount importance for molecular design from a synthetic organic chemistry perspective. We can be in a better position to design new chemical reactions and catalysts for the synthetic toolkit through thoughtfully employed quantum chemical calculations. DFT can provide unique and detailed insights into a variety of elementary chemical processes at relatively low cost. The benefits of enlightened, guided and streamlined experimental chemistry are too great to dismiss, and we anticipate that the full potential of photoredox catalysis in organic synthesis will be reached through a synergistic effort of experimental and computational research.

Acknowledgements

This work has received support from the Research Council of Norway [grant number 179568/V30] and the Department of Chemistry at UiT The Arctic University of Norway.

Notes and references

1. R. A. Angnes, Z. Li, C. R. D. Correia and G. B. Hammond, Org. Biomol. Chem., 2015, 13, 9152–9167.
2. M. Fagnoni, D. Dondi, D. Ravelli and A. Albini, Chem. Rev., 2007, 107, 2725–2756.
3. C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363.
4. N. Hoffmann, Chem. Rev., 2008, 108, 1052–1103.
5. M. A. Ischay, M. E. Anzovino, J. Du and T. P. Yoon, J. Am. Chem. Soc., 2008, 130, 12886–12887.
6. L. Furst, B. S. Matsuura, J. M. R. Narayanam, J. W. Tucker and C. R. J. Stephenson, Org. Lett., 2010, 12, 3104–3107.
7. D. A. Nicewicz and D. W. C. MacMillan, Science, 2008, 322, 77–80.
8. M. Reckenthäler and A. G. Griesbeck, Adv. Synth. Catal., 2013, 355, 2727–2744.
9. T. P. Yoon, M. A. Ischay and J. Du, Nat. Chem., 2010, 2, 527–532.
10. D. A. DiRocco, K. Dykstra, S. Krska, P. Vachal, D. V. Conway and M. Tudge, Angew. Chem., Int. Ed., 2014, 53, 4802–4806.
11. W. M. C. Sameera and F. Maseras, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 375–385.
12. N. Koga and K. Morokuma, Chem. Rev., 1991, 91, 823–842.
13. M. Torrent, M. Solà and G. Frenking, Chem. Rev., 2000, 100, 439–494.
14. Computational Modeling of Homogeneous Catalysis, ed. F. Maseras and A. Lledós, Kluwer Academic Publishers, Dordrecht, 2002.
15. D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063.
16. C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Wiley, New York, 2nd edn, 2004.
17. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
18. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
19. A. C. Tsipis, Coord. Chem. Rev., 2014, 272, 1–29.
20. J. D. Cuthbertson and D. W. C. MacMillan, Nature, 2015, 519, 74–77.
21. J. D. Nguyen, E. M. D'Amato, J. M. R. Narayanam and C. R. J. Stephenson, Nat. Chem., 2012, 4, 854–859.
22. D. M. Schultz and T. P. Yoon, Science, 2014, 343, 239176.
23. J. A. Terrett, J. D. Cuthbertson, V. W. Shurtleff and D. W. C. MacMillan, Nature, 2015, 524, 330–334.
24. J. W. Tucker, Y. Zhang, T. F. Jamison and C. R. J. Stephenson, Angew. Chem., Int. Ed., 2012, 51, 4144–4147.
25. T. B. Demissie, K. Ruud and J. H. Hansen, Organometallics, 2015, 34, 4218–4228.
26. A. A. Isse, C. Y. Lin, M. L. Coote and A. Gennaro, J. Phys. Chem. B, 2011, 115, 678–684.
27. H. G. Roth, N. A. Romero and D. A. Nicewicz, Synlett, 2016, 714–723.
28. M. N. Hopkinson, B. Sahoo and F. Glorius, Adv. Synth. Catal., 2014, 356, 2794–2800.
29. B. Sahoo, M. N. Hopkinson and F. Glorius, J. Am. Chem. Soc., 2013, 135, 5505–5508.
30. X.-z. Shu, M. Zhang, Y. He, H. Frei and F. D. Toste, J. Am. Chem. Soc., 2014, 136, 5844–5847.
31. J. Xuan, T.-T. Zeng, Z.-J. Feng, Q.-H. Deng, J.-R. Chen, L.-Q. Lu, W.-J. Xiao and H. Alper, Angew. Chem., Int. Ed., 2015, 54, 1625–1628.
32. W.-J. Yoo, T. Tsukamoto and S. Kobayashi, Angew. Chem., Int. Ed., 2015, 54, 6587–6590.
33. J.-J. Zhong, Q.-Y. Meng, B. Liu, X.-B. Li, X.-W. Gao, T. Lei, C.-J. Wu, Z.-J. Li, C.-H. Tung and L.-Z. Wu, Org. Lett., 2014, 16, 1988–1991.
34. J.-J. Zhong, C.-J. Wu, Q.-Y. Meng, X.-W. Gao, T. Lei, C.-H. Tung and L.-Z. Wu, Adv. Synth. Catal., 2014, 356, 2846–2852.
35. T. Cernak, K. D. Dykstra, S. Tyagarajan, P. Vachal and S. W. Krska, Chem. Soc. Rev., 2016, 45, 546–576.
36. N. A. Romero, K. A. Margrey, N. E. Tay and D. A. Nicewicz, Science, 2015, 349, 1326–1330.
37. T. B. Demissie and J. H. Hansen, Mechanism and site-selectivity in visible-light photocatalysed C -H functionalization: insights from DFT calculations, Submitted, 2016.
38. O. Gutierrez, J. C. Tellis, D. N. Primer, G. A. Molander and M. C. Kozlowski, J. Am. Chem. Soc., 2015, 137, 4896–4899.
39. X. Pan, C. Fang, M. Fantin, N. Malhotra, W. Y. So, L. A. Peteanu, A. A. Isse, A. Gennaro, P. Liu and K. Matyjaszewski, J. Am. Chem. Soc., 2016, 138, 2411–2425.
40. F. O'Hara, D. G. Blackmond and P. S. Baran, J. Am. Chem. Soc., 2013, 135, 12122–12134.
41. T. Iwai and M. Sawamura, ACS Catal., 2015, 5, 5031–5040.
42. M. A. Larsen and J. F. Hartwig, J. Am. Chem. Soc., 2014, 136, 4287–4299.
43. J. Xiu and W. Yi, Catal. Sci. Technol., 2016, 6, 998–1002.
44. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
45. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
46. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
47. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
48. J. M. Olsen, K. Aidas and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 3721–3734.
49. J. M. H. Olsen and J. Kongsted, in Advances in Quantum Chemistry, ed. R. S. John and B. Erkki, Academic Press, 2011, vol. 61, pp. 107–143.
50. E. v. Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
51. T. Nakajima and K. Hirao, Chem. Rev., 2012, 112, 385–402.
52. T. Saue, ChemPhysChem, 2011, 12, 3077–3094.
53. W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102.
54. M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102.
55. T. Saue and T. Helgaker, J. Comput. Chem., 2002, 23, 814–823.
56. ADF2014, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2014, http://www.scm.com/.
57. L. González, D. Escudero and L. Serrano-Andrés, ChemPhysChem, 2012, 13, 28–51.
58. M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
59. C. DanPing, L. Jie, M. HuiLi, Z. Qiao and L. WanZhen, Sci. China: Chem., 2014, 57, 48–57.

---