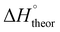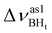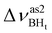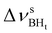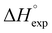Open Access Article
Open Access ArticleTwo pathways of proton transfer reaction to (triphos)Cu(η1-BH4) via a dihydrogen bond [triphos = 1,1,1-tris(diphenylphosphinomethyl)ethane]†
I. E.
Golub
a,
O. A.
Filippov
a,
N. V.
Belkova
a,
L. M.
Epstein
a,
A.
Rossin
b,
M.
Peruzzini
*b and
E. S.
Shubina
*a
aA.N. Nesmeyanov Institute of Organoelement Compounds, Russian Academy of Sciences (INEOS RAS), Vavilova 28, 119991 Moscow, Russia. E-mail: shu@ineos.ac.ru
bIstituto di Chimica dei Composti Organometallici, Consiglio Nazionale delle Ricerche (ICCOM CNR), via Madonna del Piano 10, 50019 Sesto Fiorentino (Florence), Italy. E-mail: maurizio.peruzzini@iccom.it
First published on 10th May 2016
Abstract
The interaction of the η1-tetrahydroborate copper(I) complex (triphos)Cu(η1-BH4) (1) with proton donors [CF3CH2OH (TFE), (CF3)2CHOH (HFIP), (CF3)3COH (PFTB), PhOH, p-NO2C6H4OH (PNP), p-NO2C6H4N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC6H4OH (PNAP), CF3OH] was a subject of a combined IR spectroscopic and theoretical investigation. Spectral (Δν) and thermodynamic (ΔH) parameters of dihydrogen bond (DHB) formation were determined experimentally. The terminal hydride ligand (characterized by the basicity factor Ej(BH) = 0.87 ± 0.01) is found to be a site of proton transfer which begins with nucleophilic substitution of BH4− by the alcohol oxygen atom on the copper center (BH pathway). The activation barrier computed for (CF3)2CHOH in CH2Cl2 – ΔG‡273 K = 20.6 kcal mol−1 – is in good agreement with the experimental value (ΔG‡270 K = 20.0 kcal mol−1). An abnormal dependence of the reaction rate on the proton donor strength found experimentally in dichloromethane is explained computationally on the basis of the variation of the structural and energetic details of this process with the proton donor strength. In the second reaction mechanism found (CuH pathway), DHB complexes with the initial ROH coordination to the bridging hydride lead to B–Hbr bond cleavage with BH3 elimination. “Copper assistance” via the Cu⋯O interaction is not involved. This mechanism can be evoked to explain the occurrence of proton transfer in coordinating solvents.
NC6H4OH (PNAP), CF3OH] was a subject of a combined IR spectroscopic and theoretical investigation. Spectral (Δν) and thermodynamic (ΔH) parameters of dihydrogen bond (DHB) formation were determined experimentally. The terminal hydride ligand (characterized by the basicity factor Ej(BH) = 0.87 ± 0.01) is found to be a site of proton transfer which begins with nucleophilic substitution of BH4− by the alcohol oxygen atom on the copper center (BH pathway). The activation barrier computed for (CF3)2CHOH in CH2Cl2 – ΔG‡273 K = 20.6 kcal mol−1 – is in good agreement with the experimental value (ΔG‡270 K = 20.0 kcal mol−1). An abnormal dependence of the reaction rate on the proton donor strength found experimentally in dichloromethane is explained computationally on the basis of the variation of the structural and energetic details of this process with the proton donor strength. In the second reaction mechanism found (CuH pathway), DHB complexes with the initial ROH coordination to the bridging hydride lead to B–Hbr bond cleavage with BH3 elimination. “Copper assistance” via the Cu⋯O interaction is not involved. This mechanism can be evoked to explain the occurrence of proton transfer in coordinating solvents.
Introduction
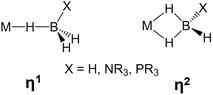
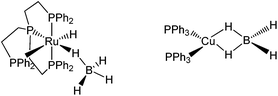
The activation of E–H (E = H, C, Si, B, N) bonds by transition metal complexes is of great interest to many research fields and constitutes a rapidly developing area of main group element chemistry, organometallic chemistry and catalysis. B–H bond activation occurs in a large variety of reactions involving boron hydrides, such as metal catalyzed hydroboration,1,2 and dehydrocoupling of amine- and phosphine-boranes.3–10 When B–H bonds coordinate to transition metal atoms, σ-complexes may be characterized in solution and even isolated in the solid state (Scheme 1).5,11–15 Such complexes are generally considered as intermediates of the B–H bond activation process.10,12,13,15,16In previous studies carried out on (Ph3P)2Cu(η2-BH4)17 and (PP3)Ru(η1-BH4),18 PP3 = κ4-P(CH2CH2PPh2)3 (Scheme 2), we have shown that coordination of the BH4− ligand to the metal decreases the proton accepting ability of the tetrahydroborate ligand (if compared with the non-coordinated BH4− anion).
In the presence of protic reagents, the simultaneous existence of multiple hydride centres (bridged and terminal BH and MH hydride ligands) may lead to the formation of a large variety of dihydrogen-bonded complexes (DHB), but only a few of them are real intermediates of the proton transfer reaction.17,18
As part of an ongoing systematic investigation addressing the reactivity of transition metal tetrahydroborates, we report here a combined theoretical (DFT) and spectroscopic study (IR, NMR) of the interaction of the known copper(I) tetrahydroborate complex (triphos)Cu(η1-BH4) (1) (Scheme 3), [triphos = κ3-H3CC(CH2PPh2)3] with a number of proton donors (OH acids). This study is aimed at unraveling the proton transfer mechanism to monodentate tetrahydroborate (η1-BH4) complexes, accompanied by the release of molecular hydrogen and at assessing the influence of the DHB complex type and the metal atom nature on the H2 evolution reaction.
Results and discussion
Theoretical investigation of DHB complexes
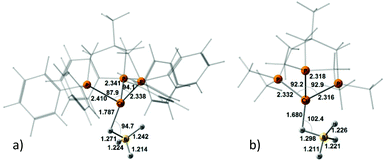
To study and model the electronic structure of the DHB complexes, in silico analysis was carried out using both the “real” complex 1 and the related copper complex bearing the methylated analogue of triphos, i.e. (triphosMe)Cu(η1-BH4) (2) (Fig. 1), where triphosMe is κ3-H3CC(CH2PMe2)3.Replacement of triphos with triphosMe does not have any meaningful effect on the initial hydride geometry, as the optimized structures of complexes 1 and 2 do not differ by more than 0.08 Å for Cu–P bond distances and 0.03 Å for the B–H bond distances (Table S1†). The angles ∠P–Cu–P and ∠H–B–H do not differ more than ±5°. The complexes 1 and 2 form the same set of DHB complexes with all alcohols, featuring similar geometries (Fig. S3–S6†). This validates the use of complex 2 as a model.
Coordination of the tetrahydroborate anion to the metal atom leads to a variety of possible DHB complexes involving BH ligands.17,18 The geometry optimization (DFT/M06) for 2·HOR gives five different types of DHB complexes (Scheme 4): bifurcated DHB complexes with preferential coordination to BHbr (IIbc) (this type was found for all alcohols except for MeOH); complex with coordination to the Cu atom (IIcb); bifurcated DHB complexes on two BHterm (IIa) and BHterm and BHbr (IIab) and trifurcated DHB complexes on BHbr and two BHterm (IIIab).
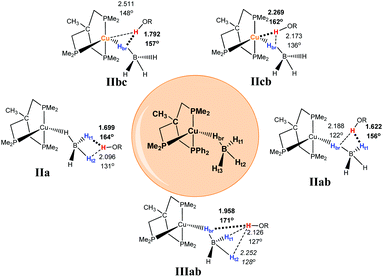 | ||
| Scheme 4 Possible types of DHB complexes between 2 and ROH. The structural parameters reported on the scheme as a representative example are coming from the adducts between 2 and (CF3)2CHOH (HFIP). | ||
Trifurcated DHB complexes such as IIIab were previously described for (PP3)RuH(η1-BH4),18 so we can assume that formation of trifurcated DHB complexes is possible only in the case of a monodentate tetrahydroborate ligand (η1-BH4).
Structural analysis
The intermolecular distances O–H⋯H–B (Table S2†) are in the range 1.622–1.985 Å for primary contacts (shorter) and 2.062–2.382 Å for secondary (longer) interactions, but, irrespective of the DHB complex type, the H⋯H contacts are shorter than the sum of van der Waals radii for the two hydrogen atoms [∑vdW(H–H) = 2.4 Å]. For primary interactions the O–H⋯H(B) angles range from 171 to 152°. A Cu⋯H separation smaller than ∑vdW(Cu–H) = 2.6 Å and the O–H⋯Cu angle falling between 140 and 170° were chosen as a criterion for classifying the Cu⋯HO contact as a hydrogen-bonded (HB) interaction. Regardless of the DHB complex type, the elongation of both the OH bond [0.008–0.020 Å] and the CuH bond [0.007–0.032 Å] was observed (Table S3†). The maximum O–H bond elongation was observed in complexes with coordination of ROH to BHterm (IIa, IIab and IIIab), while the biggest Cu–H bond elongation was found for bifurcated DHB complexes IIa and IIab. Thus, coordination to BHterm induces a general weakening of the Cu+⋯BH4− interaction with concomitant lengthening of the BHterm bond. Elongation of the BHbr bond was observed only in complexes IIbc and IIcb (with the exception of complex IIcb_TFE).Electron-density analysis
Electron density redistribution that occurs upon DHB formation was characterized in terms of the number of electrons shared between the atoms involved in the interaction. Different approaches were used: natural population analysis (NPA),19 Wiberg bond indices (WBIs)20 and Bader's Quantum Theory of “Atoms in Molecules” (QTAIM).21–23Analysis of the molecular electrostatic potential (MEP) of 2 reveals an enhanced electron density on the BH4− ligand with two minima (Vmin) at −52.1 and −54.3 kcal mol−1, located at BHterm ligands (Fig. 2). This fact suggests the preferred proton donor coordination on BHterm ligands.
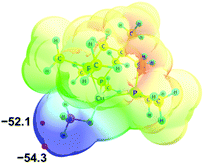 | ||
| Fig. 2 Molecular electrostatic potential map of 2 (at a distance 1.5 vdW) in the RGB scale 0.06 ÷ −0.09 a.u. Electron density minima (Vmin in kcal mol−1) marked as red spheres. | ||
As expected, upon DHB formation the charge on the proton of ROH becomes more positive, whereas the charge on the interacting hydridic hydrogen(s) becomes more negative (Table S8†).
Within the framework of the QTAIM theory, a hydrogen bond is characterized by the presence of a (3, −1) critical point; this allows for its easy identification and differentiation from other types of interactions.24 Despite the existence of several short intermolecular contacts in all DHB complexes 2·HOR, a critical point (3, −1) was found only for the shortest contact with the most linear O–H⋯H(B) and O–H⋯Cu arrangement (Table 1, Fig. S8–S13, Table S11†). The presence of additional interactions causes deviation of the OH⋯X moiety from linearity and mirrors the values of the H⋯H and H⋯Cu bond ellipticity. The maximum ellipticity value was found in complexes HFIP_IIIab (ε = 1.39), TFE_IIcb (ε = 1.03) and MeOH_IIab (ε = 0.97).
| E H⋯X, kcal mol−1 | ∇2ρc, au | ρ c, au | ε | Contact | |
|---|---|---|---|---|---|
| IIbc | −3.2 | 0.047 | 0.019 | 0.25 | BHbr⋯HO |
| IIcb | −3.0 | 0.046 | 0.019 | 0.17 | Cu⋯HO |
| IIa | −5.0 | 0.064 | 0.026 | 0.35 | BHt1⋯HO |
| IIab | −5.6 | 0.067 | 0.028 | 0.20 | BHt1⋯HO |
| IIIab | −3.2 | 0.051 | 0.018 | 1.39 | BHbr⋯HO |
WBI (bond population) is a parameter that characterizes the order of the bond between two atoms.20 The values of WBI for the primary H⋯H contact in the DHB complexes 2·HOR range from 0.008 to 0.058, while for secondary interactions the WBI values are less than 0.007 (Table S9†). In IIbc complexes, for TFE and HFIP, the WBI value of the OH⋯Cu contact is about 0.031, whereas in the IIcb complex WBI values range from 0.039 to 0.061. The WBI values for interacting OH and BH bonds decrease according to its elongation.
The electron density shift that takes place during the DHB formation was analyzed using the “base-to-acid” donation energy estimated from 2nd-order perturbative analysis (E2) of donor–acceptor interactions as implemented in NBO.25,26 Typically, the hydrogen bond entails the transfer of the electron density from the HOMO orbital of the base to an empty 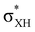 orbital (LUMO) of the acid. In all the complexes analyzed herein, the main σbase →
orbital (LUMO) of the acid. In all the complexes analyzed herein, the main σbase → 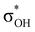 -donation corresponds to the shortest H⋯H contact. Secondary contacts possess weaker but still valuable donation and notably only the energy of primary donation is sensitive to the proton donor strength (Table S10†). For DHB complexes IIa, the identified donations are from two bonding molecular orbitals (MO) of BH ligands to the anti-bonding MO of the OH-group: σBHt1 →
-donation corresponds to the shortest H⋯H contact. Secondary contacts possess weaker but still valuable donation and notably only the energy of primary donation is sensitive to the proton donor strength (Table S10†). For DHB complexes IIa, the identified donations are from two bonding molecular orbitals (MO) of BH ligands to the anti-bonding MO of the OH-group: σBHt1 → 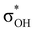 and σBHt2 →
and σBHt2 → 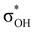 . For complexes IIab, the main donations are from the bonding MO of the BH ligand to the three-centered MO of the Cu–H–B bond: σBHt1 →
. For complexes IIab, the main donations are from the bonding MO of the BH ligand to the three-centered MO of the Cu–H–B bond: σBHt1 → 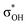 and τCu–H–B →
and τCu–H–B → 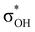 . Complexes IIbc and IIcb are both characterized by τCu–H–B →
. Complexes IIbc and IIcb are both characterized by τCu–H–B → 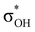 and donation from electron pairs on the Cu d-orbital to the alcohol (ndCu →
and donation from electron pairs on the Cu d-orbital to the alcohol (ndCu → 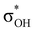 ). For IIbc the τCu–H–B →
). For IIbc the τCu–H–B → 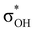 energy is larger, whereas for IIcb the ndCu →
energy is larger, whereas for IIcb the ndCu → 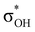 has a dominant impact on the total “base-to-acid” donation energy. Trifurcated complex IIIab with TFE and HFIP is characterized by a strong stabilization energy E2 of the primary τCu–H–B →
has a dominant impact on the total “base-to-acid” donation energy. Trifurcated complex IIIab with TFE and HFIP is characterized by a strong stabilization energy E2 of the primary τCu–H–B → 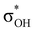 interaction and two weak σBHt1 →
interaction and two weak σBHt1 → 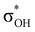 and σBHt2 →
and σBHt2 → 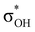 donations. For all the complexes studied, the secondary interactions provide over 15% of the total amount of stabilization energy (E2). Thus, NBO analysis confirms the multifurcated nature of DHB complexes through the existence of several donor–acceptor interactions.
donations. For all the complexes studied, the secondary interactions provide over 15% of the total amount of stabilization energy (E2). Thus, NBO analysis confirms the multifurcated nature of DHB complexes through the existence of several donor–acceptor interactions.
Interaction energies
Table 2 shows the formation energies of the DHB complexes, determined as the energy difference between the adduct and the isolated reactants (Table S4†) as well as the DHB energies derived from the AIM data. When the basis set superposition error (BSSE) was taken into account, a significant lowering of the complexation energy was obtained (up to −20%), especially for TFE and HFIP. The inclusion of nonspecific solvent effects (CH2Cl2 (DCM), THF) significantly lowers the formation energy, with bifurcated DHB complexes IIa and IIab remaining the most stable. The formation enthalpies of the DHB complexes in the gas phase, calculated from the ΔνOH (difference between stretching vibration frequencies of the OH-group of free and bonded alcohol),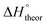 (ΔνOH) = 3.7–6.0 kcal mol−1 (Table 2) are comparable to the experimental enthalpy values determined in solution,
(ΔνOH) = 3.7–6.0 kcal mol−1 (Table 2) are comparable to the experimental enthalpy values determined in solution, 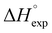 (ΔνOH) = 3.2–5.4 kcal mol−1. The energies EH⋯X, derived from the AIM data, are also larger for complexes IIa and IIab.
(ΔνOH) = 3.2–5.4 kcal mol−1. The energies EH⋯X, derived from the AIM data, are also larger for complexes IIa and IIab.
Frequency analysis
All four stretching vibrations of the BH4− group in (triphos)Cu(η1-BH4) are IR-active. The frequency analysis for the “real” molecule 1 gives three stretching vibrations for BHterm: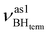 at 2492 cm−1,
at 2492 cm−1, 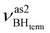 at 2419 cm−1,
at 2419 cm−1, 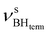 at 2313 cm−1 as well as νBHbr at 2114 cm−1. Frequency analysis for Me-model 2 gives lower energy for the
at 2313 cm−1 as well as νBHbr at 2114 cm−1. Frequency analysis for Me-model 2 gives lower energy for the 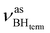 stretching vibrations (2468, 2385 cm−1) as well as for
stretching vibrations (2468, 2385 cm−1) as well as for 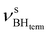 (2362 cm−1) and νBHbr (1919 cm−1) modes. Despite this frequency difference, the relative band shifts (Δν) entailed by DHB formation are of the same order.
(2362 cm−1) and νBHbr (1919 cm−1) modes. Despite this frequency difference, the relative band shifts (Δν) entailed by DHB formation are of the same order.
Formation of intermolecular complexes leads to the low-frequency shift of the stretching vibrations involved in DHB (Tables 3 and S5†). The low-frequency shift of νOH falls in the range from 144 to 357 cm−1, while the low-frequency shift of 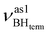 is between −4 and −17 cm−1. The largest ΔνsBH values (from −11 to −42 cm−1) were found for the complexes IIa and IIab. The low-frequency shifts νBHbr ranging from −13 to −39 cm−1 were computed for the complexes of IIbc and IIńb types only.
is between −4 and −17 cm−1. The largest ΔνsBH values (from −11 to −42 cm−1) were found for the complexes IIa and IIab. The low-frequency shifts νBHbr ranging from −13 to −39 cm−1 were computed for the complexes of IIbc and IIńb types only.
Spectral investigation of DHB
In order to assess the proton accepting ability of the BH ligand in (triphos)Cu(η1-BH4) (1), its interaction with fluorinated alcohols [CF3CH2OH (TFE), (CF3)2CHOH (HFIP) and (CF3)3COH (PFTB)] and phenols [PhOH, p-NO2C6H4OH (PNP) and p-NO2C6H4N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC6H4OH (PNAP)] was investigated in low polar media (DCM, THF) by means of IR spectroscopy in a wide temperature range (190–310 K). Upon DHB formation in DCM, the band assigned to OH stretching vibration (νOH) decreases and in the same time a new broad low-frequency band (νbondOH) appears, corresponding to stretching vibrations of the OH group linked by DHB (OHδ+⋯−δHB) (Table 4).
NC6H4OH (PNAP)] was investigated in low polar media (DCM, THF) by means of IR spectroscopy in a wide temperature range (190–310 K). Upon DHB formation in DCM, the band assigned to OH stretching vibration (νOH) decreases and in the same time a new broad low-frequency band (νbondOH) appears, corresponding to stretching vibrations of the OH group linked by DHB (OHδ+⋯−δHB) (Table 4).
| Proton donor |
P
i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ν freeOH | ν bondOH | ΔνOH | (ΔνOH) |
|---|---|---|---|---|---|
| a P i – acidity factors as characteristics of the acid proton-donating ability were taken from ref. 17 and 27. | |||||
| TFE | 0.90 | 3600 | 3419 | −181 | −3.8 |
| PhOH | 1.00 | 3569 | 3363 | −206 | −4.0 |
| HFIP | 1.07 | 3576 | 3372 | −204 | −4.0 |
| PNAP | 1.23 | 3546 | 3267 | −279 | −5.0 |
| PNP | 1.27 | 3546 | 3245 | −301 | −5.3 |
| PFTB | 1.33 | 3525 | 3245 | −290 | −5.2 |
These data allow for the calculation of the basicity factor of the BH ligand Ej(BH) = 0.87 ± 0.01. The Ej(BH) values obtained from the computed frequencies are in good agreement with the experimental outcomes (Ej(BH) = 0.87 ± 0.01 for IIa complexes and 0.84 ± 0.01 for IIab) (Tables S6 and S7, Fig. S7†). This estimation shows that the proton accepting ability of the BH ligand in (triphos)Cu(η1-BH4) is lower than that of BH in (Ph3P)2Cu(η2-BH4) (Ej = 0.91)17 and (PP3)RuH(η1-BH4) (Ej = 0.98).18
The IR spectra of complex 1 alone and in the presence of an excess of TFE (5–10 equiv.) in THF at 190 K (Fig. 3) show a change of the symmetry of BH stretching vibration bands of 1 (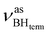 = 2387 cm−1 and new bands
= 2387 cm−1 and new bands 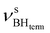 = 2351 cm−1) and the appearance of bonded BH-groups vibration,
= 2351 cm−1) and the appearance of bonded BH-groups vibration, 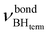 = 2338 cm−1 (Δν = −49 cm−1).
= 2338 cm−1 (Δν = −49 cm−1).
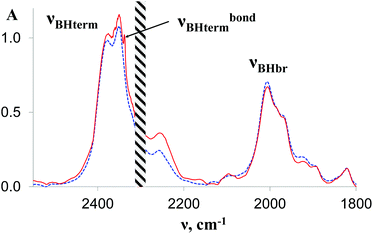 | ||
| Fig. 3 IR spectra in the νBH region of 1 (0.027 M, blue dashed line) and in the presence of TFE (10 equiv.) in THF; l = 0.4 mm, T = 190 K. | ||
Spectral investigation of the proton transfer reaction
Complex 1 reacts with excess proton donors (TFE, HFIP) in DCM even at low temperatures (200–250 K). Above 250 K, H2 evolution is observed even when a stoichiometric amount of proton donors is used. The initial bands νBHterm and νBHbr of both 1 and its DHB complexes decrease in intensity and the spectral picture characteristic of [(RO)BH3]− species formation is observed. At the same time, new low-frequency bands at 2109 and 2069 cm−1 are observed, ascribed to products of further alcoholysis, [(RO)nBH(4−n)]− (n = 2–3) (Fig. 4). The identity of the final metal containing reaction product [(triphos)Cu]+[(RO)4B]− is confirmed by NMR spectroscopy (31P{1H}: 31.29 ppm, 11B{1H}: 2.49 ppm). A similar position of 11B resonance was reported for [(RO)4B]− species characterized by NMR spectroscopy and X-ray diffraction.28,29 The low-field position of phosphorus resonance supports the formation of the [(triphos)Cu]+ cation characterized in ref. 30 in the presence of weakly coordinating counter ions. This behavior is different from that observed for (Ph3P)2Cu(η2-BH4), which gives a dimeric product [{(Ph3P)2Cu}2(μ,η2:η2-BH4)]+[(RO)4B]− upon reaction with alcohols.17 It should be noted that alcoholysis of 1 does proceed in THF in contrast to (Ph3P)2Cu(η2-BH4),17 which reacts with weak acids only in DCM. Protonation of 1 in THF takes more time and requires higher temperatures (>250 K) than in DCM, suggesting a different reaction mechanism (vide infra).The reaction scheme and its kinetic equation (Scheme 5 and eqn (1) and (2)) are similar to that obtained previously for hydride protonation in (Ph3P)2Cu(η2-BH4).17 The observed rate constants (270–315 K) range from (3.5 ± 0.1) × 10−4 to (4.7 ± 0.1) × 10−3 s−1 (Table 5). From the Eyring analysis of the temperature dependence the activation parameters were obtained for the reaction with HFIP: ΔH‡ = 9.0 ± 0.5 kcal mol−1 and ΔS‡ = −44 ± 2 cal (mol K)−1. A high negative entropy value indicates a highly organized transition state as was found previously for (Ph3P)2Cu(η2-BH4).17
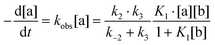 | (1) |
| k3 ≫ k−2; K1[b] ≪ 1 ⇒ kobs ∼ K1k2[b] | (2) |
| Alcohol | Ratio | k obs, (M s)−1 | Temperature |
|---|---|---|---|
| TFE | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(4.9 ± 0.1) × 10−4 | 270 K |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
(6.4 ± 0.1) × 10−4 | ||
| HFIP | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(3.5 ± 0.1) × 10−4 | 270 K |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
(5.4 ± 0.1) × 10−4 | ||
| HFIP | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(4.0 ± 0.1) × 10−4 | 290 K |
| HFIP | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(8.5 ± 0.1) × 10−4 | 300 K |
| HFIP | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(4.7 ± 0.1) × 10−3 | 315 K |
Quantum-chemical investigation of the proton transfer reaction mechanism
The quantum-chemical analysis of the proton transfer mechanism was performed at the DFT/M06 level of theory for the model compound (triphosMe)Cu(η1-BH4) (2). The proton transfer reaction at the BHterm site mediated by the DHB complex of IIa type (BH pathway) can be divided into three elementary steps: (A) nucleophilic substitution of the BH4− ligand by the alcohol oxygen atom on the copper center with concomitant Cu–H bond dissociation and O–H bond activation due to the oxygen coordination to the Lewis acidic site (Cu); (B) facilitated by the O–H bond activation, the proton transfer via the DHB intermediate (triphosMe)Cu(η1-O+(R))H⋯H4B that leads to the formation of the η2-H2 complex (triphosMe)Cu(η1-O(R))⋯(η2-H2)BH3; (C) elimination of the H2 molecule and formation of the reaction product (triphosMe)Cu(η1-O(R)BH3).Remarkably, the course of proton transfer via the BH pathway depends on the proton donor strength. Thus, for a strong proton donor like CF3OH the first transition state (TS1BHA+B) is concerted, combining the first two elementary steps: nucleophilic substitution (A) and proton transfer (B) (Fig. 5 and Fig. S14 and S15†) followed by low-barrier H2 evolution (TS1BHC). The transition state TS1BHA+B is a six-membered cycle [(B)–H–Cu⋯O⋯H⋯H–(B)] (Fig. S16†), similar to what was found for (Ph3P)2Cu(η2-BH4).17
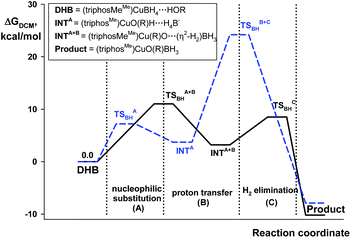 | ||
| Fig. 5 Energy profiles for the protonation of 2 by CF3OH (black solid line) and HFIP (blue dashed line) via the BH pathway. | ||
For weaker proton donors (HFIP, TFE, MeOH) the first transition state (TS1BHA) is simple nucleophilic substitution, while the second transition state is concerted (TS2BHB+C) and includes simultaneous proton transfer (B) and H2 dissociation (C) stages (Fig. 6).
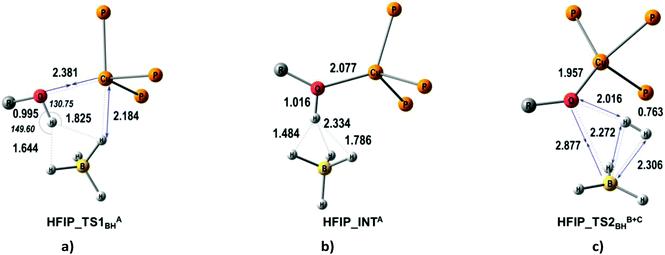 | ||
| Fig. 6 M06-optimized structures of TSs (a, c) and intermediates (b) for the BH pathway of proton transfer from HFIP to (triphosMe)Cu(η1-BH4). | ||
The concerted stage (B+C) for HFIP, TFE and MeOH is the rate determining step, and it resembles simple protonation of BH4− by a medium strength acid like TFE.31 Comparing the activation energies of BH4− protonation by ROH31 (Table 6) and by (triphosMe)Cu(η1-O(R)H) (TSBHB+C, Fig. 5), a 15–25 kcal mol−1 barrier lowering is recorded when the alcohol is coordinated to copper. The calculated value of the activation barrier for TFE is lower than that for HFIP (Table 6), in full agreement with the experimental observations (Table 5). This is obviously connected with the different “acidity enhancement” upon alcohol coordination to copper and formation of the active (triphosMe)Cu(η1-O(R)H) species. We propose that TFE has the best balance between the initial OH acidity and the basicity of the oxygen atom interacting with Cu. The combination of these two factors leads to the maximal lowering of the activation barrier of the rate determining step.
| BH pathway | CuH pathway | ||||
|---|---|---|---|---|---|
TS1BH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
TS2BH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
TSBH4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
TS1CuH | TS2CuH | |
| a TS1BH is TS1BHA+B for CF3OH or TS1BHA for other alcohols. b TS2BH is TS2BHC for CF3OH or TS2BHB+C for other alcohols. c Activation barriers of concerted proton transfer and hydrogen evolution to BH4− as suggested in ref. 31, calculated on the M06/6-311++G(d,p) level. | |||||
| CF3OH | 11.0 | 5.4 | — | 12.5 | 2.1 |
| HFIP | 7.2 | 20.6 | 35.1 | 33.2 | 1.3 |
| TFE | 10.4 | 18.9 | 44.5 | 33.3 | 0.9 |
| MeOH | 11.3 | 35.7 | 53.3 | 36.4 | 0.6 |
A second possible proton transfer mechanism is the protonation of the CuH site (CuH pathway) going through the formation of DHB complexes at the BHbr site (IIbc and IIab). The first stage of the process (TS1CuH) implies the concerted B–Hbr bond dissociation and transfer of the HO proton to the Cu–Hbr yielding the [(triphosMe)Cu(η2-H2)]+ complex weakly bound to the [(RO)BH3]− counterion (Fig. 7). The subsequent H2 elimination gives the (triphosMe)Cu(η1-O(R)BH3) product via a negligible barrier TS2CuH (less than 2.1 kcal mol−1 for all proton donors, Table 6). This CuH pathway is similar for all the proton donors studied, with an activation barrier (TS1CuH) in the 33.2–36.4 kcal mol−1 range for HFIP, TFE and MeOH. In the case of CF3OH this activation energy is much smaller: 12.5 kcal mol−1. The large energetic difference between strong and weak proton donors is somewhat similar to that found for (PP3)Ru(η1-BH4).18
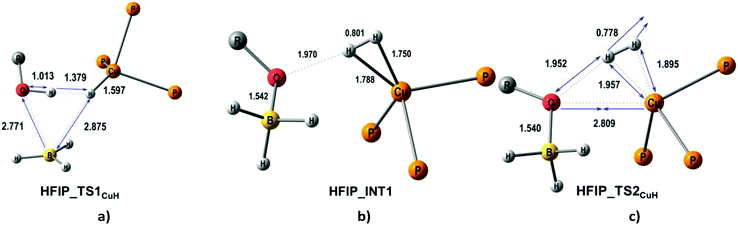 | ||
| Fig. 7 M06-optimized structures of TSs (a, c) and intermediates (b) for the CuH pathway of proton transfer from HFIP to (triphosMe)Cu(η1-BH4). | ||
The reaction with CF3OH features a higher impact of O–H bond dissociation whereas HFIP, TFE and MeOH have a predominant contribution of B–Hbr bond dissociation to the TS geometry (Fig. S16–S25†). For this reason, the activation barriers of proton transfer from CF3OH are comparable for both pathways (TS1CuH, ΔG‡theor = 12.5 kcal mol−1; TS1BHA+B, ΔG‡theor = 11.0 kcal mol−1) (Fig. S14†).
One more peculiarity of the CuH pathway is the absence of direct involvement of the copper atom in the reaction, at odds with the BH pathway. This results in the ability of the title complex to undergo proton transfer also in coordinating solvents like THF (via the CuH pathway), unlike (Ph3P)2Cu(η2-BH4).17 The latter does not react with proton donors in THF due to the Cu⋯O interaction with the solvent which prevents the “copper assisted” lower barrier proton transfer. Thus, the copper assistance along the CuH pathway for (triphos)Cu(η1-BH4) is not needed, and this reaction route becomes feasible also in the presence of coordinating solvents despite its higher activation barriers (TS1CuH, ΔG‡theor = 33.2 kcal mol−1 for HFIP) when compared with the BH pathway (TS2BHB+C, ΔG‡theor = 20.6 kcal mol−1 for HFIP). In DCM, the operating mechanism for all proton donors should be the BH pathway. The calculated activation barrier for HFIP (ΔG‡273 K = 20.6 kcal mol−1) is in good agreement with the experimental data (ΔG‡270 K = 20.0 kcal mol−1 and ΔG‡315 K = 21.8 kcal mol−1).
Experimental
General considerations
All manipulations were performed under a dry argon atmosphere using a standard Schlenk technique. Commercially available argon (99.9%) was additionally purified from traces of oxygen and moisture by sequential passage through the Ni/Cr catalyst column and 4 Å molecular sieves.HPLC grade solvents (Acros Organics) were used for sample preparation after additional purification by standard procedures. Dichloromethane (DCM) and tetrahydrofuran (THF) were dehydrated over CaH2 and Na/benzophenone, respectively. All solvents were freshly distilled under argon prior to use. Deuterated solvent (CD2Cl2) was dried on CaH2 and degassed by three freeze–pump–thaw cycles prior to use. Fluorinated alcohols were obtained from P&M (Moscow, Russia) and Fluka Analytical, were dried over anhydrous K2CO3 and distilled under argon prior to use. Other reagents were from Sigma-Aldrich and were used as received.
Variable-temperature infrared (IR) measurements
IR spectra were recorded on FTIR Nicolet 6700 and FTIR Shimadzu IR Prestige-21 spectrometers using 0.04–0.22 cm CaF2 cells. Low temperature IR studies were carried out in the 190–300 K temperature range using a home-modified cryostat (Carl Zeiss Jena). The accuracy of the experimental temperature was ±0.5 K. The cryostat modification allows for transfer of the reagents (premixed at either low or room temperature) under an inert atmosphere directly into the cells.NMR experiments
NMR spectra were recorded on a Bruker Avance II 400 MHz spectrometer. 1H chemical shifts are reported in parts per million (ppm) relative to tetramethylsilane (TMS) and were calibrated against the residual solvent resonance, while 31P{1H} NMR was referenced to 85% H3PO4 with the downfield shift taken as positive and 11B{1H} NMR was referenced to BF3·Et2O.Preparation of l,l,l-tris(diphenylphosphinomethyl)ethane copper(I) tetrahydroborate (1)
Complex 1 was synthesized according to a previously described procedure.32 Here, full spectroscopic (IR, NMR) characterization is reported, for the sake of literature data completeness. Anal. calcd for C41H43BCuP3: C, 70.04; H, 6.16; B, 1.54; P, 13.22. Found: C, 69.47; H, 6.20; B, 1.50; P, 13.06. IR (Nujol, cm−1) 2321 (s, BHasterm), 2354 (sh, BHasterm); 2233 (sh, BHsterm); 1988, 1967 (m, BHbr). 1H NMR (400 MHz, CD2Cl2, 295 K): 7.57–7.30 ppm (m, 6C6H5,30 H); 2.50 ppm (s, 3CH2, 6 H); 0.87 ppm (s, 1CH3, 3 H), 0.98 ppm (q, BH4−, 4 H); 31P{1H} NMR (400 MHz, CD2Cl2, 295 K): −25.8 ppm (s, br, 3 P); 11B{1H} NMR (400 MHz, CD2Cl2, 295 K): −32.80 ppm (s).Computational details
Full geometry optimizations were carried out with the GAUSSIAN09 (Revision C.01)33 package at the density functional theory (DFT) level using the M06 functional.34 The basis sets used were spin-state-corrected s6-31G(d) for the metal center (Cu),35 6-311++G(d,p) for atoms of the BH4− and alcohol OH-groups,36,37 6-31G(d) for the phosphorus atoms,38 and 6-31G for all the other atoms.Frequency calculations were performed for all the optimized complexes in the gas phase and are reported without the use of scaling factors. The nature of all the stationary points on the potential energy surfaces was confirmed by a vibrational analysis.39 Transition state (TS) structures showed only one negative eigenvalue in their diagonalized force constant matrices, and their associated eigenvectors were confirmed to correspond to the motion along the reaction coordinate under consideration using the Intrinsic Reaction Coordinate (IRC) method.40
The complex formation energy was calculated in the gas phase taking into account the basis sets superposition error (by the Bernardi and Boys method, BSSE),41 and ZPVE correction was determined from the unscaled harmonic frequencies.42,43
Inclusion of nonspecific solvent effects in the calculations was performed by using the SMD method.44 The interaction energy was calculated in THF (ε = 7.4) and CH2Cl2 (ε = 8.9) for the gas phase optimized geometries. Changes in Gibbs energies and enthalpies in the solvent were determined using the corresponding corrections obtained for the gas phase:45
| ΔHSolv. = ΔESolv. + ΔHcorrgas | (3) |
| ΔGSolv. = ΔESolv. + ΔGcorrgas | (4) |
Natural atomic charges and Wiberg bond indices20 were calculated using the natural-bond orbital (NBO) analysis19 implemented in Gaussian09. Topological analysis of the electron-density distribution function ρ(r) was performed using the AIMALL46 program package based on the wave function obtained by the M06 calculations. The energies of H⋯H interactions were calculated using the correlation between the binding energy (EH⋯H) and the value of the density-functional potential energy V(r) in the corresponding critical point (3, −1): EH⋯H = 0.5·V(r).47,48 Hydrogen bond ellipticity, εH⋯H, was defined as ε = (λ1/λ2 − 1), where λ1 and λ2 are the negative eigenvalues of the Hessian of the electron density at the bond critical point ordered such that λ1 < λ2 < 0.21–23
Conclusions
The interaction of alcohols of variable strength with the copper(I) borohydride complex (triphos)Cu(η1-BH4) results in a great variety of DHB complexes which encompass different mechanisms involving M–H and E–H bond (E = B, O) activation steps. The proton transfer at the terminal B–H bond begins with nucleophilic substitution of the BH4− ligand by the alcohol oxygen atom on the copper center that further activates the O–H bond for the subsequent proton transfer via the DHB intermediate (triphosMe)Cu(η1-O+(R))H⋯H4B−. A variation of the structural and energetic details of this process with the proton donor strength is found through computation, and the theoretical results are fully consistent with the experimental observations in dichloromethane showing an abnormal dependence of the reaction rate on the proton donor strength.In contrast, DHB complexes with the initial ROH coordination to the bridging B–H bond lead to B–Hbr bond cleavage with subsequent BH3 elimination and formation of the related copper hydride (triphos)CuH. This pathway does not involve any kind of “copper assistance” via the Cu⋯O interaction, so this mechanism can be evoked to explain the occurrence of proton transfer also in coordinating solvents. As copper badly stabilizes molecular hydrogen complexes (non-classical hydrides), the protonation of copper hydride is disfavored with respect to protonation of boron hydride even for strong proton donors (exemplified by CF3OH). This behavior differs from that shown by (PP3)RuH(η1-BH4),6 where the preferred pathway involves the BHbr bond dissociation followed by the ruthenium hydride protonation. The mechanism of proton transfer to monodentate tetrahydroborate (η1-BH4) complexes depends on the metal ability to stabilize η2-H2 complexes.
Acknowledgements
This work was financially supported by the Russian-Italian bilateral project CNR-RFBR no. 15-53-78027 and RFBR projects no. 16-03-00324 and 16-33-01070.Notes and references
- G. C. Fu, M. Beller and C. Bolm, in Transition Metals for Organic Synthesis, Wiley-VCH Verlag GmbH, 2008, pp. 141–146 Search PubMed.
- G. Povie, M. Marzorati, P. Bigler and P. Renaud, J. Org. Chem., 2013, 78, 1553–1558 CrossRef CAS PubMed.
- A. Staubitz, A. P. M. Robertson, M. E. Sloan and I. Manners, Chem. Rev., 2010, 110, 4023–4078 CrossRef CAS PubMed.
- A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed.
- G. Alcaraz and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2010, 49, 7170–7179 CrossRef CAS PubMed.
- N. E. Stubbs, A. P. M. Robertson, E. M. Leitao and I. Manners, J. Organomet. Chem., 2013, 730, 84–89 CrossRef CAS.
- A. John, K. I. Goldberg and D. M. Heinekey, in Organometallic Pincer Chemistry, ed. G. van Koten and D. Milstein, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 271–287 Search PubMed.
- H. C. Johnson, T. N. Hooper and A. S. Weller, in Synthesis and Application of Organoboron Compounds, ed. E. Fernández and A. Whiting, Springer International Publishing, 2015, vol. 49, ch. 6, pp. 153–220 Search PubMed.
- R. L. Melen, Chem. Soc. Rev., 2015, 45, 775–788 RSC.
- A. Rossin and M. Peruzzini, Chem. Rev., 2016 DOI:10.1021/acs.chemrev.6b00043.
- Y. Kawano, K. Yamaguchi, S.-Y. Miyake, T. Kakizawa and M. Shimoi, Chem. – Eur. J., 2007, 13, 6920–6931 CrossRef CAS PubMed.
- R. N. Perutz and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2007, 46, 2578–2592 CrossRef CAS PubMed.
- C. J. Stevens, R. Dallanegra, A. B. Chaplin, A. S. Weller, S. A. Macgregor, B. Ward, D. McKay, G. Alcaraz and S. Sabo-Etienne, Chem. – Eur. J., 2011, 17, 3011–3020 CrossRef CAS PubMed.
- A. E. Nako, A. J. P. White and M. R. Crimmin, Dalton Trans., 2015, 44, 12530–12534 RSC.
- A. Kumar, I. K. Priest, T. N. Hooper and A. Weller, Dalton Trans., 2016, 45, 6183–6195 RSC.
- Y. Kawano, M. Uruichi, M. Shimoi, S. Taki, T. Kawaguchi, T. Kakizawa and H. Ogino, J. Am. Chem. Soc., 2009, 131, 14946–14957 CrossRef CAS PubMed.
- I. E. Golub, O. A. Filippov, E. I. Gutsul, N. V. Belkova, L. M. Epstein, A. Rossin, M. Peruzzini and E. S. Shubina, Inorg. Chem., 2012, 51, 6486–6497 CrossRef CAS PubMed.
- N. V. Belkova, E. V. Bakhmutova-Albert, E. I. Gutsul, V. I. Bakhmutov, I. E. Golub, O. A. Filippov, L. M. Epstein, M. Peruzzini, A. Rossin, F. Zanobini and E. S. Shubina, Inorg. Chem., 2014, 53, 1080–1090 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohman, C. Morales and F. Weindhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory (International Series of Monographs on Chemistry), Oxford University Press, USA, 1994 Search PubMed.
- P. L. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, London, 2000 Search PubMed.
- C. Matta and R. J. Boyd, Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application, Wiley-VCH, New York, 2007 Search PubMed.
- S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 4331–4341 CrossRef CAS.
- L. M. Epstein and E. S. Shubina, Coord. Chem. Rev., 2002, 231, 165–181 CrossRef CAS.
- N. V. Belkova, E. S. Shubina and L. M. Epstein, Acc. Chem. Res., 2005, 38, 624–631 CrossRef CAS PubMed.
- A. V. Iogansen, Theor. Exp. Chem., 1973, 7, 249–256 CrossRef.
- I. E. Golub, E. S. Gulyaeva, O. A. Filippov, V. P. Dyadchenko, N. V. Belkova, L. M. Epstein, D. E. Arkhipov and E. S. Shubina, J. Phys. Chem. A, 2015, 119, 3853–3868 CrossRef CAS PubMed.
- W. G. Henderson and E. F. Mooney, in Annu. Rep. NMR Spectrosc, ed. E. F. Mooney, Academic Press, 1969, vol. 2, pp. 219–291 Search PubMed.
- C. Bianchini, C. A. Ghilardi, A. Meli, S. Midollini and A. Orlandini, Inorg. Chem., 1985, 24, 932–939 CrossRef CAS.
- O. A. Filippov, A. M. Filin, V. N. Tsupreva, N. V. Belkova, A. Lledós, G. Ujaque, L. M. Epstein and E. S. Shubina, Inorg. Chem., 2006, 45, 3086–3096 CrossRef CAS PubMed.
- P. Dapporto, S. Midollini, A. Orlandini and L. Sacconi, Inorg. Chem., 1976, 15, 2768–2774 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. Swart, M. Güell, J. M. Luis and M. Solà, J. Phys. Chem. A, 2010, 114, 7191–7197 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2262 CrossRef CAS.
- J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- J. Fritsch and G. Zundel, J. Phys. Chem., 1981, 85, 556–561 CrossRef CAS.
- R. Kramer and G. Zundel, J. Chem. Soc., Faraday Trans., 1990, 86, 301–305 RSC.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- C. Tuma, D. A. Boese and N. C. Handy, Phys. Chem. Chem. Phys., 1999, 1, 3939–3947 RSC.
- G. Buemi, in Hydrogen Bonding—New Insights, ed. S. Grabowski, Springer, Netherlands, 2006, pp. 51–107 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. Sumimoto, N. Iwane, T. Takahama and S. Sakaki, J. Am. Chem. Soc., 2004, 126, 10457–10471 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 15.05.18), TK Gristmill Software, Overland Park KS, USA, 2015 Search PubMed.
- E. Espinosa, I. Alkorta, I. Rozas, J. Elguero and E. Molins, Chem. Phys. Lett., 2001, 336, 457–461 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt01104g |
| This journal is © The Royal Society of Chemistry 2016 |