Synthesis, structure and geometrically frustrated magnetism of the layered oxide-stannide compounds Fe(Fe_3−xMn_x)Si₂Sn₇O₁₆

Abstract

Fe₄Si₂Sn₇O₁₆ has a unique crystal structure that contains alternating layers of Fe²⁺ ions octahedrally coordinated by O (oxide layer) and Sn (stannide layer), bridged by SiO₄ tetrahedra. The formula can be written as FeFe₃Si₂Sn₇O₁₆ to emphasise the distinction between the layers. Here, we report the changes in structure and properties as iron is selectively replaced by manganese in the oxide layer. Solid-state synthesis was used to produce polycrystalline samples of Fe(Fe_3−xMn_x)Si₂Sn₇O₁₆ for x ≤ 2.55, the structures of which were characterised using high-resolution synchrotron X-ray and neutron powder diffraction. Single-crystal samples were also grown at x = 0.35, 0.95, 2.60 and characterised by single crystal X-ray diffraction. We show that manganese is doped exclusively into the oxide layer, and that this layer contains exclusively magnetically active high-spin M²⁺ transition metal cations; while the stannide layer only accommodates non-magnetic low-spin Fe²⁺. All samples show clear evidence of geometrically frustrated magnetism, which we associate with the fact that the topology of the high-spin M²⁺ ions in the oxide layer describes a perfect kagomé lattice. Despite this frustration, the x = 0 and x = 2.55 samples undergo long-range antiferromagnetic ordering transitions at 3.0 K and 2.5 K, respectively.

---

1. Introduction

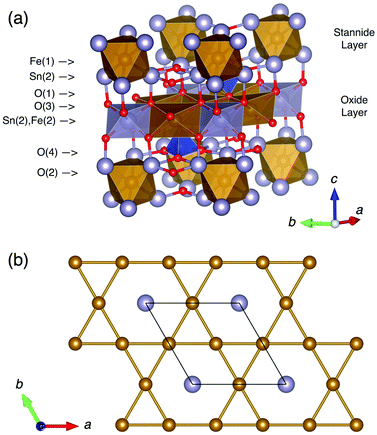
Tin oxide-based semiconductor materials find applications in a wide range of industrial technologies including sensors and battery electrodes.¹ Mixed main group metal/tin oxide semiconductors include a number of materials built on networks of oxygen linked M(SnO)₆ octahedra (M = Fe, Ru, Os).^2–4 This study concerns one such material, Fe₄Si₂Sn₇O₁₆,² which has a trigonal (P3̄m1) crystal structure consisting of alternating layers of edge-sharing FeO₆ and SnO₆ octahedra (hereafter referred to as the oxide layer) and sheets of oxygen-bridged FeSn₆ octahedra (hereafter referred to as the stannide layer), bridged by SiO₄ tetrahedra (Fig. 1a). The formula can be written as FeFe₃Si₂Sn₇O₁₆ to emphasise the fact that ¾ of the Fe sites are located in the oxide layer and ¼ in the stannide layer. Mössbauer spectroscopy was used to show that the stannide layer contains Sn²⁺ and low-spin Fe²⁺, whilst the oxide layer contains Sn⁴⁺ and high-spin Fe²⁺.² Despite the large amount of iron in the structure, this material has shown no long-range magnetic ordering down to 4.2 K.² This can be explained by the geometrically frustrated disposition of the Fe sites in both layers: a kagomé lattice, in the case of the oxide layer (highlighted in Fig. 1b); and a triangular lattice, in the case of the stannide layer (which in any case is expected to be magnetically inactive due to Fe²⁺ being low-spin d⁶, S = 0).

Fig. 1 (a) Structure of FeFe₃Si₂Sn₇O₁₆, showing FeSn₆ (gold), SnO₆ (silver) and FeO₆ (gold) octahedra with SiO₄ tetrahedra (blue) in between. The stannide and oxide layers are labelled as such. (b) The Fe and Sn sites at z = 0.5, viewed along the c axis, highlighting the kagomé lattice of high-spin Fe²⁺ sites in the oxide layer.

Materials containing transition metals arranged on the geometrically frustrated kagomé lattice have been widely studied for the exotic magnetic properties and multiply degenerate ground states that arise when all the nearest-neighbour exchange interactions on triangles (especially in the antiferromagnetic case) cannot be simultaneously satisfied.⁵ Kagomé lattice topologies can be found within in a wide variety of different crystal structure types. High-spin iron-based kagomé lattice compounds, which can be compared to those reported in the present work, include the jarosites AM₃(SO₄)₂(OH)₆ (A = alkali metal ion, M = Fe³⁺, Cr³⁺, V³⁺);^6–9 the open-framework metal phosphates AM₃(HPO₄)₂(H₂PO₄)F₂ (A = NH₄, K, M = Fe²⁺, Co²⁺);¹⁰ the amine-templated Fe(II) sulphates;^11,12 the hexagonal ferrites (BaFe_4−2xSn_2+xCo_xO₇, 0 ≤ x ≤ 2);¹³ and the intermetallic Fe₃Sn₂.¹⁴ The related triangular-lattice ferrites such as CaOFeS¹⁵ have also attracted considerable recent attention for their geometrically frustrated behaviour. Perfect geometric frustration should lead to spin ice or spin liquid states; however, in practice, the degeneracy is usually resolved at low temperatures by symmetry lowering or by the increasing dominance of non-frustrated inter-layer interactions. The examples above show a wide variety of low-temperature behaviours including antiferromagnetic spin-canting,^6–10 ferrimagnetic ordering,^11,12 spin glass freezing¹⁴ and ferromagnetic ordering.¹⁴ The manner in which the frustration is ultimately resolved for a kagomé lattice is clearly very sensitive to the symmetry and electronic structure of the crystal lattice in which is located.

The layered structure of FeFe₃Si₂Sn₇O₁₆ presents an opportunity to design materials with different combinations of magnetic and electronic properties. Here, we report the changes in structure and magnetic properties as iron is replaced by manganese. Solid-state sintering and flux growth methods were used to synthesize polycrystalline and single crystal samples of Fe(Fe_3−xMn_x)Si₂Sn₇O₁₆ with compositions x = 0, 0.81, 1.60, 2.55 and x = 0.35, 0.95, 2.60 respectively. We have studied their structural properties using single crystal X-ray diffraction, neutron powder diffraction and high-resolution synchrotron X-ray powder diffraction, as well as their magnetic properties.

2. Experimental section

Samples in this study were made using a solid-state sintering method. Varying amounts of metal and oxide powders (>99.9% purity) were ground together and placed with Sn metal oxygen buffer into corundum tubes that were then sealed in quartz tubes under air. These vessels were heated to 1173 K over a period of 48 hours followed by controlled cooling to 1023 K over 200 h before quenching in water to room temperature. Single crystals were grown using a tin flux version of the metal oxide sintering method by placing the appropriate amounts of metal and oxide powders together with Sn flux granules (99.98% purity) into corundum tubes before sealing under air in quartz. The samples were heated to 1273 K over 24 hours and held for 24 hours. The samples were cooled to 923 K over a period of 200 hours before quenching in water to room temperature.

Synchrotron X-ray powder diffraction (S-XRD) measurements were performed at the Australian Synchrotron on the Powder Diffraction beam line (λ = 0.77423 Å) from 6–86° 2θ with a step size of 0.00375° 2θ. Data were collected in transmission geometry from samples placed in 0.2 mm quartz capillaries. Variable temperature measurements from 303 to 823 K were taken using a hot-air blower. Refinements of the model against S-XRD data were performed using the Rietveld method as implemented in FullProf.¹⁶

High-resolution neutron powder diffraction (NPD) measurements were performed at room temperature using the instrument Echidna¹⁷ at the OPAL reactor, Lucas Heights, Australia. Data were collected from samples placed in 6 mm diameter vanadium cans using neutrons of wavelength λ = 1.6210 Å over a range of 2.75° to 162° 2θ with a step size of 0.125°.

Single-crystal X-ray diffraction measurements were carried out on a Bruker APEX II diffractometer equipped with a graphite monochromator and Mo K_α X-ray source (λ = 0.71073 Å) from 2–55° 2θ. Refinements were performed using the full-matrix least-squares on F² method as implemented in Shelxl-13¹⁸ with atomic displacement parameters (ADPs) for all atoms refined isotropically.

Temperature-dependent DC magnetic susceptibility measurements were carried out under zero field-cooled conditions using the VSM attachment of a Quantum Design Physical Properties Measurement System (PPMS) under a 0.1 T magnetic field between room temperature and 2 K. Field-dependent data were collected at fixed temperatures on the same instrument.

3. Results and discussion

Polycrystalline samples with four different compositions of Fe(Fe_3−xMn_x)Si₂Sn₇O₁₆ were prepared. Sublimation of manganese under our reaction conditions such as that seen in steel production¹⁹ means that it is not possible to accurately control the stoichiometry of the final product. Rietveld refinements against NPD data (discussed below) showed the compositions of the powder samples to be x = 0, 0.81, 1.60, 2.55. The products contained small amounts of Sn metal and SnO₂ as impurity phases. Single crystals recovered from Sn-flux experiments were of inhomogeneous sizes and found in large clusters on both the surface of the corundum tube and in the Sn flux.

3.1. Synchrotron X-ray powder diffraction

S-XRD data were indexed to a trigonal unit cell very close to that reported for FeFe₃Si₂SnO₁₆,² with a small number of additional peaks corresponding to small (<2.5 wt%) Sn metal impurities. Due to the difference in ionic radii between Fe²⁺ (0.78 Å) and Mn²⁺ (0.83 Å)²⁰ it was expected that there would be an increase in the a/b and c lattice constants with increasing substitution of oxide layer Fe by Mn. Unit cell parameters increase linearly with increasing Mn content in line with Vegard's law (Table 1). A March-Dollase preferred orientation in the [001] direction improved the model fit to the measured data; this reflects the layered structure and plate-like shape of the crystallites. χ² values and reliability factors obtained from Rietveld refinements (Fig. 2) for all samples indicate a good match between calculated and observed data.

Fig. 2 Powder diffraction patterns and refined fits obtained from synchrotron XRD data (λ = 0.77423 Å). Observed data points are blue crosses, the calculated fit is a red line, the difference curve is a black line below the pattern, and the peak positions are indicated by vertical bars. Lower reflection markers refer to small Sn metal impurities. (A) FeFe₃Si₂Sn₇O₁₆ (2.48(3)% Sn impurity). (B) Fe(Fe_2.19Mn_0.81)Si₂Sn₇O₁₆ (2.48(2)% Sn impurity). (C) Fe(Fe_1.40Mn_1.60)Si₂Sn₇O₁₆ (1.49(2)% Sn impurity). (D) Fe(Fe_0.45Mn_2.55)Si₂Sn₇O₁₆ (1.40(1)% Sn impurity).

Table 1 Unit cell parameters from Rietveld-refinement against S-XRD data

Sample	a [Å]	c [Å]	V [Å^3]
FeFe3Si2Sn7O16	6.826027(13)	9.14195(3)	368.8973(15)
Fe(Fe2.19Mn0.81)Si2Sn7O16	6.841036(8)	9.147802(17)	370.7585(9)
Fe(Fe1.40Mn1.60)Si2Sn7O16	6.853938(7)	9.155267(16)	372.4619(9)
Fe(Fe0.45Mn2.55)Si2Sn7O16	6.867000(10)	9.16467(2)	374.2669(11)

---

Variable-temperature S-XRD data were collected at 303, 373, 523, 673 and 823 K. Unit cell parameters were extracted as a function of temperature (Fig. 3). These materials exhibit anisotropic thermal expansion with the a/b unit cell parameters increasing at nearly twice the rate of the c parameter. Comparison between the samples shows negligible changes to the thermal expansion rates with Mn doping.

Fig. 3 Lattice parameters extracted from Rietveld-refinement against variable-temperature S-XRD data. Lines are linear fits following Vegard's law. Error bars are smaller than symbols.

3.2. Neutron powder diffraction

NPD data were used to Rietveld-refine the structural models. In addition to the greatly increased sensitivity of NPD data to the crystallographic parameters of oxygen in the presence of heavy metals such as tin, NPD has the advantage of being able to clearly distinguish between Fe and Mn, which have neutron scattering lengths of 9.45 and −3.73 fm, respectively. This allowed us to reliably refine Fe/Mn site occupancies (which is effectively impossible using X-ray diffraction data) to determine the sample compositions. χ² values and R-values for the refinements of all phases indicate good fits between the observed and calculated crystal structures (Fig. 4). The Fe(1) positions in the stannide layers are fully occupied by Fe for all phases. Fe(2) site occupancies in the oxide layer are listed in Table 2. Note that the larger sample used for NPD data collection contained a higher Sn metal impurity (9.7(6) wt%) but this was easily and adequately accounted for in the Rietveld refinement. Crystallographic information files (CIFs) from the final Rietveld refinements of the three doped phases against NPD data are available as ESI† associated with this article.

Fig. 4 Rietveld-refined fit to neutron powder diffraction data (λ = 1.6210 Å) for Fe(Fe_0.45Mn_2.55)Si₂Sn₇O₁₆. Observed data points are blue circles, the calculated fit is a red line, the difference curve is a black line below the pattern, and the peak positions are indicated by vertical bars. Lower reflection markers refer to a 9.7(6)% Sn metal impurity.

Table 2 Experimental compositions of doped samples, as determined by Rietveld refinement against NPD data

Fe(2) (occ)	Mn(2) (occ)	Experimental composition
0.729 (8)	0.271 (8)	Fe(Fe2.19Mn0.81)Si2Sn7O16
0.467 (9)	0.533 (9)	Fe(Fe1.40Mn1.60)Si2Sn7O16
0.151 (8)	0.849 (8)	Fe(Fe0.45Mn2.55)Si2Sn7O16

---

3.3. Single crystal X-ray diffraction

The structures were refined against single crystal X-ray data using FeFe₃Si₂Sn₇O₁₆ ² as a starting model, with the specific amounts of Mn in the Fe(2) positions determined from the relationship between unit cell volume and phase compositions established from powder diffraction results (Fig. 5). Refined interatomic distances are listed in Table 3. In the stannide layers, no significant changes in bond lengths are observed with increasing Mn content, supporting the conclusion from NPD refinements that Mn does not substitute into these layers. As Fe–Sn bond lengths show no significant changes compared to the iron rich phase (2.4431(2) Å), the stannide layer Fe²⁺ sites can be presumed to remain in a low-spin configuration throughout the series. In the metal oxide layer, increases in M–O (M = Fe, Mn) bond lengths are consistent with high-spin Mn²⁺ (effective ionic radius IR = 0.83 Å)¹⁹ substituting for high-spin Fe²⁺ (IR = 0.78 Å) in the MO₆ octahedra. The M(2)–O(3) bonds (shared with SnO₆ and stannide layer Sn positions) increase proportionally more than the shorter M(2)–O(1) bonds. Sn–O bond lengths in the oxide layer SnO₆ octahedra are equivalent within error for all samples. Two different Si–O bond types allow the SiO₄ tetrahedra to be orientated towards the centre of the three MO₆ octahedra.

Fig. 5 Relationship between cell volume (from S-XRD refinements) and Mn content (from NPD refinements) for powder samples. Black dots are experimental data and the blue line is a linear regression fit. Error bars are smaller than symbols.

Table 3 Bond lengths derived from refinements against single crystal XRD data

	Fe(Fe2.65Mn0.35)Si2Sn7O16	Fe(Fe2.05Mn0.95)Si2Sn7O16	Fe(Fe0.40Mn2.60)Si2Sn7O16
Fe(1)–Sn(2)	2.4453(2)	2.4462(5)	2.4520(4)
M(2)–O(1)	2.1171(16)	2.125(3)	2.138(3)
M(2)–O(3)	2.3091(16)	2.323(2)	2.335(2)
Sn(1)–O(3)	2.098(2)	2.093(4)	2.094(4)
Sn(2)–O(2)	2.0136(7)	2.0104(11)	2.0168(11)
Sn(2)–O(3)	2.055(2)	2.052(4)	2.061(4)
Sn(2)–O(4)	2.2340(15)	2.242(2)	2.248(2)
Si(1)–O(1)	1.615(2)	1.609(4)	1.619(4)
Si(1)–O(4)	1.652(5)	1.644(9)	1.629(10)

---

3.4. Magnetic property measurements

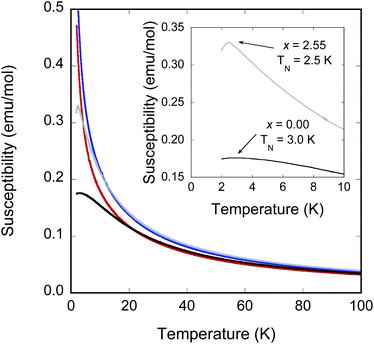
Magnetic susceptibility data (Fig. 6) for all samples were adequately fit by the Curie–Weiss law over the region 25–200 K after applying a standard diamagnetic correction.²¹ The fits yielded negative Weiss constants θ that indicate dominant antiferromagnetic (AFM) nearest-neighbour interactions. Measured effective moments per magnetic cation are summarised in Table 4. As the Fe²⁺ site in the stannide layer has been shown to be low-spin d⁶ (S = 0), only the high-spin M²⁺ sites in the metal oxide layer were considered in these effective moments calculations. All samples were found to have slightly higher effective moments compared to the expected spin-only values (calculated using the transition metal stoichiometry determined by NPD Rietveld refinements, assuming high-spin S = 2 Fe²⁺ and high-spin S = 5/2 Mn²⁺), as is normally observed in high-spin Fe²⁺ compounds due to the strong spin–orbit coupling.

Fig. 6 Temperature-dependent zero-field-cooled magnetic susceptibility of Fe(Fe_3−xMn_x)Si₂Sn₇O₁₆ samples with x = 0 (black), 0.81 (blue), 1.60 (red) and 2.55 (grey). Inset highlights the ordering transitions of the x = 0 and x = 2.55 samples.

Table 4 Summary of magnetic properties

Sample	T N (K)	θ (K)	μ eff (μB/M)	μ spin-only (μB/M)
FeFe3Si2Sn7O16	3.0	−12.8	5.36	4.90
Fe(Fe2.19Mn0.81)Si2Sn7O16	(<2)	−9.4	5.30	5.17
Fe(Fe1.40Mn1.60)Si2Sn7O16	(<2)	−8.9	5.66	5.44
Fe(Fe0.45Mn2.55)Si2Sn7O16	2.5	−14.5	6.04	5.76

---

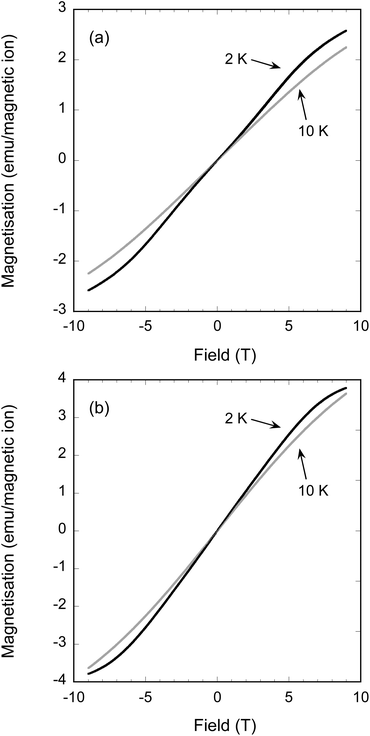
The most Fe-rich sample FeFe₃Si₂Sn₇O₁₆ and the most Mn-rich sample Fe_1.45Mn_2.55Si₂Sn₇O₁₆ undergo clear long-range ordered AFM transitions at Néel temperatures T_N = 3.0 and 2.5 K, respectively (inset to Fig. 6), while the other samples are paramagnetic down to at least 2 K. The failure to observe ordering in the other samples is consistent with the normal thermodynamic expectation that intermediate compositions on a phase diagram will have lower ordering temperatures, in this case presumably below the 2 K minimum to which we could collect data on our instrument. The behaviour of the Weiss constants θ as a function of x in Table 4 shows the same suppression in magnitude at intermediate compositions. For the phases that do order, the discrepancy between −θ and T_N can be ascribed to the geometrically frustrated nature of the kagomé lattice, with frustration indices f = |θ/T_N| of 4.3 for FeFe₃Si₂Sn₇O₁₆ and 5.8 for Fe_1.45Mn_2.55Si₂Sn₇O₁₆. Field-dependent magnetisation measurements at 10 and 2 K (Fig. 7) for these samples show no evidence for ferromagnetic components of the ordered states or metamagnetic transitions.

Fig. 7 Field-dependent magnetisation of (a) FeFe₃Si₂Sn₇O₁₆ and (b) Fe(Fe_0.45Mn_2.55)Si₂Sn₇O₁₆ measured at 10 K (grey lines) and 2 K (black lines), below and above their respective ordering temperature T_N = 3.0 K and 2.5 K, respectively.

4. Conclusions

We have shown for the first time that Mn can be substituted for Fe in FeFe₃Si₂Sn₇O₁₆, preparing six samples across the Fe(Fe_xMn_3−x)Si₂Sn₇O₁₆ solid-solution with x up to 2.55. Changes in unit cell parameters and bond lengths are consistent with substitution of high-spin Mn²⁺ for high-spin Fe²⁺ in the oxide layer. However, no Mn substitution was observed for the low-spin Fe²⁺ site in the stannide layer. This is presumably due to the unusually stable t_2g⁶ configuration of low-spin Fe²⁺ (d⁶) in an octahedral crystal field, which in turn suggests that the low-spin ion has the optimal ionic radius to stabilise this unique crystal structure type in which alternating oxide and stannide layers fit perfectly together, separated by SiO₄ bridging units. Future synthetic work will focus on preparing the nominal end-member of this solid-solution, FeMn₃Si₂Sn₇O₁₆ (x = 3), as well as attempting to incorporate other transition metal cations into this structure type.

The magnetic properties of these phases show characteristic signatures of geometric frustration, as expected given that the magnetically active cations are arranged on a kagomé lattice in the oxide layer. Nevertheless, the most Fe- and Mn-rich samples (x = 0 and 2.55) do undergo long-range ordered AFM transitions at T_N = 3.0 K and 2.5 K, respectively, and it seems likely that the intermediate compositions would do the same at temperatures below 2 K. These ordering temperatures are well below those expected on the basis of the Weiss constants θ, indicating that the systems are frustrated; the frustration indices are f = |θ/T_N| = 4.3 and 5.8 for x = 0 and 2.55, respectively. The observation of long-range magnetic ordering is surprising and worthy of further investigation. There are very few examples of undistorted kagomé lattices in oxide systems, the most obvious analogue to the present case being that of the Fe³⁺ (isoelectronic with Mn²⁺) jarosite-type compound KFe₃(OH)₆(SO₄)₂ which adopts the 120° “q = 0” triangular magnetic structure.^8,9 Future work will include magnetisation measurements below 2 K on samples of intermediate composition to determine if, and at what temperature, they magnetically order; and low-temperature neutron powder diffraction experiments to determine the ordered spin structures and their evolution across the Fe(Fe_xMn_3−x)Si₂Sn₇O₁₆ solid-solution.

Acknowledgements

The authors received financial support from the University of Auckland School of Chemical Sciences (FRDF funding, Project #3704173), the Australian Research Council (Discovery Projects), the Australian Institute for Nuclear Science and Engineering (AINSE) and the Australian Synchrotron. The authors thank Dr Qinfen Gu for assisting with powder diffraction experiments at the Australian Synchrotron.

References

1. H. Wang and A. L. Rogach, Chem. Mater., 2014, 26, 123.
2. T. Söhnel, P. Böttcher, W. Reichelt and F. E. Wagner, Z. Anorg. Allg. Chem., 1998, 624, 708.
3. W. Reichelt, T. Söhnel, O. Rademacher, H. Oppermann, A. Simon, J. Köhler and H. Mattausch, Angew. Chem., Int. Ed. Engl., 1995, 34, 19.
4. T. Söhnel and W. Reichelt, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 9.
5. J. E. Greedan, J. Mater. Chem., 2001, 11, 37.
6. M. G. Townsend, G. Longworth and E. Roudaut, Phys. Rev. B: Condens. Matter, 1986, 33(7), 4919.
7. D. Grohol, D. Papoutsakis and D. G. Nocera, Angew. Chem., Int. Ed., 2001, 40(8), 1519.
8. A. S. Wills, A. Harrison, C. Ritter and R. I. Smith, Phys. Rev. B: Condens. Matter, 2000, 61, 6156.
9. T. Inami, M. Nishiyama, S. Maegawa and Y. Oka, Phys. Rev. B: Condens. Matter, 2000, 61, 12181.
10. G. Wang, M. Valldor, B. Mallicka and A. V. Mudring, J. Mater. Chem. C, 2014, 2, 7417.
11. J. N. Behera and C. N. R. Rao, Inorg. Chem., 2006, 45, 9475.
12. G. Paul, A. Choudhury and C. N. R. Rao, Chem. Commun., 2002, 17, 1904.
13. B. Martinez, F. Sandiumenge, I. Golosovski, S. Gali, A. Labarta and X. Obradors, Phys. Rev. B: Condens. Matter, 1993, 48, 16440.
14. L. A. Fenner, A. A. Dee and A. S. Wills, J. Phys.: Condens. Matter, 2009, 21, 452202.
15. S. F. Jin, Q. Huang, Z. P. Lin, Z. L. Li, X. Z. Wu, T. P. Ying, G. Wang and X. L. Chen, Phys. Rev. B: Condens. Matter, 2015, 91, 094420.
16. J. Rodriguez-Carvajal, Physica B, 1993, 192, 55.
17. K. D. Liss, B. Hunter, M. Hagen, T. Noakes and S. Kennedy, Physica B, 2006, 385–386, 1010.
18. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112.
19. M. Selecka and A. Salak, Powder Metall. Prog., 2009, 9, 97.
20. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1976, 32, 751.
21. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic information files (CIFs) from the final Rietveld refinements of Fe(Fe_2.65Mn_0.35)Si₂Sn₇O₁₆, Fe(Fe_2.05Mn_0.95)Si₂Sn₇O₁₆ and Fe(Fe_0.40Mn_2.60)Si₂Sn₇O₁₆ against neutron powder diffraction data. See DOI: 10.1039/c6dt01074a

---