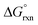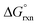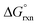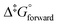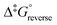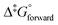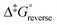Open Access Article
Open Access ArticleA DFT study to unravel the ligand exchange kinetics and thermodynamics of OsVIII oxo/hydroxido/aqua complexes in aqueous matrices†
Daniel M. E.
van Niekerk
,
Wilhelmus J.
Gerber
* and
Klaus R.
Koch
Department of Chemistry and Polymer Science, Stellenbosch University, Private Bag X1, Stellenbosch 7602, Western Cape, South Africa. E-mail: wgerber@sun.ac.za; Fax: +2721 808 3342; Tel: +27 21 808 2699
First published on 15th March 2016
Abstract
The OsVIII oxo/hydroxido complexes that are abundant in mild to relatively concentrated basic aqueous solutions are OsVIIIO4, [OsVIIIO4(OH)]− and two cis-[OsVIIIO4(OH)2]2− species. OsVIII complexes that contain water ligands are thermodynamically unfavoured w.r.t. the abovementioned species. OsVIIIO4 reacts with hydroxide in two, consecutive, elementary coordination sphere expansion steps to form the [OsVIIIO4(OH)]− complex and then the cis-[OsVIIIO4(OH)2]2− species. The Gibbs energy of activation for both reactions, in the forward and reverse direction, are in the range of 6–12 kcal mol−1 and are relatively close to diffusion-controlled. The thermodynamic driving force of the first reaction is the bonding energy of the OsVIII–OH metal-hydroxido ligand, while of the second reaction it is the relatively large hydration energy of the doubly-charged cis-[OsVIIIO4(OH)2]2− product compared to the singly-charged reactants. The DFT-calculated (PBE-D3 functional) 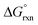 in the simulated aqueous phase (COSMO) is −2.4 kcal mol−1 for the first reaction and −0.6 kcal mol−1 for the second reaction and agree to within 1 kcal mol−1 with reported experimental values, at −2.7 and 0.3 kcal mol−1 respectively. From QTAIM and EDA analyses it is deduced that the OsVIII
in the simulated aqueous phase (COSMO) is −2.4 kcal mol−1 for the first reaction and −0.6 kcal mol−1 for the second reaction and agree to within 1 kcal mol−1 with reported experimental values, at −2.7 and 0.3 kcal mol−1 respectively. From QTAIM and EDA analyses it is deduced that the OsVIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding interactions are ionic (closed-shell) and that OsVIII–OH bonding interactions are polar covalent (dative). In contrast to QTAIM, NCI analysis allowed for the identification of relatively weak intramolecular hydrogen bonding interactions between neighbouring oxo and hydroxido ligands in both [OsVIIIO4(OH)]− and cis-[OsVIIIO4(OH)2]2− complexes.
O bonding interactions are ionic (closed-shell) and that OsVIII–OH bonding interactions are polar covalent (dative). In contrast to QTAIM, NCI analysis allowed for the identification of relatively weak intramolecular hydrogen bonding interactions between neighbouring oxo and hydroxido ligands in both [OsVIIIO4(OH)]− and cis-[OsVIIIO4(OH)2]2− complexes.
Introduction
There is extensive literature dealing with the use of OsVIIIO4 as a homogeneous catalyst for the oxidation of several organic compounds in a variety of acidic and basic aqueous solutions.1–8 However, when OsVIIIO4 is extracted from CCl4 into an aqueous hydroxide solution several possible OsVIII oxo/hydroxido/aqua complexes can form.1–3,9–12 To date, only the OsVIIIO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 and the cis-[OsVIIIO4(OH)2]2− species14–16 have been experimentally characterised, by means of X-ray diffraction spectrometry. This leaves a window for conjecture as to what other OsVIII species might exist in aqueous hydroxide solutions and which of these actually participate in reported catalytic reactions. From observed OsVIIIO4 UV-Vis spectral changes during ‘weak acid/strong base’ titrations, Galbács et al.2 proposed a reaction model given by eqn (1) and (2) with calculated Ka1 and Ka2 acid dissociation equilibrium constants, listed in Table 1.
13 and the cis-[OsVIIIO4(OH)2]2− species14–16 have been experimentally characterised, by means of X-ray diffraction spectrometry. This leaves a window for conjecture as to what other OsVIII species might exist in aqueous hydroxide solutions and which of these actually participate in reported catalytic reactions. From observed OsVIIIO4 UV-Vis spectral changes during ‘weak acid/strong base’ titrations, Galbács et al.2 proposed a reaction model given by eqn (1) and (2) with calculated Ka1 and Ka2 acid dissociation equilibrium constants, listed in Table 1. | (1) |
 | (2) |
| Lit. | K a1 | K 1 | K a2 | K 2 |
|---|---|---|---|---|
| 1 | 1.3 × 10−12 | 130 | — | — |
| 2 | 6.3 × 10−13 | 63 | 4.0 × 10−15 | 0.40 |
| 3 | 8.8 × 10−13 | 88 | 7.5 × 10−15 | 0.75 |
The OsVIII oxo/hydroxido complexes proposed to be in solution by Galbács et al.2 are all six-coordinate complexes, OsVIIIO2(OH)4, [OsVIIIO3(OH)3]− and [OsVIIIO4(OH)2]2−, with the latter presumably the cis stereoisomer. In addition, Griffith12 proposed a six-coordinate species containing a water ligand, [OsVIIIO4(OH)(H2O)]−. Apart from the abovementioned six-coordinate OsVIII species, there is experimental support for a five-coordinate OsVIII complex anion from several X-ray crystal structures of [OsVIIIO4L] derivatives (where L is a nitrogen donor ligand).17 In addition, a density functional theory (DFT) (B3LYP functional) computational study by Mayer et al.1 supports that a five-coordinate [OsVIIIO4(OH)]− complex anion may exist in the gas phase.
If a five-coordinated [OsVIIIO4(OH)]− species is present, then the reactions expected to take place are not that of a relatively weak acid reacting with water, as depicted by eqn (1) and (2), but rather coordination sphere expansion reactions (vide infra),1–3,9–12eqn (3) and (4).
 | (3) |
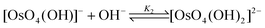 | (4) |
The equilibrium constants of the two differing reaction schemes, (1) & (2) and (3) & (4), are mathematically related to each other as shown, for example, in eqn (5) and (6).
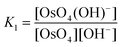 | (5) |
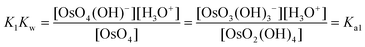 | (6) |
Although the equilibrium constants are mathematically related (eqn (6)), the actual chemical reactions are fundamentally different, giving rise to chemical species which differ significantly from a structural point of view and of course their physicochemical properties. Detailed knowledge of the chemical speciation of OsVIII complexes in basic aqueous solutions is currently unclear and is of significant importance if comproportionation11 and catalytic reactions4–8 involving these species are to be mechanistically understood. This lack of clarity is highlighted by the variety of suggestions of what the catalytically active OsVIII species could be, e.g. it has been reported that the catalytically active OsVIII species for the oxidation of olefins4 and of allyl alcohols5 in mildly acidic aqueous solutions are the OsVIIIO4 and [H2OsVIIIO5] complexes respectively. Moreover, in aqueous alkaline solutions the catalytically active OsVIII species for the oxidation of L-tryptophan,6 chloramphenicol,7 sorbitol and mannitol8 are reported to be the [OsVIIIO4(OH)2]2− and/or OsVIIIO4 complexes. To add even more complexity, Gerber et al.11 reported that the oxidation of methanol and ethanol with OsVIII in a 2.0 M NaOH aqueous solution results in an additional comproportionation reaction between an OsVIII species and a trans-[OsVIO2(OH)4]2− complex to form two postulated [OsVIIO3(OH)3]2− complexes. The formation of the OsVII complex, in addition to several OsVIII species, underlines the uncertainty pertaining to what the actual catalytically active osmium oxidant species in solution are likely to be.4–8
Electronic structure methods, and in particular density functional theory (DFT), are valuable tools used to probe chemical reactions involving transition metals.18 If progress is to be made in understanding the mechanistic aspects of reactions in which OsVIII acts as a catalyst or in terms of the synthesis of novel OsVIII complexes, it is pertinent that the most abundant OsVIII species should be identified under well-defined conditions. In this study we report a systematic DFT theoretical investigation of the following intertwined lines of inquiry. (i) Confirm whether the postulated chemical reactions (1) & (2) or (3) & (4) are responsible for the observed UV-Vis spectral changes reported in the literature;2 (ii) investigate if any OsVIII complexes that contain water ligands exist in appreciable quantities in solution; (iii) elucidate the nature of the metal–ligand bonding interactions as well as possible intramolecular hydrogen bonding interactions between neighbouring ligands; (iv) investigate the anticipated importance of hydration energies pertaining to the thermodynamic stability of OsVIII oxo/hydroxido/aqua complexes; and (v) elucidate the kinetics of interconversion between the OsVIII complexes.
Computational methods
Most calculations employed the Amsterdam Density Functional program (ADF 2012.02) developed by Baerends, Ziegler, and co-workers.19–21 Geometries were fully optimised at the scalar-relativistic zero-order regular approximation (ZORA)22–26 level using (i) the local density approximation (LDA)27 functional (ii) the generalised gradient approximation (GGA) functionals PBE,28 modified PBE (mPBE),29 PBE that include dispersion correction terms {PBE-D,30 PBE-D3,31 PBE-D3(BJ)32 and PBE-dDsC33}, BLYP34–37 and BLYP that include dispersion correction terms (BLYP-D30 and BLYP-D331), PW91,38 and (iii) the meta-GGA functional, M06L.39,40 These calculations were done with an all-electron, quadruple-ζ plus polarisation (QZ4P) function basis set for Os and the even-tempered pVQZ basis set for O and H.41 Optimisation in the gas phase as well as those using an implicit solvent model, namely the conductor-like screening model (COSMO),42–45 with the parameters of water,‡ were done with the abovementioned combinations of functionals and basis sets. All of the obtained structures were characterised as potential energy surface (PES) minima or transition states by analysing the Hessian matrix.46–50In order to identify the stable conformer geometries, conformational analyses were performed by monitoring the electronic energy, in a sequence of linear transit calculations (relaxed scans), as a function of the relevant σ O–Os–O–H torsion angle reaction coordinate constraint (partial convergence optimisation at each step) by systematic rotation. The resulting local minimum/minima obtained from the linear transit calculations were subsequently submitted for complete (full convergence optimisation) geometry optimisation calculations by the implementation of the abovementioned parameters and procedures.
Bonding analysis51,52 presented in this study is further based on the ETS-NOCV approach which is a combination of the extended transition state (ETS) method with the natural orbitals for chemical valence (NOCV) scheme.53 The colour-coded NOCV deformation-density contributions were generated with the ADF graphical user interface (GUI).54
Both the quantum theory of atoms in molecules (QTAIM)55,56 and the non-covalent interactions (NCI)57 analyses were done using the AIMAll software package58 on geometry optimised structures that were obtained with ADF.19–21 Wavefunctional files (.wfx) used for QTAIM analysis were created using Gaussian 09,59 with an effective core potential (ECP) basis set, Lanl2DZ,60–62 for Os and the correlation-consistent, cc-pVQZ,63 basis set for O and H. The conductor-like polarisable continuum model (CPCM)64,65 was used to account for aqueous solvation effects.
Experimental details
Materials
Batches of high purity potassium osmate crystals, K2[OsVIO2(OH)4], were obtained from Anglo Platinum Ltd (South Africa). Sodium hydroxide salts (Sigma-Aldrich) were of analytical reagent grade. Analytical grade orthophosphoric acid (H3PO4), hydrogen peroxide (H2O2) and carbon tetrachloride (CCl4) (Merck Chemicals) were used in the preparation of osmium tetroxide OsVIIIO4 stock solutions. Aqueous OsVIIIO4 solutions were prepared and diluted to the desired concentration using MilliQ water with a resistivity of 18.2 MΩ cm.Preparation of OsVIIIO4 solutions
OsVIIIO4 solutions were prepared by oxidative distillation of the pure K2[OsVIO2(OH)4] salt using 10% (v/v) H2O2 in an aqueous 45% (v/v) H3PO4 matrix. The evolved OsVIIIO4 vapour was trapped in CCl4. The UV-Vis spectrum of the obtained OsVIIIO4 in CCl4 was identical to that reported in literature,11,66,67 ESI Fig. S1,† and confirmed that only OsVIIIO4 was present in CCl4. Aqueous OsVIIIO4 solutions were prepared by extraction of OsVIIIO4 into MilliQ water.Instrumentation
Stopped-flow UV-Vis spectra were recorded using Applied Photophysics’ SF.3 stopped-flow accessory and Chirascan™-plus circular dichroism spectrometer and the obtained data was processed with Applied Photophysics’ Pro-Data software.Results and discussion
Thermodynamic and metal–ligand bonding analyses of OsVIII oxo/hydroxido/aqua complexes
The wavelengths at which the UV-Vis absorption maxima of OsVIIIO4 occur in condensed phases such as water and carbon tetrachloride (CCl4) and in the gas phase are essentially identical, Fig. S1,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 apart from the broader absorption lines in the solvent phases. The agreement of absorption maxima observed in these phases as a function of wavelength provides compelling evidence that OsVIIIO4 does not react with water to form OsVIII complexes with coordinated water ligands. Nonetheless, several hypothetical five- and six-coordinate OsVIII aqua complexes, e.g. [OsVIIIO4(H2O)], cis-[OsVIIIO4(H2O)2] and trans-[OsVIIIO4(H2O)2], were submitted for geometry optimisation and subsequent vibrational frequencies analysis calculations. In the gas phase, the Os–water “ligand” distance increases with each self-consistent field (SCF) iteration until unphysical bond lengths are observed (>7.0 Å). This “trend” was observed using a variety of DFT functionals (LDA, several GGA's and one MetaGGA); with the inclusion or exclusion of relativistic effects (ZORA) and irrespective of basis set quality. Conversely, in the simulated aqueous phase the geometries converge, Fig. 1, where the O4OsVIII⋯OH2 distances are 3.18 Å and 3.25 Å in the [OsVIIIO4]·H2O and [OsVIIIO4]·2H2O structures respectively. However, one negative frequency, corresponding to a bending (rocking) motion of H2O, was obtained for both the [OsVIIIO4]·H2O and [OsVIIIO4]·2H2O structures, despite performing both the geometry optimisation and frequencies analysis calculations at the highest available integration accuracy. From these results it is reasonable to conclude that there are no minima on the multidimensional potential energy surface (PES) w.r.t. OsVIII complexes that have coordinated water ligands. This corroborates the conclusion from the essentially identical UV-Vis spectra of OsVIIIO4 obtained in various solvents and in the gas phase. Moreover, the hypothetical osmium(VIII) acid, OsVIIIO2(OH)4, and [OsVIIIO4(OH)(H2O)]− species proposed by Galbács et al.2 and Griffith12 respectively, Fig. S2 and S3,† are thermodynamically much less favoured w.r.t. the found OsVIII oxo/hydroxido species associated with reaction scheme (3) & (4) (vide infra).§
11 apart from the broader absorption lines in the solvent phases. The agreement of absorption maxima observed in these phases as a function of wavelength provides compelling evidence that OsVIIIO4 does not react with water to form OsVIII complexes with coordinated water ligands. Nonetheless, several hypothetical five- and six-coordinate OsVIII aqua complexes, e.g. [OsVIIIO4(H2O)], cis-[OsVIIIO4(H2O)2] and trans-[OsVIIIO4(H2O)2], were submitted for geometry optimisation and subsequent vibrational frequencies analysis calculations. In the gas phase, the Os–water “ligand” distance increases with each self-consistent field (SCF) iteration until unphysical bond lengths are observed (>7.0 Å). This “trend” was observed using a variety of DFT functionals (LDA, several GGA's and one MetaGGA); with the inclusion or exclusion of relativistic effects (ZORA) and irrespective of basis set quality. Conversely, in the simulated aqueous phase the geometries converge, Fig. 1, where the O4OsVIII⋯OH2 distances are 3.18 Å and 3.25 Å in the [OsVIIIO4]·H2O and [OsVIIIO4]·2H2O structures respectively. However, one negative frequency, corresponding to a bending (rocking) motion of H2O, was obtained for both the [OsVIIIO4]·H2O and [OsVIIIO4]·2H2O structures, despite performing both the geometry optimisation and frequencies analysis calculations at the highest available integration accuracy. From these results it is reasonable to conclude that there are no minima on the multidimensional potential energy surface (PES) w.r.t. OsVIII complexes that have coordinated water ligands. This corroborates the conclusion from the essentially identical UV-Vis spectra of OsVIIIO4 obtained in various solvents and in the gas phase. Moreover, the hypothetical osmium(VIII) acid, OsVIIIO2(OH)4, and [OsVIIIO4(OH)(H2O)]− species proposed by Galbács et al.2 and Griffith12 respectively, Fig. S2 and S3,† are thermodynamically much less favoured w.r.t. the found OsVIII oxo/hydroxido species associated with reaction scheme (3) & (4) (vide infra).§
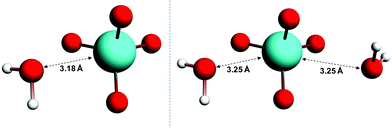 | ||
| Fig. 1 Converged geometries of [OsVIIIO4]·H2O (left) and [OsVIIIO4]·2H2O (right) in the simulated aqueous phase (PBE functional). | ||
In contrast to the abovementioned OsVIII aqua complexes, equilibrium geometries of the OsVIII species depicted by eqn (3) and (4) were found relatively easily in both the gas and simulated aqueous phase. The molecular graphs of OsVIIIO4, [OsVIIIO4(OH)]−, cis1-[OsVIIIO4(OH)2]2−, cis2-[OsVIIIO4(OH)2]2− and trans-[OsVIIIO4(OH)2]2− are shown in Fig. 2.
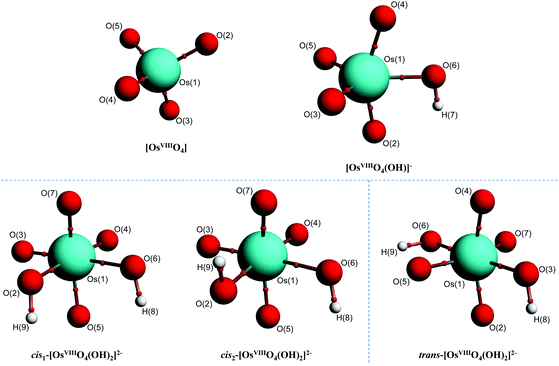 | ||
| Fig. 2 Molecular graphs of stable OsVIII oxo/hydroxido structures in the simulated aqueous phase (PBE functional) pertaining to eqn (3) and (4) with small red spheres representing (3, −1) critical points. | ||
Comparison of experimentally obtained IR vibrational frequencies and Os–O bond lengths of OsVIIIO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,68,69 agrees well with that obtained from the DFT calculations, Tables 2 and 3, supporting the computational methodology.
13,68,69 agrees well with that obtained from the DFT calculations, Tables 2 and 3, supporting the computational methodology.
| Mode | Computed (PBE) | Experimental68 | |
|---|---|---|---|
| i | Gas phase | COSMO (aqueous) | Gas phase (observed) |
| 1 (A1) | 985.1 | 984.2 | 965.2 |
| 2 (E) | 333.3 | 326.2 | 333.1 |
| 3 (T2) | 968.2 | 941.7 | 960.5 |
| 4 (T2) | 329.9 | 313.9 | 329.0 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length of OsVIIIO4 (Å)
O bond length of OsVIIIO4 (Å)
A detailed conformational analysis of the five-coordinate [OsVIIIO4(OH)]− species reveals only one stable equilibrium geometry, shown in Fig. 2, with a coordinated hydroxido ligand positioned pseudo-equatorially. The equilibrium constants listed in Table 1 can be compared to our DFT-calculated values of the coordination sphere expansion reaction, eqn (3), in order to establish its validity. Our calculated 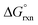 of reaction (3), Table 4, in the gas phase compare poorly with experiment (K1 is overestimated by thirty to forty orders of magnitude) for all the functionals used. This explains why Mayer et al.1 do not report their gas phase, DFT-calculated equilibrium constants to compare with the available experimental data. By contrast, apart from the LDA functional, the agreement between experiment and DFT-calculated
of reaction (3), Table 4, in the gas phase compare poorly with experiment (K1 is overestimated by thirty to forty orders of magnitude) for all the functionals used. This explains why Mayer et al.1 do not report their gas phase, DFT-calculated equilibrium constants to compare with the available experimental data. By contrast, apart from the LDA functional, the agreement between experiment and DFT-calculated 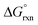 in the simulated aqueous phase is, in our opinion, excellent considering the relatively small average experimental
in the simulated aqueous phase is, in our opinion, excellent considering the relatively small average experimental 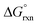 of approximately −2.7 kcal mol−1.1–3
of approximately −2.7 kcal mol−1.1–3
| Functional | Gas phase | COSMO (aqueous) | ||
|---|---|---|---|---|
| K 1 | K 1 | |||
| a Calculated average experimental value taken from ref. 1–3. | ||||
| LDA | −58.9 | 1.6 × 1043 | −15.6 | 2.8 × 1011 |
| PBE | −45.8 | 3.5 × 1033 | −1.6 | 15.0 |
| PBE-D | −46.4 | 9.6 × 1033 | −1.2 | 7.5 |
| PBE-D3 | −46.3 | 8.7 × 1033 | −2.4 | 59.2 |
| PBE-D3(BJ) | −47.0 | 2.9 × 1034 | −3.0 | 1.6 × 102 |
| PBE-dDsC | −46.9 | 2.3 × 1034 | −2.8 | 1.2 × 102 |
| mPBE | −44.0 | 1.7 × 1032 | 0.2 | 0.7 |
| BLYP | −41.5 | 2.5 × 1030 | 4.5 | 5.1 × 10−4 |
| BLYP-D | −41.1 | 1.3 × 1030 | 3.4 | 3.1 × 10−3 |
| BLYP-D3 | −41.2 | 1.5 × 1030 | 3.4 | 3.4 × 10−3 |
| PW91 | −46.9 | 2.5 × 1034 | −2.7 | 95.3 |
| M06L | −45.1 | 1.2 × 1033 | −1.0 | 5.2 |
| Experimental | −2.7 | 93.7 | ||
It may, however, be argued that the calculated values obtained by BLYP, BLYP-D and BLYP-D3 compare poorly with experiment value since they do not have the correct sign of 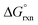 w.r.t. reaction (3). This is not problematic if the following is taken into account and to simplify the discussion we consider a relatively easy to conceptualise reaction (7).
w.r.t. reaction (3). This is not problematic if the following is taken into account and to simplify the discussion we consider a relatively easy to conceptualise reaction (7).
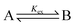 | (7) |
If Kex is equal to one there is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 concentration ratio of A and B, and
1 concentration ratio of A and B, and 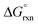 of reaction (7) is equal to zero. If the concentration ratio of A and B is 0.4
of reaction (7) is equal to zero. If the concentration ratio of A and B is 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6, then Kex is equal to 1.5 and
0.6, then Kex is equal to 1.5 and 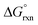 has a slight negative value equalling −1.005 kJ mol−1. By contrast, if the concentration ratio of A and B is 0.6
has a slight negative value equalling −1.005 kJ mol−1. By contrast, if the concentration ratio of A and B is 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 the Kex is equal to 0.66 and
0.4 the Kex is equal to 0.66 and 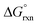 has a slight positive number of 1.005 kJ mol−1. Even though
has a slight positive number of 1.005 kJ mol−1. Even though 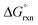 is now positive a significant amount of B is still present at equilibrium. The same argument holds for reaction (3) w.r.t. the positive BLYP, BLYP-D and BLYP-D3
is now positive a significant amount of B is still present at equilibrium. The same argument holds for reaction (3) w.r.t. the positive BLYP, BLYP-D and BLYP-D3 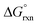 's obtained and therefore the agreement with experiment is actually quite good.
's obtained and therefore the agreement with experiment is actually quite good.
The agreement between DFT and experiment,1–3Table 4, provides strong support for the formation of a five-coordinate [OsVIIIO4(OH)]− species. Moreover, in the gas phase the DFT computational results largely favour the formation of a five-coordinate [OsVIIIO4(OH)]− species ( ) whereas in the simulated aqueous phase, COSMO, the
) whereas in the simulated aqueous phase, COSMO, the 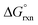 is a relatively small negative or positive number, Table 4. This suggests that hydration energy plays a large role in decreasing the relative thermodynamic stability of the [OsVIIIO4(OH)]− species w.r.t. the reactants. The COSMO calculated hydration energies of OsVIIIO4, OH− and [OsVIIIO4(OH)]− are −10.3, −96.1 and −58.9 kcal mol−1 (PBE functional) respectively. The relatively large hydration energy of the high charge density hydroxide anion compared to the other species decreases the gas phase
is a relatively small negative or positive number, Table 4. This suggests that hydration energy plays a large role in decreasing the relative thermodynamic stability of the [OsVIIIO4(OH)]− species w.r.t. the reactants. The COSMO calculated hydration energies of OsVIIIO4, OH− and [OsVIIIO4(OH)]− are −10.3, −96.1 and −58.9 kcal mol−1 (PBE functional) respectively. The relatively large hydration energy of the high charge density hydroxide anion compared to the other species decreases the gas phase 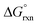 of reaction (3) by approximately 40–47 kcal mol−1, depending on the functional used. Considering the above, the thermodynamic driving force of reaction (3) is the bonding energy of a hydroxido ligand with Os. For further insight pertaining to the bonding energy and types of bonding interactions occurring between the OsVIIIO4 and OH− moieties we performed an energy decomposition analysis (EDA) as proposed by Rauk and Ziegler.51,52 Although Bader criticises energy partition schemes,70 due to fact that unique partitioning cannot be performed, there are many examples, notably by Frenking,71 where chemical insight and estimation of bond dissociation energies can be obtained to describe the physical properties of the chemical system at hand. The bond dissociation energy, −De, between two fragments Q and P (Q = OsVIIIO4, P = OH−) consist of two main energetic contributions (in the gas phase), namely the interaction (ΔEint) and preparation energy (ΔEprep), eqn (8). ΔEprep is also known as the ‘deformation energy’ and is the electronic energy difference between the prepared fragments, i.e. as Q and P occur in compound QP, and the fragments Q and P present in their equilibrium geometry. However, for EDA done in a simulated aqueous phase a third term, ΔEsolv, must also be included to account for the total change in solvation energy between compound QP and fragments Q and P as they occur in their equilibrium geometry, eqn (8). The ADF software19–21 does not automatically calculate ΔEsolv; it only prints out Esolv of QP for an EDA calculation. ΔEsolv is therefore obtained manually by subtracting the solvation energies of Q and P (equilibrium geometries) from that of QP. It should be noted that Cramer et al.72 also include solvation energy in their EDA calculations but do not specify how ΔEsolv is calculated, i.e. whether the reported values are the energy difference between compound QP and the equilibrium or the ‘deformed’ geometries of fragments Q and P.
of reaction (3) by approximately 40–47 kcal mol−1, depending on the functional used. Considering the above, the thermodynamic driving force of reaction (3) is the bonding energy of a hydroxido ligand with Os. For further insight pertaining to the bonding energy and types of bonding interactions occurring between the OsVIIIO4 and OH− moieties we performed an energy decomposition analysis (EDA) as proposed by Rauk and Ziegler.51,52 Although Bader criticises energy partition schemes,70 due to fact that unique partitioning cannot be performed, there are many examples, notably by Frenking,71 where chemical insight and estimation of bond dissociation energies can be obtained to describe the physical properties of the chemical system at hand. The bond dissociation energy, −De, between two fragments Q and P (Q = OsVIIIO4, P = OH−) consist of two main energetic contributions (in the gas phase), namely the interaction (ΔEint) and preparation energy (ΔEprep), eqn (8). ΔEprep is also known as the ‘deformation energy’ and is the electronic energy difference between the prepared fragments, i.e. as Q and P occur in compound QP, and the fragments Q and P present in their equilibrium geometry. However, for EDA done in a simulated aqueous phase a third term, ΔEsolv, must also be included to account for the total change in solvation energy between compound QP and fragments Q and P as they occur in their equilibrium geometry, eqn (8). The ADF software19–21 does not automatically calculate ΔEsolv; it only prints out Esolv of QP for an EDA calculation. ΔEsolv is therefore obtained manually by subtracting the solvation energies of Q and P (equilibrium geometries) from that of QP. It should be noted that Cramer et al.72 also include solvation energy in their EDA calculations but do not specify how ΔEsolv is calculated, i.e. whether the reported values are the energy difference between compound QP and the equilibrium or the ‘deformed’ geometries of fragments Q and P.
| −De = ΔEint + ΔEprep(+ΔEsolv) | (8) |
The ΔEint term between two fragments is defined as the sum of several main energetic contributions, eqn (9).
| ΔEint = ΔEPauli + ΔEelstat + ΔEorb + ΔEdisp | (9) |
The first two terms of ΔEint, eqn (9), are computed by using the unperturbed fragments and account for the Pauli (steric) repulsion (ΔEPauli) and electrostatic interaction (ΔEelstat), whilst the third term (ΔEorb) represents the energy ‘released’ when the fragment electron densities are allowed to relax to their equilibrium electron densities. For covalent bonds the absolute value of ΔEorb is larger than ΔEelstat, while the opposite holds true for ionic bonds. Dispersion energy (ΔEdisp) makes up the fourth contribution to the total ΔEint. It should be noted that the energy decomposition analysis is dependent on the nature and structure of the chosen fragments, especially for charged species, which makes the determination of the relative ionicity/covalency of the OsVIII–OH bond challenging.72 This is discussed further when the topological analysis of the electron density using the QTAIM method is presented (vide infra). The EDA results obtained using the above approach for the [OsVIIIO4(OH)]− anion were done in both gas and simulated aqueous phases, Table 5.
| Functional | Phase | ΔEint | ΔEPauli | ΔEelstat | ΔEorb | ΔEdisp | ΔEsolv | ΔEprep | −De |
|---|---|---|---|---|---|---|---|---|---|
| PBE | Gas | −105.0 | 270.5 | −241.6 | −133.9 | — | — | 48.7 | −56.2 |
| Aqueous | −103.8 | 270.7 | −242.3 | −132.1 | — | 47.4 | 44.6 | −11.8 | |
| PBE-D | Gas | −105.6 | 267.6 | −239.6 | −133.0 | −0.7 | — | 48.9 | −56.7 |
| Aqueous | −104.5 | 268.2 | −240.6 | −131.4 | −0.7 | 47.4 | 44.7 | −12.4 | |
| PBE-D3 | Gas | −105.6 | 269.8 | −241.1 | −133.6 | −0.6 | — | 48.9 | −56.7 |
| Aqueous | −104.4 | 270.1 | −242.0 | −132.0 | −0.6 | 47.4 | 44.6 | −12.4 | |
| PBE-D3(BJ) | Gas | −106.2 | 272.1 | −242.6 | −134.4 | −1.2 | — | 48.8 | −57.4 |
| Aqueous | −105.0 | 271.9 | −243.1 | −132.6 | −1.2 | 47.4 | 44.6 | −13.0 | |
| PBE-dDsC | Gas | −105.9 | 273.2 | −243.4 | −134.7 | −1.0 | — | 48.6 | −57.3 |
| Aqueous | −104.5 | 272.6 | −243.4 | −132.6 | −1.0 | 47.4 | 44.2 | −12.8 |
The calculated values of ΔEPauli, ΔEelstat and ΔEorb differ by less than approximately 2.1 kcal mol−1 in both the gas and simulated aqueous phase while ΔEdisp, as obtained by four different dispersion correction methods, contributes only minimally to ΔEint. In both the gas and simulated aqueous phase approximately two-thirds of the stabilisation of the OsVIII–OH metal-hydroxido bond is due to electrostatic contributions which reflect its ionic character. The ratio of ΔEelstat![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔEorb remains approximately 1.8 regardless of whether the analysis is done in the gas or simulated aqueous phase. It is the ΔEsolv contribution, of approximately 47.4 kcal mol−1, which dramatically changes −De in the simulated aqueous phase, from approximately −57 to −12 kcal mol−1. However, since the calculated −De values are negative in both phases, solvation (hydration) energy is not an essential component to promote the formation of the metal-hydroxido bond in [OsVIIIO4(OH)]−. Taking these factors into account leads to the same conclusion mentioned previously, that reaction (3) is thermodynamically driven by the bonding energy of the OsVIII–OH metal-hydroxido ligand.
ΔEorb remains approximately 1.8 regardless of whether the analysis is done in the gas or simulated aqueous phase. It is the ΔEsolv contribution, of approximately 47.4 kcal mol−1, which dramatically changes −De in the simulated aqueous phase, from approximately −57 to −12 kcal mol−1. However, since the calculated −De values are negative in both phases, solvation (hydration) energy is not an essential component to promote the formation of the metal-hydroxido bond in [OsVIIIO4(OH)]−. Taking these factors into account leads to the same conclusion mentioned previously, that reaction (3) is thermodynamically driven by the bonding energy of the OsVIII–OH metal-hydroxido ligand.
The covalent aspects of the OsVIII–OH metal-hydroxido bond was further analysed by using ETS-NOCV which is a combined charge and energy decomposition scheme for bond analysis.53 The ΔEorb stabilising contribution, Table 5, representing the interactions between the occupied molecular orbitals of one fragment with the unoccupied molecular orbitals of the other fragment, is linked to the electronic bonding effect from the formation of a chemical bond. ETS-NOCV yields the contributions from the different natural orbitals (constructed from the fragment orbitals) to the total orbitalic contribution.
The sum of the calculated energies of the two major deformation-density channels, Δρ1 and Δρ2, to the covalent contribution of the OsVIII–OH bond energy make up approximately 85% of the total orbitalic energy stabilisation, Table 6.
| Functional | Δρ1 | Δρ2 | ΔEorb |
|---|---|---|---|
| PBE | −91.5 (69.3%) | −21.2 (16.0%) | −132.1 |
| PBE-D | −91.0 (69.3%) | −21.1 (16.1%) | −131.4 |
| PBE-D3 | −91.4 (69.3%) | −21.2 (16.0%) | −132.0 |
| PBE-D3(BJ) | −91.8 (69.3%) | −21.3 (16.0%) | −132.6 |
| PBE-dDsC | −91.8 (69.2%) | −21.3 (16.0%) | −132.6 |
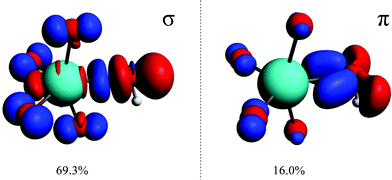
The two highest deformation-density channels, Δρ1 and Δρ2, are shown in Fig. 3. They are approximately −91.5 (69%) and −21.2 (16%) kcal mol−1 and correspond to σ- and π-donations respectively, from the occupied 2p orbitals of the hydroxido oxygen to the empty 5d orbitals of the osmium metal-centre.
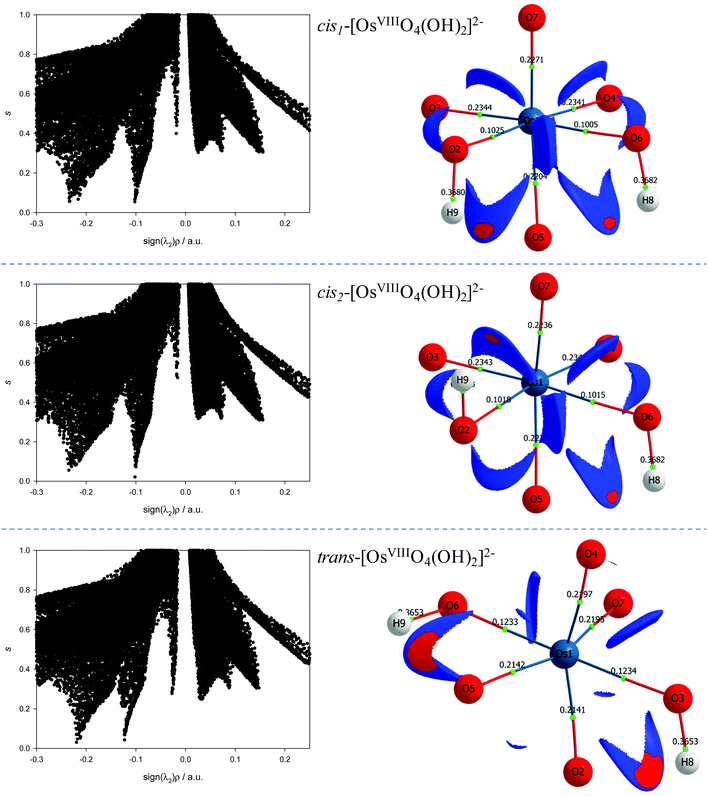
To investigate reaction (4) in more detail, conformational analyses using relaxed potential energy scans were performed in order to identify equilibrium structures of the six-coordinate OsVIII species. Three stable equilibrium geometries were found, two cis and one trans structure, as shown in Fig. 2. A diagram that briefly summarises the three possible coordination sphere expansion reactions and the stereoisomer interchange of the three six-coordinate OsVIII oxo/hydroxido species are shown in Scheme 1.
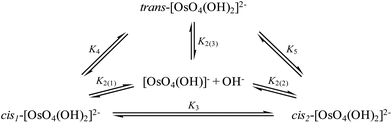 | ||
| Scheme 1 Coordination sphere expansion reactions of [OsVIIIO4(OH)]− (K2(1), K2(2) and K2(3)) and stereoisomer interchange reactions of [OsVIIIO4(OH)2]2− species (K3, K4 and K5). | ||
The DFT-calculated equilibrium constants of the isomerisation reactions (10) and (11) are K3 = 1.03 and K4 = 1.0 × 106 respectively, i.e. the two cis conformations are approximately 10 kcal mol−1 thermodynamically more stable than the trans-species. The ratio of cis- to trans-[OsVIIIO4(OH)2]2− species is approximately a million to one and therefore the trans species is not taken into account when the second coordination sphere expansion of the five-coordinate [OsVIIIO4(OH)]− to the six-coordinate [OsVIIIO4(OH)2]2− species is discussed below.
 | (10) |
 | (11) |
Experimentally, the two cis-[OsVIIIO4(OH)2]2− species in solution cannot be distinguished from one another. Therefore, in order to calculate K2 by means of DFT, eqn (4) has to be re-written as shown in eqn (12) and (13). Addition of the equilibrium expressions associated with eqn (12) and (13) results in eqn (14) which relates the equilibrium constant of eqn (4) with those in eqn (12) and (13). The associated standard reaction Gibbs free energy of the second coordination sphere expansion of the five-coordinate [OsVIIIO4(OH)]− to the six-coordinate [OsVIIIO4(OH)2]2− species is given by eqn (15).
 | (12) |
 | (13) |
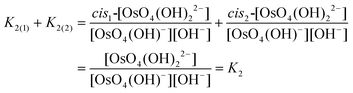 | (14) |
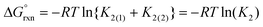 | (15) |
In the gas phase the calculated 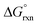 values of reaction (4) (12, 13) are large and positive, Table 7, in contrast to the large negative values of reaction (3). Conversely, the agreement between experimental and DFT-calculated standard reaction Gibbs free energies in the simulated aqueous phase are excellent, excluding the LDA functional. The hydration energies (PBE functional) of the doubly-charged cis1- and cis2-[OsVIIIO4(OH)2]2− species are −219.4 and −218.0 kcal mol−1 respectively and are relatively large compared to the hydration energies of [OH]− and [OsVIIIO4(OH)]−, −96.1 and −58.9 kcal mol−1 respectively. This implies that the hydration energy of the cis-[OsVIIIO4(OH)2]2− species is the thermodynamic driving force of reaction (4). The good agreement between experimental2,3 and calculated thermodynamic parameters provides good evidence that the OsVIII species present in basic aqueous solutions are OsVIIIO4, [OsVIIIO4(OH)]− and two cis-[OsVIIIO4(OH)2]2− complexes, i.e. reactions (3) & (4) and not reactions (1) & (2).
values of reaction (4) (12, 13) are large and positive, Table 7, in contrast to the large negative values of reaction (3). Conversely, the agreement between experimental and DFT-calculated standard reaction Gibbs free energies in the simulated aqueous phase are excellent, excluding the LDA functional. The hydration energies (PBE functional) of the doubly-charged cis1- and cis2-[OsVIIIO4(OH)2]2− species are −219.4 and −218.0 kcal mol−1 respectively and are relatively large compared to the hydration energies of [OH]− and [OsVIIIO4(OH)]−, −96.1 and −58.9 kcal mol−1 respectively. This implies that the hydration energy of the cis-[OsVIIIO4(OH)2]2− species is the thermodynamic driving force of reaction (4). The good agreement between experimental2,3 and calculated thermodynamic parameters provides good evidence that the OsVIII species present in basic aqueous solutions are OsVIIIO4, [OsVIIIO4(OH)]− and two cis-[OsVIIIO4(OH)2]2− complexes, i.e. reactions (3) & (4) and not reactions (1) & (2).
| Functional | Gas phase | COSMO (aqueous) | ||
|---|---|---|---|---|
| K eq | K eq | |||
| a Calculated average experimental value taken from ref. 2 and 3. | ||||
| LDA | 52.4 | 3.9 × 10−39 | −10.8 | 8.1 × 107 |
| PBE | 62.0 | 3.4 × 10−46 | −0.0(3) | 1.1 |
| PBE-D | 60.0 | 9.9 × 10−45 | −2.6 | 82.2 |
| PBE-D3 | 60.9 | 2.3 × 10−45 | −0.6 | 2.8 |
| PBE-D3(BJ) | 60.9 | 2.2 × 10−45 | −0.9 | 5.0 |
| PBE-dDsC | 60.6 | 3.9 × 10−45 | −1.1 | 6.9 |
| mPBE | 63.1 | 5.9 × 10−47 | 1.5 | 8.2 × 10−2 |
| BLYP | 65.3 | 1.5 × 10−48 | 3.1 | 5.1 × 10−3 |
| BLYP-D | 60.4 | 5.3 × 10−45 | −0.3 | 1.7 |
| BLYP-D3 | 61.0 | 1.8 × 10−45 | 0.4 | 0.5 |
| PW91 | 60.8 | 2.6 × 10−45 | −1.0 | 5.2 |
| M06L | 59.7 | 1.6 × 10−44 | −3.9 | 7.5 × 102 |
| Experimental | 0.3 | 0.6 | ||
The results of EDA calculations performed on the OsVIII–OH bonds of the three six-coordinate [OsVIIIO4(OH)2]2− species are encapsulated in Table 8. The two hydroxido ligands in each of the three complex species are indistinguishable from one another due to their spatial symmetry and therefore the −De values of the bonds of both ligands are the same.
| Species | Functional | Phase | ΔEint | ΔEPauli | ΔEelstat | ΔEorb | ΔEdisp | ΔEsolv | ΔEprep | −De |
|---|---|---|---|---|---|---|---|---|---|---|
| cis 1-[OsO4(OH)2]2− | PBE | Gas | 32.8 | 176.9 | −65.7 | −78.5 | — | — | 18.3 | 51.1 |
| Aqueous | 41.4 | 187.3 | −70.8 | −75.1 | — | −64.4 | 11.6 | −11.4 | ||
| PBE-D | Gas | 32.1 | 173.0 | −62.8 | −77.5 | −0.7 | — | 17.3 | 49.4 | |
| Aqueous | 40.0 | 183.0 | −67.5 | −74.1 | −1.4 | −64.6 | 11.4 | −13.1 | ||
| PBE-D3 | Gas | 31.8 | 176.3 | −65.2 | −78.3 | −1.0 | — | 18.1 | 50.0 | |
| Aqueous | 40.3 | 186.4 | −70.2 | −74.9 | −1.0 | −64.4 | 11.7 | −12.4 | ||
| PBE-D3(BJ) | Gas | 32.2 | 176.9 | −65.5 | −78.2 | −1.1 | — | 18.0 | 50.2 | |
| Aqueous | 40.9 | 186.5 | −70.1 | −74.4 | −1.1 | −64.4 | 11.2 | −12.3 | ||
| PBE-dDsC | Gas | 32.0 | 178.6 | −66.7 | −78.5 | −1.4 | — | 17.7 | 49.7 | |
| Aqueous | 40.9 | 187.0 | −70.4 | −74.5 | −1.2 | −64.4 | 11.0 | −12.5 | ||
| cis 2-[OsO4(OH)2]2− | PBE | Gas | 32.5 | 174.7 | −64.6 | −77.6 | — | — | 18.1 | 50.6 |
| Aqueous | 40.1 | 185.0 | −69.5 | −75.4 | — | −63.0 | 11.4 | −11.5 | ||
| PBE-D | Gas | 30.9 | 170.4 | −61.7 | −76.4 | −1.4 | — | 17.9 | 48.7 | |
| Aqueous | 38.7 | 179.7 | −65.5 | −74.0 | −1.5 | −63.2 | 11.3 | −13.2 | ||
| PBE-D3 | Gas | 31.4 | 173.8 | −64.1 | −77.3 | −1.0 | — | 18.1 | 49.4 | |
| Aqueous | 38.8 | 183.0 | −68.2 | −75.0 | −1.0 | −63.0 | 11.7 | −12.5 | ||
| PBE-D3(BJ) | Gas | 31.6 | 174.9 | −64.8 | −77.5 | −1.1 | — | 18.0 | 49.6 | |
| Aqueous | 39.3 | 184.4 | −69.0 | −75.1 | −1.1 | −62.9 | 11.3 | −12.4 | ||
| PBE-dDsC | Gas | 31.5 | 176.8 | −66.0 | −77.9 | −1.4 | — | 17.7 | 49.2 | |
| Aqueous | 39.3 | 184.9 | −69.3 | −75.1 | −1.2 | −63.0 | 11.1 | −12.6 | ||
| trans-[OsO4(OH)2]2− | PBE | Gas | 17.5 | 227.4 | −102.1 | −107.8 | — | — | 42.7 | 60.2 |
| Aqueous | 24.3 | 237.3 | −109.0 | −104.1 | — | −65.1 | 37.8 | −3.0 | ||
| PBE-D | Gas | 16.4 | 226.5 | −101.6 | −107.6 | −0.9 | — | 42.8 | 59.2 | |
| Aqueous | 23.0 | 234.7 | −107.3 | −103.4 | −1.0 | −65.4 | 38.5 | −3.9 | ||
| PBE-D3 | Gas | 16.7 | 227.3 | −102.1 | −107.8 | −0.7 | — | 42.7 | 59.4 | |
| Aqueous | 23.5 | 236.9 | −108.8 | −104.0 | −0.8 | −65.2 | 38.1 | −3.6 | ||
| PBE-D3(BJ) | Gas | 16.6 | 229.1 | −103.3 | −108.2 | −1.0 | — | 42.6 | 59.3 | |
| Aqueous | 23.3 | 240.4 | −111.2 | −104.9 | −1.0 | −65.3 | 38.1 | −3.8 | ||
| PBE-dDsC | Gas | 16.6 | 230.8 | −104.5 | −108.6 | −1.2 | — | 42.4 | 59.0 | |
| Aqueous | 23.5 | 241.0 | −111.5 | −105.0 | −1.0 | −65.3 | 37.8 | −4.0 |
In contrast to the OsVIII–OH bonding energetics in the [OsVIIIO4(OH)]− complex, the stabilisation contributions from the orbitalic and electrostatic interactions of all three [OsVIIIO4(OH)2]2− complexes are not large enough to yield negative ΔEint values. The large positive −De values reflect why large positive calculated 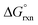 values in the gas phase, Table 7, were obtained. The ratio of ΔEelstat
values in the gas phase, Table 7, were obtained. The ratio of ΔEelstat![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔEorb in each of the two cis-[OsVIIIO4(OH)2]2− complex species is approximately 0.83 and 0.92 in the gas and simulated aqueous phase respectively and approximately 0.95 and 1.05 for the trans-[OsVIIIO4(OH)2]2− complex in the gas and simulated aqueous phase. The OsVIII–OH bonding interaction has slightly less covalent character in the trans-compared to the cis-[OsVIIIO4(OH)2]2− species. The ΔEelstat stabilisation of the OsVIII–OH interaction of all three species is less compared to that of [OsVIIIO4(OH)]− since the two fragments involved are now both anionic, resulting in less attraction as compared to when only one fragment is negatively charged. Similarly to that of the [OsVIIIO4(OH)]− complex, contributions of ΔEdisp are minimal for all three complexes. Despite the fact that the trans-[OsVIIIO4(OH)2]2− complex has a more favourable ΔEint compared to that of the two cis-[OsVIIIO4(OH)2]2− species, it is the significantly larger deformation energy contribution which makes −De, and also the relative stability of the trans-[OsVIIIO4(OH)2]2− complex, less than that of the two cis-[OsVIIIO4(OH)2]2− species. The bond dissociation energy of the trans-[OsVIIIO4(OH)2]2− species is approximately 9–10 kcal mol−1 less favourable (gas or simulated aqueous phase) compared to the two cis-[OsVIIIO4(OH)2]2− species. EDA analysis therefore provides a reason why the trans-[OsVIIIO4(OH)2]2− complex is thermodynamically less stable compared to the two cis-[OsVIIIO4(OH)2]2− species. The calculated −De values in the gas phase are relatively large positive values meaning that formation of the second OsVIII–OH metal-hydroxido bond is thermodynamically unfavourable in the absence of an adequate solvation (hydration) energy contribution. It is only when the hydration energy, ΔEsolv contribution, is present that negative −De values are obtained. Therefore, in contrast to reaction (3), reaction (4) is thermodynamically driven by the larger hydration energy of the doubly-charged [OsVIIIO4(OH)2]2− species in comparison with that of the two, singly-charged reactants, i.e. [OsVIIIO4(OH)]− and a hydroxide anion.
ΔEorb in each of the two cis-[OsVIIIO4(OH)2]2− complex species is approximately 0.83 and 0.92 in the gas and simulated aqueous phase respectively and approximately 0.95 and 1.05 for the trans-[OsVIIIO4(OH)2]2− complex in the gas and simulated aqueous phase. The OsVIII–OH bonding interaction has slightly less covalent character in the trans-compared to the cis-[OsVIIIO4(OH)2]2− species. The ΔEelstat stabilisation of the OsVIII–OH interaction of all three species is less compared to that of [OsVIIIO4(OH)]− since the two fragments involved are now both anionic, resulting in less attraction as compared to when only one fragment is negatively charged. Similarly to that of the [OsVIIIO4(OH)]− complex, contributions of ΔEdisp are minimal for all three complexes. Despite the fact that the trans-[OsVIIIO4(OH)2]2− complex has a more favourable ΔEint compared to that of the two cis-[OsVIIIO4(OH)2]2− species, it is the significantly larger deformation energy contribution which makes −De, and also the relative stability of the trans-[OsVIIIO4(OH)2]2− complex, less than that of the two cis-[OsVIIIO4(OH)2]2− species. The bond dissociation energy of the trans-[OsVIIIO4(OH)2]2− species is approximately 9–10 kcal mol−1 less favourable (gas or simulated aqueous phase) compared to the two cis-[OsVIIIO4(OH)2]2− species. EDA analysis therefore provides a reason why the trans-[OsVIIIO4(OH)2]2− complex is thermodynamically less stable compared to the two cis-[OsVIIIO4(OH)2]2− species. The calculated −De values in the gas phase are relatively large positive values meaning that formation of the second OsVIII–OH metal-hydroxido bond is thermodynamically unfavourable in the absence of an adequate solvation (hydration) energy contribution. It is only when the hydration energy, ΔEsolv contribution, is present that negative −De values are obtained. Therefore, in contrast to reaction (3), reaction (4) is thermodynamically driven by the larger hydration energy of the doubly-charged [OsVIIIO4(OH)2]2− species in comparison with that of the two, singly-charged reactants, i.e. [OsVIIIO4(OH)]− and a hydroxide anion.
Calculated results of ETS-NOCV analysis of the OsVIII–OH bond in the three six-coordinate [OsVIIIO4(OH)2]2− species are similar to that obtained in the five-coordinate [OsVIIIO4(OH)]− species. The sum of the calculated energies of the two major deformation-density channels, Δρ1 and Δρ2, to the covalent contribution of the OsVIII–OH bond energy make up approximately 71% and 16% respectively of the total orbitalic stabilisation, Table S1,† and correspond to σ- and π-donations respectively, from the occupied 2p orbitals of the hydroxido oxygen to the empty 5d orbitals of the osmium metal-centre, Fig. S4.†
To further characterise the nature of the OsVIII-oxo/hydroxido bonding interactions and to investigate whether possible intramolecular interactions occur, we performed a topological analysis of the electron density according to the quantum theory of atoms in molecules (QTAIM).55,56 The definition for atoms to be chemically bonded, according to this theory, is based on the existence of a (3, −1) bond critical point (BCP) or a saddle point along a line of maximum electron density, ρ, also called an atomic interaction line (AIL) linking the nuclei of neighbouring atoms. At the BCP the gradient of the electron density vanishes, ∇ρ(r) = 0, and the sum of the three eigenvalues (λ1 and λ2 are negative, λ3 is positive), obtained from the electron density Hessian matrix, known as the Laplacian, ∇2ρ(r)b, may have either a net positive or negative value. A positive Laplacian value at the BCP indicates a local depletion of charge. This is indicative of an ionic (closed-shell) type of bonding. A negative Laplacian value is a sign of a local concentration of charge and is indicative of a shared/covalent interaction. However, a positive Laplacian value could in some cases be misleading, as the classification of the bond between two “closed-shell” interacting atoms is also determined by a second index, the total electronic energy density, Eeb, at the BCP. This term is defined as the sum of the kinetic energy density, Gb, which usually dominates in a non-covalent bond, and the potential energy density, Vb, which is usually negative and is associated with accumulation of charge between the nuclei. In clearly covalent bonds both the ∇2ρ(r)b and Eeb = Gb + Vb are negative whilst the electron density at the BCP is larger than 0.1. In less clear cases, where the ∇2ρ(r)b has a relatively small positive value, the magnitude of Eeb can be used to further classify the bond, from being slightly covalent to purely ionic, e.g. if ∇2ρ > 0 and Eeb is negative the bond is called dative on the other hand if Eeb is positive the bond is ionic. Moreover, the Gb/ρb ratio index is generally accepted to be less than unity for shared interactions and greater than unity for closed-shell interactions. The calculated BCP's electron density topology indices of all OsVIII species in the simulated aqueous phase (PBE functional) are listed in Table S2† (see Table S3† for values obtained using PBE-D3(BJ) functional) and the molecular graphs obtained illustrated in Fig. 2.
The Laplacian at all the OsVIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O BCPs of all complexes, Table S2,† are positive, ranging from 0.76 to 0.86, and the Gb/ρb ratio is always more than unity, from 1.41 to 1.48, indicating ionic bonding interactions. Since the Eeb is negative in all cases, from −0.16 to −0.11, the interaction has a slight covalent character. The ionicity of the bonding interactions is less in the case of the OsVIII–OH BCPs in all the complexes. The Laplacian has a smaller positive value, from 0.30 to 0.38, while the Gb/ρb ratio is only slightly greater than unity, from 1.02 to 1.06. These results, along with the negative Eeb values, from −0.05 to −0.03, qualify these interactions as polar covalent (dative) and corroborate the results obtained by the EDA analysis. The O–H bonding interactions are clearly covalent as indicated by the large negative Laplacian values, from −2.36 to −2.25, Fig. 4, and the large negative Eeb values, from −0.67 to −0.66. The Gb/ρb ratio is also much smaller than unity, from 0.23 to 0.26. No qualitative changes are observed when topological analysis of the electron density is performed in the gas phase, Tables S4 and S5.† The Laplacian of the electron density, plotted along the OsVIII–O–H plane of all four OsVIII species, shown in Fig. 4, allows for the visualisation of the charge density distribution at an OsVIII
O BCPs of all complexes, Table S2,† are positive, ranging from 0.76 to 0.86, and the Gb/ρb ratio is always more than unity, from 1.41 to 1.48, indicating ionic bonding interactions. Since the Eeb is negative in all cases, from −0.16 to −0.11, the interaction has a slight covalent character. The ionicity of the bonding interactions is less in the case of the OsVIII–OH BCPs in all the complexes. The Laplacian has a smaller positive value, from 0.30 to 0.38, while the Gb/ρb ratio is only slightly greater than unity, from 1.02 to 1.06. These results, along with the negative Eeb values, from −0.05 to −0.03, qualify these interactions as polar covalent (dative) and corroborate the results obtained by the EDA analysis. The O–H bonding interactions are clearly covalent as indicated by the large negative Laplacian values, from −2.36 to −2.25, Fig. 4, and the large negative Eeb values, from −0.67 to −0.66. The Gb/ρb ratio is also much smaller than unity, from 0.23 to 0.26. No qualitative changes are observed when topological analysis of the electron density is performed in the gas phase, Tables S4 and S5.† The Laplacian of the electron density, plotted along the OsVIII–O–H plane of all four OsVIII species, shown in Fig. 4, allows for the visualisation of the charge density distribution at an OsVIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, OsVIII–OH and O–H BCP which displays the relative ionic (blue), polar covalent (green) and covalent (red) character of their bonding interactions respectively. Moreover, it is evident from the molecular graphs obtained using QTAIM, Fig. 2, that no intramolecular bonding interactions between neighbouring hydroxido and oxo ligands in any of the OsVIII species are present.
O, OsVIII–OH and O–H BCP which displays the relative ionic (blue), polar covalent (green) and covalent (red) character of their bonding interactions respectively. Moreover, it is evident from the molecular graphs obtained using QTAIM, Fig. 2, that no intramolecular bonding interactions between neighbouring hydroxido and oxo ligands in any of the OsVIII species are present.
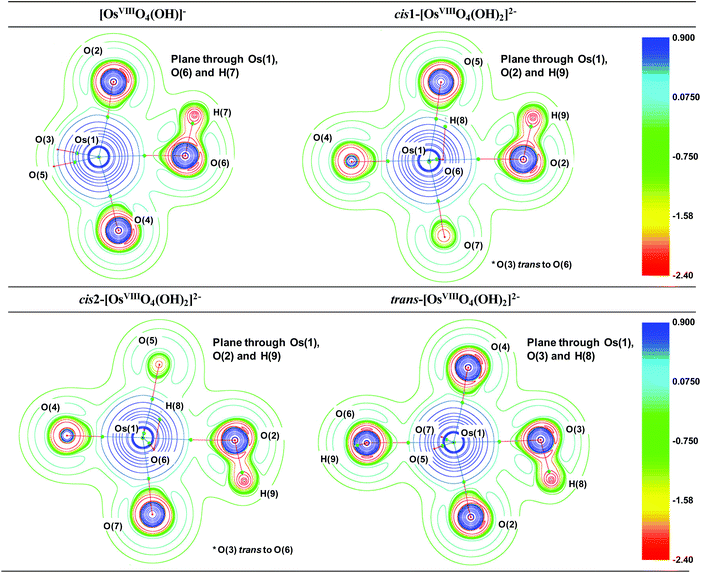 | ||
| Fig. 4 The Laplacian of the electron density (∇2ρ) of each of the OsVIII oxo/hydroxido complexes in the simulated aqueous phase (PBE functional) with numbering scheme used in Table S2.† BCPs are indicated as small green spheres. Red and blue colouring corresponds to regions of local charge accumulation and depletion respectively. | ||
The more recent Non-Covalent Interactions (NCI) analysis method is frequently used to recognise and categorise intra- and intermolecular bonding interactions in a wide variety of chemical systems.57 This is based on a 2D plot of the reduced density gradient (RDG), s, as a function of the sign of λ2 multiplied with the electron density, ρ, eqn (16). A bonding interaction according to Johnson et al.,57e.g. hydrogen bonding or π–π stacking is characterised by an accumulation of electron density in a particular region in 3D space and in these cases λ2 < 0. By contrast, repulsive interactions have a λ2 > 0.
In a recent study, Cukrowski et al.73 revealed that local properties of bonding, i.e. attractive or repulsive, based on the NCI interpretation of the electron density topology do not necessarily correlate with the physical nature of that interaction. The authors further concluded that NCI reveals only the presence or absence of possible interactions between atoms and electron density accumulation or depletion. However, in many chemical systems of less ambiguity, NCI analyses can be successfully used to identify attractive or repulsive interactions as will be shown in the following text.
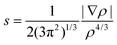 | (16) |
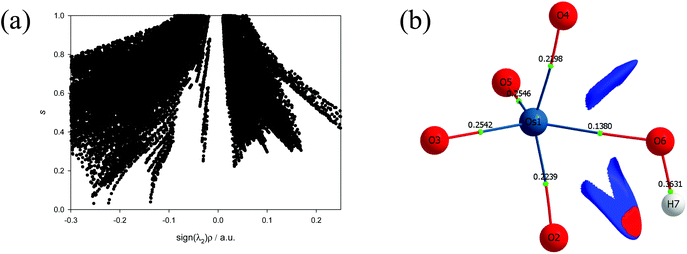
Points where s = 0 correspond to BCPs due to annihilation of the density gradient. A non-covalent interactions (NCI) analysis of the five-coordinate [OsVIIIO4(OH)]− species, Fig. 5, indicates that a relatively weak stabilisation is present between neighbouring oxo and hydroxido ligands. Although the trough at approximately sign(λ2)ρ ≈ −0.03 au does not terminate at RDG of zero, a weak attractive intramolecular hydrogen bonding interaction between H(7) & O(2) is present. The trough corresponding to this interaction is visualised in 3D space in Fig. 5(b) as a red region. The four troughs between −0.25 and −0.22 au are due to ionic (closed-shell) OsVIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds while the trough at −0.14 au is due to the polar covalent (dative) OsVIII–OH bond and these correspond with the BCPs found in the abovementioned QTAIM analysis. It is also evident that there are troughs with positive λ2 values that do not extend to a RDG of zero. These troughs are also visualised in 3D space Fig. 5(b) as blue regions and are indicative of repulsive interactions between oxygen moieties, O(4) & O(6) and O(6) & O(2), of neighbouring ligands.
O bonds while the trough at −0.14 au is due to the polar covalent (dative) OsVIII–OH bond and these correspond with the BCPs found in the abovementioned QTAIM analysis. It is also evident that there are troughs with positive λ2 values that do not extend to a RDG of zero. These troughs are also visualised in 3D space Fig. 5(b) as blue regions and are indicative of repulsive interactions between oxygen moieties, O(4) & O(6) and O(6) & O(2), of neighbouring ligands.
The NCI analyses of the cis1-[OsVIIIO4(OH)2]2−, cis2-[OsVIIIO4(OH)2]2− and trans-[OsVIIIO4(OH)2]2− species indicate relatively weak intramolecular hydrogen bonding interactions between neighbouring oxo and hydroxido ligands, Fig. 6. Both the hydroxido hydrogens in each of the three complexes have weak intramolecular hydrogen bonding interactions with a neighbouring oxo ligand. The troughs at sign(λ2)ρ range from −0.02 to −0.04 au are due to these attractive interactions and are visualised in 3D space in Fig. 6 as red regions. Several more repulsive interactions between oxygen moieties of neighbouring ligands are also present compared to the coordinatively unsaturated five-coordinate [OsVIIIO4(OH)]− complex anion.
Overall, the PBE and dispersion-corrected PBE functionals yielded good agreement with experimentally determined 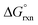 values, Tables 4 and 7. A graphical assessment of how well these DFT-calculated equilibrium constants of reactions (3) and (4) compare to the experimentally obtained values is shown in Fig. 7 where the OsVIII species distribution as a function of hydroxide concentration is plotted. For clarity, only the data for the PBE and PBE-D3 functionals are shown as examples.
values, Tables 4 and 7. A graphical assessment of how well these DFT-calculated equilibrium constants of reactions (3) and (4) compare to the experimentally obtained values is shown in Fig. 7 where the OsVIII species distribution as a function of hydroxide concentration is plotted. For clarity, only the data for the PBE and PBE-D3 functionals are shown as examples.
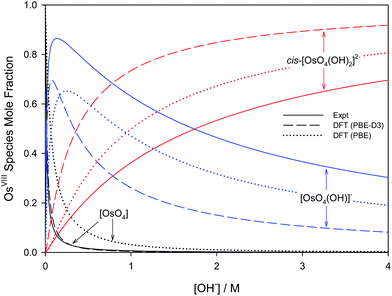 | ||
| Fig. 7 Species distribution diagram of [OsO4(OH)n]n− (n = 0, 1, 2) as a function of hydroxide concentration as calculated from DFT (PBE and PBE-D3 functionals) in contrast to experiment.74 | ||
Kinetics of coordination sphere expansion reactions (3) & (4)
It is found experimentally that when a neutral aqueous OsVIII solution is mixed with a relatively concentrated hydroxide solution that a rapid colour change occurs due to coordination sphere expansion reactions (3) & (4). Stopped-flow kinetics experiments were performed at 298.15 K in an attempt to quantify the rate at which these reactions occur. However, the spectral change occurs in such a small time scale that a ‘constant’ absorbance versus time signal is obtained, i.e. the expected absorbance when OsVIII is present at equilibrium in 2.0 M hydroxide is already observed at the first data point, at 0.001 seconds, which corresponds to the earliest possible reading that the instrument is capable of making. This indicates that the activation Gibbs energy barriers for the coordination sphere expansion reactions are relatively low. A computational study was subsequently performed to ascertain the mechanism of coordination sphere expansion and to obtain reaction energy barriers, i.e. does hydroxide coordinate directly to OsVIIIO4 and then to [OsVIIIO4(OH)]− in two, consecutive, elementary reaction steps as depicted in eqn (3) and (4)? From Fig. 8(a) it can be seen that the OsVIIIO4 species’ electrostatic surface potential defined at the 0.03 au electron density the OsVIII atom has four σ-holes75 of equal magnitude, i.e. regions where the Os atom has less electron density compared to neighbouring regions. For this reason a linear transit, relaxed scan, calculation in which a hydroxide ligand was incrementally moved closer to one of the four OsVIII σ-holes was performed. The relaxed scan calculations were only done in the simulated aqueous phase. The structure found at the maximum of the potential energy surface was subsequently submitted for a transition state search. The converged geometry structure where the OsVIII–OH distance is 3.43 Å, Fig. 8(b), has one negative vibrational frequency, corresponding to a saddle point on the PES and one degree of freedom, where the hydroxide oxygen atom vibrates towards and back w.r.t. the OsVIII atom. The Gibbs energies of activation of the forward and reverse reactions, eqn (3), and their associated rate constants were calculated using eqn (17), and are listed in Table 9.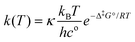 | (17) |
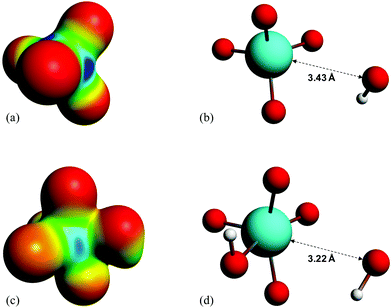 | ||
| Fig. 8 (a) and (c): Electrostatic surface potential maps of the optimised geometries of OsVIIIO4 and [OsVIIIO4(OH)]− in the simulated aqueous phase (PBE functional) corresponding to a density isosurface value of 0.03 au. Negatively and positively charged regions are indicated by red and blue colouring, respectively. (b) and (d): Molecular graphs of the calculated transition state structures (PBE functional) of reactions (3) & (4), respectively. | ||
It is assumed that the transmission factor or transmission coefficient, κ, is equal to one and do not vary as a function of temperature. The rate constants obtained of reaction (3) are relatively large and falls in the range of a diffusion-controlled rate-limiting step.76
From Fig. 8(c) it is observed that the [OsVIIIO4(OH)]− species has two equivalent σ-holes. In a similar fashion to the method used to describe the mechanism of reaction (3), the “incoming” hydroxido ligand was placed in line with the OsVIII atom σ-hole and a linear transit relaxed scan calculation was performed. The transition state geometry structure where the OsVIII–OH distance is 3.22 Å, Fig. 8(d), has one negative vibrational frequency. Reactions (3) & (4) occur as two elementary steps. The Gibbs energies of activation of the forward and reverse reactions, eqn (4) (or more specifically reaction (13)), and their associated rate constants were calculated using eqn (17) and are listed in Table 10.
The calculated rate constants obtained for reaction (13), Table 10, are relatively large, yet on estimation an order of magnitude less when compared to reaction (3). We attribute this result in part to the repulsion between the two negatively charged species which increases the Δ‡G° activation energy barrier. From reactions (3) and (13), the rate law eqn (18)–(20) are derived. Using the rate constants obtained with the PBE-dDsC functional, the species concentration evolution curves as a function of time were calculated, Fig. 9. The initial conditions in this hypothetical “stopped-flow” kinetics calculation are two aqueous solutions of equal volume where one syringe contains OsVIIIO4 at 10.0 mM and the other contains 4.0 M [OH]−. It is seen in Fig. 9 that reactions (3) and (13) reach equilibrium in less than 0.00003 seconds which explains our experimental stopped-flow kinetics results.
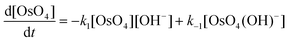 | (18) |
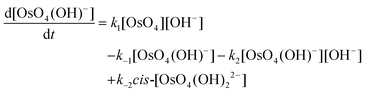 | (19) |
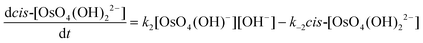 | (20) |
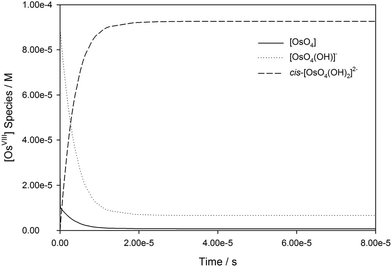 | ||
| Fig. 9 Simulated kinetic traces of OsVIIIO4 reacting with OH− in 2 M NaOH as a function of time (PBE-dDsC functional). | ||
Conclusions
We have demonstrated that DFT computational methodologies, mainly with GGA functionals, are successful in elucidating the equilibrium structures and energies of OsVIII oxo/hydroxido species that are present in aqueous basic solutions. Our calculations provide evidence that the OsVIII species present in basic aqueous solutions are OsVIIIO4, [OsVIIIO4(OH)]− and two cis-[OsVIIIO4(OH)2]2− complexes and that water-bonded OsVIII species most likely do not exist. Good agreement with reported, experimentally obtained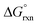 values pertaining to the two coordination sphere expansion reactions validates the DFT methodology used. The thermodynamic driving force of the first coordination sphere expansion reaction is the bonding energy of the OsVIII–OH metal-hydroxido ligand present in [OsVIIIO4(OH)]− and of the second reaction it is the larger hydration energy of the doubly-charged cis-[OsVIIIO4(OH)2]2− species in comparison with that of the two, singly-charged reactants. Both coordination sphere expansion reactions have relatively low transition state energy, Δ‡G°, barriers.
values pertaining to the two coordination sphere expansion reactions validates the DFT methodology used. The thermodynamic driving force of the first coordination sphere expansion reaction is the bonding energy of the OsVIII–OH metal-hydroxido ligand present in [OsVIIIO4(OH)]− and of the second reaction it is the larger hydration energy of the doubly-charged cis-[OsVIIIO4(OH)2]2− species in comparison with that of the two, singly-charged reactants. Both coordination sphere expansion reactions have relatively low transition state energy, Δ‡G°, barriers.
QTAIM and EDA analyses indicate that OsVIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding interactions are ionic (closed-shell) whereas the OsVIII–OH bonding interactions are polar covalent (dative). NCI analysis of both the [OsVIIIO4(OH)]− and cis-[OsVIIIO4(OH)2]2− species indicate the presence of weak intramolecular hydrogen bonding interactions between neighbouring oxo and hydroxido ligands.
O bonding interactions are ionic (closed-shell) whereas the OsVIII–OH bonding interactions are polar covalent (dative). NCI analysis of both the [OsVIIIO4(OH)]− and cis-[OsVIIIO4(OH)2]2− species indicate the presence of weak intramolecular hydrogen bonding interactions between neighbouring oxo and hydroxido ligands.
The results obtained in this study allow for subsequent investigations which aim to describe the mechanism of the proposed comproportionation reaction by Gerber et al.11 Furthermore, the clarity w.r.t. the OsVIII speciation can now be used to make informed suggestions regarding which OsVIII complexes are the active catalysts in future studies done in aqueous solutions.
References
- A. Dehestani, W. H. Lam, D. A. Hrovat, E. R. Davidson, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2005, 127, 3423 CrossRef CAS PubMed.
- Z. M. Galbács, A. Zsednai and L. J. Csányi, Transition Met. Chem., 1983, 8, 328 CrossRef.
- B. J. McFadzean, PhD Dissertation, NMMU, South Africa, 2008.
- A. H. Éll, A. Closson, H. Adolfsson and J.-E. Bäckvall, Adv. Synth. Catal., 2003, 345, 1012 CrossRef.
- S. M. Desai, N. N. Halligudi and S. T. Nandibewoor, Int. J. Chem. Kinet., 1999, 31, 583 CrossRef CAS.
- N. P. Shetti, R. R. Hosamani and S. T. Nandibewoor, Res. Lett. Inorg. Chem., 2008, 216058, 1 CrossRef.
- K. Byadagi, M. Meti, S. Nandibewoor and S. Chimatadar, Ind. Eng. Chem. Res., 2013, 52, 9011 CrossRef CAS.
- M. P. Singh, H. S. Singh, M. C. Gangwar, P. Thakur and A. K. Singh, Proc. - Indian Acad. Sci., Sect. A, 1975, 41, 178 CAS.
- N. N. Ivan-Emin, N. A. Nevskaya, N. N. Nevskii and A. S. Izmailovich, Russ. J. Inorg. Chem., 1984, 29, 710 Search PubMed.
- H. C. Jewiss, W. Levason, M. Tajik, M. Webster and N. P. C. Walker, J. Chem. Soc., Dalton Trans., 1985, 199 RSC.
- T. E. Geswindt, W. J. Gerber, H. E. Rohwer and K. R. Koch, Dalton Trans., 2011, 40, 8581 RSC.
- W. P. Griffith, The Chemistry of the Rarer Platinum Metals (Os, Ru, Ir & Rh), Interscience, 1967, ch. 3 Search PubMed.
- B. Krebs and K. D. Hasse, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1334 CrossRef.
- N. N. Nevskii, B. Ivan-Emin, O. N. A. Nevskaya and N. V. Belov, Dokl. Akad. Nauk SSSR, 1983, 226, 245 Search PubMed.
- Z. Y. Lin and M. B. Hall, Coord. Chem. Rev., 1993, 123, 149 CrossRef CAS.
- D. T. Richens, The Chemistry of Aqua Ions, John Wiley and Sons, New York, 1997 Search PubMed.
- D. W. Nelson, A. Gypser, P. T. Ho, H. C. Kolb, T. Kondo, H.-L. Kwong, A. McGrath, E. A. Rubin, P.-O. Norbby, K. P. Gable and K. B. Sharpless, J. Am. Chem. Soc., 1997, 119, 1840 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757 RSC.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed.
- E. J. Baerends, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, G. van Kessel, F. Kootstra, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, P. R. T. Schipper, G. Schreckenbach, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo, A. L. Yakovlev and T. Ziegler, ADF2012.02, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http:/www.scm.com Search PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- E. van Lenthe, A. E. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505 CrossRef CAS.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58(8), 1200 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1996, 116, 5933 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- S. Grimme, J. Anthony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1457 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Theor. Comput., 2011, 7, 3567 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS.
- B. G. Johnson, P. M. W. Gill and J. A. Pople, J. Chem. Phys., 1993, 98, 5612 CrossRef CAS.
- T. V. Russo, R. L. Martin and P. J. Hay, J. Chem. Phys., 1994, 101, 7729 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Sing and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1992, 46, 6671 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224 CrossRef CAS.
- A. Klamt and V. Jones, J. Chem. Phys., 1996, 105, 9972 CrossRef CAS.
- A. Bérces, R. M. Dickson, L. Fan, H. Jacobsen, D. Swerhone and T. Ziegler, Comput. Phys. Commun., 1997, 100, 247 CrossRef.
- H. Jacobsen, A. Bérces, D. Swerhone and T. Ziegler, Comput. Phys. Commun., 1997, 100, 263 CrossRef CAS.
- S. K. Wolff, Int. J. Quantum Chem., 2005, 104, 645 CrossRef CAS.
- L. Fan and T. Ziegler, J. Chem. Phys., 1992, 96, 9005 CrossRef CAS.
- L. Fan and T. Ziegler, J. Phys. Chem., 1992, 96, 6937 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755 CrossRef CAS.
- M. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theor. Comput., 2009, 5, 962 CrossRef CAS PubMed.
- GUI 2014, SCM, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- J. I. Rodríguez, R. F. W. Bader, P. W. Ayers, C. Michel, A. W. Götz and C. Bo, Chem. Phys. Lett., 2009, 472, 149 CrossRef.
- J. I. Rodríguez, J. Comput. Chem., 2013, 34, 681 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 15.05.18), TK Gristmill Software, Overland Park KS, USA, 2015 Search PubMed (http://aim.tkgristmill.com).
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669 CrossRef CAS PubMed.
- E. J. Wells, A. D. Jordan, D. S. Alderdice and I. G. Ross, Aust. J. Chem., 1967, 20, 2315 CrossRef CAS.
- J. L. Roebber, R. N. Wiener and C. A. Russel, J. Chem. Phys., 1974, 60, 3166 CrossRef CAS.
- R. S. McDowell and M. Goldblatt, Inorg. Chem., 1971, 10(3), 625 CrossRef CAS.
- H. M. Seip and R. Stølevik, Acta Chem. Scand., 1966, 20, 385 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- M. von Hopffgarten and G. Frenking, WIREs Comput. Mol. Sci., 2012, 2, 43 CrossRef CAS.
- Y. Jeanvoine, P. Miró, F. Martelli, C. J. Cramer and R. Spezia, Phys. Chem. Chem. Phys., 2012, 14, 14822 RSC.
- I. Cukrowski, J. H. de Lange, A. S. Adeyinka and P. Mangondo, Comput. Theor. Chem., 2015, 1053, 60 CrossRef CAS.
- E. C. Hosten, Complex Species Distribution (version 3.1), NMMU Search PubMed.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291 CrossRef CAS PubMed.
- O. von Berg and P. H. von Hippel, Ann. Rev. Biophys. Chem., 1985, 14, 131 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary UV-Vis spectrum, additional computational results and Cartesian coordinates of all optimised structures. See DOI: 10.1039/c6dt00657d |
| ‡ ε = dielectric constant = 78.39 and Rad = radius of the rigid sphere H2O molecules = 1.93 Å. |
| § Detailed DFT calculations are presented and discussed in the ESI.† |
| This journal is © The Royal Society of Chemistry 2016 |