Achirality in the low temperature structure and lattice modes of tris(acetylacetonate)iron(III)

Abstract

Tris(acetylacteonate) iron(III) is a relatively ubiquitous mononuclear inorganic coordination complex. The bidentate nature of the three acetylacteonate ligands coordinating around a single centre inevitably leads to structural isomeric forms, however whether or not this relates to chirality in the solid state has been questioned in the literature. Variable temperature neutron diffraction data down to T = 3 K, highlights the dynamic nature of the ligand environment, including the motions of the hydrogen atoms. The Fourier transform of the molecular dynamics simulation based on the experimentally determined structure was shown to closely reproduce the low temperature vibrational density of states obtained using inelastic neutron scattering.

---

Introduction

Tris(acetylacetonate) iron(III), Fe(acac)₃ where acac = OC(CH₃)CHC(CH₃)O, is a staple coordination complex of undergraduate studies the world over. Relatively easy to synthesise in high quality crystalline samples having a rich red coloration,^1–3 it continues to be a useful tool for the teaching of elementary coordination chemistry and molecular magnetism.⁴ It is maybe surprising therefore that it has recently been the topic of several works, with some debate over the precise crystal structure. As with all tris-bidentate systems based upon octahedral coordination, Fe(acac)₃ is inherently chiral at the molecular level. However in 1967 the structure was first refined using Weissenberg images into the centrosymmetric orthorhombic Pbca space group.⁵ Indeed, unlike other members of the first row transition metal tris-acetylacetonates, Fe(acac)₃ is not readily resolved into enantiomerically pure samples, in accord with this space group setting. However, in 1996, a ‘re-interpretation’ of the structure assigned it to one of the 65 Sohncke space groups that can support a chiral structure,⁶ orthorhombic P2₁2₁2₁.⁷ A curiosity of this space group setting is that the asymmetric unit contains two independent molecules, one of each enantiomer. Crystallographically this would be an extremely rare situation, whereas in Pbca the pseudo-inversion centre that relates the two enantiomer molecules corresponds to a real crystallographic inversion. Indeed, this interpretation was later shown to be inaccurate in two subsequent low temperature X-ray structure determinations at T = 20 and 150 K,^8,9 both placing it once again in the centrosymmetric space group Pbca as recently as 2007. Enantiomerically pure samples of Fe(acac)₃ were prepared for the first time in 2011 by co-crystallising the molecule with CCl₄, to yield [Fe(acac)₃](CCl₄) in the trigonal Sohncke space group R3.¹⁰ It must be noted that almost all batches of these crystals were twinned by inversion such that most individual crystals essentially contained a racemic mixture. Only one batch out of very many was ever found with crystals giving a Flack parameter of X = 0 representing enantiometrically pure crystals.¹¹ Subsequent solvent-based stability studies displayed a relaxation in the optical activity, thereby demonstrating the highly labile ligand environment in solution. So what is it to be – do racemates of Fe(acac)₃ crystallise in a chiral crystal structure in which the unit cell consists of a single enantiomer under an achiral space group, or does it crystallise in a truly achiral crystal structure consisting of a racemic mixture of the two enantiomers? Further, a recent report makes claim of an additional Fe(acac)₃ polymorph, although the reported structure appears to largely be a lower symmetry monoclinic representation based around one half of the unit cell of the orthorhombic structure.¹² In order to elucidate the various questions that persist around the structure of this familiar small molecule, we have undertaken single crystal neutron diffraction studies at temperatures down to 3 K, directly determining the positions of all atoms in the molecules for the first time. By studying the evolution of the atomic displacement parameters as a function of temperature, an insight into the molecular dynamics was obtained, which was then compared to inelastic neutron scattering (INS) data obtained on the same material. Finally, making use of the high quality crystal structure, we were able to perform detailed molecular dynamic modelling to arrive at a simulated INS spectrum, providing for the first time a complete picture of the molecular packing and dynamics of pure Fe(acac)₃. Our findings are fully in accord with those recently reported by one of us (UAJ) investigating the iron-weighted density of states using nuclear inelastic scattering (NIS).¹³

Experimental section

Synthesis

All materials used are of reagent grade and were used without further purification.

Iron(III) chloride anhydrous (5 g, 30.8 mmol) was dissolved in water (50 mL) and the 0.1 M KOH was added with vigorous stirring until the pH reached 8.¹⁴ The precipitate was collected by vacuum filtration and washed with copious amounts of distilled water. The solid was dried in a desiccator overnight forming the dried iron hydroxide. Acetylacetone (5 mL, 48.7 mmol) was heated with stirring and the iron hydroxide was added slowly with stirring, until the added iron hydroxide no longer dissolved. The mixture was then filtered hot through cotton wool and the eluent was allowed to cool slowly over several days, crystallizing the crystals for this study. The crystals were collected by vacuum filtration and washed lightly with cold ethanol and finally were dried under vacuum.

Single crystal neutron diffraction

Single-crystal neutron diffraction patterns were collected at 3, 50, 100 and 150 K on the Koala Laue diffractometer at the Open Pool Australian Light-water reactor operated by the Australian Nuclear Science and Technology Organisation. This Laue diffractometer uses polychromatic thermal neutrons coupled with a large solid-angle (8 steradians) cylindrical image-plate detector. An Fe-acac crystal of approximate dimensions 1.5 × 1.5 × 1.5 mm was mounted on an aluminum pin with silicone grease. The diffraction patterns were indexed using the program LAUEGEN^15,16 and the reflections integrated using a 2D version of the σ(I)/I algorithm described by Wilkinson et al.¹⁷ and Prince et al.¹⁸ No absorption correction was found to be necessary. The reflections were normalized to the same incident wavelength using a curve derived by comparing equivalent reflections and multiple observations via the program LAUENORM.¹⁹ Only reflections with wavelengths between 1.0 and 2.9 Å were accepted for the normalization procedure because those outside this range were too weak or had too few equivalents to allow determination of the normalization curve confidently. The structure was determined using Jana 2006 ²⁰ with the starting model derived from single-crystal X-ray diffraction.²¹ The program VESTA²² was used for 3D visualization of the difference Fourier maps to identify structural disorder. The crystallographic data have been deposited in the CCDC and can be obtained from The Cambridge Crystallographic Data Centre by quoting: CCDC 1471349–1471352 for the data at the four temperatures measured.

One disadvantage of the Laue method is the inability to accurately determine the cell dimensions due to the quasi-polychromatic beam. However in this case this is irrelevant as literature determinations have shown that the cell dimensions are invariant as a function of temperature from 20–293 K,^5,7–9 presumably due to the flexible nature of the molecular units. Indeed, the dimensions quoted in the structural models used herein are those determined from the neutron Laue method and are within 3% of the mean of the reported cell volumes.

Inelastic neutron scattering

INS measurements were performed on the IN4 thermal time-of-flight spectrometer at the Institut Laue-Langevin, France.²³ A polycrystalline sample (0.75 g of Fe-acac) was placed into a cylindrical torroidal Al can of sample thickness 1 mm (93% transmission) and inserted into a cryostat to obtain the low sample temperatures at 135° to the incident beam at two wavelengths λ₁ = 1.17 Å and λ₂ = 1.53 Å, (E¹_i = 59.6 meV and E²_i = 34.9 meV). The data were collected over scattered angles of 15° ≤ 2θ ≤ 120° at a range of temperatures, 1.5 ≤ T ≤ 30 K and manipulated using the LAMP routine.²⁴

Molecular dynamics calculations

In order to rationalise the measured INS data to the determined crystal structure, detailed solid-state molecular dynamics simulations were performed based upon optimised structural models. A single unit-cell was used for the density functional theory (DFT) geometry optimisations which were carried out with VASP^25–28 using the project augmented wave potential²⁹ (PAW) and the Perdew–Burke–Ernzerhof³⁰ (PBE) exchange correlation functional, with the unit-cell parameters being constrained to the experimental values. The atomic positions for all cells were optimised by minimising the forces acting on the atoms using VASP with high precision: energy cut-off of 500 eV, a convergence condition of 10⁻⁴ eV and a 3 × 3 × 6 Monkhorst–Pack³¹k-point mesh. These minimisations were in excellent agreement with the experimentally determined crystal structures other than slight changes to the methyl-group orientations. These minimised structures were used as the start-point for the MD simulations that were carried out at lower precision with an energy cut-off of 300 eV and a single k-point. All MD simulations used a time-step of 1 fs with a target temperature of 40 K. An initial isokinetic run with velocity scaling of 4 ps was made followed by a thermalisation run in the microcanonical ensemble of 8 ps and a production run of 17 ps. Trajectories from the production run were stored for analysis.

Results and discussion

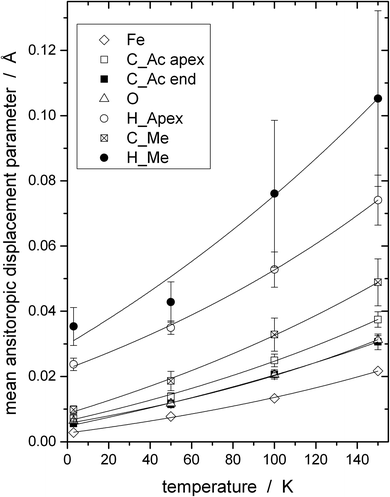
The crystal structure was refined into the achiral orthorhombic space group Pbca, with 8 molecules in the unit cell (a = 15.254 Å, b = 13.436 Å, c = 16.465 Å, α = β = γ = 90°). The Fe atoms sit in layers in the ab plane that stack into columns running along the c-axis, in accord with most of the literature and effectively eliminating the assignment of a Sohncke space group. This was found to be invariant with temperature. As neutron diffraction provides an accurate determination of all of the atoms present, including hydrogens, the evolution of the atomic displacement parameters as a function of temperature, Fig. 1, provides a unique insight into the thermally excited dynamics present in the molecule that has not been available to previous diffraction studies. As the heaviest atom, Fe sits at the centre of the molecular framework and its displacements are very small, even at 150 K. Most of the atomic displacements are centered on the acetylacetonate ligands, with the methyl groups dominant and their motions evolving more rapidly with temperature, Fig. 2. Here, the dominant displacements are found for the hydrogen atoms of the terminal methyl groups and the hydrogen atoms of the apical site of the acac ligand. This is replicated in the behaviour of the carbon atoms associated with these hydrogens, the methyl and apical carbons having significantly greater displacement parameters than the carbon atoms directly bonded to the coordinating oxygens. Indeed the mean of the anisotropic displacement parameters for these two atoms types are inseparable. The emergent picture is then of a highly floppy ligand environment around the hydrogen positions, with the Fe coordination sphere more rigidly pinned.

Fig. 1 Molecular structure of Fe(acac)₃ obtained at the indicated temperatures. All ellipsoids are shown at the 50% occupation level; orange = Fe, red = oxygen, grey = carbon and white = hydrogen.

Fig. 2 Temperature dependence of the averaged anisotropic displacement parameters for each of the different types of atom in Fe(acac)₃. The error bars represent the standard deviation across the individual values.

Analysis of the Hirshfeld surface using the CrystalExplorer software, Fig. 3,^32,33 shows that the dominant intermolecular interactions are essentially H⋯H in nature, making up around 62% of the surface, with hydrogen-bonding O⋯H interactions accounting for 24% of the contacts, Fig. 4. The temperature dependence of these contacts is consistent with thermally-activated dynamics which populate excited states in the low-lying hydrogen-bonded configurations.

Fig. 3 Hirshfeld surface of Fe(acac)₃ at T = 3 K. All interactions are shown on a common scale in which close interactions are shown in red (−0.005 Å relative to the Hirshfeld surface) and interactions at the surface are shown in blue.

Fig. 4 Temperature evolution of the dominant intermolecular contacts, H⋯H and O⋯H. The insets show the fingerprint plots of the Hirshfeld surface, specific to the particular interactions.

Inelastic neutron scattering, INS, is a well established technique with numerous manuscripts describing the theory and applications.³⁴ Hydrogenous systems provide INS spectra that are dominated by the scattering from the hydrogen atoms. This is because of first, the incoherent neutron scattering cross-section of hydrogen (ca. 80 barns) is about 20 times greater than that for most other atoms and second, hydrogen, being the lightest atom, tends to have the largest amplitude of motion in the normal mode. The dynamic structure factor that is measured in an INS experiment at low temperature (<20 K) is given by the expression,³⁵

where is the mean square displacement of atom n in mode i; σ_H is the incoherent cross section for a hydrogen atom, and Q is the momentum transfer vector. The empirical parameter γ is an average mean square amplitude of all motions of the hydrogen atoms.

The fact that the INS spectrum is dominated by hydrogen modes is demonstrated in Fig. 5 in which the cross-section for each atom type is calculated based upon the mean square displacement being congruent with the anisotropic displacement parameters obtained from the NPD experiments. The total cross-section summed over all Q, S(ω), can be seen to be dominated by the hydrogen atom motions, >99%, ca. 90% of which is due to the methyl hydrogen motions. As such the experimental data is predominantly methyl-weighted, with only around 8% contribution from the single hydrogen atoms at the apical positions of the acetylacetonate ligand.

Fig. 5 Contribution to S(Q,ω) as determined for thermally-activated dynamics based upon the anisotropic displacement parameters obtained from neutron diffraction. The energy scale assumes equal Boltzmann populations at the temperature at which the structure was obtained.

The main validation of the MD simulations coupled to the measured structures, is the ability to reproduce the measured INS spectra, achieved using the program nMoldyn.³⁶ The measured dynamical structure factor, S(Q,ω) is related to the simulated trajectories via a Fourier transform of the incoherent intermediate scattering function:

where the momentum transfer, Q, and time, t, are on a regular grid, R(0) is the atomic position at t = 0 and b is the total scattering cross-section (in the incoherent approximation). The summation is over all atoms, i, but approximates to a sum over only the hydrogen atoms due to the very large incoherent cross section of H. A comparison of the calculated spectra of the analogues with the spectra measured on IN4 (Fig. 6) shows a reasonable agreement, and is certainly adequate for an assignment of the regions of spectral intensity. It must be noted here that no fitting of the model to the data was performed, Fig. 6 represents a straight comparison of the calculated S(Q,ω) convoluted with an instrument resolution function. In particular, the dominant region of intensity between 13–35 meV is satisfactorily reproduced, along with the acoustic phonons to lower energy. The agreement, without energy scaling, between the measured INS spectrum and that calculated from the MD simulation, which is based solely upon the determined structure and accepted interatomic interactions, provides additional validation of the structural model – this is found to not only to best reproduce the measured diffraction data, but also the molecular dynamics.

Fig. 6 INS spectra obtained at 1.5 K at two incident energies, E_i = 34.9 (filled squares) and 59.6 meV (open circles). The simulated spectrum obtained from MD calculations is superimposed as a solid line.

Conclusion

Fe(acac)₃ has been shown to crystallise in the achiral space group Pbca. There are no structural phase transitions down to 3 K. The molecular dynamics are dominated by the flexibility of the acetylacetonate ligands, with the coordination environment about the Fe centre more rigidly defined. A molecular dynamics simulation was used to reproduce the inelastic neutron scattering spectrum, essentially validating the structural model as determined from the neutron diffraction data.

Acknowledgements

We are grateful to the ILL and ANSTO for providing facilities and beamtime for this investigation. TKE was supported by a UNSW Postgraduate Award.

References

1. R. G. Charles and S. Barnartt, J. Phys. Chem., 1958, 62, 315.
2. T. G. Dunne and F. A. Cotton, Inorg. Chem., 1963, 2, 263.
3. M. K. Chaudhuri and S. K. Ghosh, J. Chem. Soc., Dalton Trans., 1983, 839–840.
4. N. C. Pernicone, J. B. Geri and J. T. York, J. Chem. Educ., 2011, 88, 1323–1327.
5. J. Iball and C. H. Morgan, Acta Crystallogr., 1967, 23, 239–244.
6. H. D. Flack, Helv. Chim. Acta, 2003, 86, 905–921.
7. M. Kabak, A. Elmali, S. Ozbey, O. Atakoi and A. Kenar, Z. Kristallogr., 1996, 211, 831–832.
8. M.-L. Hu, Z.-M. Jin, Q. Miao and L.-P. Fang, Z. Kristallogr. – New Cryst. Struct., 2001, 216, 597–598.
9. P. A. Stabnikov, N. V. Pervukhina, I. A. Baidina, L. A. Sheluudyakpva and S. V. Borisov, J. Struct. Chem., 2007, 48, 186–192.
10. A. Lennartson, Inorg. Chim. Acta, 2011, 365, 451–453.
11. H. D. Flack, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1983, 39, 876–881.
12. T. M. Baker, K. M. Howard, W. W. Brennessel and M. L. Neidig, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2015, 71, m228–m229.
13. U. A. Jayasooriya, J. N. T. Peck, J. E. Barclay, S. M. Hardy, A. I. Chumakov, D. J. Evans, C. J. M. Pickett and V. S. Oganesyan, Chem. Phys. Lett., 2011, 518, 119–123.
14. M. K. Chaudhari, S. K. Dehury, S. S. Dhar, U. Bora, B. M. Choudary and L. K. Mannepalli, United States Patent Application: 0040127690 - Process for Making Metal Acetylacetonates, A120040127690, 2004.
15. J. W. Campbell, J. Appl. Crystallogr., 1995, 28, 228–236.
16. J. W. Campbell, Q. Hao, M. M. Harding, N. D. Nguti and C. J. Wilkinson, Appl. Crystallogr., 1998, 31, 496–502.
17. C. Wilkinson, H. W. Khamis, R. F. D. Stansfield and G. J. McIntyre, J. Appl. Crystallogr., 1988, 21, 471–478.
18. E. Prince, C. Wilkinson and G. J. McIntyre, J. Appl. Crystallogr., 1997, 30, 133–137.
19. J. W. Campbell, J. Habash, J. R. Helliwell and K. Moffat, Inform. Q. Protein Crystallogr., 1986, 18, 23–31.
20. V. Petricek, M. Dusek and L. Palatinus, Jana2006. The crystallographic computing system, Institute of Physics, Praha, Czech Republic, 2006.
21. N. V. Pervukhina, I. A. Baidina, L. A. Sheluudyakpva and S. V. Borisov, J. Struct. Chem., 2007, 48, 186–192.
22. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
23. G. Cicognani, H. Mutka and F. Sacchetti, Physica B, 2000, 276–278, 83–84.
24. LAMP, the Large Array Manipulation Program, http://wwwold.ill.fr/data_treat/lamp/lamp.html.
25. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
26. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558–561.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775.
29. P. E. Blochl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
32. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
33. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816.
34. P. C. H. Mitchell, S. F. Parker and A. J. Ramirez-Cuesta, in Vibrational Spectroscopy with Neutrons: With applications in Chemistry, Biology, Materials Science and Catalysis, World Scientific Publishing, London, 2005.
35. D. A. Braden, S. F. Parker, J. Tomkinson and B. S. Hudson, J. Chem. Phys., 1999, 111, 429–437.
36. G. R. Kneller, V. Keiner, M. Kneller and M. Schiller, Comput. Phys. Commun., 1995, 91, 191–214.

---

Footnote

† CCDC 1471349–1471352. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt00517a

---