On the mechanism of water oxidation catalyzed by a dinuclear ruthenium complex: a quantum chemical study

Abstract

The development of efficient and robust catalysts for H₂O oxidation is an essential element in solar water splitting. The reaction mechanism for a previously reported dinuclear Ru water oxidation catalyst (1) has been investigated in detail through quantum chemical calculations. The predicted mechanism starts from a Ru₂^III,III complex with two aqua ligands. After three sequential oxidations, O–O bond formation occurs at a formal Ru₂^IV,V state via the direct coupling of two adjacent oxo moieties while the water nucleophilic attack mechanism was found to be associated with a higher energy barrier. Two H₂O molecules are then inserted with subsequent release of O₂, which was found to be the rate-limiting step with a barrier of 22.7 kcal mol⁻¹. In a previous work, it was revealed that the ligand scaffold in the studied Ru complex has a non-innocent function. Here, we further highlight this behavior, where the ligand was shown to mediate proton transfer events and accept/donate electrons during the catalytic cycle, which can significantly decrease the redox potentials and facilitate the access to high-valent redox states. This study provides further insight into the H₂O oxidation mechanism and principles for designing improved catalysts for activation of small molecules, such as H₂O.

---

Introduction

The splitting of H₂O into H₂ and O₂ is an appealing solution to solar energy conversion. Here, the development of efficient water oxidation catalysts (WOCs) is a vital element for the construction of catalytic systems capable of converting solar energy to storable fuels.^1–2 To date, several molecular complexes based on Ru,^3–11 Ir,^12–15 Mn,^16–20 Fe,^21–25 Co,^26–30 and Cu,^31–35 have been identified to catalyze the four-electron oxidation of H₂O to O₂ (eqn 1). In addition to the large thermodynamic requirement for oxidizing H₂O, generation of O₂ is kinetically cumbersome, which makes it difficult to develop viable catalysts for this transformation.

A majority of the reported WOCs require a strong sacrificial oxidant, Ce^IV, to drive H₂O oxidation. However, an appealing approach is the incorporation of negatively charged moieties into the ligand scaffolds of the WOCs. This results in WOCs with significantly reduced redox potentials compared to catalysts comprising neutral ligands,^36–40 and enables the use of the mild one-electron oxidant [Ru(bpy)₃]³⁺ (bpy = 2,2′-bipyridine) to drive H₂O oxidation.^41–45 These catalysts possess the ability to generate the essential high-valent metal–oxo species at low redox potentials, which promotes O–O bond formation, either via water nucleophilic attack (WNA) or through the direct coupling (DC) of the metal–oxo units (see Fig. 1).⁴⁶

Fig. 1 Schematic representation of the pathways for O–O bond formation for artificial WOCs. WNA = water nucleophilic attack. DC = direct coupling.

In order to rationally design more efficient WOCs, it is crucial to gain mechanistic insight into how these catalysts promote the oxidation of H₂O and to elucidate how the O–O bond formation event occurs. During the recent years, quantum chemical calculations have been proven to be a powerful tool for studying artificial WOCs. The comprehensive mechanistic quantum chemical studies regarding Ru-based WOCs have generated a wealth of chemical insight, especially in the regard of the mechanistic descriptions and for detailing scenarios for O–O bond formation.^47–49 Our group has recently developed dinuclear Ru^II,III complex 1′ (Fig. 2) housing a hexacoordinating pyrazole-based ligand. The developed Ru complex 1′ was found to promote both chemical and photochemical oxidation of H₂O using either pregenerated or photochemcially generated [Ru(bpy)₃]³⁺-type oxidants.⁵⁰ Preliminary mechanistic studies suggest that H₂O oxidation proceeds through a high-valent Ru^IV,V species as the catalytically competent intermediate for promoting O–O bond formation.⁵¹

Fig. 2 (Left) Molecular structure of dinuclear Ru^II,III complex 1′ and (right) calculated structure.

In the present study, we further explore the mechanistic details associated with dinuclear Ru complex 1′ through quantum chemical calculations. It was found that O–O bond formation takes place at the formal Ru₂^IV,V state, which is also consistent with experiments, via direct coupling of two adjacent oxo units. An alternative mechanism involving the nucleophilic attack of H₂O was associated with a significantly higher barrier. The ligand was shown to be non-innocent by participating in proton transfer processes and by accepting/donating electrons during the catalytic cycle. These findings shed new light on the principles for designing improved catalysts for the multi-electron oxidation of H₂O and the possibility of implementing these key features to other transition metal-based WOCs.

Experimental section

Computational details

The density functional calculations were performed using the hybrid B3LYP⁵² functional, as implemented in the Gaussian 09 code.⁵³ Geometries were optimized with the 6-31G(d,p) basis set for the C, N, O, H elements and the effective core potential SDD⁵⁴ basis set for Ru. Based on these optimized geometries, the final and the solvation energies were calculated as single-point corrections using the SMD⁵⁵ continuum solvation model using the B3LYP*⁵⁶ functional (15 % exact exchange) and a larger basis set, where all elements, except Ru, were described by 6-311+G(2df,2p). It has been shown that B3LYP* gives better results in describing relative energies in transition metal complexes⁵⁶ and also redox potentials in Photosystem II and some synthetic water oxidation catalysts.⁵⁷ For the solvation free energy of H₂O, the experimental value of −6.3 kcal mol⁻¹ is used. The concentration correction of 1.9 kcal mol⁻¹ at room temperature (obtained from the free energy change of 1 mol of an ideal gas from 1 atm (24.5 L mol⁻¹, 298.15 K) to 1 M in the solution phase) was added for all species except H₂O, for which 4.3 kcal mol⁻¹ was used as the standard state of the H₂O solvent is 55.6 M. The values reported here are the B3LYP*-D2 energies, including Gibbs free energy corrections and D2 dispersion correction⁵⁸ from B3LYP.

For the calculation of the redox potentials, exactly the same procedure as in our previous article was used; therefore, only some essential points are repeated here. The experimental absolute redox potential of the [Ru(bpy)₃]³⁺/[Ru(bpy)₃]²⁺ couple (1.26 + 4.281 V)⁵⁹ was used as a reference, which corresponds to an electron affinity of 127.8 kcal mol⁻¹. For the proton-coupled electron transfer processes, the experimental value of −264.0 kcal mol⁻¹ (ref. 60) (corresponding to 1 atm in the gas phase and 1 M in the solution phase) for the solvation free energy of a proton is used.

Results and discussion

Redox properties of Ru complex 1

The redox properties of this catalyst with different ligand compositions have been studied in detail in our previous paper.⁵¹ Importantly, the Pourbaix diagram for Ru complex 1′ was constructed to understand the pH-dependent behavior of redox potentials. Here, we only present the relevant catalytic species at the working pH (pH 7.2). The reaction begins from Ru complex 1 (Ru₂^III,III, Fig. 3), which has four picoline ligands in the axial positions, and one aqua and one hydroxide ligand in the equatorial positions. The Mulliken spin densities on Ru1 and Ru2 are 0.83 and 0.71, respectively. Importantly, the spin density on the designed ligand is 0.38, suggesting a non-innocent behavior of the ligand by stabilizing the two Ru^III centers by electron donation. A strong hydrogen bond can be seen between the aqua and the hydroxide ligands, with a distance of only 1.41 Å.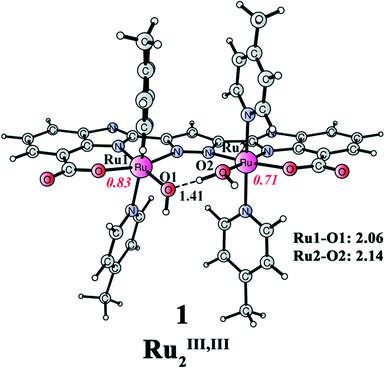

Fig. 3 Optimized structure of dinuclear Ru complex 1 ([(L)Ru₂^III,III(OH₂)(OH)(pic)₄]; total charge of 0). Distances are given in Angstrom and spin densities on the metal are given in red italic.

From complex 1, a proton-coupled electron transfer (PCET) oxidation proceeds to form a formal Ru₂^III,IV complex 2 ([(L)Ru₂^III,IV(O)(OH₂)(pic)₄], Fig. 4). The ground state of intermediate 2 is a quartet with the corresponding doublet at 2.1 kcal mol⁻¹ higher energy. The redox potential for the oxidation of 1 to 2 was calculated to be 0.66 V vs. NHE (see Fig. 13 and Table 1) and is in good agreement with the experimentally obtained value (0.64 V). When the redox potential for the [Ru(bpy)₃]³⁺/[Ru(bpy)₃]²⁺ couple (1.26 V vs. NHE) is used as the reference, the formation of complex 2 by the oxidation of 1 is exergonic by 13.9 kcal mol⁻¹. During the oxidation, both the proton and the electron are released from the Ru1-bound hydroxide as a spin population analysis suggests the generation of an oxyl radical (O1; 0.70, see Table 2). The electronic structure of complex 2 is best described as a low-spin Ru^III (S = 1/2) ferromagnetically coupled to an oxyl radical (S = 1/2) with an additional low-spin Ru^III center (S = 1/2).

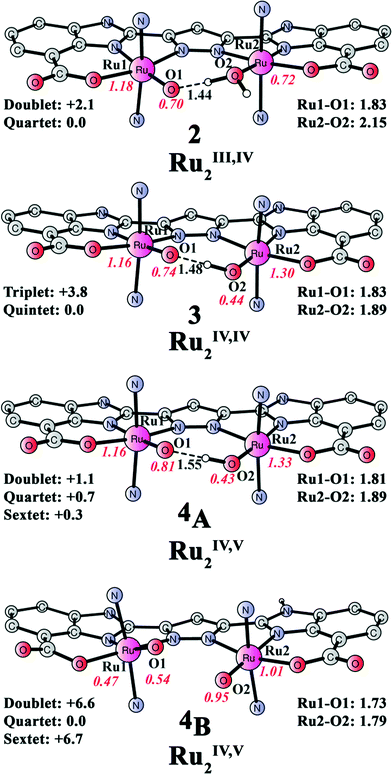Fig. 4 Optimized structures of species 2 ([(L)Ru₂^III,IV(O)(OH₂)(pic)₄]), 3 ([(L)Ru₂^IV,IV(O)(OH)(pic)₄]), and 4 ([(L)Ru₂^IV,V(O)(OH)(pic)₄]). Distances are given in Angstrom and spin densities on selected atoms are indicated in red italic. Relative energies of different spin states are given in kcal mol⁻¹. The energy of 4_A is relative to 4_B. In all intermediates, considerable spin density is localized on the ligand backbone, see Table 2. For clarity, the picoline ligands are represented by nitrogen atoms and unimportant hydrogen atoms are not shown.

Table 1 Comparison of calculated and experimental redox potentials (in V vs. NHE) for dinuclear Ru complex 1 (ref. 50)

	Calculated	Experimental
Ru2^III,IV/Ru2^III,III	0.66	0.64
Ru2^IV,IV/Ru2^III,IV	0.85	0.86
Ru2^V,IV/Ru2^IV,IV	1.14	1.12

---

Table 2 Summary of spin densities on selected atoms and the ligand backbone for various intermediates

Species	Ru1	Ru2	O1	O2	Ligand
1	0.83	0.71	0.08	0.01	0.38
2	1.18	0.72	0.70	0.02	0.40
3	1.16	1.30	0.74	0.44	0.42
4A	1.16	1.33	0.81	0.43	1.32
4B	0.47	1.01	0.54	0.95	0.04
TS1 A	0.83	0.88	0.16	0.01	1.16
Int1 A	0.87	0.84	0.14	0.03	1.16
TS1 B	1.12	0.93	0.10	0.45	0.42
Int1 B	0.13	0.73	−0.08	0.07	0.17
4dp	0.93	0.93	0.93	0.93	−0.71
TS1 dp	1.05	1.05	0.25	0.25	0.43
Int1 dp	0.56	0.56	−0.17	−0.17	0.25
TS2 A	0.98	0.99	0.25	0.05	1.09
TS2 B	1.23	0.96	0.64	0.26	0.26
TS2 dp	0.96	1.27	0.25	0.53	0.33
Int3	0	0	0	0	0
TS3	0.89	0.80	−0.25	−0.48	1.08
Int4	0.65	0.82	−0.27	−0.43	1.24
Int4 dp	−0.76	1.29	0.29	0.61	0.24
TS4	−0.68	1.05	0.55	0.63	0.27

---

The subsequent PCET oxidation, with a redox potential of 0.85 V, leads to the formation of a formal [Ru₂^IV,IV(O)(OH)(pic)₄] species (3, see Fig. 4). Intermediate 3 is a quintet, where the triplet is 3.8 kcal mol⁻¹ higher in energy. Here, a proton is removed from the Ru2-bound aqua molecule and an electron is released from Ru2, thus generating an additional Ru^IV center. However, significant spin delocalization on the hydroxide oxygen (0.44) can be seen and the spin density on Ru2 is merely 1.30.

A subsequent one-electron oxidation occurs to produce the formal [(L)Ru₂^IV,V(O)(OH)(pic)₄] complex 4 (Fig. 4). This redox step was found to be associated with a redox potential of 1.15 V. The direct removal of an electron from species 3 would generate 4_A, in which the doublet, quartet, and sextet are all close in energy. However, proton transfer from the Ru2-bound hydroxide to the imidazole nitrogen (4_B) via deprotonation and reprotonation facilitated by the water solution can slightly lower the energy by 0.3 kcal mol⁻¹. This proton relocation should occur readily and lead to an equilibrium between intermediates 4_A and 4_B. Loss of the proton, which should be plausible at pH 7.2, yields intermediate 4_dp (vide infra). Species 4_B is a quartet, where the doublet and the sextet are 6.6 and 6.7 kcal mol⁻¹ higher in energy, respectively. The generated Ru₂^IV,V intermediate (4, see Fig. 5) has the ability of mediating O–O bond formation, which is also supported experimentally,⁵¹ and will be discussed in the following section. During these three oxidation steps, the total spin density on the designed ligand evolves from 0.38 in 1, to 0.40 in 2, to 0.42 in 3, and further to 1.32 in intermediate 4_A (see Table 2).

Fig. 5 Energetic profile for the formation of Ru₂^IV,V (4). Energies are given in kcal mol⁻¹ and are relative to Ru₂^III,III complex 1.

These results suggest a non-innocent function of the ligand, which can donate electrons during the oxidation and become partially oxidized. By doing this, the redox potentials are significantly decreased and high-valent redox states can be accessed with lower energy requirements. From species 4_A to 4_B, the ligand accepts a proton (highlighted in Fig. 5), which is coupled with an electron transfer from the Ru2-bound hydroxide to the ligand, generating an oxygen radical at O2. The ligand thus facilitates the generation of the second oxygen radical, which is necessary for the following O–O bond formation via direct-coupling.

O–O bond formation by direct coupling at the Ru₂^IV,V state

From Ru₂^IV,V intermediate 4, there are two mechanistic possibilities for O–O bond formation; (1) direct coupling (DC) of two oxo units, or (2) water nucleophilic attack (WNA) by an incoming H₂O molecule on one of the ruthenium-oxo moieties. In this section, the DC mechanism is presented and the alternative WNA mechanism will be presented in the following section.

As shown in Fig. 4, intermediate 4 can exist as two isomers (4_A {[(L)Ru₂^IV,V(O)(OH)(pic)₄]} and 4_B {[(HL)Ru₂^IV,V(O)₂(pic)₄]}). Consequently, O–O bond formation from 4_A takes place via coupling of an oxo and a hydroxide moiety. However, from isomer 4_B, the coupling of two oxo units from isomer 4_B was found to be more favorable (see Fig. 8). These two transition states are labeled as TS1_A and TS1_B, respectively, and are depicted in Fig. 6. For TS1_A, the barriers for the doublet and quartet were calculated to be 17.7 and 16.5 kcal mol⁻¹, respectively, relative to 4_B. For TS1_B, the barrier in the doublet and quartet were found to be significantly lower, 8.6 and 8.5 kcal mol⁻¹, respectively, relative to 4_B. In TS1_B, the critical O1–O2 bond was calculated to be 1.83 Å. The coupling of two oxo units from isomer 4_B is associated with a significantly lower barrier and is thus preferred compared to the coupling of an oxo and a hydroxide moiety from isomer 4_A. This can be realized by comparing the different driving force for the O–O bond formation. The coupling of an oxo and a hydroxide to produce Int1_A is endergonic by as much as 15.1 kcal mol⁻¹, while it is slightly exergonic (1.2 kcal mol⁻¹) for the formation of Int1_B.

Fig. 6 Optimized structures of the transition states of the O–O bond formation via direct coupling from intermediate 4 ([(L)Ru₂^IV,V(O)(OH)(pic)₄]). Energies of the different spin states are given in kcal mol⁻¹ relative to 4_B.

We also considered the deprotonated form 4_dp ([(L)Ru₂^IV,V(O)₂(pic)₄], Fig. 7), as its pK_a was calculated to be 8.2. This suggests that the generation of 4_dp is possible at the working pH (pH 7.2), with an energy penalty of only 1.5 kcal mol⁻¹. Upon deprotonation, a ligand radical is generated at the highly-conjugated planar ligand, as the ligand has a formal total charge of −5. The doublet, quartet, and sextet are close in energy, with a difference of merely ∼0.1 kcal mol⁻¹. The O–O bond formation from 4_dp turns out to be very facile and the transition state TS1_dp (Fig. 7) lies at only +3.2 kcal mol⁻¹ for the quartet (+4.6 kcal mol⁻¹ for the doublet) higher than 4_dp. In TS1_dp, the nascent O1–O2 bond is 1.79 Å and the spin density on both O1 and O2 is 0.25. This is different from that of TS1 in which the spin density on O2 is higher. The resulting peroxido intermediate Int1_dp ([(L)Ru₂^III,IV(O₂)(pic)₄]) has a O–O bond distance of 1.37 Å and is shown in Fig. 7. When the energetic penalty for the deprotonation is added, the total barrier for the O–O bond formation viaTS1_dp becomes 4.7 kcal mol⁻¹, which is 3.8 kcal mol⁻¹ lower than that viaTS1_B. Importantly, the alternative mechanism involving the coupling of an oxo and a hydroxide moiety is highly unfavorable and can be ruled out.

Fig. 7 Optimized structure of stationary points of O–O bond formation via direct coupling from species 4_dp ([(L)Ru₂^IV,V(O)₂(pic)₄]; total charge: 0). Energies of different spin states are given in kcal mol⁻¹ relative to 4_dp.

It is pertinent to mention that O–O bond formation by direct coupling at the Ru₂^IV,IV state has also been considered. The direct coupling of an oxo and a hydroxide moiety from complex 3 (the optimized transition state and intermediate are shown in Fig. S1†) has a barrier of 21.1 kcal mol⁻¹, which is 4.6 kcal mol⁻¹ higher than that from 4_A. The alternative pathway via the coupling of two oxo moieties has an even higher barrier, 24.3 kcal mol⁻¹. These results further confirm that O–O bond formation takes place at the Ru₂^IV,V state.

O–O bond formation by water attack at the Ru₂^IV,V state

The alternative O–O bond formation mechanism via WNA on a ruthenium-oxo moiety was also considered (see Fig. 8). From intermediate 4_A, the Ru2-bound hydroxide can act as a base to promote the abstraction of a proton from the incoming nucleophilic H₂O molecule (transition state TS2_A shown in Fig. 9). The barrier was calculated to be 20.9 kcal mol⁻¹ relative to 4_A + H₂O or 21.2 kcal mol⁻¹ relative to 4_B + H₂O. Similarly, the transition state for H₂O attack on 4_B (TS2_B) was located and is displayed in Fig. 9. In 4_B, the imidazole adjacent to Ru1 is deprotonated while the other imidazole unit close to Ru2 is protonated. This renders O1 more nucleophilic than O2 and thus O2 has a more electrophilic character compared to O1. Therefore, the Ru1–O1 moiety functions as a base to facilitate the nucleophilic attack of H₂O on Ru2–O2. The barrier for this step was calculated to be 21.4 kcal mol⁻¹ relative to 4_B + H₂O. WNA on 4_dp has a slightly lower barrier, being 18.2 kcal mol⁻¹ relative to 4_dp + H₂O. The total barrier becomes 19.7 kcal mol⁻¹ when the energy cost for the deprotonation step is included. These findings show that O–O bond formation via direct coupling is associated with a significantly lower barrier compared to the nucleophilic attack of H₂O on the ruthenium–oxo unit. This is similar to the results observed for the “blue dimer” and the dinuclear Ru-pyrazole catalyst developed by Llobet, in which the direct coupling of two oxo groups is also preferred.^57a

Fig. 8 Energetic profile for O–O bond formation. Energies are given in kcal mol⁻¹ and are relative to Ru₂^III,III complex 1.

Fig. 9 Optimized structures of transition states of O–O bond formation via H₂O attack from intermediates 4 (TS2_A and TS2_B) and 4_dp (TS2_dp). Energies of TS2 and TS2_dp are given in kcal mol⁻¹ relative to 4 + H₂O and 4_dp + H₂O, respectively.

Water insertion into the peroxide intermediate

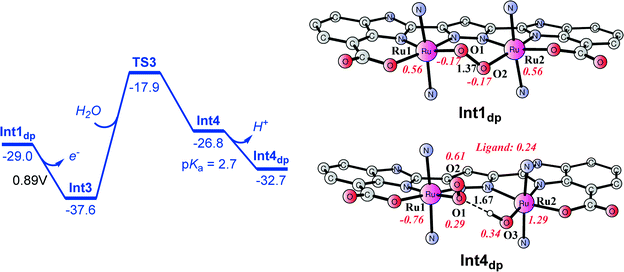
From peroxido intermediate Int1_dp ([(L)Ru₂^III,IV(O₂)(pic)₄]), a very facile one-electron oxidation to generate Int3 ([(L)Ru₂^IV,IV(O₂)(pic)₄]; total charge of +1, Fig. 10) takes place and was calculated to have a potential of 0.89 V, suggesting that this step is exergonic by 8.6 kcal mol⁻¹. The oxidized peroxido species Int3 is a closed-shell singlet, where the triplet and quintet are 8.0 and 3.3 kcal mol⁻¹ higher in energy. A H₂O molecule can then be inserted into Int3via transition state TS3. The barrier for this step was calculated to be 19.7 kcal mol⁻¹ for the triplet state (see Fig. 10), which is dramatically higher than that for the O–O bond formation step (4.7 kcal mol⁻¹). The singlet and quintet pathways were shown to have higher barriers than the triplet (Fig. 10). During the H₂O insertion process, a spin crossing is needed from the singlet to triplet state. In transition state TS3, the distance between the incoming H₂O oxygen O3 and Ru2 is 2.29 Å, while the Ru2–O2 distance is 2.62 Å. The resulting triplet species Int4 ([(L)Ru₂^IV,IV(O₂)(OH₂)(pic)₄]) lies at 10.8 kcal mol⁻¹ relative to Int3 + H₂O. The pK_a of Int4 was calculated to be 2.7, indicating that it is deprotonated at pH 7.2. The deprotonated form is labeled as Int4_dp ([(L)Ru₂^IV,IV(O₂)(OH)(pic)₄]) and is depicted in Fig. 11 and 12. The energetic profile for the H₂O insertion process is depicted in Fig. 11. In Int4_dp, O2 (spin density of 0.61) has a more radical character than O1 (0.29), and therefore a hydrogen bond is formed between the Ru2-bound hydroxide and O1.

Fig. 10 Optimized structures of intermediates and transition state for the H₂O insertion to the peroxide intermediate. Energies of TS3 and Int4 are given in kcal mol⁻¹ relative to Int3 + H₂O.

Fig. 11 Energetic profile for H₂O insertion into peroxido intermediate Int1_dp ([(L)Ru₂^III,IV(O₂)(pic)₄]). Energies are given in kcal mol⁻¹ and are relative to Ru₂^III,III complex 1.

Fig. 12 Optimized structures of intermediates and transition state for O₂ release. Energies of TS4 are given in kcal mol⁻¹ relative to Int4_dp+H₂O.

O₂ release and catalyst regeneration

From the [(L)Ru₂^IV,IV(O₂)(OH)(pic)₄] species Int4_dp, release of O₂ can occur from the Ru1 center, coupled with the binding of a second H₂O molecule. The optimized transition state, TS4, for the release of O₂ is shown in Fig. 12. The barrier was calculated to be 17.8 kcal mol⁻¹ relative to Int4_dp + H₂O, making the total barrier 22.7 kcal mol⁻¹ when taking into account the energetic penalty for the formation of Int4_dp from Int3. We have also tried to include more water molecules to account for the effect of hydrogen bonding during the O₂ release process. The inclusion of one water molecule to bridge the incoming water molecule and the O₂ molecule leads to a slight increase in the barrier by 0.8 kcal mol⁻¹ (see the ESI,† Fig. S2). The addition of a second water molecule to bridge the hydroxide moiety and the O₂ molecule further increases the barrier by 6.8 kcal mol⁻¹. These results suggest that the inclusion of water molecules does not facilitate the ligand exchange. In any case, the O₂ release has a much higher barrier than that for the O–O bond formation. Importantly, this step was determined to be the rate-limiting step for the whole catalytic cycle. The turnover frequency for this catalyst has been experimentally measured to be 1.3 s⁻¹,⁵⁰ which can be converted into a barrier of ∼17 kcal mol⁻¹. Compared with the experimental data, the calculated barrier is somewhat overestimated and may have originated from the density functional and/or the continuum solvation model. At TS4, the Ru1–O1 and Ru1–O4 distances are 2.25 and 2.56 Å, respectively. This step leads to the regeneration of Ru complex 1 and completes the catalytic cycle. The complete energetic profile and catalytic cycle are shown in Fig. 13 and Scheme 1, respectively. Briefly, the consecutive PCET events of the staring complex Ru₂^III,III1 furnishes the oxidized Ru₂^IV,V species 4_dp, which has the ability to trigger O–O bond formation. Here, the direct coupling of the two oxo units was found to be favored over the nucleophilic attack of H₂O on one of the oxo moieties. The direct coupling yields Ru₂^III,IV peroxido species Int1_dp, which loses an electron and one proton to produce the Ru₂^IV,IV intermediate Int4_dp from which O₂ is liberated, regenerating the starting Ru complex 1 to complete the catalytic cycle.

Fig. 13 Energetic profile for H₂O oxidation catalyzed by Ru complex 1. Energies are given in kcal mol⁻¹. To set up the relative energies, 1.26 V vs. NHE (redox potential for [Ru(bpy)₃]³⁺/[Ru(bpy)₃]²⁺) is used as a reference.

Scheme 1 Proposed catalytic cycle for H₂O oxidation by dinuclear Ru complex 1.

Conclusions

In the present paper, the H₂O oxidation mechanism has been investigated for a dinuclear Ru complex by quantum chemical calculations. Relevant redox intermediates, redox potentials, and reaction pathways for O–O bond formation and O₂ release were calculated and compared. H₂O oxidation commences from the Ru₂^III,III complex 1, housing two aqua ligands. Two sequential PCET oxidations lead to the formation of a formal [(L)Ru₂^IV,IV(O)(OH)(pic)₄] complex 3, which is followed by a one-electron oxidation to generate the formal [(HL)Ru₂^IV,V(O)₂(pic)₄] complex 4_B containing two oxo moieties.

O–O bond formation can occur via the direct coupling of the two oxo groups with a barrier of 8.5 kcal mol⁻¹. The alternative scenario, WNA, was determined to have a barrier of 21.2 kcal mol⁻¹, suggesting that this is not a viable pathway. It was also revealed that the deprotonation of Ru₂^IV,V intermediate 4 to form 4_dp ([(L)Ru₂^IV,V(O)₂(pic)₄]) is slightly endergonic and the coupling of the two oxo groups from this intermediate to give Int1_dp has an even lower barrier, being only 4.7 kcal mol⁻¹ when the energy cost for the deprotonation step to produce 4_dp is included.

A subsequent one-electron oxidation of Int1_dp takes place, resulting in the formation of the formal [(L)Ru₂^IV,IV(O₂)(pic)₄] peroxido intermediate Int3. This is followed by H₂O insertion into the peroxido intermediate to generate Int4 ([(L)Ru₂^IV,IV(O₂)(OH₂)(pic)₄]), which can be deprotonated at pH 7.2 as its pK_a was calculated to be 2.7. Finally, insertion of a second H₂O molecule proceeds, concomitant with the release of O₂. This step was calculated to be rate-limiting with a total barrier of 22.7 kcal mol⁻¹.

The computed mechanism involves three key features: generation of a Ru₂^IV,V intermediate, direct coupling of two metal-oxo units, and O₂ release to regenerate the catalyst. For the studied Ru catalyst, the ligand motif was also found to be non-innocent by participating in proton transfer and by accepting/donating electrons during the catalytic process. This strategy can significantly lower the redox potentials and help accessing high-valent oxidation states, which is required for promoting O–O bond formation, and could be a general strategy for designing more efficient metal-based WOCs.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21503083), startup funding from Huazhong University of Science and Technology, the Swedish Research Council (621-2012-2404 and 621-2013-4872), and the Knut and Alice Wallenberg Foundation. Computer time was generously provided by the Swedish National Infrastructure for Computing.

Notes and references

1. M. D. Kärkäs, O. Verho, E. V. Johnston and B. Åkermark, Chem. Rev., 2014, 114, 11863–12001.
2. J. D. Blakemore, R. H. Crabtree and G. W. Brudvig, Chem. Rev., 2015, 115, 12974–13005.
3. L. Alibabaei, B. D. Sherman, M. R. Norris, M. K. Brennaman and T. J. Meyer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5899–5902.
4. H. Li, F. Li, B. Zhang, X. Zhou, F. Yu and L. Sun, J. Am. Chem. Soc., 2015, 137, 4332–4335.
5. T.-T. Li, W.-L. Zhao, Y. Chen, F.-M. Li, C.-J. Wang, Y.-H. Tian and W.-F. Fu, Chem. – Eur. J., 2014, 20, 13957–13964.
6. N. Song, J. J. Concepcion, R. A. Binstead, J. A. Rudd, A. K. Vannucci, C. J. Dares, M. K. Coggins and T. J. Meyer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4935–4940.
7. R. Matheu, L. Francàs, P. Chernev, M. Z. Ertem, V. Batista, M. Haumann, X. Sala and A. Llobet, ACS Catal., 2015, 5, 3422–3429.
8. J. J. Concepcion, D. K. Zhong, D. J. Szalda, J. T. Muckerman and E. Fujita, Chem. Commun., 2015, 51, 4105–4108.
9. M. D. Kärkäs, E. V. Johnston, E. A. Karlsson, B.-L. Lee, T. Åkermark, M. Shariatgorji, L. Ilag, Ö. Hansson, J.-E. Bäckvall and B. Åkermark, Chem. – Eur. J., 2011, 17, 7953–7959.
10. M. Natali, E. Deponti, D. Vilona, A. Sartorel, M. Bonchio and F. Scandola, Eur. J. Inorg. Chem., 2015, 3467–3477.
11. K. Tanaka, H. Isobe, S. Yamanaka and K. Yamaguchi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15600–15605.
12. S. W. Sheehan, J. M. Thomsen, U. Hintermair, R. H. Crabtree, G. W. Brudvig and C. A. Schmuttenmaer, Nat. Commun., 2015, 6, 6469.
13. O. Diaz-Morales, T. J. P. Hersbach, D. G. H. Hetterscheid, J. N. H. Reek and M. T. M. Koper, J. Am. Chem. Soc., 2014, 136, 10432–10439.
14. A. Volpe, A. Sartorel, C. Tubaro, L. Meneghini, M. Di Valentin, C. Graiff and M. Bonchio, Eur. J. Inorg. Chem., 2014, 665–675.
15. J. M. Thomsen, S. W. Sheehan, S. M. Hashmi, J. Campos, U. Hintermair, R. H. Crabtree and G. W. Brudvig, J. Am. Chem. Soc., 2014, 136, 13826–13834.
16. E. A. Karlsson, B.-L. Lee, T. Åkermark, E. V. Johnston, M. D. Kärkäs, J. Sun, Ö. Hansson, J.-E. Bäckvall and B. Åkermark, Angew. Chem., Int. Ed., 2011, 50, 11715–11718.
17. L. Ma, Q. Wang, W.-L. Man, H.-K. Kwong, C.-C. Ko and T.-C. Lau, Angew. Chem., Int. Ed., 2015, 54, 5246–5249.
18. W. A. A. Arafa, M. D. Kärkäs, B.-L. Lee, T. Åkermark, R.-Z. Liao, H.-M. Berends, J. Messinger, P. E. M. Siegbahn and B. Åkermark, Phys. Chem. Chem. Phys., 2014, 16, 11950–11964.
19. J. Limburg, J. S. Vrettos, L. M. Liable-Sands, A. L. Rheingold, R. H. Crabtree and G. W. Brudvig, Science, 1999, 283, 1524–1527.
20. E. A. Karlsson, B.-L. Lee, R.-Z. Liao, T. Åkermark, M. D. Kärkäs, V. Saavedra Becerril, P. E. M. Siegbahn, X. Zou, M. Abrahamsson and B. Åkermark, ChemPlusChem, 2014, 79, 936–950.
21. Z. Codolà, L. Gómez, S. T. Kleespies, L. Que, Jr., M. Costas and J. Lloret-Fillol, Nat. Commun., 2015, 6, 5865.
22. W.-P. To, T. W.-S. Chow, C.-W. Tse, X. Guan, J.-S. Huang and C.-M. Che, Chem. Sci., 2015, 6, 5891–5903.
23. P. Tan, H.-K. Kwong and T.-C. Lau, Chem. Commun., 2015, 51, 12189–12192.
24. M. K. Coggins, M.-T. Zhang, A. K. Vannucci, C. J. Dares and T. J. Meyer, J. Am. Chem. Soc., 2014, 136, 5531–5534.
25. W. C. Ellis, N. D. McDaniel, S. Bernhard and T. J. Collins, J. Am. Chem. Soc., 2010, 132, 10990–10991.
26. B. Das, A. Orthaber, S. Ott and A. Thapper, Chem. Commun., 2015, 51, 13074–13077.
27. T. Nakazono, A. R. Parent and K. Sakai, Chem. – Eur. J., 2015, 21, 6723–6726.
28. X. Zhou, F. Li, H. Li, B. Zhang, F. Yu and L. Sun, ChemSusChem, 2014, 7, 2453–2456.
29. H. Jia, Z. Sun, D. Jiang and P. Du, Chem. Mater., 2015, 27, 4586–4593.
30. H.-Y. Wang, E. Mijangos, S. Ott and A. Thapper, Angew. Chem., Int. Ed., 2014, 53, 14499–14502.
31. X.-J. Su, M. Gao, L. Jiao, R.-Z. Liao, P. E. M. Siegbahn, J.-P. Cheng and M.-T. Zhang, Angew. Chem., Int. Ed., 2015, 54, 4909–4914.
32. P. Garrido-Barros, I. Funes-Ardoiz, S. Drouet, J. Benet-Buchholz, F. Maseras and A. Llobet, J. Am. Chem. Soc., 2015, 137, 6758–6761.
33. J. S. Pap, Ł. Szyrwiel, D. Srankó, Z. Kerner, B. Setner, Z. Szewczuk and W. Malinka, Chem. Commun., 2015, 51, 6322–6324.
34. D. L. Gerlach, S. Bhagan, A. A. Cruce, D. B. Burks, I. Nieto, H. T. Truong, S. P. Kelley, C. J. Herbst-Gervasoni, K. L. Jernigan, M. K. Bowman, S. Pan, M. Zeller and E. T. Papish, Inorg. Chem., 2014, 53, 12689–12698.
35. M.-T. Zhang, Z. Chen, P. Kang and T. J. Meyer, J. Am. Chem. Soc., 2013, 135, 2048–2051.
36. L. Duan, F. Bozoglian, S. Mandal, B. Stewart, T. Privalov, A. Llobet and L. Sun, Nat. Chem., 2012, 4, 418–423.
37. D. L. Ashford, B. D. Sherman, R. A. Binstead, J. L. Templeton and T. J. Meyer, Angew. Chem., Int. Ed., 2015, 54, 4778–4781.
38. A. C. Sander, S. Maji, L. Francàs, T. Böhnisch, S. Dechert, A. Llobet and F. Meyer, ChemSusChem, 2015, 8, 1697–1702.
39. X. Ding, Y. Gao, L. Zhang, Z. Yu, J. Liu and L. Sun, ACS Catal., 2014, 4, 2347–2350.
40. M. V. Sheridan, B. D. Sherman, Z. Fang, K.-R. Wee, M. K. Coggins and T. J. Meyer, ACS Catal., 2015, 5, 4404–4409.
41. M. D. Kärkäs, T. Åkermark, E. V. Johnston, S. R. Karim, T. M. Laine, B.-L. Lee, T. Åkermark, T. Privalov and B. Åkermark, Angew. Chem., Int. Ed., 2012, 51, 11589–11593.
42. M. D. Kärkäs, T. Åkermark, H. Chen, J. Sun and B. Åkermark, Angew. Chem., Int. Ed., 2013, 52, 4189–4193.
43. W. Rabten, M. D. Kärkäs, T. Åkermark, H. Chen, R.-Z. Liao, F. Tinnis, J. Sun, P. E. M. Siegbahn, P. G. Andersson and B. Åkermark, Inorg. Chem., 2015, 54, 4611–4620.
44. M. D. Kärkäs, R.-Z. Liao, T. M. Laine, T. Åkermark, S. Ghanem, P. E. M. Siegbahn and B. Åkermark, Catal. Sci. Technol., 2016, 6, 1306–1319.
45. W. Rabten, T. Åkermark, M. D. Kärkäs, H. Chen, J. Sun, P. G. Andersson and B. Åkermark, Dalton Trans., 2016, 45, 3272–3276.
46. X. Sala, S. Maji, R. Bofill, J. García-Antón, L. Escriche and A. Llobet, Acc. Chem. Res., 2014, 47, 504–516.
47. For quantum chemical calculations on single-site Ru-based water oxidation catalysts, see for example: (a) Y. Wang and M. S. G. Ahlquist, Dalton Trans., 2014, 43, 13776–13782; (b) R. Kang, K. Chen, J. Yao, S. Shaik and H. Chen, Inorg. Chem., 2014, 53, 7130–7136; (c) Z.-L. Lang, G.-C. Yang, N.-N. Ma, S.-Z. Wen, L.-K. Yan, W. Guan and Z.-M. Su, Dalton Trans., 2013, 42, 10617–10625; (d) L. Vigara, M. Z. Ertem, N. Planas, F. Bozoglian, N. Leidel, H. Dau, M. Haumann, L. Gagliardi, C. J. Cramer and A. Llobet, Chem. Sci., 2012, 3, 2576–2586; (e) L. Tong, Y. Wang, L. Duan, Y. Xu, X. Cheng, A. Fischer, M. S. G. Ahlquist and L. Sun, Inorg. Chem., 2012, 51, 3388–3398; (f) J. L. Valles-Pardo, M. C. Guijt, M. Iannuzzi, K. S. Joya, H. J. M. de Groot and F. Buda, ChemPhysChem, 2012, 13, 140–146; (g) X. Lin, X. Hu, J. J. Concepcion, Z. Chen, S. Liu, T. J. Meyer and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15669–15672; (h) L. Wang, L. Duan, B. Stewart, M. Pu, J. Liu, T. Privalov and L. Sun, J. Am. Chem. Soc., 2012, 134, 18868–18880; (i) T. F. Hughes and R. A. Friesner, J. Phys. Chem. B, 2011, 115, 9280–9289; (j) T. Privalov, B. Åkermark and L. Sun, Chem. – Eur. J., 2011, 17, 8313–8317; (k) X. Sala, M. Z. Ertem, L. Vigara, T. K. Todorova, W. Chen, R. C. Rocha, F. Aquilante, C. J. Cramer, L. Gagliardi and A. Llobet, Angew. Chem., Int. Ed., 2010, 49, 7745–7747; (l) J. Nyhlén, L. Duan, B. Åkermark, L. Sun and T. Privalov, Angew. Chem., Int. Ed., 2010, 49, 1773–1777.
48. For quantum chemical calculations on dinuclear Ru-based water oxidation catalysts, see for example: (a) H. Isobe, K. Tanaka, J.-R. Shen and K. Yamaguchi, Inorg. Chem., 2014, 53, 3973–3984; (b) I. Lopez, M. Z. Ertem, S. Maji, J. Benet-Buchholz, A. Keidel, U. Kuhlmann, P. Hildebrandt, C. J. Cramer, L. Gagliardi and A. Llobet, Angew. Chem., Int. Ed., 2014, 53, 205–209; (c) R. Bianco, P. J. Hay and J. T. Hynes, J. Phys. Chem. B, 2013, 117, 15761–15773; (d) S. Ghosh and M.-H. Baik, Angew. Chem., Int. Ed., 2012, 51, 1221–1224; (e) R. Bianco, P. J. Hay and J. T. Hynes, Energy Environ. Sci., 2012, 5, 7741–7746; (f) X. Li, G. Chen, S. Schinzel and P. E. M. Siegbahn, Dalton Trans., 2011, 40, 11296–11307; (g) R. Bianco, P. J. Hay and J. T. Hynes, J. Phys. Chem. A, 2011, 115, 8003–8016; (h) F. Bozoglian, S. Romain, M. Z. Ertem, T. K. Todorova, C. Sens, J. Mola, M. Rodriguez, I. Romero, J. Benet-Buchholz, X. Fontrodona, C. J. Cramer, L. Gagliardi and A. Llobet, J. Am. Chem. Soc., 2009, 131, 15176–15187; (i) X. Yang and M.-H. Baik, J. Am. Chem. Soc., 2008, 130, 16231–16240; (j) X. Yang and M.-H. Baik, J. Am. Chem. Soc., 2006, 128, 7476–7485.
49. For quantum chemical calculations on a tetranuclear Ru-based water oxidation catalysts, see: S. Piccinin, A. Sartorel, G. Aquilanti, A. Goldoni, M. Bonchio and S. Fabris, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4917–4922.
50. T. M. Laine, M. D. Kärkäs, R.-Z. Liao, T. Åkermark, B.-L. Lee, E. A. Karlsson, P. E. M. Siegbahn and B. Åkermark, Chem. Commun., 2015, 51, 1862–1865.
51. T. M. Laine, M. D. Kärkäs, R.-Z. Liao, P. E. M. Siegbahn and B. Åkermark, Chem. – Eur. J., 2015, 21, 10039–10048.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
54. D. Andrae, U. Häuβermann, M. Dolg, H. Stoll and H. Preuβ, Theor. Chim. Acta, 1990, 77, 123–141.
55. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
56. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55.
57. (a) X. Li, G. Chen, S. Schinzel and P. E. M. Siegbahn, Dalton Trans., 2011, 40, 11296–11307; (b) P. E. M. Siegbahn and M. R. A. Blomberg, J. Chem. Theory Comput., 2014, 10, 268–272; (c) R.-Z. Liao, X. Li and P. E. M. Siegbahn, Eur. J. Inorg. Chem., 2014, 728–741; (d) R.-Z. Liao and P. E. M. Siegbahn, ACS Catal., 2014, 4, 3937–3949; (e) R.-Z. Liao, M. D. Kärkäs, B.-L. Lee, B. Åkermark and P. E. M. Siegbahn, Inorg. Chem., 2015, 54, 342–351.
58. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
59. A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899.
60. D. M. Camaioni and C. A. Schwerdtfeger, J. Phys. Chem. A, 2005, 109, 10795–10797.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates for optimized structures. See DOI: 10.1039/c6cy00083e

---