 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fe/γ-Al2O3 and Fe–K/γ-Al2O3 as reverse water-gas shift catalysts†
Jason A.
Loiland
a,
Matthew J.
Wulfers
a,
Nebojsa S.
Marinkovic
b and
Raul F.
Lobo
*a
aCenter for Catalytic Science and Technology, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA. E-mail: lobo@udel.edu; Fax: +302 831 1048; Tel: +302 831 1261
bDepartment of Chemical Engineering, Columbia University, New York, NY 10027, USA
First published on 15th January 2016
Abstract
The reverse water-gas shift (RWGS) reaction was investigated on Fe/γ-Al2O3 and Fe–K/γ-Al2O3 catalysts at temperatures between 723 K and 753 K and atmospheric pressure. Both materials exhibited fast catalytic CO formation rates and high CO selectivity (>99%). Reaction rates displayed a strong dependence on H2 partial pressure (reaction orders of 0.58 and 0.54 on Fe/γ-Al2O3 and Fe–K/γ-Al2O3, respectively), and a weak dependence on CO2 partial pressure (reaction orders of 0.37 and 0.21, respectively) under nearly equimolar CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 composition. The catalysts were stable under excess H2 but deactivated slowly (1–2% h−1 of the overall reaction rate) under an equimolar mixture of CO2 and H2. Addition of potassium to the Fe/γ-Al2O3 material (Fe/K mass ratio = 1.24) led to a threefold increase in reaction rate, but also doubled the deactivation rate (CO2
H2 composition. The catalysts were stable under excess H2 but deactivated slowly (1–2% h−1 of the overall reaction rate) under an equimolar mixture of CO2 and H2. Addition of potassium to the Fe/γ-Al2O3 material (Fe/K mass ratio = 1.24) led to a threefold increase in reaction rate, but also doubled the deactivation rate (CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Gas-switching experiments (CO2 or H2 only) and DRIFTS spectra collected in situ showed that stable intermediates formed on Fe–K/Al2O3 but not on Fe/Al2O3. This suggests, although does not prove, that a redox mechanism is the only reaction pathway on the Fe/Al2O3 catalyst, and is the predominant pathway on the Fe–K/Al2O3 catalyst. The potassium promoter activates a secondary pathway for CO formation, which may be the so-called associative pathway.
1). Gas-switching experiments (CO2 or H2 only) and DRIFTS spectra collected in situ showed that stable intermediates formed on Fe–K/Al2O3 but not on Fe/Al2O3. This suggests, although does not prove, that a redox mechanism is the only reaction pathway on the Fe/Al2O3 catalyst, and is the predominant pathway on the Fe–K/Al2O3 catalyst. The potassium promoter activates a secondary pathway for CO formation, which may be the so-called associative pathway.
1. Introduction
The reverse-water gas shift (RWGS) reaction (eqn (1)) is the reaction of carbon dioxide (CO2) and hydrogen (H2) to form carbon monoxide (CO) and water (H2O). The reaction is endothermic (ΔH°298 = 41.2 kJ mol−1) and the chemical equilibrium favors CO and H2O as the temperature increases. The water-gas shift (WGS) reaction should be mechanistically related to the RWGS reaction through the principle of microscopic reversibility, and has been investigated in great detail on many catalysts. With the growing importance of limiting anthropogenic CO2 emissions, the RWGS reaction presents a straightforward alternative for the reduction of CO2 to CO if an economically viable and carbon-neutral source of H2 can be developed.CO2 + H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⇌ ⇌![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO + H2O CO + H2O | (1) |
The WGS reaction is carried out on an industrial scale in two reactors connected in series; the first reactor is operated at “high temperature” (623–723 K) and uses FexOy-based catalysts with various promoters (Pt, Cu, Ag, Ba, K, Cr, etc.) and supports (Cr2O3, CeO2–ZrO2, MnO).1 Magnetite is believed to be the active phase of iron under high temperature WGS conditions, and, when promoted with chromium, is the customary industrial catalyst for the high-temperature WGS reaction.2 Chromium is a structural promoter that helps prevent the iron from sintering.3,4 The second WGS reactor is operated at “low temperature” (453–523 K) and uses Cu–Zn/Al2O3 as the catalyst.5
In addition to WGS, supported iron is known to catalyze the RWGS reaction6 and a number of other industrially important reactions, including: i) Fischer–Tropsch synthesis,7 ii) ammonia synthesis,8 iii) ethylbenzene dehydrogenation to styrene,9 and iv) selective catalytic reduction of nitrogen oxides (NOx) with ethanol (EtOH-SCR).10 The RWGS and WGS reactions are often carried out in conjunction with Fischer–Tropsch synthesis on iron catalysts,11 in which case iron carbide is believed to be the active phase for hydrocarbon production,12 and iron oxide is the active phase for WGS and RWGS.1
Promoters are often used with iron catalysts to enhance Fischer–Tropsch or RWGS rates and tune the selectivity to the desired products.13–17 One known effect of potassium on iron is an increased CO2 adsorption capacity.12 Alkali metals are considered electronic promoters, as they can facilitate electron transfer and enhance electrostatic interactions with reacting molecules.18,19 Chen et al showed that for RWGS on Cu/SiO2, promotion with potassium leads to the creation of new active sites at the copper–potassium interface.20 Structural promoters such as Cr or Al are often used to prevent iron from sintering.12,21
Two key issues remain unresolved in regard to the WGS and RWGS reaction mechanism(s): i) distinction between the ‘redox’ and ‘associative’ mechanisms, and ii) determination of the structure of the carbon-containing intermediate in the associative mechanism. The redox and associative models were proposed in 1920 by Armstrong and Hilditch,22 and provided the basis for many subsequent investigations with different catalysts.9,23–26 Temkin and coworkers proposed that the redox mechanism is active for the WGS reaction on iron catalysts promoted with chromium.27–29 In this mechanism, the catalyst is first reduced by adsorbed H2 (or CO in WGS), and is subsequently oxidized by CO2 (or H2O in WGS) to complete the redox cycle. A distinguishing feature of the redox mechanism is that the products can be generated in the absence of either reactant (as in a reactant switching-type experiment). The associative mechanism is a Langmuir–Hinshelwood (LMHW) type mechanism, and was suggested by Oki and coworkers to be the dominant mechanism for the WGS reaction on iron oxide catalysts.30,31 In this mechanism, both reactants must be adsorbed on the catalyst surface at the same time to create products. A number of carbon-containing intermediates have been proposed for the associative mechanisms, the most frequently suggested being a formate species.32 Other suggested intermediates include carbonate,33 carbonyl,34 and carboxyl35 species.
In this report it is shown that iron supported on alumina (Fe/Al2O3) is a highly selective catalyst for the RWGS reaction at temperatures between 723 K and 753 K. It is also shown that the specific rate (per gram of material) is enhanced by addition of potassium. While it is not possible to establish the precise role(s) of potassium on a molecular level, it is shown that addition of potassium i) enhances reaction rates, ii) leads to the formation of stable carbon-containing surface species, and iii) changes the catalyst behavior during H2/CO2 gas switching experiments. It is suggested that the simple redox and associative mechanisms are insufficient to explain the observations from the gas-switching experiments, and a more complex reaction model is proposed.
2. Experimental
2.1 Materials
Fe/Al2O3 and Fe–K/Al2O3 were prepared using the wetness impregnation method. Gamma alumina (γ-Al2O3, Alfa Aesar, 99.97%) was added to an aqueous solution of 0.1 M iron nitrate (Fe(NO3)3·9H2O, Aldrich, 99.99%), with or without potassium carbonate (K2CO3, Sigma Aldrich, ≥99.0%), and the mixture was stirred with a magnetic stir bar at room temperature for 1 h. The quantities of metal precursor and γ-Al2O3 added to each solution are given in Table S1;† the final elemental composition of the samples was determined by ICP-OES (Galbraith Laboratories, TN). The suspension was then heated to 353 K to evaporate water, and the resulting slurry was dried in a static oven at a temperature of 383 K for 24 h in air. The dried samples were subsequently calcined in a Thermolyne furnace in air by heating at a rate of 300 K h−1 to 823 K and holding at that temperature for 4 h. Hematite (Fe2O3, Aldrich, 99.99%) and iron foil were used as standards for X-ray absorption near edge structure (XANES) experiments. Magnetite (Fe3O4, Aldrich, 99.99%) was used as a catalyst for comparison to the alumina-supported catalysts. Gases used were: CO2 (Keen, Grade 5.0), H2 (Matheson, UHP), helium (He, Keen, Grade 5.0), argon (Ar, Keen, Grade 5.0) and D2 (Cambridge Isotopes, 99.6% gas purity, 99.8% isotope purity). Potassium bromide (KBr, Alfa Aesar, spectroscopy grade) was used as the background in DRIFTS experiments.2.2 Analytical
X-Ray Diffraction (XRD) patterns of catalyst powders were collected at room temperature on a Philips X'pert diffractometer using Cu Kα radiation (λ = 1.5418 Å). Measurements were taken over the range of 5° < 2θ < 80° with a step size of 0.02° and a count time of 2 s at each step. Physisorption of N2 was performed using a Micromeritics 3Flex instrument at a temperature of 77 K. The Brunauer–Emmett–Teller (BET) surface areas were calculated from data points at relative pressures (p/p0) between 0.05 and 0.25. Before adsorption, samples were degassed under vacuum (P < 150 mTorr) for 8 h at a temperature of 573 K. An Auriga 60 high resolution focused ion beam and scanning electron microscope (SEM) was used to collect SEM micrographs and energy-dispersive X-ray (EDX) spectra to provide information regarding sample morphology and elemental composition, respectively. The microscope was operated at an accelerating voltage of 3–10 kV and a current of 10 μA.2.3 Flow apparatus used for kinetics and gas-switching experiments
Reaction rate and selectivity were evaluated using a packed-bed microreactor operated in down-flow mode. Gas flows through the reactor were controlled by mass flow controllers (Brooks Instrument). Catalyst powders were pressed and sieved to obtain particle sizes within the range of 250–425 μm; the catalyst particles were supported on a quartz wool plug within a quartz tube reactor (7 mm I.D.). The quartz tube was placed inside a ceramic radiant full cylinder heater (Omega, CRFC-26/120-A), and the reaction temperature was controlled by an Omega CN/74000 temperature controller using the input from a thermocouple (Omega, K-type, 1/16 in diameter) placed around the outside of the quartz tube at the middle of the catalyst bed. Gas transfer lines for the effluent stream were heated to a temperature above 373 K and vented to atmospheric pressure. The composition of the effluent stream was analyzed online either by a gas chromatograph (GC, Agilent, 7890A) during continuous flow experiments or a mass spectrometer (MS, Pfeiffer, GSD320) during gas switching experiments. The GC was equipped with both a thermal conductivity detector (TCD) and a flame-ionization detector (FID). The TCD was used to quantify CO2, CO, and H2 concentrations, and the FID was used to quantify hydrocarbon concentrations. A Hayesep Q column (Agilent, 2 mm ID × 12 ft) was used in the GC to separate products quantified with the TCD, and a HP-Plot Q column (Agilent, 0.32 mm ID × 30 m) was used to separate products quantified with the FID.2.4 Measurement of product formation rates
Catalyst samples were pretreated before all experiments in the microreactor by increasing the reactor temperature at a rate of 5 K min−1 to 773 K in a gas flow containing 10 kPa H2. After being held at 773 K for 2 h, the temperature was lowered to the initial reaction temperature. The total flow rate under all conditions, including pretreatment, was 75 sccm. Helium was used as the balance gas.Rates of CO formation were calculated assuming differential reactor operation according to eqn (2):
 | (2) |
| robs. = r+ − r− = r+(1 − η) | (3) |
 | (4) |
 | (5) |
Experiments were designed to i) determine reaction rates in excess (i.e. non-equimolar) CO2 or H2, and ii) determine kinetic parameters. In the first case, CO2 and H2 were fed to the catalyst—4.5% Fe/Al2O3 (43 mg) or 4.2% Fe–3.4% K/Al2O3 (23 mg)—with the reactor temperature held at 753 K. The initial partial pressures of both CO2 and H2 were 15 kPa. After a break-in period of 15 h, the partial pressure of CO2 was increased to 60 kPa, while the partial pressure of H2 was held at 15 kPa. After another period of 3 h, the partial pressure of CO2 was decreased to 15 kPa and the partial pressure of H2 was increased to 60 kPa. Finally, both partial pressures were returned to 15 kPa. CO2 conversion was quantified under the same conditions on a sample of magnetite (100 mg) and γ-Al2O3 (98 mg), but only with CO2 and H2 partial pressures of 15 kPa.
For the second case, kinetic parameters were determined with near equimolar concentrations of CO2 and H2 on both 4.5% Fe/Al2O3 (45 mg) and 4.2% Fe–3.4% K/Al2O3 (22 mg), and under large H2 excess on both 4.5% Fe/Al2O3 (42 mg) and 4.2% Fe–3.4% K/Al2O3 (23 mg). With equimolar or near equimolar concentrations of CO2 and H2, the reaction was first performed for 15–16 h at a temperature of 753 K with reactant partial pressures of 15 kPa. The temperature was then lowered in 10 K increments to 723 K, with 5–6 GC injections (a period of about 60 min) taken at each temperature. After the period at 723 K, the CO2 partial pressure was reduced to 10 kPa and increased in 2.5 kPa increments to a final partial pressure of 20 kPa. Finally, the CO2 partial pressure was returned to 15 kPa and the H2 partial pressure was lowered to 10 kPa and increased in 2.5 kPa increments. The basic outline of the experiments conducted with excess H2 was the same as that used for near equimolar reactant concentrations. Reactant partial pressures during the initial period were 90 kPa H2 and 10 kPa CO2. During the variable CO2 partial pressure period, the H2 partial pressure was maintained at 85 kPa and the CO2 partial pressure was varied between 5 kPa and 12.5 kPa in 2.5 kPa increments. To investigate the effect of H2 partial pressure, the CO2 partial pressure was kept at 10 kPa and the H2 partial pressure was varied between 70–90 kPa in 5 kPa increments. At the end of the experiments, and several times throughout, reaction parameters were returned to a condition that had already been tested to determine if deactivation had occurred.
The kinetic isotope effect (KIE) of H2/D2 was investigated on 4.5% Fe/Al2O3 (42 mg) and 4.2% Fe–3.4% K/Al2O3 (24 mg). After pretreatment, the reaction began at a temperature of 753 K with CO2 and H2 partial pressures of 15 kPa. After 16 h, the temperature was lowered to 723 K and, after 1.5 h, H2 in the feed was replaced by D2.
2.5 Measurement of reaction rates with intermittent CO2 and H2 flows
CO formation rates were measured while alternating between CO2 and H2 gas flows. Catalysts were pretreated as described in section 2.4, with a minor difference being that the gas flow rates were 36 sccm He and 4 sccm H2. After pretreatment, the H2 flow was stopped and was replaced by 4 sccm of CO2. After 20 min, CO2 in the gas stream was replaced by H2. This sequence was repeated three times. The reactor was then purged with He for 20 min before CO2 was readmitted to the gas stream. After 20 min, the reactor was again purged with He before H2 was readmitted to the gas stream. All sequences with a given gas composition lasted for 20 min, and the temperature of the reactor was held at 773 K throughout the duration of the gas switching portion of the experiment. All gas switches were performed by simultaneously turning off the mass flow controller of the reactant gas flowing into the reactor and turning on the mass flow controller of the other reactant. The hydrodynamic behavior of the gas flow during the transient experiments was analysed in a separate experiment by switching the flow from 10% H2/He to 10% CO2/1% Ar/He. The response time of the inert Ar (m/z = 40) relative to those of the products formed during the reaction was monitored to ensure that no artifacts were present.Additional gas-switching experiments involving purge times of varying length with an inert gas (Ar) were carried out on Fe/Al2O3 at 753 K. Following a reduction of the catalyst in 10 kPa H2 for 2 h at 773 K, 15 kPa CO2 was admitted to the reactor. After 20 min, CO2 was replaced by 15 kPa H2 for 20 min. Then, the reactor was purged with Ar for 5 min. This sequence (CO2 → H2 → Ar) was repeated several times, but each time the length of the inert purge was increased by 5 min. After the inert purge reached 20 min, the cycle was repeated a final time with a 5 min inert purge to monitor any effects from catalyst deactivation.
2.6 Diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) measurements
Infrared (IR) spectra were collected with a Nicolet Nexus 470 spectrometer equipped with a mercury cadmium telluride (MCT) detector. A Praying Mantis accessory (Harrick Scientific) was used in conjunction with a HVC-VUV environmental chamber (Harrick Scientific) to collect diffuse reflectance spectra. Catalyst powders were held in the chamber on top of a wire mesh screen, and gases were delivered to the chamber by mass flow controllers. Potassium bromide was heated in the chamber to a temperature of 723 K under He flow and used to collect the background spectrum. Potassium bromide was also used to dilute catalyst samples in a mass ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Catalysts were pretreated by heating from room temperature to 773 K at a rate of 5 K min−1 and holding at that temperature for 2 h in a flow of 30 sccm He and 10 sccm H2. The temperature of the chamber was then lowered to 723 K and the reactant gas in the feed was switched between H2 and CO2 two times, in 30 min intervals, for a total of two periods in CO2 flow. After the final period in CO2 flow, the chamber was purged with He. The IR spectra presented are the average of 128 scans collected with a resolution of 2 cm−1.
1. Catalysts were pretreated by heating from room temperature to 773 K at a rate of 5 K min−1 and holding at that temperature for 2 h in a flow of 30 sccm He and 10 sccm H2. The temperature of the chamber was then lowered to 723 K and the reactant gas in the feed was switched between H2 and CO2 two times, in 30 min intervals, for a total of two periods in CO2 flow. After the final period in CO2 flow, the chamber was purged with He. The IR spectra presented are the average of 128 scans collected with a resolution of 2 cm−1.
2.7 X-ray absorption near-edge structure (XANES) spectroscopy
XANES spectra were collected at the National Synchrotron Light Source (NSLS) at Brookhaven National Laboratory on beamline X18A. Spectra of iron standards with known oxidation states (hematite and metallic iron) were collected after placing the materials on Kapton tape. In situ experiments were performed using the apparatus previously described by Paredis et al.36 About 15 mg of catalyst was used in all experiments.In situ experiments were performed after an initial reduction. During reaction, gas flows consisted of either i) an equimolar mixture of CO2 and H2, or ii) alternating flows of CO2 and H2. For continuous flow experiments, the temperature was increased from room temperature to 823 K under a gas flow consisting of 5 sccm H2 and 5 sccm He. After a period of time in which the iron was almost completely reduced to Fe2+ (see below), He in the feed was replaced by CO2. For experiments in which the flow was alternated between CO2 and H2, the temperature was increased to 773 K under a gas flow of 2 sccm H2 and 8 sccm He and held at that temperature until the iron was almost completely reduced to Fe2+. Then, the catalyst was purged for 15 min with He, and 2 sccm of CO2 was added to the feed. The reactor was then purged with He for another 15 min before 2 sccm of H2 was added to the feed.
XANES data were analysed using the Athena extension of IFEFFIT software. All spectra were normalized by adjusting the pre- and post-edge line parameters in Athena so the regression lines passed through the middle of the data in their respective regions. Iron oxidation states and Fe3+/Fetot ratios were estimated by linear-combination fitting (LCF) analysis, assuming that the collected data are linear combinations of Fe2+ and Fe3+. The edge energies (Eo) for Fe0 and Fe3+ were determined from the standard materials to be 7111.9 eV and 7123.5 eV, respectively. These values correspond to the energies with the maximum first derivatives, and provide a linear relation that relates the oxidation state of iron to the edge energy. Then, the edge energies of spectra collected during the in situ measurements were determined and fit to the linear relation to quantify the amounts of Fe2+ and Fe3+ present in the samples.
3. Results
3.1 Elemental composition and dispersion of iron in supported catalysts
Table 1 summarizes the elemental compositions and surface areas of the catalyst samples. Iron loadings were between 0.9 and 9.1%, and were within 10% of their nominal values (see Table S1†). The surface areas of all supported iron samples were 60–80 m2 g−1, with most samples having a surface area slightly below that of γ-Al2O3 (a representative adsorption isotherm is shown in Fig. S1†). In general, increased potassium loading led to a reduction in surface area by 10–20%. Powder XRD patterns (see Fig. S2†) showed no reflections indicating the presence of bulk iron or iron oxides in the samples. Elemental mapping images (see Fig. S3 and S4†) revealed a uniform distribution of iron and potassium, consistent with the absence of bulk iron diffraction peaks in the XRD patterns.| Material | Fea (wt%) | Ka (wt%) | Surface areab (m2 g−1) |
|---|---|---|---|
| a Determined from elemental analysis (ICP-OES, Galbraith Laboratories). b Brauner–Emmett–Teller (BET) surface area from N2 adsorption isotherm. | |||
| 1Fe 3K | 0.9 | 3.5 | 69.7 |
| 4Fe | 4.5 | — | 79.0 |
| 10Fe | 9.1 | — | 76.1 |
| 8Fe 3K | 7.7 | 3.4 | 65.1 |
| 5Fe 1K | 6.7 | 2.3 | 68.3 |
| 4Fe 4K | 4.2 | 3.4 | 60.5 |
| γ-Al2O3 | — | — | 77.4 |
3.2 Reaction rates and stability of Fe/Al2O3, Fe–K/Al2O3, and bulk iron oxide
Fig. 1 shows catalytic CO formation rates on Fe/Al2O3, Fe–K/Al2O3, and bulk iron oxide. Bare γ-Al2O3 catalyzed CO formation with a rate of 3 mmol h−1 g−1, which was lower than the rates on all other samples by at least an order of magnitude (data not shown). Bulk iron oxide was loaded as magnetite (Fe3O4), and, after a short induction period, produced CO at a steady rate of 30 mmol h−1 g−1, which was the lowest specific rate on any of the iron-containing materials. The selectivity to CO on all of the materials under equimolar CO2 and H2 was always greater than 99%, methane (CH4) being the only minor side product. 4.5% Fe/Al2O3 catalyzed CO formation with an initial rate of 50 mmol h−1 g−1, higher than the rate on bulk iron oxide, but deactivated at a nearly linear rate of 0.48 mmol h−1 g−1 per h. The initial rate of CO formation on 4.2% Fe–3.4% K/Al2O3 was 140 mmol h−1 g−1, which is much higher than the rate on both bulk iron oxide and 4.5% Fe/Al2O3, but deactivation occurred at an initial rate of 3.96 mmol h−1 g−1 per h before gradually decreasing to 1.2 mmol h−1 g−1 per h.After an initial 800 min break-in period at a temperature of 753 K, both supported catalysts operated without further deactivation when the temperature was lowered by 30 K under equimolar CO2 and H2 partial pressures (see Fig. S5†). This was determined by measuring the CO formation rate at the very end of the experiment under the same conditions used during the break-in period. Rates collected in the middle of the experiment, during which gas flow rates and temperatures were changed (lowered), were used to determine reaction orders and activation energies. Because the CO formation rate measured after the series of gas flow rate and temperature changes was the same as before the changes, the kinetic parameters extracted from the rate measurements were not corrupted by deactivation.
As shown in Fig. 1, rates of CO formation increased on both catalysts when the gas composition was changed from an equimolar CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 mixture to 60 kPa CO2 and 15 kPa H2. The rate of deactivation on 4.5% Fe/Al2O3 increased to 2.6 mmol h−1 g−1 per h but remained linear. The 4.2% Fe–3.4% K/Al2O3 catalyst also continued to deactivate under excess CO2, but showed an exponential deactivation profile. When the gas composition was changed to 15 kPa CO2 and 60 kPa H2, the CO formation rate increased on both catalysts. The rate on 4.5% Fe/Al2O3 increased steadily with time on stream, whereas the rate on 4.2% Fe–3.4% K/Al2O3 first increased rapidly to a maximum of 222 mmol g−1 h−1, exhibited stable activity for approximately 80 min, and then began to slowly deactivate at a rate of 1.5 mmol h−1 g−1 per h. The selectivity to CO decreased to 95% under excess H2 on the 4.5% Fe/Al2O3 catalyst (CH4 is the main side product). On 4.2% Fe–3.4% K/Al2O3, the selectivity to CO remained greater than 99% under excess H2. Returning the gas composition to 15 kPa CO2 and 15 kPa H2 resulted in an initial rate of 116.8 mmol g−1 h−1 on Fe–K/Al2O3 (compared to 103.6 mmol g−1 h−1 observed at the end of the first period of flowing this gas composition). The rate decreased to 102.5 mmol g−1 h−1 over the course of an additional hour. On Fe/Al2O3, returning the gas composition to 15 kPa of CO2 and 15 kPa of H2 resulted in a rate of 45.2 mmol g−1 h−1 (compared to 43.7 mmol g−1 h−1 observed at the end of the first period of flowing this gas composition), and the catalyst showed no deactivation over the course of an additional hour.
H2 mixture to 60 kPa CO2 and 15 kPa H2. The rate of deactivation on 4.5% Fe/Al2O3 increased to 2.6 mmol h−1 g−1 per h but remained linear. The 4.2% Fe–3.4% K/Al2O3 catalyst also continued to deactivate under excess CO2, but showed an exponential deactivation profile. When the gas composition was changed to 15 kPa CO2 and 60 kPa H2, the CO formation rate increased on both catalysts. The rate on 4.5% Fe/Al2O3 increased steadily with time on stream, whereas the rate on 4.2% Fe–3.4% K/Al2O3 first increased rapidly to a maximum of 222 mmol g−1 h−1, exhibited stable activity for approximately 80 min, and then began to slowly deactivate at a rate of 1.5 mmol h−1 g−1 per h. The selectivity to CO decreased to 95% under excess H2 on the 4.5% Fe/Al2O3 catalyst (CH4 is the main side product). On 4.2% Fe–3.4% K/Al2O3, the selectivity to CO remained greater than 99% under excess H2. Returning the gas composition to 15 kPa CO2 and 15 kPa H2 resulted in an initial rate of 116.8 mmol g−1 h−1 on Fe–K/Al2O3 (compared to 103.6 mmol g−1 h−1 observed at the end of the first period of flowing this gas composition). The rate decreased to 102.5 mmol g−1 h−1 over the course of an additional hour. On Fe/Al2O3, returning the gas composition to 15 kPa of CO2 and 15 kPa of H2 resulted in a rate of 45.2 mmol g−1 h−1 (compared to 43.7 mmol g−1 h−1 observed at the end of the first period of flowing this gas composition), and the catalyst showed no deactivation over the course of an additional hour.
3.3 Rate orders, kinetic isotope effect, and CO2/H2 switching experiments
After the initial break-in period, reaction rates on both catalysts were stable at a temperature of 723 K. This allowed for the determination of kinetic parameters without having to model deactivation profiles (Arrhenius plots are shown in Fig. S6†). Table 2 summarizes these data at near equimolar CO2 and H2, and in large H2 excess. Under near equimolar CO2 and H2 composition, the reaction order with respect to H2 was nearly the same on both catalysts (0.58 and 0.54 on Fe/Al2O3 and Fe–K/Al2O3, respectively). In contrast, the reaction order with respect to CO2 on 4.2% Fe–3.4% K/Al2O3 was nearly half the order of that on 4.5% Fe/Al2O3 (0.37 and 0.21 on Fe/Al2O3 and Fe–K/Al2O3, respectively). Under excess H2, the reaction rate on Fe/Al2O3 was nearly first order with respect to CO2 and was independent of H2 pressure. The activation energy increased by 6 kJ mol−1 with respect to the value determined at equimolar concentrations of CO2 and H2. In contrast, the rate on Fe–K/Al2O3 under excess H2 depended on the concentrations of both reactants (CO2 reaction order = 0.65, H2 reaction order = 0.53), and the activation energy of 23 kJ mol−1 was significantly lower than the value of 69 kJ mol−1 determined under equimolar CO2 and H2.| Catalyst | E meas. (kJ mol−1) | Order in CO2 | Order in H2 |
|---|---|---|---|
| Equimolar CO2 and H2 | |||
| 4.5% Fe/Al2O3 | 46 | 0.37 | 0.58 |
| 4.2% Fe–3.4% K/Al2O3 | 69 | 0.21 | 0.54 |
| Excess H2 | |||
| 4.5% Fe/Al2O3 | 52 | 0.87 | 0.01 |
| 4.2% Fe–3.4% K/Al2O3 | 23 | 0.65 | 0.53 |
The reaction rate on 4.5% Fe/Al2O3 was considerably higher under CO2/D2 flow compared to CO2/H2 flow, indicating the occurrence of an inverse KIE (the average value of rH/rD was ∼0.65, see Fig. S7†). In contrast, the reaction rates on 4.2% Fe–3.4% K/Al2O3 under CO2/D2 flow and CO2/H2 flow were nearly identical, with an average rH/rD value of 1.03.
CO and H2O were the main products formed during gas-switching experiments (top panel in Fig. 2). On 4.5% Fe/Al2O3, CO was formed only when switching from H2 to CO2, whereas H2O was formed when switching from H2 to CO2 and when switching from CO2 to H2. However, when the catalyst was purged with He before switching from H2 to CO2, water was not formed, even though CO was produced. The potassium promoted catalyst showed different properties (bottom panel in Fig. 2). First, CO was produced when switching from CO2 to H2. Additionally, after flowing H2 and purging the reactor with He, water was produced upon admission of CO2. Concurrent with water formation, H2 was observed as determined from the mass spectrometer signal at m/z = 2 (see Fig. S8†).
The hydrodynamic behavior of the system was monitored by switching the gas flow from 10% H2/He to 10% CO2/1% Ar/He (see Fig. S9†). The transient response curve of Ar (m/z = 40) appeared much faster compared to response curves of CO2 (m/z = 44, 28) and CO (m/z = 28), indicating that the hydrodynamic behavior of the gas flow in the system did not obscure our ability to accurately detect a kinetic response upon the gas switch.37 It should also be noted that GC data collected during the gas-switching experiments verified the observations seen with the MS, although only the MS data are presented because of the higher time resolution. The CO2 contribution to the m/z = 28 signal was accounted for in order to identify the production of CO.
3.4 DRIFTS
IR spectra of the 9.1% Fe/Al2O3 and 7.7% Fe–3.4% K/Al2O3 catalysts after pretreatment in H2 showed only weak absorption bands (Fig. 3). In the spectra of both materials, a small band at 3550 cm−1 was visible, and on 7.7% Fe–3.4% K/Al2O3, additional minor bands at 1379 cm−1 and 1538 cm−1 were also observed. The overall reflectance of the reduced materials increased dramatically after admission of CO2, which is consistent with the change in color of the materials from dark grey to orange. The spectrum of 9.1% Fe/Al2O3 in Fig. 3 shows bands at 3550–3750 cm−1 from gas phase CO2, and minor inflections at 1308 cm−1 and 1595 cm−1. On 7.7% Fe–3.4% K/Al2O3, several intense bands formed at 1343 cm−1, 1568 cm−1, 2613 cm−1, and 2904 cm−1 after admission of CO2 (the band at 1343 cm−1 has a shoulder on the high energy side). The changes in intensity of the bands during the course of a 30 min purge with inert gas were small (see Fig. S10†). The IR spectra were collected at 723 K, since results from the packed-bed reactor experiments indicated that the materials are stable at this temperature (see Fig. S5†). Additionally, note that the actual bed temperature in commercial in situ spectroscopic environmental chambers, such as the one used in this work, is below the set point.38,39 Thus, it is highly unlikely that there were any changes to the materials caused by deactivation during the course of the DRIFTS experiments.3.5 XANES spectroscopy
XANES spectra were acquired during H2/CO2 gas switching experiments on 4.5% Fe/Al2O3 and 4.2% Fe–3.4% K/Al2O3 (see Fig. S11 and S12†). Before pretreatment, the positions of the absorption edge energy and pre-edge energy were 7123 eV and 7114.5 eV, respectively. During heating and flow of H2, the absorption edge energy shifted to 7119.5 eV by the time a temperature of ∼773 K was reached, and remained at that energy for the duration of the period in H2 flow. When H2 was replaced by CO2, the position of the absorption edge energy shifted immediately to 7122.2 eV. The fraction of Fe3+ in both catalysts as determined from LCF analysis was ∼0.85 during H2 pretreatment (up to a temperature of nearly 773 K). At 773 K, no Fe3+ was observed within the detection limits of the technique. When CO2 was admitted, the fraction of Fe3+ increased rapidly to ∼0.65.XANES spectra were also collected during a continuous equimolar flow of CO2/H2 (see Fig. S13 and S14†). For both catalysts, the fraction of Fe3+ was ∼0 after the pretreatment. During equimolar CO2/H2 flow on 4.2% Fe–3.4% K/Al2O3, the fraction of Fe3+ increased with time on stream for the first 25 minutes until a steady value of 0.08 was reached. A different behavior was noted with 4.5% Fe/Al2O3; with this catalyst, the position of the absorption edge energy did not change upon admission of CO2, and the fraction of Fe3+ remained ∼0 during the period of feeding CO2 and H2.
Table 3 summarizes the average fraction of Fe3+ present in both catalysts during different gas flows as calculated from the XANES data. The values indicate that the iron is present as mostly Fe2+ under flow of H2 and mostly Fe3+ under flow of CO2. Under an equimolar flow of CO2 and H2, the majority of Fe was in the 2+ oxidation state on both catalysts.
| Gas flow | Fe3+/Fetot. for Fe/Al2O3 | Fe3+/Fetot. for Fe–K/Al2O3 |
|---|---|---|
| 50% CO2 + 50% H2 | 0.01 | 0.08 |
| 20% H2/He | 0 | 0.02 |
| 20% CO2/He | 0.61 | 0.65 |
| He | 0.59 | 0.65 |
3.6 Summary of experimental results
Table 4 compares key properties and results from experiments carried out with Fe/Al2O3 and Fe–K/Al2O3, and clearly shows that major differences exist between the two materials for nearly every experiment. Most significant are the inverse KIE observed on Fe/Al2O3 but no KIE observed on Fe–K/Al2O3, the observation of stable surface intermediates on Fe–K/Al2O3 but not on Fe/Al2O3, differences in kinetic parameters, and the production of H2O on Fe/Al2O3 during the gas switch from H2 to CO2, but the production of CO and H2O on Fe–K/Al2O3 during the same gas switch.| Experiment | Fe/Al2O3 | Fe–K/Al2O3 |
|---|---|---|
| KIE (rH/rD) | 0.65 | 1.03 |
| Gas-switching (CO2 → H2) | CO and H2O produced | CO and H2O produced |
| Gas-switching (H2 → CO2) | H2O produced | CO and H2O produced |
| DRIFTS | No intermediate | Stable intermediate(s) |
| CO2 reaction order (∼equimolar inlet) | 0.37 | 0.21 |
| H2 reaction order (∼equimolar inlet) | 0.58 | 0.54 |
| E meas. (kJ mol−1) | 46 | 69 |
4. Discussion
4.1 Stable surface species on Fe–K/Al2O3
Experiments in which gas flows were alternated between H2 and CO2 on 4.2% Fe–3.4% K/Al2O3 (Fig. 2) indicate that stable surface species form when the reduced catalyst is contacted with CO2. After reduction in H2 and upon admission of CO2, CO and H2O were produced. However, CO was also produced when H2 was readmitted, even after an intermediate purge with He. Consequently, a stable carbon-containing intermediate must form during the period in CO2 flow; the intermediate does not desorb or react in He, and H2 is required to decompose it and form products. It is possible that the CO released during the switch from CO2 to H2 on Fe–K/Al2O3 could result from the preferential adsorption of H2 on iron, which causes desorption of CO from iron. However, no evidence was observed of adsorbed CO on Fe–K/Al2O3 or Fe–K/Al2O3 in the DRIFTS spectra. CO typically shows strong IR absorption bands around 2100 cm−1 and 1830–1880 cm−1,40 but none of these bands were observed. The bond dissociation energies for Fe–CO complexes are in the range of 145–274 kJ mol−1,41 while the bond dissociation energy for Fe–H is 162 kJ mol−1.42 The difference between these bond dissociation energies indicates that the Fe–CO bond tends to be stronger than the Fe–H bond, and therefore CO will not likely desorb because of the introduction of H2. In contrast to the potassium promoted sample, the 4.5% Fe/Al2O3 catalyst did not release CO upon switching gas flows from CO2 to H2, suggesting that stable intermediates do not form on this material.DRIFTS spectra verified that stable intermediates form only on the catalyst containing potassium. After pretreatment in H2, the maximum intensity across the IR spectrum decreased by ∼50% on both materials (Fig. 3), a change consistent with the change in sample color from orange to grey and the reduction of Fe3+ to Fe2+ (evidence for the reduction of Fe3+ was also observed using XANES, section 4.4). Although the Fe/Al2O3 catalyst was oxidized by CO2, as indicated by the overall increase in reflectance of the material and its change in color from grey to orange, only weak absorption bands were observed around 1308 cm−1 and 1595 cm−1. In contrast, when Fe–K/Al2O3 was contacted with CO2, intense absorption bands formed that disappeared very slowly when CO2 was removed from the gas stream (see Fig. S10†). The formation of intense absorption bands on Fe–K/Al2O3 (but not on Fe/Al2O3) is in agreement with the results from the gas-switching experiments and confirms the presence of a stable, carbon-containing surface species on Fe–K/Al2O3.
The most intense IR bands on Fe–K/Al2O3 were observed at 1343 cm−1 and 1568 cm−1. A smaller band at 2904 cm−1 is likely from the νCH vibration of a formate. The intense bands at 1300–1600 cm−1 appear to be the superposition of bands from several species. When the catalyst was purged with He, two bands at 1651 cm−1 and 1292 cm−1 (identified from a difference plot of the spectra, see Fig. S10†) slowly disappear, while the majority of the absorbing species remain unchanged. A shoulder at ∼1380 cm−1 is also visible, and might be paired with the band at 1550 cm−1, both of which did not completely disappear after re-reduction in H2. It is likely that the remainder of the band intensity comes from another species, with bands at 1343 cm−1 and 1568 cm−1.
This analysis indicates that there are at least three surface species that form on Fe–K/Al2O3, one of which is a formate. The formate ion exhibits characteristic IR vibrations at 1555 cm−1 (asymm νCO), 1376 cm−1 (δCH), and 1348 cm−1 (symm νCO) on α-Fe2O3.43 IR bands were observed at 1568 cm−1 and 1380 cm−1 here and, together with the band at 2904 cm−1, strongly suggest that formate is present on the catalyst surface. Other possible surface species that can form during exposure to CO2/H2 include bicarbonate, carboxylate, and carbonate. Carboxylates show IR vibrations at 1560 cm−1 and 1340 cm−1 on iron-oxide materials.43 The bands we observed at 1550 cm−1 and 1343 cm−1 agree well with these previous assignments and indicate that carboxylates may also form on the Fe–K/Al2O3 material. This is also expected since this sample is basic. The bands at 1651 cm−1 and 1292 cm−1, which disappear during the He purge, could potentially be assigned to bicarbonate (1655–1615 cm−1 [asym νCO], 1400–1370 cm−1 [symm νCO], 1300 cm−1 [δOH]), carboxylate (1660–1560 cm−1[νCO]), or bidentate carbonate (1730–1660 cm−1 and 1270–1230 cm−1 on Al2O3) species, based on assignments from the literature.43
IR bands in the 3600–3800 cm−1 region of the spectra, which are associated with surface hydroxyl (–OH) groups, were not detected for the catalysts (see Fig. 3). This is peculiar, as typically these bands appear very strongly in IR spectra. For instance, IR spectra of bare Al2O3 did reveal IR bands associated with –OH groups (spectra not shown). Thus, the absence of detectable –OH groups on the catalyst samples is not an artifact, and suggests that the incorporation of iron and potassium into the sample has an effect on these groups.
4.2 Redox and associative reaction pathways on Fe/Al2O3 and Fe–K/Al2O3
The associative pathway has often been proposed as the dominant mechanism for WGS.44–48 However, in a recent review Burch et al.49 concluded that the associative pathway typically accounts for less than 10–15% of the overall WGS reaction rate50–52 and that formates are often only spectator species.38,53 The authors found that the associative pathway49 can be dominant on low-activity materials such as MgO (ref. 44) and 0.2% Rh/CeO2,45 but that the vast majority of investigations in which an associative pathway was said to be dominant lacked the quantitative data necessary to validate the claim.46–48 Steady-state isotopic transient kinetic analysis (SSITKA) is often coupled with DRIFTS and MS to elucidate reaction mechanisms and differentiate between active reaction intermediates and spectator species, and has been applied several times to the WGS and RWGS reactions. In a study of the RWGS reaction on 10% Cu/SiO2, Yang et al used 12C/13C isotopic transient analysis with MS and IR to simultaneously measure the site coverage and residence time of adsorbed formate species.54 Their results showed that the formate removal rate was two orders of magnitude greater than the catalytic RWGS reaction rate, and thus the reaction has no influence on the formate surface coverage. Using SSITKA–DRIFTS–MS, Burch and co-workers showed that surface carbonates were exchanged significantly faster than formates on 2% Pt/CeO2, and thus formates observed by IR were not actually a major reaction intermediate.35,55 Finally, in a study of the WGS reaction on 2% Pt/CeO2, Kalamaras et al. used SSITKA–DRIFTS and SSITKA–MS to show that formates present on the catalyst could not be considered important reaction intermediates, and proposed that a redox mechanism is dominant relative to the associative mechanism.56Gas-switching experiments in which flows of H2 and CO2 were alternated (Fig. 2) were used here to distinguish and quantify contributions from redox and associative pathways.57 CO formation, when the reduced forms of both Fe/Al2O3 and Fe–K/Al2O3 catalysts are contacted with CO2, even after the reduced catalysts were purged with He to ensure the absence of H2, is evidence of a redox pathway. In the simplest form of the redox mechanism, gas-phase CO2 adsorbs on a reduced site to form CO and an oxidized site (eqn (6)), which can then be re-reduced by gas phase H2 to reform the reduced site (eqn (7)).
| CO2 (g) + sred. → CO (g) + O·s | (6) |
| H2 + O·s → H2O (g) + sred. | (7) |
 | (8) |
| Material | Period | Rate after H2 → CO2 gas switch (μmol L−1 s−1 gcat.−1) | Rate after CO2 → H2 gas switch (μmol L−1 s−1 gcat.−1) | (H2 → CO2 rate)/CO2 → H2 rate) ratio |
|---|---|---|---|---|
| 4.5% Fe/Al2O3 | 1st CO2 | 1.48 | — | — |
| 2nd CO2 | 1.24 | — | — | |
| 3rd CO2 | 1.15 | — | — | |
| 4th CO2 (after He purge) | 0.47 | — | — | |
| 4.2% Fe–3.4% K/Al2O3 | 1st CO2 | 0.43 | 0.28 | 1.53 |
| 2nd CO2 | 1.07 | 0.26 | 4.19 | |
| 3rd CO2 | 1.48 | 0.26 | 5.63 | |
| 4th CO2 (after He purge) | 2.31 | 0.11 | 21.5 | |
The presence of a stable, carbon-containing surface intermediate on Fe–K/Al2O3, (see section 4.1) may be evidence of a concurrent associative pathway. Apparently, potassium allows for a new reaction pathway to CO that involves a stable intermediate. In the associative pathway, described generally by eqn (9), CO2 and H2 adsorb on the catalyst surface to form a carbon-containing intermediate (i.e. formate, carbonate, or bicarbonate), which then decomposes in the presence of H2 to form CO and H2O.
| CO2 (g) + H2 (g) → CO2·s + 2H·s → CO·s + H2O·s | (9) |
In summary, CO formed upon switching from H2 to CO2 is evidence supporting the redox mechanism, while the CO formed upon switching from CO2 to H2 is evidence in support of the associative mechanism. Both the redox and associative reaction pathways then appear to contribute to the overall RWGS rate on Fe–K/Al2O3, while only the redox pathway is active on Fe/Al2O3. The ratios of the rates during CO2 flow to H2 flow for Fe–K/Al2O3 (Table 5) indicate that the redox pathway is the dominant contributor to the overall reaction rate.
4.3 Kinetics parameters and formulation of a kinetic model on Fe/Al2O3
There are few detailed kinetic investigations of the RWGS reaction on Fe-based catalysts. Osaki et al reported an activation energy of 78.2 kJ mol−1 on 20% Fe/Al2O3, determined in the temperature range of 500–800 K.58 This value is significantly higher than the 46 kJ mol−1 observed here on 4.5% Fe/Al2O3. The reaction orders of 0.37 for CO2 and 0.58 for H2 obtained on Fe/Al2O3 under 15 kPa CO2 and 15 kPa H2 (Table 2) appear to follow the power-law rate relation described by eqn (10); that is, reaction orders are not independent. Additionally, under excess H2 conditions the reaction orders of 0.87 for CO2 and 0.01 for H2 also follow this relation.| r = kapp.[CO2]n[H2]1−n | (10) |
As shown in Table 2, the activation energy (Emeas.) for the reaction on Fe–K/Al2O3 (69 kJ mol−1) is significantly greater than that on Fe/Al2O3 (46 kJ mol−1), even though Fe–K/Al2O3 showed higher catalytic rates. This is surprising, as normally reaction rates increase with a decrease in the activation energy. The higher rate on Fe–K/Al2O3, despite its greater Emeas., indicates that the pre-exponential factor of the rate determining step is large. According to Transition State Theory, a large pre-exponential factor indicates a small negative (or even positive) entropy of formation of the transition state (ΔS‡), and is characteristic of monomolecular reactions.60 A monomolecular RDS typically involves bond dissociation; in this reaction it would likely involve C–O bond breaking. The lower reaction rates observed on Fe/Al2O3, in spite of a lower Emeas., indicate that the RDS is likely bimolecular and possibly involves C–H bond formation. As such, ΔS‡ will be much more negative for this reaction pathway, resulting in a smaller pre-exponential factor that reduces the rate constant.60
We observed an inverse KIE on Fe/Al2O3, with a rH/rD ratio of ∼0.65; this value is nearly the inverse of the typical rH/rD ratio of ∼1.4 for a normal H/D KIE.61 In general, isotope effects are such that kH/kD > 1 and KH/KD < 1, and therefore a switch from H2 to D2 can affect both of these ratios in opposite directions. This leads to the possibility of observing a normal, inverse, or negligible isotope effect, depending on the relative magnitudes of change for these ratios.62 The inverse KIE observed on Fe/Al2O3 suggests, then, that the equilibrium isotope effects have a significant influence on the measured overall isotope effect and prevail over normal kinetic isotope effects associated with C–H bond formation. The isotopic substitution from H2 to D2 is known to change the equilibrium of certain elementary steps, such as hydrogen adsorption.63 Therefore, the thermodynamic terms of the apparent rate constant, which depend on the relative chemisorption enthalpies of D2 and H2 on the catalyst surface, are affected.63 Previous studies have indicated that chemisorption of D2 is preferred over that of H2 on Fe catalysts, and thus KH/KD is less than 1.64 In contrast, switching from H2 to D2 on Fe–K/Al2O3 had very little effect on the CO formation rate, as the rH/rD ratio was observed to be 1.03. The absence of a significant KIE on Fe–K/Al2O3 indicates that the RDS does not involve bond breaking or forming with H, which is consistent with the occurrence of a redox mechanism in which CO2 dissociation is the RDS. The difference between the observed KIEs on the two catalysts implies that the incorporation of potassium alters the RDS of the reaction mechanism.
The gas-switching experiments with CO2 and H2 led us to conclude that a redox pathway is active on both Fe/Al2O3 and Fe–K/Al2O3 (see above). Based on this result, an initial model for the reaction pathway for both catalysts is given in Scheme 1. The mechanism shown is a classical redox pathway that includes steps for CO2 adsorption, CO desorption, and H2O desorption.
Using CO formation on the surface (step 2) as the rate-determining step (RDS), a rate expression can be derived for CO formation in the gas phase at differential conversion (eqn (11)).
 | (11) |
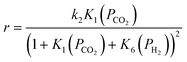 | (12) |
Considering the inverse KIE that was observed on Fe/Al2O3, a different reaction mechanism can be proposed in which C–H bond formation is the RDS (Scheme 2). The model depicted in Scheme 2 is an associative mechanism involving the reaction of adsorbed CO2 with dissociated H2 to form a surface intermediate (step 4), which subsequently desorbs as CO (g) and H2O (g) (step 5). This reaction scheme also incorporates competitive adsorption by H2 (step 1) and H2 dissociation on the surface (step 2).
Evidence for H2 dissociation (step 2 in Scheme 2) was observed when H2/D2 mixtures were fed to the catalyst in the presence or absence of CO2 (see Fig. S15†). HD formation occurs quickly (on the same time scale as the chemical conversion of CO2 to CO), indicating that H2 dissociation is reversible and not rate limiting. The intermediate formed in step 4 of Scheme 2 should not be observable by in situ IR spectroscopy because, by definition, its formation is rate limiting and it rapidly decomposes (recall that such intermediates were not observed on Fe/Al2O3 catalysts). The rate equation for CO formation according to Scheme 2 is presented in eqn (13), assuming that step 4 is the RDS and that conversion levels are low.
 | (13) |
Eqn (13) has both CO2 and H2 terms in the numerator, agreeing with the experimental results in which positive reaction orders were observed for both of these reactants. The fit of this equation is good for both catalysts (Table 6), with the only exception being that the fitted reaction orders for H2 differ from the experimentally determined values. For instance, Table 6 shows that the H2 reaction orders on Fe/Al2O3 and Fe–K/Al2O3 are 0.58 and 0.54, respectively, while the H2 reaction orders fitted from the model are 0.50 for both catalysts. Note that the apparent rate constant in the rate expression (eqn (13)) is a product of the elementary rate constant for step 4 (k4) and the equilibrium constants of steps 1–3 (K1, K2, K3). Equilibrium isotope effects are typically less than 1, and therefore these terms could be the reason for the inverse KIE observed experimentally.62 Only K1 or K2 can be the cause of the inverse KIE, though, since only these steps involve H2.
| Material | E a (kJ mol−1) | Order in CO2 | Order in H2 | |
|---|---|---|---|---|
| Fe/Al2O3 | Experimental | 46 | 0.37 | 0.58 |
| Fitted (step 4 RDS) | 46 | 0.37 | 0.50 | |
| Fitted (step 5 RDS) | 45 | 0.38 | 0.59 | |
| Fe–K/Al2O3 | Experimental | 69 | 0.21 | 0.54 |
| Fitted (step 4 RDS) | 70 | 0.22 | 0.50 | |
| Fitted (step 5 RDS) | 71 | 0.22 | 0.98 | |
Finally, it is also possible that step 5 of Scheme 2 (decomposition of the surface intermediate) is the RDS on Fe–K/Al2O3, since stable carbon-containing intermediates were observed on this catalyst during the DRIFTS experiments. In this case, the rate expression shown in eqn (14) is obtained.
 | (14) |
It is unlikely that step 5 is the RDS on Fe/Al2O3, since no carbon-containing intermediates were observed during the IR experiments; nonetheless, an attempt was made to fit the experimental data to the rate expression in eqn (14) for this scenario. As Table 6 shows, the assumption that step 5 is the RDS results in a better fit with the experimental data for Fe/Al2O3, as opposed to the case when step 4 was assumed to be the RDS and the H2 reaction orders did not match well. The assumption of step 5 as the RDS for the reaction on Fe–K/Al2O3 results in poor agreement between the fitted (0.98) and experimentally determined (0.54) reaction orders for H2. It is clear from the results that the simple redox and associative mechanisms proposed are not sufficient to describe all of the experimental results. This suggests that a more complex mechanism or combination of competing pathways may be occurring, as is often the case in the WGS and RWGS reactions.
5. Conclusions
Packed-bed microreactor studies indicated that incorporation of potassium into Fe/Al2O3 results in a significant increase (∼3 times) in CO formation rates. Fe/Al2O3 and Fe–K/Al2O3 slowly deactivated under excess CO2, but excess H2 resulted in stable catalytic rates. Reaction rates depend more strongly on H2 (orders 0.58 and 0.54 for Fe/Al2O3 and Fe–K/Al2O3, respectively) compared to CO2 (orders 0.37 and 0.21 for Fe/Al2O3 and Fe–K/Al2O3, respectively) under equimolar CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 composition. Gas-switching experiments on Fe/Al2O3 revealed that CO was formed only when switching from H2 to CO2, whereas H2O was formed when switching from H2 to CO2 and when switching from CO2 to H2. The results of the gas-switching experiments on Fe/Al2O3 suggest that a redox mechanism is active, since the order in which the reactants are adsorbed on the surface affects the products that are observed. On Fe–K/Al2O3, both CO and H2O were produced when switching from H2 to CO2 and from CO2 to H2, which suggests that an associative reaction mechanism may also be occurring. Evidence of carbon-containing surface intermediates on Fe–K/Al2O3—supporting the occurrence of an associative mechanism—was obtained using DRIFTS. IR bands associated with formate, and possibly carbonate, bicarbonate, and carboxylate, were observed in the presence of CO2 and H2. No such IR bands were observed on the Fe/Al2O3 material, in agreement with the results from the gas-switching experiments, in which CO was not produced when switching from CO2 to H2. Reaction rates measured under H2 or D2 revealed an inverse KIE on Fe/Al2O3 (rH/rD = 0.65), but no KIE on Fe–K/Al2O3 (rH/rD = 1.03). The observed inverse KIE suggests that the RDS for the mechanism on Fe/Al2O3 involves hydrogen addition, while that on Fe–K/Al2O3 does not. Although the experimental evidence suggested that a redox mechanism is the only (on Fe/Al2O3) or dominant (on Fe–K/Al2O3) mechanism occurring, the rate expression obtained from a proposed redox mechanism (Scheme 1) did not show a dependence on H2 pressure, that is, it is inconsistent with the experimental results in which a clear dependence on H2 pressure was observed. The associative model provided an excellent fit to the experimental reaction data, but did not explain other experimental results, which strongly suggested a redox mechanism.
H2 composition. Gas-switching experiments on Fe/Al2O3 revealed that CO was formed only when switching from H2 to CO2, whereas H2O was formed when switching from H2 to CO2 and when switching from CO2 to H2. The results of the gas-switching experiments on Fe/Al2O3 suggest that a redox mechanism is active, since the order in which the reactants are adsorbed on the surface affects the products that are observed. On Fe–K/Al2O3, both CO and H2O were produced when switching from H2 to CO2 and from CO2 to H2, which suggests that an associative reaction mechanism may also be occurring. Evidence of carbon-containing surface intermediates on Fe–K/Al2O3—supporting the occurrence of an associative mechanism—was obtained using DRIFTS. IR bands associated with formate, and possibly carbonate, bicarbonate, and carboxylate, were observed in the presence of CO2 and H2. No such IR bands were observed on the Fe/Al2O3 material, in agreement with the results from the gas-switching experiments, in which CO was not produced when switching from CO2 to H2. Reaction rates measured under H2 or D2 revealed an inverse KIE on Fe/Al2O3 (rH/rD = 0.65), but no KIE on Fe–K/Al2O3 (rH/rD = 1.03). The observed inverse KIE suggests that the RDS for the mechanism on Fe/Al2O3 involves hydrogen addition, while that on Fe–K/Al2O3 does not. Although the experimental evidence suggested that a redox mechanism is the only (on Fe/Al2O3) or dominant (on Fe–K/Al2O3) mechanism occurring, the rate expression obtained from a proposed redox mechanism (Scheme 1) did not show a dependence on H2 pressure, that is, it is inconsistent with the experimental results in which a clear dependence on H2 pressure was observed. The associative model provided an excellent fit to the experimental reaction data, but did not explain other experimental results, which strongly suggested a redox mechanism.
Author contributions
J. A. L. and M. J. W. contributed equally to this report by conducting experiments, analyzing the results, and co-writing the manuscript. N. S. M. assisted in conducting the XANES experiments at Brookhaven National Laboratory and helped with the data analysis. R. F. L. supervised the research and co-wrote the manuscript.Acknowledgements
The authors thank E. Schreiner and H. Sheng from the University of Delaware for their help in collecting XANES data at Brookhaven National Laboratory. This research was funded by the U.S. Army under grant GTS-S-14-392. The authors would also like to acknowledge the Synchrotron Catalysis Consortium funded by the U.S. Department of Energy under grant DE-SC0012335.References
- C. Ratnasamy and J. Wagner, Catal. Rev.: Sci. Eng., 2009, 51, 325–440 CAS.
- A. Hakeem, R. Vasquez, J. Rajendran, M. Li, R. Berger, J. Delgado, F. Kapteijn and M. Makkee, J. Catal., 2014, 313, 34–35 CrossRef CAS.
- D. Newsome, Catal. Rev.: Sci. Eng., 1980, 21, 275–318 CAS.
- H. Topsoe and M. Boudart, J. Catal., 1973, 31, 346–359 CrossRef CAS.
- D. Jeong, W. Jang, J. Shim, W. Han, H. Roh, U. H. Jung and W. L. Yoon, Renewable Energy, 2014, 65, 102–107 CrossRef CAS.
- A. Sun, Z. Qin, S. Chen and J. Wang, J. Mol. Catal. A: Chem., 2004, 210, 189–195 CrossRef CAS.
- F. Farias, R. Rabelo Neto, M. Baldanza, M. Schmal and F. Fernandes, Braz. J. Chem. Eng., 2011, 28, 495–504 CrossRef CAS.
- H. Hinrichs and R. Thoma, Process for the production of iron oxide catalysts, US Pat., US 3417031A, 17 Dec. 1968 Search PubMed.
- C. Nederlof, G. Talay, F. Kapteijn and M. Makkee, Appl. Catal., A, 2012, 423–424, 59–68 CrossRef CAS.
- D. Worch, W. Suprun and R. Glaser, Chem. Pap., 2014, 68, 1228–1239 CAS.
- M. Kumaran Gnanamani, W. Shafer, D. Sparks and B. Davis, Catal. Commun., 2011, 12, 936–939 CrossRef.
- P. Sai Prasad, J. Bae, K. Jun and K. Lee, Catal. Surv. Asia, 2008, 12, 170–183 CrossRef.
- D. Bukur, D. Mukesh and S. Patel, Ind. Eng. Chem. Res., 1990, 29, 194–204 CrossRef CAS.
- J. Dun, E. Gulari and K. Ng, Appl. Catal., 1985, 15, 247–263 CrossRef CAS.
- G. Maiti, R. Malessa and M. Baerns, Appl. Catal., 1983, 5, 151–170 CrossRef CAS.
- A. Pour, M. Zare and Y. Zamani, J. Nat. Gas Chem., 2010, 19, 31–34 CrossRef CAS.
- Y. Yang, H. Ziang, Y. Xu, L. Bai and Y. Li, Appl. Catal., A, 2004, 266, 181–194 CrossRef CAS.
- D. Miller and M. Moskovits, J. Phys. Chem., 1988, 92, 6081–6085 CrossRef CAS.
- A. Kotarba, A. Baranski, S. Hodorowicz, J. Sokolowski, A. Szytula and L. Holmlid, Catal. Lett., 2000, 67, 129–134 CrossRef CAS.
- C. Chen, W. Cheng and S. Lin, Appl. Catal., A, 2003, 238, 55–67 CrossRef CAS.
- H. Wan, B. Wu, C. Zhang, H. Xiang, Y. Li, B. Xu and F. Yi, Catal. Commun., 2007, 8, 1538–1545 CrossRef CAS.
- E. Armstrong and T. Hilditch, Proc. R. Soc. London, Ser. A, 1920, 97, 265 CrossRef CAS.
- C. Chen, W. Cheng and S. Lin, Catal. Lett., 2000, 68, 45–48 CrossRef CAS.
- C. Chen and W. Cheng, Catal. Lett., 2002, 83, 121–126 CrossRef CAS.
- L. Wang, M. Khazaneh, D. Widmann and R. Behm, J. Catal., 2013, 302, 20–30 CrossRef CAS.
- S. Fujita, M. Usui and N. Takezawa, J. Catal., 1992, 134, 220–225 CrossRef CAS.
- N. Kulkova and M. Temkin, Zh. Fiz. Khim., 1949, 23, 695–698 CAS.
- M. Temkin, in Advances in Catalysis, ed. D. Eley, H. Pines and P. Weisz, Academic Press, New York, 1979, vol. 28 Search PubMed.
- G. Shchibrya, N. Morozov and M. Temkin, Kinet. Catal., 1965, 6, 1057–1059 CAS.
- R. Mezaki and S. Oki, J. Catal., 1973, 30, 488–489 CrossRef CAS.
- S. Oki, J. Happel, M. Hinatow and Y. Kancko, Catal., Proc. Int. Congr., 5th, 1973, 1, 173–183 CAS.
- J. Ladebeck and J. Wagner, in Handbook of Fuel Cells- Fundamentals, Technology and Applications, ed. W. Vielstich, A. Lamm and H. A. Gasteiger, John Wiley & Sons, Ltd, Chichester, 2003, pp. 190–201 Search PubMed.
- D. Tibiletti, A. Goguet, F. Meunier, J. Breen and R. Burch, Chem. Commun., 2004, 1636–1637 RSC.
- A. Goguet, F. Meunier, D. Tibiletti, J. Breen and R. Burch, J. Phys. Chem. B, 2004, 108, 20240–20246 CrossRef CAS.
- A. Gokhale, J. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402–1414 CrossRef CAS PubMed.
- K. Paredis, L. Ono, F. Behafarid, Z. Zhang, J. Yang, A. Frenkel and B. Cuenya, J. Am. Chem. Soc., 2011, 133, 13455–13464 CrossRef CAS PubMed.
- A. M. Efstathiou and X. E. Verykios, Appl. Catal., A, 1997, 151, 109–166 CrossRef CAS.
- F. C. Jentoft, Adv. Catal., 2009, 52, 129–211 CAS.
- H. Li, M. Rivallan, F. Thibault-Starzyk, A. Travert and F. C. Meunier, Phys. Chem. Chem. Phys., 2013, 15, 7321–7327 RSC.
- E. Kock, M. Kogler, T. Bielz, B. Klotzer and S. Penner, J. Phys. Chem. C, 2013, 117, 17666–17673 Search PubMed.
- C. P. McNary and P. B. Armentrout, Phys. Chem. Chem. Phys., 2014, 16, 26467–26477 RSC.
- R. G. Pearson, Chem. Rev., 1985, 85, 41–49 CrossRef CAS.
- G. Busca and V. Lorenzelli, J. Mater. Chem., 1982, 7, 89–126 CrossRef CAS.
- A. Ueno, T. Onishi and K. Tamaru, Trans. Faraday Soc., 1970, 66, 756–763 RSC.
- T. Shido and Y. Iwasawa, J. Catal., 1993, 141, 71–81 CrossRef CAS.
- G. Jacobs and B. Davis, Appl. Catal., A, 2007, 333, 192–201 CrossRef CAS.
- R. Leppelt, B. Schumacher, V. Plzak, M. Kinne and R. Behm, J. Catal., 2006, 244, 137–152 CrossRef CAS.
- C. Kalamaras, G. Olympiou and A. Efstathiou, Catal. Today, 2008, 138, 228–234 CrossRef CAS.
- R. Burch, A. Goguet and F. Meunier, Appl. Catal., A, 2011, 409–410, 3–12 CrossRef CAS.
- D. Tibiletti, F. Meunier, A. Goguet, D. Reid, R. Burch, M. Boaro, M. Vicario and A. Trovarelli, J. Catal., 2006, 244, 183–191 CrossRef CAS.
- F. Meunier, A. Goguet, C. Hardacre, R. Burch and D. Thompsett, J. Catal., 2007, 252, 18–22 CrossRef CAS.
- F. Meunier, D. Reid, A. Goguet, S. Shekhtman, C. Hardacre, R. Burch, W. Deng and M. Flytzani-Stephanopoulos, J. Catal., 2007, 247, 277–287 CrossRef CAS.
- C. Kalamaras, P. Panagiotopoulou, D. Kondarides and A. Efstathiou, J. Catal., 2009, 264, 117–129 CrossRef CAS.
- Y. Yang, C. A. Mims, R. S. Disselkamp, C. H. F. Peden and C. T. Campbel, Top. Catal., 2009, 52, 1440–1447 CrossRef CAS.
- F. C. Meunier, D. Tibiletti, A. Goguet and R. Burch, Oil Gas Sci. Technol., 2006, 61, 497–502 CAS.
- C. M. Kalamaras, S. Americanou and A. M. Efstathiou, J. Catal., 2011, 279, 287–300 CrossRef CAS.
- S. Kim, H. Lee and S. Hong, Appl. Catal., A, 2012, 423–424, 100–107 CAS.
- T. Osaki, N. Narita, T. Horiuchi, T. Sugiyama, H. Masuda and K. Suzuki, J. Mol. Catal. A: Chem., 1997, 125, 63–71 CrossRef CAS.
- M. Ginés, A. Marchi and C. Apesteguia, Appl. Catal., A, 1997, 154, 155–171 CrossRef.
- I. Chorkendorff and J. Niemantsverdriet, in Concepts of Modern Catalysis and Kinetics, Wiley-VCH, Darmstadt, 2007, 2nd edn Search PubMed.
- M. Kumaran Gnanamani, G. Jacobs, W. Shafer, D. Sparks and B. Davis, Catal. Lett., 2011, 141, 1420–1428 CrossRef.
- M. Ojeda, A. Li, R. Nabar, A. Nilekar, M. Mavrikakis and E. Iglesia, J. Phys. Chem., 2010, 114, 19761–19770 CAS.
- S. Krishnamoorthy, M. Tu, M. P. Ojeda, D. Pinna and E. Iglesia, J. Catal., 2002, 211, 422–433 CrossRef CAS.
- P. Biloen, H. Helle and W. Sachtler, J. Catal., 1979, 44, 439 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cy02111a |
| This journal is © The Royal Society of Chemistry 2016 |





