Strain-induced helical chirality in polyaromatic systems

Abstract

Helicity in a molecule arises when the molecule contains a stereogenic axis instead of a stereogenic centre. In a molecule that is not inherently helically chiral, helicity can be induced by designing the molecule such that an unfavourable steric interaction, or strain, is present in its planar conformation. The release of this strain forces the molecule to adopt a helical twist against the cost of the torsional strain induced in the backbone, an interplay of forces, which must be balanced in favour of the helical conformation over the planar one. In this tutorial review, design principles that govern this process are analysed and the selected examples are categorised into three main (I, II and III) and two related (IV and V) classes, simply by their relation to one of the three types of helically twisted ribbons or two types of helically twisted cyclic ribbons, respectively. The presented examples were selected such that they illustrate their category in the best possible way, as well as based on availability of their solid-state structures and racemisation energy barriers. Finally, the relationship between the structure and properties is discussed, highlighting the cases in which induced helicity gave rise to unprecedented phenomena.

---

Michel Rickhaus (left), Marcel Mayor (middle) and Michal Juríček (right)

Michel Rickhaus obtained his MSc (2011) and PhD (2015) from the University of Basel under the supervision of Professor Marcel Mayor. His research interests involve the development of new concepts for inducing twists and strain in aromatic materials. Under the supervision of Professor Lawrence T. Scott at Boston College, he worked as a visiting scholar on planarisation of curved aromatic systems.

Marcel Mayor received his PhD in 1995 supervised by Professor Rolf Scheffold and Professor Lorenz Walder. After working with Professor Jean-Marie Lehn at the University Louis Pasteur in Strasbourg and at the Collège de France in Paris, he founded his own research group at the Karlsruhe Institute of Technology in 1998. On defending his habilitation in 2002, he became Professor of Chemistry at the University of Basel in 2004. His current research interests are supramolecular chemistry, molecular electronics, nanoscale architectures, functional materials and hybrid materials.

Michal Juríček received his MSc from Comenius University in Bratislava before he pursued his PhD at Radboud University Nijmegen with Professor Alan E. Rowan. In 2011, he joined the group of Professor J. Fraser Stoddart at Northwestern University as a postdoctoral fellow. He currently leads an independent research group at the University of Basel, where he investigates polycyclic hydrocarbons with delocalised spin densities.

---

Key learning points

(1) Chirality can arise without stereogenic centres.

(2) Strain introduced into a sufficiently rigid backbone can induce helical chirality.

(3) Linked or fused aromatic rings are ideally suited to relay helicity within a structure.

(4) Strained helical molecules often show surprisingly low racemisation barriers and are more flexible than is generally believed.

(5) Helicity induced in a π-conjugated system often leads to an unusual electronic structure and unexpected properties.

1. Introduction

Since its elucidation in 1953, the double-helix structure of DNA has fostered the role that chirality plays¹ in living systems, namely, providing function with complexity. Helical chirality, in particular, governs² formation of many supramolecular assemblies composed of chiral or even achiral molecular building blocks in both biological and artificial systems. The helical secondary structure often defines the function of complex assemblies beyond a single stereogenic centre and translates chirality from the molecular level to the nanometer scale. Understanding how complexity arises from simple building blocks and the role of chirality in this process is the key to the design of functional systems.

Helical chirality is a property of chiral systems³ that do not contain stereogenic centres, that is, asymmetric units where four non-equivalent points represent the vertices of a tetrahedron. In a helical stereogenic unit, four points that can be identical are placed in a three-dimensional space such that the system is not superimposable on its mirror image. This type of chirality is also known as axial chirality because of the presence of a stereogenic axis instead of a centre. In molecules that are not inherently helically chiral, helicity can be induced. Flexible molecules, such as DNA, can be folded into a helical conformation by specific directional non-covalent interactions, for example, hydrogen bonding. In rigid molecules, helical conformations can arise if unfavourable steric interactions, or strain, are present in their non-helical conformations, which is the driving force towards formation of the energetically favoured helical conformations. This second type of helical chirality, here referred to as strain-induced, is the subject of this tutorial review.

The helical conformation is induced⁴ by minimising the steric interactions present in the planar conformation against the energy cost of the torsional strain, or deformation, induced upon twisting the molecule. The main requirement for a molecule to adopt a helical conformation is therefore the right balance of the two forces, the first one being the driving force. As a consequence, it is necessary that the molecule is both rigid and flexible at the same time. Fused or linked polyaromatic systems are ideally suited to serve this purpose because their core is sufficiently rigid. In parallel, the induced deformation is typically spread over a large number of bonds, which makes the core relatively flexible. Conceptually different types of strain-induced polyaromatic helices have been reported in the literature. These numerous significant achievements notwithstanding, there is still intellectual space left for designing conceptually new helical systems, which are induced by strain and which adopt well-defined geometries. Understanding how helicity arises and how it is translated into properties in these systems is crucial for understanding the interplay between chirality and function.

It is important to note that numerous examples are known in the literature, many of which could not be included in this review because of space restrictions. As most of these have recently been reviewed exhaustedly, we focused on the qualitative rather than quantitative analysis and classification of the selected examples. Previous reviews on helically chiral strained polyaromatic compounds include four recent, extensive reviews on [n]helicenes^5–7 and twistacenes⁸ and one other review⁹ highlighting specific examples. Each review, however, deals mostly with one class of helical molecules and focuses on different synthetic approaches, including stereoselective synthesis, to these targets. A general concept bringing all the structural motifs together in a systematic way has been missing in the literature and is addressed in this conceptual review. The strain-induced helical architectures are organised by means that they adopt a helical conformation, and their structural design and its consequences are discussed. Because of the vast number of examples, the presented structures were selected thoroughly, such that they illustrate the differences between various types of strain-induced helical systems as clearly and simply as possible. To qualitatively assess the amount of induced strain, structural and dynamic parameters are discussed in detail. Therefore, compounds, whose solid-state structures as well as the Gibbs free energy barriers (ΔG^‡) of racemisation are available, were selected preferentially. In the case of less recent examples, the ΔG^‡ values were estimated from the activation energies (E_a) of racemisation and the corresponding A values, using the Arrhenius and Eyring equations. In addition, we have tried to include as many recent significant examples as possible, which have not been reviewed before.

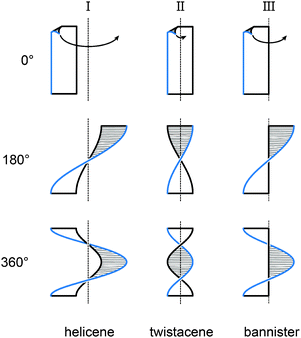
Fig. 1 illustrates three limiting cases of twisting a ribbon with edges highlighted in black and blue for clarity. Depending on the position of the stereogenic axis, three types, namely, I, II and III, can be recognised. A type I helical ribbon coils around an axis, which does not have an intersection with the ribbon, leading to a structure reminiscent of a staircase. As a result, the blue and black edges do not have the same length, the blue edge being consistently the longer one in this review (except for the case of equal lengths of the two edges). Molecular analogues are known as helicenes (Section 2), the most archetypal examples of helical polyaromatic systems. The steric interaction between overlapping or partially overlapping rings forces helicenes to adopt a helical conformation against the energy cost of the torsional strain induced in the helicene backbone.

Fig. 1 Three types of helically twisted ribbons. The stereogenic axis is placed such that it (I) does not have an intersection with the ribbon (helicene-type), (II) is identical to the main axis of the ribbon (twistacene-type) or (III) is identical to the black edge of the ribbon (bannister-type). In type II, the blue and black edges have the same length, while in types I and III, the blue edge is longer than the black one. Twists of 180 and 360° are shown.

Type II features a stereogenic axis that is identical to the main axis of the untwisted, planar ribbon. When the ribbon is twisted around this axis, both edges have the same length and are pirouetting around the axis similarly to the strands of double-helix DNA. The closest molecular analogues of type II ribbon are known as twistacenes (Section 3). Unfavourable steric interactions are achieved by introducing steric crowdedness around the periphery. The energy benefit of minimising these steric interactions is optimised against the energy cost of distorting the π-system from planarity.

In type III, the stereogenic axis and the black edge of a ribbon, instead of the main axis of its planar form, are identical. Twisting the ribbon around the stereogenic axis leads to a system, in which the blue edge is longer than the black one and coils around the black edge, similarly to the case of a bannister (Section 4). Known molecular analogues of type III system have a rigid oligo(para-phenylene) backbone (black edge) and a bannister-like flexible part (blue edge), encircling a “hollow” ribbon. Ring strain in the bannister systems induces the helically twisted conformation against the torsional strain generated in the oligo(para-phenylene) backbone, which is energetically less costly.

Section 5 of this review focuses on helical systems in which a “circular ribbon” (ribbon where both ends are “fused” together) is twisted around one or three axes to provide more complex helically twisted systems, namely, figure-of-eight (type IV) and propeller (type V) helices, respectively. In Section 6, the properties emerging from the helical nature of these systems are discussed.

2. Helicenes

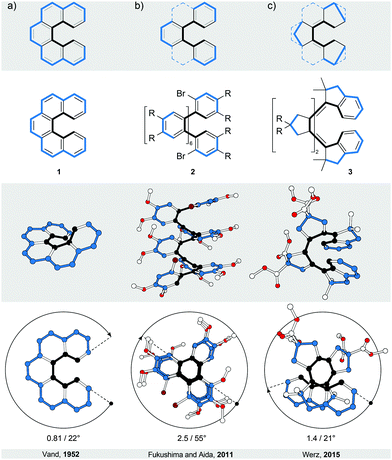
Helicenes^5–7 and truncated helicenes are the first structural type of strain-induced helical architectures shown in Fig. 1, in which both edges of a ribbon, one shorter (black) and one longer (blue), coil around an axis that does not have an intersection with the ribbon. In other words, the edges coil around circular cylinders that have a common axis but different diameters. The structure of an [n]helicene (Fig. 2a) comprises ortho-fused benzene rings (n is the number of rings), which represent the body of the ribbon. In truncated [n]helicenes, some rings are omitted (Fig. 2, top) such that the black edge remains intact, while the blue edge is interrupted. The number of turns (Fig. 2, bottom) in [n]helicenes and truncated [n]helicenes can be estimated using the formula n/6. According to this formula, [6]helicene shows approximately one and [12]helicene approximately two turns.

Fig. 2 Helicenes and truncated helicenes: structural formulae of 1–3 (top), and perspective (middle) and top (bottom) views of their corresponding solid-state structures (XRD). The truncation process is illustrated using the backbone of the parent [5]helicene (a) with a continuous annulation. Partial truncation of [n]helicenes leads to ortho-[m]phenylenes (b), and full truncation and embedding of five-membered rings leads to all-s-cis all-Z polyenes (c). The overall number of turns/average torsion-angle value per phenanthrene (a) or biphenyl (b and c) subunit are shown. The edges are highlighted in black and blue for clarity. In 2, R = OMe; in 3, R = COOMe.

2.1. [n]Helicenes

In a two-dimensional drawing of an [n]helicene, some benzene rings overlap with one another and therefore suffer from steric interaction. The number of overlapping rings depends on the number of fused rings (n). When n ≤ 6, the terminal benzene rings only partially overlap¹⁰ with each other (1, Fig. 2a). When n > 6, every k fused ring (k > 6) overlaps with the (k − 6) ring and the steric interaction between these rings causes repulsion (Fig. 3a). To minimise the steric interaction, the structure undergoes a helical twist and the final thermodynamically most favoured conformation results from the optimisation of the energy cost of the induced torsional strain against the energy benefit of the minimised steric interaction. The induced torsional strain is best visible by looking at distortions in the bay region (black) of the phenanthrene subunits of [n]helicenes. While in phenanthrene (the shortest [n]helicene) the bay-region torsion-angle value is close to 0°, in [n]helicenes with n > 3, the average bay-region torsion-angle values vary from 19° in [4]helicene⁵ to 24° in [16]helicene¹¹ (4), the longest [n]helicene (Fig. 3a) made to date. (Note: the average torsion-angle value is calculated from the torsion-angle values of all possible phenanthrene subunits in an [n]helicene.) The roughly constant values of the torsion angles across the series of [n]helicenes are the result of the close contact between the rings positioned above each other, with an average distance of ∼3.5 Å (the π–π stacking distance), by which [n]helicenes gain additional stabilisation. [n]Helicene can be thus viewed as a tension spring.

Fig. 3 Helicenes and ortho-naphthylenes: structural formulae of 4–7 (top), and perspective (middle) and top (bottom right) views of their corresponding solid-state structures (XRD). The overall number of turns/average torsion-angle value per phenanthrene (a), phenanthrene/fluorene (b) or binaphthyl (c and d) subunit are shown. The edges are highlighted in black and blue for clarity. In 7, R = CHO.

Although the values of torsion angles are approximately uniform, the racemisation ΔG^‡ values of [n]helicenes increase⁶ with increasing n (n/ΔG^‡ (kcal mol⁻¹) at 300 K: 5/24.1, 6/35.6, 7/41.7, 8/42.4 and 9/43.5). In [n]helicenes with n > 6, in which at least two rings are fully overlapped, a plateau is reached and the energy barrier values of [7]- and higher [n]helicenes are very similar. This observation indicates that [n]helicenes are “much more flexible than is generally believed” as pointed out¹² by Martin and Mislow. It has been shown¹² that the racemisation of [n]helicenes most likely occurs through a conformational pathway, rather than an internal double Diels–Alder reaction, because the necessary molecular deformations are spread over a large number of bonds. Substituents introduced in the bay region of the terminal rings increase⁶ the energy barrier of racemisation in [n]helicenes, as they induce an additional steric interaction, reflected by an increased average “bay-region” angle.

A unique example of an [n]helicene is compound 5¹³ (Fig. 3b), in which five- and six-membered rings are fused together in an alternating ortho/meta fashion. As a result of this topology, a less curved structure, compared to all-ortho-fused helicenes, is obtained. To induce a helical conformation in this system, four phenyl substituents were introduced at the inside (black edge) and two tert-butyl substituents at the outside (blue edge) peripheries, respectively, to cause sufficient unfavourable steric interaction. The structure adopts a helical conformation, which is reminiscent of a spiral staircase, in which the four phenyl groups represent four parallel steps. Compared to all-ortho-fused helicenes, the ortho-/meta-fused helical “spring” makes a full turn over a longer distance. It can therefore be categorised as a helicene that is, in part, twistacene-like. The structure is further stabilised by π–π stacking interactions between the parallel phenyl rings, which rotate around the single aryl–aryl bond with energy-barrier values between 12.6 kcal mol⁻¹ at 283 K and 14.3 kcal mol⁻¹ at 298 K. The energy barrier of racemisation was not determined for this compound, but it is expected to be stable against racemisation at room temperature.

2.2. Truncated [n]helicenes

Truncation of every second ring in [n]helicene with n ≥ 5 (Fig. 2b) leads to an ortho-[m]phenylene structure (m = (n + 1)/2 for an ortho-[m]phenylene made by truncation of [n]helicene). Similarly to [n]helicenes, ortho-[m]phenylenes¹⁴ also adopt a helically twisted conformation to minimise the steric interaction between each pair of alternating phenylene rings. In contrast to [n]helicenes, however, ortho-[m]phenylenes do not contain phenanthrene but biphenylene subunits, which makes them more flexible as conformational changes involve rotation of phenylene rings around single aryl–aryl bonds. Because of their flexibility, ortho-[m]phenylenes adopt¹⁴ multiple helical conformations in solution. In the most stable helical conformation (“closed” helix) of ortho-[m]phenylenes, the phenylene rings are oriented with respect to each other such that every phenylene ring interacts through an offset π–π stacking¹⁵ with every third phenylene ring, forming a well-defined helical architecture with small disorder at the ends. The steric interaction is minimised against torsional strain induced in each biphenylene subunit. For illustration, the average biphenylene torsion-angle value in ortho-[8]phenylene 2¹⁶ is 55°, which is higher than the value (∼45°) of the optimum biphenyl torsion angle. The induction of the torsional strain in biphenyl, however, is less energy-costly compared with phenanthrene, and ortho-[m]phenylenes are thus less strained than [n]helicenes.

The lack of strain and higher flexibility of ortho-[m]phenylenes are also reflected in the lower values of their racemisation ΔG^‡ when compared with [n]helicenes. The shortest ortho-[m]phenylene that could be partially resolved¹⁷ into its enantiomers by chiral-stationary-phase HPLC was ortho-[10]phenylene. Helical inversion of ortho-[16]phenylene and ortho-[24]phenylene is sufficiently slow and both compounds could be fully resolved, which allowed determination¹⁷ of their racemisation ΔG^‡ values at 298 K (23.4 and 23.9 kcal mol⁻¹, respectively). The longest reported ortho-phenylene contains¹⁶ 48 phenylene units, however, its racemisation barrier was not reported. An ortho-[8]phenylene derivative of 2 (with an NO₂ group instead of each Br atom) was successfully resolved¹⁶ into its enantiomers by crystallisation. Its racemisation ΔG^‡ value at 283 K was determined to be 20.4 kcal mol⁻¹, indicating fast helical inversion (half-life of 352 s) in solution. Interestingly, this compound adopts¹⁶ a tighter helical conformation (shorter π–π stacking distance between phenylene rings) upon oxidation, which dramatically changes its racemisation barrier at 283 K to 23.9 kcal mol⁻¹ (half-life of 44 h), a value similar to those of longer neutral analogues. The racemisation barrier can be increased by replacing the phenylene subunits with the naphthalene ones (Fig. 3c and d). Because of the increased steric interaction, naphthalene-1,2-diyl system 7¹⁸ does not undergo racemisation even at elevated temperatures (the racemisation ΔG^‡ value of a related trimer at 453 K is 36.8 kcal mol⁻¹). Topologically, while in extended systems 6¹⁹ a full offset overlap between the naphthalene moieties is expected based on the solid-state structure, in extended systems 7, only partial offset overlap between the naphthalene moieties should take place. An extension of ortho-[m]phenylenes are oligo(ortho-phenylacetylenes),²⁰ which in some cases adopt a helical conformation in the solid state. In these systems, the helical conformation is not induced by strain and is usually one of many possible conformations that are in equilibrium in solution. Because oligo(ortho-phenylacetylenes) can be therefore categorised as foldamers,²¹ they do not fit into the category of strain-induced helices and are not discussed in more detail.

Truncation of all rings in an [n]helicene leads to a polyene structure (Fig. 2c). To induce a helical conformation in such a polyene system, five-membered aliphatic rings were annulated at the site of the single bonds. In this way, the polyene system was forced to adopt an all-s-cis all-Z arrangement. Milde reported²² the first example of such a polyene (3, truncated [9]helicene), which is coiled into a helical conformation with an average bay-region torsion angle of 21°. Double bonds connecting the five-membered rings induce rigidity in the system, which is, similar to [n]helicenes, more strained than ortho-[m]phenylenes. In fact, the racemisation ΔG^‡ value of 3 was determined to be 28.1 kcal mol⁻¹ at 383 K. For a comparison, the racemisation ΔG^‡ value of non-truncated [9]helicene is 51.5 kcal mol⁻¹ at 383 K, which makes [n]helicenes more stable against racemisation than truncated [n]helicenes.

3. Twistacenes

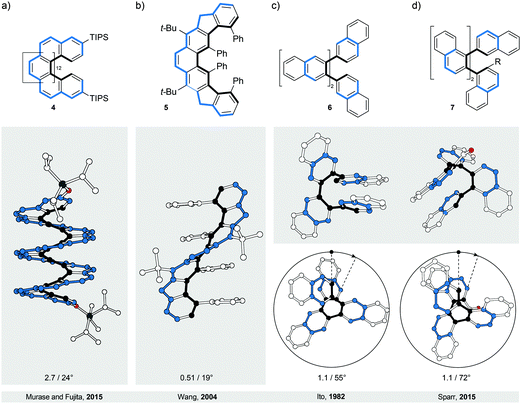
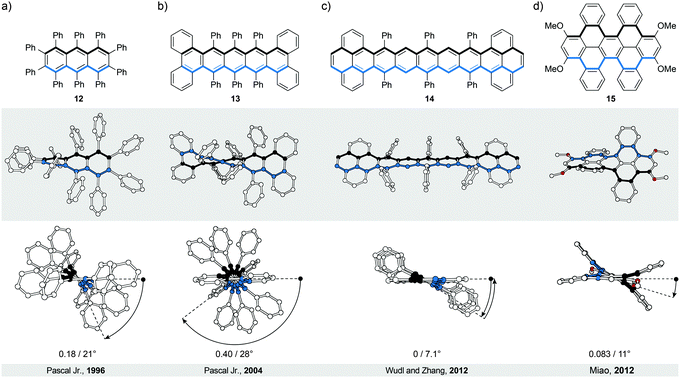
The most intuitive deformation of a planar ribbon is the twist along its main molecular axis (Fig. 1, middle). Both edges of the resulting helically twisted ribbon have the same length and this degree of symmetry simplifies the synthesis of the molecular analogues. Acenes, polyaromatic hydrocarbons comprising linearly (or meta-) fused benzene rings, are ideally suited for induction of such a helical twist. They have well-defined chemically addressable rims, which allow substituents or annulated rings to be held in close proximity to each other. The steric crowdedness around the periphery forces an acene to adopt a helical conformation, which is energetically more favoured than the planar one. Such twisted acenes are known⁸ as twistacenes. Steric crowdedness can be achieved (Fig. 4) by the use of bulky substituents, such as phenyl groups, at all (a, crowded twistacenes)²³ or selected (b, equatorenes)²⁴ positions, by benzannulation (c, π-extended twistacenes),²⁵ or by embedding an acene into a bicyclic system (d, bicyclic twistacenes).²⁶ In the latter case, two pairs of opposing peripheral carbon atoms are bridged, one pair above and one below the acene plane. In this constitution, the carbon atoms are pulled out of the plane, each pair in the opposing relative direction, inducing helicity. Cases, where bulky substituents in combination with benzannulated rings are employed to induce helical twist, have also been described.²⁷ In this section, representative examples of all four types and their combinations are discussed.

Fig. 4 Twistacenes: structural formulae of 8–11 (top), and perspective (middle) and side (bottom) views of their corresponding solid-state structures (XRD). A continuous helical twist of naphthalene around its main molecular axis was achieved by (a) substitution at all peripheral positions, (b) substitution at the positions on one side only, (c) benzannulation and (d) embedding naphthalene unit into a bicyclic system. The overall number of turns/average torsion-angle value per benzene ring are shown. The edges are highlighted in black and blue for clarity.

To assess qualitatively the amount of induced torsional strain in a twistacene, the average torsion-angle values per benzene ring are compared, instead of the overall end-to-end torsion-angle values. Notably, twistacenes are less sensitive to light, heat, oxygen, dimerisation or polymerisation compared with planar acenes. They, however, retain⁸ the electronic and spectroscopic properties of the parent acenes, presumably because the twist is relatively small and continuous across the entire “ribbon”.

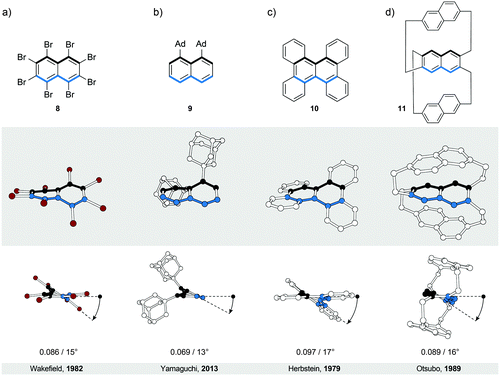
3.1. Crowded twistacenes

In perbrominated naphthalene 8²³ (Fig. 4a), every hydrogen atom is substituted by a bromine atom. The shortest distance between the neighbouring bromine atoms at the 1-/4- and 8-/5-positions in planar 8 is ∼2.5 Å, while the average distance between the neighbouring bromine atoms in helically twisted 8 is ∼3.3 Å. Since the sum of the van der Waals radii of two bromine atoms is ∼3.8 Å, a significant amount of strain energy is released upon twisting 8. Indeed, X-ray diffraction analysis of the solid-state structure of 8 revealed an end-to-end twist of 31° (or ∼15° per benzene ring), which was attributed solely to the effect of minimising steric interactions between the substituents. The steric effect is clearly visible when the end-to-end twist of 8 is compared with that (24°) of octachloronaphthalene,⁸ as chlorine (radius 175 pm) is less bulky than bromine (radius 190 pm). When the bromine atoms in 1 were replaced by phenyl substituents to afford octaphenylnaphthalene,⁸ it was found that the naphthalene unit in this compound is almost perfectly planar in the solid state. The calculations performed on octaphenylnaphthalene and comparison with other analogues suggest⁸ that such planarisation should not be favoured, indicating that crystal-packing forces overcompensated the induced steric strain in this case. Solution studies, if possible, are therefore an important addition to the solid-state analysis of the induced helical twist.

The perphenylated anthracene 12²⁸ (Fig. 5a), an extended analogue of octaphenylnaphthalene, shows a 63° twist (or ∼21° per benzene ring) in the solid-state structure. Notably, its ¹³C NMR spectrum in solution features only 16 signals instead of the expected 22 for the D₂ symmetric structure, indicating that 12 is relatively flexible to yield a time-averaged D_2h or D₂ symmetry. The obtained spectroscopic data revealed a fine vibrational structure similar to anthracene, which suggests that distortions of up to 21° per benzene ring do not significantly affect the π-conjugation in acenes.

Fig. 5 Longer twistacenes: structural formulae of 12–15 (top), and side (middle) and top (bottom) views of their corresponding solid-state structures (XRD). (a) Fully substituted anthracene derivative, (b) pentacene with both bulky substituents and π-extended benzannulated ends, (c) the first example of a nonatwistacene, which adopts an achiral meso conformation and (d) naphthalene-based bicyclic cyclophane. The overall number of turns/average torsion-angle value per benzene ring are shown. The edges are highlighted in black and blue for clarity.

Twistacene 13 shows²⁷ an astonishing end-to-end torsion-angle value of 144° (∼28° per benzene ring) in the solid state (Fig. 5b), the largest induced twist to date. As a consequence, 13 is highly soluble in common organic solvents and air-stable at room temperature in the dark. It is also one of the few twistacenes that undergo a relatively slow racemisation (half-life ∼9 h, ΔG^‡ = 23.8 kcal mol⁻¹, 298 K), which allowed separation of its enantiomers. For a comparison, most of its analogues, which afforded enantiomerically pure crystals, undergo⁸ a much faster racemisation in solution. Racemisation of twistacenes occurs⁸ over several nonplanar intermediates with lower energy transition states, compared with a hypothetical planar transition state, which is the main reason for fast racemisation of most twistacenes.

The importance of sufficient steric crowdedness around the periphery for inducing the helical twist in acenes is demonstrated²⁹ best in the case of nonatwistacene 14. In 14, the periphery is decorated (Fig. 5c) with bulky substituents and benzannulated rings, however, four crucial positions around the centre of the acene are unsubstituted. The steric strain at each end (between phenyl and annulated benzene rings) induces a helical twist, with positive (at one end) and negative (at the other end) helicities. Because of the four missing substituents, the helical twist at one end does not propagate to the other end; rather it changes helicity in the centre of the acene. This conformation is energetically more favoured than that with a continuous twist because it results in a decreased average torsion-angle value of ∼7.1° per benzene ring (∼28° in 13) and consequently less induced strain. The central benzene ring has no twist (0° torsion angle), while the third-to-last benzene rings experience the largest twist (14° torsion angle). Such a disrupted-helix conformation has a plane of symmetry and represents an achiral meso form. A continuous crowdedness around the periphery is therefore of central importance for inducing helicity in acenes by strain. In contrast to the planar nonacene, which is extremely unstable and has never been isolated as a solid material, twistacene 14 is stable in air for more than five days. The increased stability is presumably the consequence of steric bulk and extended π-conjugation at the ends (pyrene subunits), which proved to increase the stability under oxygen and light exposure in shorter twistacenes. The twist, which typically does not affect significantly the electronic structure, might contribute to stability, but due to steric factors, as well. An example of an extended type II system is compound 15,³⁰ in which dibenzo[cd,lm]perylene is employed instead of an acene as the “ribbon” (Fig. 5d). The helical conformation is induced by annulation of four benzene rings, which are part of two [5]helicene subunits that display the same helicity within the structure. The induced torsional twist of 11° is lower compared to most of the twistacenes, presumably as a result of the fact that the induced strain is spread over a larger number of bonds in dibenzo[cd,lm]perylene compared with an acene of the same length. The second possible isomer is the anti-conformer (not shown), which is chiral despite the fact that the [5]helicene subunits show opposite helicities. Theoretical calculations predict similar energies for both stereoisomers and, indeed, heating of one or the other conformer leads to a mixture of both. Substitution of the methoxy groups in 15 for the hexyloxy groups allowed determination³⁰ of the conformer-interconversion barriers of the corresponding derivative (27.7 kcal mol⁻¹ for the twisted-to-anti and 28.7 kcal mol⁻¹ for the anti-to-twisted processes at 383 K) by ¹H NMR spectroscopy. These values, in principle, also correspond to the racemisation-barrier values for both conformers.

3.2. Equatorenes

A recently described type of longitudinally twisted acenes that is closely related to twistacenes are the equatorenes. Similarly to twistacenes, the torsional twist in equatorenes is caused by steric strain at the periphery, however, only on one side, resulting in a lower symmetry compared to twistacenes. Equatorene 9²⁴ (Fig. 4b) bearing two adamantyl (Ad) groups at the 1- and 8-positions shows an end-to-end twist of almost 25° (∼13° per benzene ring). Notably, the blue edge in 9 shows no deviation from planarity, as the twist affects solely the black (substituted) edge. Such dissymmetry is also present if the unsubstituted part of the acene (blue edge) is annulated, which distorts only the substituted part of the conjugated system from planarity. Remarkably, equatorenes do not racemise at room temperature, as the racemisation energy barriers have typically higher values than those of twistacenes. For example, the racemisation ΔG^‡ value of 9 was determined to be 26 kcal mol⁻¹ at 343 K. Benzannulation of the unsubstituted part of the acene core further increases this barrier. As the induced twist is higher in twistacenes than in equatorenes, the increase of the energy-barrier values in the case of equatorenes can be attributed to the substituent rather than the twist effect, as the equatorene substituents are usually much bulkier than those of twistacenes (adamantly versus phenyl). Compared with the planar parent acenes, the emission maxima of equatorene analogues are typically red-shifted²⁴ due to the decrease of the energy of the HOMO while maintaining the LUMO energy level.

3.3. π-Extended twistacenes

Benzannulation of an acene leads to structures with an interesting diversity of twists, when looking at their solid-state structures. Strictly speaking, they no longer belong to the category of acenes but are an entirely new class of polycyclic aromatic hydrocarbons (PAHs). They are related to acenes in the sense that they adopt a twisted-ribbon conformation similar to twistacenes. The torsional twist is caused by the steric interaction between the annulated rings. One selected example is given here but many more exist in the literature, often not being recognised as chiral molecules. Tetrabenzonaphthalene 10²⁵ (Fig. 4c) demonstrates the principle of introducing steric strain by benzannulation, which induces a helical end-to-end twist of 35° (∼17° per benzene ring) in 10. For a comparison, the value of this end-to-end twist is very close to that (31°) of crowded twistacene 8 (Fig. 4a).

3.4. Bicyclic twistacenes

A conceptually different approach to induce a helical twist in acenes is by crosswire-like bridging of two pairs of opposing edge positions. One bridge, if short enough, distorts an acene into a boat-like conformation. With two bridges of such length, the acene is distorted into a helically twisted conformation (Fig. 4d) if one bridge connects the two ends above and one below the plane of the acene. Tanaka et al. demonstrated²⁶ this concept in a naphthalene-based “triple-decker” bicyclic cyclophane 11 (Fig. 4d). The resulting end-to-end twist of the central naphthalene unit in 11 is 32° (∼16° per benzene ring), and is caused solely by the bicyclic strain without the contribution of steric bulk.

4. Bannisters

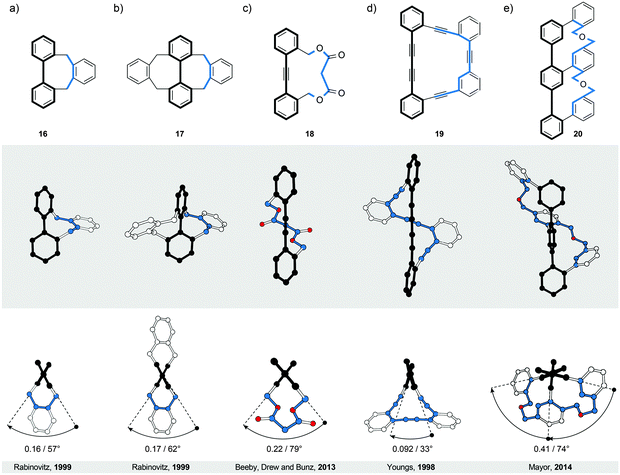
Similarly to helicenes and twistacenes described in Sections 2 and 3, respectively, the bannister-like structures also display a continuous helical twist along the stereogenic axis. The difference between the twistacene and bannister ribbon types is that in twistacenes, the stereogenic axis is identical to the main axis of the ribbon, while in bannisters, the stereogenic axis and the black edge of the ribbon are identical (Fig. 1, right). From a different perspective, a bannister system can be viewed as one half of the twistacene system, in which the axis becomes the black edge. In this constitution, the blue edge resembles a bannister of a staircase rather than the steps, as it is longer and coils around the shorter black edge (the axis), which remains linear. The structures of the known molecular bannister analogues consist (Fig. 6) of an oligo(para-phenylene)^31–34 (a, b and e) or a phenylene–acetylene^35,36 (c and d) backbone, representing the black edge, and a linker bridging the terminal phenylene rings (blue edge), forming a macrocycle encircling a “hollow” ribbon. The energy barrier for the relative rotation of the individual phenylene rings in an unbridged oligo(para-phenylene) is relatively low and the rings are “free” to rotate around the single aryl–aryl bonds under ambient conditions. The macrocyclic strain of the hypothetically planar bannister oligomers forces the linker to coil around the oligo(para-phenylene) backbone in a helical fashion, inducing torsional strain in each biphenylene subunit. The general rule³³ to follow while designing bannister structures is to interlink two phenylene rings with a bridge that is longer than the distance between the two rings.

Fig. 6 Bannisters: structural formulae of 16–20 (top), and side (middle) and top (bottom) views of their corresponding solid-state structures (XRD). Singly (a) and doubly (b) bridged biphenyl, singly bridged diphenylacetylene (tolane, c) and bis(phenylacetylene) (d) with an extended molecular axis compared with biphenyl, and singly bridged terphenyl (e) featuring one continuous bridge, which is connected to each ring of the backbone. The overall number of turns/average torsion-angle value per biphenyl subunit are shown. The edges are highlighted in black and blue for clarity.

4.1. Bridged biphenyls

The smallest known bannister structures are bridged biphenyls⁴² (Fig. 6a, b and 7). The axially chiral ortho-substituted biphenyls do not fall into this category because their chirality is not merely induced by steric interactions between the substituents. An additional criterion for ortho-substituted biphenyls to be axially chiral is that the two ortho-substituents of each phenyl ring are not equivalent. For example, the doubly bridged biphenyl 17³² (Fig. 6b) bearing four equivalent ortho-substituents is C₂-symmetric (62° torsional twist) and therefore chiral, while its unbridged analogue 2,2′,6,6′-tetramethyl-1,1′-biphenyl is not because it has a plane of symmetry (∼90° torsional twist⁴³). Unsubstituted biphenyl⁴² itself has ∼45° torsional twist in the lowest-energy conformation, which defines its chirality as a geometrical object. The energy barrier of rotation around the aryl–aryl bond in biphenyl is, however, relatively low and fast rotation under ambient conditions does not allow differentiation between the two enantiomers.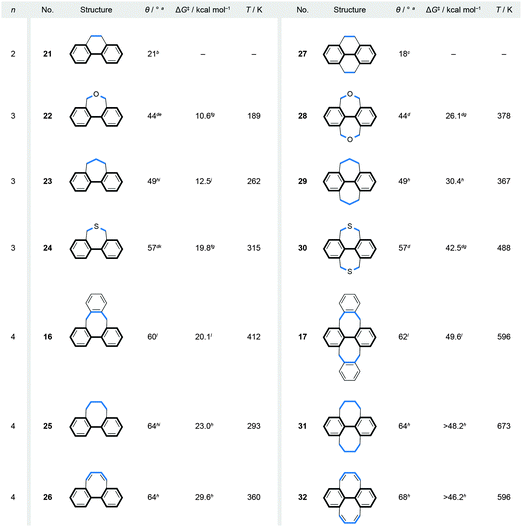

Fig. 7 Correlation between the values of the biphenyl torsion angles (θ), Gibbs free energy barriers (ΔG^‡) of racemisation and the lengths (n) of the bridges (highlighted in blue) in singly (16 and 21–26) and doubly (17 and 27–32) bridged biphenyls. ^a Calculated value. ^b XRD Value, ref. 37. ^c XRD Value, ref. 38. ^dRef. 39; the torsion-angle values were calculated only for singly bridged biphenyls. ^e 43° from XRD of a 4,4′-dibromo-derivative, ref. 40. ^fRef. 41. ^g Estimated from the E_a and log A values by using Eyring and Arrhenius equations; ΔG^‡ = ΔH^‡ − TΔS^‡, where ΔH^‡ = E_a − RT and ΔS^‡ = R(ln A − 1 − ln(k_BT/h)); for 22 and 24, the log A values of 28 and 30, respectively, were used. ^hRef. 42. ⁱ 45° (23) and 59° (25) from XRD of 4,4′-dicyano-derivatives, ref. 43. ^jRef. 43. ^k 58° from XRD, ref. 44. ^lRef. 32; 58° (16) and 57° (17) from XRD.

A series of singly and doubly ortho,ortho′-bridged biphenyls in Fig. 7 demonstrate the dependence of the induced torsional twist (θ) in a biphenyl on the length (n, the number of bridging atoms) and the number (one versus two) of its bridges, as well as the effect of the twist and the number of bridges on the racemisation barrier ΔG^‡. The torsional twist is induced by minimising strain that is present in the ring formed by the bridge and the backbone in an untwisted, planar biphenyl. When the length (n) of the X_n-bridge exceeds one atom, the coplanar phenyl units, as in the case of C₁-bridged biphenyl (fluorene), adopt a helically twisted conformation by rotation around the single aryl–aryl bond. For both singly and doubly bridged biphenyls, the biphenyl torsion-angle values increase with increasing n, varying (Fig. 7) from 21° (C₂-bridged 21³⁷) to 64° (C₄-bridged 25 and 26⁴²) in the singly bridged series and from 18° (C₂-bridged 27³⁸) to 68° (C₄-bridged 32⁴²) in the doubly bridged series. The torsion angles of the singly and doubly bridged biphenyls featuring the same bridge types have similar values with differences of <4°, in accord with expectations for such C₂ symmetric systems. Fig. 7 further illustrates that the racemisation ΔG^‡ values increase with increasing torsion-angle values in each series. Although this trend cannot be generalised to all bridged biphenyls, it can be applied to systems, such as 22–24 and 28–30, in which deformations induced during racemisation are equal in number and in kind. In these systems, the three-atom bridges comprise either an oxygen, a carbon or a sulphur atom in the middle, and the size of the central atom defines³⁹ the torsional twist and the racemisation barrier. It is also of interest to note that although the torsion-angle values of the singly and doubly bridged biphenyls featuring the same bridge are similar, the racemisation-barrier values of the doubly bridged biphenyls are 2.1–2.5 times higher than those of the corresponding singly bridged biphenyls. An additional (second) bridge thus helps “locking” the helical conformation in the bannister-type biphenyls, which makes all doubly bridged biphenyls with n > 2 stable against racemisation under ambient conditions. The doubly bridged biphenyls can be viewed as “double-bannister”, or double-helix, systems, in which each bridge coils around the stereogenic axis similarly to the coiling of the two edges in twistacenes. Increasing the rigidity of the bridge(s)⁴² in the case of 26 and 32 also leads to a significant increase of the racemisation-barrier values, when compared to flexible systems 25 and 31, although all four compounds display similar values of torsional twists.

4.2. Extended bannisters

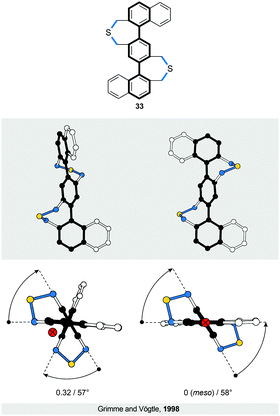
Introduction of one and two acetylene linkers in between the two rings of a bridged biphenyl leads to elongated bannister systems 18³⁵ and 19,³⁶ respectively (Fig. 6c and d). The ease of induction of the torsional twist in such systems leads to an astonishing 79° twist in the case of 18. The energy barrier of racemisation for this compound was not reported. Considering the flexibility of the system, however, the barrier is expected to be relatively low. In the case of 19, the rigidity of the bridge accounts for the relatively low torsional twist (33°) and, presumably, for a higher energy barrier of racemisation compared to 18, as evidenced by obvious deformations induced in the bridge (Fig. 6d).

The successful induction of helical chirality in bridged biphenyls encouraged the design and realisation of extended analogues, namely, terphenyls, with the backbone extended for an additional phenylene ring compared to biphenyls. Vögtle and co-workers pioneered³¹ the work in this field and synthesised the first doubly bridged terphenyl 33 (Fig. 8), using the same –CH₂SCH₂– bridge as in biphenyls 24 and 30. Because the bridges in 33 link one terminal ring each to the central ring, the bridges do not display a continuous helical twist around the backbone but around an axis that is parallel to the backbone (Fig. 8, left). From this view, 33 represents a type I helix rather than type III (Fig. 1), despite the fact that Vögtle introduced³¹ the term bannister (German Geländer) for this system. From a “bannister perspective”, 33 can be viewed as two bannister subunits linked together, each being able to undergo helicity inversion independently of one another.

Fig. 8 Structural formula of 33 (top), and side (middle) and top (bottom) views of the solid-state structures (XRD) of its two diastereomers, a chiral (left, (P)-enantiomer shown) and an achiral (right, (P,M)-meso-form) one. The two diastereomers exist because both bannister subunits can adopt either (P) or (M) helicities independently of each other. The overall number of turns/average torsion-angle value per biphenyl subunit are shown. The edges are highlighted in black and blue for clarity. The crossed red-filled ring indicates the stereogenic axis.

As a result of two stereogenic units being present in 33, two diastereomers of 33 exist, a pair of enantiomers (P,P and M,M) with a helical conformation (Fig. 8, left) and an achiral (P,M)-meso-form (Fig. 8, right) that is more stable than the chiral conformers. All three stereoisomers are in equilibrium with each other in solution, as confirmed by ¹H NMR spectroscopy. The fact that the two bannister subunits in 33 are independent of each other is evidenced³¹ by the torsion angles (57° on average) and the energy barrier of racemisation (>23 kcal mol⁻¹ at 298 K) for 33, values that are similar to those of singly bridged 24 (57°, 19.8 kcal mol⁻¹ at 315 K), rather than doubly bridged 30 (57°, 42.5 kcal mol⁻¹ at 488 K). Rathore and co-workers later extended³³ this system to a quadruply bridged pentaphenyl analogue. No crystal structure has been reported for this compound but, in principle, eight different diastereomers are possible with four stereogenic units.

A true bannister oligomer 20 with a continuous helical twist around the terphenyl backbone (Fig. 6e) has been recently reported^33,34 by Mayor and co-workers, who presented a new concept that is related to Vögtle's and Rathore's idea of bannister oligomers. Instead of using two independent bridges as in 33, only one continuous bridge attached to each ring of the backbone in a ladder-like fashion was employed in 20. Similarly to other bannister oligomers, a helically twisted conformation is induced in 20 by strain that is present because the bridge and the terphenyl backbone do not have equal lengths. The new feature in this design is that the bridge is connected to each ring of the backbone with a linker (a phenyl ring), which acts as a relay. Once one end of the molecule adopts a helical conformation, the relay unit translates the helical twist onto the next segment, inducing a continuous twist of the bridge around the backbone that is collinear with the stereogenic axis. In this design, only (P) and (M) helical conformers, and not the meso-conformer, exist. Indeed, the X-ray crystallography, NMR spectroscopy and dynamic CD measurements confirmed the exclusive formation of two enantiomeric species, which presumably racemise via a uniform “dance-ribbon-like” pathway, with the racemisation ΔG^‡ value (∼23.8 kcal mol⁻¹ at 298 K) similar to that of 33. Compound 20 is to date the longest bannister oligomer that does not have a meso-form. Its stability against racemisation could be further increased by either increasing the rigidity of the bridge or employing the “double-bannister” strategy, as in the case of doubly bridged biphenyls.

5. Figure-of-eights and propellers

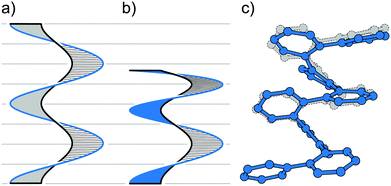
This section covers polyaromatic structures that can be represented by a cyclic ribbon helically twisted around one or three axes (Fig. 9), which results in the figure-of-eight (type IV) or propeller-like (type V) helical architectures, respectively. Typically, these helices feature several structural elements that induce a helical twist continuously and with a high degree of symmetry. They illustrate how a variety of possibilities can arise by combining the right pieces and inspire the design of more complex and extended strain-induced helical polyaromatics.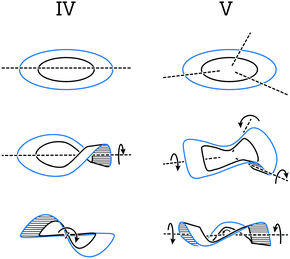

Fig. 9 Cyclic ribbon helically twisted around one (type IV) and three (type V) axes to afford figure-of-eight and propeller helices, respectively.

5.1. Figure-of-eights

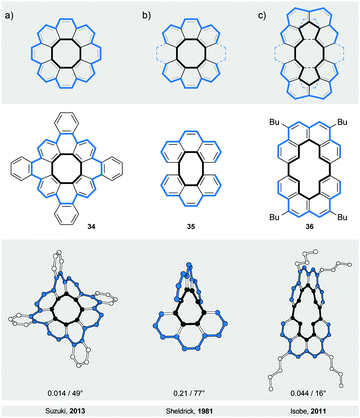
The first type (IV) of helically twisted cyclic ribbons is represented by molecules, in which aromatic rings are fused to form a circle, such as [8]circulene⁴⁵ (34, Fig. 10a).

Fig. 10 Figure-of-eights: structural formulae of 34–36 (top), and perspective (bottom) views of their corresponding solid-state structures (XRD). (a) Tetrabenzo[8]circulene with a helically twisted conformation. (b and c) Cyclic bis[n]helicenes related to [8]circulene with well-defined helical twists. The overall number of turns/average torsion-angle value between opposing carbon–carbon bonds of the inner eight-membered ring (34) or between opposing carbon–carbon bonds linking the [n]helicene subunits (35 and 36) are shown. The edges are highlighted in black and blue for clarity.

Because of the strain within the inner eight-membered ring (black), 34 adopts a saddle-like conformation that displays a negative curvature. Based on DFT calculations, this conformation is achiral and has a D_2d symmetry, which is in accord with NMR observations. The helically twisted S₄ symmetric conformation observed in the solid state (Fig. 10a) is therefore most likely the result of the packing forces. This conformation is approximately 1.8 kcal mol⁻¹ higher in energy than the D_2d conformation according to DFT. The average torsion-angle value of the helically twisted S₄ conformation, calculated from the dihedral angles between the opposing carbon–carbon bonds of the inner eight-membered ring, is 49°.

Truncation (and extension) of [8]circulene leads to phenanthrene- (Fig. 10b) and [4]helicene-based (Fig. 10c) cyclic structures 35⁴⁶ and 36,⁴⁷ respectively. In these structures, two [n]helicene subunits are linked together to form a cycle twisted around one axis, a shape reminiscent of a figure-of-eight. The twist is induced either (1) by the strain present in the eight-membered ring in the case of 35 or (2) by the steric interactions within the [4]helicene and biphenyl subunits in the case of 36. In 35 and 36, both helically twisted subunits show the same helicity as the overall structure, which has a helical twist of 77° and 16°, respectively. The racemisation ΔG^‡ values have not been determined for any of these structures, but a ΔG^‡ value of 10.1 kcal mol⁻¹ has been estimated for 36 by theoretical calculations. Structures 35 and 36 are unique in the sense that they represent⁴⁷ the illusory molecular expression of the “Penrose stairs”.

5.2. Propellers

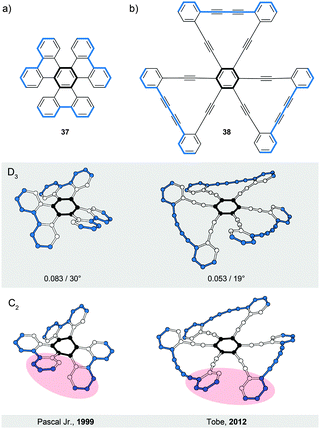
Compounds 37⁴⁸ and 38⁴⁹ represent (Fig. 11) the second type (V) of helically twisted cyclic ribbons. They are reminiscent of a propeller because of their blade-shaped subunits. Compound 37, also known as cloverphene (from “clover-like starphene”), is one of the first reported propellers and one of the smallest possible propellers derived from benzene. It adopts a D₃ symmetric helical conformation, in which three blades (blue-edged biphenyl subunits) are twisted out of the central-benzene-ring plane (black) by 30° on average per blade, as a result of the steric interaction between the blades. The structure of 37 also features three [5]helicene subunits, which share three rings each with one another. The average torsional twist of the [5]helicene subunits is 25°, a value slightly higher than that of parent [5]helicene (Fig. 2a). In addition to the propeller D₃ conformation (Fig. 11a, middle), 37 can, in principle, also adopt a chiral C₂ symmetric conformation (Fig. 11a, bottom). While in the D₃ conformation the blades are twisted in an “up-down–up-down–up-down” fashion, the C₂ conformation displays an “up-down–up-up–down-down” packing sequence of the blades. Consequently, the central benzene ring is almost planar (shallow chair conformation) in the first case, while it is significantly distorted in the latter case (twisted boat conformation). According to DFT calculations, the D₃ conformation of 37 is lower in energy than the C₂ conformation by 5.0 kcal mol⁻¹, which is in agreement⁴⁸ with the fact that only single crystals of D₃-37 could be obtained. The racemisation barrier of D₃-37 was not determined but it likely has a magnitude similar to that of [5]helicene. The racemisation process of D₃-37 occurs presumably via the C₂ intermediate.

Fig. 11 Propellers: structural formulae of 37 and 38 (top), and perspective views of their D₃ (XRD, middle) and C₂ (model, bottom) conformations. The D₃ and C₂ conformations are twisted in an “up-down–up-down–up-down” and “up-down–up-up–down-down” fashions, respectively. The overall number of turns/average torsion-angle value per blade are shown for D₃ conformations. The edges are highlighted in black and blue for clarity. The red-filled circles highlight the parts of the C₂ conformations, where the packing sequence of the blades differs from that of the corresponding D₃ conformations.

The D₃ propeller conformation is sometimes less stable than the C₂ conformation, for example, in the case of perchloro- or perfluorotriphenylene.⁴⁸ Pascal Jr. and co-workers carried out an extensive investigation of the D₃/C₂ dichotomy and found a simple rule-of-thumb⁴⁸ for the prediction of conformation in overcrowded D_3h polycyclic aromatics (D_3h is the symmetry of these structures when drawn flat on a paper): “if the central ring is expected to be aromatic (possessing shorter, benzene-like bonds), then a D₃ conformation should be preferred, but if the central ring is nonaromatic (possessing some very long “single” bonds and great bond alteration), then a C₂ conformation will be observed.” In other words, if the central ring is more resistant to deformation, the twist occurs on the blades. If the blades are more resistant towards deformation, the core benzene ring is distorted. From these observations, the D₃/C₂ dichotomy seems to be mainly an electronic effect.

The second example of a D₃ symmetric helical propeller is compound 38,⁴⁹ an ethynylene-extended analogue of 37. The two outer benzene rings of each blade in 38 are linked by a diethynylene unit, which pushes these rings towards the rings of the neighbouring blades. The steric interaction between the neighbouring outer benzene rings forces the blades to twist by 19° on average with respect to the central benzene ring. In solution, 38 shows a rapid D₃/C₂ interconversion relative to the NMR timescale. Upon additional benzannulation of the blades, the barrier of the D₃/C₂ interconversion for the corresponding derivative was determined⁴⁹ to be ∼25 kcal mol⁻¹ at 220 K.

6. Properties arising from helicity

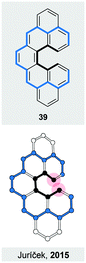
The overviewed concepts to induce helical chirality have merit in its own way. They, however, often provide us with structures that show unique properties or behaviour, some of which are discussed in this section. In particular, helical chirality in polyaromatic systems holds a promise to enhance optical and chiroptical properties, among others. Many of these promises have been met over the years, underlining the importance of design principles for making new strain-induced helices.

An induced helical twist can have a strong impact on the electronic structure of a π-conjugated system. For helicenes, this phenomenon is illustrated by a biradicaloid cethrene (39, Fig. 12), a dibenzo-annulated [5]helicene derivative. It has been shown⁵⁰ that the helical twist in 39 results in a significantly decreased singlet–triplet gap (5.6 kcal mol⁻¹), when compared to that (8.9 kcal mol⁻¹) of its planar analogue heptazethrene. Upon twisting hypothetically planar 39, an antibonding and a bonding interaction within the HOMO and the LUMO, respectively, appear between the carbon atoms highlighted by red-filled circles (Fig. 12). In the triplet state, the HOMO and the LUMO contain one electron each, and the bonding and antibonding interactions roughly cancel out. In the singlet state, the two electrons are predominantly paired in the HOMO and singlet 39 suffers from the antibonding interaction more than triplet 39, which results in the stabilisation of the triplet relative to singlet state and the decrease of the singlet–triplet gap. The interactions within the frontier MOs are visible also from the torsion-angle values of the [5]helicene subunit in the optimised geometries. While the average torsion-angle value in triplet 39 is 22°, singlet 39 features an increased torsion of 24°.

Fig. 12 Structural formula of 39 (top), a dibenzo-annulated [5]helicene, and the perspective view (bottom) of the optimised geometry of its singlet ground state. The edges are highlighted in black and blue for clarity.

As mentioned briefly in Section 2.2, an NO₂ analogue of ortho-[8]phenylene 2 was successfully resolved¹⁶ into its enantiomers by crystallisation. Although its helical inversion in solution is fast, one-electron oxidation dramatically changes the half-life of inversion from 352 s to 44 h as it triggers compression of the helix by shortening the average π–π stacking distance between the phenylene rings from 3.26 to 3.22 Å. The phenomenon of a helix compression in ortho-[m]phenylenes was also observed upon photoexcitation. Hartley et al. studied¹⁴ a series of ortho-[m]phenylenes with m ranging from 4 to 8 and found that the effective conjugation length (ECL) in this series is ∼4 and ∼5, as determined by experiments and calculations, respectively. The ECL value 4 means that the UV/Vis absorption maximum shifts bathochromically with the increasing length up to m = 4 and then remains approximately constant for oligomers with m > 4. This observation does not come as a surprise, as the biphenyl torsional twist makes the π-conjugation less effective compared to planar systems.

Interestingly, the emission maximum shifts hypsochromically with an increasing length for all members of this series as a result of a helix compression, which occurs¹⁴ on one end only in oligomers with m > 5 (Fig. 13). In the excited state, biphenyls typically adopt a planar quinoidal structure, but in ortho-[m]phenylenes, planarisation of the biphenyl units is not possible because of strain. As a result, the biphenyl torsion-angle values decrease upon photoexcitation to approximately 20–30° (quinoid-like structure), but are not zero. Furthermore, this compression occurs on one end only in oligomers with m > 5. Because longer oligomers are less able to accommodate the excited-state planarisation, stability of the excited state decreases as the length of ortho-[m]phenylenes increases, which is the reason for the observed hypsochromic shift in the emission spectra. The emission behaviour of ortho-[m]phenylenes thus directly reflects the relationship between their conformational behaviour and their electronic structure.

Fig. 13 Illustration of ground (a) and excited (b) states of ortho-[8]phenylene (c). In the excited state (blue in c), ortho-[8]phenylene adopts a helical conformation that is compressed on one end, in contrast to its ground state (gray in c) with no compression.

The induced twist in twistacenes increases their stability. Because the twist does not significantly alter the electronic properties of the parent acene, this approach allows the preparation of longer acenes, which are otherwise not accessible or unstable. The elongation of acenes decreases the HOMO–LUMO gap and this feature makes longer acenes suitable candidates for constructing semiconductors. The access to stable longer acenes is therefore desired. Zhang et al. have recently synthesised and characterised²⁹ the longest stable acene, namely, nonacene derivative 14 (Fig. 5c). As mentioned in Section 3.1, nonacene 14 features an average 7° twist per benzene unit, but as it is not sufficiently crowded, it contains a plane of symmetry and is not chiral. The HOMO–LUMO energy gap in 14 was determined to be 1.7 eV by UV/Vis spectroscopy and cyclic voltammetry, which is a value in between those of hexacene (1.84 eV) and heptacene (1.36 eV). Although 14 does not display a continuous helical twist along the backbone, it is a proof-of-principle example, which demonstrates that an induced helical twist should allow for the preparation of even longer acenes that are not accessible by other methods.

Bannister compound 18 (Fig. 6c) demonstrates³⁵ how an induced helical twist can, quite unexpectedly, affect the absorption and emission behaviour. In contrast to biphenyl, an unsubstituted tolane (diphenylacetylene) has a flat energy profile of rotation around the alkyne unit, with an energy barrier of less than 1 kcal mol⁻¹. Similarly to biphenyl, however, the twisted conformation of tolane can be enforced by increasing steric bulk at the phenyl rings or by linking them. The linking approach is particularly appealing because it allows the tolane unit to adopt a planar conformation, which is more stable than the twisted one in the excited state. Compared with an unsubstituted tolane, a tolane with a fixed planar conformation displays a red-shifted absorption, while a tolane with a fixed twisted conformation shows a blue-shifted absorption. Bunz and co-workers have recently described³⁵ a malonate-bridged tolane 18 that exhibits an almost 80° twist in the solid state, a torsion which was later confirmed in solution. What makes this structure unique is its unexpected long-lived (4 s) phosphorescence at low temperature (77 K), which is most likely the result of the large twist that stabilises the triplet state. While the ground state of 18 is twisted, the system planarises upon excitation to the singlet S₁ state and at elevated temperature (298 K) fluoresces at a maximum wavelength similar to those of planar tolanes. At low temperature (77 K) in a glassy matrix, however, the twisted excited state conformation is fixed and instead of fluorescence, an inter-system crossing to the twisted triplet T₁ state, which enables phosphorescence, occurs. Presumably, this feature is possible if a large twist (>70°) is induced in a tolane, which has not yet been achieved by steric bulk.

7. Conclusion

Helical architectures have inspired artists, designers, engineers and scientists alike for centuries, because in helices, chirality is expressed in a highly symmetric fashion that appeals naturally to the eye. It is fascinating to realise that helical structures featuring an axis of symmetry look simpler than most of other chiral structures, and more beautiful than most of other achiral structures. It is not just their visage, however, that captured the attention of chemists. Helicity often gives rise to unprecedented properties, which would not exist without the helical twist. Polyaromatic systems, in particular, are ever-sought targets to induce helical chirality. Helical twisting of a π-conjugated backbone can often quite dramatically alter the electronic properties, or even lead to new unexpected features, as shown in the preceding section. Understanding the principles that govern the induction of helical chirality and its impact on the electronic structure is therefore of crucial importance. We hope that the classification concepts and principles to induce helicity that are presented in this review will inspire the design and synthesis of new “complex yet simple” helical structures. As many helices known from the literature are not configurationally stable at room temperature, structures with increased values of racemisation energy barriers would certainly represent an invaluable advancement in this field.

Available CCDC numbers

1 (1137287), 2 (773552), 3 (1020999), 4 (1051159), 6 (267858), 7 (1405203), 8 (1110604), 9 (947431), 10 (1268345), 11 (1192755), 12 (1314918), 13 (252291), 14 (857476), 15 (913485), 16 (1210912), 17 (1210914), 18 (918377), 19 (1170129), 20 (995567), 21 (1157531), 24 (726382), 27 (670511), 33 (101385), 34 (949624), 35 (1104816), 36 (806565), 37 (114449), 38 (872771).

Acknowledgements

The Swiss National Science Foundation (SNF, M. J./PZ00P2_148043; SNF, M. M./200020_159730) and the Novartis University of Basel Excellence Scholarship for Life Sciences (M. J.) are kindly acknowledged for their financial support.

References

1. G. H. Wagniere, On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image, VHCA and Wiley-VCH, Zürich, 2007.
2. Y. Wang, J. Xu, Y. Wang and H. Chen, Chem. Soc. Rev., 2013, 42, 2930–2962.
3. K. Mislow, Molecular Chirality, in Topics in Stereochemistry, ed. S. E. Denmark, John Wiley & Sons, Inc., Hoboken, 1999, pp. 1–82.
4. H. Förster and F. Vögtle, Angew. Chem., Int. Ed. Engl., 1977, 16, 429–441.
5. M. Gingras, Chem. Soc. Rev., 2013, 42, 968–1006 and references cited therein.
6. M. Gingras, G. Félix and R. Peresutti, Chem. Soc. Rev., 2013, 42, 1007–1050 and references cited therein.
7. M. Gingras, Chem. Soc. Rev., 2013, 42, 1051–1095 and references cited therein.
8. R. A. Pascal Jr., Chem. Rev., 2006, 106, 4809–4819 and references cited therein.
9. C. Schmuck, Angew. Chem., Int. Ed., 2003, 42, 2448–2452.
10. A. O. McIntosh, J. M. Robertson and V. Vand, Nature, 1952, 169, 322–323.
11. K. Mori, T. Murase and M. Fujita, Angew. Chem., Int. Ed., 2015, 54, 6847–6851.
12. R. H. Martin and M. J. Marchant, Tetrahedron, 1974, 30, 347–349 and ref. 9 cited therein.
13. W. Dai, J. L. Petersen and K. K. Wang, Org. Lett., 2004, 6, 4355–4357.
14. C. S. Hartley, J. Org. Chem., 2011, 76, 9188–9191 and ref. 5–7 cited therein.
15. S. M. Mathew, J. T. Engle, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2013, 135, 6714–6722.
16. E. Ohta, H. Sato, S. Ando, A. Kosaka, T. Fukushima, D. Hashizume, M. Yamasaki, K. Hasegawa, A. Muraoka, H. Ushiyama, K. Yamashita and T. Aida, Nat. Chem., 2011, 3, 68–73.
17. S. Ando, E. Ohta, A. Kosaka, D. Hashizume, H. Koshino, T. Fukushima and T. Aida, J. Am. Chem. Soc., 2012, 134, 11084–11087.
18. D. Lotter, M. Neuburger, M. Rickhaus, D. Häussinger and C. Sparr, Angew. Chem., Int. Ed., 2015 DOI:10.1002/anie.201510259.
19. T. Motomura, H. Nakamura, M. Suginome, M. Murakami and Y. Ito, Bull. Chem. Soc. Jpn., 2005, 78, 142–146.
20. R. H. Grubbs and D. Kratz, Chem. Ber., 1993, 126, 149–157.
21. Foldamers: Structure, Properties and Applications, ed. S. Hecht and I. Huc, Wiley-VCH, Weinheim, 2007.
22. B. Milde, M. Leibeling, M. Pawliczek, J. Grunenberg, P. G. Jones and D. B. Werz, Angew. Chem., Int. Ed., 2015, 54, 1331–1335.
23. J. H. Brady, A. D. Redhouse and B. J. Wakefield, J. Chem. Res., 1982, 137, 1541–1554.
24. K. Yamamoto, N. Oyamada, S. Xia, Y. Kobayashi, M. Yamaguchi, H. Maeda, H. Nishihara, T. Uchimaru and E. Kwon, J. Am. Chem. Soc., 2013, 135, 16526–16532.
25. F. H. Herbstein, Acta Crystallogr., 1979, B35, 1661–1670.
26. T. Otsubo, Y. Aso, F. Ogura, S. Misumi, A. Kawamoto and J. Tanaka, Bull. Chem. Soc. Jpn., 1989, 62, 164–170.
27. J. Lu, D. M. Ho, N. J. Vogelaar, C. M. Kraml and R. A. Pascal Jr., J. Am. Chem. Soc., 2004, 126, 11168–11169.
28. X. Qiao, M. A. Padula, D. M. Ho, N. J. Vogelaar, C. E. Schutt and R. A. Pascal Jr., J. Am. Chem. Soc., 1996, 118, 741–745.
29. J. Xiao, H. M. Duong, Y. Liu, W. Shi, L. Ji, G. Li, S. Li, X.-W. Liu, J. Ma, F. Wudl and Q. Zhang, Angew. Chem., Int. Ed., 2012, 51, 6094–6098.
30. J. Luo, X. Xu, R. Mao and Q. Miao, J. Am. Chem. Soc., 2012, 134, 13796–13803.
31. B. Kiupel, C. Niederalt, M. Nieger, S. Grimme and F. Vögtle, Angew. Chem., Int. Ed., 1998, 37, 3031–3034.
32. L. Eshdat, E. Shabtai, S. A. Saleh, T. Sternfeld, M. Saito, Y. Okamoto and M. Rabinovitz, J. Org. Chem., 1999, 64, 3532–3537.
33. M. Rickhaus, L. M. Bannwart, M. Neuburger, H. Gsellinger, K. Zimmermann, D. Häussinger and M. Mayor, Angew. Chem., Int. Ed., 2014, 53, 14587–14591 and ref. 4 cited therein.
34. M. Rickhaus, O. T. Unke, R. Mannancherry, L. M. Bannwart, M. Neuburger, D. Häussinger and M. Mayor, Chem. – Eur. J., 2015, 21, 18156–18167.
35. S. Menning, M. Krämer, B. A. Coombs, F. Rominger, A. Beeby, A. Dreuw and U. H. F. Bunz, J. Am. Chem. Soc., 2013, 135, 2160–2163.
36. K. P. Baldwin, R. S. Simons, D. A. Scheiman, R. Lattimer, C. A. Tessier and W. J. Youngs, J. Chem. Crystallogr., 1998, 28, 353–360.
37. R. Cosmo, T. W. Hambley and S. Sternhell, J. Org. Chem., 1987, 52, 3119–3123.
38. H. Dang, T. Maris, J.-H. Yi, F. Rosei, A. Nanci and J. D. Wuest, Langmuir, 2007, 23, 11980–11985.
39. K. Mislow, M. A. W. Glass, H. B. Hopps, E. Simon and G. H. Wahl, J. Am. Chem. Soc., 1963, 86, 1710–1733.
40. H.-Q. Zhang, B. Li, G.-D. Yang and Y.-G. Ma, Acta Crystallogr., 2008, E64, o1304.
41. R. J. Kurland, M. B. Rubin and W. B. Wise, J. Chem. Phys., 1964, 40, 2426–2427.
42. K. Müllen, W. Heinz, F.-G. Klärner, W. R. Roth, I. Kindermann, O. Adamczak, M. Wezze and J. Lex, Chem. Ber., 1990, 123, 2349–2371.
43. J. Rotzler, H. Gsellinger, A. Bihlmeier, M. Gantenbein, D. Vonlanthen, D. Häussinger, W. Klopper and M. Mayor, Org. Biomol. Chem., 2013, 11, 110–118 and ref. 4 cited therein.
44. N. Yoshinari and T. Konno, Acta Crystallogr., 2009, E65, o774.
45. Y. Sakamoto and T. Suzuki, J. Am. Chem. Soc., 2013, 135, 14074–14077.
46. H. Irngartinger, W. R. K. Reibel and G. M. Sheldrick, Acta Crystallogr., 1981, B37, 1768–1771.
47. W. Nakanishi, T. Matsuno, J. Ichikawa and H. Isobe, Angew. Chem., Int. Ed., 2011, 50, 6048–6051.
48. L. Barnett, D. M. Ho, K. K. Baldridge and R. A. Pascal Jr., J. Am. Chem. Soc., 1999, 121, 727–733.
49. S. Nobusue, Y. Mukai, Y. Fukumoto, R. Umeda, K. Tahara, M. Sonoda and Y. Tobe, Chem. – Eur. J., 2012, 18, 12814–12824.
50. P. Ravat, T. Šolomek, M. Rickhaus, D. Häussinger, M. Neuburger, M. Baumgarten and M. Juríček, Angew. Chem., Int. Ed., 2015 DOI:10.1002/anie.201507961.

---