Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The mechanics of tessellations – bioinspired strategies for fracture resistance
Peter
Fratzl
*a,
Otmar
Kolednik
b,
F. Dieter
Fischer
c and
Mason N.
Dean
a
aMax Planck Institute of Colloids and Interfaces, Department of Biomaterials, Research Campus Golm, 14424 Potsdam, Germany. E-mail: fratzl@mpikg.mpg.de
bErich Schmid Institute of Materials Science, Austrian Academy of Sciences, Leoben, Austria
cInstitute of Mechanics, Montanuniversität Leoben, Austria
First published on 17th September 2015
Abstract
Faced with a comparatively limited palette of minerals and organic polymers as building materials, evolution has arrived repeatedly on structural solutions that rely on clever geometric arrangements to avoid mechanical trade-offs in stiffness, strength and flexibility. In this tutorial review, we highlight the concept of tessellation, a structural motif that involves periodic soft and hard elements arranged in series and that appears in a vast array of invertebrate and vertebrate animal biomaterials. We start from basic mechanics principles on the effects of material heterogeneities in hypothetical structures, to derive common concepts from a diversity of natural examples of one-, two- and three-dimensional tilings/layerings. We show that the tessellation of a hard, continuous surface – its atomization into discrete elements connected by a softer phase – can theoretically result in maximization of material toughness, with little expense to stiffness or strength. Moreover, the arrangement of soft/flexible and hard/stiff elements into particular geometries can permit surprising functions, such as signal filtering or ‘stretch and catch’ responses, where the constrained flexibility of systems allows a built-in safety mechanism for ensuring that both compressive and tensile loads are managed well. Our analysis unites examples ranging from exoskeletal materials (fish scales, arthropod cuticle, turtle shell) to endoskeletal materials (bone, shark cartilage, sponge spicules) to attachment devices (mussel byssal threads), from both invertebrate and vertebrate animals, while spotlighting success and potential for bio-inspired manmade applications.
Key learning points(1) Learn from nature how to design fracture-resistant composite materials(2) The principles of crack propagation in elastically modulated materials (3) A look into the diversity of tessellated materials in natural organisms (4) Brick and mortar arrangements of ceramic and polymeric components of composites (5) Defect-tolerant designs of hybrid materials found in natural organisms |
Introduction
Modern engineering materials used to build mechanical support structures are often made of steel or other metal alloys, materials that are non-existent in the natural world. Metals have the advantage of being stiff and strong enough to not give way under normal mechanical load, while being plastic enough to deform without breaking when the typical load (i.e. the yield stress) is exceeded. The combination of these properties has made metals integral to a huge technological success in human history, from copper to bronze and iron ages all the way to modern times, with our reliance on the current portfolio of metallic alloys.1Natural organisms have nothing comparable to metals at their disposal and, still, they are able to grow stiff and very fracture-resistant materials, such as bones, wood or spider silk. None of these materials have the possibility of dislocation movement, which enables the plasticity of metals, and so their fracture resistance must have other origins. In fact, many mechanisms that increase the fracture resistance of natural materials are linked to the geometric arrangement of different components in tissues.2 Rather than discussing such mechanisms in an exhaustive way, in this review we will focus on a widespread strategy common among them, which we call tessellation, and which has not received sufficient attention in the last years. The general underlying concept is a combination of hard elements and relatively soft connecting layers, very much like in bathroom tiling. Such tessellations exist at all scales in natural materials, from molecular arrangements to macroscopic units, and they provide a range of interesting properties, such as prevention of crack propagation, flexibility and protection for biological armors, hardness and stretchiness for biological coatings (sometimes with self-healing properties as well), and even strain enhancement and signal filtering for mechanosensing.
Our goal in this review is to describe a unifying concept related to failure tolerance found in many materials grown by different animals, from molluscs to arthropods and vertebrates, and to highlight naturally evolved applications of these principles as a potential inspiration for engineering. The tutorial review starts with some relevant background on mechanics and then illustrates one-, two- and three-dimensional tilings as a concept to reduce crack propagation and, thus, fragility of glass sponge skeletons, bone or spider cuticle. The concept of tension–compression asymmetry is then discussed as a means of tuning bending properties of the turtle carapace or the shark skeleton. This principle is also relevant to the high abrasion resistance of the coatings of mussel byssus fibers. In vibration sensors of spiders, tessellation allows geometric signal amplification, a property very useful in designing highly sensitive mechanosensors. Finally, the concept of tessellation is generalized to the molecular level, where the coexistence of strong and weak molecular bonds in fibers results in unusual mechanical properties, such as self-healing.
Bending or breaking
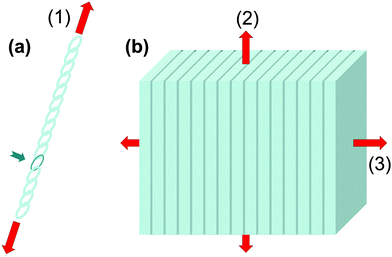
As known from the ancient legends, bending is often be better than breaking. Both phenomena are dependent on the geometry of the objects: a slender reed bends more easily than the thick oak (from Aesop's fables, 6th century BCE). But there are also material properties that distinguish these two phenomena. Stiffness (generally measured by the Young's modulus) determines the load required for a given elastic deformation (e.g. under bending) and for buckling for a given specimen geometry. (Ultimate) strength is the resistance to failure. More precisely, it is the force per unit area to break a piece of material in tension or compression. Even more important than strength is (fracture) toughness which measures the energy required to create a unit surface of crack between two parts of the same structure. Roughly speaking, toughness measures the capacity to absorb or dissipate much of the energy introduced by external loads into the material during crack extension. The reason for delineating such differences in material properties is that strength and toughness are hard to reconcile within any given material.3 In most materials, they would be inversely related: ceramics, for example, are typically strong but not tough (that is, they are brittle). Elastomeric materials often behave in just the opposite way.Natural organisms have developed a plethora of strategies to reduce the susceptibility of their materials to fracturing, while maintaining the required stiffness for necessary biological functions, such as standing upright or protecting the body. Many of these strategies hinge on material inhomogeneities, combinations of materials with different properties in arrangements (e.g. layers, tessellations) that achieve emergent properties beyond those of the constituent parts. In natural systems, such material inhomogeneities can occur at all scales, from the nanometer to nearly organ size. Unfortunately, it is far from obvious how material inhomogeneities influence the overall mechanical properties and, in particular, strength and toughness. To illustrate how important it is to assess the nature of material inhomogeneities to estimate these properties, it may be useful to consider the situations sketched in Fig. 1, a long chain with one weak element and a multilayer of sheets glued together.
Material stiffness can be described by material parameters such as the Young's modulus.4 In general, it is a tensorial quantity that depends on all geometric dimensions; for the sake of easier discussion here we describe it by a single scalar parameter, Young's modulus E, which is the load per unit surface per relative elongation of the chain. Hence, the larger the value of E, the more the chain needs to be pulled in order to achieve a given elongation. The purpose of this exercise is to estimate the change in E due to the introduction of a weak chain element (red in Fig. 1a). Assume that there are 100 chain elements in total. The modulus of the normal element is E, while the modulus of the weak one is just E/10. Then, according to a simple equation that can be found in textbooks,5 the overall modulus ET and the overall strength σfT of the chain are:
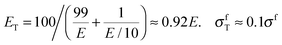 | (1) |
Fig. 1b extends this discussion to a three-dimensional structure. The case considered is a multilayered composite, consisting of alternating layers of stiff (light grey) and soft layers (dark), the latter being one hundred times thinner than the former. To maintain the analogy with the case of the linear chain, we suppose that the (isotropic) Young's modulus of the stiff layers is E and that of the soft layers is E/10. We assume the same ratio for the strength σf in the thick layers and σf/10 in the thin layers. Again, using calculations from text books, one obtains different answers for different directions of the load. For the transverse direction perpendicular to the layers (direction 3 in Fig. 2b), one recovers exactly eqn (1). For the longitudinal direction (2), one obtains:
| EL ≈ (99E + E/10)/100 ≈ 0.99E, σfL ≈ 0.99σf | (2) |
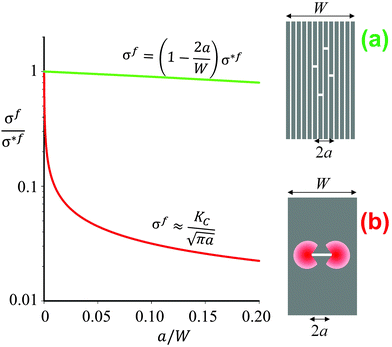 | ||
| Fig. 2 Schematics and graphical representation of the strength σf of a brittle material as a function of the crack length 2a, for a multilayer (a) and a block (b) of same geometric dimensions (width W). The quantity σ*f is the intrinsic strength of the material. In panel (a) the total length of all the individual cracks appearing in different layers equals 2a. The stress decreases linearly as a function of the total crack length. In the compact block (b) the red areas indicate regions of stress concentration, which reduce the strength according to Irwin's relation4 as indicated above the red line. The term KC is the critical stress intensity, which is a measure of the fracture toughness of the material. | ||
Why it is hard to tear a book
The longitudinal load case (2) described in Fig. 1b is rather interesting, as the soft interlayers only moderately reduce both the overall strength and Young's modulus of the material. As a matter of fact, this configuration represents a clear advantage with respect to fracture resistance as sketched in Fig. 2b. In this example, a brittle material, such as ceramic, glass or dry paper, is either loaded as a compact block (Fig. 2b) or as a pile of sheets (Fig. 2a), as for instance in a book. The difference in Fig. 1b is that now cracks with a total length 2a have been placed in the multilayer (Fig. 2a) or in the block (Fig. 2b). Stress concentrations appear near crack tips,4 leading to crack growth at rather low loads and a strong reduction of the fracture load of the material. The red line in Fig. 2b demonstrates, in an exemplary manner, how strongly even a small crack reduces the strength σf of the compact block, according to Griffith's law and the relation by Irwin indicated above the line (see ref. 4 and references therein). Although the overall crack length is the same in the cases in Fig. 2a and b, the stress concentration shown in 2b will not appear in the multilayer and, thus, the composite strength decreases only very slowly when more and more layers break.The effect of material layering on crack propagation has been investigated for a variety of materials, including a pile of paper simulating a book6 (Fig. 3). In essence, the driving force for crack propagation is reduced to zero at every interface between two pages and a new crack needs to be nucleated in the following page for crack propagation. This means that the toughness of the book is more than one order of magnitude larger than the toughness of paper, in reasonable agreement with the simple estimate discussed in Fig. 2.
 | ||
| Fig. 3 Crack propagating in a pile of paper (top) and in a single layer (bottom).6 The diagram shows the energy required to produce a new unit of crack surface (called JR) which is more than an order of magnitude larger in the stack (blue symbols) than the fracture energy of a plain paper (red symbols). Δa is the crack extension. The high fracture resistance of the stack is demonstrated by a sequence of photos taken (from left to right) at increasing tensile loads applied in the vertical direction. | ||
A similar mechanism has been found in multilayers consisting of a high-strength aluminum alloy, separated by thin, soft polymer interlayers. The polymer has a much lower Young's modulus and strength than the aluminum alloy and prevents crack propagation into the next aluminum sheet. The required fracture energy JR of the composite is more than two orders of magnitude higher than that of the homogeneous aluminum alloy.7 Even interlayers made of pure aluminum between the alloy layers, which has the same modulus but a much lower strength than the aluminum alloy, can work as effective crack arresters. Here an increase in JR by a factor 30 has been observed.
Materials with periodically varying modulus
In the previous example with the book, Young's modulus varies abruptly from the value for paper to zero between the pages. However, the main conclusions stay valid also for materials where the modulus varies in a more complex though still periodic way. In a series of publications, some of the authors have performed fracture mechanics analyses of materials with periodically varying Young's modulus. Materials of this type are very common in nature and include multilayered silica in glass sponges8,9 (Fig. 5), the nacreous layer of some sea shells,10 layered carapaces of insects and arthropods11,12 consisting of chitin layers with varying fiber orientation, as well as lamellar bone13,14 (Fig. 6). The toughness of these materials is generally remarkable being sometimes several hundred times tougher than the stiffer homogeneous material (see below).Many models have been developed in the past to account for this exceptional property. However, the simple fact that periodic variations in local Young's modulus already provide a significant toughness increase has not been considered in most cases and will be discussed here. The fracture mechanics analysis of systems with periodically varying modulus is summarized in Fig. 4. It is generally accepted that a crack propagates more easily in the direction of decreasing Young's modulus, since the crack driving force is increased15 (green arrow in Fig. 4a). The crack driving force J is defined as the (specific) energy that would be available for creating a new crack surface. This energy would generally be provided by the work of the external load challenging the material or the strain energy stored in the material. Since a certain energy is required to produce a new crack surface, see Fig. 4, the crack grows more easily, i.e. at a lower external load, if the crack driving force J is high.15 On the contrary, J is reduced when the modulus increases (red arrow). In this case, it is more difficult for the crack to grow and a higher external load is needed.
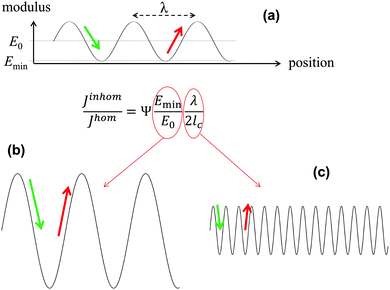 | ||
| Fig. 4 Equation for the relative magnitude of the crack driving force in an elastically inhomogeneous system, Jinhom, relative to a homogeneous system, Jhom, with the same average Young's modulus E0, where the graph on top (a) shows a sinusoidal Young modulus variation with wavelength λ and a minimum value Emin in the inhomogeneous material. In the equation, the parameter Ψ is a constant close to 1 and lc represents the intrinsic crack length of the homogeneous system,16 describing its inherent toughness. (b and c) show schematically two ways of reducing the driving force, either by increasing the amplitude or decreasing the wavelength of the modulus oscillation shown in (a). | ||
Analytical and numerical studies of this problem16–18 show that the effective driving force of the crack in an inhomogeneous system (Jinhom) is generally smaller than the crack driving forces in the homogeneous system with the same average modulus (Jhom). Interestingly, this reduction depends on the amplitude and the wavelength of the modulus variation (see Fig. 4 and eqn (3)).
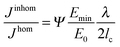 | (3) |
Glass sponge skeleton
Although the skeletons of most sponges are comprised of a complex meshwork of small, mineralized spicules, typically much less than 1 mm in size, the silica anchor spicule of the deep-sea glass sponge Monorhaphis chuni can be up to one meter in length (Fig. 5a). The silica, like glass, is inherently brittle, but the massive anchor spicule of M. chuni consists of concentric silica layers (Fig. 5b). The thickness of these layers varies according to the direction of the local current bending the spicule, being ∼5 μm (Fig. 5c) on the side of the spicule loaded in tension and slightly larger on the compression side,9 where crack propagation is less critical. The layers are separated by thin organic sheets (dark lines in Fig. 5c) and the elastic moduli of both the silica and the organic interlayer19 have been measured by modulus mapping (Fig. 5d). Inserting these values and an intrinsic defect size lc ≈ 20 μm into the equation in Fig. 4, we get E0/Emin ≈ 36/0.7 ≈ 50 and 2lc/λ ≈ 8, illustrating that the layering seen in the anchor spicule results in an overall improvement of the fracture energy JR by a factor of about 400 relative to homogeneous silica.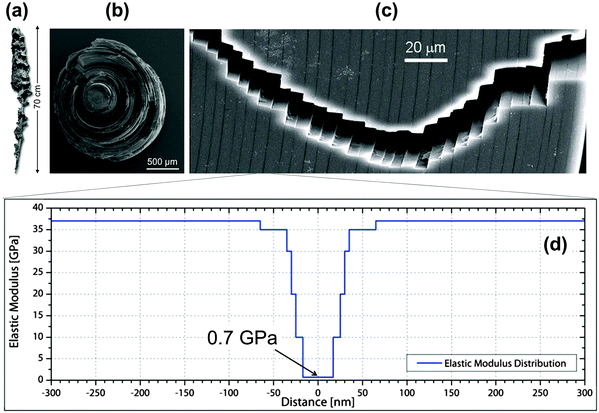 | ||
| Fig. 5 Lamellar structure of the silica spicule of the glass sponge M. chuni: (a) complete sponge, (b) fractured cross-section and (c) crack path. The vertical arrow in (a) indicates a length of 0.7 m. Vertical dark lines in the scanning electron microscopy image (c) are due to organic interlayers. (d) Young's moduli of the constituents measured by modulus mapping and plotted along the distance from the mid-plane of the interlayers.19 This results in a periodic variation of Young's modulus between 0.7 and about 37 GPa. | ||
Lamellar bone and arthropod cuticle
Lamellar bone13,14,20 and the cuticle of insects and arthropods11 are based on different fiber types (mineralized collagen and chitin, respectively). However, these materials share a similar layered structural organization. The fibers in each layer are parallel, but in each successive layer, the fibers run at a gradually different angle, resulting in an overall structure similar to plywood13,14,20 with each layer rotated with respect to its neighbors. This is shown for the case of lamellar bone in Fig. 6. The zigzagging crack path is similar to that observed in Fig. 5, indicating that the lamellae in bone also hinder crack propagation. For the crack to propagate in the direction perpendicular to the lamellae (that is, in the vertical direction in Fig. 6c), a tensile load has to be applied in the direction parallel to the lamellae to tear them apart (horizontal direction in Fig. 6c). However, due to the fact that the Young's modulus of mineralized fibrils is not the same in the direction parallel and perpendicular to the fiber direction, the in-plane modulus varies along the crack path, from a high value when the fibers run parallel to the load direction to low when they run perpendicular to it (that is, when the fibers point out of the page in Fig. 6c). The arrangement of lamellae then provides the periodic variation of the Young's modulus.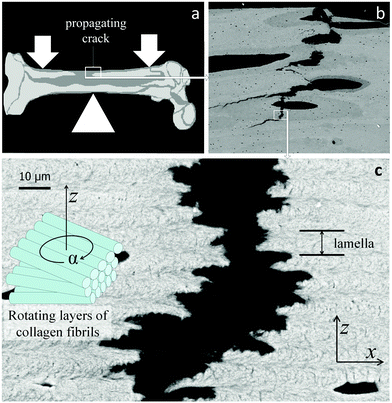 | ||
| Fig. 6 Lamellar structure of human cortical bone with a crack extending roughly in the vertical direction. (a) Sketch of the human femur with site of crack propagation; (b) back-scattering electron micrographic overview of the crack path which connects large defects such as blood vessels (black ovals); (c) crack extending within lamellar bone21 (as enlarged from the white rectangle in (b)). Each lamella consists of piled layers consisting of parallel fibrils the orientations of which rotate between successive layers (see sketch on the left side). The thickness of one lamella is indicated on the right. (x, y, z) is a coordinate system with y perpendicular to the figure. | ||
In order to estimate the contribution of the Young's modulus variation to fracture resistance of lamellar bone, we assume that mineralized collagen fibrils constitute an orthotropic material with moduli of E11 in the direction of the fibrils and E22 in all directions perpendicular to the fibrils. We call z the direction perpendicular to the lamellae. The crack plane is (y,z) with the crack propagation in the z-direction (that is, disrupting the layers as in Fig. 6c). A (tensile) load is applied in the x-direction; given the plywood structure, the fibers will have different orientations with respect to the axis of loading, x. When they are parallel to the load axis, The Young's modulus is just E11. As soon as the fiber direction turns by an angle α (see inset in Fig. 6c), the modulus in the x-direction changes and becomes5
| Ex = m4E11 + 2m2n2 (E12 + 2E66) + n4E22, | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and n = sin
α and n = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. The term E12 + 2E66 is due to additional components of the elasticity tensor and essentially describes shear between the fibrils, which has only a minor effect on the periodic variation. This yields a periodic function of α with a periodicity of π (180°), as plotted in Fig. 7 for E11/E22 = 3 and for several values of the shear contribution (E12 + 2E66)/E22. For any reasonable value of the shear (that is, E22 ≤ E12 + 2E66 ≤ E11), this function is close to a sine-function, where Emin ≈ E22 and E0 = (E11 + E22)/2.
α. The term E12 + 2E66 is due to additional components of the elasticity tensor and essentially describes shear between the fibrils, which has only a minor effect on the periodic variation. This yields a periodic function of α with a periodicity of π (180°), as plotted in Fig. 7 for E11/E22 = 3 and for several values of the shear contribution (E12 + 2E66)/E22. For any reasonable value of the shear (that is, E22 ≤ E12 + 2E66 ≤ E11), this function is close to a sine-function, where Emin ≈ E22 and E0 = (E11 + E22)/2.
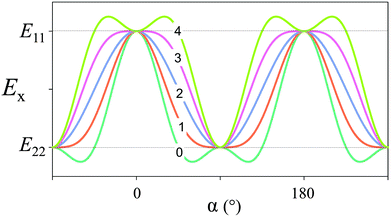 | ||
| Fig. 7 Elastic modulus in the x-direction, according to eqn (4). We have taken E11/E22 = 3 (i.e. Young's modulus is three times larger in the direction of the fiber compared to perpendicular to the fiber axis) and the number (0 to 4) indicated for each graph corresponds to the value of (E12 + 2E66)/E22 (the shear contribution) inserted in the equation. | ||
With these values is it possible to estimate how the crack driving force is reduced just by the fact that the Young's modulus oscillates. A reasonable value22 for E0/Emin is 2. The intrinsic defect length is estimated to be lc = E0JR/π(σf)2 = 100 μm, where the average modulus is E0 = 10 GPa, the fracture energy is JR = 300 J m−2 and the strength is σf = 100 MPa. Taking a typical lamellar thickness of 5 microns, the fracture energy improves by a factor of about 80 compared to a compact bone without a lamellar structure.21
Similar considerations can also be made for the chitin cuticle of arthropods,12 where the plywood structure is also likely to reduce the crack driving force by one to two orders of magnitude.
Generalization to planar or spatial tessellations
Skeletons of sharks and rays
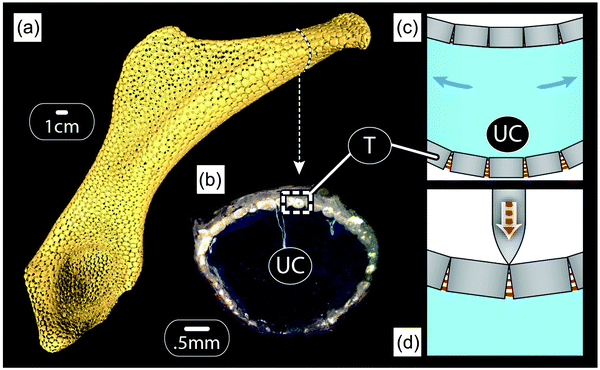
A different kind of layering is seen in shark and ray skeletons. Rather than having bone in their skeletons, they possess what is effectively an armored cartilage, comprised of an unmineralized hyaline-like cartilage covered with a layer of mineralized tiles called tesserae23 (Fig. 8). Tesserae are typically hundreds of microns wide and deep and arranged in a single layer, connected to one another by short organic fibers,23 with a modulus probably 1–3 orders of magnitude lower than that of tesserae.24 The whole skeleton is then wrapped in stout collagen fibers, resulting in a constrained surface tessellation.23,25 From a mechanical standpoint, tesserae apparently serve to stiffen the tissue relative to a non-tessellated system,24 especially when loading is in-plane with the mat of tesserae.26 Indeed, cartilage is a relatively soft tissue, which would not be sufficiently stiff to prevent bending of a shark jaw during biting, for example.26The hard, ceramic-like covering of the skeletal elements effectively stiffens them in bending. However, if this hard layer were continuous, the slightest defect in this layer would initiate cracking in tension due to the stress concentration explained in Fig. 2. Separating this layer into a tiling has a similar beneficial effect as the paving of roads with segmental paving stones or bricks. Indeed, a continuous stone (or concrete) covering of the road inevitably leads to cracking of the surface when the soil swells due to water uptake or freezing. This is why roads have been paved with segmental elements since Roman times and only the invention of tough and viscous bitumen in the last century allowed for a continuous covering of roads.
In addition, the tiling of skeletal elements has other, more biological benefits. Indeed, since cartilage cannot repair or remodel, all the growth of skeletal elements occurs at the margins of tesserae.23 From a mechanical standpoint though, these joints represent a transition in modulus, that is, a discontinuity between tiles preventing crack propagation and localizing damage. While there are no in vivo or in situ data on how the tessellated layer behaves under physiological loading, the tiling would theoretically prevent cracking of the brittle tesserae and protect the cells living in tesserae when the skeletal element is bending.23,24
It is interesting to note that multiple layers of tesserae can be seen in skeletons of large species and those that eat hard foods, with up to 5 or 6 layers observed in individuals of some species.27 It is not known yet how the joints interact in different layers. Presumably, the more ‘typical’ single layer tessellation imparts a balance of stiffness and flexibility;24 in multi-layered systems, however, staggering and/or aligning joints in specific ways could be a means of improving the mechanics of the tessellated layer in three dimensions.
Materials made of interlocking elements
The combination of stiff elements connected by fibers seen in shark and ray skeletons is not foreign to manmade designs. In recent years, materials scientists have developed concepts for interlocking materials where the individual elements are held together without any glue, either because they are blocked within a frame, held together by wires (Fig. 9) or because the elements interlock like a puzzle game. This just extends the concept of one-dimensional periodicity to higher dimensions (two-dimensional periodicity in Fig. 9). Such interlocking materials have shown to be defect-tolerant, exhibit tunable bending stiffness and even allow for acoustic absorption.28 | ||
| Fig. 9 Material stabilized by the interlocking of osteomorphic blocks. (a) Individual blocks shown from different directions. The planar material (b) is held together by the tension of metallic fibers (two of which are seen in the front of the picture) and by the interlocking of the osteomorphic blocks (from Molotnikov et al.28 with permission by the author). | ||
A natural (but largely unexamined) example of such geometric interlocking structures is seen among the several genera of durophagous (hard-prey crushing) myliobatid stingrays.27 The teeth of these fishes look nothing like the familiar pointed cusps of sharks, rather ranging in form from blunt-ended bars to extended hexagons to chevrons, nesting together with interlocking morphologies described anecdotally as “overlapping shelve” or “tongue-groove” mechanisms and with varying degrees of tightness of fit29 (Fig. 10). The observed interlocking of ray teeth suggests that stability for durophagy may be imparted by tooth–tooth interactions: although the teeth are unsocketed and only anchored at their base into the dental ligament, the tooth arrays are largely self-supporting (e.g.Fig. 10c), suggesting a degree of load-sharing among teeth during feeding events. The range of dental morphologies in durophagous stingrays offers a fascinating natural experiment for testing the mechanical effects of interlocking morphologies, particularly in a high-performance system where failure of individual elements would not endanger the entire structure.
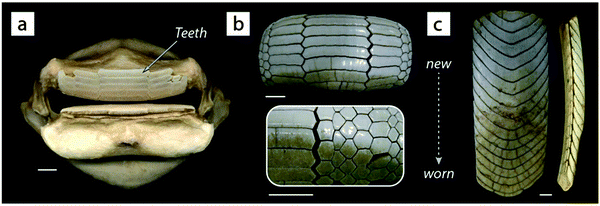 | ||
| Fig. 10 The pavement-like teeth of durophagous (hard-prey eating) stingrays. Unlike most other batoid fishes (including stingrays and their relatives), durophagous stingrays possess extremely stout jaws (a) with very flat teeth (b and c). The shapes of these teeth vary by species ((a and b) = species of Rhinoptera, (c) = Aetobatus) and typically interlock in an imbricated framework that is largely self-supporting, as in the lower jaw tooth array shown in the lateral view in the far right image in (c); note that each “band” in the arrays is an individual tooth. Rays and sharks have continuous dental replacement: the teeth in (b) and (c) are progressively older toward the bottom of the page, with the teeth in use discernible by their discoloration and wear. Rays, like sharks, possess tessellated cartilage; the jaw in (a) is covered in tesserae (see Fig. 8 and 13). All scale bars are 1 cm. | ||
Brick and mortar structure
Another variant of tessellated structure has been proposed30 in 2000 to describe materials such as nacre or the mineralized collagen fibril.31 The general idea is that stiff mineral platelets are arranged in a staggered fashion as sketched in Fig. 11a, with the orange layer in between being a soft matrix that connects the platelets by shear-resistant connectors. Because of its conceptual simplicity, this model has been extensively studied in recent years to determine the effects of such arrangements on the Young's modulus as well as the energy to failure of tissues;32 for a recent review, see ref. 33 and the references therein.A simple analytical expression has been derived for the Young's modulus EC of such a composite as:
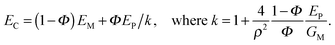 | (5) |
While the length-to-thickness ratio ρ of the particles controls the elastic properties of the composite, it has also been shown32 that the energy to failure of the composite can be dramatically increased if the matrix yields and flows at a shear stress below a certain critical limit. Indeed, during elastic deformation, it has been shown that τM = 2σP/ρ, where τM is the shear stress in the matrix and σP the tensile stress in the particles. If one assumes that the matrix flows at a shear stress τYM, that relates to the strength σFP of the mineral forming the platelets by τYM ≤ 2σFP/ρ, then the mineral platelets are protected and the composite deforms until the shear limit or until the tensile limit of the matrix. This is shown for an example in Fig. 11c, where the critical shear stress is set to be as large as possible to comply with the limit above. This leads to a dramatic increase in the energy to failure when the platelet volume fraction drops from 100% to somewhat lower values. As an example, at a volume fraction of 50% (which would be the mineral content in mineralized collagen fibrils in bone22), the energy to failure increases by a factor of 35, while the Young's modulus of the composite decreases by only a factor of 3 relative to that of the mineral component.
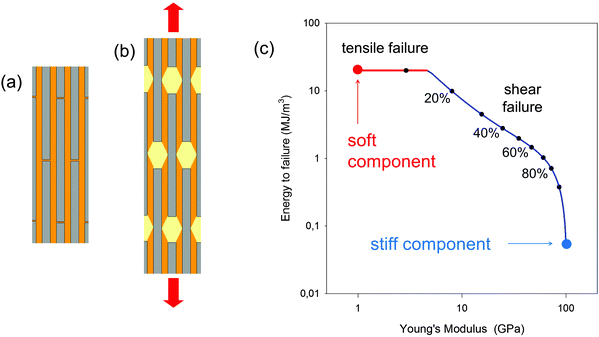 | ||
| Fig. 11 Mechanical behavior of the staggered (brick and mortar) model.30,31 (a) Stiff (mineral) platelets, viewed edge-on in grey, are embedded in a much softer matrix (orange). (b) The in-plane deformation in tension is characterized predominantly by shearing of the organic matrix connecting the platelets, rather than deformation of the platelets themselves. (c) Young's modulus and energy to failure for a composite with platelets with a length-to-thickness ratio of 30 and a Young's modulus of 100 GPa, and with an interstitial matrix with a Young's modulus of 1 GPa. The matrix properties are set to allow flow under shear beyond a critical shear stress, chosen so as to prevent the tensile stress of the mineral platelets exceeding their strength (100 MPa). The ultimate strain of the matrix is considered to be 50% in shear and 15% in tension. With these parameters, both Young's modulus and energy to failure (i.e., the energy per unit volume needed to break the material in a tensile test without notching the specimen) are plotted for different values of the volume fraction of platelets (as indicated by dots on the curve) according to the model eqn (5) and given in ref. 32. The shape of the curve highlights the trade-off mentioned in the Introduction that is often seen between material toughness and stiffness. | ||
This model has been studied by a number of authors in much more detail34,35 and a review of the Young's modulus in staggered brick-and-mortar models can be found in ref. 33. Many attempts have also been made to synthesize artificial nacre-like composites, involving platelets with thin layers of mortar between them and following mechanical principles similar to those described by the model, resulting in composites with superior mechanical properties combining stiffness and toughness (for a review, see ref. 36).
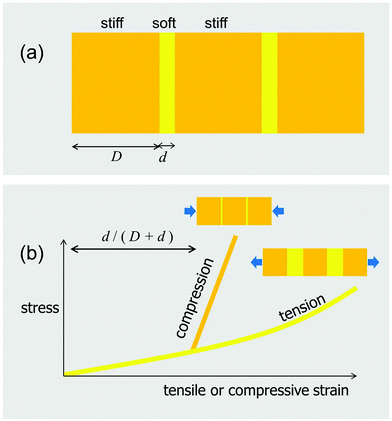
Constrained flexibility
To this point, the advantage of separating a homogeneously stiff block into stiff tiles connected by thin soft layers has been discussed only in terms of controlling the crack driving force. There is, however, another fundamental advantage of tessellations, connected to their inherently constrained flexibilities. The simplest version of this constraint is the tension–compression asymmetry sketched in Fig. 12, which expands the case presented in Fig. 1b to a situation where the axial load can be either in tension or compression. As shown in this figure, the composite, consisting of stiff blocks connected by soft interlayers, behaves in a much softer way in tension than in compression. As a consequence, despite the soft interlayers, the composite is nearly as stiff in compression as the plain orange block (Fig. 12).Skeletons of sharks and rays
Our previous discussion of the tessellated cartilage of shark and ray skeletons was focused largely on simple, localized, single-layer tessellations. However, it is important to note that this skeletal tiling is not simply restricted to one region of the skeleton, but rather forms an outer sheath that covers the majority of most skeletal elements in the body23 (Fig. 13a and b). As with bony skeletons, pieces of the skeleton exhibit complex 3D shapes that can be loaded in complex ways; the relationship of the tiling morphology to the skeletal form and loading has yet to be examined though.From experiments on shark and ray behaviors (e.g.ref. 37), it is safe to assume that bending is a normal mode of loading. This would result in one side of the skeleton loaded in compression, while the other is loaded in tension, as sketched in Fig. 13c. The tessellated layer may therefore experience a diversity of loading regimes, making it important to consider both the “upper” and “lower” tessellated layers. Although there are no data on how the tessellated skeleton (or the tessellated layer) deforms during physiological loading, modeling the effects of bending on a tessellated sandwich composite with simplified, but biologically-relevant geometries and material properties can give us some insight into the advantages of such tiling.24 The idea shown in Fig. 13c considers that tesserae pull apart on the tensile side, loading intertesseral fibers in tension, but transfer the load by contact on the compressive side. This means that the layer of tesserae would behave approximately like the yellow curve in Fig. 12b on the tension side and like the orange curve in Fig. 12b on the compression side. Therefore, the intertesseral fiber modulus is more relevant to the tensile side, whereas the tesseral compressive modulus is more relevant to the compressive side.24
One consequence of the different behaviors of tesserae on the tensile and the compressive sides (according to Fig. 13c) is that the neutral axis of bending of the skeleton (the transition point between tensile and compressive stresses in bending) shifts more toward the compressive side of the skeleton.24 Moreover, due to the geometry in beam bending (Fig. 13c), the largest compressive and tensile stresses appear in the outermost layers of the beam, which correspond to the tessellated layers in the shark skeleton. In other words, in addition to the tessellated covering dramatically reducing the danger of cortical fracturing (relative to a continuously mineralized layer, as outlined previously), it also serves to distribute loads to the tissues best able to bear them, thereby also avoiding damage to the whole skeleton.
The tessellated skeletons of sharks and ray stand to tell us a great deal regarding the mechanics of both simple and complex tilings, but also morphologies that allow tunable responses to different loading regimes. We can also imagine that, in extreme bending cases or indentation (e.g. the result of point loads from teeth during predation events; see schematic in Fig. 13d), the behavior of joints between tesserae may be more complex than suggested in Fig. 13c, with the bottom part of the joint experiencing tension, even as the top is loaded in compression. For this to occur the intertesseral joints must be much narrower than being taller, a condition suggested by a previous morphological study.23
Armored fish scales
Armored fish scales have been studied in some detail by various groups.38,39 These scales need to be flexible (at small deformations) but also stiff and protective when higher loads are applied, such as the indentation that might result from a biting predator. A sketch of the periodic arrangement of mineralized scales anchored in the demis is shown in Fig. 14, for the example of salmon. Conceptually, this is again a periodic succession of hard and soft layers, athough in a tilted arrangement. Given that the scales are embedded in a soft matrix, the elastic response at small deformations is going to be relatively soft. For some other challenges (such as compression from the outside, see Fig. 14), it is easy to imagine that scales will get in contact with each other and generate a much stiffer response. This is the most wanted property for all kinds of armor, namely to be flexible at small deformations (leading to little restriction of the mobility of the animal), but to show a stiff protective reponse when the (especially compressive) stresses become large. This is only one simple example of a protective armor and there are much more complex designs.38,39 | ||
| Fig. 14 Scales of the Atlantic salmon, Salmo salar (a), enlarged in (b) to show local variation in the scale morphology. (c) Shows mineral platelets in scales (black) embedded in the dermal soft tissue as imaged by microcomputed tomography. The sketch in (d) depicts the general organization, involving periodic arrangement of stiff (mineralized) scales within a soft dermal matrix; however, scales are different sizes and arranged at different angles to the surface in different regions of the body. The overall mechanical properties depend on the aspect ratio, separation and tilt angle of the scales (adapted from Browning et al.,38 with permission by Elsevier). | ||
Turtle carapace
Through evolution, the red-eared slider turtle has adapted its thoracic cage to become a protective carapace as shown in Fig. 15. In the carapace, bony structures corresponding to the ribs are joined through a suture where extensions emanating from each rib interdigitate without forming mineralized bridges (Fig. 15). This is a striking example of constrained flexibility. Indeed, at small deformations, ribs can easily move relative to each other because only the soft matrix between the extensions in the suture needs to be deformed. This facilitates small movements associated with breathing and swimming. Under larger external loads (e.g. those applied to the carapace by teeth of a predator), however, the extensions come into contact with each other, yielding a stiff response that protects the animal.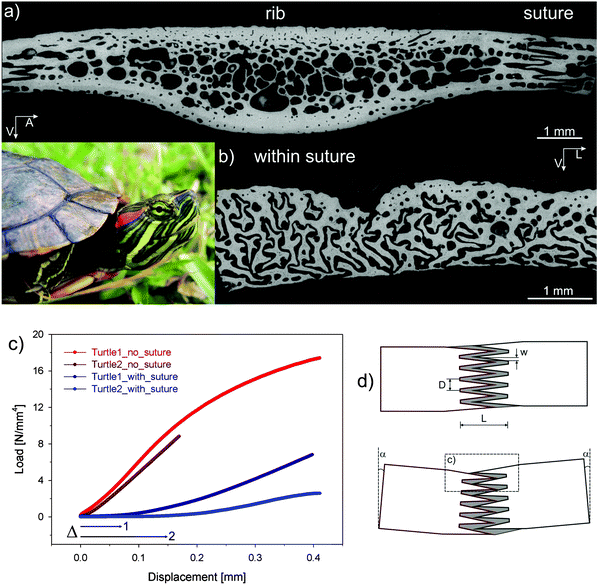 | ||
| Fig. 15 Carapace of the red-eared slider turtle (inset). (a) Cross-section through one of the modified ribs forming the carapace; carapace ribs are considerably widened relative to the ribs of other vertebrates, adjoining with adjacent ribs at complex sutures. The greyscale corresponds to the mineral content measured by back-scattered electron imaging (black meaning no mineral). (b) Cross-section across the suture showing that there are no mineralized bridges between the ribs, but rather a complex interdigitation of processes emanating from each of the ribs. (c) Mechanical bending data showing that the suture provides an initial displacement (labelled Δ) before a rigid reaction starts. In parts of the rib without suture, the stiff response is immediate. (d) Shows a model where – upon bending of the carapace – the processes emanating from each rib initially move almost freely inside the soft (unmineralized) sutural matrix until they bump into each other and the stiff response begins (adapted from ref. 40 with permission by Wiley). | ||
Cuticle of the mussel byssus
Mussels anchor themselves to rocks in wave-swept habitats using a group of protein fibers, the byssus, glued to the stone surface (Fig. 16a). These fibers have very special mechanical properties that have attracted much interest in recent years,41 particularly their large extensibility and self-healing capacities. Moreover, byssus fibers are covered by a relatively hard and yet extensible coating (the cuticle) that is believed to provide abrasion resistance (Fig. 16b). This raises the question how a hard material can be extensible at the same time. A recent study42 showed that the cuticle consists mainly of protein containing clusters of cross-links (granules) comprised of Fe ions coordinating specific amino acid (DOPA) residues on the protein chains. These roughly half-micron-sized granules are harder than the matrix that surrounds them, and therefore are believed to provide the abrasion resistance of the cuticle. However, it is the soft matrix surrounding them that is believed to be the root of the cuticle extensibility; Fig. 16c and 15d illustrate the model for the combined hardness (in compression) and extensibility (in tension). When the cuticle is compressed, the hard granules get in contact with each other providing an overall hard response. When the fiber is tensed, the granules stay essentially undeformed while the (much softer) matrix between them extends. This is, therefore, a perfect example of constrained flexibility and tensile compression asymmetry illustrated in Fig. 12.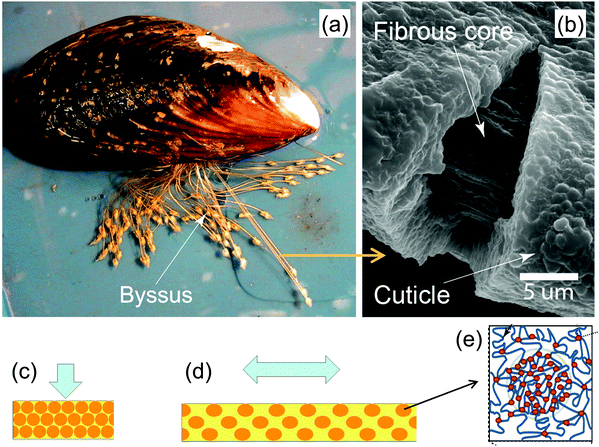 | ||
| Fig. 16 Hard and extensible cuticle of the byssus fibers by which mussels attach to rocks (a). The fibrous core of the fibers is coated by a protein-based cuticle (b). The cuticle is hardened by inclusions consisting of granules (schematic orange balls in (c) and (d)) of clustered cross-links (red dots in (e)) between otherwise extensible proteins (yellow matrix in (c) and (d)). A model for the deformation of the cuticle in compression (c) and tension (d) shows that the hard granules provide a strong resistance to compression, whereas most of the tensile deformation occurs in the surrounding soft matrix (yellow) (adapted from ref. 42 with permission by Science). | ||
Geometric amplification and sensing
A quite different function of geometric tessellations is seen in the lyriform sensor of some spiders43 (Fig. 17). The sensor consists of slits in the chitin cuticle of the spider leg (Fig. 17b) that amplify and filter tiny vibrations in the leaf on which the spider is sitting. Fig. 17c shows a series of slits in the stiff cuticle on the medial surface. A thin membrane at the base of the slits inside the cuticle connects the vibration sensing organ to nerve cells. The deformation of this membrane is sensed by a nerve cell that then triggers a reaction by the organism. This is a somewhat unique system, since most vibration and tactile sensing in arthropods is performed by hair.43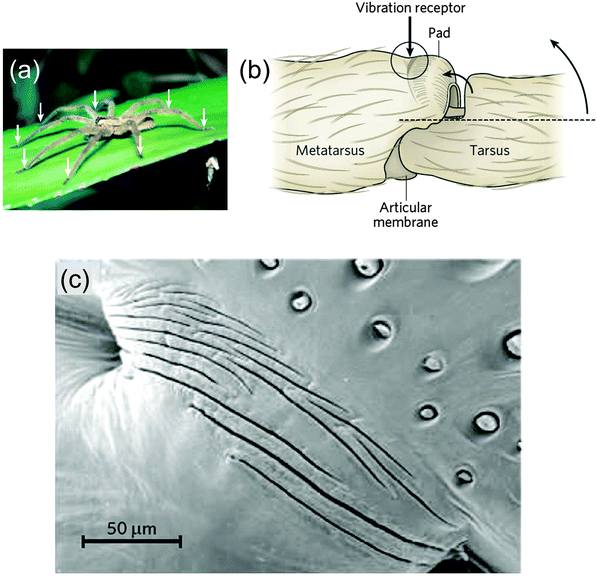 | ||
| Fig. 17 Vibration-sensitive slit organ of Cupiennius salei (a), with arrows pointing to the location of the vibration sensors, on the legs. (b) The vibration sensor, on the dorsal surface of the metatarsus, is stimulated by compression following the upward movement of the tarsus, indicated by the two curved arrows. (c) Scanning electron micrograph of the vibration detector (dorsal view, area depicted in circle in b, adapted from ref. 44). | ||
Taking a rough approximation, each slit can generally be considered as a strain amplification system, as sketched in Fig. 18. This situation is actually reminiscent of the load acting into the (3)-direction in Fig. 1, where soft and stiff regions are stacked in a series along the load direction. The Young's modulus of the composite can be calculated according to eqn (1). Here we are interested in the strain in the soft tissue between the stiff blocks compared to the strain in the composite system. Taking the simplest case, where the blocks are so much stiffer than the slit between them, we can write the overall strain of the composite εC as a function of the elongation strain of the slit width, εS:
| εC = εSLS/(LB + LS) | (6) |
 | ||
| Fig. 18 Principle of strain amplification in a tessellated structure. If the length of the stiff blocks (orange) is hundred times larger than the width of the soft interspace between them, small length changes of the composite (resulting from the vibrations of the structure) are amplified and are 100 times larger in the interspace between the stiff (orange) tiles.46 | ||
Conclusions and related concepts at the molecular level
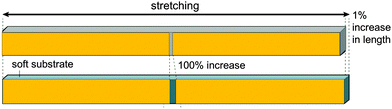
Most of the examples discussed above consider tessellations where the widths of the soft and stiff components are in the range of micrometers (or at least tens to hundreds of nanometers). Although this is not the topic of this review, it is tempting to generalize the concept to the molecular level where the soft component would conceptually be replaced by weak bonds and the stiff component by strong bonds, as sketched in Fig. 19. This figure illustrates the concept of sacrificial bonds and hidden length41,47,48 which has been introduced to explain the fracture resistance of certain natural materials. The idea is that (reversible) weak bonds are the first to break under an applied load, thus liberating a large hidden length by the unfolding of covalent chains. The weak bonds may be hydrogen bonds as in spider silk or metal coordination bonds as in mussel byssus and other fibers.49 The rupture of the weak (sacrificial) bonds allows for large deformation without disrupting the whole structure. When the molecules later refold, weak bonds may reconnect and restore the original length and mechanical behavior of the fibers.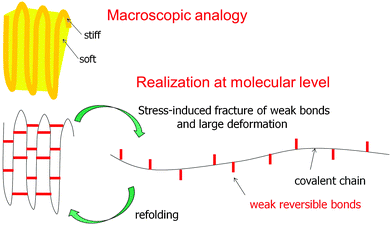 | ||
| Fig. 19 The concept of sacrificial bonds and hidden length.47 Weak reversible bonds (red) are the first to break under an applied load. This allows covalent chains to unfold and provide substantial deformation without disrupting the chain. In some systems (e.g. the mussel byssus41), after release of the load and refolding of the covalent chain, the weak bonds may reform and restore the original properties. Conceptually, this is not far from a composite containing a soft and a stiff component, as sketched above, although this analogy should not be overemphasized. | ||
This review highlights just one general structural concept which allows tuning of the mechanical properties of (biological) materials. The examples shown above demonstrate how a comparatively simple alteration to a continuous structure, mainly subdividing the surface or volume into space-filling tiles, can greatly influence the mechanical behavior of materials. All the examples are taken from natural organisms, which synthesize their mechanical support structures from minerals and natural polymers, such as proteins or polysaccharides. Due to the inherently rather poor mechanical properties of some of these constituent parts, structuring has become an essential tool in the evolution of tissues and materials. Putting all of these examples into the common perspective of tessellated structures – which can, in some cases, be successfully modeled by simple repetitive patterns of soft/extensible and hard/stiff structural elements – will hopefully inspire the design of new artificial materials with exceptional properties.
Acknowledgements
PF is grateful for support by the DFG, in the framework of the Gottfried Wilhelm Leibniz Prize. FDF acknowledges support by the Humboldt Foundation through the Humboldt Research Prize. OK acknowledges support by the Austrian Federal Government and the Styrian Provincial Government under the frame of the Austrian COMET Competence Center Programme (K2 Competence Center on “Integrated Research in Materials, Processing and Product Engineering”, Strategic Project A4.20-WP1 and WP2). MND is grateful for support from an HFSP Young Investigator's Grant (RGY0067-2013); a SYNTHESYS grant (GB-TAF-2289) to MND funded a collection visit to the Natural History Museum (London) to photograph the museum specimens in Fig. 8 and 10. Laura Ekstrom, Allison Luger, James Maclaine, Ronald Seidel and Kady Lyons generously provided images and specimens for Fig. 8, 10 and 13.References
- M. Ashby, Materials – a brief history, Philos. Mag. Lett., 2008, 88, 749–755, DOI:10.1080/09500830802047056.
- J. W. C. Dunlop and P. Fratzl, Biological Composites, Annu. Rev. Mater. Res., 2010, 40, 1–24, DOI:10.1146/annurev-matsci-070909-104421.
- R. O. Ritchie, The conflicts between strength and toughness, Nat. Mater., 2011, 10, 817–822, DOI:10.1038/NMAT3115.
- W. D. Callister, Jr., Materials Science and Engineering – An Introduction, John Wiley & Sons, Inc., 4th edn, 1997, p. 852 Search PubMed.
- L. A. Carlsson and R. B. Pipes, Experimental Characterization of Advanced Composite Materials, Taylor & Francis, 4th edn, 2014, p. 379 Search PubMed.
- J. Zechner and O. Kolednik, Paper multilayer with a fracture toughness of steel, J. Mater. Sci., 2013, 48, 5180–5187, DOI:10.1007/s10853-013-7304-y.
- J. Zechner and O. Kolednik, Fracture resistance of aluminum multilayer composites, Eng. Fract. Mech., 2013, 110, 489–500, DOI:10.1016/j.engfracmech.2012.11.007.
- J. Aizenberg, et al., Skeleton of Euplectella sp.: Structural hierarchy from the nanoscale to the macroscale, Science, 2005, 309, 275–278, DOI:10.1126/science.1112255.
- A. Miserez, et al., Effects of laminate architecture on fracture resistance of sponge biosilica: Lessons from nature, Adv. Funct. Mater., 2008, 18, 1241–1248, DOI:10.1002/adfm.200701135.
- A. P. Jackson, J. F. V. Vincent and R. M. Turner, The Mechanical Design of Nacre, Proc. R. Soc. London, Ser. B, 1988, 234, 415–440, DOI:10.1098/rspb.1988.0056.
- Y. Bouligand, Twisted Fibrous Arrangements In Biological-Materials and Cholesteric Mesophases, Tissue Cell, 1972, 4, 189–190, DOI:10.1016/s0040-8166(72)80042-9.
- D. Raabe, C. Sachs and P. Romano, The crustacean exoskeleton as an example of a structurally and mechanically graded biological nanocomposite material, Acta Mater., 2005, 53, 4281–4292, DOI:10.1016/j.actamat.2005.05.027.
- N. Reznikov, R. Shahar and S. Weiner, Three-dimensional structure of human lamellar bone: The presence of two different materials and new insights into the hierarchical organization, Bone, 2014, 59, 93–104, DOI:10.1016/j.bone.2013.10.023.
- S. Weiner, T. Arad, I. Sabanay and W. Traub, Rotated plywood structure of primary lamellar bone in the rat: Orientations of the collagen fibril arrays, Bone, 1997, 20, 509–514, DOI:10.1016/S8756-3282(97)00053-7.
- O. Kolednik, in Wiley Enzyclopedia of Composites, ed. L. Nicolais and A. Borzachiello, John Wiley & Sons, 2012, vol. 2, pp. 1126–1141 Search PubMed.
- O. Kolednik, J. Predan, F. D. Fischer and P. Fratzl, Improvements of strength and fracture resistance by spatial material property variations, Acta Mater., 2014, 68, 279–294, DOI:10.1016/j.actamat.2014.01.034.
- O. Kolednik, J. Predan, F. D. Fischer and P. Fratzl, Bioinspired Design Criteria for Damage-Resistant Materials with Periodically Varying Microstructure, Adv. Funct. Mater., 2011, 21, 3634–3641, DOI:10.1002/adfm.201100443.
- P. Fratzl, H. S. Gupta, F. D. Fischer and O. Kolednik, Hindered crack propagation in materials with periodically varying Young's modulus – Lessons from biological materials, Adv. Mater., 2007, 19, 2657–2661, DOI:10.1002/adma.200602394.
- I. Zlotnikov, In situ elastic modulus measurements of ultrathin protein-rich organic layers in biosilica: towards deeper understanding of superior resistance to fracture of biocomposites, RSC Adv., 2013, 3, 5798–5802, 10.1039/c3ra40574e.
- M. M. Giraud-Guille, L. Besseau and R. Martin, Liquid crystalline assemblies of collagen in bone and in vitro systems, J. Biomech. Eng., 2003, 36, 1571–1579, DOI:10.1016/S0021-9290(03)00134-9.
- H. Peterlik, P. Roschger, K. Klaushofer and P. Fratzl, From brittle to ductile fracture of bone, Nat. Mater., 2006, 5, 52–55, DOI:10.1038/nmat1545.
- P. Fratzl, H. S. Gupta, E. P. Paschalis and P. Roschger, Structure and mechanical quality of the collagen-mineral nano-composite in bone, J. Mater. Chem., 2004, 14, 2115–2123, 10.1039/b402005g.
- M. N. Dean, C. G. Mull, S. N. Gorb and A. P. Summers, Ontogeny of the tessellated skeleton: Insight from the skeletal growth of the round stingray Urobatis halleri, J. Anat., 2009, 215, 227–239 CrossRef PubMed.
- X. Liu, M. N. Dean, A. P. Summers and J. C. Earthman, Composite model of the shark's skeleton in bending: a novel architecture for biomimetic design of fatigue resistant materials, Mater. Sci. Eng., C, 2010, 30, 1077–1084 CrossRef CAS.
- N. E. Kemp and S. K. Westrin, Ultrastructure of calcified cartilage in the endoskeletal tesserae of sharks, J. Morphol., 1979, 160, 75–101, DOI:10.1002/jmor.1051600106.
- X. Liu, M. N. Dean, H. Youssefpour, A. P. Summers and J. C. Earthman, Stress relaxation behavior of tessellated cartilage from the jaws of blue sharks, J. Mech. Behav. Biomed. Mater., 2014, 29, 68–80, DOI:10.1016/j.jmbbm.2013.08.014.
- A. P. Summers, Stiffening the stingray skeleton – An investigation of durophagy in myliobatid stingrays (Chondrichthyes, Batoidea, Myliobatidae), J. Morphol., 2000, 243, 113–126 CrossRef CAS PubMed.
- A. Molotnikov, R. Gerbrand, Y. Qi, G. P. Simon and Y. Estrin, Design of responsive materials using topologically interlocked elements, Smart Mater. Struct., 2015, 24, 025034, DOI:10.1088/0964-1726/24/2/025034.
- K. M. Claeson, et al., First Mesozoic record of the stingray Myliobatis wurnoensis from Mali and a phylogenetic analysis of Myliobatidae incorporating dental characters, Acta Palaeontol. Pol., 2010, 55, 655–674, DOI:10.4202/app.2009.1117.
- I. Jager and P. Fratzl, Mineralized collagen fibrils: A mechanical model with a staggered arrangement of mineral particles, Biophys. J., 2000, 79, 1737–1746 CrossRef CAS PubMed.
- H. J. Gao, B. H. Ji, I. L. Jager, E. Arzt and P. Fratzl, Materials become insensitive to flaws at nanoscale: Lessons from nature, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5597–5600, DOI:10.1073/pnas.0631609100.
- P. Fratzl and R. Weinkamer, Nature's hierarchical materials, Prog. Mater. Sci., 2007, 52, 1263–1334, DOI:10.1016/j.pmatsci.2007.06.001.
- B. Bar-On and H. D. Wagner, Structural motifs and elastic properties of hierarchical biological tissues – A review, J. Struct. Biol., 2013, 183, 149–164, DOI:10.1016/j.jsb.2013.05.012.
- B. H. Ji and H. J. Gao, Mechanical properties of nanostructure of biological materials, J. Mech. Phys. Solids, 2004, 52, 1963–1990, DOI:10.1016/j.jmps.2004.03.006.
- J. W. Pro, R. K. Lim, L. R. Petzold, M. Utz and M. R. Begley, GPU-based simulations of fracture in idealized brick and mortar composites, J. Mech. Phys. Solids, 2015, 80, 68–85, DOI:10.1016/j.jmps.2015.03.011.
- A. R. Studart, R. Libanori and R. M. Erb, Replicating Biological Design Principles in Synthetic Composites, RSC Smart Mater., 2013, 322–358, 10.1039/9781849737555-00322.
- L. J. Macesic and A. P. Summers, Flexural stiffness and composition of the batoid propterygium as predictors of punting ability, J. Exp. Biol., 2012, 215, 2003–2012 CrossRef PubMed.
- A. Browning, C. Ortiz and M. C. Boyce, Mechanics of composite elasmoid fish scale assemblies and their bioinspired analogues, J. Mech. Behav. Biomed. Mater., 2013, 19, 75–86, DOI:10.1016/j.jmbbm.2012.11.003.
- W. Yang, et al., Structure and fracture resistance of alligator gar (Atractosteus spatula) armored fish scales, Acta Biomater., 2013, 9, 5876–5889, DOI:10.1016/j.actbio.2012.12.026.
- S. Krauss, E. Monsonego-Ornan, E. Zelzer, P. Fratzl and R. Shahar, Mechanical Function of a Complex Three-Dimensional Suture Joining the Bony Elements in the Shell of the Red-Eared Slider Turtle, Adv. Mater., 2009, 21, 407–412, DOI:10.1002/adma.200801256.
- M. J. Harrington and J. H. Waite, How Nature Modulates a Fiber's Mechanical Properties: Mechanically Distinct Fibers Drawn from Natural Mesogenic Block Copolymer Variants, Adv. Mater., 2009, 21, 440–444, DOI:10.1002/adma.200801072.
- M. J. Harrington, A. Masic, N. Holten-Andersen, J. H. Waite and P. Fratzl, Iron-Clad Fibers: A Metal-Based Biological Strategy for Hard Flexible Coatings, Science, 2010, 328, 216–220, DOI:10.1126/science.1181044.
- F. G. Barth, A Spider's World – Senses and Behavior, Springer, 2002 Search PubMed.
- P. Fratzl and F. G. Barth, Biomaterial systems for mechanosensing and actuation, Nature, 2009, 462, 442–448, DOI:10.1038/nature08603.
- D. Kang, et al., Ultrasensitive mechanical crack-based sensor inspired by the spider sensory system, Nature, 2014, 516, 222–226, DOI:10.1038/nature14002.
- P. Fratzl, The virtues of tiling, Nature, 2014, 516, 178–179 CrossRef CAS PubMed.
- G. E. Fantner, et al., Sacrificial bonds and hidden length: Unraveling molecular mesostructures in tough materials, Biophys. J., 2006, 90, 1411–1418, DOI:10.1529/biophysj.105.069344.
- S. Keten, Z. P. Xu, B. Ihle and M. J. Buehler, Nanoconfinement controls stiffness, strength and mechanical toughness of beta-sheet crystals in silk, Nat. Mater., 2010, 9, 359–367, DOI:10.1038/NMAT2704.
- E. Degtyar, M. J. Harrington, Y. Politi and P. Fratzl, The Mechanical Role of Metal Ions in Biogenic Protein-Based Materials, Angew. Chem., Int. Ed., 2014, 53, 12026–12044, DOI:10.1002/anie.201404272.
| This journal is © The Royal Society of Chemistry 2016 |