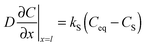Untangling surface oxygen exchange effects in YBa₂Cu₃O_6+x thin films by electrical conductivity relaxation

Abstract

The kinetics of oxygen incorporation (in-diffusion process) and excorporation (out-diffusion process), in YBa₂Cu₃O_6+x (YBCO) epitaxial thin films prepared using the chemical solution deposition (CSD) methodology by the trifluoroacetate route, was investigated by electrical conductivity relaxation measurements. We show that the oxygenation kinetics of YBCO films is limited by the surface exchange process of oxygen molecules prior to bulk diffusion into the films. The analysis of the temperature and oxygen partial pressure influence on the oxygenation kinetics has drawn a consistent picture of the oxygen surface exchange process enabling us to define the most likely rate determining step. We have also established a strategy to accelerate the oxygenation kinetics at low temperatures based on the catalytic influence of Ag coatings thus allowing us to decrease the oxygenation temperature in the YBCO thin films.

---

Introduction

The use of low-cost techniques such as chemical solution deposition (CSD) for the growth of high performance REBa₂Cu₃O_6+x (REBCO) coated conductors (CCs) is one of the major requirements for a widespread use of superconductivity in large scale applications.^1–6 CSD has become a very competitive, cost-effective and scalable methodology to produce REBCO, especially YBCO, epitaxial thin films, and so an extensive analysis of all the relevant processing steps is worthwhile.

The last step in any CC manufacturing process is oxygenation. Achieving an optimal oxygen content in YBCO films is actually a critical issue in the development of high critical current superconductors. This process depends on the kinetics of the surface oxygen exchange and bulk oxygen diffusion processes. Therefore, an improved understanding of oxygen incorporation (in-diffusion process) and excorporation (out-diffusion process) in YBCO films is needed to design an optimal oxygenation.

The oxygen exchange processes have been investigated extensively in the past using different techniques such as secondary ion mass spectrometry,^7–10 thermogravimetry,^11,12 spectroscopic ellipsometry¹³ or electrical conductivity relaxation.^14–20 However, in most of the cases the kinetics of oxygen exchange have been analyzed in terms of a volume diffusion process governed by Fick's laws^21,22 and the surface reactions that the oxygen molecules experience on the YBCO films have been scarcely considered.¹⁸

However, in recent years, the mechanisms of oxygen exchange and bulk diffusion in functional oxides have become a topic generating high interest. The relevance of surface reactions, which may become the slowest step in the whole chain of oxygen exchange, has been stressed. This is particularly important in thin films, because the short diffusion distance makes bulk diffusion very fast leading to homogeneously oxygenated films. The research about this issue in the field of solid oxide fuel cells (SOFCs) where mixed ionic and electronic conductors (MIECs) are used is especially relevant.^23–25 In these materials, the oxygen molecules have to complete four different steps before diffusing through the volume: (i) adsorption/ionization, (ii) surface diffusion to find a vacancy, (iii) dissociation and (iv) migration of the second ion to find another vacancy.^26–28

Among these steps, the slowest one limits the overall rate of the surface reaction and, for this reason, it is known as the rate determining step (rds). The rds can vary depending on the particular case that is being considered. Similar proposals have been made for many MIECs, such as SrTiO₃ (STO), Fe-doped STO or Ba_1−xSr_xCo_yFe_1−yO_3−z.^29–33 Also, extensive analyses of the oxygen surface reactions have been carried out in CeO_2−z (ceria) and gadolinium doped ceria (GDC) as recognized oxygen-deficient compounds which may serve as model systems. The complexity of the surface oxygen-ion transfer was demonstrated on these systems and it was shown that surface phenomena can limit in some cases the rate of the overall oxygen exchange processes.^34–40 However, the possibility that the surface reactions limited the oxygen exchange processes in YBCO films or single crystals was mostly discarded, and only recently the role of surface reactions was pointed out.^10,13,18,41 Therefore, further analysis of the oxygen exchange mechanisms in YBCO films is needed to determine when this process is surface limited and under which conditions the volume bulk diffusion in films is indeed fast enough.

For this reason, in this work, we analyze, by electrical conductance relaxation measurements, the effect that several parameters, such as temperature (T) and oxygen partial pressure (P_O2), have on the oxygenation kinetics of CSD YBCO films. After concluding that surface exchange effects play the key role in oxygenating our YBCO films, we also investigate the influence of including Ag as a catalyst to enhance the low-temperature oxygenation rate. The results are the base for designing optimal oxygenation processes in minimal time for YBCO films having different oxygen contents.

Theoretical aspects

The problem of oxygen diffusion in YBCO thin films is addressed, in a simple way, as a one-dimensional diffusion process in a homogeneous medium bound by two parallel infinite planes, e.g. the planes at x = 0 and x = l (actually, we only have one limiting surface because the other one is in contact with the substrate). These conditions apply in practice to diffusion into a plane sheet of material so thin that effectively all the diffusing substance enters through the plane faces and a negligible amount through the edges. In this case, the problem is reduced to solve Fick's second law in one dimension (eqn (1)):^21,22,42with boundary conditions of zero flux at the film–substrate interface,
and a linear reaction rate at the free surface,
where D is the mean value of the bulk diffusion coefficient in the material, k_S is the surface reaction rate constant, l is the film thickness and C, C_S and C_eq are the oxygen concentration at any point, at the surface and that in equilibrium with the surrounding gas, respectively.

For an initial homogeneous oxygen concentration, C₀, this problem has an exact analytical solution.⁴² This solution integrated over the film thickness delivers the time-dependence of the average oxygen concentration, C̄ (eqn (2)):

where

The values β_n are the n'th positive roots of (eqn (3)):

β_n tan β_n = δ (3)

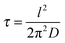For a volume diffusion-controlled process (δ ≫ 1) and for a surface-controlled process (δ ≪ 1), the only relevant term of the series of the solution is the first one; the other terms have much shorter time constants and much lower amplitudes. Consequently, in both cases the evolution of C̄ with time can be described by a single time constant (eqn (4)):where or τ = l/k_S is the relaxation time if the process is volume-diffusion or surface exchange-controlled, respectively.

In the case when the process is volume-diffusion controlled, the exponential function should be multiplied by a factor very close to one (8/π²).

Finally, since the oxygen content controls the electronic carrier concentration in YBCO films, its evolution will result in a parallel evolution of the film conductance, G = 1/R. We will assume that C̄ and G are proportional (i.e., the mobility of the carriers is assumed to be constant during the course of relaxation) and, consequently, the electrical conductance transients will be fitted to the time dependence of eqn (5), where the concentrations must be substituted by the conductances (eqn (5)):

Eventually, if there are two different parallel oxygenation channels it would be necessary to consider two conductivity relaxation processes with different relaxation times.¹⁸

Results

Structural and superconducting characterization of the films

All the 250 nm CSD YBCO films employed in this study present excellent biaxial texture as observed in the 2D XRD θ–2θ frame (Fig. 1a) and confirmed by ϕ-scan and ω-scan measurements (typically Δω ∼ 0.6°). The YBCO grains exhibit a perfect epitaxial (00l) orientation (Fig. 1b). The presence of other grain orientations or secondary phases is not detected. X-ray diffraction was used to determine the film lattice parameters which are strongly sensitive to the YBCO oxygen content (see Fig. S2, ESI†).

Fig. 1 2D XRD θ–2θ (a) frame and (b) integrated patterns of a 250 nm CSD YBCO film studied in this work. The film displays a perfect 2D texture.

On the other hand, the SEM image shown in Fig. 2 demonstrates that the obtained films have a dense and homogenous surface without the presence of precipitates or grains with the {100} planes oriented perpendicular to the substrate (a–b grains). The presence of pores (marked with white arrows) is also noticeable. These pores have actually a great importance in accelerating the oxygen diffusion processes, as will be discussed later, even if their density is not high enough to influence adversely the superconducting properties such as the critical current density.^43–46 Actually, previous investigations of the origin of residual pores in YBCO CSD films showed that pores are formed at the stage of metallorganic pyrolysis and they are healed during the growth stage, therefore it is very important to perform a fine tuning of the processing conditions to reach this stage.⁴⁷ The TEM images of the cross section of the CSD films after optimized growth confirm their high quality epitaxy and the limited density of pores (see Fig. S3, ESI†). The critical temperature of the superconducting films corresponds to T^onset_c and it was measured by inductive measurements using a superconducting quantum interference device (SQUID) magnetometer at a low magnetic field (H ∼ 1–5 Oe). This SQUID magnetometer was also used to determine the critical current density J_c of the YBCO films using the Bean critical state model of thin discs.^48,49

Fig. 2 SEM image of a typical 250 nm CSD YBCO film showing a dense and homogeneous surface with the presence of some pores (white arrows).

Temperature dependence of oxygenation kinetics

The electrical conductivity relaxation after consecutive steps of P_O2, either going towards a lower value (P_L = 2 × 10⁻⁴ atm) or towards a higher value (P_H = 1 atm), can be observed in Fig. 3a. The consecutive conductance steps are measured at different temperatures.

Fig. 3 (a) Evolution of the conductance with time at different temperatures with alternating changes of P_O2 (A: P_H = 1 atm and B: P_L = 2 × 10⁻⁴ atm). (b) Example of a non-saturated conductance relaxation measurement made at very long times (15 h) for an out-diffusion process at 400 °C. (c) Typical fitting (red curve) of an experimental conductivity relaxation measurement (black curve) using expression (5) to determine the τ values (in-diffusion process at 450 °C).

When P_O2 decreases, oxygen ions leave the YBCO structure (we will refer to this process as “out-diffusion”), thus decreasing the carrier concentration and so causing a decrease of the film conductance (Fig. 3b). This process leads to a final stoichiometry close to YBa₂Cu₃O₆ and, therefore, a change from the orthorhombic phase to the tetragonal phase yielding a non-superconducting film. The oxygen level can be estimated from the T–P_O2 phase diagram.^50–52 On the other hand, when P_O2 increases, oxygen ions enter into the YBCO structure (process referred as “in-diffusion”) and an increase of the conductance is observed (Fig. 3c). During the in-diffusion process, we return to the orthorhombic phase and the films become superconducting again. The different values of oxygen stoichiometry can be again estimated from the T and P_O2 and this will determine the T_c of the films.⁵³ In the ESI† (Fig. S2), we report typical examples of how the different oxygen contents of YBCO films influence the T_c, critical current density J_c(T) and c-axis parameter of the thin films. Notice that the values of saturation conductance at P_L and at P_H increase at lower temperatures. This evolution is mainly due to the increase of the equilibrium oxygen content at low temperatures and higher P_O2 values.^50,54 The saturation conductance is shown to decrease at high temperatures, independent of the metallic to semiconducting transition of the YBCO films at an oxygen content of δ ∼ 0.6. This would indicate that the influence of the carrier concentration change on conductance overcomes the intrinsic temperature dependence of the electric conductivity of the YBCO phase in the semiconductor or metallic regimes. Fig. 3a and b also show that at low temperatures (below 550 °C for out-diffusion and below 400 °C for in-diffusion), the saturation of the conductance is not reached. This is because, at such low temperatures, the oxygen exchange process is so slow that the equilibrium is not reached at lab scale times (maximum 2 h in the present experiments). This conclusion is also supported by the low T_c and J_c values measured on such partially oxygenated YBCO films (see Fig. S2, ESI†). Fig. 3b shows one example of the non-saturated out-diffusion conductance relaxation process measured at 400 °C, even if much longer annealing times are used (>15 h).

The conductance transients corresponding to oxygen out- and in-diffusion were fitted using eqn (6) to obtain the τ values (Fig. 3c). It is observed that good fits are achieved which correspond either to a process limited by surface reactions or by bulk diffusion, as discussed in Section 3. It has to be considered that only the transients that reach an equilibrium process can be properly fitted. The curves that are not saturated after the corresponding oxygen exchange process are not valid for the fitting and, therefore, all the graphs in this work only contain τ values obtained from equilibrium states. Fig. 4 displays the temperature dependence of τ values for the out- and in-diffusion processes. The τ values are longer for the out-diffusion process (∼7 min at 500 °C to ∼0.4 min at 800 °C) than for in-diffusion (∼4 min at 400 °C to ∼0.5 min at 500 °C). In the case of in-diffusion, above 500 °C, the process is so fast that it is not possible to obtain an accurate value of τ.

Fig. 4 Evolution of τ values with temperature and k_Svs. 1000/T curves for the out-diffusion (black) and in-diffusion (red) processes of a 250 nm pristine YBCO film following the P_O2 changes shown in Fig. 3.

On the right Y axis of Fig. 4, the values of the surface reaction rates k_s obtained by application of eqn (5) are also indicated. The log k_svs. 1/T series of points have been fitted to a linear dependence to extract the activation energy, E_a and k₀ (k_s = k₀ exp^E_a/kT). For out-diffusion, it is found that E_a = 0.25 ± 0.05 eV in the 550–800 °C range, whereas a much higher value of 0.8 ± 0.2 eV is obtained for in-diffusion E_a in the 400–500 °C range.

The in-diffusion E_a value is similar to those previously reported for sputtered YBCO thin films and bulk and liquid phase epitaxy (LPE) samples,^16,20,55,56 while the E_a value of the out-diffusion process is considerably smaller (no similar analyses have been previously reported). The k₀ values determined from the intercepts of the straight lines in Fig. 4 also strongly differ between out- and in-diffusion processes: k₀ = 1.5 × 10⁻⁶ ± 8 × 10⁻⁷ cm s⁻¹ and 0.29 ± 0.09 cm s⁻¹ for the out- and in-diffusion processes, respectively.

At this stage, we wonder if the asymmetric behavior between out- and in-diffusion processes is real or if it arises from an experimental artifact associated with the conductivity relaxation experiments which might be influenced by different electrical current percolation paths between both experiments.^56,57 To ensure that this is not the case, we performed thermogravimetric analysis (TGA) experiments on YBCO powders with small particle size (10 μm of diameter) to ascertain if asymmetry is also observed in this case. We indeed found that under similar conditions of temperature and P_H and P_L values, similar τ values are obtained and the asymmetry is maintained (see Fig. 5). Hence, we confirm that the asymmetric behavior of oxygen exchange is an intrinsic characteristic of YBCO under the experimental conditions used in our experiments.

Fig. 5 TGA measurements of the mass change due to the oxygen out-diffusion (solid) and in-diffusion (dashed) processes in a YBCO polycrystalline powder sample.

Oxygen pressure dependence of the conductivity relaxation

The oxygen partial pressure P_O2 is a key parameter to analyze the mechanisms limiting the kinetics of oxygen exchange processes on any oxide. Hence, we have carried out a series of conductance relaxation measurements where P_L was changed within the range P_L = 5 × 10⁻⁵ to P_H = 1 atm, while P_H was kept constant to 1 atm. A first set of experiments was performed to analyze the temperature dependence of τ values at different P_O2 values for the out-diffusion process. The experimental results show that P_O2 has a strong influence on the corresponding τ values (Fig. 6).

Fig. 6 Measurements of the out-diffusion process showing the evolution of τ values with temperature at different P_L values and P_H = 1 atm. Dependence of k_S on 1/T at different P_L values is also indicated together with the corresponding E_a values.

At higher P_L, τ values are smaller at all temperatures (values shown in Fig. 6). Consequently, k_S increases with P_L at all temperatures and it follows a thermally activated behavior whose activation energy depends on P_O2. E_a has been found to decrease with P_L (Fig. 6).

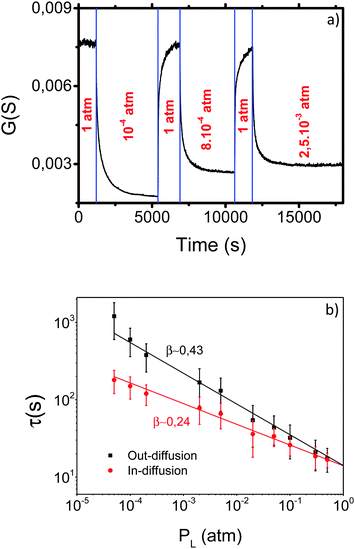
More insight into the influence of P_O2 on the oxygenation kinetics was gained from a second series of experiments where the dependence of τ on P_L was determined by measuring the conductance relaxation at 500 °C for both in-diffusion and out-diffusion processes. The procedure is illustrated in Fig. 7a where the conductance transients are observed when P_O2 is switched from P_L to P_H and vice versaFig. 7b displays the corresponding τ values as a function of P_L. The figure shows that τ follows a power law, i.e., τ ∝ P_O2^β with β values differing between in- and out-diffusion processes. Consequently, the corresponding τ values are progressively different when P_L moves away from P_H.

Fig. 7 (a) Evolution of the electrical conductance with time at 500 °C when different out-and in-diffusion processes are carried out with different P_L values and P_H = 1 atm. (b) Evolution of τ values for the in- and out-diffusion processes shown in (a). In the in-diffusion and out-diffusion experiments the initial or final P_L values were variable, respectively. The slope of the power law curves indicates that the factor β is ∼0.43 ± 0.04 for out-diffusion and ∼0.24 ± 0.05 for in-diffusion.

Actually, the reaction rates of surface reactions usually follow a power law dependence P_O2^β, where β depends on each particular reaction. Hence, the conductance relaxation times should also follow such a dependence (τ ∝ P_O2^β) if oxygen exchange is dominated by surface reactions.^30,31,58 The power law dependence of the reaction rates has a thermodynamic origin derived from the equilibrium constant of the chemical reaction and also from the influence of oxygen adsorbate coverage on P_O2.^56,58 The analysis of the τ power dependence on P_O2 can therefore provide more information on the rds of the surface reactions. It can also further clarify the origin of some controversial observations concerning the possible existence of an asymmetric behavior between in and out-diffusion oxygenation kinetics in YBCO.^59–62 The results reported in Fig. 7b draw a plausible scenario for this controversy: in any experimental analysis of the asymmetry issue it is required that P_L and P_H differ by a significant amount to detect the corresponding effects.

At this stage, we should stress that bulk diffusion might also introduce some dependence of oxygenation kinetics on P_O2 because the equilibrium oxygen content δ of YBCO depends on P_O2,⁵⁰ and this brings some dependence on P_O2 on the chemical diffusion constant D, an usual feature in most MIEC oxides.^63–66 However, in YBCO the dependence of D on δ seems to be rather weak, even if a thorough investigation of this effect in single crystals or epitaxial films would be worthwhile to handle properly the YBCO diffusion constant anisotropy effects.^{9,12,16,56,57,67–72}

The results shown in Fig. 3–7 provide, therefore, an adequate framework to disentangle the corundum of the surface oxygen exchange mechanisms in CSD YBCO films. For instance, the strong divergence between in-diffusion and out-diffusion kinetics (i.e., modified τ values and a strong decrease of E_a for the out-diffusion process) can only be attributed to the asymmetry of the surface reactions.

An additional parameter which may influence the observed oxygenation kinetic asymmetries is the temperature, so we investigated the τ dependence on P_L at different temperatures. Fig. 8 shows that the ratio of τ values for in- and out-diffusion follows a P_O2 power law dependence with β independent of temperature within the investigated temperature range.

Fig. 8 Plot of the ratio of τ values of in- and out-diffusion at different temperatures vs. P_L, when P_H is fixed at 1 atm, as shown in Fig. 6.

This behavior provides more understanding of the surface reaction processes limiting the oxygen exchange. Since, as commented above, one does not expect an asymmetry in the kinetics of in- and out-diffusion for a process controlled by bulk diffusion, the continuous lines of Fig. 8 are extrapolated to the different P_L values where τ_in/τ_out ∼ 1, i.e., when the experimental behavior is indistinguishable from that of bulk diffusion. Under these conditions, the difference in P_O2 between both processes become very small and the equilibrium states are reached very fast. Our analysis clarifies, therefore, why previous reports in single crystals showed that the τ values of in- and out-diffusion were indistinguishable: the departures from the equilibrium were too small.^16,68 The asymmetric behavior associated with oxygen surface reactions, therefore, can only be detected when large enough P_O2 steps are used.

Finally, we can conclude this section by analyzing in more detail the rds associated with surface reactions from the P_O2 dependence of τ values.

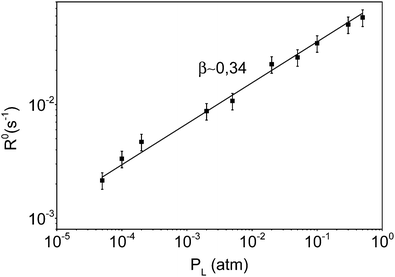
This analysis is mainly grounded on the determination of β exponents which always depend on the particular rds to be considered. In the case of STO films, Merkle and Maier described in detail the values of the exponent corresponding to each particular surface reaction.³⁰ For the case of YBCO films, on the other hand, Chen et al. proposed that the β parameter associated with the surface reactions should be 1/2.¹⁸

In the most complete analysis of these issues, reported by Merkle and Maier for STO films,³⁰ a useful approach was to determine the equilibrium reaction rate (R⁰) from the τ values of the in- and out-diffusion processes. The following equation was proposed (eqn (6)):

In the case of STO films, the relationship between R⁰ and P_O2 for each step of the surface reactions was described.³⁰ These reactions are similar to those proposed by Kuklja et al. for the case of (Ba,Sr)(Co,Fe)O_3−z films and already mentioned in the Introduction.²⁶ By representing a log–log plot of the obtained R⁰ values vs. P_L for our CSD YBCO films at 500 °C, one can determine the coefficient of the power law dependence (Fig. 9). The obtained value β ∼ 0.34 suggests, following the proposal for the STO films, that the rds in our case could be either the chemisorption process, leading to the formation of O₂²⁻ molecules from O₂ in the gas phase, or the dissociation of an O₂²⁻ molecule to form two O⁻ ions on the film surface. We should note, however, that the results obtained here for CSD YBCO films cannot be directly compared with the coefficients derived for STO films.³⁰ The calculations were performed in that case assuming the adsorption equilibrium to be in the limit of low coverage and based on the bulk defect chemical data. Bearing this in mind, it is clear that our identification of the rds in CSD YBCO films can only be considered as a first approximation to a complex problem requiring further theoretical and experimental investigation.

Fig. 9 Dependence of the equilibrium reaction rate R⁰ on P_L for YBCO CSD films. The observed P^0.34_L dependence measured at 500 °C suggests that the rds is linked to the chemisorption or dissociation of O₂²⁻ molecules.

The use of silver to accelerate the kinetics of the YBCO oxygen exchange

The analysis of the oxygenation kinetics in CSD YBCO films presented up to now has demonstrated that the surface reactions limit the rate of oxygen exchange. It was also found that at low temperatures (below 550 °C and 400 °C for out- and in-diffusion, respectively) the processes are too slow to reach the equilibrium state within the experimental time window. Consequently, it is not possible to carry out oxygenation processes below 400 °C in reasonable times because the oxygen incorporation will be incomplete (Fig. 3b). However, oxygenation at low temperatures would be interesting because one can further modify the oxygen content of the YBCO films.^73–76 To overcome the low temperature limitation in the oxygenation of functional oxides, it has been shown that silver can be used as a catalyst to enhance the rate of oxygen incorporation. The use of silver as a catalyst for selective oxidation processes is well-known in different fields, especially in the hydrocarbon industry.^77,78 Additionally, it has excellent oxygen solubility and permeability, two critical properties required to achieve a fast oxygen exchange.⁷⁹ The role of silver is to facilitate the O₂ molecule dissociation and reduction. When O₂ molecules are adsorbed on a silver surface, there is an electron transfer from silver to the π* orbitals of the O₂ molecules. This causes a decrease in the binding energy of the O=O bond facilitating its rupture.⁸⁰ This strategy was successfully tested in STO films.²⁹ A layer of silver (100 nm) was deposited on top of STO by sputtering. After a 7-day annealing process at 1023 K, the silver layer transforms into micro/nanoparticles on the STO surface. The STO films with these silver nanoparticles on the top showed lower E_a and also much higher k₀ values than the pristine samples.²⁹

In our case, we have introduced silver either directly in the YBCO solution or as evaporated metallic layers, on the YBCO surface. In the first case, a YBCO + 5% M Ag solution is prepared by adding Ag–TFA salt to the YBCO solution and the films were synthesized using similar growth processes as pristine YBCO films. The structure and superconducting properties are similar to those of the previously investigated films.⁸¹ Silver shows a tendency to diffuse towards the film surface before its sublimation and, at 810 °C, some traces of silver remain on the surface (at 720 °C, some silver NPs are still detected at the surface after growth).⁸¹

In the case of Ag coating of the YBCO films, its typical initial thickness is ∼100 nm, however, after thermal annealing at 300 °C for about 5 h, the typical surface microstructure corresponds to that of nanometric or micrometric Ag particles (Fig. S2 in ESI†).

Conductivity relaxation experiments, both for the out- and in-diffusion processes, have been performed on these films at temperatures below 350 °C where the pristine YBCO films displayed very long oxygenation times. A comparison of the typical conductance relaxation of pristine and YBCO–Ag coated films at 350 °C and 300 °C is shown in Fig. 10a and b. It can be observed that the equilibrium oxygenation in YBCO–Ag coated films is reached within reasonable oxygenation times, while in pristine YBCO films saturation is not reached, even after times as long as 12–15 h (Fig. 3b).

Fig. 10 (a) Conductance relaxation due to an in-diffusion process originated with a P_O2 step from P_L = 5 × 10⁻³ atm to P_H = 1 atm in pristine and YBCO–Ag coated films at 350 °C. The difference in the oxygen exchange rate between both types of films is clearly observed. (b) Evolution of the conductance during in- and out-diffusion processes at 300 °C with P_L = 5 × 10⁻³ atm and P_H = 1 atm. The corresponding τ values are also indicated.

These results demonstrate that the oxygenation kinetics is much faster when Ag is deposited on the film surface.

It is clear that oxygen in-diffusion is favored at low temperatures by silver. When silver is deposited on the surface of YBCO, the number of O₂ molecules that are adsorbed and dissociated is larger due to the reduction of the bond energy and, probably, also due to an enhanced sticking probability of the molecules. It has been suggested that oxygen atoms diffuse into bulk silver and reach the film surface. This oxygen path was proposed for a silver membrane kept at temperatures above 310 °C. Below this temperature, the atomic oxygen is found to be locked at the silver surface without diffusion into the silver layer.^82–84 The overall result of this phenomenon is the acceleration of the surface reactions. Probably silver is able to accelerate the rds, which has been suggested to be the dissociation of O₂²⁻ molecules (or the formation of O₂²⁻). A thorough analysis of the temperature and P_O2 dependence of these films will be required to properly analyze the microscopic mechanisms responsible for such a strong modification of the oxygen exchange processes.

Discussion

The results presented in the previous sections have provided compelling evidence of the oxygen surface exchange reactions as the limiting step in the oxygenation processes of CSD YBCO films. In other words, the surface reactions are slower than the bulk diffusion process in these thin films. It is a useful exercise, however, to compare the surface reaction rates to the expected bulk diffusion rates in YBCO crystals. For this purpose, we need to take into account that along the a–b planes the bulk oxygen diffusion coefficient is much larger than the diffusion constant along the c-axis (D_ab ≈ 10⁶D_c).^9,10 Since volume diffusion is faster than the surface oxygen surface exchange, we can estimate from our data an upper bound of the oxygen diffusion length parallel to the ab planes, based on previously determined chemical diffusion constants.

A comparative analysis of oxygenation rates in bulk melt textured ceramics and thin films has been performed previously, where it is assumed that bulk oxygen diffusion is the limiting step. The upper bound of the grain size (or bulk diffusion length) can be determined using the following formula (eqn (7)):¹⁶

Base on the experimental τ values for the oxygen in-diffusion process at 700 °C in our CSD films, L is estimated to be in the range of L ∼ 0.3–0.7 μm, depending on the D_ab values chosen in the calculation. The diffusion lengths estimated by other authors for different YBCO samples from their experimental τ values were: L ∼ 10³–10⁴ μm for melt textured bulk ceramics YBCO,²⁰L ∼ 10¹–10² μm for LPE films⁵⁵ and L ∼ 0.2 μm for sputtered films.^16,68 The upper bound of our CSD films is therefore similar to the values previously reported for sputtering films.

Fig. 11 compares typical Ln(1/τ) vs. 1000/T curves for the oxygen in-diffusion process of the above mentioned YBCO samples. It is observed that the CSD film curve is shown in the top left part, thus indicating that the τ values are the smallest in this range of temperatures. The E_a values for the in-diffusion process of the CSD films are similar to those of LPE, sputtering or bulk ceramics. In the case of CSD YBCO films, the values vary in the range 0.8–1 eV, which are similar to the previously reported values (1.1–1.25 eV) in other types of samples. For the out-diffusion process, however, as we mentioned before, the E_a values are reduced to E_a = 0.2–0.3 eV, thus pointing towards a modified rds mechanism,^23,85 or an asymmetry of the surface reactions during oxygen exchange.⁵⁶

Fig. 11 In-diffusion Ln(1/τ) vs. 1000/T curves for the YBCO LPE films,⁵⁵ sputtering films,^16,68 MTG bulk samples²⁰ and CSD films.

With regard to the observed τ₀ values in Fig. 11, the obtained results for each technique are quite different. The τ₀ values for CSD and sputtering films are in the range of 10⁻⁵–10⁻⁷ s, while in the case of the LPE and MTG samples the τ₀ values are in the range of 10⁻²–10⁻³ s, a reflection of the larger L values in these materials. We suggest therefore that in YBCO films with a thickness in the range of hundreds of nanometers and with small grain sizes (below ∼1 μm), the surface reactions are the rate limiting factor for oxygen exchange. When the sample thickness increases above several micrometers and the grain sizes also increases, as in the case of the LPE samples (10 μm thickness with large grains of 10¹–10² μm), the rate limiting factor is bulk diffusion.

The microscopic mechanisms underlying the obtained E_a values arise actually from different sources, depending on whether bulk diffusion or surface exchange is the rds. In the case of bulk controlled mechanisms, the E_a correspond to the energy barrier that the oxygen ions have to overcome to diffuse inside the YBCO structure. On the other hand, the E_a values in a surface controlled mechanism arise from one of the energy barriers that the oxygen molecules have to overcome: chemisorption, diffusion or dissociation.

After reaching the conclusion that oxygen diffuses along lengths shorter than 0.3–0.7 μm, we may wonder if these are reasonable values taking into account the microstructure of the CSD films. Actually, the scenario suggested for the present CSD YBCO films is quite similar to that previously suggested by other authors for epitaxial functional oxide films.^18,19,86 These works proposed that the oxygen exchange in epitaxial films takes place through two different exchange channels: the native surface and dislocations usually present in the films. The claim is that the oxygen exchange rate through these two channels strongly differs. Oxygen diffusion through dislocations is much faster than through the native surface because in defective structures the oxygen mobility is higher^87,88 and the number of oxygen vacancies is larger than in the bulk,^87,89 thus enhancing the bulk diffusion.

In the case of the CSD YBCO films, we propose a slightly modified scenario. First, the surface reactions are completed at the native surface. In the case of YBCO films grown by CSD, no threading dislocations exist even at very low thicknesses,⁹⁰ so it is considered that oxygen ion exchange towards the bulk of the film happens mainly through pores or low angle grain boundaries. Actually, as observed in Fig. 3, the density of pores in the 250 nm thick CSD YBCO films is high enough to facilitate oxygen diffusion through the small angle grain boundaries existing in CSD YBCO films. These low angle grain boundaries have been shown to play some role in the superconducting transport properties and so they are probably also active as fast oxygen diffusion paths.^56,60,91 Due to the fact that bulk oxygen diffusion is faster than oxygen surface exchange rates, we should not expect that electronic percolation effects influence the measured bulk conductance. We propose, therefore, that oxygen ions penetrate into the films along the vertical direction through these pores, where the surface reactions may also occur, as well as along the low angle grain boundaries remaining in the CSD epitaxial films.^62,67 These oxygen exchange paths should be much faster than bulk diffusion along the c-axis within the bulk of the film due to the low values of D_c mentioned before. Actually, we estimate that oxygen ions can diffuse over a distance between 300 and 700 times longer along the a–b planes than along the c-axis. We should note here that the mean separation distance between pores is in the range of the diffusion length (or probably grain size), L, calculated using eqn (7). Therefore, oxygen ions can diffuse fast enough along the a–b planes to achieve a homogeneous distribution.

Summarizing, the in-diffusion of oxygen proceeds through the five steps indicated in Fig. 12, four of them linked to the surface reactions and the last one linked to bulk diffusion. First, the O₂ molecules are chemisorbed onto the free surface. Then, the ionized molecules diffuse into existing defects and dissociate leading to O²⁻ ions which then require further surface diffusion to find available oxygen vacancies.⁹² Once the oxygen molecules complete the surface reactions, if the resulting ions are near a pore, they diffuse through it in the vertical direction and then along the a–b plane (Fig. 12). Molecular oxygen may probably also diffuse within the pores where the surface reactions can be also completed. Anyway, considering vertical diffusion through the pores or grain boundaries is the only way to justify the observed small τ values.

Fig. 12 Complete picture of the oxygen exchange process in CSD YBCO films including the surface reactions and the bulk/volume diffusion. The complete process follows these steps: (1) chemisorption of O₂ molecules, (2) surface diffusion to find a vacancy, (3) dissociation of O₂ molecules, (4) migration of the second ion to another vacancy and (5) volume diffusion.

This scenario is compatible with the reported experimental results and it also clarifies the role of the silver nanoparticles at the surface. At low temperatures, when the oxygen exchange through pores and grain boundaries is still effective, the exchange rate is too small because the rds has been slowed down. When some silver nanoparticles are deposited on the film surface they accelerate the oxygen surface reactions, and probably the oxygen ion surface chemisorption as well. The huge τ values observed in pristine films at low temperatures are then strongly reduced and the conductivity transients become measurable. Essentially, the catalytic effect of silver nanoparticles accelerates the molecular oxygen dissociation reactions on the native surface thus increasing the formation rate of O²⁻ ions at low temperatures and hence enhancing the efficiency of the oxygen exchange channels to diffuse towards the bulk of the films.

Conclusions

This work was devoted to the study of oxygen incorporation and excorporation processes in CSD YBCO films in order to clarify the limiting factors of the oxygen exchange in these kinds of films and we have unequivocally proved that the surface reactions are the limiting factor in the kinetics of the oxygen exchange processes in CSD YBCO films. The P_O2 dependence of conductance relaxation times and the asymmetric behavior of the in- and out-diffusion processes cannot be explained without consideration of oxygen exchange as a surface controlled process. The study of the P_O2 influence in the relaxation times is also essential to establish the rate determining step (rds) of the surface reactions. We suggest that the chemisorption process leading to the formation of ionized O₂²⁻ molecules, or the dissociation of an O₂²⁻ molecule to form two O⁻ ions at the surface, is the rds in the present case. Finally, we have also shown that silver is an effective catalytic agent to accelerate the rate of the oxygen exchange rates at lower temperatures than those we can achieve in pristine YBCO films. The reduction of relaxation times in Ag coated YBCO films was quite significant at low temperatures, thus allowing the shortening of the oxygenation times of the films at low temperatures where the pristine films cannot be fully oxygenated. It is suggested that silver reduces the strength of the O=O bond and decreases drastically the overall surface reaction times. After completing the surface reactions, the oxygen ions diffuse parallel to the ab planes into the volume of the films benefiting from the existing pores and grain boundaries.

Experimental

The films studied in this work were prepared by CSD following the trifluoroacetate (TFA) route. YBCO metallorganic precursor solutions based on anhydrous TFA salts were prepared and characterized as described in detail previously.^81,93 Basically, YBCO solid ceramic powder was dissolved in trifluoroacetic acid, trifluoroacetic anhydride and acetone. Further, the mixture was purified to finally obtain a 0.25 M (with respect to the Y content) YBCO–TFA solution. Alternative YBCO + 5% mol Ag solutions were prepared by adding the corresponding stoichiometric amount of Ag–TFA precursor salts into the original 0.25 M YBCO–TFA solution. These solutions were deposited by spin-coating on 5 × 5 mm² LaAlO₃(00l) (LAO) substrates. The subsequent pyrolysis and growth processes are also described elsewhere.^93–95 The phase analysis of the YBCO films was performed by X-ray diffraction using a Bruker AXS GADDS diffractometer equipped with a 2D detector. The lattice parameters were determined using a Siemens model D-5000 X-ray diffractometer with a step size of 0.01°. The morphology of the fully grown films was studied to observe the presence of precipitates, porosity and the degree of grain disorientation. The scanning electron microscopy (SEM) images were obtained using a SEM Quanta 200 ESEM FEG equipment. TEM images were obtained on a Philips CM30 operated at 300 kV and a Jeol 2010 FEG operated at 200 kV.

The films conductance was determined by electrical measurements carried out using a standard system reported elsewhere.^18,19,95,96 It consists of a 4-probe contact in a Van der Pauw configuration. The sample is held in the center of a 22 mm furnace tube that allows controlling the temperature and gas atmosphere. All experiments have been performed at atmospheric pressure. The P_O2 was set by mixing N₂ and O₂ using appropriate mass-flow meters. The in-diffusion conductance transients were measured after P_O2 was switched from a low-value, P_L, to a high value, P_H; and the reverse was done for the out-diffusion experiments.

The influence of gas flow on the oxygen exchange kinetics was analyzed for out-diffusion experiments in order to evaluate the proper flow to be used in all the kinetic experiments. Out-diffusion experiments were performed at gas flows in the range from 0.15 to 0.6 l min⁻¹ at different temperatures (300–800 °C) (Fig. S1 in the ESI†). It was found that some dependence on gas flow exists which is enhanced at low temperatures and which tends to stabilize at 0.6 l min⁻¹. This gas flow dependence at low gas flow rates arises probably from insufficient oxygen diffusion across the boundary layer formed on top of the films. For this reason, all the reported experiments were performed under the highest gas flow allowed in our experimental set up, i.e., 0.6 l min⁻¹.

Acknowledgements

The authors acknowledge the MICIN (NANOSELECT, CSD2007-00041 and MAT2014-51778-C2-1-R and C2-2-R), Generalitat de Catalunya (2014SGR 753 and Xarmae), the EU (EU-FP7 NMP-LA-2012-280432 EUROTAPES project, Cost Action MP1201) and ERC ADG-2014-669504. M. C. is grateful to the MINECO for the “Ramon y Cajal” contract RYC-2013-12448. We also acknowledge the MINECO for the Center of Excellence award Severo Ochoa (SEV-2015-0496). C. F. Sánchez-Valdés acknowledges the support received from CSIC under JAE-Predoctorals program. We also acknowledge useful discussions with Dr S. Ricart.

References

1. X. Obradors and T. Puig, Supercond. Sci. Technol., 2014, 27, 44003.
2. X. Obradors, T. Puig, A. Pomar, F. Sandiumenge, N. Mestres, M. Coll, A. Cavallaro, N. Romà, J. Gázquez, J. C. González, O. Castaño, J. Gutiérrez, A. Palau, K. Zalamova, S. Morlens, A. Hassini, M. Gibert, S. Ricart, J. M. Moretó, S. Piñol, D. Isfort and J. Bock, Supercond. Sci. Technol., 2006, 19, S13–S26.
3. X. Obradors, T. Puig, A. Pomar, F. Sandiumenge, S. Piñol, N. Mestres, O. Castaño, M. Coll, A. Cavallaro, A. Palau, J. Gázquez, J. C. González, J. Gutiérrez, N. Romà, S. Ricart, J. M. Moretó, M. D. Rossell and G. van Tendeloo, Supercond. Sci. Technol., 2004, 17, 1055–1064.
4. T. Izumi, M. Yoshizumi, J. Matsuda, K. Nakaoka, Y. Kitoh, Y. Sutoh, T. Nakanishi, A. Nakai, K. Suzuki, Y. Yamada, A. Yajima, T. Saitoh and Y. Shiohara, Phys. C, 2007, 463, 510–514.
5. Y. Shiohara, T. Taneda and M. Yoshizumi, Jpn. J. Appl. Phys., 2012, 51, 10007.
6. Y. Shiohara, M. Yoshizumi, Y. Takagi and T. Izumi, Phys. C, 2013, 484, 1–5.
7. S. Tsukui, R. E. Koritala, M. Li, K. C. Goretta, M. Adachi, J. E. Baker and J. L. Routbort, Phys. C, 2003, 392, 841–846.
8. R. Mogilevsky, R. Levi-Setti, B. Pashmakov, L. Liu, K. Zhang, H. M. Jaeger, D. B. Buchholz, R. P. H. Chang and B. W. Veal, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 6420–6423.
9. S. J. Rothman, J. L. Routbort, U. Welp and J. E. Baker, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 2326–2333.
10. S. I. Bredikhin, G. A. Emelchenko, V. S. Shechtman, A. A. Zhokhov, S. Carter, R. J. Chater, J. A. Kilner and B. C. H. Steele, Phys. C, 1991, 179(4–6), 286–290.
11. T. B. Tang and W. Lo, Phys. C, 1991, 174, 463–466.
12. K. Kishio, K. Suzuki, T. Hasegawa, T. Yamamoto, K. Kitazawa and K. Fueki, J. Solid State Chem., 1989, 82, 192–202.
13. A. Michaelis, E. A. Irene, O. Auciello and A. R. Krauss, J. Appl. Phys., 1998, 83, 7736.
14. G. S. Grader, P. K. Gallagher, J. Thomson and M. Gurvitch, Appl. Phys. A: Solids Surf., 1988, 45, 179–183.
15. S. H. Lee, S. C. Bae, J. K. Ku and H. J. Shin, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 9142–9146.
16. S. Kittelberger, U. Bolz, R. P. Huebener, B. Holzapfel and L. Mex, Phys. C, 1998, 302, 93–101.
17. C. Krauns and H.-U. Krebs, Z. Phys. B: Condens. Matter, 1993, 92, 43–46.
18. L. Chen, C. L. Chen and A. J. Jacobson, IEEE Trans. Appl. Supercond., 2003, 13, 2882–2885.
19. T. Qu, Y. Xue, F. Feng, R. Huang, W. Wu, K. Shi and Z. Ha, Phys. C, 2013, 494, 148–152.
20. H. Zhang, H. Ye, K. Du, X. Y. Huang and Z. H. Wang, Supercond. Sci. Technol., 2002, 15, 317.
21. A. Fick, Ann. Phys. Chem., 1855, 170, 59–86.
22. A. Fick, London, Edinburgh Dublin Philos. Mag. J. Sci., 1855, 10, 30–39.
23. S. B. Adler, Chem. Rev., 2004, 104, 4791–4844.
24. S. B. Adler, X. Y. Chen and J. R. Wilson, J. Catal., 2007, 245, 91–109.
25. A. J. Jacobson, Chem. Mater., 2010, 22, 660–674.
26. M. M. Kuklja, E. A. Kotomin, R. Merkle, Yu. A. Mastrikov and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 5443.
27. M. V. Ananyev, E. S. Tropin, V. A. Eremin, A. S. Farlenkov, A. S. Smirnov, A. A. Kolchugin, N. M. Porotnikova, A. V. Khodimchuk, A. V. Berenov and E. Kh. Kurumchin, Phys. Chem. Chem. Phys., 2016, 18, 9102–9111.
28. C. Körber, A. Wachau, P. Ágoston, K. Albe and A. Klein, Phys. Chem. Chem. Phys., 2011, 13, 3223.
29. M. Leonhardt, R. A. De Souza, J. Claus and J. Maier, J. Electrochem. Soc., 2002, 149, J19.
30. R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2002, 4, 4140–4148.
31. R. Merkle and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874–3894.
32. L. Wang, R. Merkle and J. Maier, J. Electrochem. Soc., 2010, 157, B1802.
33. V. Metlenko, W. Jung, S. R. Bishop, H. L. Tuller and R. A. De Souza, Phys. Chem. Chem. Phys., 2016, 18, 29495–29505.
34. Z. A. Feng, F. El Gabaly, X. Ye, Z.-X. Shen and W. C. Chueh, Nat. Commun., 2014, 5, 966–978.
35. A. Karthikeyan and S. Ramanathan, Appl. Phys. Lett., 2008, 92, 243109.
36. Y. Shi, A. H. Bork, S. Schweiger and J. L. M. Rupp, Nat. Mater., 2015, 14, 721–727.
37. S. V. Kalinin, A. Borisevich and D. Fong, ACS Nano, 2012, 6, 10423–10437.
38. A. Sawa, Mater. Today, 2008, 11, 28–36.
39. C. Moreno, C. Munuera, S. Valencia, F. Kronast, X. Obradors and C. Ocal, Nano Lett., 2010, 10, 3828–3835.
40. N. Knoblauch, L. Dörrer, P. Fielitz, M. Schmücker and G. Borchardt, Phys. Chem. Chem. Phys., 2015, 17, 5849–5860.
41. J. L. Routbort and S. J. Rothman, J. Appl. Phys., 1994, 76, 5615.
42. J. Crank, The mathematics of diffusion, Clarendon Press, 1975.
43. A. Pomar, J. Gutiérrez, A. Palau, T. Puig and X. Obradors, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214–522.
44. E. Bartolomé, A. Palau, J. Gutiérrez, X. Granados, A. Pomar, T. Puig, X. Obradors, V. Cambel, J. Soltys, D. Gregusova, D. X. Chen and A. Sánchez, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 895–899.
45. A. Palau, T. Puig, X. Obradors, E. Pardo, C. Navau, A. Sánchez, A. Usoskin, H. C. Freyhardt, L. Fernández, B. Holzapfel and R. Feenstra, Appl. Phys. Lett., 2004, 84, 230.
46. O. Castaño, A. Cavallaro, A. Palau, J. C. González, M. Rosell, T. Puig, S. Piñol, N. Mestres, F. Sandiumenge, A. Pomar and X. Obradors, IEEE Trans. Appl. Supercond., 2003, 13, 2504–2507.
47. K. Zalamova, A. Pomar, A. Palau, T. Puig and X. Obradors, Supercond. Sci. Technol., 2010, 23, 14012.
48. C. P. Bean, Phys. Rev. Lett., 1962, 8, 250–253.
49. C. P. Bean, Rev. Mod. Phys., 1964, 36(1), 31–39.
50. J. Shimoyama, S. Horii, K. Otzschi and K. Kishio, MRS Proc., 2001, 689, E8.18.
51. E. D. Specht, C. J. Sparks, A. G. Dhere, J. Brynestad, O. B. Cavin, D. M. Kroege and H. A. Oye, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 7426–7434.
52. J. Ye and K. Nakamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 7554–7564.
53. R. Liang, D. A. Bonn and W. N. Hardy, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 180505.
54. T. B. Lindemer, J. F. Hunley, J. E. Gates, A. L. Sutton, J. Brynestad, C. R. Hubbard and P. K. Gallagher, J. Am. Ceram. Soc., 1989, 72, 1775–1788.
55. H. Zhang, X. Yao and X. Zeng, Phys. Status Solidi, 2004, 201, 2305–2311.
56. K. Conder, Mater. Sci. Eng., R, 2001, 32, 41–102.
57. N. K. Tu, N. C. Yeh, S. I. Park and C. C. Tsuei, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 304–314.
58. Y. A. Mastrikov, R. Merkle, E. Heifets, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2010, 114, 3017–3027.
59. J. R. LaGraff and D. A. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 3380–3390.
60. J. R. LaGraff and D. A. Payne, Phys. C, 1993, 212, 470–477.
61. J. R. LaGraff and D. A. Payne, Phys. C, 1993, 212, 478–486.
62. J. R. LaGraff and D. A. Payne, Phys. C, 1993, 212, 487–496.
63. M. Søgaard, P. Vang Hendriksen and M. Mogensen, J. Solid State Chem., 2007, 180, 1489–1503.
64. I. Yasuda and M. Hishinuma, J. Solid State Chem., 1996, 123, 382–390.
65. J. A. Lane and J. A. Kilner, Solid State Ionics, 2000, 136, 927–932.
66. D. Rupasov, T. Makarenko and A. J. Jacobson, Solid State Ionics, 2014, 265, 68–72.
67. M. D. Vázquez-Navarro, A. Kursumovic and J. E. Evetts, Supercond. Sci. Technol., 1999, 12, 1117–1122.
68. S. Kittelberger, O. M. Stoll and R. P. Huebener, Supercond. Sci. Technol., 1998, 11, 744–750.
69. S. Elschner, W. Becker, H. Bestgen and M. Brand, Phys. C, 1992, 202, 401–407.
70. A. Erb, B. Greb and G. Müller-Vogt, Phys. C, 1996, 259, 83–91.
71. S. Kittelberger, U. Bolz, R. P. Huebener, B. Holzapfel, L. Mex and R. A. Schwarzer, Phys. C, 1999, 312, 7–20.
72. M. Burriel, H. Téllez, R. J. Chater, R. Castaing, P. Veber, M. Zaghrioui, T. Ishihara, J. A. Kilner and J.-M. Bassat, J. Phys. Chem. C, 2016, 120, 17927–17938.
73. J. L. Tallon, IEEE Trans. Appl. Supercond., 2015, 25, 1–6.
74. E. F. Talantsev, S. C. Wimbush, N. M. Strickland, J. A. Xia, P. D’Souza, J. G. Storey, J. L. Tallon, B. Ingham, R. Knibbe and N. J. Long, IEEE Trans. Appl. Supercond., 2013, 23.
75. G. Deutscher, APL Mater., 2014, 2, 96108.
76. G. Deutscher, J. Appl. Phys., 2012, 111, 112603.
77. G. Ertl, Handbook of heterogeneous catalysis, Wiley-VCH, 2008.
78. R. A. Van Santen and H. P. C. E. Kuipers, Adv. Catal., 1987, 35, 265–321.
79. C. C. Yu, J. D. Baek, C. H. Su, L. Fan, J. Wei, Y. C. Liao and P. C. Su, ACS Appl. Mater. Interfaces, 2016, 8, 10343–10349.
80. S. T. Oyama, Mechanisms in homogeneous and heterogeneous epoxidation catalysis, Elsevier, 2008.
81. X. Obradors, F. Martínez-Julián, K. Zalamova, V. R. Vlad, A. Pomar, A. Palau, A. Llordés, H. Chen, M. Coll, S. Ricart, N. Mestres, X. Granados, T. Puig and M. Rikel, Phys. C, 2012, 482, 58–67.
82. C. Backx, C. P. M. De Groot and P. Biloen, Surf. Sci., 1981, 104, 300–317.
83. V. I. Bukhtiyarov, V. V. Kaichev and I. P. Prosvirin, J. Chem. Phys., 1999, 111, 2169.
84. B. A. Sexton and R. J. Madix, Chem. Phys. Lett., 1980, 76, 294–297.
85. J. Liu, G. Collins, M. Liu and C. Chen, APL Mater., 2013, 1, 31101.
86. L. Yan and P. A. Salvador, ACS Appl. Mater. Interfaces, 2012, 4, 2541–2550.
87. K. Szot, W. Speier, G. Bihlmayer and R. Waser, Nat. Mater., 2006, 5, 312–320.
88. K. Otsuka, A. Kuwabara, A. Nakamura, T. Yamamoto, K. Matsunaga and Y. Ikuhara, Appl. Phys. Lett., 2003, 82, 877.
89. R. F. Klie, W. Walkosz, G. Yang and Y. Zhao, J. Electron Microsc., 2009, 58, 185–191.
90. J. Gázquez, M. Coll, N. Romà, F. Sandiumenge, T. Puig and X. Obradors, Supercond. Sci. Technol., 2012, 25, 65009.
91. V. Solovyov, I. K. Dimitrov and Q. Li, Supercond. Sci. Technol., 2013, 26, 13001.
92. S. K. R. S. Sankaranarayanan and S. Ramanathan, J. Phys. Chem. C, 2010, 114, 6631–6639.
93. N. Romà, S. Morlens, S. Ricart, K. Zalamova, J. M. Moretó, A. Pomar, T. Puig and X. Obradors, Supercond. Sci. Technol., 2006, 19, 521–527.
94. X. Obradors, T. Puig, S. Ricart, M. Coll, J. Gázquez, A. Palau and X. Granados, Supercond. Sci. Technol., 2012, 25, 123001.
95. C. F. Sánchez-Valdés, T. Puig and X. Obradors, Supercond. Sci. Technol., 2015, 28, 24006.
96. H. Chen, K. Zalamova, A. Pomar, X. Granados, T. Puig and X. Obradors, J. Mater. Res., 2010, 25, 2371–2379.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01855j

---