Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DFT-D3 study of H2 and N2 chemisorption over cobalt promoted Ta3N5-(100), (010) and (001) surfaces
Constantinos D.
Zeinalipour-Yazdi
 a,
Justin S. J.
Hargreaves
b,
Said
Laassiri
b and
C. Richard A.
Catlow
*ac
a,
Justin S. J.
Hargreaves
b,
Said
Laassiri
b and
C. Richard A.
Catlow
*ac
aKathleen Lonsdale Materials Chemistry, Department of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: c.r.a.catlow@ucl.ac.uk
bWestCHEM, School of Chemistry, Joseph Black Building, University of Glasgow, Glasgow G12 8QQ, UK
cSchool of Chemistry, Cardiff University, Park Place, Cardiff CF10 1AD, UK
First published on 24th April 2017
Abstract
The reactants for ammonia synthesis have been studied, employing density functional theory (DFT), with respect to their adsorption on tantalum nitride surfaces. The adsorption of nitrogen was found to be mostly molecular and non-activated with side-on, end-on and tilt configurations. At bridging nitrogen sites (Ta–N–Ta) it results in an azide functional group formation with a formation energy of 205 kJ mol−1. H2 was found also to chemisorb molecularly with an adsorption energy in the range −81 to −91 kJ mol−1. At bridging nitrogen sites it adsorbs dissociatively forming >NH groups with an exothermic formation energy of −175 kJ mol−1 per H2. The nitrogen vacancy formation energies were relatively high compared to other metal nitrides found to be 2.89 eV, 2.32 eV and 1.95 eV for plain, surface co-adsorbed cobalt and sub-surface co-adsorbed cobalt Ta3N5-(010). Co-adsorption of cobalt was found to occur mostly at nitrogen rich sites of the surface with an adsorption energy that ranged between −200 to −400 kJ mol−1. The co-adsorption of cobalt was found to enhance the dissociation of molecular hydrogen on the surface of Ta3N5. The studies offer significant new insight with respect to the chemistry of N2 and H2 with tantalum nitride surfaces in the presence of cobalt promoters.
1. Introduction
Understanding the mechanism of catalytic reactions is critical in the development of new catalyst formulations and process conditions that have lower energy requirements. In catalytic reactions, the role of defects and promoters is generally not well understood at the atomistic level. We have previously shown via a semi-empirical thermodynamic DFT approach that the number of nitrogen vacancies on Co3Mo3N surfaces can be of the order of 1013 per cm2 even at ambient temperature.1 These nitrogen vacancies, due to their high concentration, could participate in catalytic reactions in competing pathways that occur on the catalyst surface and at steps. In a detailed study of the adsorption and activation of N2 and H2 on Co3Mo3N surfaces2 with such nitrogen vacancies, we found that N2 becomes activated at such defect sites. The effect of oxygen impurities and nitrogen vacancies on the electronic structure and surface stability of Ta3N5 low index surfaces has been previously investigated which showed that the former stabilise the material3 and that the latter results in the 720 nm sub-band-gap optical absorption.4 A rationale for the enhanced, improved photoelectrochemical activities of Ta3N5(110) surfaces was given based on the low dissociation barrier of water and barrier for hydrogen migration from Ta to N.5 Although the potential development tantalum nitride based water splitting photocatalysts is well recognised, the reactivity of these materials for ammonia synthesis is acknowledged to a smaller extent. Our recent experimental reactivity screening of Co, Fe and Re doped Ta3N5 materials has shown a pronounced effect on the catalytic activity in Co-doped Ta3N5.6 Currently, the exact role of Co in the ammonia synthesis mechanism is, however, not well understood, nor is it known whether it can participate as a promoter in surface reactions of H2 and N2 over Ta3N5. In this dispersion-corrected periodic DFT study we attempt to gain further insight about the effect that Co promoters can have on the formation of nitrogen defects (i.e. nitrogen vacancies) and the chemisorption of the reactants of ammonia synthesis (i.e. H2, N2) to Ta3N5(001), (010) and (100) surfaces.In order to model the bulk and surfaces of Ta3N5 we have used the coordinates as determined by time-of-flight neutron diffraction (TOF-ND).7 The bulk 3 × 1 × 1 unit cell of Ta3N5 is shown in Fig. 1a and is composed of irregular TaN6 octahedra with both three (N3) and four coordinate nitrogen (N4) atoms and has the pseudo-brookite (Fe2TiO5) structure8–10 shown in Fig. 1a. The 3D-framework generates channels that are 4 Å in width along the [0 0 1] lattice direction. The interstitial nitrogen was found to be labile and reactive to hydrogen that generates ammonia under reducing conditions.6,11 The porous structure of Ta3N5 offers the possibility of adsorbing metal atoms to its structure. The effect of co-adsorbed cobalt atoms with respect to the adsorption of H2 and N2 has not been previously studied theoretically.
We have therefore calculated, via periodic DFT, the adsorption sites for Co atoms on Ta3N5. We then investigate the effect of cobalt promoters on the nitrogen vacancy formation energy on Ta3N5-(100), (010) and (001) surfaces. We also study the chemisorption of H2 and N2 on the Co promoted and plain Ta3N5 surfaces in order to understand the effect of Co promoters with respect to the chemisorption of the ammonia synthesis reactants.
2. Computational methods
The optimised geometry of bulk of Ta3N5 was modelled with 3 × 1 × 1 supercell where the corresponding 1 × 1 × 1 unit cell belongs to the space group CmCm (63), where a = 3.932 Å, b = 10.339 Å, c = 10.384 Å, α = β = γ = 90°. These were in good agreement with the neutron diffraction derived lattice parameters (a = 3.8862 Å, b = 10.2118 Å, c = 10.2624 Å, α = β = γ = 90°).7 The supercell dimensions was therefore set to a = 11.795 Å, b = 10.339 Å, c = 10.384 Å, α = β = γ = 90°. The surfaces were modelled via slabs about 1 nm in width that had a 20 Å vacuum gap for which the surface structure is shown in Fig. 1b–d. All DFT calculations were periodic Γ-point12 spin-polarised obtained with the use of the VASP 5.4.1 code, as Ta3N5 is a relatively narrow gap material, we would expect any surface dipolar effects to be compensated electronically rather than by surface reconstruction.13,14 Exchange and correlation effects were considered within the generalized gradient approximation (GGA) using the revised Perdew–Burke–Ernzerhof (revPBE) exchange–correlation (XC) functional,15 with the projector augmented-wave (PAW) method16,17 used to represent core states. These were 1s to 4f for Ta, 1s for N and H, and 1s to 3p for Co. The cut-off energy for the energy of the planewaves for the bulk 3 × 1 × 1 unit cell was 800 eV, and therefore this was also used in the periodic slab calculations. Geometry optimizations were performed with a residual force threshold on each atom of 0.01 eV Å−1 using the conjugate-gradient algorithm. The convergence criterion for electronic relaxation was 10−4 eV. The initial charge density was obtained by superposition of atomic charges. Initial adsorption configurations where such that the distance between the adsorbate and the nearest surface site was set to 2 Å in an end-on configuration for N2 and side-on for H2. The various adsorption sites were every symmetry unique surface site shown in Fig. 1, which resulted in 3, 8 and 3 sites for (100), (010) and (001)-surfaces, respectively. The adsorption energy was taken as the total energy difference between the fully relaxed bound state of the surface–adsorbate complex from that of the fully relaxed surface slab and the isolated molecules given by:| ΔEads,D3 = Eslab-X2 − Eslab − EX2, | (1) |
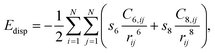 | (2) |
3. Results and discussion
The adsorption of N2 and H2 on Ta3N5 was studied systematically at every symmetry unique site shown in Fig. 1. We have also tested briefly whether the final configuration for an adsorption site would differ when placing the adsorbate mid-way between two symmetry unique sites but this was found to have no effect. The adsorption energies along with the relevant structural parameters of the optimised adsorbate configuration are given in Tables 1 and 2 for the (010) and (100)/(001) surface of Ta3N5, respectively.| Property | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Site 6 | Site 7 | Site 8 | Units |
|---|---|---|---|---|---|---|---|---|---|
| a Percent N2 activation is defined as [r(N2,ads) − 1.098] × 100/1.098. b Percent H2 activation is defined as [r(H2,ads) − 0.74] × 100/0.74. | |||||||||
| Nitrogen adsorption (010) | |||||||||
| ΔEN2,D3 | −22 | −27 | 205 | 205 | −22 | −22 | −14 | −11 | kJ mol−1 |
| r(N–N) | 1.117 | 1.118 | 1.146 | 1.146 | 1.116 | 1.117 | 1.116 | 1.117 | Å |
| a(S–N–N) | 131.4 | 163.3 | 178.7 | 178.0 | 115.8 | 140.5 | 129.7 | 128.3 | ° |
| r(S–N) | 3.467 | 2.637 | 1.239 | 1.240 | 3.539 | 3.144 | 3.459 | 3.262 | Å |
| Type | Tilt | Tilt | End-on | End-on | Tilt | Tilt | Tilt | Tilt | |
| Bound to | Ta | Ta | N3 | N3 | N4 | Ta | N3 | N3 | |
| N2 activationa | 2 | 2 | 4 | 4 | 2 | 2 | 2 | 2 | % |
| Hydrogen adsorption (010) | |||||||||
| ΔEH2,D3 | −89 | −90 | −81 | −175 | −86 | −86 | −82 | −82 | kJ mol−1 |
| r(H–H) | 0.750 | 0.753 | 0.748 | 2.413 | 0.748 | 0.749 | 0.747 | 0.747 | Å |
| a(S–H–H) | 88.6 | 87.5 | 165.9 | n/a | 128.7 | 105.1 | 138.2 | 124.7 | ° |
| r(S–H) | 3.103 | 2.810 | 2.709 | 1.021 | 3.095 | 3.109 | 2.923 | 3.086 | Å |
| Type | Side-on | Side-on | End-on | Atomic | Tilt | Tilt | Tilt | Tilt | |
| Bound to | N4 | Ta | N3 | N3 | N4 | N4 | N3 | N3 | |
| H2 activationb | 1 | 2 | 1 | n/a | 1 | 1 | 1 | 1 | % |
| Property | Site 1 | Site 2 | Site 3 | Site 1 | Site 2 | Site 3 | Units |
|---|---|---|---|---|---|---|---|
| Nitrogen adsorption (001) | Nitrogen adsorption (100) | ||||||
| a Percent N2 activation is defined as [r(N2,ads) − 1.098] × 100/1.098. b Percent H2 activation is defined as [r(H2,ads) − 0.74] × 100/0.74. | |||||||
| ΔEH2,D3 | −29 | 0 | −32 | −13 | 201 | −23 | kJ mol−1 |
| r(N–N) | 1.123 | 1.113 | 1.118 | 1.112 | 1.158 | 1.116 | Å |
| a(S–N–N) | 159 | 92 | 168 | 152 | 177 | 174 | ° |
| r(S–N) | 2.504 | 2.939 | 2.348 | 3.476 | 1.231 | 2.476 | Å |
| Type | Tilt | Side-on | End-on | Tilt | End-on | End-on | |
| Bound to | Ta | N4 | Ta | N4 | N4 | Ta | |
| N2 activationa | 2 | 1 | 2 | 1 | 5 | 2 | % |
| Property | Site 1 | Site 2 | Site 3 | Site 1 | Site 2 | Site 3 | Units |
|---|---|---|---|---|---|---|---|
| Hydrogen adsorption (001) | Hydrogen adsorption (100) | ||||||
| ΔEH2,D3 | −86 | −81 | −91 | −85 | −87 | −90 | kJ mol−1 |
| r(H–H) | 0.752 | 0.749 | 0.7623 | 0.752 | 0.748 | 0.749 | Å |
| a(S–H–H) | 151 | 163 | 86 | 134 | 155 | 84 | ° |
| r(S–H) | 2.568 | 2.738 | 2.387 | 2.842 | 2.814 | 3.161 | Å |
| Type | Tilt | End-on | Side-on | Tilt | Tilt | Side-on | |
| Bound to | N3 | N4 | Ta | N4 | N4 | Ta | |
| H2 activationb | 2 | 1 | 3 | 2 | 1 | 1 | % |
3.1 N2 adsorption on Ta3N5
For the adsorption of nitrogen we find that at most sites it is molecular without any activation of the N–N bond (e.g.Table 1 sites 1, 2, 5–8). From the dispersion-corrected adsorption energies which range between −11 to −32 kJ mol−1, the adsorption of N2 on Ta3N5-(010) is considered to be physisorption both to Ta and N surface atoms, with the former interaction being somewhat stronger. The larger the tilt angle, a(S–N–N) the shorter the distance, r(S–N) between N2 and the surface. For the (010)-surface a small enhancement of the adsorption energy is observed when N2 is adsorbed at N4 sites compared to N3 sites, which shows that the chemical nature of the four-coordinated and the three-coordinated nitrogen atoms differs slightly with the first having slightly more exothermic adsorption energies for molecular nitrogen.Among the eight symmetry adsorption sites studied, two sites had a drastically different adsorption energy (Table 1, site 3 and 4) which was endothermic by 205 kJ mol−1. We find that at these adsorption sites molecular nitrogen adsorbing to the surface will form an azide functional group (N3) as shown in Scheme 1 and therefore these are in fact formation energies. The azide functional group forms on bridging surface nitrogen atoms (i.e. N3). The N–N bond length of the azide in closer proximity from the surface was found to be 1.239 Å whereas the other N–N bond length was 1.146 Å, in close agreement with X-ray data of azides formed in bridging copper complexes, found to be 1.196 Å and 1.161 Å, respectively.19 In this functional group N2 is moderately activated based on the % bond elongation which was found to be 4–5%. Based on the formation energy of the azide, this functional group appears to be quite unstable on the (010) surface of Ta3N5. A simplified schematic showing the adsorption site geometry of the azide group formation and the formation of >NH species due to H2 chemisorption are shown in Scheme 1.
3.2 H2 adsorption on Ta3N5
For the adsorption of H2 we find that it is mostly molecular with only one site dissociating it and forming surface >NH groups (see Scheme 1). These >NH groups form again on bridging surface nitrogen atoms (i.e. N3 sites) and their formation energy is exothermic by −175 kJ mol−1 for H2 dissociating at these sites (site 4). Formation of the >NH groups can be clearly seen from structural parameters of the adsorption site shown in Table 1 for site 4. The N–H bond length is 1.021 whereas for every other adsorption site where the adsorption is molecular the N–H distance is between 2.7–3.1 Å. Furthermore this effect can be observed from the H–H distance which for the N–H groups is 2.413 Å compared to an average of 0.75 Å found for the molecularly adsorbed H2. Based on the exothermicity of molecular H2 adsorption, which was found between −81 to −90 kJ mol−1, the adsorption here can be classified as close to chemisorption. It is very interesting to observe that although the adsorption energy of H2 is almost −100 kJ mol−1 on most sites, it does not result in the dissociation of molecular hydrogen which preserves its chemical bond. Additionally, the distance at which molecular hydrogen absorbs in these configurations is quite large, ranging between 2.7 and 3.1 Å. Furthermore, we find that the adsorption energy is not very sensitive to the molecular orientation of hydrogen which adsorbs mostly in a tilt configuration but also in end-on and side-on configurations. It is interesting therefore to note how a closed shell molecule can develop such a strong interaction on Ta3N5-(010) surfaces even in the absence of surface metal atoms that usually have the tendency to coordinate strongly with hydrogen. Here again similarly to the adsorption of N2, we observe a small enhancement of the adsorption energies when N2 is adsorbed to N4 sites compared to N3 sites, which can be interpreted to be result of the higher polarizability of four-coordinated N atoms compared to three-coordinated N, as each Ta–N bond introduces additional polarizability due to the nature of covalent bonds observed in this semiconductor. It is interesting that based on only energetic and structural considerations the existence of the azide and NH groups can be clearly identified among the various adsorbed configurations studied.3.3 Effect of Co-doping on nitrogen vacancy formation energies
We have investigated whether the enhanced ammonia synthesis reactivity could be attributed to the easier formation of nitrogen vacancies, as these could be potential sites for nitrogen activation.2 In particular, we have investigated the single (SVFE) and double (DVFE) vacancy formation energy of nitrogen on the (010)-surface of Ta3N5. Energies refer to abstraction on lattice N to form molecular nitrogen. The formation of nitrogen vacancies is schematically shown in Fig. 2 where the successive removal of a N3 atom from the surface of Ta3N5-(010) is shown. The choice of single and double vacancy was such that the co-adsorbed Co could interact with both defects through nearest neighbour interactions. Other combinations of double nitrogen vacancies where the N were not in nearby positions have been omitted.In particular, The formation of nitrogen vacancies was tested only on the (010) surface of Ta3N5 and the effect of cobalt dopant was examined by placing Co at two surface sites adjacent to the vacancy site (i.e. pos1 and pos2) and at two sub-surface sites (i.e. pos3 and pos4) shown in Fig. 3.
The single nitrogen vacancy formation (SVFE) energy in Ta3N5 is 2.89 eV, which is considerably higher than calculated for another active catalyst for ammonia synthesis, Co3Mo3N. There the SVFE was found to be 2.35 eV for five-coordinated nitrogen and 1.39 to 1.68 eV for three-coordinated nitrogen.1 Therefore the surface concentration of nitrogen vacancies will be less than on Co3Mo3N surfaces, which, however, maybe be compensated by nitrogen vacancies at sub-surface sites, which in Ta3N5 may become available to the reactants due to the structure which results in 4 Å wide channels along the [001] direction as shown in Fig. 1d. We find that in Ta3N5 single vacancies (SV) rather than adjacent double vacancies (DV) are more stable as shown by the higher VFE in Table 3 that show that the DVFE > SVFE per vacancy by an average of 0.37 eV except at pos3, where the SV were found to be less stable than the DV. For pos4 we observe that surface and sub-surface Co co-adsorbate at nearby positions can reduce the SVFE and DVFE for nitrogen by as much as 0.94 eV. It appears that the bonding of Co at adjacent sites destabilises somewhat the Ta–N bonds, which can be attributed to the electron withdrawing nature of Co in an attempt to fill its incomplete d-shell. Therefore the effect of these Co promoters on the pronounced reactivity of the Co-doped Ta3N5 could be attributed to the easier formation of nitrogen vacancies in a mechanism that involves activation of nitrogen at such sites. In addition, the results tabulated in Table 3 indicate that sub-surface co-adsorption of Co results in the greatest reduction of the SVFE on Ta3N5, an aspect that may guide synthetic efforts generating Ta3N5 materials that have a large density of nitrogen vacancies, for optoelectronic applications.
| SVFE (eV) | DVFE (eV) | |
|---|---|---|
| No-dop | 2.89 | 3.16 |
| pos1 | 2.52 | 2.66 |
| pos2 | 2.32 | 2.78 |
| pos3 | 2.72 | 2.38 |
| pos4 | 1.95 | 2.57 |
3.4 Effect of Co promoters on H2 chemisorption
We have further studied the adsorption of cobalt at various sites on the surface of Ta3N5 in order to understand its bonding and locate the energetically lowest doping sites. These results are tabulated in Table 4.We find that cobalt generally adsorbs more strongly when it is coordinated to surface nitrogen atoms rather than surface tantalum atoms, which can be clearly seen by the adsorption studies of Co atoms at the various symmetry unique adsorption sites of Ta3N5. We have studied the adsorption of Co at the sites shown in Fig. 1. Although the adsorption structure of Co at each site has its own distinct stereochemical structure, we observed a trend of the adsorption energy as a function of the number of nitrogen atoms with which cobalt is coordinated. In particular, we found that the weakest adsorption of cobalt occurs when it interacts with a single surface tantalum atom (100-site 3) where the adsorption energy is −151 kJ mol−1, which is more than 50 kJ mol−1 lower than the adsorption energy of Co when it interacts only with a nitrogen atom (010-site 1) which ranges between −200 to −266 kJ mol−1. The adsorption energy of Co with two surface nitrogen atoms is in the range of −301 to −376 kJ mol−1. Lastly the adsorption energy of Co with 3 or 4 surface nitrogen atoms is in the range −373 to −397 kJ mol−1. These results show that the attachment of Co to nitrogen is more energetically favourable and depends on the number of Co–N bonds formed. In particular we find that Co will adsorb more favourably at sites that are nitrogen rich and where the nitrogen can complex with cobalt in a square planar configuration where one ligand is missing (e.g. 010-site 8 and 010-site 5). The average Co–N bond length was found to be 1.86 Å in close agreement with the sum of the covalent radius of values N:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 pm and Co:
71 pm and Co:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 pm which is 1.96 Å.20 Based on the sphere-in-contact model this result suggests the formation of covalent bonds between nitrogen and cobalt.21 However, the electronic structure of Ta3N5 does not have any unpaired electrons on the surface nitrogen, which indicates when cobalt is co-adsorbed, these sites are re-hybridized into states with unpaired electrons, that can then form the covalent Co–N.
126 pm which is 1.96 Å.20 Based on the sphere-in-contact model this result suggests the formation of covalent bonds between nitrogen and cobalt.21 However, the electronic structure of Ta3N5 does not have any unpaired electrons on the surface nitrogen, which indicates when cobalt is co-adsorbed, these sites are re-hybridized into states with unpaired electrons, that can then form the covalent Co–N.
We next study how Co promoters affect the chemisorption of H2. Here we have again studied the adsorption of a single H2 molecule in a side-on configuration at each site depicted in Fig. 1.
The adsorption of H2 on Ta3N5 is mainly molecular with adsorption energies in a narrow range (i.e. −81 to −90 kJ mol−1) apart from one site on the (010)-surface which is shown by a white arrow in Fig. 4. At this site is chemisorbs dissociatively to form surface >NH species. Upon addition of cobalt to the surface of Ta3N5 at the various adsorption sites depicted in Fig. 1, we observe that the chemisorption of H2 changes drastically with more sites promoting the dissociation of molecular hydrogen in the form of atomically chemisorbed –H species. Based on the average length of the Co–H bond, we find that it is in close agreement with the sum of the covalent radius of Co and H and therefore indicates covalent bonding of H with cobalt. Additionally for every site the adsorption energy becomes more exothermic apart from two sites shown by the black arrows in Fig. 4, where the adsorption remains molecular. At both these sites Co is coordinated to 3 nitrogen atoms and therefore does not dissociatively chemisorb H2, but only adsorbs it in a side-on configuration. This result clearly suggests that co-adsorbed cobalt atoms on the various surfaces of Ta3N5 will promote the formation of –H species which could be active intermediates in the hydrogenation of surface nitrogen in surface reactions mechanism of the Langmuir–Hinshelwood type, where both –N and –H originates from surface adsorbates.
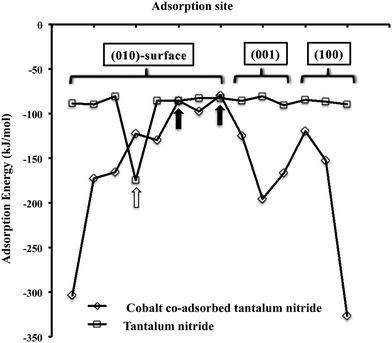 | ||
| Fig. 4 Graph showing the dispersion-corrected adsorption energy of H2 on plain and Co-doped Ta3N5-(001), (010) and (001) surfaces. | ||
4. Conclusions
In this periodic DFT study we studied systematically the adsorption of the reactants of ammonia synthesis (i.e. H2 and N2) on Ta3N5 and have found potential reaction intermediates relevant to the ammonia synthesis reaction and have explained the effect of Co promoters. The adsorption of nitrogen was found to be mostly molecular and non-activated with side-on, end-on and tilt configurations. At bridging nitrogen sites (Ta–N–Ta) it results in an azide functional group formation with a formation energy of 205 kJ mol−1. H2 was found to also chemisorb molecularly with an adsorption energy in the range −81 to −91 kJ mol−1. At bridging nitrogen sites it adsorbs dissociatively forming >NH groups with an exothermic formation energy of −175 kJ mol−1 per H2. Co-adsorption of cobalt was found to occur mostly at the nitrogen rich sites of the surface, with an adsorption energy that ranged between −200 to −400 kJ mol−1. We have shown how cobalt can lower the vacancy formation energy for nitrogen in Ta3N5 and become active centres for dissociative hydrogen chemisorption.Acknowledgements
This study was supported by EPSRC funding (EP/L026317/1, EP/L02537X/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202/1), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).References
- C. D. Zeinalipour-Yazdi, J. S. J. Hargreaves. and C. R. A. Catlow, J. Phys. Chem. C, 2015, 119, 28368 CAS.
- C. D. Zeinalipour-Yazdi, J. S. J. Hargreaves and C. R. A. Catlow, J. Phys. Chem. C, 2016, 120, 21390 CAS.
- J. Wang, A. Ma, Z. Li, J. Jiang, J. Feng and Z. Zou, Phys. Chem. Chem. Phys., 2015, 17, 23265 RSC.
- J. Wang, A. Ma, Z. Li, J. Jiang, J. Feng and Z. Zou, Phys. Chem. Chem. Phys., 2015, 17, 8166 RSC.
- J. Wang, A. Ma, Z. Li, J. Jiang, J. Feng and Z. Zou, Phys. Chem. Chem. Phys., 2016, 18, 7938 RSC.
- S. Laassiri, C. D. Zeinalipour-Yazdi, C. R. A. Catlow and J. S. J. Hargreaves, Catal. Today, 2017, 286, 147 CrossRef CAS.
- N. E. Brese, M. O'Keeffe, P. Rauch and F. J. DiSalvo, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 2291 CrossRef.
- S. J. Henderson and A. L. Hector, J. Solid State Chem., 2006, 179, 3518 CrossRef CAS.
- N. E. Brese, M. O'Keeffe, P. Rauch and F. J. DiSalvo, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 2291 CrossRef.
- J. Strähle, Z. Anorg. Allg. Chem., 1974, 402, 47 CrossRef.
- A. M. Alexander, J. S. J. Hargreaves and C. Mitchell, Top. Catal., 2012, 55, 1046 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and D. Jouber, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Matsumoto, S. I. Ooi, K. Nakatsuka, W. Mori, S. Suzuki, A. Nakahara and Y. Nakao, J. Chem. Soc., Dalton Trans., 1985, 2095 RSC.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
- C. D. Zeinalipour-Yazdi, D. P. Pullman and C. R. A. Catlow, J. Mol. Model., 2016, 22, 40 CrossRef PubMed.
| This journal is © the Owner Societies 2017 |