Separation of water–ethanol solutions with carbon nanotubes and electric fields

Abstract

Bioethanol has been used as an alternative energy source for transportation vehicles to reduce the use of fossil fuels. The separation of water–ethanol solutions from fermentation processes is still an important issue in the production of anhydrous ethanol. Using molecular dynamics simulations, we investigate the effect of axial electric fields on the separation of water–ethanol solutions with carbon nanotubes (CNTs). In the absence of an electric field, CNT–ethanol van der Waals interactions allow ethanol to fill the CNTs in preference to water, i.e., a separation effect for ethanol. However, as the CNT diameter increases, this ethanol separation effect significantly decreases owing to a decrease in the strength of the van der Waals interactions. In contrast, under an electric field, the energy of the electrostatic interactions within the water molecule structure induces water molecules to fill the CNTs in preference to ethanol, i.e., a separation effect for water. More importantly, the electrostatic interactions are dependent on the water molecule structure in the CNT instead of the CNT diameter. As a result, the separation effect observed under an electric field does not diminish over a wide CNT diameter range. Moreover, CNTs and electric fields can be used to separate methanol–ethanol solutions too. Under an electric field, methanol preferentially fills CNTs over ethanol in a wide CNT diameter range.

---

1 Introduction

In addition to its wide use in industrial processes, ethanol has been considered a potential energy resource to reduce the use of fossil fuels, such as fuels for engines.^1–4 The use of ethanol as an automobile engine fuel has significantly increased the production of bioethanol,^5–7 which is produced from various plants or biomass through ethanol fermentation processes.^8–11 To obtain a homogeneous ethanol–gasoline mixture, water must not be present in the ethanol, and hence nearly pure ethanol (≥99.5 vol%) or anhydrous ethanol is required.^12–14 However, the presence of water in the fermentation processes cannot be avoided. With simple distillation, the purity of the ethanol can only be increased to a maximum of 95 wt% owing to the azeotropic point. Further anhydrous ethanol enrichment can be achieved with azeotropic distillation or extractive distillation. Unfortunately, such distillation processes consume a large amount of energy, around 31% to 64% of the heating value of the anhydrous ethanol.¹³ Therefore, a more efficient method is urgently required. Although some alternative methods have been developed and applied, such as membrane pervaporation^15,16 and adsorption by zeolites,^17–19 water–ethanol separation still remains an important problem in anhydrous ethanol production.

The fact that carbon nanotubes (CNTs) can transport fluid^20–22 has inspired their potential application as membranes.²³ CNT membranes have been proposed for the separation of various substances, such as gas separation,^24,25 desalination,^26–28 gas–water separation,²⁹ water–methanol separation^31–34 and the separation of organic molecules from water.³⁰ Moreover, the study of CNT-based water–ethanol separation has attracted considerable attention.^33–36 Because the van der Waals interaction between CNTs and ethanol is stronger than that between CNTs and water, ethanol molecules preferentially fill CNTs over water molecules.^33–36 However, the preference of ethanol to occupy CNTs decreases significantly as the diameter of the CNTs increases.³⁶

A difference in ion concentration across a biological membrane can induce a strong electric field, which can measure from 0.06 to 0.3 V nm⁻¹.^37,38 The existence of such electric fields in biological membranes has led to an increased number of studies on water confined in nanoscale spaces under electric fields in recent years.^39–49 Beyond its importance in biological science, the effect of electric fields at the nanoscale is promising for nanotechnology-based applications, such as nano pumping^50–54 and water purification.⁵⁵ Under electric fields, water in CNTs assembles into a rich variety of structures.^43,45,46,56 Recently, we demonstrated that water structures induced by electric fields show potential for the separation of water–methanol solutions.³⁴

In this work, we demonstrate the water and ethanol separation effect of CNTs under electric fields for water–ethanol solutions using molecular dynamics (MD) simulations. Without the presence of an electric field, the van der Waals interactions between CNTs and ethanol causes ethanol to preferentially occupy CNTs over water, resulting in a separation effect. However, as the CNT diameter increases, the selectivity for ethanol significantly decreases owing to a decrease in the strength of the van der Waals interaction. In contrast, under an electric field, water preferentially fills the CNTs over ethanol, i.e., selectivity for water. The electrostatic interactions within the structure of the water molecules is an important factor in the separation effect under an electric field. Interestingly, the electrostatic interaction depends on the structure of the water molecules in the CNTs instead of the CNT diameter. As a result, under an electric field the strength of the separation effect does not significantly decrease with increasing CNT diameter. Furthermore, the separation of methanol–ethanol solutions is also possible. Under an electric field, methanol preferentially flows into CNTs over ethanol for a wide range of CNT diameters.

2 Method

The model system for the MD simulation was the same as that in our earlier studies,^34,56 which consisted of a 2.95 nm length of CNT embedded in two graphene sheets with reservoirs at each side. To demonstrate the separation effect, we used a wide range of CNT diameters, i.e., 0.81 nm, 0.95 nm, 1.08 nm, 1.22 nm, 1.36 nm, 1.63 nm, 2.03 nm, 2.71 nm, 3.39 nm, and 4.07 nm for (6,6), (7,7), (8,8), (9,9), (10,10), (12,12), (15,15), (20,20), (25,25), and (30,30) CNTs, respectively. The reservoirs were filled with water–ethanol mixtures with water mole fractions (χ_water) of 0.81 (the number of molecules in each reservoir was N_water = 4000 and N_ethanol = 964) and 0.19 (N_water = 964 and N_ethanol = 4000), equivalent to mass fractions of 61.9% and 8.6%, respectively. To clarify the separation effect, we also investigated the effect of an electric field on ethanol molecules. In these cases, (8,8) and (10,10) CNTs were used and the reservoirs were filled with ethanol molecules only. All components were placed in a rectangular box that was subjected to periodic boundary conditions in all directions (x, y, and z-axes).

The SPC⁵⁷ model was used for the water molecules and the OPLS united-atom^58,59 model was used for the ethanol molecules. It has previously been shown that the OPLS-UA model can well reproduce the properties of ethanol,⁶⁰ and it has been widely used for molecular dynamics studies.^19,35,61 In this model, each ethanol molecule is represented by four interaction sites, i.e., hydrogen atom (H), oxygen atom (O), methylene group (CH₂), and methyl group (CH₃). The Lennard-Jones (LJ) parameters and charges for each site are shown in Table 1. The LJ parameters used to obtain the interactions of different sites were calculated with the combination rule and . An electric field of up to 2 V nm⁻¹ was applied in the direction of the positive z-axis. It was assumed that the applied electric field does not influence the electron population of carbon atoms in the CNTs. The electric field was assumed uniform in the CNTs. It is noted here that the threshold at which an electric field induces the dissociation of water molecules is 3.5 V nm⁻¹.⁶²

Table 1 The Lennard-Jones parameters and charges for water, ethanol, and carbon nanotubes

Site	σ [nm]	ε [kJ mol^−1]	q [e]
Water, SPC model
O	0.3166	0.6500	−0.820
H	0	0	0.410
Ethanol, OPLS-UA model
CH3	0.3775	0.8661	0
CH2	0.3905	0.4937	0.265
O	0.3070	0.7113	−0.700
H	0	0	0.435
Carbon nanotubes
C	0.3400	0.3612	0

---

The simulations were performed using GROMACS 4.5.5 software.⁶³ The van der Waals interactions were cut off at 1.5 nm, and the electrostatic interactions were treated using the particle mesh Ewald (PME) method⁶⁴ with the real space cut off also set to 1.5 nm. The length of the chemical bonds of the water and ethanol molecules and the angles between them were kept constant with the SHAKE algorithm.⁶⁵ Torsional motion about the C–O bond was the only intramolecular dynamics considered in the simulation. The CNTs and graphene were made rigid by keeping the length and angle of the chemical bonds constant. The simulation was performed with NL_xL_yP_zT, and the temperature (T) was kept at 300 K with the Nosé–Hoover coupling scheme.^66,67 The pressure in the axial direction (z-axis) was maintained at 0.1 MPa using the Parrinello–Rahman technique.⁶⁸ The time step was set to 2 fs and the simulations were performed for production runs of around 10 ns.

3 Results and discussion

The simulation results are presented in the following order. First, the results of the separation effect for water–ethanol solutions are discussed. Then, we clarify the separation effect from two viewpoints, i.e., by comparing the molecular structures and potential energies of ethanol and water. Finally, the separation effect for a methanol–ethanol solution is also discussed.

3.1 Separation effect for water–ethanol solutions

The separation effect was investigated by filling the reservoirs with mixtures of water–ethanol molecules. The same as in our previous study on water–methanol mixtures,³⁴ the separation effect was obtained by calculating the mole fractions in the CNTs and comparing them with those in the reservoirs, as shown in Fig. 1. At 0 V nm⁻¹, χ_water in the CNTs is lower (or χ_ethanol in the CNTs is higher) than both χ_water = 0.81 and 0.19 (black dotted-lines) in the reservoirs, as shown in Fig. 1A and B, respectively. Without an electric field, ethanol molecules preferentially fill the CNTs over water molecules. This preference produces a separation effect for ethanol. The separation effect is strong for small CNT diameters, but significantly decreases with increasing CNT diameter when no electric field is present. A similar trend was also confirmed in a previous study on the separation of water–ethanol solutions.³⁶

Fig. 1 Mole fraction of water molecules χ_water (or ethanol molecules χ_ethanol) in (6,6) to (30,30) CNTs under various electric fields. The black dotted lines show the mole fraction in the reservoir, i.e., (A) χ_water = 0.81, and (B) χ_water = 0.19. The error bars represent the standard deviation.

In contrast, in the presence of an electric field, χ_water in the CNTs is higher than that in the reservoirs. At 1 and 2 V nm⁻¹, χ_water = 1.0 in all of the CNTs, i.e., only water occupies the CNTs (Fig. 1A). At 0.5 V nm⁻¹, χ_water = 1.0 in all of the CNTs, except for the (6,6) CNT. Even when χ_water in the reservoirs is very low, χ_water in the (6,6) to (15,15) CNTs is 1.0 at 2 V nm⁻¹. This decreases to 0.82, 0.95, and 0.77 in the (20,20), (25,25), and (30,30) CNTs, respectively (Fig. 1B). Under an electric field, water molecules preferentially fill CNTs over ethanol molecules, resulting in a separation effect for water. Interestingly, this separation effect under an electric field is stronger than that without the presence of an electric field and does not significantly decrease as the CNT diameter increases.

The dependency of the mole fractions of water and ethanol in the CNTs on the strength of the electric field is shown in Fig. 2. χ_water in the CNTs increases with the strength of the electric field E. It is obvious that the effect of E ≤ 0.5 V nm⁻¹ on the separation effect with the (6,6) CNT is weaker than that with larger CNTs. As explained in the following paragraph, the structure of water molecules in the CNTs plays an important role in the separation effect under an electric field. Water molecules in the (6,6) CNT have a single file structure.^20,69,70 This changes to a zig-zag structure under E ≥ 0.5 V nm⁻¹,³⁴i.e., a more stable structure.

Fig. 2 Dependency of χ_water (or χ_ethanol) on electric field strength E in (6,6) to (30,30) CNTs. The mole fraction in the reservoirs are: (A) χ_water = 0.81 (black dotted-line), and (B) χ_water = 0.19 (black dotted-line).

Fig. 3 shows snapshots of the molecular structures in an (8,8) CNT for χ_water = 0.19 in the reservoirs. At 0 V nm⁻¹, only ethanol molecules appear in the snapshot. Very few water molecules appear in the (8,8) CNT under these conditions (Fig. 1). At 0.25 V nm⁻¹, the number of water molecules in the CNT increases as seen in the snapshot. At E ≥ 0.5 V nm⁻¹, only water molecules fill the CNT, and they form ordered (helical) structures. These ice-nanotube structures are induced by the electric field.^43,45,46,56 The formation of this ordered structure makes water more stable than ethanol in the CNT. As a result, the CNT prefers to adsorb water instead of ethanol. Under the electric field, the water structure in the CNT becomes more stable owing to electrostatic interaction within the structure, as shown in the next section. We also performed simulations with a TIP4P water model, (8,8) CNT and χ_water = 0.19 in the reservoirs to clarify the dependency of the separation effect on the water model. At E ≥ 0.5 V nm⁻¹, only water molecules occupy the CNT (see Table S1 in ESI†). Moreover, the water molecules form helical structures in the CNT as well (Fig. S1, ESI†). This result suggests that the separation effect with an electric field shows little dependence on the water model.

Fig. 3 Structures of molecules in the (8,8) CNT under E = 0, 0.25, 0.5, and 2 V nm⁻¹ for χ_water = 0.19 in the reservoir. Green, yellow, pink, and blue spheres represent the hydrogen, oxygen, methylene, and methyl of the ethanol molecules, respectively. Red and white spheres represent the oxygen and hydrogen of the water molecules, respectively. At E ≥ 0.5 V nm⁻¹, only water molecules occupy the CNT and they form a helical structure.

The effect of an electric field on the separation of water–ethanol solutions as presented in Fig. 1 to 3 is similar to that for water–methanol solutions.³⁴ With an electric field, χ_water is obviously higher in the (25,25) CNT than in (20,20) and (30,30) CNTs (Fig. 1). The same trend is also observed for the separation of water–methanol solutions.³⁴ This suggests that the water structure in the (25,25) CNT is more stable than that in the (20,20) CNT. Moreover, it implies that the separation effect with the electric field is more dependent on this molecular structure than on the CNT diameter. We analyzed hydrogen bond (HB) auto correlation functions of the water structures in (20,20), (25,25) and (30,30) CNTs to clarify the HB dynamics in the structures (see Fig. S2 and S3 in ESI†). As shown in Fig. S3 (ESI†), the lifetime of the HBs in the water structure in the (25,25) CNT is longer than that in the (20,20) and (30,30) CNTs. This indicates that the water structure in the (25,25) CNT is stronger than that in the (20,20) and (30,30) CNTs.

To clarify the separation mechanism, we investigated the effect of electric fields on ethanol by filling the reservoirs with only ethanol molecules. The average number of ethanol molecules occupying the (8,8) and (10,10) CNTs are shown in Table 2. The occupancy of ethanol in the CNTs tends to increase with electric field strength. The electric field does not decrease the number of ethanol molecules in the CNTs. As with water molecules,^34,56 the electric field facilitates the filling of the CNTs with ethanol molecules. The mechanism of this separation effect can be explained by comparing the structure and potential energy of ethanol with those of water as follows.

Table 2 The average number of ethanol molecules in the CNTs and the standard deviation

E [V nm^−1]	(8,8) CNT	(10,10) CNT
0	12.0 ± 0.6	22.4 ± 1.0
1	12.8 ± 0.5	23.9 ± 0.8
2	12.8 ± 0.6	23.6 ± 0.8

---

3.2 Orientations and structures of molecules in CNTs

The direct effect of applying an electric field to ethanol is a change in dipole moment orientation. This is caused by the action of the forces induced by the electric field on the positive charges of hydrogen (H) and methylene (CH₂) and on the negative charge of oxygen (O). These forces produce a moment that aligns the direction of the dipole moment parallel to that of the electric field. Fig. 4 shows the direction of the dipole moment of the ethanol molecules in the (8,8) and (10,10) CNTs under electric fields of 0, 1, and 2 V nm⁻¹. The direction of the dipole moment is indicated by the angle α between the dipole vector μ and the electric field E. At 0 V nm⁻¹, the dipole moment of ethanol in the (8,8) CNT has a particular orientation of cos α = −0.9. This differs from the dipole moment of the water molecules, which have two opposing orientations of cos α = −0.8 and 0.8,⁵⁶ in the (8,8) CNT. It seems that molecular size is the origin of the different dipole orientations of ethanol and water. At 0 V nm⁻¹ in the larger (10,10) CNT, the dipole moment orients in all directions with two small-peaks at cos α = −0.9 and 0.9, which are similar to those of the water molecules. At 1 and 2 V nm⁻¹, the direction of the dipole moment of ethanol in the (8,8) and (10,10) CNTs is parallel to the electric field E, which is the same as the direction of the dipole moment of the water molecules under the electric field.

Fig. 4 Orientation of the dipole moment of ethanol molecules in (8,8) and (10,10) CNTs. The direction of the dipole moment is indicated by angle α, which is the angle between the dipole moment μ and the electric field E. O, H, and CH₂ represent the oxygen, hydrogen, and methylene of ethanol, respectively. The vertical axis shows the probability distribution function (PDF).

Distribution of the dihedral angle associated with the torsional motion of the O–C bond is shown in Fig. 5. The central peak at α = 180° and the two mirror-image peaks at α = 72° and 288° (black curve) arise from ethanol in the reservoirs. The central peak corresponds to the trans conformer, while the other two peaks correspond to the gauche conformer. The fraction of each conformer was obtained by integrating the distribution curves from 0° to 120° and from 240° to 360° for the gauche conformer, and from 120° to 240° for the trans conformer. At 0 V nm⁻¹, the population of trans conformer in the reservoirs is 50%. This is in very good agreement with that of bulk ethanol at 298 K.^59,60 The population of trans conformer in the reservoirs increases slightly to 51% and 52% at 1 and 2 V nm⁻¹, respectively.

Fig. 5 Distribution of the dihedral angle of ethanol molecules in the (8,8) CNT (top) and the (10,10) CNT (bottom) at 0, 1, and 2 V nm⁻¹. The black curve (Res.) shows the distribution of ethanol in the reservoirs at 0 V nm⁻¹. The inset orthographic projection snapshots show the structure of ethanol in the (8,8) CNT at 2 V nm⁻¹ (top) and in the (10,10) CNT at 0 and 2 V nm⁻¹ (bottom).

In the (8,8) CNT, ethanol tends to form the gauche conformer, which is different from the dihedral angle distribution in the reservoirs. The proportion of gauche conformer is 82%, 85%, and 81% at 0, 1, and 2 V nm⁻¹, respectively. The snapshot in Fig. 5 (top) shows an orthographic projection of the ethanol molecule structure in the (8,8) CNT at 2 V nm⁻¹. The ethanol molecules form a semicircular structure with their hydrogen bond between the hydrogen (green) and the oxygen (yellow) atoms at the middle. The ethanol molecules form the gauche conformer to follow the contour of the CNT wall. The ethanol molecules in the (8,8) CNT have similar structures at 0 and 1 V nm⁻¹. The ethanol molecule structures in the CNTs are shown in more detail in Fig. 6 (discussed in the next section). In the larger diameter (10,10) CNT at 0 V nm⁻¹, the distribution of the dihedral angle becomes similar to that in the reservoirs, i.e., 49% trans conformer. As shown by the snapshot in Fig. 5 (bottom), at 0 V nm⁻¹ the ethanol structure is disordered. At 1 or 2 V nm⁻¹, ethanol forms two structures in the (10,10) CNT, each of which is similar to that in the (8,8) CNT. However, the ethanol molecules tend to form the trans conformer instead of the gauche conformer seen in the (8,8) CNT. At 1 and 2 V nm⁻¹, the proportion of trans conformer in the (10,10) CNT is 67%. Thus, the CNT diameter could be an important factor affecting the dihedral angle.

Fig. 6 Snapshots of ethanol molecules in CNTs. (A) Perspective projection in the (8,8) CNT at 2 V nm⁻¹ (left) and in the (10,10) CNT at 2 V nm⁻¹ (right). (B) Two-dimensional structures at 2 V nm⁻¹ in the (8,8) CNT (left) and in the (10,10) CNT (right). Green, yellow, pink, and blue represent hydrogen, oxygen, methylene, and methyl, respectively.

The structures of ethanol molecules in the CNTs are shown in perspective projection and two-dimensions (2D) in Fig. 6A and B, respectively. The radial positions of oxygen atoms in the CNTs were averaged to determine the radius of each tube. Then, all atoms of the ethanol molecules were radially projected on the tube wall. Finally, the tube wall was opened to obtain the 2D structures. In the (8,8) CNT at 2 V nm⁻¹, ethanol forms a single line structure as shown in Fig. 6A (left) and B (left). In the (10,10) CNT at 2 V nm⁻¹, ethanol forms two parallel structures as shown in Fig. 6A (right) and B (right).

We employed geometrical criteria to analyze the hydrogen bonds (HBs). A pair of ethanol molecules were considered to have HBs if they fulfilled the following three conditions: R_OO < 0.35 nm, R_OH < 0.26 nm, and angle of HO⋯O < 30°.⁶⁰R_OO and R_OH denote oxygen–oxygen and oxygen–hydrogen distances, respectively. The average numbers of HBs per molecule in the (8,8) CNT are 1.90, 1.85, and 1.79 at 0, 1, and 2 V nm⁻¹, respectively. The average numbers of HBs per molecule in the (10,10) CNT are 1.85, 1.91, and 1.87 at 0, 1, and 2 V nm⁻¹, respectively. The electric field does not significantly increase the number of HBs. However, HBs under an electric field are stronger than those without an electric field. As shown in the next section, the Coulomb potential energy per molecule in the presence of an electric field is lower than that without an electric field. This indicates that the electric field strengthens the electrostatic interaction within the ethanol molecule structure.

Ethanol forms a HB network only with oxygen and hydrogen atoms, and methyl and methylene groups cannot contribute to the HB network. As seen in the (10,10) CNT in Fig. 6B (right), methyl groups from each structure are close to each other. This causes the formation of two parallel structures that have no outward-facing HBs. Bulk ethanol shows a similar linear chain HB structure.⁶⁰ Water molecules can form a HB bond network with their all atoms. Therefore, the number of HBs per water molecule is higher than that for ethanol, i.e., 2.84, 2.93, and 2.77 in the (8,8) CNT at 0, 1, and 2 V nm⁻¹, respectively.³⁴ This makes the electrostatic interaction within the water structure stronger than that within the ethanol structure. In other words, water structures in CNTs under an electric field are more stable than those of ethanol.

3.3 Potential energies

3.3.1 Lennard-Jones potential energy. To investigate the interaction between the CNT and ethanol molecules, we calculated the Lennard-Jones (LJ) potential energy of ethanol in the reservoirs and in the CNT. The distribution of the LJ potential energy at 0 and 2 V nm⁻¹ is shown in Fig. 7. The difference between the LJ potential energy in the CNT and in the reservoirs, ΔU_LJ = U_LJ,CNT − U_LJ,Res, indicates the van der Waals interaction between the CNT and ethanol molecules. At 0 V nm⁻¹, the average LJ potential in the reservoirs and in the (8,8) CNT is −22.79 kJ mol⁻¹ and −43.03 kJ mol⁻¹, respectively (Table 3). This means that ΔU_LJ = −20.24 kJ mol⁻¹. The negative value of ΔU_LJ indicates an attractive CNT–ethanol interaction. At 2 V nm⁻¹, ΔU_LJ slightly increases to −19.34 kJ mol⁻¹. Thus, the electric field does not significantly change the CNT–ethanol van der Waals interaction.

Fig. 7 Distribution of the Lennard-Jones (LJ) potential energy of ethanol molecules in reservoirs and in CNTs at 0 and 2 V nm⁻¹. The LJ potential energy in the CNTs is lower than that in the reservoirs, denoting an attractive van der Waals interaction between the CNTs and ethanol. This attractive interaction decreases with increasing CNT diameter, as shown by the higher distribution for the (10,10) CNT compared with that for the (8,8) CNT.

Table 3 Average potential energies per molecule for ethanol in reservoirs (Res.) and in the (8,8) CNT. ΔU is the difference between the potential energy in the CNT (U_CNT) and the reservoirs (U_Res), ΔU = U_CNT − U_Res. The 6th column shows ΔU for the (10,10) CNT

E [V nm^−1]	Energy (U)	In Res. [kJ mol^−1]	In CNT [kJ mol^−1]	ΔU [kJ mol^−1]	ΔU10,10 [kJ mol^−1]
0	LJ	−22.79	−43.03	−20.24	−16.69
	Coulomb	−58.89	−60.80	−1.91	2.18
			Total:	−22.15	−14.51
2	LJ	−24.25	−43.59	−19.34	−15.48
	Coulomb	−61.68	−73.21	−11.53	−12.10
	Dipole	−7.07	−8.29	−1.22	−1.24
			Total:	−32.09	−28.82

---

The ΔU_LJ for water in the (8,8) CNT at 0 V nm⁻¹ is −10.37 kJ mol⁻¹,³⁴ which is higher than that for ethanol. This means that the CNT–ethanol interaction is stronger than the CNT–water interaction. Moreover, this implies that the CNT–ethanol van der Waals interaction facilitates the filling of the CNT with ethanol in preference to water (Fig. 1). At 2 V nm⁻¹, ΔU_LJ for water becomes positive, 6.29 kJ mol⁻¹. This indicates a repulsive CNT–water interaction. Thus, in the presence of the electric field, the CNT–water van der Waals interaction does not contribute to the preferential filling of CNTs by water (Fig. 1). This repulsive interaction supports the previous result that an ice-nanotube structure induced by an electric field can flow through a CNT.⁵⁶

The ΔU_LJ for the (10,10) CNT is shown in the 6th column of Table 3, i.e., −16.69 and −15.48 kJ mol⁻¹ at 0 and 2 V nm⁻¹, respectively. This higher ΔU_LJ in the (10,10) CNT, compared to that in the (8,8) CNT, implies that the strength of the attractive CNT–ethanol interaction decreases with increasing CNT diameter. Fig. 7 confirms this result; the distribution of U_LJ for the (10,10) CNT is shifted to a higher energy compared with that for the (8,8) CNT.

3.3.2 Coulomb potential energy. Fig. 8 shows the distribution of the Coulomb potential energy of ethanol in the reservoirs and CNTs. At 0 V nm⁻¹, there is no significant difference between the potential energy in the reservoirs and in the CNTs. For the (8,8) CNT, the average potential energies are −58.89 kJ mol⁻¹ in the reservoirs and −60.80 kJ mol⁻¹ in the CNT (Table 3). At 2 V nm⁻¹, the Coulomb potential energy decreases from −61.68 kJ mol⁻¹ in the reservoirs to −73.21 kJ mol⁻¹ in the (8,8) CNT. The electric field makes the electrostatic interactions within the ethanol molecule structure in the CNT stronger than that in the reservoirs. ΔU_coulomb decreases from −1.91 kJ mol⁻¹ to −11.53 kJ mol⁻¹ at 0 and 2 V nm⁻¹, respectively. This means that under an electric field the Coulomb potential energy drives the ethanol molecules to fill the CNT. ΔU_coulomb does not increase with CNT diameter, i.e., −12.10 kJ mol⁻¹ in the (10,10) CNT at 2 V nm⁻¹. Unlike the van der Waals interaction, the electrostatic interaction in the molecule structure in the CNTs under an electric field does not decrease with increasing CNT diameter. Fig. 8 shows that the distribution of U_coulomb for the (10,10) CNT is not shifted to higher energy compared with that of the (8,8) CNT.

Fig. 8 Distribution of Coulomb potential energy of ethanol molecules in reservoirs and in CNTs at 0 and 2 V nm⁻¹. Under an electric field, the potential energy in the CNTs is lower than that in the reservoirs. The electric field strengthens the electrostatic interactions within the ethanol molecule structure in the CNTs.

The ΔU_coulomb for water at 0 and 2 V nm⁻¹ are 12.13 and −31.55 kJ mol⁻¹, respectively.³⁴ Without an electric field, the Coulomb potential energy does not act as a driving energy for water to fill the CNT. Conversely, with an electric field, the Coulomb potential energy is the main factor facilitating water to fill the CNT. At 2 V nm⁻¹ in the larger (10,10) CNT, ΔU_coulomb decreases to −35.1 kJ mol⁻¹. This supports the notion that the electrostatic interaction between molecules in CNTs under electric fields does not decrease with increasing CNT diameter. The Coulomb potential energy per molecule for water in the (8,8) CNT at 2 V nm⁻¹ is −129.01 kJ mol⁻¹, which is much lower than that for ethanol. This clarifies that the electrostatic interaction in the water structure is stronger than that in the ethanol structure.

3.3.3 Dipole potential energy. When a dipole moment is subjected to an external electric field, it has a dipole potential energy as follows

U_dipole = −μ·E (1)

where μ is the vector of the dipole moment and E is the electric field. The potential energy becomes a minimum if the direction of the dipole moment is parallel to that of the electric field. However, under an electric field, the direction of the dipole moment is not statically parallel to the electric field but oscillates around it. The presence of graphene sheets causes polarization in the reservoirs. This polarization induces an internal electric field in the direction opposite to the external electric field.⁵⁶ As a result, the effective electric field in the reservoir becomes lower than that in the CNT. This makes the amplitude of the dipole oscillation in the reservoir larger than that in the CNT. Consequently, the distribution of the dipole potential in the reservoirs is broader (see Fig. 9), and the average dipole potential in the reservoirs is slightly higher than that in the CNT (Table 3). ΔU_dipole for the (8,8) and (10,10) CNTs are −1.22 kJ mol⁻¹ and −1.24 kJ mol⁻¹, respectively. The diameter of the CNT does not significantly influence ΔU_dipole. The ΔU_dipole for water is slightly lower, −5.06 kJ mol⁻¹. This is because the dipole moment of water is higher than that of ethanol, i.e., 2.27 D and 2.22 D, respectively. Thus, the polarization effect is stronger for water and the effective electric field in the reservoirs becomes lower. As a result, the amplitude of the rotational motion of water molecules in the reservoirs is larger, and hence the distribution of the dipole potential is broader.

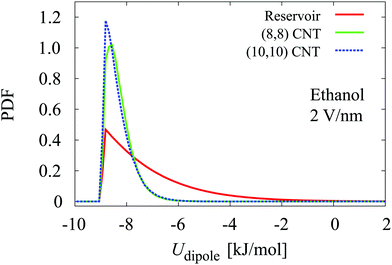Fig. 9 Distribution of the dipole potential energy for ethanol molecules in reservoirs and in CNTs at 2 V nm⁻¹.

The ΔU_total per molecule decreases under an electric field, from −22.15 to −32.09 kJ mol⁻¹ in the (8,8) CNT and from −14.51 to −28.82 kJ mol⁻¹ in the (10,10) CNT at 0 and 2 V nm⁻¹, respectively. A decrease in ΔU_total denotes that the electric field causes ethanol molecules to preferentially fill the CNTs. This agrees with the occupancy data, which indicates that the presence of an electric field increases the number of ethanol molecules in CNTs (Table 2).

3.3.4 The sum of the potential energies. To clarify the separation effect, we calculated ΔU_system, which is defined as the ΔU_total per molecule given in Table 3 multiplied by the number of all molecules in the CNT (Table 2). The results are compared with the ΔU_system of water and methanol³⁴ in Table 4 and displayed in Fig. 10. At 0 V nm⁻¹, the ΔU_system of ethanol is lower than that of water, i.e., −265.80 and 63.18 kJ mol⁻¹, respectively. This explains why ethanol preferentially fills CNTs over water (Fig. 1). The LJ potential energy or the interaction between the CNT and ethanol is the dominant factor determining the ΔU_system of ethanol (Table 3). ΔU_LJ increases with CNT diameter, hence without an electric field the separation effect significantly decreases with increasing CNT diameter.

Table 4 ΔU_system for the (8,8) CNT and reservoirs filled with water molecules (CNT–water system), methanol molecules (CNT–methanol system), and ethanol molecules (CNT–ethanol system). ΔU_system is defined as the ΔU_total per molecule multiplied by the number of molecules occupying the (8,8) CNT

E [V nm^−1]	Molecule	ΔUtotal [kJ mol^−1]^a	Occupancy in CNT^b	ΔUsystem [kJ mol^−1]
a Those for water and methanol were taken from ref. 34. b That for water was taken from ref. 56 and methanol from ref. 34.
0	Water	1.76	35.9	63.18
	Methanol	−10.72	16.7	−179.02
	Ethanol	−22.15	12.0	−265.80
0.5	Water	−11.60	40.6	−470.96
	Methanol	−24.71	19.6	−484.32
	Ethanol	−30.37	12.6	−382.66
1	Water	−20.68	47.7	−986.44
	Methanol	−29.58	19.7	−582.73
	Ethanol	−32.92	12.8	−421.38
2	Water	−30.32	49.6	−1503.87
	Methanol	−32.14	19.3	−620.30
	Ethanol	−32.09	12.8	−410.75

---

Fig. 10 Comparison of ΔU_system for water (CNT–water system), methanol (CNT–methanol system), and ethanol (CNT–ethanol system) in the (8,8) CNT. Under an electric field, ΔU_system of water is lower than that of methanol and ethanol. This suggests that water fills the CNT in preference to methanol and ethanol.

The ΔU_system of water tends to be lower than that of ethanol and methanol in the presence of an electric field. At 1 V nm⁻¹ and 2 V nm⁻¹, the ΔU_system of water is much lower than that of both ethanol and methanol (Table 4). This causes water to strongly preferentially fill CNTs over both ethanol (Fig. 1) and methanol.³⁴ Under an electric field, the Coulomb potential energy or the electrostatic interaction within the water molecule structure is the main factor that determines its ΔU_system. The electrostatic interaction does not become weaker with increasing the CNT diameter. As a result, the separation effect under an electric field does not decrease over a wide range of CNT diameters.

Actually, at 0.5, 1, and 2 V nm⁻¹, the ΔU_total per molecule for ethanol is lower than that for water owing to the contribution of ΔU_LJ and ΔU_coulomb. However, because the occupancy of water molecules in the CNT is much higher than that of ethanol molecules, the ΔU_system for water is much lower. More water molecules can occupy a CNT than ethanol molecules because water molecules are smaller than ethanol molecules. Another reason is that water molecules can form a hydrogen bond network with all of their atoms. This makes the structure of water molecules in the CNT more compact and so it can contain more molecules. This result suggests that water can be effectively separated from other longer alcohol molecules such as propanol and butanol using an electric field and CNTs.

3.4 Separation of methanol–ethanol solution with CNTs and electric fields

There is a significant difference between the ΔU_system of ethanol and methanol both with and without the presence of an electric field (see Fig. 10). It is thus expected that the separation of a methanol–ethanol solution can be achieved using CNTs both with and without an electric field. To examine the separation effect for methanol–ethanol solutions, we carried out simulations by filling the reservoirs with a mixture of methanol and ethanol molecules in which the mole fraction of methanol (or ethanol) is 50%. The CNT diameter was varied from 0.95 nm to 4.07 nm, corresponding to (7,7) and (30,30) CNTs, respectively.

Fig. 11 shows the separation effect for a methanol–ethanol solution with and without the presence of an electric field. At 0 V nm⁻¹, χ_ethanol in the CNTs is larger than that in the reservoirs. Without an electric field, ethanol molecules preferentially fill the CNTs over methanol, resulting in a separation effect for ethanol. This result confirms the results shown in Fig. 10 in which the ΔU_system for ethanol is lower than that for methanol. At 0 V nm⁻¹, the ethanol–CNT van der Waals interaction is the main factor determining the separation effect. However, the strength of this interaction significantly decreases with increasing CNT diameter. As a result, the separation effect decreases with increasing CNT diameter (Fig. 11).

Fig. 11 Mole fraction of methanol molecules χ_methanol (or ethanol molecules χ_ethanol) in (7,7) to (30,30) CNTs under 0, 0.5, 1, and 2 V nm⁻¹ electric fields. The black dotted lines indicate the mole fraction in the reservoir (res.), i.e., χ_methanol = χ_ethanol = 0.5. The error bars show the standard deviation.

In contrast, under 0.5, 1, and 2 V nm⁻¹ electric fields, χ_methanol in the CNTs is larger than that in the reservoirs (Fig. 11). This indicates that methanol preferentially flows into the CNTs over ethanol, producing a separation effect for methanol. This confirms the results also shown in Fig. 10 where the ΔU_system of methanol is lower than that of ethanol. The electrostatic interaction within the methanol molecule structure determines the separation effect under an electric field. The interaction depends on the molecule structure instead of the CNT diameter. As a result, the separation effect under an electric field is strong over a wide range of CNT diameters.

Under an electric field, the ΔU_total per molecule for ethanol and methanol is not significantly different (Table 4). However, the difference in occupancy, which arises from the difference in molecular size, means that the ΔU_system of methanol is significantly lower than that of ethanol. This suggests that CNTs and electric fields can be used to separate one type of alcohol from another based their molecular size.

4 Conclusions

We demonstrate the effect of axial electric fields on the separation of water–ethanol solutions using CNTs. Without an electric field, CNTs prefer to adsorb ethanol over water, producing a separation effect for ethanol. The CNT–ethanol van der Waals interaction is an important factor that determines the separation effect without the presence of an electric field. However, as CNT diameter increases, the strength of this separation effect decreases significantly owing to the decrease in the strength of the van der Waals interaction. In contrast, under an electric field, water fills CNTs in preference to ethanol, resulting in a separation effect for water. The electrostatic interactions within the water molecule structure play an important role in the separation under an electric field. The electric field aligns and induces the formation of ordered structures of water molecules in the CNTs. The formation of the ordered structures strengthens the electrostatic interactions or hydrogen bonds within the structures. The electrostatic interactions are more dependent on the water structure in the CNT than on the CNT diameter. As a result, the strength of the separation effect under an electric field does not significantly decrease with increasing CNT diameter.

CNTs under electric fields are also able to separate methanol–ethanol solutions. In the presence of an electric field, methanol preferentially occupies CNTs over ethanol, resulting in a separation effect. The electrostatic interaction between methanol molecules in the CNTs is an important factor in the separation effect under an electric field. The interaction depends on the molecule structures in the CNT instead of CNT diameter, hence the separation of a methanol–ethanol solution under an electric field does not significantly decrease with CNT diameter.

Acknowledgements

This work was supported by JSPS KAKENHI [Grant-in-Aid for Challenging Exploratory Research] Grant No. 25630070 and Core Research for Evolutionary Science and Technology (CREST) of the Japan Science and Technology Agency. EY was funded by a MEXT Grant-in-Aid from the “Program for Leading Graduate Schools”.

References

1. L. R. Lynd, J. H. Cushman, R. J. Nichols and C. E. Wyman, Science, 1991, 251, 1318–1323.
2. A. E. Farrell, R. J. Plevin, B. T. Turner, A. D. Jones, M. O'hare and D. M. Kammen, Science, 2006, 311, 506–508.
3. J. Goldemberg, Science, 2007, 315, 808–810.
4. K. Kohse-Höinghaus, P. Oßwald, T. A. Cool, T. Kasper, N. Hansen, F. Qi, C. K. Westbrook and P. R. Westmoreland, Angew. Chem., Int. Ed., 2010, 49, 3572–3597.
5. O. J. Sanchez and C. A. Cardona, Bioresour. Technol., 2008, 99, 5270–5295.
6. M. Balat and H. Balat, Appl. Energy, 2009, 86, 2273–2282.
7. A. Gupta and J. P. Verma, Renewable Sustainable Energy Rev., 2015, 41, 550–567.
8. I. Gelfand, R. Sahajpal, X. Zhang, R. C. Izaurralde, K. L. Gross and G. P. Robertson, Nature, 2013, 493, 514–517.
9. H. Chen, D. Zhou, G. Luo, S. Zhang and J. Chen, Renewable Sustainable Energy Rev., 2015, 47, 427–437.
10. R. L. Costa, T. V. Oliveira, J. de Souza Ferreira, V. L. Cardoso and F. R. X. Batista, Bioresour. Technol., 2015, 181, 330–337.
11. M. Wang, X. Pan, X. Xia, B. Xi and L. Wang, Bioresour. Technol., 2015, 187, 113–119.
12. F. Yüksel and B. Yüksel, Renewable Energy, 2004, 29, 1181–1191.
13. S. Kumar, N. Singh and R. Prasad, Renewable Sustainable Energy Rev., 2010, 14, 1830–1844.
14. A. Kyriakides, V. Dimas, E. Lymperopoulou, D. Karonis and E. Lois, Fuel, 2013, 108, 208–215.
15. X. Feng and R. Y. Huang, Ind. Eng. Chem. Res., 1997, 36, 1048–1066.
16. L. M. Vane, J. Chem. Technol. Biotechnol., 2005, 80, 603–629.
17. J. Z. Yang, Q. L. Liu and H. T. Wang, J. Membr. Sci., 2007, 291, 1–9.
18. M. Simo, S. Sivashanmugam, C. J. Brown and V. Hlavacek, Ind. Eng. Chem. Res., 2009, 48, 9247–9260.
19. A. Phan, D. R. Cole and A. Striolo, Langmuir, 2014, 30, 8066–8077.
20. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190.
21. M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Nature, 2005, 438, 44.
22. J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037.
23. B. J. Hinds, N. Chopra, T. Rantell, R. Andrews, V. Gavalas and L. G. Bachas, Science, 2004, 303, 62–65.
24. G. Arora and S. I. Sandler, Nano Lett., 2007, 7, 565–569.
25. G. Arora and S. I. Sandler, J. Chem. Phys., 2006, 124, 084702.
26. W.-F. Chan, H.-y. Chen, A. Surapathi, M. G. Taylor, X. Shao, E. Marand and J. K. Johnson, ACS Nano, 2013, 7, 5308–5319.
27. B. Corry, Energy Environ. Sci., 2011, 4, 751–759.
28. A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180.
29. J. Lee and N. Aluru, Appl. Phys. Lett., 2010, 96, 133108.
30. O. Sae-Khow and S. Mitra, J. Phys. Chem. C, 2010, 114, 16351–16356.
31. J. Zheng, E. M. Lennon, H.-K. Tsao, Y.-J. Sheng and S. Jiang, J. Chem. Phys., 2005, 122, 214702.
32. W.-H. Zhao, B. Shang, S.-P. Du, L.-F. Yuan, J. Yang and X. C. Zeng, J. Chem. Phys., 2012, 137, 034501.
33. X. Tian, Z. Yang, B. Zhou, P. Xiu and Y. Tu, J. Chem. Phys., 2013, 138, 204711.
34. Winarto, D. Takaiwa, E. Yamamoto and K. Yasuoka, Nanoscale, 2015, 7, 12659–12665.
35. L. Lu, Q. Shao, L. Huang and X. Lu, Fluid Phase Equilib., 2007, 261, 191–198.
36. S.-p. Du, W.-h. Zhao and L.-f. Yuan, Chin. J. Chem. Phys., 2012, 25, 487.
37. A. Philippsen, W. Im, A. Engel, T. Schirmer, B. Roux and D. J. Müller, Biophys. J., 2002, 82, 1667–1676.
38. M. L. Berkowitz, D. L. Bostick and S. Pandit, Chem. Rev., 2006, 106, 1527–1539.
39. S. Vaitheeswaran, J. C. Rasaiah and G. Hummer, J. Chem. Phys., 2004, 121, 7955.
40. J. Dzubiella, R. Allen and J.-P. Hansen, J. Chem. Phys., 2004, 120, 5001–5004.
41. F. Mikami, K. Matsuda, H. Kataura and Y. Maniwa, ACS Nano, 2009, 3, 1279–1287.
42. B. Xu, Y. Qiao, Q. Zhou and X. Chen, Langmuir, 2011, 27, 6349–6357.
43. Z. Fu, Y. Luo, J. Ma and G. Wei, J. Chem. Phys., 2011, 134, 154507.
44. S. O. Diallo, E. Mamontov, W. Nobuo, S. Inagaki and Y. Fukushima, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021506.
45. Z. Qian, Z. Fu and G. Wei, J. Chem. Phys., 2014, 140, 154508.
46. Y. He, G. Sun, K. Koga and L. Xu, Sci. Rep., 2014, 4, 6596.
47. D. Bratko, C. D. Daub, K. Leung and A. Luzar, J. Am. Chem. Soc., 2007, 129, 2504–2510.
48. H. Qiu and W. Guo, Phys. Rev. Lett., 2013, 110, 195701.
49. W.-H. Zhao, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Chem. Sci., 2014, 5, 1757–1764.
50. J. Su and H. Guo, ACS Nano, 2010, 5, 351–359.
51. K. F. Rinne, S. Gekle, D. J. Bonthuis and R. R. Netz, Nano Lett., 2012, 12, 1780–1783.
52. J. Kou, X. Zhou, H. Lu, Y. Xu, F. Wu and J. Fan, Soft Matter, 2012, 8, 12111–12115.
53. S. De Luca, B. Todd, J. Hansen and P. J. Daivis, J. Chem. Phys., 2013, 138, 154712.
54. S. De Luca, B. D. Todd, J. S. Hansen and P. J. Daivis, Langmuir, 2014, 30, 3095–3109.
55. M. Suk and N. Aluru, Phys. Chem. Chem. Phys., 2009, 11, 8614–8619.
56. Winarto, D. Takaiwa, E. Yamamoto and K. Yasuoka, J. Chem. Phys., 2015, 142, 124701.
57. H. Berendsen, J. Postma, W. Van Gunsteren and J. Hermans, Intermol. Forces, 1981, 14, 331–342.
58. W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646.
59. W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284.
60. L. Saiz, J. Padro and E. Guardia, J. Phys. Chem. B, 1997, 101, 78–86.
61. Q. Shao, L. Huang, J. Zhou, L. Lu, L. Zhang, X. Lu, S. Jiang, K. E. Gubbins, Y. Zhu and W. Shen, J. Phys. Chem. C, 2007, 111, 15677–15685.
62. A. M. Saitta, F. Saija and P. V. Giaquinta, Phys. Rev. Lett., 2012, 108, 207801.
63. B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
64. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
65. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
66. S. Nosé, J. Chem. Phys., 1984, 81, 511.
67. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
68. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182.
69. A. Berezhkovskii and G. Hummer, Phys. Rev. Lett., 2002, 89, 64503.
70. G. Zuo, R. Shen, S. Ma and W. Guo, ACS Nano, 2010, 4, 205–210.

---

Footnote

† Electronic supplementary information (ESI) available: Separation effect with the TIP4P water model and water structures in (20,20), (25,25) and (30,30) CNTs. See DOI: 10.1039/c6cp06731j

---