Chirped-pulse Fourier transform millimeter-wave spectroscopy of ten vibrationally excited states of i-propyl cyanide: exploring the far-infrared region

Abstract

We report here further spectroscopic investigation of the astrochemically relevant molecule i-propyl cyanide. We observed and analysed the rotational spectra of the ground state of the molecule and ten vibrationally excited states with energies between 180–500 cm⁻¹. For this, we used a segmented W-band spectrometer (75–110 GHz) and performed the experiments under room temperature conditions. This approach thus provides access to high-resolution, pure rotational data of vibrational modes that occur in the far-infrared fingerprint region, and that can be difficult to access with other techniques. The obtained, extensive data set will support further astronomical searches and identifications, such as in warmer regions of the interstellar space where contributions from vibrationally excited states become increasingly relevant.

---

1 Introduction

With almost 200 molecules detected in interstellar space the overwhelming complexity of interstellar chemistry is prevalent (see http://www.astro.uni-koeln.de/cdms/molecules, Cologne Database for Molecular Spectroscopy). The molecular species range from unsaturated molecular carbon chains to heavy-metal containing triatomics. Among these 200 molecules, the family of cyanide containing molecules constitutes a considerable fraction (approximately 10%). The most recent detections of complex cyanides have been performed toward the Galactic center source Sagittarius B2 (Sgr B2), identifying a variety of cyanide species (such as aminoacetonitrile, n-propyl cyanide,^1–3 isotopologues of vinyl cyanide and ethyl cyanide,⁴E-cyanomethanimine,⁵ methyl isocyanate and methyl cyanate^6,7).

Recently, Belloche et al. detected the first branched alkyl molecule, i-propyl cyanide toward Sgr B2, with an abundance 0.4 times that of its straight-chain structural isomer n-propyl cyanide.⁸ Based on astrochemical models, the authors proposed that both isomers, i-propyl cyanide and n-propyl cyanide, are produced on dust grain ice mantles through the addition of molecular radicals. For the branched i-propyl cyanide species, the addition of a functional group to the non-terminal carbon would be required. This detection was based on an extensive laboratory spectroscopy investigation of i-propyl cyanide in selected regions between 6 and 600 GHz.⁹

A considerable proportion of complex molecules reside in low-lying vibrationally excited states at the elevated temperatures that were determined for i-propyl cyanide towards Sgr B2 (around 150 K). These vibrationally excited states, along with isotopologues that can often be seen in natural abundance, are associated with the so-called ‘weeds’ in radioastronomy data.¹⁰ These weeds can occupy many channels in a very complex, warm, dense astronomical dataset, therefore, it is important that the vibrationally excited states and isotopologues of abundant astronomical species are characterised. In 1974, Durig and Li reported the analysis of the ground state and three energetically low-lying vibrational states of i-propyl cyanide in a room-temperature microwave spectroscopy study (26.5–40 GHz).¹¹

In the present work, we identified and characterised up to ten vibrationally excited states of i-propyl cyanide on our new segmented chirped-pulse W-band instrument, which is presented here. The energies of the vibrationally exited states ranged up to 500 cm⁻¹, reinforcing how millimeter-wave spectroscopy of room temperature samples provides us with detailed molecular parameters of low-lying vibrationally excited states. We also observed the ¹³C isotopologues of the vibronic ground state of i-propyl cyanide in natural abundance (1.1%) in the millimeter-wave frequency range. This allowed us to precisely determine the ground-state structure of the molecule.

2 Experimental and computational methods

The rotational spectrum of i-propyl cyanide was recorded using the chirped-pulse Fourier transform millimeter-wave spectrometer purchased from BrightSpec, Inc. It is based on the work from the University of Virginia, in which the chirped-pulse technique was extended into the millimeter wave regime.¹² It covers the frequency range from 75–110 GHz (W-band) and employs the segmented approach.¹³ The spectrometer can operate in two segmented modes: fast mode and high dynamic range (HDR) mode. In fast mode, the entire 35 GHz frequency range is divided into 48 chirps, each having a bandwidth of 720 MHz. These 48 pulses (from here on referred to as the pulse train) and the following molecular response are collected subsequently on a real time digitiser, so that the entire spectrum is collected in 130 μs. Fast mode is used to quickly run and analyse a spectrum (with 10 000 averages taking about 1 min). In the HDR mode, the segments are further divided, thus increasing the acquisition time but decreasing the number of spurious signals present in the spectrum. It provides spectra with a higher dynamic range than fast mode. A typical measurement strategy would be to first record fast-mode spectra to get an initial overview of the spectral features, and then to refine these measurements using the HDR mode. In the following, we only show spectra recorded using the HDR mode.

The spectrometer is combined with a stainless-steel single-pass vacuum chamber, which is 67 cm long and sealed with two Teflon windows at each side. The sample of interest is placed in a sample reservoir and can be heated to increase the vapour pressure. In this case, the i-propyl cyanide (99% pure, purchased from Alfa Aesar and used without further purification) did not require additional heating to generate sufficient vapour pressure. A flow of about 4 μbar of i-propyl cyanide was maintained inside the chamber during the experiment. The pulse train was broadcast with a horn antenna and coupled into the vacuum chamber through the first Teflon window. The molecular response, in the form of a free induction decay (FID), was coupled out of the chamber via the second Teflon window and detected by a receiving horn antenna. The pulse train and corresponding FIDs were collected on the real-time digitiser, averaged, and finally Fourier transformed via a fast Fourier transformation from the time domain to the frequency domain. A typical excitation pulse duration is 500 ns, and the FID is collected for 4 μs, as was the case for this experiment. The achieved frequency accuracy of the instrument is approximately 30 kHz with line widths of about 550 kHz. For this experiment, 500 000 FIDs were recorded and averaged in HDR mode, which corresponds to a measurement time of 50 minutes.

Because of the fact that i-propyl cyanide is of C_s symmetry and the Ray's asymmetry parameter value is κ = −0.57, i-propyl cyanide is a near-prolate asymmetric molecule. However, to be consistent with previous datasets,⁹ the data were fitted to a Watson's S reduction Hamiltonian in a I^r representation. The spectral assignment was performed with the AABS package^14,15 and fit with Pickett's programs (SPFIT/SPCAT).¹⁶ The experimental analysis was supported with harmonic and anharmonic quantum-chemical calculations using the program package Gaussian 09.¹⁷ These calculations, performed at the B3LYP/aug-cc-pVTZ level of theory, provided the rotational constants of the individual vibrationally excited states. The overall dipole moment of i-propyl cyanide is large, with μ_a = 4.02 D and μ_c = 0.62 D. For facilitating the assignment of the rich experimental spectrum, the calculated rotational constants for the vibrationally excited states were shifted by the difference we obtained between the calculated and the experimental rotational constants for the ground state (see Table S1 of the ESI† that provides a summary of the quantum-chemical results and the discrepancies between experiment and calculations).

For the rotational spectra of the non-perturbed vibrational states, we assigned between 66 to 128 transitions with a signal to noise ratio of 1200 : 1 for the strongest transitions and fit them to a rigid-rotor Hamiltonian including centrifugal distortion within experimental accuracy (30 kHz). The transitions involved rotational quantum numbers J ranging between 11 and 17 and K_a values in the range 0 to 12 for R-type transitions, i.e., those following the selection rule ΔJ = +1. K_a is the quantum number associated with the projection of the rotational angular momentum onto the inertial axis a in the limit of the prolate symmetric top. Note that we also recorded weak Q-type transitions (obeying the selection rule ΔJ = 0) for which we observed higher J values. The rotational constants A, B and C, and the quartic centrifugal distortion rotational parameters of each state are well determined (see Table 1). The precision on the D_K values is limited by the range of K_a values observable in this spectral region. For the perturbed vibrational states (those that lie close in energy), we only included transitions with low K_a values (up to 7) into the fit, which impacts the accuracy of the D_K values. Therefore, in order to determine reliable rotational constants for those states, the D_K constant has been kept fixed to its ground state value.

Table 1 Molecular parameters for the ground state and vibrationally excited states of i-propyl cyanide, which has C_s symmetry. Ten vibrationally excited states were experimentally observed, two further states were predicted, but not observed. ΔE^a and ΔE^h are based on ab initio calculations with and without anharmonic corrections (B3LYP/aug-cc-pVTZ), respectively. Note the larger rms values for states ν₁₇, ν₃₀ + ν₂₉ and 2ν₂₉, which might arise from coupling with the near-degenerate states ν₂₉, ν₃₀ + ν₁₇, and ν₂₉ + ν₁₇, respectively. Perturbed states are marked with a *. J_m and K_a,m are the maximum values included in the fits

	GS	ν 30	ν 29*	ν 17*	ν 16	ν 15	2ν30	(ν30 + ν29)*	(ν30 + ν17)*	(ν29 + ν17)*	2ν29*	2ν17*	(ν30 + ν16)
Symmetry		A′′	A′′	A′	A′	A′	A′	A′	A′′	A′′	A′	A′	A′′
ΔE^a (cm^−1)	0	191.2	216.7	218.9	281.7	357.8	383.2	408.8	411.2	429.6	430.3	437.3	473.7
ΔE^h (cm^−1)	0	189.7	220.9	218.3	281.9	353.2	379.3	410.6	408.0	439.3	441.8	436.7	471.6
A (MHz)	7940.8746(16)	7896.7463(15)	7932.513(51)	7993.882(26)	7923.1764(24)	7928.435(15)	7853.1241(69)	7879.481(28)	7945.628(27)		7926.817(25)		7875.091(21)
B (MHz)	3968.08888(52)	3980.03092(59)	3964.9749(93)	3971.8633(50)	3970.27231(63)	3978.7235(14)	3991.94840(76)	3976.7219(54)	3983.3608(56)		3963.9296(49)		3981.9721(22)
C (MHz)	2901.05458(53)	2899.86118(61)	2898.2195(46)	2904.7205(20)	2902.82671(69)	2900.5124(14)	2898.60041(73)	2896.9396(33)	2903.4154(23)		2896.3754(36)		2901.5706(16)
D J (kHz)	0.6127(12)	0.6386(13)	0.630(16)	0.6085(79)	0.6129(14)	0.6155(16)	0.6603(15)	0.6349(75)	0.6205(82)		0.5585(60)		0.6320(34)
D JK (kHz)	12.1698(43)	11.4510(21)	11.38(24)	13.162(99)	11.9422(17)	12.2310(37)	10.7860(38)	10.363(50)	12.519(92)		11.231(95)		11.279(13)
D K (kHz)	−5.231(27)	−7.869(10)	[−5.231]	[−5.231]	−5.236(10)	−4.07(11)	−9.356(85)	[−5.231]	[−5.231]		[−5.231]		−7.20(55)
d 1 (kHz)	−0.24393(11)	−0.25602(18)	−0.2637(72)	−0.2486(39)	−0.25187(18)	−0.25600(83)	−0.27202(36)	−0.3044(60)	−0.2550(48)		−0.2516(46)		−0.2556(22)
d 2 (kHz)	−0.189404(63)	−0.183884(73)	−0.1774(31)	−0.2025(13)	−0.185515(88)	−0.19630(55)	−0.17902(17)	−0.1983(24)	−0.1934(15)		−0.1929(25)		−0.1760(10)
H JK (Hz)	0.0347(16)		−2.55(77)	−1.55(31)					−1.59(26)
h 2 (Hz)	0.000931(72)
h 3 (Hz)	0.000326(33)
No. lines	173	128	45	71	109	88	89	42	68		37		66
rms (kHz)	26.9	32.3	58.5	44.1	33.1	33.7	32.0	64.4	50.3		51.9		32.7
J m/Ka,m	40/10	35/12	16/6	17/8	40/14	40/13	38/12	17/8	17/8		17/6		17/11

---

The additional rotational constants due to ¹³C isotopic substitution in natural abundance were used to determine the substitution structure of i-propyl cyanide using Kraitchman's equations¹⁸ as implemented in the KRA program package.¹⁴

3 Results and discussion

The broadband spectrum covering 75–110 GHz for i-propyl cyanide is shown in Fig. 1a, illustrating the high line density arising from the large number of vibrational states. Despite the spectrum's richness, the high resolution and sensitivity of the spectrometer result in well separated and distinguishable rotational transitions. This is illustrated in the zoom-in (Fig. 1b) of the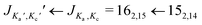 rotational transition (left component of the doublets) and the 16_1,15 ← 15_1,14 rotational transition (right component of the doublets) for the vibronic ground state and several vibrational states. Note that no ¹⁴N nuclear quadrupole coupling was observed because it collapses for the high J, K_a, and K_c values populated at the elevated temperatures used in the experiment and observed in this high frequency range. As in previous rotationally resolved spectroscopy studies on i-propyl cyanide, we also observed no line splittings due to methyl group internal rotation.^9,11 The calculated barriers associated with this motion amount to 13.1 kJ mol⁻¹ (B3LYP/6-311G++ level of theory) and are too high to cause detectable line splittings for our experiment.

Fig. 1 (a) Broadband rotational spectrum of i-propyl cyanide and (b) zoom of the 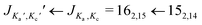and 16_1,15 ← 15_1,14 transitions of the vibronic ground and ten vibrationally excited states as labelled in the spectrum. The upper traces are the experimental spectra, while the lower traces are simulations of the fitted rotational parameters (see also Table 1 and the text for more details). The S/N ratios for these transitions corresponds to 475 : 1 for the 16_2,15 ← 15_2,14 transition and to 324 : 1 for the 16_1,15 ← 15_1,14 transition for the vibronic ground state.

Based on the shifted calculated rotational constants (see Section 2 and Table S1 of the ESI†) the assignment of most of the vibrationally excited states was straight forward. We could unambiguously identify ten energetically low-lying vibrationally excited states and fit their rotational transitions to an asymmetric-top Hamiltonian, as described in Section 2. The rotational constants for the ground state and the vibrationally excited states are summarised in Table 1. The calculated vibrational frequencies of the respective states are also included (B3LYP/aug-cc-pVTZ level of theory with and without anharmonic corrections). However, for some pairs of states, such as ν₂₉/ν₁₇ as well as (ν₃₀ + ν₂₉)/(ν₃₀ + ν₁₇), the analysis was more challenging. We found that these vibrationally excited states, which are within only a few cm⁻¹ energetically, perturb each other. Without being able to identify the band centers, this perturbation cannot be analysed in detail. Such a study would require high-resolution far-infrared data, where vibrational transitions are probed, and our anharmonic frequency calculations predict the relevant vibrational transitions to be too weak to be observed. Even though the standard deviation for these states of the corresponding fits are larger than the frequency accuracy of our spectrometer, they are still sufficiently determined to obtain useful molecular parameters to support their radioastronomic detection, which is one of the motivations of the present work.

The results of our quantum-chemical calculations allow us to assign motions for some of the vibrational states. The lowest frequency vibrational state, ν₃₀, corresponds to the C–C≡N out-of-plane bending motion, and ν₁₇ can be assigned to the associated in-plane motion. The ν₁₆ and ν₂₉ modes concern the symmetric and asymmetric methyl torsional modes, respectively. Finally, the last fundamental mode assigned, ν₁₅, refers to a CC₂ deformation involving a bending motion between the two C–CH₃ bonds. All the other modes observed in this study are combinations of the previously described motions. The (ν₂₉ + ν₁₇) and 2ν₁₇ modes could not be observed experimentally. We assume that they are too strongly perturbed because they are involved (with 2ν₂₉) in a three party perturbation.

Note that three of the vibrationally excited states (namely ν₂₉, ν₁₇, ν₁₆) were also observed in the previous study by Durig et al. (Table 3 of ref. 11). By comparing the respective rotational constants, we can make the following correlation: the ν_α, ν_β and ν_γ states from ref. 11 correspond to our ν₂₉, ν₁₇, and ν₁₆ states, respectively. Based on transition intensities, the authors of ref. 11 ordered their states according to ν_β, ν_α, and ν_γ, which generally agrees with our findings. However, they did not report on the lowest vibrational state, i.e., ν₃₀ in Table 1. This missing state ν₃₀ thus led to some confusion in the initial assignments.

The authors of ref. 11 also derived an approximate molecular structure for i-propyl cyanide. The length of the C–CN bond is particularly interesting since it is expected to be rather short as a result of the very strong electron-withdrawing cyano group. In ref. 11, the bond length r(C–CN) was determined to be 1.501 Å and the angle between the C≡N bond and the CCC plane was estimated to be σ = 53.8°. In the present work, we recorded the rotational spectra of all three singly substituted ¹³C isotopologues of the vibronic ground state of i-propyl cyanide. These additional sets of rotational constants allowed us to determine its substitution structure (r_s) of the carbon backbone using the Kraitchman's equations (see also Table S2 of the ESI†). This method exploits mono-isotopic substitution information and provides a straightforward way to use the isotopic changes in the moments of inertia to determine the atom coordinates in the principal axis frame.

Fig. 2 shows a comparison between the calculated structure of i-propyl cyanide (B3LYP/aug-cc-pVTZ) and the experimentally determined r_s structure. As can be seen, the experimental atom positions match those from the calculated structure with small deviations. The substitution structure yields the following structural parameters: r(C–CN) = 1.4600(46) Å, which is 0.04 Å shorter than determined in ref. 11, and r(C–CH₃) = 1.5359(42) Å. The angle between the C≡N bond and the CCC plane was determined to be σ = 51.52(32)°, which is also smaller than in ref. 11. This is in line with the qualitative discussions in ref. 11 that a shorter C–CN bond results in smaller σ angles. The discrepancy between our structural parameters and those from Durig and Li might arise from the various assumptions they had to adopt for their analysis. Their data only allowed them to produce a partial structure, and they presented parameters that were determined with the aid of i-propyl chloride.¹¹ In the present work, the complete carbon backbone structure is determined solely based on the experimental data.

Fig. 2 Comparison between experimentally determined (r_s) structure and calculated structure (B3LYP/aug-cc-pVTZ) at the equilibrium for i-propyl cyanide. The calculated structure is comprised of the transparent gray carbon atoms, while the orange spheres represent the r_s atom positions. Experimental values for selected bond lengths and angles are also given.

The comparison of the C–CN bond length obtained for i-propyl cyanide can be extended to other cyanide containing molecules. Keeping in mind that the electron-withdrawing cyano group is expected to produce a shortening of that C–CN single bond, Table 2 compares the C–CN bond length in i-propyl cyanide with analogous, short-chain cyanides as well as with average C–C bond lengths for different orbital hybridisation regimes. The C–CN bond in i-propyl cyanide is on the same order of magnitude as an average C(sp³)–C(sp) bond, being only slightly shorter by 0.01 Å. Indeed, the bond is substantially shorter than a typical C–C single bond (C(sp³)–C(sp³)) by 0.07 Å. In addition, the C–CN bond length in i-propyl cyanide is in keeping with those of analogous alkyl cyanides – it amounts to 1.46 Å (when errors are considered), regardless of the adjacent alkyl chains. The shortest C–CN bond is the one in benzonitrile, likely due to electronic effects of the aromatic ring giving it some double bond character. The experimental data are compared to computed bond distances that we performed at the B3LYP/aug-cc-pVTZ level of theory. The similar bond lengths in the alkyl cyanides and the respective shorter value for benzonitrile is well reproduced by the calculations.

Table 2 A comparison of the C–CN bond length in a variety of alkyl cyanides. Included in the table, for reference, are average C–C bond lengths for different orbital hybridisation regimes as well as calculated bond lengths (this work, B3LYP/aug-cc-pVTZ level of theory)

Compound	r(C–CN)exp (Å)	r(C–CN)calc (Å)
Methyl cyanide	1.4594(6)^19	1.455
Ethyl cyanide	1.459(1)^20	1.460
n-Propyl cyanide	1.4621(43)^21	1.459
i-Propyl cyanide	1.501^11	1.466
i-Propyl cyanide	1.4600(46) (this work)	1.466
n-Butyl cyanide		1.459
t-Butyl cyanide	1.46(2)^22	1.472
Benzonitrile	1.4509(6)^23	1.430
C(sp^3)–C(sp^3)	1.53^24
C(sp^3)–C(sp)	1.47^24

---

4 Conclusions

We performed high-resolution chirped-pulse Fourier transform rotational spectroscopy in the 75–110 GHz frequency range on i-propyl cyanide, a branched molecule of astronomical interest. For this, we used a W-band spectrometer employing the segmented approach. In the HDR mode, 500 000 averages and spectral coverage over the whole frequency range is achieved in about 50 minutes, maintaining a high resolution (on the order of 30 kHz) and high sensitivity. Because of this high resolution and sensitivity, we could identify and characterise ten vibrationally excited states up to 500 cm⁻¹ and record the rotational signatures of the three singly substituted ¹³C isotopologues of the vibronic ground state in the millimeter-wave frequency range. Spectral information for the isotopologues allowed us to determine the carbon backbone structure of i-propyl cyanide and to compare it with similar molecules and previous studies. This rather complete data set will support further astronomical searches and identifications, such as in warmer regions of interstellar space where the contribution of vibrationally excited states might be even more relevant.

Acknowledgements

This work has been supported by the ERC Starting grant ASTROROT (grant agreement number 638027). B.E.A. acknowledges the financial support of the IMPRS-UFAST. A.L.S. is supported by the Louise Johnson Fellowship.

References

1. A. Belloche, K. M. Menten, C. Comito, H. S. P. Müller, P. Schilke, J. Ott, S. Thorwirth and C. Hieret, Detection of amino acetonitrile in Sgr B2(N), Astron. Astrophys., 2008, 482, 179–196.
2. A. Belloche, R. T. Garrod, H. S. P. Müller, K. M. Menten, C. Comito and P. Schilke, Increased complexity in interstellar chemistry: detection and chemical modeling of ethyl formate and n-propyl cyanide in Sagittarius B2(N), Astron. Astrophys., 2009, 499, 215–232.
3. H. S. P. Müller, A. Walters, N. Wehres, A. Belloche, O. H. Wilkins, D. Liu, R. Vicente, R. T. Garrod, K. M. Menten, F. Lewen and S. Schlemmer, Laboratory spectroscopic study and astronomical detection of vibrationally excited n-propyl cyanide, 2016, arXiv:1608.08129v1.
4. H. S. P. Müller, A. Belloche, K. M. Menten, C. Comito and P. Schilke, Rotational spectroscopy of isotopic vinyl cyanide, H₂CCHCN, in the laboratory and in space, J. Mol. Spectrosc., 2008, 251, 319–325.
5. D. P. Zaleski, N. A. Seifert, A. L. Steber, M. T. Muckle, R. A. Loomis, J. F. Corby, Jr., O. Martinez, K. N. Crabtree, P. R. Jewell, J. M. Hollis, F. J. Lovas, D. Vasquez, J. Nyiramahirwe, N. Sciortino, K. Johnson, M. C. McCarthy, A. J. Remijan and B. H. Pate, Detection of E-cyanomethanimine toward Sagittarius B2(N) in the green bank telescope PRIMOS survey, Astrophys. J., Lett., 2013, 765(1), L10.
6. J. Cernicharo, Z. Kisiel, B. Tercero, L. Kolesniková, I. R. Medvedev, A. López, S. Fortman, M. Winnewisser, F. C. de Lucia, J. L. Alonso and J.-C. Guillemin, A rigorous detection of interstellar CH₃NCO: an important missing species in astrochemical networks, Astron. Astrophys., 2016, 587, L4.
7. L. Kolesniková, J. L. Alonso, C. Bermúdez, E. R. Alonso, B. Tercero, J. Cernicharo and J.-C. Guillemin, The millimeter wave spectrum of methyl cyanate: a laboratory study and astronomical search in space, Astron. Astrophys., 2016, 591, A75.
8. A. Belloche, R. T. Garrod, H. S. P. Müller and K. M. Menten, Detection of a branched alkyl molecule in the interstellar medium: iso-propyl cyanide, Science, 2014, 345(6204), 1584–1587.
9. H. S. P. Müller, A. Coutens, A. Walters, J.-U. Grabow and S. Schlemmer, Rotational spectroscopy, dipole moment and ¹⁴N nuclear hyperfine structure of iso-propyl cyanide, J. Mol. Spectrosc., 2011, 267, 100–107.
10. S. M. Fortman, I. R. Medvedev, C. F. Neese and F. C. De Lucia, The complete, temperature-resolved experimental spectrum of ethyl cyanide (CH₃CH₂CN) between 210 and 270 GHz, Astrophys. J., 2010, 725(2), 1682.
11. J. R. Durig and Y. S. Li, Microwave spectrum, dipole moment and structure of isopropyl cyanide, J. Mol. Struct., 1974, 21(2), 289–297.
12. A. L. Steber, B. J. Harris, J. L. Neill and B. H. Pate, An arbitrary waveform generator based chirped pulse Fourier transform spectrometer operating from 260 to 295 GHz, J. Mol. Spectrosc., 2012, 280, 3–10.
13. J. L. Neill, B. J. Harris, A. L. Steber, K. O. Douglass, D. F. Plusquellic and B. H. Pate, Segmented chirped-pulse Fourier transform submillimeter spectroscopy for broadband gas analysis, Opt. Express, 2013, 21, 19743–19749.
14. Z. Kisiel, PROSPE, Programs for Rotational Spectroscopy, 2015, http://info.ifpan.edu.pl/^~kisiel/orospe.htm.
15. Z. Kisiel, L. Pszczolkowski, I. R. Medvedev, M. Winnewisser, F. C. De Lucia and E. Herbst, Rotational spectrum of trans–trans diethyl ether in the ground and three excited vibrational states, J. Membr. Sci., 2005, 233, 231–243.
16. H. M. Pickett, The fitting and prediction of vibration–rotation spectra with spin interactions, J. Mol. Spectrosc., 1991, 148(2), 371–377.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009.
18. J. Kraitchman, Determination of molecular structure from microwave spectroscopic data, Am. J. Phys., 1953, 21, 17–24.
19. M. Le Guennec, G. Wlodarczak, J. Burie and J. Demaison, Rotational spectrum of CH₂DCN and structure of methyl cyanide, J. Mol. Spectrosc., 1992, 154, 305–323.
20. H. M. Heise, H. Lutz and H. Dreizler, Molecular structure, quadrupole coupling tensor and dipole moment of ethyl cyanide, Z. Naturforsch., 1974, 29a, 1345–1355.
21. M. Traetteberg, P. Bakken and H. Hopf, Structure and conformation of gaseous butyronitrile: C–H–π interaction?, J. Mol. Spectrosc., 2000, 556, 189–196.
22. R. L. Livingston and C. N. R. Rao, The molecular structure of pivalonitrile by electron diffraction, J. Am. Chem. Soc., 1959, 81, 3584–3586.
23. J. Casado, L. Nygaard and G. Ole Sørensen, Microwave spectra of isotopic benzonitriles. Refined molecular structure of benzonitrile, J. Mol. Spectrosc., 1971, 8, 211–224.
24. F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp06297k

---