Early events in the photochemistry of 5-diazo Meldrum's acid: formation of a product manifold in C–N bound and pre-dissociated intersection seam regions

Abstract

5-Diazo Meldrum's acid (DMA) undergoes a photo-induced Wolff rearrangement (WR). Recent gas-phase experiments have identified three photochemical products formed in a sub-ps scale after irradiation, a carbene formed after nitrogen loss, a ketene formed after WR and a second carbene formed after nitrogen and CO elimination (A. Steinbacher, et al. Phys. Chem. Chem. Phys., 2014, 16, 7290–7298). In this work, ground- and excited-state potential energy surfaces (PESs) have been investigated at the MS-CASPT2//CASSCF level. The key element of the PESs is an extended S₀/S₁ conical intersection seam along the C–N dissociation coordinate. The C–N predissociated region of the seam is accessed after excitation to the bright S₂ state, and decay paths from the seam to the three primary products have been characterized. For the ketene and carbene II products, we show two possible formation pathways, a direct and a stepwise one, which suggests that these products may be formed in a bi-modal fashion. We have also characterized two possible mechanisms for triplet formation, one occurring before C–N dissociation involving a (S₁/T₂/T₁) crossing region, and another one through the carbene. In contrast, excitation to S₁ leads to a C–N bound region of the seam from where DMA regeneration or diazirine formation is possible, with a preference for the first case. The results are in good agreement with experimental data. Together with our previous work on diazonaphthoquinone, they show the importance of an extended seam in the photochemistry of α-diazoketones.

---

Introduction

Diazo carbonyl compounds are widely used in organic synthesis, drug delivery, peptide design, DNA cleavage, photoaffinity labeling, and photolithography.¹ These applications are primarily based on the Wolff rearrangement (WR) which yields a ketene by loss of dinitrogen with accompanying 1,2-rearrangement.² Although the WR has been known for more than a century, its mechanism is still a subject of disputation. One aspect is whether the dinitrogen extrusion is concerted with the carbon–carbon bond migration, or whether it occurs via a carbene intermediate and a subsequent rearrangement.^3–7 The mechanistic details depend on the particular molecule. Early in 1966, Kaplan and Meloy proposed that the syn conformers of diazoketones undergo WR in favor of a concerted mechanism, while the anti conformers prefer a stepwise manner.⁸ Kaplan's initial rule has been confirmed and extended by plentiful experiments. Burdzinski and Platz pointed out that the WR process proceeds by both concerted (major) and stepwise (minor) pathways in all cyclic diazo carbonyl compounds, which are structurally locked in a syn conformation.⁹ This conjecture is supported by photolysis of diazonaphthoquinone (DNQ) in methanol¹⁰ and ultrafast spectroscopy experiments.¹¹ Recently, dynamics calculations by our groups and others showed that in DNQ the key step of the rearrangement is the passage of the excited molecule through an extended seam of conical intersection (CI) from where different products can be formed.^12–14 Decay from the extended seam can lead to the ketene final product and the carbene intermediate, which explains the concurrent experimental observation of both pathways.^10,11

The focus of the present work is another prototypical diazo compound, 5-diazo Meldrum's acid (DMA). DMA is of great practical interest because of its potential for deep-UV photoresist and imaging applications.¹⁵ It shows a rich photochemistry where several products, including some that are not observed in DNQ, are formed in a sub-ps time scale, and the main focus of our work is to explain this complex mechanistic scenario with the extended seam of intersection model. Experimental studies have investigated its spectroscopic properties,¹⁶ thermochemical decomposition,^3,17–19 and photolysis under various conditions.^{3,15,17,18,20–23} The proposed primary processes of DMA upon UV photoexcitation are illustrated in Scheme 1.

Scheme 1

Early work shows that the photolysis of DMA is wavelength dependent.^15,21 Irradiation at 254 nm in methanol, which populates the S₂ state, gives 34% of photo-Wolff products, while irradiation at 355 nm, which populates S₁, only leads to approximately 2% of diazirine formation.¹⁸ More recent fs resolution studies show that the products formed at 266 nm have formation times below 1 ps, i.e. in the ultrafast range, providing the main motivation for our work. After UV excitation at 266 nm in chloroform, DMA rapidly interconverts from the S₂ state to the S₁ state, which has a lifetime of not more than 300 fs.²⁰ Carbene and ketene formation was observed within the first 300 fs and 1 ps after irradiation, respectively. Similar dynamics was disclosed in time- and wavenumber-resolved experiments in methanol, where about 30% excited DMA molecules on S₂ (266 nm) undergo WR to form ketene, while the rest relax to the S₁ state, from where they can decay to the ground state (∼97%), isomerize to a diazirine (∼2%) or generate a triplet carbene (1–2%).²² Recently, femtosecond time-resolved photofragment ion spectroscopy was employed to investigate the gas-phase photochemistry of DMA, where solvent and vibrational energy loss effects are avoided, simplifying comparisons to theoretical studies.²³ These results show that DMA rearranges to form a ketene within a time scale of 27 fs after 267 nm excitation, which provides strong evidence for the concerted WR mechanism.²³ In addition, the formation of the carbene II product was observed with a time constant of 358 fs.

On the theoretical side, time-dependent density functional theory (TD-DFT) calculations suggest that the S₁ state lies at 3.4–3.5 eV (353–369 nm) and has a small oscillator strength.^17,20 This is in good agreement with the experimental UV spectrum, which shows a transition at 329 nm with a low extinction coefficient. DFT and MP2 calculations also suggest that the WR of DMA is a concerted process because the carbene-to-ketene reaction is barrierless.^5,17 However, no study of the excited-state potential energy surface, which is mandatory to understand the mechanism of photolysis, has appeared up to now. Here, we present such a study using the CASSCF and MS-CASPT2 methods, which allow for an accurate characterization of the excited-surface potential energy surface.

Our work shows that the ultrafast formation of the primary product manifold can be understood in terms of an extended seam of CI between the excited and ground states. CIs are crossings between potential energy surfaces (PESs) of the same multiplicity that act as funnels that enable efficient transfer of population.^24–32 CIs are not isolated points but form part of multidimensional seams of intersection.^24–27 The intersection seams are usually composed of several segments associated with the formation of different photoproducts or recovery of the reactant.³³ This topological feature has been successfully used to explain, among others, the photodynamics of ethylene,^34,35 benzene,^36–38 azobenzene,³⁹ fulvene,^40–42 thymine,⁴³ adenine,⁴⁴ cytosine,⁴⁵ 5-bromouracil,⁴⁶o-hydroxybenzaldehyde,⁴⁷ malonaldehyde,⁴⁸ DNQ,¹³ the retinal chromophore,⁴⁹ the HBI chromophore of the green fluorescent protein⁵⁰ or aggregation induced emitters.^31,51 In the present case, the seam can be accessed without an energy barrier after excitation to S₂, and there are barrierless paths from different parts of the seam to the diazirine, carbene I, ketene and carbene II products. Overall, this comprehensive mechanistic picture explains the first steps of the photolysis of DMA.

Computational details

The calculations were carried out using the MS-CASPT2//CASSCF approach,⁵² which is well established in computational photochemistry. Thus, critical points (minima, transition states (TSs) and CIs) and minimum energy paths (MEPs) were optimized at the complete active space self-consistent field (CASSCF) level, and the energies were recalculated at the multi-state complete active space second-order perturbation (MS-CASPT2) level to account for dynamic correlation. All the minima and TS structures have been characterized by vibrational frequency calculations. The CASSCF calculations have been carried out using Gaussian 09⁵³ and the MS-CASPT2 calculations using Molcas 8.0.^54,55 The standard 6-31g* basis set was employed for CASSCF optimizations and the ANO-S basis set with 3s2p1d contraction for C, N and O and 2s1p contraction for H was used for MS-CASPT2 single point calculations. The absolute and relative energies of all critical points are provided in Tables S1 and S2 in the ESI.†

The active space of the CASSCF calculations for DMA (see Fig. 1 for the structure and atomic labeling) is composed of ten electrons distributed in nine orbitals, assigned as CAS(10,9) hereafter, which includes seven π and π* orbitals perpendicular to the six-membered ring and the two in-plane π orbitals of the diazo group (labeled π_NN and π*_NN). The two σ/σ* orbital pairs of the C₅–N₈ and the C₅–C₇ bonds are also included in the active space in case of the C₅–N₈ bond cleavage and the ring rearrangement. For the other bond breaking processes, the active space orbitals relaxed to the most suitable ones for each case. For a reliable estimation of the overall energetics, the MS-CASPT2 energies of all structures (critical points and points along the paths) were calculated with a (12,11) active space ((10,8) for carbene structures). The orbitals for Franck–Condon (FC) like structures are shown as an example in Fig. 1. The suitability of this approach was checked making sure that there were no large discrepancies between the CASSCF and MS-CASPT2 energy profiles.

Fig. 1 DMA structure and active space orbitals used for the calculations at FC-like geometries.

In the MS-CASPT2 calculations, three roots were computed with equal weights in the CASSCF reference calculation of the singlet or triplet states. The number of states was chosen in order to always include the ground state as well as ππ*_NN and ππ* excited states (the ground state and two ππ* excited states in the case of C₆H₆O₄) in the reference function and avoid orbital rotations that would change the composition of the active space. An ionization potential-electron affinity (IPEA) parameter⁵⁶ of 0.0 a.u. and an imaginary level shift⁵⁷ of 0.1 a.u. were used in MS-CASPT2 calculations. The spin–orbital coupling (SOC) strength between the singlet state and the triplet state was computed with atomic mean-field integrals by using a one-electron operator implemented in Molcas 8.0.^54,55

The CI structures have been optimized at the CASSCF level, and the seam has been characterized by a series of optimizations constraining the C₅–N₈ distance to different values, using a recently developed algorithm based on a double Newton–Raphson step.⁵⁸ Because of differential correlation between the intersecting states, the MS-CASPT2 single-point energies for some of the structures have substantial S₁/S₀ energy gaps of up to 0.6 eV, even though the CASSCF energy gap is <0.05 eV in all cases. To provide a more accurate characterization of the intersections at the MS-CASPT2 level, it would be necessary to optimize them at this level of theory or use a larger active space in the CASSCF optimization. However, this is out of the scope of our work. Therefore, as an approximation we provide the average S₁/S₀ MS-CASPT2 single-point energies at the CIs, and in Fig. 4 we display the energy gap as an error bar. Although the MS-CASPT2 energies along the seam are only approximate, the shape of the seam gives a clear view of its role in the reactivity.

The MEP calculations involving a TS were started from the TS structure following the numerical or analytical force constants in forward and reverse directions, using the intrinsic reaction coordinate (IRC) algorithm.^59,60 The decay MEPs from the FC geometry and from the CI seam to the DMA reactant and the diazirine and carbene I products were calculated using hypersphere geometry optimizations to determine the initial relaxation direction (IRD),⁶¹ with step sizes of 0.1–0.5 Bohr amu^1/2, followed by an IRC calculation. In each case, the hypersphere calculation was started in the direction of the desired product. For the ketene, carbene II and acetone products, the hypersphere calculations with this step size failed to converge in the desired relaxation direction and led to points on the MEP to carbene I. Therefore, the decay paths to these products were calculated running first a series of IRD calculations of decreasing step size, starting with approximately 40 Bohr amu^1/2, until the hypersphere optimization failed to converge in the desired direction. This happened at 7.5, 19.8, and 17.5 Bohr amu^1/2 for ketene, carbene II and acetone, respectively. The initial part of the paths from the seam to reach these points was then completed by linear interpolations in internal coordinates (LIICs). A similar approach has been used previously by us to compute the excited-state tautomerization paths of 1-methyl cytosine.⁶²

Results

The optimized structures of the critical points on the PES of DMA are displayed in Fig. 2, where some key bond lengths are shown, and the atom numbering is provided in Scheme 1. Our approach to explain the reactivity is based on calculating the excited-state decay paths from the FC structure, DMA-S₀. As we explain below, these paths lead to the seam of CI, and the main mechanistic insight is obtained by calculating the decay paths from the different regions of the seam to the products. These paths are shown in Fig. 3–7 and are discussed in the following subsections.

Fig. 2 Optimized structures of the critical points on the potential energy surface with the key bond lengths in Å. Energies are relative to DMA-S₀ except for the C–N dissociated structures (m–r), which are relative to boat-like carbene.

Fig. 3 MS-CASPT2 energy profiles for the MEP from the FC geometry to (S₂/S₁)_X and from (S₂/S₁)_X to the (S₁/S₀) CI seam. Inset: Singly occupied orbitals at (S₁/S₀)_X.

Fig. 4 Average MS-CASPT2 energy profile of S₀ and S₁ at the (S₁/S₀)_X seam along the C₅–N₈ stretching coordinate. The error bars correspond to MS-CASPT2 energy gaps in the CI structures (see Computational details). Insets: Singly occupied molecular orbitals at (S₁/S₀)_X-CN1.6 and (S₁/S₀)_X-CN2.2.

Fig. 5 MS-CASPT2 energy profile for the MEP from FC to (S₂/S₁)_X, LIIC from (S₁/S₂)_X to (S₀/S₁)_X-CN2.2 and MEP from (S₀/S₁)_X-CN2.2 to carbene I.

Fig. 6 MS-CASPT2 energy profile for the direct decay path from (S₁/S₀)_X-CN2.2 to the ketene. Inset: Structures along the path with representative interatomic distances in Å.

Fig. 7 MS-CASPT2 energy profile for the direct decay path from (S₁/S₀)_X-CN2.2 to carbene II. Inset: Structures along the path with representative interatomic distances in Å.

Ground-state equilibrium structure and vertical excitation energies

The ground-state minimum DMA-S₀ adopts an envelope conformation of C_s symmetry with a linear C₅–N₈–N₉ moiety and a puckered C₂ atom. The vertical excitation energies, oscillator strengths, and dominant configurations at DMA-S₀, calculated at the MS-CASPT2 level, are presented in Table 1. According to our calculations, S₁ lies at 3.71 eV (334 nm) and is a dark state with negligible oscillator strength (7.2 × 10⁻⁶). It corresponds to electronic promotion from the delocalized π₄ orbital to the in-plane diazo π*_NN orbital. S₂ is a bright state at 5.16 eV (240 nm) with significantly higher oscillator strength (0.24) than the other states. The excitation involves the π₄ orbital and the diazo π₁* orbital perpendicular to the plane. S₃–S₅ are weakly absorbing states with energies 5.32, 7.48 and 7.64 eV, respectively. These results are in good agreement with the experimental observations of a strong absorbance at 248 nm (5.00 eV) and a much weaker band at 329 nm (3.77 eV) virtually independent of the polarity of the solvent.¹⁷ Moreover, they suggest that excitation at 266 nm or 267 nm in time-resolved UV-vis spectroscopic experiments populates the S₂ state of DMA.^20,22,23 Our calculations are also in good agreement with previous TD-DFT calculations, which give an S₁ energy of 3.4–3.5 eV and an energy of 5.2–5.3 eV for the bright state.^17,20 These calculations give a number of additional states with near zero oscillator strength between 4.3 and 5.3 eV that are probably Rydberg states not considered in our calculations.

Table 1 Relative MS-CASPT2 vertical excitation energies (ΔE) and wavelengths (λ) of DMA-S₀, including the dominant electronic configuration (orbitals in Fig. 1) and the oscillator strength (f)

State	Electronic configuration^a	ΔE (eV)	λ (nm)	f
a Orbital occupation of the leading configuration, following the order given in Fig. 1. 2 stands for doubly occupied orbitals, u and d stand for singly occupied orbitals and 0 stands for empty ones. The reference configuration (S0) is 22222200000. b Calculated with the (14,11) active space shown in Fig. S1 (ESI).
S1	22222ud0000 (ππ*NN)	3.71	334	7.2 × 10^−6
S2	22222u0d000 (ππ*)	5.16	240	0.24
S3	2u222220d00^b (nOπ*NN)	5.32	233	3.6 × 10^−5
S4	2u2222d0000 (ππ*NN)	7.48	166	1.8 × 10^−4
S5	2222u2d0000 (ππ*NN)	7.64	162	2.7 × 10^−6

---

Initial decay from DMA-S₀

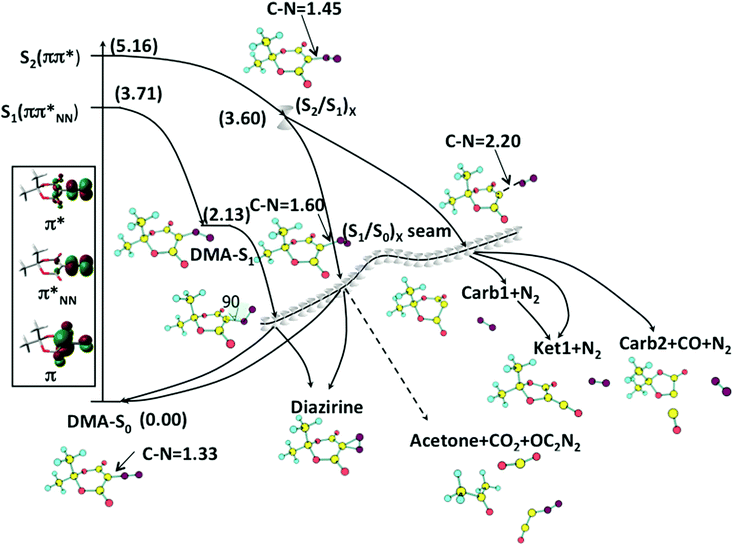
Excitation at 266 nm or 267 nm (approximately 4.65 eV)^20,22,23 populates the ππ* state, which is S₂ at DMA-S₀. The relaxation path is initially dominated by C₅–N₈ bond stretching followed by bending of the quasi-linear C₅–N₈–N₉ moiety until a CI point between the ππ* state and ππ*_NN states is reached, (S₂/S₁)_X (see Fig. 3), with an approximate energy 3.60 eV. At (S₂/S₁)_X, the C₅–N₈ bond is stretched from 1.33 Å at DMA-S₀ to 1.44 Å, and the C₅–N₈–N₉ angle decreases from 179° to 132° (see the structures in Fig. 2). From (S₂/S₁)_X, there are two possible decay paths. The first one leads without any barrier to a CI seam between the ππ*_NN state and the ground state (see the energy profile and orbitals in Fig. 3). The minimum energy point of the seam, (S₁/S₀)_X−Min, has an energy of approximately 2.18 eV. At (S₁/S₀)_X−Min, the C₅–N₈ bond length is 1.45 Å and the N₈–N₉ diazo group is rotated by about 40° out of the ring plane. The decay MEP from (S₁/S₀)_X−Min leads back to the DMA-S₀ reactant (see Fig. S2 in the ESI†).

The alternative decay path from (S₂/S₁)_X leads to a minimum on S₁, DMA-S₁ (see Fig. 2), with a relative energy of 2.13 eV. For this structure, the C₅–N₈–N₉ angle is 124.5°. DMA-S₁ is separated from (S₁/S₀)_X−Min by a barrier of approximately 0.4 eV, estimated by a LIIC (see Fig. S3, ESI†). This barrier is low enough to allow for further decay to the ground state thanks to the vibrational excess energy carried by the molecule after excitation. Overall, the paths calculated from the FC structure through (S₂/S₁)_X match well with the experimental finding that more than a half of S₂ excited DMA molecules relax back to the S₀ ground state without reacting.^17,20,22,23

Extended S₁/S₀ seam of intersection

The fact that the decay MEP from (S₁/S₀)_X leads to DMA-S₀ suggests that the formation of the primary photoproducts in a sub-ps time scale implies the passage of the molecule through other regions of the intersection seam. This is consistent with our previous work on DNQ, where we characterized an extended seam of intersection along the carbon–diazo dissociation coordinate.¹³ Following this idea, we have characterized a segment of extended seam along the C₅–N₈ coordinate, with distances ranging from 1.3 to 3.2 Å. The results are shown in Fig. 4, where we plot the average MS-CASPT2 energy of the optimized CI structures (see Computational details). The seam is composed of two low-energy regions, one with a short C₅–N₈ distance (1.3–1.7 Å, approximately) and another one with a longer C₅–N₈ distance (>2.0 Å, approximately). We refer to the two regions as the C–N bound and pre-dissociated regions of the seam, respectively. They are separated by a segment of seam of higher energy where the C₅–N₈ distance is 1.8–2.0 Å. Importantly, the two regions of the seam are associated with different products, and both are accessible from the DMA-S₀ structure after excitation on S₂. As we explain in the following subsections, this explains the formation of different products.

Diazirine formation from the C–N bound seam region

The bound seam region is energetically accessible after excitation (see Fig. 3). To study the reactivity associated with this region we have characterized additional decay paths from representative CIs with C₅–N₈ distances of 1.5 and 1.6 Å, referred to as (S₁/S₀)_X-CN1.5 and (S₁/S₀)_X-CN1.6, respectively. We have also characterized a segment of seam where the bent diazo group is perpendicular to the plane of the ring and the C₄–C₅–N₇–N₈ angle is 90°, (S₁/S₀)_X-D90. There are two MEPs for the decay from (S₁/S₀)_X-CN1.6, one leading back to DMA-S₀ and another one to the diazirine product (Fig. S4 and S5, ESI†). Ground state diazirine has C_s symmetry with the diazo group perpendicular to the C₄–C₅–C₇ plane and almost equal C₅–N₈ (1.47 Å) and C₅–N₉ (1.50 Å) bond lengths (see the structure in Fig. 2). For comparison, the barrier for DMA to diazirine isomerization in the ground state is 2.21 eV, and that for the reverse process is 1.46 eV (see the TS-iso-S₀ structure in Fig. 2 and the energy profile in Fig. S6, ESI†). An MEP to diazirine was also characterized starting from (S₁/S₀)_X-D90 (see Fig. S7, ESI†), and a LIIC from (S₁/S₀)_X-CN1.5 also leads without a barrier to diazirine (Fig. S8, ESI†).

Overall, these results show that diazirine can be formed as a side product during the decay of the S₂ excited molecule in the bound seam region, which is in agreement with experimental observations.²² The results also explain the formation of small amounts of diazirine after excitation to S₁,¹⁷ since this will initially populate the DMA-S₁ minimum, followed by decay in the bound region of the seam, where reactant regeneration will predominate over diazirine formation. We have also located a pathway for the ultrafast, direct formation of acetone from (S₁/S₀)_X-CN1.6 (see Fig. S9, ESI†). Compared to the other pathways, this is the less favoured one, energetically. This is consistent with the kinetic model presented in ref. 23, where acetone is only formed after a sequence of fragmentations and no evidence for its ultrafast formation is provided.

Decay paths from the C–N predissociated seam region: carbene I, ketene and carbene II formation

The reactivity associated with the predissociated seam region has been studied using a point with a C₅–N₈ distance of 2.2 Å as a reference, (S₁/S₀)_X-CN2.2. In spite of the energy barrier along the seam, the predissociated seam region is also accessible energetically from (S₂/S₁)_X, as shown by a LIIC between the two structures (see Fig. 5). The MEP for decay in S₀ from (S₁/S₀)_X-CN2.2 leads to carbene I (Fig. 5). The singlet carbene species has three configurations, two closed-shell configurations and an open-shell one, differing in the occupations of the π and p_x orbitals of C₅. Accordingly, three singlet carbene conformers were optimized and are shown in Fig. 2: a boat-like (closed-shell), a chair-like (closed-shell), and a planar one (open-shell). The boat-shaped conformer is the most stable one, with an energy relative to DMA-S₀ of approximately 2.2 eV, while the chair-shaped one and the planar one are 0.08 eV and 0.51 eV higher, respectively. This is consistent with previous DFT results showing that the singlet carbene resulting from DMA has a boat-like conformation.¹⁷

A transition state (labelled TS-CK-S₀ in Fig. 2) connecting the singlet carbene and the ketene was located at the CASSCF level. The CASSCF barrier is approximately 0.2 eV (see Fig. S10, ESI†), but the MS-CASPT2 energy profile along the MEP shows no barrier (see Fig. S11, ESI†). This is in agreement with previous DFT and MP2 results which found barriers of less than 1 kcal·mol⁻¹.¹⁷ It implies that the singlet carbene lies in a very shallow minimum on the PES, which facilitates further formation of the ketene in a short time scale through a formal stepwise pathway.

As an alternative to the stepwise pathway, we have located a direct, barrierless decay path from (S₁/S₀)_X-CN2.2 to the ketene that follows a concerted, asynchronous mechanism (see Fig. 6). We show three points along the path to illustrate the evolution of the C₅–N₈ and C₅–O₁ distances. In contrast to the pathway leading to carbene I, the direct path to the ketene is not an MEP (see Computational details), and the slope along the path to carbene I is higher than for the direct path. This suggests that the probability to populate the direct ketene formation path during the decay will be lower than that of the stepwise one, even though the time scale of direct ketene formation will be shorter than that along the stepwise path.

In the most recent photolysis experiments in the gas phase, the formation of carbene II was also detected in a sub-ps time scale.²³ We have characterized two pathways for this reaction. The first one is stepwise formation via CO elimination from ground-state ketene. The barrier for this reaction is 1.50 eV (see Fig. S12, ESI†). Such a high barrier may be too high to explain the ultrafast formation of carbene II through the stepwise mechanism, since this process will require considerable intramolecular vibrational energy redistribution to the C–C dissociation mode and this may take a longer time than that measured experimentally. As an alternative, we have located a decay path for the direct formation of carbene II from (S₁/S₀)_X-CN2.2 (see Fig. 7) which may also explain the ultrafast appearance of this species. The structures at the bottom of Fig. 7 illustrate that the process is asynchronous, and the rearrangement of the six- to a five-membered ring precedes the CO elimination.

Triplet carbene formation

Based on the transient spectroscopic signature at 1613 cm⁻¹, it has been suggested that low amounts of the triplet carbene (1–3%) might be formed by an intersystem crossing (ISC) mechanism within 39 ps after the formation of singlet carbene.²² The formation of traces of Meldrum's acid after direct photolysis of DMA has also been taken as an indication of triplet carbene formation.¹⁷ Following this idea, we have investigated two possible mechanisms for this process. The first one is population transfer to the triplet state from the singlet carbene. The triplet carbene minimum, labeled as carbene-triplet in Fig. 2, lies 0.58 eV below the singlet boat-like carbene and has a quasi-planar structure. The singlet–triplet energy gaps at the three singlet carbene minima are shown in Table S3 (ESI†). At the boat- and chair-like S₀ minima, the gap to the triplet is approximately 0.1 eV, and the SOC parameter is approximately 6 cm⁻¹. The small singlet–triplet gaps are in agreement with previous DFT calculations,³ and the SOC values suggest that ISC to the triplet is possible. However, ISC at the carbene competes with the barrierless rearrangement to the ketene, and we have located an alternative mechanism.

The alternative is the formation of the triplet before nitrogen elimination, i.e. directly after passage through (S₂/S₁)_X. ISC for another diazo compound, 3-thienyldiazomethane, has been recently proposed by Fang et al. to take place via T₂, i.e. through a S₁ → T₂ → T₁ sequence.⁶³ Inspired by this work, we have located the (S₁/T₂)_X and (T₂/T₁)_X structures in DMA (see Fig. 2), with relative energies of 3.18 and 2.99 eV, respectively. Interestingly, the calculated SOC between S₁ and T₂ at (S₁/T₂)_X is large (17.8 cm⁻¹). This is due to the fact that S₁ and T₂ correspond to excitation from π₄ to different orbitals, π*_NN for S₁ and π₁* for T₂ (see Fig. 1), and the different orientation of the π*_NN and π₁* orbitals gives rise to a large SOC, in agreement with El-Sayed's rule.⁶⁴ This is different from 3-thienyldiazomethane⁶³ and the related 2-thiothymine,⁶⁵ where the strong spin–orbital interaction is due to the heavy atom effect caused by a sulphur atom. According to this mechanism, ISC at (S₁/T₂)_X may result in the population of the DMA-T₁ minimum after internal conversion from T₂ to T₁. The formation of the triplet carbene from DMA-T₁ can then take place after a barrier of 0.35 eV is surmounted (see Fig. S13, ESI†).

Discussion

The mechanistic picture explaining the early events of DMA photochemistry is summarized in Fig. 8. The key element is the S₁/S₀ seam of intersection, which contains a C–N bound and a C–N predissociated region separated by an energy barrier. Photoexcitation at 266 nm populates the bright S₂ state, which has a ππ* character. The relaxation path goes through the (S₂/S₁)_X CI without any barrier and leads to the S₁/S₀ seam. Decay in the bound region leads preferentially to the regeneration of ground-state DMA or to the formation of diazirine. This is consistent with the low quantum yields of WR and isomerization indicating that the majority of excited DMA will go back to the ground state through internal conversion.^6,17,20 In contrast, decay in the pre-dissociated region leads to the carbene I and II and ketene products.

Fig. 8 Overview of the decay paths on the potential energy surface of DMA, showing the C₅–N₈ distance (in Å), C₄–C₅–N₈–N₉ dihedral angle (in degree), and relative energy (in parenthesis, in eV) of the key structures. Inset: Orbitals involved in the excitations at DMA-S₀ geometry.

The reactivity of the different (S₁/S₀)_X seam regions can be rationalized with the help of the orbitals involved in the excitation. At a short C₅–N₈ distance (e.g. 1.6 Å), the two orbitals in question are the orbital delocalized on the ring and the in-plane π orbital of the diazo group π*_NN (see the orbitals of (S₁/S₀)_X-CN1.6 in Fig. 4). The two intersecting states correspond to a biradical with the configuration (π₁)¹(π*_NN)¹ and a zwitterionic structure with the configuration (π₁)²(π*_NN)⁰. As the C₅–N₈ bond is stretched, the π*_NN orbital mixes with the σ* orbital of the stretched C₅–N₈ bond, and the biradical state turns to a dissociative (πσ*)-type state. Finally, when the C₅–N₈ bond nearly dissociates (see the orbitals of (S₁/S₀)_X-CN2.2 in Fig. 4), the excitation localizes on the π₁ and p_x orbitals of C₅, resulting in a formal carbene (configurations of the intersecting states: (π₁)¹(p_x)¹ and (π₁)²(p_x)⁰). Therefore, it can be concluded that the changes in reactivity are due to the changes in character of the states along the seam. In turn, the barrier that separates the bound and pre-dissociated seam regions explains the wavelength dependence of photolysis. Excitation at long wavelengths only gives access to the bound regions of the seam, where only the diazirine side-product can be formed, whereas excitation at shorter wavelengths provides enough energy to reach the photochemically relevant pre-dissociated seam region.

The calculated decay paths explain the ultrafast formation of the products observed experimentally. The ‘instantaneous’ observation of carbene I in the most recent gas-phase experiments²³ is consistent with the almost barrierless decay path to this product. In the same experiments, the ketene was detected within 27 fs of the excitation. We have located two paths for this product, a stepwise one through carbene I, where the second step has virtually no barrier, and a direct one from the seam which is less favourable energetically. These paths can be considered as limiting cases for the paths followed in the real dynamics, but they suggest that the ketene may be formed in a bi-modal fashion. In this hypothesis, a small fraction of excited molecules would follow the energetically less favoured direct path for ketene formation and would give rise to the signal detected at 27 fs, whereas the main fraction of ketene product would be formed in a longer time scale, along the formal stepwise path. Dynamics calculations are required to provide further support for this hypothesis. Similarly, there are two paths for the formation of carbene II, a direct one and one through the ketene. Therefore, carbene II could also follow a bi-modal appearance.

Conclusions

The early photochemical events of DMA after excitation to S₁ and S₂ are rationalized by the presence of an extended seam of intersection along the C–N dissociation coordinate. The seam is similar to the one described previously by us for DNQ,¹³ and it explains the formation of different primary photoproducts.

DMA stands out among other molecules that have ultrafast photochemistry because three primary products are formed in a sub-ps scale. This is due to the existence of several paths that lead directly from the seam to the products. The spectroscopically bright state lies high compared to other molecules, 5.16 eV, and excitation provides sufficient energy to populate the direct paths. For comparison, the formation of the carbene II analogue mediated by CO elimination is not observed in DNQ. Presumably there is a path similar to that described for DMA, but the excitation energy of DNQ (3.50 eV), which is lower due to the presence of the aromatic chromophore, is not enough to allow access to it.

Going back to DMA, the identification of a stepwise path and a direct path from the seam for ketene and carbene II formation also suggests that these products may be formed in a bi-modal fashion. In addition, the C–N bound and pre-dissociated regions of the seam are separated by a barrier, which explains the absence of WR products after excitation to S₁. Overall, the seam along the C–N coordinate appears as the key mechanistic element to explain the photochemistry of α-diazocarbonyl compounds.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (21303007); the Excellent Young Scholars Research Fund of Beijing Institute of Technology (2013YR1917); the Spanish Ministerio de Economía y Competitividad (RYC-2011-09582, CTQ2015-69363-P, FIS2012-37549-C05-02, and UNGI-10-4E-801) together with the European Funds for Regional Development (FEDER); and the Generalitat de Catalunya (2014-SGR-301, 2014-SGR-1202, and Xarxa de Referència en Química Teòrica i Computacional).

References

1. W. Kirmse, Eur. J. Org. Chem., 2002, 2193–2256.
2. L. Wolff, Justus Liebigs Ann. Chem., 1902, 325, 129–133.
3. A. Bogdanova and V. V. Popik, J. Am. Chem. Soc., 2004, 126, 11293–11302.
4. N. K. Urdabayev and V. V. Popik, J. Am. Chem. Soc., 2004, 126, 4058–4059.
5. V. V. Popik, Can. J. Chem., 2005, 83, 1382–1390.
6. Y. Zhang, G. Burdzinski, J. Kubicki and M. S. Platz, J. Am. Chem. Soc., 2009, 131, 9646–9647.
7. G. T. Burdzinski, J. Wang, T. L. Gustafson and M. S. Platz, J. Am. Chem. Soc., 2008, 130, 3746–3747.
8. F. Kaplan and G. K. Meloy, J. Am. Chem. Soc., 1966, 88, 950–956.
9. G. Burdzinski and M. S. Platz, J. Phys. Org. Chem., 2010, 23, 308–314.
10. J. J. M. Vleggaar, A. H. Huizer, P. A. Kraakman, W. P. M. Nijssen, R. J. Visser and C. Varma, J. Am. Chem. Soc., 1994, 116, 11754–11763.
11. D. Wolpert, M. Schade and T. Brixner, J. Chem. Phys., 2008, 129, 094504.
12. G. L. Cui and W. Thiel, Angew. Chem., Int. Ed., 2013, 52, 433–436.
13. Q. S. Li, A. Migani and L. Blancafort, J. Phys. Chem. Lett., 2012, 3, 1056–1061.
14. Q. Li, A. Migani and L. Blancafort, J. Phys. Chem. A, 2009, 113, 9413–9417.
15. T. Lippert, A. Koskelo and P. O. Stoutland, J. Am. Chem. Soc., 1996, 118, 1551–1552.
16. R. A. Abramovitch, Can. J. Chem., 1959, 37, 361–365.
17. A. Bogdanova and V. V. Popik, J. Am. Chem. Soc., 2003, 125, 14153–14162.
18. A. Bogdanova and V. V. Popik, J. Am. Chem. Soc., 2003, 125, 1456–1457.
19. M. Lang, F. Holzmeier, I. Fischer and P. Hemberger, J. Phys. Chem. A, 2014, 118, 11235–11243.
20. G. Burdzinski, J. Rehault, J. Wang and M. S. Platz, J. Phys. Chem. A, 2008, 112, 10108–10112.
21. M. Jones, W. Ando, M. E. Hendrick, A. Kulczycki, P. M. Howley, K. F. Hummel and D. S. Malament, J. Am. Chem. Soc., 1972, 94, 7469–7479.
22. P. Rudolf, J. Buback, J. Aulbach, P. Nuernberger and T. Brixner, J. Am. Chem. Soc., 2010, 132, 15213–15222.
23. A. Steinbacher, S. Roeding, T. Brixner and P. Nuernberger, Phys. Chem. Chem. Phys., 2014, 16, 7290–7298.
24. M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH Publishers, Inc., New York, 1995.
25. F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321–328.
26. D. R. Yarkony, J. Phys. Chem. A, 2001, 105, 6277–6293.
27. Conical Intersections: Electronic Structue, Dynamics & Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2004.
28. Q. S. Li, A. Migani and L. Blancafort, Phys. Chem. Chem. Phys., 2012, 14, 6561–6568.
29. D. A. Horke, Q. S. Li, L. Blancafort and J. R. R. Verlet, Nat. Chem., 2013, 5, 711–717.
30. Q. S. Li and L. Blancafort, Photochem. Photobiol. Sci., 2013, 12, 1401–1408.
31. Q. S. Li and L. Blancafort, Chem. Commun., 2013, 49, 5966–5968.
32. D. Polli, P. Altoe, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440–443.
33. L. Blancafort, ChemPhysChem, 2014, 15, 3166–3181.
34. M. Ben-Nun and T. J. Martínez, Chem. Phys., 2000, 259, 237–248.
35. M. Barbatti, M. Ruckenbauer and H. Lischka, J. Chem. Phys., 2005, 122, 174307.
36. B. Lasorne, M. J. Bearpark, M. A. Robb and G. A. Worth, J. Phys. Chem. A, 2008, 112, 13017–13027.
37. Q. S. Li, D. Mendive-Tapia, M. J. Paterson, A. Migani, M. J. Bearpark, M. A. Robb and L. Blancafort, Chem. Phys., 2010, 377, 60–65.
38. L. Blancafort and M. A. Robb, J. Chem. Theory Comput., 2012, 8, 4922–4930.
39. I. Conti, M. Garavelli and G. Orlandi, J. Am. Chem. Soc., 2008, 130, 5216–5230.
40. D. Mendive-Tapia, B. Lasorne, G. A. Worth, M. J. Bearpark and M. A. Robb, Phys. Chem. Chem. Phys., 2010, 12, 15725–15733.
41. L. Blancafort, F. Gatti and H. D. Meyer, J. Chem. Phys., 2011, 135, 134303.
42. S. Ruiz-Barragan and L. Blancafort, Faraday Discuss., 2013, 163, 497–512.
43. D. Asturiol, B. Lasorne, G. A. Worth, M. A. Robb and L. Blancafort, Phys. Chem. Chem. Phys., 2010, 12, 4949–4958.
44. M. Barbatti and H. Lischka, J. Am. Chem. Soc., 2008, 130, 6831–6839.
45. K. A. Kistler and S. Matsika, J. Chem. Phys., 2008, 128, 215102.
46. M. Kobylecka, A. Migani, D. Asturiol, J. Rak and L. Blancafort, J. Phys. Chem. A, 2009, 113, 5489–5495.
47. A. Migani, L. Blancafort, M. A. Robb and A. D. Debellis, J. Am. Chem. Soc., 2008, 130, 6932–6933.
48. J. D. Coe, M. T. Ong, B. G. Levine and T. J. Martinez, J. Phys. Chem. A, 2008, 112, 12559–12567.
49. A. Migani, M. A. Robb and M. Olivucci, J. Am. Chem. Soc., 2003, 125, 2804–2808.
50. T. Mori and T. J. Martinez, J. Chem. Theory Comput., 2013, 9, 1155–1163.
51. X.-L. Peng, S. Ruiz-Barragan, Z.-S. Li, Q.-S. Li and L. Blancafort, J. Mater. Chem. C, 2016, 4, 2802–2810.
52. L. Serrano-Andrés and M. Merchán, THEOCHEM, 2005, 729, 99–108.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01., Gaussian, Inc., Wallingford, CT, 2013.
54. G. Karlstrom, R. Lindh, P. A. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239.
55. F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P.-A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247.
56. G. Ghigo, B. O. Roos and P. A. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
57. N. Forsberg and P. A. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
58. S. Ruiz-Barragan, M. A. Robb and L. Blancafort, J. Chem. Theory Comput., 2013, 9, 1433–1442.
59. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
60. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
61. P. Celani, M. A. Robb, M. Garavelli, F. Bernardi and M. Olivucci, Chem. Phys. Lett., 1995, 243, 1–8.
62. Q. Li and L. Blancafort, Photochem. Photobiol. Sci., 2013, 12, 1401–1408.
63. P. J. Guan and W. H. Fang, Theor. Chem. Acc., 2014, 133, 1532.
64. S. K. Lower and M. A. Elsayed, Chem. Rev., 1966, 66, 199.
65. G. L. Cui and W. H. Fang, J. Chem. Phys., 2013, 138, 44315.

---

Footnote

† Electronic supplementary information (ESI) available: Absolute and relative energies and Cartesian coordinates of critical points, energy profiles for decay paths mentioned in the text, singlet–triplet energy gaps and spin–orbit coupling constants at the carbene minima. See DOI: 10.1039/c6cp06290c

---