Open Access Article
Open Access ArticleDeprotonation of formic acid in collisions with a liquid water surface studied by molecular dynamics and metadynamics simulations†
Garold
Murdachaew
 *a,
Gilbert M.
Nathanson
b,
R.
Benny Gerber
acd and
Lauri
Halonen
a
*a,
Gilbert M.
Nathanson
b,
R.
Benny Gerber
acd and
Lauri
Halonen
a
aLaboratory of Physical Chemistry, Department of Chemistry, P. O. Box 55 (A.I. Virtasen aukio 1), FI-00014 University of Helsinki, Finland. E-mail: garold.murdachaew@helsinki.fi
bDepartment of Chemistry, University of Wisconsin-Madison, Madison, Wisconsin 53706, USA
cInstitute of Chemistry and the Fritz Haber Research Center, The Hebrew University, 91904 Jerusalem, Israel
dDepartment of Chemistry, University of California, Irvine, California 92697, USA
First published on 10th October 2016
Abstract
Deprotonation of organic acids at aqueous surfaces has important implications in atmospheric chemistry and other disciplines, yet it is not well-characterized or understood. This article explores the interactions of formic acid (FA), including ionization, in collisions at the air–water interface. Ab initio molecular dynamics simulations with dispersion-corrected density functional theory were used. The 8–50 picosecond duration trajectories all resulted in the adsorption of FA within the interfacial region, with no scattering, absorption into the bulk or desorption into the vapor. Despite the known weak acidity of FA, spontaneous deprotonation of the acid was observed at the interface on a broad picosecond timescale, ranging from a few picoseconds typical for stronger acids to tens of picoseconds. Deprotonation occurred in 4% of the trajectories, and was followed by Grotthuss proton transfer through adjacent water molecules. Both sequential and ultrafast concerted proton transfer were observed. The formation of contact ion pairs and solvent-separated ion pairs, and finally the reformation of neutral FA, both trans and cis conformers, occurred in different stages of the dynamics. To better understand the deprotonation mechanisms at the interface compared with the process in bulk water, we used well-tempered metadynamics to obtain deprotonation free energy profiles. While in bulk water FA deprotonation has a free energy barrier of 14.8 kJ mol−1, in fair agreement with the earlier work, the barrier at the interface is only 7.5 kJ mol−1. Thus, at the air–water interface, FA may dissociate more rapidly than in the bulk. This finding can be rationalized with reference to the dissimilar aqueous solvation and hydrogen-bonding environments in the interface compared to those in bulk liquid water.
1 Introduction
Acid deprotonation and proton transfer (PT) at aqueous interfaces is a fundamental chemical reaction important in many fields. The interface is most often air–water (“soft”) or a wetted icy or mineral interface (“hard”).1 In particular, the protonation state of common strong acids (HCl and HNO3) at air–aqueous interfaces has been studied both experimentally,2–4 and theoretically.1,3–8 Particular interest in these studies has been determining if the acid's strength and deprotonation mechanisms and timescales at aqueous interfaces differ compared to their known behavior in bulk ambient liquid water. HNO3, while a strong acid in liquid water, was found to remain mainly in its neutral form at the air–water interface (also depending on its concentration).1–7 With regard to HCl, just as in the bulk, deprotonation occurs at the interface. However, while in the bulk PT quickly leads to a solvent-separated ion pair (SSIP) of Cl−⋯(H2O)n⋯H3O+, n ≥ 1, recently, Baer et al.1 have shown that at the interface the contact ion pair (CIP) of Cl−⋯H3O+ is uniquely stable. Therefore, the simple impression of the higher concentration of under-coordinated water molecules at the interface leading to enhanced reactivity need not always be true.Our own recent theoretical studies have examined the behavior of HCl and H2SO4 at hard interfaces: the air-wetted hydroxylated quartz interface9,10 and HNO3 at the air–ice interface including defective ice and ice with a quasi-liquid layer.11–13 It has been suggested that while ideal ice surfaces may significantly reduce deprotonation of such strong acids, real ice surfaces at temperatures greater than about 250 K will allow deprotonation due to the presence of the apparently ubiquitous quasi-liquid layer or defects,11–13 while domains of nearly-perfect proton-ordered ice monolayers on quartz may enhance deprotonation of HCl and H2SO4.9,10,13
Here, we follow two recent ab initio studies that compared the behavior of various strong acids at the air–water interface to their bulk behavior.1,3 Experiments have stimulated such studies and have provided useful insights into the dynamical behavior of acids at aqueous surfaces. The experimental approaches have included the surface sensitive spectroscopic technique of vibrational sum frequency generation (VSFG),14 and X-ray photoelectron spectroscopy (XPS).3 An alternate approach ideally suitable for examining the liquid surface structure, kinetics, and the presence of delayed as well as prompt chemical reactions is molecular scattering from a continually renewed air–liquid interface.15–18 A recent development by introducing liquid microjets has enabled the study of liquids with significant vapor pressure such as water at near-ambient temperatures.19,20 The time dependence of acid deprotonation and PT can be monitored in such studies by observing isotopic D to H exchange by mass-spectrometric detection. Inspired by this experimental development and with a view to complementing the insights to be gained in these studies, we have recently completed an ab initio study of HCl scattering and deprotonation at the air–water interface.21
Organic acids such as carboxylic acids RCOOH and dicarboxylic acids as well have importance in various contexts. The simplest carboxylic acids, formic acid (FA, R = H; and also acetic acid, R = CH3) exist in significant concentrations in the environment.22–26 These carboxylic acids are some of the less reactive volatile organic compounds (VOCs) emitted by vegetation and ants for FA, and have significant concentrations in the clean troposphere in forested areas.26 They contribute a large fraction of observed gas-phase acidity22,25 and constitute a major portion of the nonmethane organic mixture of the clean atmosphere. Furthermore, their concentrations may be increased in the polluted atmospheres in urban areas,25 where FA is a contributor to photochemical smog.23 Thus, they contribute to particle formation and growth, rainwater and cloud acidity, and corrosion of metals by FA.27 The acids are removed from the atmosphere through wet or dry deposition.23 Since they have a high solubility, scavenging by rainwater and wet deposition is the preferred removal route.25 Despite being weaker acids (the pKa of FA is 3.75, the while pKa of acetic acid is 4.75) than the strong mineral acids such as sulfuric and nitric acids, the carboxylic acids usually have much larger concentrations,22 and thus may have a stronger overall effect on the free acidity of rainwater. Recently, FA has been proposed as a hydrogen storage medium for a hydrogen economy.28
Despite the prevalence of organic acids in the environment, fewer studies exist for these species, including formic acid, at interfaces. The behavior of FA in aqueous environments has been studied in both experiments and in simulations. Recent experiments have examined the protonation state of FA at the air–water interface. Brown et al.29,30 and Ottosson et al.31 have employed X-ray photoelectron spectroscopy (XPS), while the group of Johnson et al.32,33 have used VSFG. Both techniques see no or minimal deprotonation of this medium-strength acid at the air–water interface. The theoretical studies included those examining the binding energies and minimum energy structures of FA–water clusters,34–37 equilibrium and biased (metadynamics) studies of the deprotonation barrier of FA in bulk ambient water,38 classical potential studies of the free energy of solvation profile of FA at air–aqueous interfaces, including the air–water interface39 and the air–ice interface.40 The computed free energy profiles between vapor and solution39,40 support the experimentally known partitioning of FA into water, as quantified by the Henry's Law constant of ≈9000 M per atm at 298 K.41–43 In addition, the simulations confirm that FA has a preference for adsorption at the air–water interface, as expected by a species RCOOH comprised of the hydrophilic hydroxyl (–OH) and hydrophobic R-groups.
In this work, in order to guide and assist the interpretation of ongoing experimental work, we have employed ab initio simulations with density functional theory to study the mechanisms, on a timescale of a few to tens of picoseconds, of adsorption and deprotonation of formic acid at the ambient air–water interface, both with (gentle) collisions and also with biased sampling (metadynamics) to better understand the free-energy barrier to deprotonation at the interface in comparison to the bulk.
2 Systems and methods
2.1 Equilibrium and collision simulations
The QUICKSTEP module within the CP2K package44 was employed for all ab initio simulations with the density functional theory (DFT) using the BLYP exchange–correlation functional45,46 combined with a dispersion correction (BLYP-D247). The wave function was represented by double-zeta valence polarization (DZVP) basis sets on atoms in combination with GTH pseudopotentials.48 The energy cutoff for the expansion in plane waves was 280 Ry (where 1 Ry = 0.5 Hartree = 2.1798 × 10−18 J). The wave function was converged to 3 × 10−7 Hartree. A 0.4 fs time step was used initially but then 0.5 fs was used for the majority of the calculations. All systems were modeled with periodic boundary conditions. To reduce computational costs, the interface was modeled using a relatively thin water slab containing 72 H2O molecules within a 13.4724 × 15.5566 × 40 Å3 rectangular supercell, the same size as that reported in ref. 21 and 49–51. As in previous work,21,52,53 a harmonic constraint K(z − z0)2 with a spring constant K = 1 Hartree bohr−2 (1 bohr = 0.529177 Å, 1 Å = 10−10 m) was always used to ensure that the center of mass (COM) of the water slab remained at the origin of the coordinate system. Note that the constraints discussed below had this form but with a smaller spring constant, K = 0.1 Hartree bohr−2, and were applied to the COM of FA. In addition, the system contained a single FA molecule initially placed approximately 5 Å above the water surface. The amount of vacuum between adjacent images in the z direction was thus 25–30 Å. For comparison, calculations of FA in bulk liquid water were also performed. The model system contained a single FA and 63 water molecules in a cubic box with a side length of 12.4138 Å. All simulations were commenced using trans-FA since the cis conformer is 16.7 kJ mol−1 higher in energy (in vacuo) and not stable at ambient temperatures.54,55 The systems are displayed in Fig. 1.Prior to addition of FA, to prepare the water systems, canonical ensemble (NVT) simulations of durations 25.0 ps and 12.0 ps using a massive Nosé–Hoover thermostat56,57 at 300 K were performed for the bare water slab (72 water molecules) and the bulk liquid water box (64 water molecules), respectively. The initial portions of the trajectories were considered to be equilibration portions, and therefore averages were computed only for the final 15.0 ps and 10.0 ps portions of the trajectories for the slab and the bulk liquid, respectively. For computing radial distribution functions (RDFs) and hydrogen bond (H-bond) populations for the slab, the top and bottom surfaces were averaged together. A standard geometric criterion was used to identify hydrogen bonding between two molecules with molecular groups containing a hydrogen donor and a hydrogen acceptor.21,52,53 An H-bond was considered to exist between a donor D and an acceptor A if the distance D–A was less than 3.2 Å and the D–H⋯A angle was greater than 140°. With regard to the bulk water simulation, we confirmed that the internal energy per molecule or the heat of vaporization and the structure in the form of the RDFs were in good agreement with the values expected from BLYP-D simulations and with the experiment (see, e.g., ref. 53 and references therein for similar studies on water slabs and bulk water). As in ref. 52 and 53, we consider the center of the slab to be at z = 0 Å, and fit the density profile ρ(z) to the hyperbolic tangent function
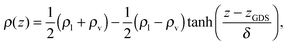 | (1) |
Besides the density, the relative H-bond population types of the water molecules at the surface are also of importance for surface reactivity. A water molecule in the bulk will prefer to form four H-bonds with its neighbors, two as a donor (D) and two as an acceptor (A). Such a water molecule is of the H-bond type DDAA. Water molecules at the surface may prefer to be under-coordinated and may be of H-bond types ADD, DAA, DA, or A. The H-bond population profiles of the bare water slab are summarized in Fig. 2(b). These results are in good agreement with those obtained using BLYP-D2 with a thick slab.59 As expected, DDAA dominates in the center, while at the surface the largest portion of water molecules are of the type DA. Such under-coordinated water molecules account for the enhanced reactivity of the surface compared to bulk systems, assisting in molecular adsorption and reaction, as we find in our simulations. While we are using a thin slab in our definition of bulk and surface regions, it is gratifying that the main characteristics of the slab are reproduced compared to the thicker slabs used in ref. 52, 53 and 59.
Trajectories in the microcanonical ensemble (NVE) of FA impacting the water slab were obtained as follows. For each trajectory, the initial geometry of the water slab came from a different snapshot (to enhance sampling) in the production portion of the NVT simulation described above. Then, the FA molecule was introduced 4–5 Å above the water surface. The COM of the FA molecule was constrained at this height and a further 2 ps NVT equilibration was performed. This served to allow rotations and translations of the FA molecule that are steered by interactions with the surface to lower energy states relative to the surface since the height was close to the surface at the start for reasons of efficiency. Next, the constraint was released and the actual NVE collision simulation was performed with initial thermal velocities selected from the Maxwell–Boltzmann distribution at 300 K. In 37 trajectories, the initial velocities of the FA molecule were purely thermal. In addition, 2 trajectories each were computed in which the COM of FA had an additional 1, 2, 4, or 10 kBT (2.5, 5.0, 10.0, or 24.9 kJ mol−1, respectively) of kinetic energy added, with the impact directed at 45° toward the air–water interface. Thus, there were 45 trajectories computed, whose durations were mainly 8–10 ps, and 5 trajectories were extended to about 50 ps, giving about 590 ps of the total NVE trajectory time. During the trajectories, the height z of the FA molecule above the surface, its acidic hydroxyl bond length rOH, and its orientation angles were monitored (see Fig. 1(b)). Other quantities that were monitored include the other bond distances, the H–C–O–H dihedral angle and the possibility of trans to cis isomerization, and FA–water H-bonds.
To better understand the solvation of formic acid in various aqueous environments and also to provide starting points for the metadynamics simulations described below, we performed equilibrium simulations in the canonical ensemble (NVT). Similarly to the approach used in ref. 1 and 3, we examined the activity of the interface by constraining the COM of FA at three positions in the slab, two in the interfacial region, at the surface (z = zGDS + 1 Å) and at the subsurface (z = zGDS − 1 Å), and at the center of the slab, at z = 0 Å. The last position can be compared to the analogous calculation where FA is solvated in the bulk liquid water with 63 water molecules. After equilibration, the production portions of these simulations were 14–24 ps in duration to ensure sufficient sampling.
2.2 Metadynamics simulations
In order to explore the deprotonation mechanisms of aqueous FA and obtain the free energy of dissociation barriers, an enhanced sampling method was required. We employed metadynamics,60,61 in particular, well-tempered metadynamics (WTMetaD),62 which has been shown to converge asymptotically.63 As in ref. 1 and 3, we examined the activity of the interface in various aqueous environments: bulk water, and center, subsurface, and surface of the water slab. The WTMetaD simulations always began with an equilibrated structure (with neutral, trans-FA) coming from the equilibrium simulations described above and were likewise performed in the NVT ensemble. Thus, the free energy differences are properly Helmholtz free energy differences ΔF, but, with our slab setup, where the internal pressure will be approximately constant, they approximate Gibbs free energy differences ΔG.After some experimentation and tuning, the following parameters, which are typically found in ref. 62 and 63 as well, were selected. The reaction coordinate, also termed the collective variable (CV), drives the deprotonation and PT and unambiguously differentiates protonated and deprotonated states. It was chosen to be nOH, which measures the coordination of the hydroxyl oxygen of FA by its H atom,
 | (2) |
3 Results and discussion
3.1 Collision simulations
We will discuss mainly six representative thermal collision trajectories: two trajectories where spontaneous dissociation was observed (labeled 1 and 2) and four trajectories where it was not (labeled 3–6). Trajectory 1 was 10 ps in duration, while trajectories 2–5 lasted 50 ps. The collisions with added kinetic energy had similar outcomes, with the exception that they took longer to equilibrate to the surface, and thus had a reduced likelihood for deprotonation within the duration of the computed trajectory. In our study of HCl at the air–water interface,21 it was observed that adding energy to the system, either by raising the temperature of the water slab, or by adding collision energy to HCl, typically reduced the time required for HCl to deprotonate. With formic acid, this seems not to be the case either because FA is a weak acid and more collision energy is needed or because the energy can be distributed among more modes of the larger molecule. The results for all 45 scattering trajectories can be found in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (adsorbed
1 (adsorbed![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vapor), 1 × 103
vapor), 1 × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (absorbed
1 (absorbed![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vapor), and 20
vapor), and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (adsorbed
1 (adsorbed![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) absorbed). Our results are in general agreement with these partitioning predictions. Experimentally, the Henry's Law constant43 of 9000 M per atm at 25 °C also reflects the high solubility of FA, although it does not distinguish between adsorption in the surface region and absorption into the bulk. We note that the trapping observed in all collisions and the absence of desorption over the 50 ps trajectories is also in accord with separate molecular beam scattering experiments19,20 of FA collisions with 8 molal LiBr/H2O at 250 K. These microjet experiments show that almost every FA impinging at thermal collision energies disappears into solution, and does not evaporate over the 100 microsecond observation window.66
absorbed). Our results are in general agreement with these partitioning predictions. Experimentally, the Henry's Law constant43 of 9000 M per atm at 25 °C also reflects the high solubility of FA, although it does not distinguish between adsorption in the surface region and absorption into the bulk. We note that the trapping observed in all collisions and the absence of desorption over the 50 ps trajectories is also in accord with separate molecular beam scattering experiments19,20 of FA collisions with 8 molal LiBr/H2O at 250 K. These microjet experiments show that almost every FA impinging at thermal collision energies disappears into solution, and does not evaporate over the 100 microsecond observation window.66
 | ||
| Fig. 3 The vertical position of FA carbon atom relative to the center of the water slab is shown for collision trajectories 1–6. The black lines mark the position of the Gibbs dividing surface zGDS of the water slab and the interfacial width ±2δ of the surface. The colored dotted lines (blue, center of the slab; red, subsurface region; and green, surface region, see Fig. 2) mark the vertical positions at which FA was fixed in the metadynamics simulations and are drawn here to show how often the unrestrained trajectories visit these regions. The arrows labeled b–f refer to the snapshots shown in Fig. 5 (trajectory 1) and 6 (trajectory 2). | ||
Fig. 4 presents the formic acid hydroxyl bond length rOH as a function of time for the six selected trajectories. The dotted line and labels on the right axis mark the approximate stretched O–H bond lengths when an H-bond is formed through donation of the H to a water oxygen atom (rOH = 1.1 Å), when the proton is shared (1.4 Å), when dissociation occurs and a contact ion pair or CIP is formed (1.6 Å), and when a minimal-distance solvent-separated ion pair or SSIP is formed (1.8 Å). Fig. 4 shows that while a number of trajectories exhibited stretched FA (O)H bonds, only two of the 45 collision trajectories (4%) underwent spontaneous deprotonation.
 | ||
| Fig. 4 The O–H separation in FA is shown for collision trajectories 1–6. The dashed black lines mark the approximate O–H separations for various states of aqueous FA. See the text for details. | ||
Fig. 5 shows snapshots from trajectory 1 (top view). FA first establishes an (O)H donor hydrogen bond (H-bond, panel (a)) with a surface-water oxygen atom. FA then deprotonates at 3.88 ps. At this time, FA is solvated by three H-bonds, the mentioned donor H-bond of FA and two H-bonds accepted by FA from nearby water molecules at (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O. Panels (b–f) show the deprotonation and formation of the CIP and SSIP as PT proceeds. Both Eigen (H3O+) and Zundel (H5O2+) charged water species were present. To summarize, following deprotonation, the proton defect migrates through a ring of four water molecules and neutral FA is reformed in the cis conformation. The whole process is completed within approximately 6 ps. In Fig. 3, the red arrows for trajectory 1, marked b–f, indicate that the entire deprotonation and reprotonation process occurs near the top of the interface, z ∼ zGDS + 1, mainly z > zGDS, what we refer to as the “surface” region.
)O. Panels (b–f) show the deprotonation and formation of the CIP and SSIP as PT proceeds. Both Eigen (H3O+) and Zundel (H5O2+) charged water species were present. To summarize, following deprotonation, the proton defect migrates through a ring of four water molecules and neutral FA is reformed in the cis conformation. The whole process is completed within approximately 6 ps. In Fig. 3, the red arrows for trajectory 1, marked b–f, indicate that the entire deprotonation and reprotonation process occurs near the top of the interface, z ∼ zGDS + 1, mainly z > zGDS, what we refer to as the “surface” region.
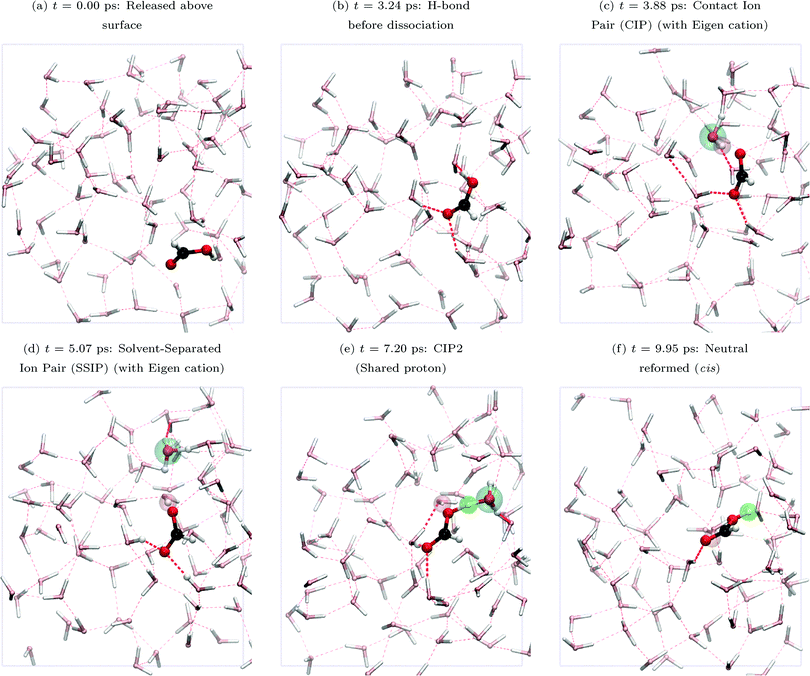 | ||
| Fig. 5 Snapshots (top view) from trajectory 1 showing FA deprotonation and PT at the air–water interface. Key used throughout this paper: carbon, black; oxygen, red; hydrogen, white; background atoms, pastel colors; hydrogen bonds shown with dotted red lines. Important atoms or states are highlighted by bubbles: (1) cyan bubble (large) – indicates an Eigen (one cyan bubble) or Zundel (two cyan bubbles) species produced after FA deprotonation and proton migration; (2) red bubble – initial proton from FA after FA deprotonation; (3) green bubble – another proton which covalently attaches to the same FA oxygen atom (making neutral FA again, either trans or cis); (4) blue bubble (not in this figure but present in, e.g., trajectory 2, see Fig. 6) – another proton which covalently attaches to the other FA oxygen atom (making neutral FA again, either trans or cis). | ||
Fig. 6 shows snapshots from trajectory 2. Note the differences in FA orientations exhibited between the panels showing the start of the trajectory (a) and the H-bond prior to dissociation at (b). Likely due to the necessity to establish an optimum orientation and solvation, this trajectory required a long wait before the deprotonation process was observed at 29.230 ps but PT was rapid once it commenced. Panel (c) shows that at dissociation FA exhibits a tilt relative to the surface normal. As in trajectory 1, FA is involved in three H-bonds with surface water molecules. However, here it donates (O)H and accepts one H-bond at O(H) and one H-bond at (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O. Following deprotonation, the proton defect migrates through a wire of three water molecules. Neutral FA is reformed in the trans conformation but with the proton attached to the other FA oxygen atom. The whole ultrafast process is completed in about 120 fs. In Fig. 3, the green arrows for trajectory 2, marked b–f, indicate that again this deprotonation–reprotonation process occurs within the top of the interface.
)O. Following deprotonation, the proton defect migrates through a wire of three water molecules. Neutral FA is reformed in the trans conformation but with the proton attached to the other FA oxygen atom. The whole ultrafast process is completed in about 120 fs. In Fig. 3, the green arrows for trajectory 2, marked b–f, indicate that again this deprotonation–reprotonation process occurs within the top of the interface.
 | ||
| Fig. 6 Snapshots (top view) from trajectory 2 showing the FA deprotonation and PT at the air–water interface. Also see Fig. 5. | ||
To better understand how the issues discussed impact our system, we performed a detailed structure and dynamics analysis of the deprotonation and PT events in trajectories 1 and 2. This analysis is shown graphically in Fig. 7 and 8.
In trajectory 1, as mentioned above, Fig. 7 shows that the deprotonation of trans-FA, the series of PT events, and reprotonation processes ending in neutral cis-FA occur via PT through a ring of four H-bonded water molecules attached to the hydroxyl oxygen, O(H) (here labeled O(I); similarly the carbonyl oxygen (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O is labeled O(II)); see panel (a) which displays a snapshot at t = 4.665 ps. While in bulk ice and at lower temperatures PT may rely mainly on proton tunneling, water molecule mobility due to thermal fluctuations in liquid water (and even the greater mobility of water molecules at the surface of defect-rich ice11 or at the ice quasi-liquid layer12) permits the occasional shrinkage of O–O distances which significantly reduces the barrier to PT, and allows the process to proceed without invoking proton tunneling.77,79 The sequences of O–O distances and PT coordinates in Fig. 7(a–c) are defined as rOO,i = |rO,i−1 − rO,i| and ξi = |rO,i−1 − rH,i| − |rH,i − rO,i|. Thus, for a proton i, ξi < 0, ξi = 0, and ξi > 0 prior to, at the moment of, and after the PT event, respectively.
)O is labeled O(II)); see panel (a) which displays a snapshot at t = 4.665 ps. While in bulk ice and at lower temperatures PT may rely mainly on proton tunneling, water molecule mobility due to thermal fluctuations in liquid water (and even the greater mobility of water molecules at the surface of defect-rich ice11 or at the ice quasi-liquid layer12) permits the occasional shrinkage of O–O distances which significantly reduces the barrier to PT, and allows the process to proceed without invoking proton tunneling.77,79 The sequences of O–O distances and PT coordinates in Fig. 7(a–c) are defined as rOO,i = |rO,i−1 − rO,i| and ξi = |rO,i−1 − rH,i| − |rH,i − rO,i|. Thus, for a proton i, ξi < 0, ξi = 0, and ξi > 0 prior to, at the moment of, and after the PT event, respectively.
The insets in panels (b) and (c) of Fig. 7 focus attention on the PT events. It it seen that the ith proton is transferred when rOO,i ≈ 2.4 Å. The PT of protons 1 and 2 is nearly concerted. The remaining PT events are sequential, separated by rest periods. This is in agreement with the new understanding of PT events in liquid water:67 containing both intense bursts of activity in the form of concerted transfers, on a timescale of tens to hundreds of femtoseconds, and sequential PT events as well, separated by rest periods, resulting in a slower, few picosecond timescale. Here, the timescale of the overall process is dominated by sequential transfers/rest periods, and thus occupies approximately 6 ps. Since the ring of water molecules starts and ends on O(I), the overall result of these PT events is to transform trans-FA into cis-FA.
In trajectory 2, Fig. 8 shows that the deprotonation of trans-FA, the series of PT events, and reprotonation processes ending again in neutral trans-FA occur via PT through a wire of three H-bonded water molecules connecting O(I) to O(II); see panel (a) which displays a snapshot at t = 29.293 ps. Such an arrangement is known to be a low-energy configuration from gas phase (cluster) experimental and theoretical studies, with particularly strong and therefore short H-bonds.35 The sequences of O–O distances rOO,i and PT coordinates ξi in Fig. 8(a–c) are defined similarly as in Fig. 7(a–c).
The long wait for the PT events in trajectory 2 can be partially understood by seeing that in panel (b) of Fig. 8 the relative distance between water molecules 2 and 3 is initially large. Thus, the wire of three waters facilitating PT in this trajectory takes a long time to assemble. Once the wire is assembled, panel (c) shows that all the PT events are ultrafast: there is concerted transfer of protons 2 and 3 and nearly concerted transfer of the other protons. Thus, concerted PT is fully dominant in this trajectory and only the shorter timescale is relevant, allowing the whole process to be completed in about 120 fs. The result of the overall PT events is to reform trans-FA, while switching the identity of the hydroxyl and carbonyl oxygen atoms.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O⋯Hw. If FA sinks deeper into the water surface and the solvation shell continues to form, FA can accept up to two additional relatively weak H-bonds at each oxygen atom. These observations are in agreement with experimental and theoretical studies of FA microsolvation in small water clusters, where it is seen that one strong and typically 1–2 or 3 weaker H-bonds with water molecules can be formed.34,35 The rightmost panels in Fig. 9 show the total number of H-bonds that FA establishes with water. It is seen that the two instances of deprotonation, in trajectories 1 and 2, are often correlated with FA forming about 4 H-bonds. However, such an H-bonding or solvation state does not always lead to deprotonation. Deprotonation and Grotthuss migration of the proton defect also depends on the state of the second solvation shell surrounding the acid.78 This is in agreement with the behavior of other acids whose deprotonation also depends on some minimal solvation.80
)O⋯Hw. If FA sinks deeper into the water surface and the solvation shell continues to form, FA can accept up to two additional relatively weak H-bonds at each oxygen atom. These observations are in agreement with experimental and theoretical studies of FA microsolvation in small water clusters, where it is seen that one strong and typically 1–2 or 3 weaker H-bonds with water molecules can be formed.34,35 The rightmost panels in Fig. 9 show the total number of H-bonds that FA establishes with water. It is seen that the two instances of deprotonation, in trajectories 1 and 2, are often correlated with FA forming about 4 H-bonds. However, such an H-bonding or solvation state does not always lead to deprotonation. Deprotonation and Grotthuss migration of the proton defect also depends on the state of the second solvation shell surrounding the acid.78 This is in agreement with the behavior of other acids whose deprotonation also depends on some minimal solvation.80
 | ||
Fig. 9 The number of H-bonds that FA forms with water molecules is shown for four selected collision trajectories. The rows, top to bottom, show collision trajectories 1–4. Left to right, the column in each row shows the number of FA–water H-bonds involving the FA hydroxyl group (–OH), the FA carbonyl group (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and the total number of H-bonds, respectively. The dotted black line at 4 H-bonds in the panels in the rightmost column marks the approximate H-bonding threshold for FA ionization (3–4 H-bonds). The arrows labeled b–f refer to the snapshots shown in Fig. 5 (trajectory 1) and 6 (trajectory 2). O), and the total number of H-bonds, respectively. The dotted black line at 4 H-bonds in the panels in the rightmost column marks the approximate H-bonding threshold for FA ionization (3–4 H-bonds). The arrows labeled b–f refer to the snapshots shown in Fig. 5 (trajectory 1) and 6 (trajectory 2). | ||
3.2 Equilibrium simulations
To better understand the state of formic acid in the various aqueous environments, we also performed equilibrium simulations with formic acid in bulk liquid water and constrained at three depths (center and subsurface and surface of the slab). The results of the simulations are described below. We observed spontaneous dissociation when formic acid was at the subsurface (see the ESI† for details).| Ref. | (O)H⋯Ow and O(H)⋯Hw | (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O⋯Hw )O⋯Hw |
Total | |
|---|---|---|---|---|
| a The data were obtained by averaging the data shown in Fig. S5 of the ESI. b Estimated from the hydration number of 3.1 obtained from the O–Hw radial distribution function reported in ref. 81. c This is the hydration number obtained from the O–Ow radial distribution function. Such a hydration number will always be an overestimate of the number of H-bonds. d Total hydration numbers of formate as estimated from X-ray diffraction and Raman/ATR-IR experiments, extrapolated to infinite dilution. e Experiments and theory. | ||||
| Bulk water | This work | 2.1 | 1.2 | 3.3 ± 0.8 |
| Center of slab | This work | 1.8 | 1.0 | 2.8 ± 0.9 |
| Subsurface of slab | This work | 1.2 | 1.8 | 3.0 ± 0.5 |
| Subsurface of slab (formate ion) | This work | 1.9 | 2.2 | 4.1 ± 0.6 |
| Surface of slab | This work | 1.9 | 1.1 | 3.0 ± 0.6 |
| Bulk water | 81 (Theory: DFT) | 3.0b | ||
| Bulk water (formate ion) | 81 (Theory: DFT) | (<4.4c) | ||
| Bulk water (formate ion) | 82 (Theory: DFT) | (<4.9c) | ||
| Bulk water (formate ion) | 83 and 84 (Experiment) | (<4.6–4.9d) | ||
| Bulk water (formate ion) | 85 (Experiment: IR) | >3e | ||
At the surface and subsurface of the slab, the number of H-bonds was slightly reduced, to 3.0. After the spontaneous deprotonation at the subsurface, however, the average number of H-bonds that formate participated in was 4.1, in reasonable agreement with ref. 81 and other studies.82–85 Such an increase in H-bonds and hydration numbers of the anion compared to the neutral acid is expected since the anion can form stronger H-bonds, and thus better compete with water–water H-bonds.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 42–57°. Since VSFG is most sensitive to molecules at the top of interfaces, this can be compared to our values of θsurfaceCH = 42 ± 12° and θsurfaceC
O = 42–57°. Since VSFG is most sensitive to molecules at the top of interfaces, this can be compared to our values of θsurfaceCH = 42 ± 12° and θsurfaceC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 38 ± 14°. In the subsurface region, FA undergoes a rotation to a tilted orientation, with θsubsurfaceCH = 83 ± 18° and θsubsurfaceC
O = 38 ± 14°. In the subsurface region, FA undergoes a rotation to a tilted orientation, with θsubsurfaceCH = 83 ± 18° and θsubsurfaceC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 78 ± 16°. Such a rotation may be energetically favored since it will place the carbonyl (–C
O = 78 ± 16°. Such a rotation may be energetically favored since it will place the carbonyl (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) group of FA closer to the under-coordinated water molecules present at the surface, thereby allowing for (C
O) group of FA closer to the under-coordinated water molecules present at the surface, thereby allowing for (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )O⋯Hw H-bond formation without necessitating a competition with other water molecules. Comparing the relatively sharp orientational angle distributions of FA at the surface to the broader ones at the subsurface, it is seen that an average increase in depth of merely 2 Å quickly causes loss of a well-defined orientational preference. Thus, it may be that the VSFG spectroscopic method used by Johnson, dependent as it is on a well-defined molecular orientation and insensitive to a homogeneous environment, does not detect the subsurface FA where deprotonation is most enhanced (see below) due to this rapid loss of orientational preference.
)O⋯Hw H-bond formation without necessitating a competition with other water molecules. Comparing the relatively sharp orientational angle distributions of FA at the surface to the broader ones at the subsurface, it is seen that an average increase in depth of merely 2 Å quickly causes loss of a well-defined orientational preference. Thus, it may be that the VSFG spectroscopic method used by Johnson, dependent as it is on a well-defined molecular orientation and insensitive to a homogeneous environment, does not detect the subsurface FA where deprotonation is most enhanced (see below) due to this rapid loss of orientational preference.
 | ||
Fig. 10 Distributions of the cosines of two orientation angles of neutral trans-FA at two depths in the interfacial region obtained from equilibrium simulations: (a) cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCH and (b) cos θCH and (b) cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θC θC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. The extracted average values and standard deviations of the angles and the comparison to the experimental values reported in ref. 32 are: (a) θsurfaceCH = 42 ± 12° (θexpCH = 27–43°), θsubsurfaceCH = 83 ± 18°; and (b) θsurfaceC O. The extracted average values and standard deviations of the angles and the comparison to the experimental values reported in ref. 32 are: (a) θsurfaceCH = 42 ± 12° (θexpCH = 27–43°), θsubsurfaceCH = 83 ± 18°; and (b) θsurfaceC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 38 ± 14° (θexpC O = 38 ± 14° (θexpC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 42–57°), θsubsurfaceC O = 42–57°), θsubsurfaceC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 78 ± 16°. Also see the ESI† for the cos O = 78 ± 16°. Also see the ESI† for the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn and cos θn and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCO distributions. θCO distributions. | ||
3.3 Metadynamics simulations
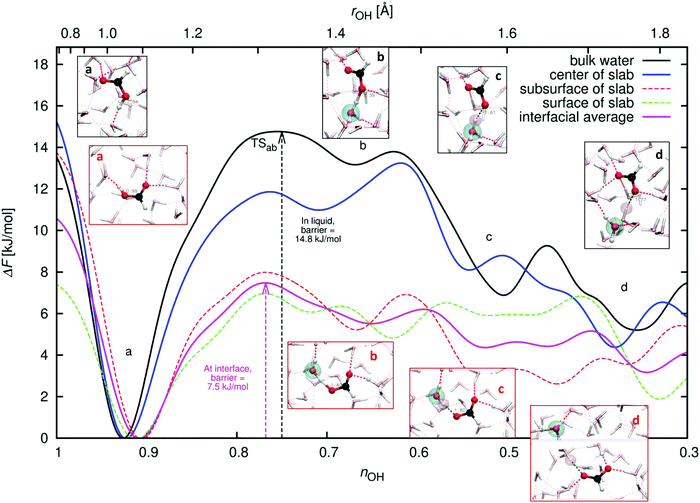
Fig. 11 presents the results of the WTMetaD simulations of FA deprotonation. We sampled sufficiently to explore the configurational space and obtain convergence (see ESI†). Fig. 11 shows the free energies and barriers for the deprotonation and PT processes in the configurational snapshots. The states of the system can be characterized by the value of CV nOH defined in eqn (2) (or, equivalently, rOH, which is shown on the top axis). These system states are: state a – the FA initial neutral or the FA (O)H hydrogen bonded to a water oxygen atom, nOH ≈ 0.9 (rOH ≈ 1.1 Å); state b – the shared-proton configuration, nOH ≈ 0.7 (rOH ≈ 1.4 Å); state c – the contact-ion pair (CIP), nOH ≈ 0.5 (rOH ≈ 1.6 Å); and state d – the closest solvent-separated ion pair (SSIP), nOH ≈ 0.3 (rOH ≈ 1.8 Å). The largest barrier to deprotonation (the transition state marked TSab) is located between states a and b.Fig. 11 compares the results of the simulations of FA in bulk liquid water (black line) and in the center of the slab (blue line). The two curves are in reasonable agreement given that our slab is relatively thin. Next, the results for FA sampled at two depths in the interfacial region, the subsurface (z = zGDS − 1 Å) and surface (z = zGDS + 1 Å) are shown (see also Fig. 2). Their deprotonation barriers are similar, and the two curves have been averaged together to obtain the average behavior at the interface.
Our barrier to FA deprotonation in liquid water is somewhat low at 14.8 kJ mol−1, compared to barriers of about 16.7–18.0 kJ mol−1 found by Lee et al.38 The underestimation of the barrier in the bulk liquid is due to an underestimation of free energy which we attribute mainly to our use of a relatively small DZVP basis set, since our preliminary calculations using the larger MOLOPT-DZVP-SR basis set86 indicate that the barrier becomes about 2.1 kJ mol−1 deeper in the bulk liquid. Here, we are ignoring nuclear quantum effects and any possible deficiencies of the DFT BLYP-D2 description of the electronic structure, which would also account for differences with respect to, for example, experimental and calculated pKas. We do not attempt to compute pKas since that would require converging states c (CIP) or d (SSIP). The uncertainty in the interfacial curve, if considered as the deviation between the subsurface and surface curves becomes large in the c and d regions.
Considering the interfacial curve, we obtain a barrier of 7.5 kJ mol−1, a reduction of nearly 50% relative to the barrier in the bulk of 14.8 kJ/mol. Our results imply that formic acid deprotonates faster at the air–water interface than when fully solvated in water. This observation may be reconciled with the lack of observed deprotonated FA at the air–water interface in the XPS experiments by Brown et al.29,30 and in the VSFG experiments by Johnson et al.32,33 by noting that deprotonation is a relatively rare event.
4 Concluding remarks and atmospheric chemistry implications
We have employed ab initio molecular dynamics with dispersion-corrected density functional theory to study an atmospherically prevalent medium-strength acid, formic acid (FA), at the air–water interface. Our scattering simulations confirm that FA is strongly surface active, and remains adsorbed even in our longest simulations of 50 ps. Deprotonation happens in only about 4% of our simulations. When it occurs, it initiates PT whose duration ranges from fractions of a picosecond to a few picoseconds, indicative of concerted and sequential proton transfer mechanisms, respectively. PT terminates with the reformation of neutral FA, which may however have undergone a trans to cis conformational change. With respect to our total trajectory time of collisions of about 590 ps, we observed the existence of deprotonated FA in only about 1% of the time (about 6 ps in the two trajectories) before the neutral FA was reformed by various mechanisms. With regard to neutral FA, our simulations show an agreement between the orientation of FA at the top of the air–water interface and those obtained in the VSFG experiments by Johnson et al.32,33 We may partially reconcile the lack of observed deprotonated formic acid in these VSFG experiments by appealing to the rapid homogenization of formic acid orientation with depth, making VSFG experiments less sensitive to the depth where deprotonation appears to be more favored.Our metadynamics simulations comparing the deprotonation barriers of FA at the air–water interface and in the bulk indicate that it has a smaller barrier to dissociation at the interface which implies that FA deprotonates faster at the interface. A detailed examination of the equilibrium solvation and H-bonding state of FA in interfacial compared to bulk solvation is inconclusive since approximately the same average number of H-bonds are obtained. Thus, the faster deprotonation at the interface may be partially due to the faster water re-orientational and H-bond dynamics at the interface or it may be due to the effects in the second solvation shell. Regardless of the cause, since all carboxylic acids have a strong surface preference, the faster deprotonation at the interface implies that these acids, particularly formic and acetic acids which can have significant concentrations especially in polluted atmospheres and in rain and cloud water, may contribute more strongly to atmospheric acidity than previously believed, and produce ionic products, which even if short-lived, can enhance pickup and reactions with adsorbed species such as amines.
The behavior of FA at the air–water interface is contrary to that of many strong acids. Baer et al.1 have shown that HCl has a similarly small barrier to deprotonation at the interface as in the bulk (but the CIP is only stable at the interface), while HNO3 has an exceptionally large barrier at the surface due to insufficient solvation and exceptional stability of neutral HNO3. Thus at the surface, HNO3, depending also on its concentration, can be effectively a weak acid and may be observed to be neutral.2,3 Therefore, the simple impression of the higher concentration of under-coordinated water molecules at the interface leading to enhanced reactivity need not always be true.
It should be of considerable interest to extend this work to other carboxylic acids RCOOH, many of which are known to participate in atmospheric systems and processes, e.g., in secondary organic aerosols. A point that merits attention is how does the organic residue R affect the ionization mechanism and dynamics. What is well-known is that with increasing size of the (relatively hydrophobic) R group, the molecule's solubility (i.e., absorption into the water bulk) decreases. This can be quantified by, for example, the Henry's Law constant, which for acetic acid is about 40% less41 than that of formic acid. Also, given the amphiphilic nature of carboxylic acids, the orientational preference observed with formic acid, with the R group oriented along the surface normal, is maintained. However, more work is merited on the deprotonation propensity, dynamics, and mechanisms of other RCOOH, at the interface, in comparison to their fully solvated behavior. Biological chemistry and astrochemistry/prebiotic chemistry are other disciplines where the interactions of such acids in an aqueous environment are potentially of much interest.87–89
Acknowledgements
We are grateful to Finland's Center for Scientific Computing (CSC) for providing computational resources. RBG thanks the Israel Science Foundation (ISF Grant 172/12), the US National Science Foundation (NSF Grants CHE 0909227 and 1443140), and AirUCI for partial support of this project. GMN thanks the National Science Foundation (CHE-1152737) for financial support. LH thanks the Academy of Finland (grant numbers 257479 and 294752) for financial support. GM acknowledges discussions with Lauri Partanen and thanks him for reading and commenting on the manuscript.References
- M. D. Baer, D. J. Tobias and C. J. Mundy, J. Phys. Chem. C, 2014, 118, 29412–29420 CAS.
- M. C. Kido Soule, P. G. Blower and G. L. Richmond, J. Phys. Chem. A, 2007, 111, 3349–3357 CrossRef CAS PubMed.
- T. Lewis, B. Winter, A. C. Stern, M. D. Baer, C. J. Mundy, D. J. Tobias and J. C. Hemminger, J. Phys. Chem. C, 2011, 115, 21183–21190 CAS.
- T. Lewis, B. Winter, A. C. Stern, M. D. Baer, C. J. Mundy, D. J. Tobias and J. C. Hemminger, J. Phys. Chem. B, 2011, 115, 9445–9451 CrossRef CAS PubMed.
- E. S. Shamay, V. Buch, M. Parrinello and G. L. Richmond, J. Am. Chem. Soc., 2007, 129, 12910–12911 CrossRef CAS PubMed.
- S. Wang, R. Bianco and J. T. Hynes, J. Phys. Chem. A, 2009, 113, 1295–1307 CrossRef CAS PubMed.
- D. Ardura and D. J. Donaldson, Phys. Chem. Chem. Phys., 2009, 11, 857–863 RSC.
- C. D. Wick, J. Phys. Chem. A, 2013, 117, 12459–12467 CrossRef CAS PubMed.
- G. Murdachaew, M.-P. Gaigeot, L. Halonen and R. B. Gerber, J. Phys. Chem. Lett., 2013, 4, 3500–3507 CrossRef CAS.
- G. Murdachaew, M.-P. Gaigeot, L. Halonen and R. B. Gerber, Phys. Chem. Chem. Phys., 2014, 16, 22287–22298 RSC.
- S. Riikonen, P. Parkkinen, L. Halonen and R. B. Gerber, J. Phys. Chem. Lett., 2013, 4, 1850–1855 CrossRef CAS PubMed.
- S. Riikonen, P. Parkkinen, L. Halonen and R. B. Gerber, J. Phys. Chem. A, 2014, 118, 5029–5037 CrossRef CAS PubMed.
- R. B. Gerber, M. E. Varner, A. D. Hammerich, S. Riikonen, G. Murdachaew, D. Shemesh and B. J. Finlayson-Pitts, Acc. Chem. Res., 2015, 48, 399–406 CrossRef CAS PubMed.
- Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154 CrossRef CAS PubMed.
- G. M. Nathanson, Annu. Rev. Phys. Chem., 2004, 55, 231–255 CrossRef CAS PubMed.
- I. Chorny, I. Benjamin and G. M. Nathanson, J. Phys. Chem. B, 2004, 108, 995–1002 CrossRef CAS.
- S. M. Brastad and G. M. Nathanson, Phys. Chem. Chem. Phys., 2011, 13, 8284–8295 RSC.
- L. P. Dempsey, S. M. Brastad and G. M. Nathanson, J. Phys. Chem. Lett., 2011, 2, 622–627 CrossRef CAS.
- J. A. Faust and G. M. Nathanson, Chem. Soc. Rev., 2016, 45, 3609–3620 RSC.
- J. A. Faust, T. B. Sobyra and G. M. Nathanson, J. Phys. Chem. Lett., 2016, 7, 730–735 CrossRef CAS PubMed.
- L. Partanen, G. Murdachaew, R. B. Gerber and L. Halonen, Phys. Chem. Chem. Phys., 2016, 18, 13432–13442 RSC.
- B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications, Academic Press, San Diego, CA, USA, 2000 Search PubMed.
- R. P. Wayne, Chemistry of Atmospheres: An Introduction to the Chemistry of the Atmospheres of Earth, the Planets, and their Satellites, Oxford University Press, Oxford, 2000 Search PubMed.
- A. Chebbi and P. Carlier, Atmos. Environ., 1996, 30, 4233–4249 CrossRef CAS.
- P. Khare, N. Kumar, K. M. Kumari and S. S. Srivastava, Rev. Geophys., 1999, 37, 227–248 CrossRef CAS.
- S. Schobesberger, F. D. Lopez-Hilfiker, D. Taipale, D. B. Millet, E. L. D'Ambro, P. Rantala, I. Mammarella, P. Zhou, G. M. Wolfe, B. H. Lee, M. Boy and J. A. Thornton, Geophys. Res. Lett., 2016, 2016GL069599 Search PubMed.
- J. Hedberg, J. Henriquez, S. Baldelli, C. M. Johnson and C. Leygraf, J. Phys. Chem. C, 2009, 113, 2088–2095 CAS.
- S. Enthaler, J. von Langermann and T. Schmidt, Energy Environ. Sci., 2010, 3, 1207–1217 CAS.
- M. A. Brown, F. Vila, M. Sterrer, S. Thürmer, B. Winter, M. Ammann, J. J. Rehr and J. A. van Bokhoven, J. Phys. Chem. Lett., 2012, 3, 1754–1759 CrossRef CAS PubMed.
- J. G. Pruyne, M.-T. Lee, C. Fábri, A. Beloqui Redondo, A. Kleibert, M. Ammann, M. A. Brown and M. J. Krisch, J. Phys. Chem. C, 2014, 118, 29350–29360 CAS.
- N. Ottosson, E. Wernersson, J. Söderström, W. Pokapanich, S. Kaufmann, S. Svensson, I. Persson, G. öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2011, 13, 12261–12267 RSC.
- C. M. Johnson, E. Tyrode, A. Kumpulainen and C. Leygraf, J. Phys. Chem. C, 2009, 113, 13209–13218 CAS.
- C. M. Johnson and S. Baldelli, Chem. Rev., 2014, 114, 8416–8446 CrossRef CAS PubMed.
- D. Priem, T.-K. Ha and A. Bauder, J. Chem. Phys., 2000, 113, 169–175 CrossRef CAS.
- S. Aloisio, P. E. Hintze and V. Vaida, J. Phys. Chem. A, 2002, 106, 363–370 CrossRef CAS.
- E. G. Goken and A. W. Castleman, J. Geophys. Res.: Atmos., 2010, 115, D16203 CrossRef.
- E. G. Goken, K. L. Joshi, M. F. Russo, A. C. T. van Duin and A. W. Castleman, J. Phys. Chem. A, 2011, 115, 4657–4664 CrossRef CAS PubMed.
- J.-G. Lee, E. Asciutto, V. Babin, C. Sagui, T. Darden and C. Roland, J. Phys. Chem. B, 2006, 110, 2325–2331 CrossRef CAS PubMed.
- L. B. Pártay, P. Jedlovszky, P. N. M. Hoang, S. Picaud and M. Mezei, J. Phys. Chem. C, 2007, 111, 9407–9416 Search PubMed.
- P. Jedlovszky, G. Hantal, K. Neuróhr, S. Picaud, P. N. M. Hoang, P. v. Hessberg and J. N. Crowley, J. Phys. Chem. C, 2008, 112, 8976–8987 CAS.
- B. J. Johnson, E. A. Betterton and D. Craig, J. Atmos. Chem., 1996, 24, 113–119 CrossRef CAS.
- J. Staudinger and P. V. Roberts, Chemosphere, 2001, 44, 561–576 CrossRef CAS PubMed.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CAS.
- The CP2K developers group, http://www.cp2k.org/, 2000–2014.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- A. D. Hammerich and V. Buch, J. Phys. Chem. A, 2012, 116, 5637–5652 CrossRef CAS PubMed.
- A. D. Hammerich, B. J. Finlayson-Pitts and R. B. Gerber, J. Phys. Chem. Lett., 2012, 3, 3405–3410 CrossRef CAS PubMed.
- A. D. Hammerich, B. J. Finlayson-Pitts and R. B. Gerber, Phys. Chem. Chem. Phys., 2015, 17, 19360–19370 RSC.
- I.-F. W. Kuo, C. J. Mundy, B. L. Eggimann, M. J. McGrath, J. I. Siepmann, B. Chen, J. Vieceli and D. J. Tobias, J. Phys. Chem. B, 2006, 110, 3738–3746 CrossRef CAS PubMed.
- G. Murdachaew, C. J. Mundy, G. K. Schenter, T. Laino and J. Hutter, J. Phys. Chem. A, 2011, 115, 6046–6053 CrossRef CAS PubMed.
- M. Pettersson, J. Lundell, L. Khriachtchev and M. Räsänen, J. Am. Chem. Soc., 1997, 119, 11715–11716 CrossRef CAS.
- K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Phys. Chem. A, 2007, 111, 2040–2042 CrossRef CAS PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- D. J. Tobias, G. J. Martyna and M. L. Klein, J. Phys. Chem., 1993, 97, 12959–12966 CrossRef CAS.
- A. P. Willard and D. Chandler, J. Phys. Chem. B, 2010, 114, 1954–1958 CrossRef CAS PubMed.
- M. D. Baer, C. J. Mundy, M. J. McGrath, I.-F. W. Kuo, J. I. Siepmann and D. J. Tobias, J. Chem. Phys., 2011, 135, 124712 CrossRef PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302 CrossRef PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- J. F. Dama, M. Parrinello and G. A. Voth, Phys. Rev. Lett., 2014, 112, 240602 CrossRef PubMed.
- M. Sprik, Chem. Phys., 2000, 258, 139–150 CrossRef CAS.
- G. Murdachaew, M. E. Varner, L. F. Phillips, B. J. Finlayson-Pitts and R. B. Gerber, Phys. Chem. Chem. Phys., 2012, 15, 204–212 RSC.
- G. M. Nathanson and T. B. Sobyra, et al., article in preparation.
- A. Hassanali, F. Giberti, J. Cuny, T. D. Kühne and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13723–13728 CrossRef CAS PubMed.
- M. J. Cox, R. L. A. Timmer, H. J. Bakker, S. Park and N. Agmon, J. Phys. Chem. A, 2009, 113, 6599–6606 CrossRef CAS PubMed.
- B. J. Siwick and H. J. Bakker, J. Am. Chem. Soc., 2007, 129, 13412–13420 CrossRef CAS PubMed.
- P. Maurer, V. Thomas and R. Iftimie, J. Chem. Phys., 2011, 134, 094505 CrossRef PubMed.
- S. Miura, M. E. Tuckerman and M. L. Klein, J. Chem. Phys., 1998, 109, 5290–5299 CrossRef CAS.
- J. Kohanoff, S. Koval, D. A. Estrin, D. Laria and Y. Abashkin, J. Chem. Phys., 2000, 112, 9498–9508 CrossRef CAS.
- C. Drechsel-Grau and D. Marx, Phys. Rev. Lett., 2014, 112, 148302 CrossRef PubMed.
- X. Meng, J. Guo, J. Peng, J. Chen, Z. Wang, J.-R. Shi, X.-Z. Li, E.-G. Wang and Y. Jiang, Nat. Phys., 2015, 11, 235–239 CrossRef CAS.
- C. Drechsel-Grau and D. Marx, Nat. Phys., 2015, 11, 216–218 CrossRef CAS.
- V. R. I. Kaila and G. Hummer, Phys. Chem. Chem. Phys., 2011, 13, 13207–13215 RSC.
- D. Marx, ChemPhysChem, 2007, 8, 209–210 CrossRef CAS.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS.
- K. R. Leopold, Annu. Rev. Phys. Chem., 2011, 62, 327–349 CrossRef CAS PubMed.
- Q. Chen, Z. Liu and C. H. Wong, J. Theor. Comput. Chem., 2012, 11, 1019–1032 CrossRef CAS.
- K. Leung and S. B. Rempe, J. Am. Chem. Soc., 2004, 126, 344–351 CrossRef CAS PubMed.
- Y. Kameda, K. Fukuhara, K. Mochiduki, H. Naganuma, T. Usuki and O. Uemura, J. Non-Cryst. Solids, 2002, 312, 433 CrossRef.
- Y. Kameda, T. Mori, T. Nishiyama, T. Usuki and O. Uemura, Bull. Chem. Soc. Jpn., 1996, 69, 1495–1504 CrossRef CAS.
- M. Smiechowski, E. Gojlo and J. Stangret, J. Phys. Chem. B, 2011, 115, 4834–4842 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- T. C. Freitas, K. Coutinho, M. T. d. N. Varella, M. a. P. Lima, S. Canuto and M. H. F. Bettega, J. Chem. Phys., 2013, 138, 174307 CrossRef CAS PubMed.
- A. N. Borkar, M. K. Rout and R. V. Hosur, PLoS One, 2011, 6, e19830 CAS.
- R. T. Garrod, S. L. W. Weaver and E. Herbst, Astrophys. J., 2008, 682, 283–302 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp06071d |
| This journal is © the Owner Societies 2016 |