Micellization of alkyltrimethylammonium bromide surfactants in choline chloride:glycerol deep eutectic solvent

Abstract

Deep eutectic solvents have shown the ability to promote the self-assembly of surfactants in solution. However, some differences have been found compared with self-assembly in pure water and other polar organic solvents. The behaviour of alkyltrimethylammonium bromides in choline chloride:glycerol deep eutectic solvent has been studied by means of surface tension, X-ray and neutron reflectivity and small-angle neutron scattering. The surfactants were found to remain surface active and showed comparable critical micelle concentrations to the same surfactants in water. Our scattering studies demonstrate that these surfactants form globular micelles with ellipsoidal shape in solution. The size, shape and aggregation number of the aggregates were found to vary with the chain length of the surfactant. Specific solvent-headgroup interactions were not found in this system, unlike those we have previously postulated for anionic surfactants in choline chloride deep eutectic solvents.

---

Introduction

Ionic liquids and deep eutectic solvents (DES) have been studied as an alternative to traditional solvents in many applications. The environmentally friendly, “green”, nature of these solvents, together with their tuneable properties has led to their promotion for use in organic, inorganic and electrochemistry processes.^1,2 Some of the recent interest has focused on the ability of ionic liquids to support the self-assembly of amphiphiles.³ Since the first study of the micellization of surfactants in ionic liquids in 1982,⁴ there are an increasing number of investigations demonstrating that a variety of ionic liquids are capable of sustaining amphiphile self-assembly, including protic⁵ and aprotic liquids.⁶ The aggregation of anionic,⁷ cationic^4,8,9 and non-ionic¹⁰ surfactants has been studied through common, well-established techniques.

In some respects DES share characteristics and properties with ionic liquids. DES are generally made by the complexation of a hydrogen bond donor with a salt capable of sustaining a hydrogen bond network, unlike ionic liquids which are formed from a discrete anion and cation.^2,11,12 The favourable interaction between these components in the liquid state leads to a large depression in the melting point, with the term DES coined for systems where this results in the mixture being liquid at room temperature. Unlike ionic liquids, DES are formed by non-toxic, organic precursors and many possible combinations can be reached through the complexation of different salts with alcohols, carboxylic acids, amines and other naturally-occurring compounds.¹³ The various combinations of different salts and hydrogen bond donors lead to changes in the physicochemical properties of the solvent, which may allow the possibility to control such properties.

The compatibility of DES with water has been reported and this offers another variable with which the characteristics of the solvent may be controlled.¹⁴ Properties such as the viscosity are particularly influenced by the presence of water, although the mechanism by which this occurs is not yet understood.

Since the first application of a deep eutectic solvent as an electrodeposition agent,¹⁵ these solvents have been used as green alternatives in synthesis (of zeolitic materials,¹⁶ metal organic frameworks¹⁷ and nanostructured materials¹⁸) and in liquid–liquid extraction,¹⁹ selective adsorption of CO₂²⁰ and pharmaceutical applications.²¹

Recent investigations have found the ability of DES to support the aggregation of amphiphiles. Phospholipid vesicles have been reported by Gutierrez et al., highlighting the importance of DES as alternative solvent to support self-assembly.²² More recently it has been shown that such vesicles can form spontaneously in DES.²³ DES can also support surfactants that have self-assembled into ordered structures. Rengstl et al. reported the evidence of aggregation of choline dodecylsulfate surfactant in low-melting mixtures of dicarboxilic acid-based DES.²⁴ In subsequent studies a mixture of choline chloride:urea with water was found to promote the self-assembly of sodium dodecyl sulfate (SDS).²⁵ Cationic surfactants were also found to be soluble and form aggregates in choline chloride:glycerol, although no structural detail on such aggregates has yet been reported.²⁶ Tan et al. have shown the self-assembly of long chain ionic liquids in choline chloride:glycerol DES.²⁷

We have recently published a detailed analysis of the micellization process of SDS in pure choline chloride:urea.^28,29 Small-angle neutron scattering (SANS) data showed the formation of elongated micelles above the critical micelle concentration (CMC), unlike the same surfactant in water and other polar organic solvents where it forms globular micelles.^30,31 In water an increase of the aggregation number can be promoted by the presence of electrolytes, where the adsorption of ions to the headgroups screens the charge and enables micelle growth.³² We therefore inferred that the presence of ions within the structure of the deep eutectic solvent has a similar effect and results in larger micelles at low SDS concentrations. The addition of water to the DES was found to substantially reduce this effect and suggested that small quantities of water could be used to control aggregate morphology.

The work presented here is part of a series of studies in which we aim to understand micellization in deep eutectic solvents. Here we report the aggregation of cationic surfactants, alkyltrimethylammonium bromides (C_nTAB), in a DES. Different chain lengths (n = 12, 14 and 16) were studied in order to elucidate the effect of the lyophobic moiety of the surfactant on micellization in DES.

Alkyltrimethylammonium bromide surfactants have widely been studied in water and other solvents. The formation of globular micelles has been reported as the preferable shape for these surfactants in pure solvents.^33–35 However the transition to elongated micelles can be achieved by specific ion interactions between salt in solution and the surfactant headgroup.^36–38 These surfactants were found to have a very low solubility in the choline chloride:urea DES used in our previous work. In the work presented here we have used choline chloride:glycerol DES (eutectic composition: 1 : 2 molar ratio; melting point = −40 °C) which represents one of the most studied DES and showed high solubility for these surfactants.³⁹ It has physical properties that may be more useful for many applications such as lower viscosity and is liquid over a wider range of temperatures. We present here the results of our investigations of the properties of these systems using surface tension, X-ray and neutron reflectivity, and small-angle neutron scattering (SANS). Use of selective deuteration of both surfactant and solvent molecules allowed us to check for any significant interaction between micelles and components of the DES.

Experimental

Materials

Choline chloride (>98%, Sigma) and glycerol (>99%, Sigma) (1 : 2 mole equivalence) were mixed at 80 °C on a hot plate until a transparent, homogeneous mixture was achieved. The mixture was afterwards equilibrated for at least 24 hours in an oven at 40 °C. Isotopic mixtures were identically prepared using d₉-choline chloride (N,N,N-trimethyl-d₉, 99% atom, 99.9% D, Cambridge Isotope Laboratories) and d₈-glycerol (99% atom, 98.5% D, Qmx Laboratories).

C₁₂TAB (Acros Organics, 99%), C₁₄TAB (Acros Organics, 99%) and C₁₆TAB (Sigma, >99%) were purchased and used without further purification. Versions of the surfactants with either just tail or both head and tail deuterated were supplied by the STFC ISIS Deuteration Facility. We have chosen not to further purify either the DES materials or the surfactants because we are interested in the behaviour of these systems under the conditions in which they may be used in potential applications. Impurities in choline chloride are likely to be trimethylamine and ethylene glycol,⁴⁰ and in the C_nTABs are most likely to be long chain amines which were not fully quarternised during synthesis. Based on their behaviour in water we believe that none of these impurities are likely to significantly alter the phase behaviour of the C_nTABs in this DES.

The surfactants were used to prepare high-concentration stock solutions in order to reduce the variability between samples whilst low concentrations were prepared by dilution of the stock solution with pure DES for the protonated samples. In order to minimise the waste of deuterated chemicals, samples for the SANS experiments were prepared by direct mixing of the DES with the surfactants. The resulting solutions were sealed and kept in an oven at 40 °C for at least 24 hours to equilibrate.

The resulting samples were found to absorb water from the atmosphere due to the hygroscopicity of the solvent. In order to control the presence of water in the system, samples were freeze-dried before each experiment and water content was determined through Karl–Fischer titration (Mettler Toledo DL32 Karl–Fischer Coulometer Aquiline electrolyte A (Fisher Scientific), Aqualine Catholyte CG A). The water content was therefore maintained below 0.35 wt% during the experimental procedure discussed here.

Methods

Surface tension. Drop-shape analysis of a pendant drop was used to determine the surface tension of the samples and solvent in a Krüss DSA100. The samples were equilibrated in the oven at 40 °C prior to measurement. Several drops for each concentration were suspended using a dispensing needle. Pictures of a drop were taken after equilibration and the contour of those was fitted to the Young–Laplace equation. The values of surface tension were measured repeatedly for at least three measurements of each concentration and averaged to obtain the final value. The temperature was not controlled during measurement. Although we expect some variability in temperature that adds some uncertainty to our measurements, we have found that this method provides self-consistent measurements.²⁸

X-Ray and neutron reflectivity. Reflectivity measurements were intended to determine the scattering length density of the pure solvent and subsequently calculate the molecular volume of the DES. Three different contrasts of the pure solvent were measured using X-ray and neutron reflectivity. The X-ray reflectivity (XRR) measurements were taken on I07 beamline at Diamond Light Source, at 12.5 keV using the double-crystal-deflector system.⁴¹ Samples were placed in temperature-controlled PTFE trough at 30 °C and kept in an inert helium atmosphere. Data were collected after at least one hour of equilibration.

Data were collected in four different regimes of angle and attenuation to provide a total momentum transfer (q) from 0.018 to 0.7 Å⁻¹. Data reduction consisted of stitching the attenuation regimes together and normalising to the critical edge, a footprint correction to account for over-illumination ignoring meniscus effects and background subtraction. This background was measured simultaneously by integrating two regions of interest on a Pilatus 100k detector, one for the specular reflection and the other offset for the background.

The neutron reflectivity (NR) measurements were performed on the FIGARO instrument at the Institut Laue-Langevin.⁴² This time-of-flight instrument was used with a chopper pair giving pulses with 7% dλ/λ in the wavelength range λ = 2–30 Å. Data acquisitions were carried out at incident angles of Θ = 0.62 and 3.8°, providing a q-range from 0.005 to 0.4 Å⁻¹.

Delrin adsorption troughs (50 mm × 60 mm surface) were used to load the sample. These troughs were placed in an inert nitrogen atmosphere (a box with sapphire windows) to avoid the adsorption of water. As with X-rays, at least 90 minutes was allowed for equilibration. Data was collected and reduced using the standard procedures of the beamline.

Two different contrasts were measured, varying the isotopic mixtures in the system: fully protonated solvent, h-choline chloride:h-glycerol, and partially deuterated solvent, h/d-choline chloride:h/d-glycerol (a mix of protonated and deuterated materials were used rather than fully deuterated to minimise the cost of obtaining the substantial volume of DES required for the experiment).

Small-angle neutron scattering. The SANS measurements were performed on SANS2D at ISIS Pulsed Neutron Source.⁴³ SANS2D is a time-of-flight instrument with two movable detectors. The rear detector was placed at 4 m distance from the sample giving, together with the front detector, a momentum transfer range of 0.004–1.40 Å⁻¹. Samples were loaded into a temperature-controlled sample changer using 1 mm path length, 1 cm wide, quartz Hellma cells. The temperature was kept at 30 °C during the collection of the data for the C₁₂TAB and C₁₄TAB surfactants whilst samples with C₁₆TAB were measured at 40 °C, in order to avoid the solidification of samples with high surfactant concentration.

Data were reduced using the routines within Mantid.⁴⁴ The data were normalised to the sample transmission, and corrected for detector efficiencies, then scattering from the empty cell was subtracted. The output data were the absolute scattered intensity, I(q) in cm⁻¹, versus the momentum transfer, q in Å⁻¹. The scattering of the pure solvents were afterwards subtracted accounting for the incoherent contribution to each sample using SasView.⁴⁵ Instrument resolution was accounted for by smearing of the model functions using a Gaussian function at a constant 8% dq/q.

Samples were prepared in different concentrations above the critical micelle concentration (CMC) point and different isotopic mixtures. Different contrasts were measured to model the micelle structure formed by each surfactant: h-choline chloride:h-glycerol + d-C_n-d-TAB, d-choline chloride:h-glycerol + h-C_n-h-TAB, d-choline chloride:d-glycerol + h-C_n-h-TAB and h-choline chloride:h-glycerol + d-C_n-h-TAB. Note that for ease reading we refer to a ‘fully deuterated’ solvent in fact an isotopic mixture, which contains a partially deuterated precursor, d₉-choline chloride.

Data analysis

Small-angle neutron scattering. Model-based fitting was used for the whole range of concentrations studied here. The scattered intensity in SANS of isotropic, centrosymmetric particles can be described by the function:

I(q) = NV²(ΔSLD)²P(q)S(q)

where N is the number of particles, V the volume of the particles and ΔSLD corresponds to the difference in the scattering length density between the solvent and the particles. P(q) and S(q) are respectively the form factor and the structure factor. P(q) depends on the intraparticle scattering and thus on the shape of the particle. S(q) corresponds to the interparticle interactions within the system and generally depends on the concentration of particles in the system.

As in our recent study of SDS in DES, a range of different analytical models were tested to find the best option to fit the present data.²⁹ These models included a sphere model (Schulz-radius distribution), a cylinder model, an ellipsoidal model, and both prolate and oblate core–shell ellipsoid model. In addition we also considered both micelle and reverse micelle models. A complete record of these tests is included in the ESI.†

The core–shell ellipsoid model (prolate distribution of mass) was chosen as being most suitable approach. This model describes an ellipsoidal particle with a core–shell radial distribution.^37,46 The structural parameters of the model are: equatorial radius of the core (r_eq,core), shell thickness on the equatorial axis (T_eq,shell), axial ratio of the core (X_core) and axial ratio of the shell (X_shell). Where X_core = r_po,core/r_eq,core and X_shell = T_po,shell/T_eq,shell, (r_po,core = polar radius of the core; T_po,shell = shell thickness in the polar axis).

As in our previous study (and for the same reasons) we have used a hard-sphere structure factor (Percus–Yevick approximation) to account for the intermicellar interactions between charged particles.²⁹ This structure factor is described by two parameters, effective radius and S(q) volume fraction. Since the potential interactions are dominated not only by the charged headgroup but also the media, these parameters were not constrained to the dimensions of the form factor. Although this apparent structure factor does not provide a direct physical interpretation of the intermicellar contribution, we believe that it is a good approximation that allows the deconvolution of the interparticle and intraparticle contributions to the scattering. The rescaled mean square approximation was initially used for S(q), however the limited information about the physicochemical properties of the solvent means that such an analysis is not sufficiently reliable.^47,48

In order to resolve the micelle structure, we have followed a systematic fitting procedure for all the surfactant–DES mixtures. The system h-choline chloride:h-glycerol + d-C_n-h-TAB, dominated by the scattering of the micelle core, was used to obtain the size of the micelle core by averaging the results from intermediate concentrations (with better statistics than low concentrations and less affected by S(q) than high concentrations). Subsequently, we have fixed those values for all the contrasts and simultaneously fit them in order to determine the structural parameters of the entire micelle, including the headgroup shell. The radius of interaction used in the structure factor approximation was calculated as that of a sphere with the same second viral coefficient as the ellipsoidal shape and the value was fixed during the fitting procedure.⁴⁹

Results

Surface tension

Fig. 1 shows surface tension data for each of the C_nTABs in choline chloride:glycerol DES. The surface tension values are plotted against the concentration of surfactant in the solvent. The diffusion rate of the different surfactants to the surface has been evaluated in order to assess the validity of our experiments (see ESI†). The surface tension of the pure solvent and surfactant-DES system were measured as a function of time in order to follow the equilibration of the sample. Our experiments demonstrate that equilibration is achieved after a few seconds in concentrations around the CMC, however these kinetics are much slower at concentrations far below the CMC. Due to the difficulty of assessing the equilibrium at these really low concentrations, we can not draw further conclusions about surfactant thermodynamics at the interface from this data.

Fig. 1 Surface tension of different C_nTAB in 1 : 2 choline chloride : glycerol against the concentration of surfactant. The black dashed lines help to show the trend which finds the CMC.

The absolute value of surface tension of the pure DES is 63.5 ± 0.5 mN m⁻¹. This value was found to be higher than values previously reported by Abbott et al. using a Wilhelmy plate technique, 48 mN m⁻¹ at 40 °C.³⁹ However we do not know the source of this difference. The surface tension is slightly lower than our measurement of choline chloride:urea system, 66 ± 1 mN m⁻¹, which was made using the same apparatus.²⁸

For each surfactant, the shapes of the surface isotherm exhibit the classic behaviour of a surfactant in aqueous solution. The surface tension is gradually reduced with the addition of surfactant until it reaches the CMC.⁵⁰ We have determined the CMC from these plots to be 0.9 ± 0.1 mM for C₁₆TAB, 3.9 ± 0.2 mM for C₁₄TAB and 22 ± 2 mM for C₁₂TAB. Table 1 shows the CMCs of different C_nTABs in various solvents for comparison. The CMC was found to decrease with increasing the surfactant chain length, suggesting a lower solubility of free surfactant monomers for the longer chains. This behaviour is well known in polar solvents where the lyophobic effect drives the aggregation. Our measurement of the CMCs in choline chloride:glycerol were found to be slightly higher than in water in the case of C₁₂TAB and C₁₄TAB, and in the case of C₁₆TAB similar to the value observed in water.^51–53 However our values are not in agreement with the previously reported values obtained using fluorescence spectroscopy, which were reported to be one order of magnitude above ours.²⁶ Evans et al. reported significantly higher CMCs of akyltrimethylammonium bromides in an ionic liquid, ethylammonium nitrate.⁴ These considerably higher CMC values were explained by the greater affinity of the ionic liquid for lyophobic moieties by comparison to water. In protic ionic liquids, the non-polar domain of the solvent shows a higher capacity to solubilize free surfactant monomers and, hence, the CMCs of these surfactants appear to be higher.

Table 1 Critical micelle concentration (mM) from surface tension measurements for C₁₂TAB, C₁₄TAB and C₁₆TAB in a variety of polar solvents where these surfactants were found to form micelles

Surfactant	Solvent	Temp./°C	CMC/mM
C12TAB	1 : 2 choline chloride : glycerol	40	22 ± 2
	Water^51	40	15.0
	Ethylammonium nitrate^4	50	190
C14TAB	1 : 2 choline chloride : glycerol	40	3.9 ± 0.1
	Water^52	30	3.51
	Ethylammonium nitrate^4	50	46
C16TAB	1 : 2 choline chloride : glycerol	40	0.9 ± 0.1
	Water^53	25	0.92 ± 0.02
	Ethylammonium nitrate^4	50	18

---

X-Ray and neutron reflectivity

The scattering length density (SLD) of the DES can be obtained from the position of the critical edge from reflectivity experiments. This value depends from the exact composition of the solvent (the scattering length) and the molecular volume, and can also be calculated based on the atomic composition of the sample. Our reflectivity measurements were therefore intended to calculate the molecular volume of the solvent and in order to use these values to validate the volume of each component used during the SANS data fitting.

Fig. 2 shows the reflectivity data from XRR (one contrast) and NR (two isotopic contrasts). The fits shown were obtained using Motofit.⁵⁴ This package uses the Abeles optical matrix method to simulate the reflectivity profile. For fitting the pure solvent profiles a subphase model was used with the following parameters: the SLD of the solvent, the surface roughness (σ) and a residual background level. The results from the co-refinement of the three contrasts are included in Table 2.

Fig. 2 (a) Reflectivity profiles and best fits to the data (dashed lines) and (b) scattering length density profiles of each contrast: (red circles) X-ray contrast, (green squares) h/d choline chloride:h/d glycerol, and (blue triangles) h-choline chloride:h-glycerol.

Table 2 Scattering length density and surface roughness of pure solvent obtained from the fits. The scattering length was calculated by accounting for the atomic contribution to the scattering of each component (1 mole of choline chloride, 2 moles of glycerol) and subsequently used to calculate the molecular volume

Contrast	SLD/×10^−2 Å^−2	σ/Å	Scattering length/fm	Volume/Å^3
X-Ray	10.8 ± 0.1	3.3 ± 0.1	496	459 ± 4
h/d-Choline chloride:h/d-glycerol	3.15 ± 0.02	3.3 ± 0.1	140	445 ± 4
h-Choline chloride:h-glycerol	0.45 ± 0.03	3.3 ± 0.1	20.5	455 ± 30

---

The molecular volume of the solvent was calculated from the reflectivity results and averaged to a value of 453 ± 8 ų.

Small-angle neutron scattering

A core–shell ellipsoid model was used to fit the SANS data using SasView. Different concentrations of the surfactants were measured and fitted between 0.006 and 0.4 Å⁻¹ of momentum transfer. The SLD of each component of the system was calculated by accounting for the scattering length of each component and the volume that it occupies (see Table 3). The molecular volumes of the DES precursors were validated through the reflectivity results, shown to be in agreement, and subsequently used during the SANS data fitting. The SLD values of the solvents and micelle tails were fixed during the data analysis. The core of the micelle, composed of surfactant tails, was considered not to be affected by solvent penetration, while the SLD of the headgroup layer was fitted in order to account for solvation by the DES. The systems containing partially deuterated surfactants were intended to resolve the structure of the micelle core (see ESI†). Fixing those parameters, the four contrasts were simultaneously fitted in order to obtain a detailed picture of the micelles in choline chloride:glycerol.

Table 3 Scattering lengths, volumes and extended lengths of each constituent of the system

Unit	Length/Å	Volume/Å^3	Neutron scattering length/fm
a Extended lengths and volume for surfactant tails were obtained from Tanford equations.^55 Scattering lengths were calculated as the summation of the neutron scattering lengths of the atoms which form the unit.
C5H14NOCl	—	198	5.6
C5H5D9NOCl	—	198	99.3
C3H8O3	—	126	7.4
C3D8O3	—	126	90.7
N(CH3)3^−	—	135^53	−4.3
N(CD3)3^−	—	135^53	89.3
C12H25	16.68^a	350^a	−13.7
C12D25	16.68^a	350^a	246
C14H29	19.21^a	404^a	−15.4
C14D29	19.21^a	404^a	286
C16H33	21.74^a	458^a	−17.1
C16D33	21.74^a	458^a	326

---

Fig. 3 shows the SANS data and one of the isotopic mixtures (deuterated solvent, protonated surfactant) of the three surfactants. The results of the simultaneous fits are included in Tables 4, 5 and 6 for C₁₂TAB, C₁₄TAB and C₁₆TAB, respectively. The plots corresponding to the other isotopic mixtures are included in the ESI,† as well as a detailed summary with all of the results from the fits.

Fig. 3 SANS patterns and best fits for different concentrations of surfactant in choline chloride:glycerol DES: (a) h-C₁₂-h-TAB in d-choline chloride:d-glycerol, (b) h-C₁₄-h-TAB in d-choline chloride:d-glycerol and (c) h-C₁₆-h-TAB in d-choline chloride:d-glycerol. Surfactant concentrations are quoted in the legend of each graph. The black-dashed lines represent the best fits obtained through co-refinement of all the contrasts.

Table 4 Fitting parameters for SANS data of different concentrations of C₁₂TAB in choline chloride:glycerol shown in Fig. 3a. The shell SLD column is distributed as follows for the different contrasts: h-C₁₂-h-TAB + d-choline chloride:d-glycerol, h-C₁₂-h-TAB + d-choline chloride:h-glycerol

Conc./mM	r eq,core/Å	X core	T eq,shell/Å	X shell	SLDshell/×10^−6 Å^−2	ϕ fit/×10^−2	ϕ calc/×10^−2	ϕ S(q)/×10^−2
43.5 ± 3	14.8 ± 0.3	1.64 ± 0.01	4.4 ± 1.8	1.8 ± 0.5	5.1 ± 0.8, 1.2 ± 0.4	0.7 ± 0.2	0.5 ± 0.1	1.8 ± 0.3
79.7 ± 3.1	14.8 ± 0.3	1.64 ± 0.01	3.8 ± 1.5	1.5 ± 0.4	4.6 ± 1.1, 0.6 ± 1.2	1.6 ± 0.4	1.6 ± 0.1	2.1 ± 0.2
205 ± 12	14.8 ± 0.3	1.64 ± 0.01	4.6 ± 0.4	1.3 ± 0.2	4.2 ± 0.3, 0.0 ± 0.4	4.8 ± 0.4	5.2 ± 0.1	7.4 ± 0.1
422 ± 44	14.8 ± 0.3	1.64 ± 0.01	4.4 ± 0.2	1.4 ± 0.2	3.6 ± 0.2, 0.1 ± 0.1	11 ± 0	11 ± 1	15 ± 1
943 ± 92	14.8 ± 0.3	1.64 ± 0.01	4.9 ± 0.1	1.8 ± 0.1	4.3 ± 0.1, 0.1 ± 0.2	22 ± 1	23 ± 2	27 ± 1

---

Table 5 Fitting parameters for SANS data of different concentrations of C₁₄TAB in choline chloride:glycerol shown in Fig. 3b. The shell SLD column is distributed as follows for the different contrasts: h-C₁₄-h-TAB + d-choline chloride:d-glycerol, d-C₁₄-d-TAB + h-choline chloride:h-glycerol, h-C₁₄-h-TAB + d-choline chloride:h-glycerol

Conc./mM	r eq,core/Å	X core	T eq,shell/Å	X shell	SLDshell/×10^−6 Å^−2	ϕ fit/×10^−2	ϕ calc/×10^−2	ϕ S(q)/×10^−2
40.3 ± 3.4	18.9 ± 0.1	1.71 ± 0.04	4.2 ± 2.3	1.1 ± 1.0	4.5 ± 1.2, 2.9 ± 1.6, 0.1 ± 0.2	1.0 ± 0.2	1.3 ± 0.1	2.9 ± 0.4
77.9 ± 7.1	18.9 ± 0.1	1.71 ± 0.04	5.3 ± 1.1	1.3 ± 0.4	4.6 ± 0.5, 3.1 ± 0.7, 0.8 ± 0.6	2.5 ± 0.2	2.6 ± 0.3	5.2 ± 0.3
182 ± 9	18.9 ± 0.1	1.71 ± 0.04	4.4 ± 0.2	1.6 ± 0.1	4.1 ± 0.2, 3.2 ± 0.3, 0.5 ± 0.3	5.8 ± 0.2	6.1 ± 0.5	11 ± 1
390 ± 36	18.9 ± 0.1	1.71 ± 0.04	4.7 ± 0.1	1.6 ± 0.1	3.3 ± 0.3, 4.8 ± 0.1, 0.2 ± 0.1	9.9 ± 0.6	12 ± 1	18 ± 1

---

Table 6 Fitting parameters for SANS data of different concentrations of C₁₆TAB in choline chloride:glycerol shown in Fig. 3c. The shell SLD column is distributed as follows for the different contrasts: h-C₁₆-h-TAB + d-choline chloride:d-glycerol, d-C₁₆-d-TAB + h-choline chloride:h-glycerol, h-C₁₆-h-TAB + d-choline chloride:h-glycerol

Conc./mM	r eq,core/Å	X core	T eq,shell/Å	X shell	SLDshell/×10^−6 Å^−2	ϕ fit/×10^−2	ϕ calc/×10^−2	ϕ S(q)/×10^−2
36.3 ± 3	19.6 ± 0.1	1.82 ± 0.05	5.6 ± 1.5	1.8 ± 0.2	4.0 ± 0.6, 2.4 ± 0.5, 0.4 ± 0.2	1.3 ± 0.2	1.2 ± 0.1	—
68.3 ± 4.8	19.6 ± 0.1	1.82 ± 0.05	5.4 ± 0.5	1.9 ± 0.1	4.0 ± 0.3, 2.3 ± 0.3, 0.2 ± 0.1	2.5 ± 0.2	2.3 ± 0.1	—
172 ± 8	19.6 ± 0.1	1.82 ± 0.05	5.7 ± 0.5	1.7 ± 0.1	4.8 ± 0.2, 2.4 ± 0.2, 0.8 ± 0.1	5.3 ± 0.1	5.5 ± 0.2	0.7 ± 0.1
352 ± 17	19.6 ± 0.1	1.82 ± 0.05	6.1 ± 0.2	1.7 ± 0.1	3.6 ± 0.1, 2.6 ± 0.1, 0.3 ± 0.1	11 ± 1	11 ± 1	8.9 ± 0.1

---

Micelle dimensions were successively used to calculate other parameters of interest. The volume of the core of a single micelle, containing only surfactant tails, was calculated and used to determine the aggregation number of the micelles (N_agg).⁵⁵ The contrast protonated surfactant in partially deuterated solvent, was used to evaluate the possibility of selective solvation of the headgroup region by either glycerol or choline chloride from the DES.

The effective radius for the structure factor model was determined for different concentrations of surfactant and the resulting values were averaged to obtain a value fixed during the fitting procedure: 22 ± 2 Å for C₁₂TAB, 26.0 ± 0.5 Å for C₁₄TAB and 28.0 ± 0.2 Å for C₁₆TAB. Therefore, changes in the structure factor volume fraction were observed with varying concentration of surfactant. The fitted volume fraction of micelles (ϕ_fit) and structure factor volume fraction (ϕ_S(q)) were obtained during the data analysis.

Fig. 4 shows the results for the equatorial radius of the micelle core (R_eq,core), core axial ratio (X_core, ratio between the equatorial radius and the polar radius). Surfactant tails are situated inside the micelle while the headgroups form a shell at the interface with the liquid. The size of the micelles was found to be dependent on the surfactant chain length and are bigger for longer surfactant chain lengths (R_g,C12 = 17.7 ± 0.9 Å, R_g,C14 = 18.9 ± 0.1 Å, R_g,C16 = 26.1 ± 0.6 Å, average). For the reported structural parameters in water and ethylammonium nitrate,^8,9,56 the radius of gyration of the micelles in those solvents were calculated and compared with our results. The radius of gyration in choline chloride:glycerol were found to be larger than in water (R_g,C12 = 16.8 Å, R_g,C16 = 25.4 Å) and in ethylammonium nitrate (R_g,C12 = 12.4 Å, R_g,C16 = 15.5 Å).

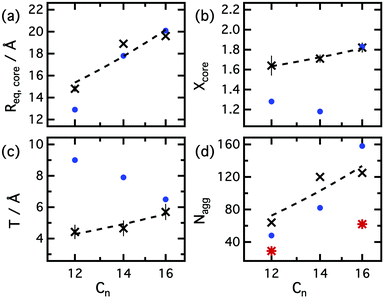Fig. 4 Comparison between the averaged structural parameters of micelles in different solvents: (black crosses) choline chloride:glycerol, (blue dots) water^36,37,56 and (red stars) ethylammonium nitrate.^8,9 The plots represent the number of carbons in the tail of the surfactant against (a) the equatorial radius of the core, (b) the axial ratio of the core, (c) the shell thickness on the equatorial axis and (d) the aggregation number of the micelles. Error bars are included for all of our experimental data. Where not visible, the error bars are within the marker.

For each individual surfactant, the shape and size of the micelle were found to show small variations with concentration. Although we have not found evidence of large variations related to the modelling of the structure factor, we believe that these rather small fluctuations may arise from the fitting procedure for data from low concentrations of surfactant, where the statistics are more affected by the background subtraction at low concentrations, and also the effects of S(q) at high concentrations.

The equatorial radius of the micelle core was found to vary with the size of the surfactant. This dimension was fitted to 14.8 ± 0.3 Å, 18.9 ± 0.1 Å and 19.6 ± 0.1 Å for C₁₂TAB, C₁₄TAB and C₁₆TAB, respectively. The polar radius was found to be bigger for all surfactants, as expected from a prolate distribution of mass (X_core > 1). Also the equatorial radii of the core were found to be comparable but smaller than in water, while the axial ratio observed in this DES is larger than in water (Fig. 4).

The presence of a structure factor contribution is negligible up to a relatively high surfactant concentration, whereas intermicellar interactions are effective at lower surfactant concentration in water.^8,36,37 Although there is limited physicochemical information about the solvent, we can qualitatively infer that the high ionic strength of the DES reduces the intermicellar interaction in comparison with water.

The aggregation number in DES was found to not change with surfactant concentration, unlike anionic surfactants in choline chloride:urea DES.²⁹ In choline chloride:glycerol DES, the average number of surfactant molecules per micelle increases with the chain length of the surfactant (N_agg,C12 = 64 ± 2, N_agg,C14 = 120 ± 1, N_agg,C16 = 125 ± 2), as they vary in water and ethylammonium nitrate.^9,37

Although we previously reported a morphology transition in micelles of an anionic surfactant, SDS,²⁹ we do not observe a similar effect with the cationic surfactants studied here. The unusual behaviour of SDS in such a solvent was suggested to arise from specific interactions in the headgroup region, which we do not see with the cationic surfactants in the present DES. Although a similar type of transition was found for alkyltrimethylammonium bromides and salts in aqueous solutions,^36,38,57,58 the ammonium group does not show affinity for the positively charged choline ion, meaning that such a mechanism for screening and curvature modification is not present in these cationic surfactant – DES systems.

Discussion

The cationic surfactants studied in the present work were found to remain surface-active in the present DES as shown by the surface tension data. Pal et al. previously reported evidence of aggregation of alkyltrimethylammonium surfactants in choline chloride:glycerol.²⁶ Their values for the CMCs of these surfactants were found to be in disagreement with our measurements, although our SANS data confirms the presence of micelles below the values reported in such work (see Fig. 3 and Table 4).

The values of the CMCs determined in the present work were found to be comparable to those in water but considerably lower than in ethylammonium nitrate. Therefore, our values of the CMCs suggest that the micellization process in this DES is more similar to that in water rather than in ionic liquids, and, as evidenced by the SANS results from isotopic variations, also the interaction lack the surfactant-solvent interactions previously reported for anionic surfactants in DES.²⁹

Differences in the shape of the SANS data are observed with changing surfactant chain length, suggesting variation in the morphology of the aggregates. Micelle morphology can be understood through the packing parameter, v/a₀l_c, where v corresponds to the volume of the surfactant hydrocarbon tail, l_c is the length of such tail and a₀ is the apparent area per monomer at the headgroup-tail interface.⁵⁹ Spherical micelles can be found with values less than or equal to 1/3, rod-like for a packing parameter between 1/3 and 1/2, and surfactant bilayers are found for values between 1/2 and 1. The formation of micelles by analogous surfactants with the same headgroup but differing chain lengths will lead to variations in the packing parameter. Therefore, in the present case, changes in micelle structure can be related to variations in the surfactant chain length.

Micelles were indeed found to vary in shape and size with different surfactant chain lengths, from smaller micelles formed by C₁₂TAB and larger for C₁₆TAB. With increasing the length of the surfactant tail, the axial ratio of the micelle varies and the aggregate curvature slightly decreases. Although a trend can be observed from our fits, the variance between concentrations does not allow us to draw further conclusions about this effect.

These surfactants in DES show larger aggregates than in water, unlike other ionic surfactants in solvents with lower polarity than water.^30,31 The aggregates were also found to be smaller in ethylammonium nitrate (see Fig. 4). The aggregation numbers of micelles increase with larger surfactants, as reported for water and ethylammonium nitrate. The axial ratio of the micelles was found to be larger in DES than in the water. In water, the interaction between headgroups is driven by the electrostatic interactions, modulated mainly by counterion binding. In the DES, the high ionic strength reduces such interactions and permits closer surfactant packing, thus the formation of aggregates that are more elongated than in water.

The structure factor volume fraction for C₁₂TAB and C₁₄TAB was found to be systematically larger than the physical volume fraction of micelles (see Tables 4 and 5). This indicates that the intermicellar contribution cannot be simply described using the excluded volume approximation, but some other contributions need to be accounted for. Although we cannot extract direct physical information from these values, this approach allows us to successfully analyse the form factor. Interestingly, this behaviour was not seen for C₁₆TAB. In that case a structure factor was not required (and could not be reliably fitted) for the two lowest concentrations, whilst the highest two concentrations showed structure factor volume fractions that were lower than the physical volume fraction. These results clearly show the limitations of the approach of approximating the structure factor as a hard sphere interaction. Future work making use of neutron diffraction should provide information about the specific environments of the headgroups in each of these surfactants. Combined with computational studies, more information about the interaction potentials in these solvents can be obtained.

For this type of cationic surfactants, SANS studies from different systems have been used to elaborate different pictures of the micelle. The first studies concluded that these surfactants form globular micelles with a headgroup layer thickness between 2 and 8 Å, depending on the hydration number.^{33,35–37,56} A more recent study through the use of wide q-range neutron diffraction provided an atomistic configuration of a C₁₀TAB micelle in pure water with the micelle headgroup layer composed of a hydrated shell of thickness about 7.5 Å.⁶⁰ This detailed model of the aggregate offered an important advance in understanding the hydration effect and the location of the counterions in the Stern layer. The limited resolution of SANS at high q, in comparison with wide-angle neutron diffraction, does not allow us to elaborate a highly accurate model of the micelle interface. The complexity of the system, where preferential adsorption of individual DES constituents may be taking place, complicates the determination of the characteristics of the headgroup layer and solvation effects. The variations of the shell SLD indicate solvation of the headgroup layer (see Tables 4–6) with a possible preferential adsorption of glycerol. However, our estimation of the shell thickness (4.4 ± 0.5 Å, 4.7 ± 0.5 Å, 5.7 ± 0.5 Å, averaged for C₁₂TAB, C₁₄TAB and C₁₆TAB respectively) and solvation of the headgroups can probably be refined through the application of liquid neutron diffraction experiments.

Conclusions

This study furthers the understanding of the self-assembly of alkyltrimethylammonium bromide in a choline chloride:glycerol deep eutectic solvent. Unlike the previously studied choline chloride:urea deep eutectic solvent, which has a low solubility for these surfactants, the present solvent was found to solubilise and promote the self-assembly of cationic surfactants. Surface tension measurements have shown comparable CMCs to those values in water but they are considerably lower than the CMCs in ethylammonium nitrate, an ionic liquid. This experiment suggest that the solubility of free monomers in the choline chloride:glycerol DES is comparable to that in pure water, implying that the formation of micelles will be akin to that in water. The CMCs were also found to increase with the length of the surfactant chain, suggesting that the lyophobic effect drives the formation of micelles in this solvent.

Small-angle neutron scattering data shows the presence of self-assembled structures with similar shapes and sizes to those found in water. The polar radius of the aggregates was found to increase with the number of carbon atoms in the surfactant tail. Nonetheless, the axial ratio increases at longer surfactant molecules, as seen in pure water. The interaction between the colloidal particles in the system was, however, found to be increased compared to that in water, probably as a result of the high ionic strength of the deep eutectic solvent in comparison with water. The core–shell ellipsoid model in choline chloride:glycerol showed a similar micelle dimension to aggregates in pure water but with a slightly larger axial ratio. Such a difference was attributed to the weaker interaction between headgroups at the micelle interface due to the high ionic strength of the deep eutectic solvent. The modelling of the four isotopic contrasts has helped to find an approximate dimension of the headgroup shell surrounding the core of the micelle. However, since solvent penetration affects the contrast resolution further investigations, ideally using wide-angle liquid diffraction, will be needed to make firm conclusions about the precise composition of the micelle-solvent interface.

Acknowledgements

We thank the ISIS Spallation Source, Diamond Light Source and the Institut Laue-Langevin for the awarded beamtime (experiment numbers RB1510328, SI10546-1 and 9-13-612⁶¹). We also thank the Diamond Light Source for the offline access to the Kruss Tensiometer, and the authors also thank the Division of Physical Chemistry, Lund University, for supporting the visit of A. S.-F. We acknowledge University of Bath Alumni Fund and European Spallation Source for funding A. S.-F. This work used SasView software, originally developed by the DANSE project (NSF award DMR-0520547).

References

1. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150.
2. E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082.
3. T. L. Greaves and C. J. Drummond, Chem. Soc. Rev., 2008, 37, 1709–1726.
4. D. F. Evans, A. Yamauchi, R. Roman and E. Z. Casassa, J. Colloid Interface Sci., 1982, 88, 89–96.
5. R. Atkin, S. M. C. Bobillier and G. G. Warr, J. Phys. Chem. B, 2010, 114, 1350–1360.
6. S. C. Sharma, R. Atkin and G. G. Warr, J. Phys. Chem. B, 2013, 117, 14568–14575.
7. J. L. Anderson, V. Pino, E. C. Hagberg, V. V. Sheares and D. W. Armstrong, Chem. Commun., 2003, 2444–2445,  10.1039/b307516h.
8. A. Dolan, R. Atkin and G. G. Warr, Chem. Sci., 2015, 6, 6189–6198.
9. C. R. López-Barrón and N. J. Wagner, Langmuir, 2012, 28, 12722–12730.
10. M. U. Araos and G. G. Warr, Langmuir, 2008, 24, 9354–9360.
11. O. S. Hammond, D. T. Bowron and K. J. Edler, Green Chem., 2016, 18, 2736–2744.
12. S. Kaur, A. Gupta and H. K. Kashyap, J. Phys. Chem. B, 2016, 120, 6712–6720.
13. Y. Dai, J. van Spronsen, G. J. Witkamp, R. Verpoorte and Y. H. Choi, Anal. Chim. Acta, 2013, 766, 61–68.
14. Y. Dai, G.-J. Witkamp, R. Verpoorte and Y. H. Choi, Food Chem., 2015, 187, 14–19.
15. A. P. Abbott, G. Capper, D. L. Davies, H. L. Munro, R. K. Rasheed and V. Tambyrajah, Chem. Commun., 2001, 2010–2011,  10.1039/b106357j.
16. E. R. Parnham, E. A. Drylie, P. S. Wheatley, A. M. Z. Slawin and R. E. Morris, Angew. Chem., Int. Ed., 2006, 45, 4962–4966.
17. C. F. J. Faul and M. Antonietti, Adv. Mater., 2003, 15, 673–683.
18. A. Abo-Hamad, M. Hayyan, M. A. AlSaadi and M. A. Hashim, Chem. Eng. J., 2015, 273, 551–567.
19. A. P. Abbott, P. M. Cullis, M. J. Gibson, R. C. Harris and E. Raven, Green Chem., 2007, 9, 868–872.
20. R. B. Leron and M. H. Li, J. Chem. Thermodyn., 2013, 57, 131–136.
21. K. D. Weaver, H. J. Kim, J. Sun, D. R. MacFarlane and G. D. Elliott, Green Chem., 2010, 12, 507–513.
22. M. C. Gutiérrez, M. L. Ferrer, C. R. Mateo and F. del Monte, Langmuir, 2009, 25, 5509–5515.
23. S. J. Bryant, R. Atkin and G. G. Warr, Soft Matter, 2016, 12, 1645–1648.
24. D. Rengstl, V. Fischer and W. Kunz, Phys. Chem. Chem. Phys., 2014, 16, 22815–22822.
25. M. Pal, R. Rai, A. Yadav, R. Khanna, G. A. Baker and S. Pandey, Langmuir, 2014, 30, 13191–13198.
26. M. Pal, R. K. Singh and S. Pandey, ChemPhysChem, 2015, 16, 2538–2542.
27. X. Tan, J. Zhang, T. Luo, X. Sang, C. Liu, B. Zhang, L. Peng, W. Li and B. Han, Soft Matter, 2016, 12, 5297–5303.
28. T. Arnold, A. J. Jackson, A. Sanchez-Fernandez, D. Magnone, A. E. Terry and K. J. Edler, Langmuir, 2015, 31, 12894–12902.
29. A. Sanchez-Fernandez, K. J. Edler, T. Arnold, R. K. Heenan, L. Porcar, N. J. Terrill, A. E. Terry and A. J. Jackson, Phys. Chem. Chem. Phys., 2016, 18, 14063–14073.
30. J. B. Hayter and J. Penfold, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 1851–1863.
31. T. Perche, X. Auvray, C. Petipas and R. Anthore, Langmuir, 1997, 13, 1475–1480.
32. L. Arleth, M. Bergström and J. S. Pedersen, Langmuir, 2002, 18, 5343–5353.
33. J. B. Hayter and J. Penfold, Colloid Polym. Sci., 1983, 261, 1022–1030.
34. R. Zana, C. Picot and R. Duplessix, J. Colloid Interface Sci., 1983, 93, 43–53.
35. J. Tabony, Mol. Phys., 1984, 51, 975–989.
36. M. Bergstrom and J. S. Pedersen, Phys. Chem. Chem. Phys., 1999, 1, 4437–4446.
37. S. S. Berr, E. Caponetti, J. S. Johnson, R. R. M. Jones and L. J. Magid, J. Phys. Chem., 1986, 90, 5766–5770.
38. T. H. Ito, R. K. Rodrigues, W. Loh and E. Sabadini, Langmuir, 2015, 31, 6020–6026.
39. A. P. Abbott, R. C. Harris, K. S. Ryder, C. D'Agostino, L. F. Gladden and M. D. Mantle, Green Chem., 2011, 13, 82–90.
40. Choline Chloride MSDS, INCHEM, http://www.inchem.org/documents/sids/sids/67481.pdf, accessed 18 July 2016.
41. T. Arnold, C. Nicklin, J. Rawle, J. Sutter, T. Bates, B. Nutter, G. McIntyre and M. Burt, J. Synchrotron Radiat., 2012, 19, 408–416.
42. R. A. Campbell, H. P. Wacklin, I. Sutton, R. Cubitt and G. Fragneto, Eur. Phys. J. Plus, 2011, 126, 107.
43. R. K. Heenan, S. E. Rogers, D. Turner, A. E. Terry, J. Treadgold and S. M. King, Neutron News, 2011, 22, 3.
44. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
45. M. Doucet, S. King, P. Butler, P. Kienzle, P. Parker, J. Kyzywon, A. Jackson, T. Richter, M. Gonzales, T. Nielsen, R. Ferraz Leal, A. Makvardsen, R. Heenan, J. Bakker and G. Alina, Gervaise, SasView version 3.1.2, http://www.sasview.org, DOI: 10.5282/zenodo.35065.
46. M. Kotlarchyk and S. H. Chen, J. Chem. Phys., 1983, 79, 2461–2469.
47. J.-P. Hansen and J. B. Hayter, Mol. Phys., 1982, 46, 651–656.
48. J. B. Hayter and J. Penfold, Mol. Phys., 1981, 42, 109–118.
49. A. Isihara, J. Chem. Phys., 1950, 18, 1446–1449.
50. P. H. Elworthy and K. J. Mysels, J. Colloid Interface Sci., 1966, 21, 331–347.
51. M. J. Schick, J. Phys. Chem., 1963, 67, 1796–1799.
52. R. L. Venable and R. V. Nauman, J. Phys. Chem., 1964, 68, 3498–3503.
53. J. R. Lu, M. Hromadova, E. A. Simister, R. K. Thomas and J. Penfold, J. Phys. Chem., 1994, 98, 11519–11526.
54. A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276.
55. C. Tanford, J. Phys. Chem., 1972, 76, 3020–3024.
56. S. S. Berr, J. Phys. Chem., 1987, 91, 4760–4765.
57. L. J. Magid, Z. Han, Z. Li and P. D. Butler, Langmuir, 2000, 16, 149–156.
58. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
59. J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568.
60. R. Hargreaves, D. T. Bowron and K. Edler, J. Am. Chem. Soc., 2011, 133, 16524–16536.
61. K. J. Edler, T. Arnold, R. A. Campbell, A. Sanchez-Fernandez and A. J. Jackson, Langmuir Film Formation on Deep Eutectic Solvents, Institut Laue-Langevin (ILL), 2015,  DOI:10.5291/ILL-DATA.9-13-612.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison of different reciprocal space models fitted to the experimental data and results from isotopic mixtures not included in the main text. See DOI: 10.1039/c6cp06053f

---