Intramolecular torque, an indicator of the internal rotation direction of rotor molecules and similar systems

Abstract

Rotation-inducing torque is ubiquitous in many molecular systems. We present a straightforward theoretical method based on forces acting on atoms and obtained from atomistic quantum mechanics calculations to quickly and qualitatively determine whether a molecule or sub-unit thereof has a tendency to rotate and, if so, around which axis and in which sense: clockwise or counterclockwise. The method also indicates which atoms, if any, are predominant in causing the rotation. Our computational approach can in general efficiently provide insights into the internal rotational degrees of freedom of all molecules and help to theoretically screen or modify them in advance of experiments or to efficiently guide a detailed analysis of their rotational behavior with more extensive computations. As an example, we demonstrate the effectiveness of the approach using a specific light-driven molecular rotary motor which was successfully synthesized and analyzed in prior experiments and simulations.

---

Introduction

The concept of torque^1–5 – the induction of rotation, as opposed to translation, by external or internal forces – is ubiquitous in dynamic molecular phenomena such as collisions, chemical reactions, vibrations and electronic excitations. The concept is especially useful for rotor molecules, in which energy from some source (e.g. chemical reaction, electron–electron or optical excitation) is converted to rotational motion^6–11 through the action of a net torque on the whole molecule or on a part of the molecule (often called rotor or rotator), as in the bacterial flagella^12,13 and F₁-ATPase,^4,5 for example. Furthermore, the development of artificial molecular motors^14–25 holds much promise for sourcing sustainable energy, developing advanced medical devices, etc.²⁶ The Nobel Prize in Chemistry for 2016 has been awarded jointly to J.-P. Sauvage, J. F. Stoddart and B. L. Feringa for “the design and synthesis of molecular machines”; this remarkable progress also begs for a deeper understanding of the functioning of molecular machines, including in particular rotor motors, in order to enable full exploitation of the broad potential of these novel devices.

While torque has been used extensively to analyze rotor behavior in molecules,^1–5 we shall here utilize this concept predictively, i.e. to predict whether a particular molecule prepared in a specific state (e.g. photoexcited or twisted in a collision) will internally rotate or not; also, the torque vector will make it possible to predict the dominant direction of rotation: around which axis and in what sense (clockwise vs. counterclockwise). Our approach will be general, making no a priori assumptions about the rotational properties of the molecule under study, and thus will consider a wide variety of possible rotational behaviors. As an illustration, we take a well-studied rotor molecule (9-(2,4,7-trimethyl-2,3-dihydro-1H-inden-1-ylidene)-9H-fluorene, called “motor 1” in this work)^27–29 consisting of a rotator and a stator. It is known that this molecule presents a unidirectional motor behavior by appropriate chirality, radiationless decay and two stable equilibria. To reveal its underlying mechanism, theoretical studies^28,29 have been performed for extensive mapping of the detailed geometry of the molecule during the rotation to determine its configurational trajectories in multidimensional space, which is computationally very demanding but cannot confidently predict the rotation direction due to the need to explore a very-high-dimensional structural space with exhaustive search methods. In this work, we propose to obtain the rotational character much more easily by calculating the torque at a few selected geometries. Such a quick study of the molecule's global behavior would very much reduce the need to explore large volumes of configuration space and thus can guide a subsequent detailed study more efficiently toward a full understanding of the rotational mechanism of the system.

Our efficient approach produces a qualitative answer, not e.g. a precise speed of rotation about a precisely determined axis. Its aim is to rapidly, confidently and qualitatively predict the rotational evolution of the system. It is possible to obtain qualitative answers via a single total-energy calculation in the molecule's initial state which yields forces on all the atoms and, hence, atom-derived torques after choosing a suitable rotation center: that qualitative information may, for example, be sufficient to screen out unpromising candidate molecules from a search for useful rotor molecules, saving the time and expense of more detailed simulations of these candidates; likewise, this torque method allows quickly exploring alternate molecules.

To study either initial rotation or subsequent rotation, the torque referred to a selected rotation center can be very easily calculated from the forces acting on the individual atoms and may be projected accordingly if an obvious axis of rotation is available, such as a single strong atom–atom bond acting as an “axle” between a stator and a rotator. Even when the preferred axis of rotation is not so obvious, considering the torque components along three orthogonal axes will suffice to clearly indicate the general direction of initial rotation, or the absence of a tendency to rotate. Once the initial direction of rotation is obtained, one may follow the rotation by turning the rotator rigidly through a few steps in that direction, repeating the foregoing at each step. It is assumed that a rigid rotator is particularly valid in ultrafast light-driven processes, as observed experimentally for another similar rotor molecule where rotation happens on a 100 fs timescale after the photo-excitation,³⁰ much faster than the relaxation of the functional groups in the excited state. Afterwards, on the longer timescale, the radiationless transition back to the ground state conformer should be studied with a local optimization by constraining a suitable dihedral angle for updating the direction of rotation due to shape and state changes in this soft rotor molecule. This situation is analogous to a spacecraft^31,32 in which a multitude of components can rotate irregularly, e.g. antennae, solar panels, astronauts, liquids, gases, pumps and fans, affecting the spacecraft's orientation and spin, and thus complicating navigation. Thus, this approach includes the frequent case of flexible molecules, which can change their shape and electronic structure during rotation.

Our general approach to torque calculation can also be applied to more complex systems than simple stator + rotator molecules; for example, a molecule may have multiple rotators (including a rotator within a rotator), or the molecule may have a more complex link between the stator and the rotator than a single bond (e.g. consecutive units in a flexible polymer, or three consecutive CC bonds in stilbene). Then the same calculation can yield torques around each bond or rotation axis to evaluate its individual tendency and direction of rotation, at negligible extra computational cost since all the atomic positions and forces are available for each atom from a single calculation.

Methodology

We consider the classical motion of individual atoms and groups of atoms in a molecule of arbitrary complexity, induced by internal or external forces acting on the individual atoms. We shall distinguish between translational, rotational and flexing motions of the molecule; these types of motion normally occur simultaneously, but can be disentangled using classical mechanics. The translational motion is more relevant to vibrational analysis, while the rotational motion is of special interest when examining rotor molecules. The flexing motion distorts a molecule or its subunits beyond rigid translation and rigid rotation: flexing results not only from inhomogeneous forces but also from induced changes in the electronic structure during deformation; we shall illustrate this effect further below through an iterative approach. For the present purpose, we neglect the translational motion.

Single point calculations of density functional theory (DFT) or time-dependent DFT (TD-DFT) can generate atomic force vectors, i.e., the analytical gradients of total energies with atomic coordinates, which can be used to further calculate the needed torques for rotation predictions according to the following scheme.

The total torque on a rotator (or on any molecule or subunit of a molecule) is obtained as the vector 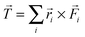, where i runs over all atoms of the rotator (or other subunit of interest), F⃑_i is the total force acting on atom i due to all other atoms in the molecule, and r⃑_i is the position of atom i relative to a reference point. The choice of reference point is arbitrary in general, but it will be useful to place it on the resulting rotation axis. At this stage the location and orientation of the rotation axis are undecided: although there can be multiple axes in a molecule for the rotations of its components, there may be a principal axis of rotation which is chosen by the system (respecting mechanical conservation laws) and will result from the vector summation of the atomic torques in the system, but will also be affected by the constraints imposed by any rigidity of the linkage to a stator and by the different masses of the atoms, i.e. inertia. Some degree of insight is needed to choose the reference point. For colliding molecules or reaction fragments in a vacuum, the point could be located at the center of mass of each separate molecule or fragment, since a free object will rotate around its center of mass. For a molecule like “motor 1”, a relatively rigid bond connecting the stator and rotator favors a reference point anywhere along that bond.

For convenience and clarity, we shall in the following discussion assume that the stator has a fixed orientation, but that it can still deform somewhat during the rotation of the rotator: this may be achieved strictly by fixing the mutual orientation of a particularly important triplet of atoms of the stator. (In a free stator + rotator molecule, both stator and rotator will actually turn in opposite directions to conserve the total angular momentum, so the designation of stator vs. rotator becomes arbitrary. If the stator is relatively large and bulky, or is itself rigidly attached to a larger mass, it will be nearly static.) We also assume zero temperature, i.e. no thermal vibrations.

If the total torque vector T⃑ on a rotator is small (e.g. comparable to or smaller than the average individual atomic torque), then there is only a weak tendency to rotate; this indicates that the atomic torques largely cancel each other (while possibly leading to distortions within the rotator) or are individually small. This outcome shows that the molecule actually does not behave like a rotator in its assumed configuration and state: it may not be a suitable “rotor molecule”, so one may consider alternate molecules instead.

Now consider the more interesting case where the total torque vector T⃑ is larger (e.g. significantly larger than individual atomic torques or dominated by a few atomic torques). If T⃑ is found to be parallel to a fixed bond between the stator and the rotator, it is clear that the rotator will (at least initially) rotate around that bond axis, like a top spinning with a steady vertical axis on a table. The direction of rotation (clockwise or counterclockwise as seen from the rotator to the stator in this paper) will simply be given by the direction in which T⃑ points (“up” vs. “down”). But if T⃑ is tilted away from that bond axis, there is also a torque component that will make the rotator tilt to the side, like a spinning top tilting sideways from the vertical on a table; the rotator may then precess like a tilted top, but that motion will depend also on any other deformations taking place in the molecule during the subsequent rotation.

For simplicity, a flexible axis along the C2=C3 bond of the rotor 1 molecule is chosen for studying the rotation around it and the reference point for calculating torques is set at the middle point of the C2=C3 bond. The total calculated torque is projected onto the C2=C3 axis, see Fig. 1. If we wish to inspect the effect of a tilt of the rotation axis away from the bond axis (resulting in a constrained rotation about the fixed Z-axis), we may simply take the projection T⃑_z of the total torque T⃑ onto the Z-axis and use it to predict the sense of rotation about that fixed direction. Also, our torque method easily provides the component of the total torque perpendicular to the bond axis, T⃑_⊥ = T⃑ − T⃑_∥ = T⃑_X + T⃑_Y: that perpendicular component shows the approximate direction in which this tilting would happen, and roughly how strong the tendency of such tilting is.

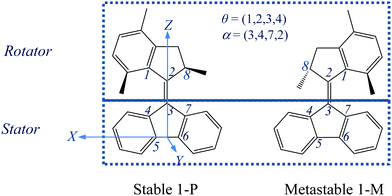Fig. 1 A schematic representation of the stable and metastable states of the “motor 1” molecule, with labelling of key atoms and definition of two dihedral angles θ and α and of the coordinate axes. The C6–C5 bond defines the X-axis, with the origin midway between C5 and C6, while the Z-axis is perpendicular to X and passes through C3, and the Y-axis is perpendicular to X and Z. Thus the pentagon of the stator is in the XZ plane, while the bond C3=C2 is approximately parallel to the Z-axis. The rotational trajectory of “motor 1” is analyzed in ref. 28 and 29 in terms of potential energy surfaces (PESs) for the ground state S0 and the excited state S1, calculated and displayed as a function of the torsion angle, θ, around the linking C2=C3 bond and the “pyramidalization angle”, α, which essentially describes the tilting of the C2=C3 bond away from the initial orientation. Note that the lower methyl group is shown in front of the plane of the figure in both states, so that these two states are not equivalent by 180° rotation about the C2=C3 bond, due to the chiral nature of the molecule.

Application

Motor 1 has two equilibrium states: stable (1-P) and metastable (1-M) conformers.^28,29,33 As depicted in Fig. 1, the upper half of motor 1 is defined as the rotator and the lower half as the stator, which are connected via a “vertical” C2=C3 double bond axis. The key atoms and dihedral angles are labelled and defined in Fig. 1. The fluorene-based stator has 2-fold axial and mirror symmetries about the C2=C3 axis and the figure plane, respectively, when it is disconnected from the rotator. Such a design splits the 360° rotation into two identical 180° rotations with a total of four steps, 1–4: two identical photoisomerizations (1 and 3) and two identical thermal relaxations (2 and 4), shown as a cycle in Fig. 2; in this work, we only model step 1 (and the identical step 3). Thus the geometries of stable 1-P and stable 1-P′ are mutually identical (after 180° rotation) and so are those of metastable 1-M and metastable 1-M′. The rotation can be described as follows: the C2=C3 double bond favors a co-planar arrangement of the rotator and the stator in the 1-P state, but the steric hindrance of the lower methyl group seen at the left in state 1-P in Fig. 1 forces a twist on the rotator (hence this methyl is drawn above the plane of the figure and the molecule is chiral); in step 1 (Fig. 2), the rotator turns about the C2=C3 axis so that this lower methyl swings around in front of the plane of the figure until it hits the right-hand side of the stator in the 1-M state (in the ground state this twisting of the C2=C3 bond has a large energy barrier of nearly 40 kcal mol⁻¹,³³ which is overcome by photoexcitation followed by isomerization); in step 2, the rotator bends over the stator so that the methyl can rotate behind the plane of the figure until it has the 1-P geometry again, labeled as 1-P′ to indicate that a total rotation of 180° from 1-P has been achieved (this “helix inversion” involves a smaller energy barrier that can be overcome thermally); the process then repeats itself identically to complete the second 180° via 1-M′ and reach 1-P again, etc.

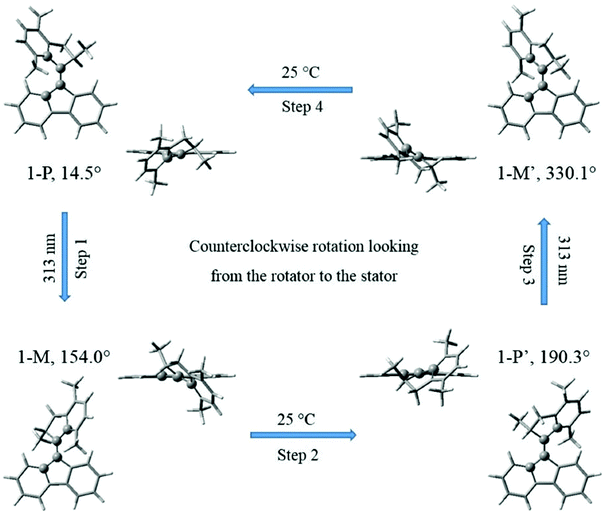Fig. 2 The two photochemical and two thermal steps of a complete 360° rotary cycle of motor 1 (after ref. 27–29). The pairs of images in the 4 states 1-P, 1-M, 1-P′ and 1-M′ show the orientations of the stator, rotator phenyl plane and rotator pentagon, looking toward the –Y direction (external images) vs. the –Z-axis (i.e. along the C2=C3 bond; inner images). The dihedral angle θ is given for each state and marked with atomic balls to track the C2=C3 torsion.

In this work, we choose the CAM-B3LYP^34–36 functional with a 6-31+G* basis set to carry out the calculations conducted using the Gaussian 09 code.³⁷ The reliability of this functional is validated by comparing the excitation energies with reported higher levels of TD-DFT (see Table 1).

Table 1 Comparisons of the excitation energies in kcal mol⁻¹ and corresponding wavelengths in nm (in parentheses) of the bistable isomers 1-P and 1-M at various levels of calculations. The numerical values are taken from ref. 29

Method, basis set	1-P	1-M
CAM-B3LYP, 6-31+G*	86.94 (329)	78.40 (364)
TD-BH&HLYP, 6-31G*	87.17 (328)	78.17 (366)
SA-REBH&HLYP, 6-31G*	87.63 (327)	78.40 (365)
OM2/GUGA-MRCI, 6-31G*	90.63 (315)	86.48 (331)

---

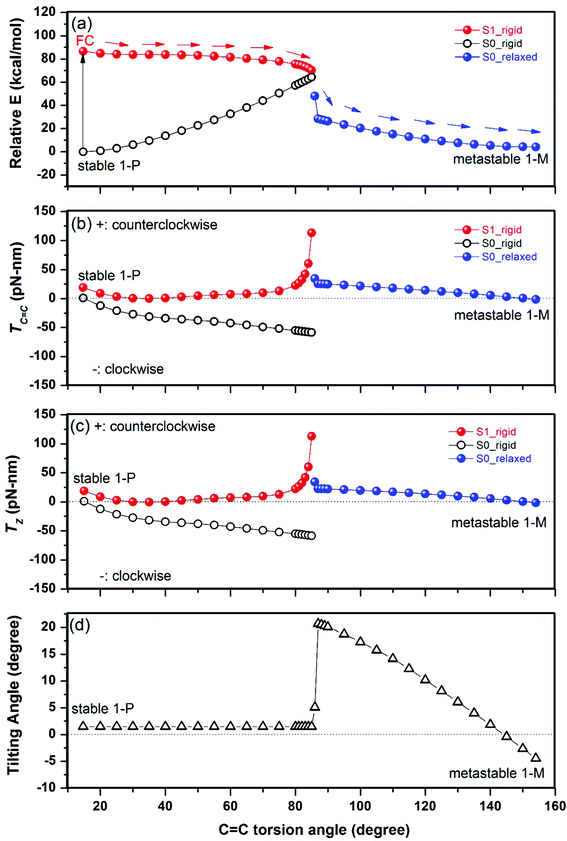
In the initial lowest-energy stable state (1-P), there are no net forces on any atom, so the total torque on the rotator is zero. The photoexcitation to the excited state S1 first leads to the Franck–Condon (FC) state in which the atomic geometry has not changed while the electronic level occupation has changed; this causes non-zero net forces on most atoms and results, due to the chirality of the molecule, in a significant positive total torque on the rotator, as projected onto the C=C bond axis (see Fig. 3b near the ground state's torsion angle of 15°). The positive sign implies a counterclockwise rotation, looking from the rotator toward the stator. This counterclockwise rotation is reflected by a negative slope of the PES surface of the S1 state (seen as a downward slope marked by arrows in Fig. 3a), driving the system in the counterclockwise direction.

Fig. 3 (a) Profiles of the energy E of the S0 and S1 PESs (the arrows show the expected counterclockwise system evolution), (b) total torque T_C=C (in units of piconewton × nanometer = 10⁻²¹ N m) of the rotator of motor 1 projected onto the C=C double bond as a function of the torsion angle θ from 1-P to 1-M, assuming rigid rotation of the rotator until 85°, then optimized rotation beyond 85° (see the text for details), (c) profiles of the S0 and S1 total torques T_Z (in units of piconewton × nanometer = 10⁻²¹ N m) of the rotator of motor 1 projected onto the Z direction, (d) tilting angle of the C=C axis relative to the Z direction as a function of the torsion angle (θ) from 1-P to 1-M, assuming rigid rotation of the rotator until 85°, then optimized rotation beyond 85° (see the text for details).

We see here the contrast in the two approaches for obtaining the direction of rotation. The PES approach requires multiple total-energy calculations in high-dimensional search space to find a path of descending energy; it is not sufficient to observe that a particular dihedral angle between four atoms will turn counterclockwise, since the rest of the rotator could be turning in any other direction, e.g. clockwise. By contrast, the total torque uses a single total-energy calculation at the initial geometry to indicate the overall rotation direction of the rotator.

For further rotation away from 1-P, the torque method can efficiently simulate a simple rigid rotation of the rotator to explore qualitatively whether there is continued tendency to rotate counterclockwise. At this simplest level, we obtain the total torque (and total energy) shown in Fig. 3 until a torsion angle of 85° (where the total energies of S0 and S1 states are closest). We see that the total torque on the rotator remains positive or close to zero, so the rotation can continue in the counterclockwise direction (the more exact PES analysis of ref. 28 and 29 confirms a continuous downward slope in the counterclockwise direction). We have calculated the FC state every 5° or 1° for Fig. 3 (with relatively rapid electronic optimization but without time-consuming geometric optimization): we could have skipped most of those points by using larger steps of 30°, for example, to save even more computation time.

The barrier for twisting the C=C double bond on the ground state PES, as seen in Fig. 3a, occurs near a torsion angle of 85°, causing high energies in that region. Also, near 85° the ground state S0 and the excited state S1 approach each other in energy (Fig. 3a): this facilitates de-excitation to the ground state S0. Beyond 85°, we thus follow the further rotation in the ground state S0 until the metastable state 1-M (near 154°). Due to the deexcitation timescale impact, we now allow the rotator (and stator) to be non-rigid in the ground state S0. This requires optimizing the structure at several fixed torsion angles (specified as particular dihedral angles involving the C=C bond), which we did every 1° or 5° for Fig. 3. We observe again a positive total torque, approaching zero near the equilibrium state 1-M, as it should; so the rotation continues in the counterclockwise direction (as also confirmed in the more complete PES analysis²⁹). The sudden switch to optimized geometries causes the observed discontinuities near 85° in Fig. 3, which are therefore not physical. Thus, the real geometric evolution might happen between the rigid and relaxed S0 PES in the range of 86°–90°.

To examine whether tilting the C=C axis could significantly change the effect of the torque described above, we project the torque of the rotator onto the Z direction (T⃑_z) to compare it with the above T⃑_C=C. As shown in Fig. 3c, T_Z is almost the same as T_C=C of Fig. 3b, implying that the tilting effect on the axis is minor. Fig. 3d shows that the tilting angle of the C=C axis from the Z direction remains ∼1.5° before a torsion angle of 85° due to the rigid rotation and varies in the range of 0–21° for the relaxed geometries after a torsion angle of 86°.

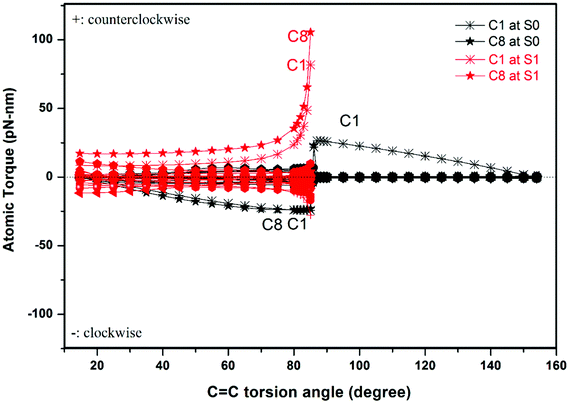
Our method allows us to easily identify those atoms that dominate the unidirectional rotation, namely those atoms which are subject to the largest torques. We plot the individual atomic torques of the rotator in Fig. 4 as a function of the torsion angle θ. During the rotation in the S1 state from 15° to 85°, the C1 and C8 atoms bear the largest torques. In the S0 state from 86° to 154°, the C1 atom basically bears the entire torque, all other atoms experiencing negligible torque. The C1 and C8 atoms belong to the same five-membered ring, and are connected together by C2 of the C2=C3 bond, as shown in Fig. 1. This shows that the optical response is still the cis–trans isomerization of the vinyl bond, but is blended into the structure of the more complex motor 1. After photoexcitation to state S1, the C1 and C8 atoms undergo most of the torque that drives the rotator to rotate in a counterclockwise direction until the intermediate configuration at 85°, where the rotator and stator are almost perpendicular to each other. Then after de-excitation from S1 to S0, the remaining rotation to 1-M will be driven by the C1 atom. As demonstrated above, the atomic torque analysis reveals very clearly that a single atom can dominate the rotation direction and can further deepen the study of the working mechanism of the motor. At the same time, in our example, the excitation to the S1 state produces a distribution of atomic torques on multiple atoms with both negative and positive signs. This is unfavorable for starting a unidirectional rotation as these atoms will tend to rotate in opposite directions. Thus, our atomic torque profile can reveal the absolute preference of rotation direction so as to help judge whether unidirectionality in a molecular motor is favored or not.

Fig. 4 The atomic torques in the rotator in the S0 and S1 states as a function of the C2=C3 double bond torsion angle from 1-P (at left) to 1-M (at right). Only atoms C1 and C8 are labelled, as they are subject to the largest torques.

Conclusion and remarks

In conclusion, we have developed an approach to use torque from DFT and TD-DFT calculations to predict the rotational behavior of a molecular rotor. The approach has been successfully applied in the study of the photoisomerization of a light-powered molecular rotary motor twisting around its central C=C axis. Through vector summation of the torques acting on each atom and projected onto the rotation axis, we can optionally inspect the impact of a certain part within a motor on the unidirectional rotation with explicit rotation direction and magnitude. The method illustrates clearly how, for this rotor molecule, the unidirectional rotation can be realized by switching from the S1 state to the S0 state. Also, our approach highlights that the significant atomic torques can be localized on a few atoms (here two C atoms attached directly to the C=C axis in the rotator). It is also seen that atomic torques with widely variable directions on multiple atoms after the photoexcitation are not favorable for driving a unidirectional rotation in this molecule.

Our work shows that the torque profile reveals the rotation direction, even though it is only an alternative expression of the ground and excited-state PESs. Since the potential energy is a scalar quantity, it cannot be decomposed and projected; by contrast, the calculated torque projected onto the rotational axis can clearly distinguish between the rotational directions in any configuration. The method thus can help experiments in the design of motor molecules with better performance. The approach is very helpful in our ongoing research to study the mechanical motions of other molecular motors.

Our torque approach can also easily be applied to molecular collisions, chemical reactions, vibrations or electronic excitations for given atomic positions (e.g. distortion of a molecule by a collision, by reaction with another molecule, by vibration or by excitation). A single total-energy calculation can obtain the forces acting on each atom and therefore lead to the torque acting on any part of the molecule(s), thus predicting the presence and direction of a resulting rotation (of course, with colliding molecules one should also consider the linear and angular momenta of the incoming and outgoing molecules or fragments, as in standard collision dynamics).

Acknowledgements

The work described in this paper was supported by grants from the Research Grants Council of the Hong Kong SAR (Project No. CityU 11304415 and HKBU 12301814). We acknowledge the High Performance Cluster Computing Centre at the Hong Kong Baptist University, which receives funding from the Research Grants Council, the University Grants Committee of the HKSAR and HKBU, and the National Supercomputing Center in Shenzhen for providing the computational resources, and Jing Xia for her participation in the early period of this work. Klaus Hermann greatly acknowledges support by the ICTS at HKBU.

References

1. A. J. Stone, The Description of Bimolecular Potentials, Forces and Torques: the S and V Function Expansions, Mol. Phys., 1978, 36, 241–256.
2. S. L. Price, A. J. Stone and M. Alderton, Explicit Formulae for the Electrostatic Energy, Forces and Torques between a Pair of Molecules of Arbitrary Symmetry, Mol. Phys., 1984, 52, 987–1001.
3. Theoretical Models of Chemical Bonding Part 4: Theoretical Treatment of Large Molecules and Their Interactions, ed. Z. B. Maksic, Springer, 1991.
4. S. Mukherjee and A. Warshel, Dissecting the Role of the γ-Subunit in the Rotary–Chemical Coupling and Torque Generation of F₁-ATPase, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2746–2751.
5. S. Mukherjee, R. P. Bora and A. Warshel, Torque, Chemistry and Efficiency in Molecular Motors: a Study of the Rotary-Chemical Coupling in F₁-ATPase, Q. Rev. Biophys., 2015, 48, 395–403.
6. K. Mislow, Molecular Machinery in Organic Chemistry, Chemtracts: Org. Chem., 1989, 2, 151–174.
7. V. Balzani, M. Gömez-Löpez and J. F. Stoddart, Molecular Machines, Acc. Chem. Res., 1998, 31, 405–414.
8. J.-P. Sauvage, Transition Metal-Containing Rotaxanes and Catenanes in Motion: Toward Molecular Machines and Motors, Acc. Chem. Res., 1998, 31, 611–619.
9. V. Balzani, A. Credi, F. M. Raymo and J. F. Stoddart, Artificial Molecular Machines, Angew. Chem., Int. Ed., 2000, 39, 3348–3391.
10. N. Koumura, R. W. J. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Light-Driven Monodirectional Molecular Rotor, Nature, 1999, 401, 152–155.
11. J. Michl and E. C. H. Sykes, Molecular Rotors and Motors: Recent Advances and Future Challenges, ACS Nano, 2009, 3, 1042–1048.
12. H. C. Berg, The Rotary Motor of Bacterial Flagella, Annu. Rev. Biochem., 2003, 72, 19–54.
13. M. Kim, J. C. Bird, A. J. Van Parys, K. S. Breuer and T. R. Powers, A Macroscopic Scale Model of Bacterial Flagellar Bundling, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 15481–15485.
14. S. Shinkai, T. Ogawa, Y. Kusano, O. Manabe, K. Kikukawa, T. Goto and T. J. Matsuda, Photoresponsive Crown Ethers. 4. Influence of Alkali Metal Cations on Photoisomerization and Thermal Isomerization of Azobis(benzocrown ether)s, J. Am. Chem. Soc., 1982, 104, 1960–1967.
15. B. L. Feringa, W. F. Jager, B. de Lange and E. W. Meijer, Chiroptical Molecular Switch, J. Am. Chem. Soc., 1991, 113, 5468–5470.
16. T. R. Kelly, M. C. Bowyer, K. V. Bhaskar, D. Bebbington, A. Garcia, F. Lang, M. H. Kim and M. P. Jette, A Molecular Brake, J. Am. Chem. Soc., 1994, 116, 3657–3658.
17. B. L. Feringa, N. P. M. Huck and H. A. van Doren, Chiroptical Switching between Liquid Crystalline Phases, J. Am. Chem. Soc., 1995, 117, 9929–9930.
18. T. C. Bedard and J. S. Moore, Design and Synthesis of a ‘Molecular Turnstile’, J. Am. Chem. Soc., 1995, 117, 10662–10671.
19. F. Würthner and J. Rebek Jr., Light-Switchable Catalysis in Synthetic Receptors, Angew. Chem., Int. Ed. Engl., 1995, 34, 446–448.
20. G. M. Tsivgoulis and J.-M. Lehn, Photonic Molecular Devices: Reversibly Photoswitchable Fluorophors for Nondestructive Readout for Optical Memory, Angew. Chem., Int. Ed. Engl., 1995, 34, 1119–1122.
21. W. F. Jager, J. C. de Jong, B. de Lange, N. P. M. Huck, A. Meetsma and B. L. Feringa, A Highly Stereoselective Optical Switching Process Based on Donor-Acceptor Substituted Dissymmetric Alkenes, Angew. Chem., Int. Ed. Engl., 1995, 34, 348–350.
22. M. Klok, N. Boyle, M. T. Pryce, A. Meetsma, W. R. Browne and B. L. Feringa, MHz Unidirectional Rotation of Molecular Rotary Motors, J. Am. Chem. Soc., 2008, 130, 10484–10485.
23. D. Pijper, M. G. M. Jongejan, A. Meetsma and B. L. Feringa, Light-Controlled Supramolecular Helicity of a Liquid Crystalline Phase Using a Helical Polymer Functionalized with a Single Chiroptical Molecular Switch, J. Am. Chem. Soc., 2008, 130, 4541–4552.
24. T. Kudernac, N. Ruangsupapichat, M. Parschau, B. Maciá, N. Katsonis, S. R. Harutyunyan, K.-H. Ernst and B. L. Feringa, Electrically Driven Directional Motion of a Four-Wheeled Molecule on a Metal Surface, Nature, 2011, 479, 208–211.
25. G. Du, E. Moulin, N. Jouault, E. Buhler and N. Giuseppone, Muscle-like Supramolecular Polymers: Integrated Motion from Thousands of Molecular Machines, Angew. Chem., Int. Ed., 2012, 51, 12504–12508.
26. M. A. Haidekker and E. A. Theodorakis, Molecular Rotors—Fluorescent Biosensors for Viscosity and Flow, Org. Biomol. Chem., 2007, 5, 1669–1678.
27. M. M. Pollard, A. Meetsma and B. L. Feringa, A Redesign of Light-Driven Rotary Molecular Motors, Org. Biomol. Chem., 2008, 6, 507–512.
28. A. Kazaryan, J. C. M. Kistemaker, L. V. Schäfer, W. R. Browne, B. L. Feringa and M. Filatov, Understanding the Dynamics Behind the Photoisomerization of a Light-Driven Fluorene Molecular Rotary Motor, J. Phys. Chem. A, 2010, 114, 5058–5067.
29. A. Kazaryan, Z. Lan, L. V. Schäfer, W. Thiel and M. Filatov, Surface Hopping Excited-State Dynamics Study of the Photoisomerization of a Light-Driven Fluorene Molecular Rotary Motor, J. Chem. Theory Comput., 2011, 7, 2189–2199.
30. J. Conyard, A. Cnossen, W. R. Browne, B. L. Feringa and S. R. Meech, Chemically Optimizing Operational Efficiency of Molecular Rotary Motors, J. Am. Chem. Soc., 2014, 136, 9692–9700.
31. Torque in spacecraft: reaction wheel http://https://en.wikipedia.org/wiki/Reaction_wheel & attitude control http://https://en.wikipedia.org/wiki/Attitude_control.
32. A. H. de Ruiter, C. Damaren and J. R. Forbes, Spacecraft Dynamics and Control: An Introduction, Wiley, 2013.
33. M. Filatov and M. Olivucci, Designing Conical Intersections for Light-Driven Single Molecule Rotary Motors: From Precessional to Axial Motion, J. Org. Chem., 2014, 79, 3587–3600.
34. T. Yanai, D. P. Tew and N. C. Handy, A New Hybrid Exchange–Correlation Functional using the Coulomb-Attenuating Method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
35. I. V. Rostov, R. D. Amos, R. Kobayashi, G. Scalmani and M. J. Frisch, Studies of the Ground and Excited-State Surfaces of the Retinal Chromophore using CAM-B3LYP, J. Phys. Chem. B, 2010, 114, 5547–5555.
36. I. V. Rostov, R. Kobayashi and R. D. Amos, Comparing Long-Range Corrected Functionals in the Cis–Trans Isomerisation of the Retinal Chromophore, Mol. Phys., 2012, 110, 2329–2336.
37. M. J. Frisch, et al., Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009.

---

Footnote

† Authors who contributed equally to this work.

---