 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The computational prediction of Raman and ROA spectra of charged histidine tautomers in aqueous solution
Salvatore
Cardamone
ab,
Beth A.
Caine
ab,
Ewan
Blanch
c,
Maria G.
Lizio
ab and
Paul L. A.
Popelier
*ab
aManchester Institute of Biotechnology (MIB), 131 Princess Street, Manchester M1 7DN, UK. E-mail: paul.popelier@manchester.ac.uk; Tel: +44 (0)161 3064511
bSchool of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK
cSchool of Science, Royal Melbourne Institute of Technology (RMIT), 124a La Trobe Street, Melbourne, VIC 3001, Australia
First published on 12th September 2016
Abstract
Histidine is a key component of a number of enzymatic mechanisms, and undertakes a myriad of functionalities in biochemical systems. Its computational modelling can be problematic, as its capacity to take on a number of distinct formal charge states, and tautomers thereof, is difficult to capture by conventional techniques. We demonstrate a means for recovering the experimental Raman optical activity (ROA) spectra of histidine to a high degree of accuracy. The resultant concordance between experiment and theory is of particular importance in characterising physically insightful quantities, such as band assignments. We introduce a novel conformer selection scheme that unambiguously parses snapshots from a molecular dynamics trajectory into a smaller conformational ensemble, suitable for reproducing experimental spectra. We show that the “dissimilarity” of the conformers within the resultant ensemble is maximised and representative of the physically relevant regions of molecular conformational space. In addition, we present a conformer optimisation strategy that significantly reduces the computational costs associated with alternative optimisation strategies. This conformer optimisation strategy yields spectra of equivalent quality to those of the aforementioned alternative optimisation strategies. Finally, we demonstrate that microsolvated models of small molecules yield spectra that are comparable in quality to those obtained from ab initio calculations involving a large number of solvent molecules.
1. Introduction
Raman optical activity (ROA) is a powerful chiroptical technique that can be used to probe a number of molecular properties. In the early days of its inception, ROA was used to deduce stereochemical information of molecular species by comparison with band patterns of related molecules.1 Unlike a number of other spectroscopies, ROA intensities in the low wavenumber region of the spectrum are rich in information, since these regions correspond to, for example, torsional degrees of freedom2 and large scale conformational modes of motion.3,4 ROA also possesses the capacity to determine the proportions of enantiomers within a sample, which is of great importance in purification processes.5The structural features of biochemical systems make them particularly amenable to ROA spectroscopy. ROA offers a far more robust analysis of biomolecular structure than more common forms of vibrational spectroscopy because of its sensitivity to chirality. The ROA signal of a system is largely dominated by the more rigid and chiral elements of that system, and in the case of proteins and peptides this corresponds to the secondary structure motifs exhibited by the polypeptides. This makes ROA highly useful for structural characterisation of complex biomolecules, in contrast to Raman spectroscopy, where amino acid sidechain signals typically dominate the spectrum.6 ROA is by no means constrained to peptide systems, and the ROA signals of other biochemical species, such as DNA bases7 and oligomeric nucleic acids,8 also prove informative. The utility of ROA in structural analysis has been exemplified over the years by a number of studies on the folding,6,9 assembly10 and dynamical properties11 of biochemical systems.
Histidine is somewhat unique in its ability to perform a number of biochemical roles. Traditionally characterised as a polar amino acid, histidine does not substitute particularly well with other amino acids.12 The nitrogen atoms of the imidazole group have long been known to act as proton shuttles, and grant functionality for a number of enzymatic mechanisms. However, histidine has also been shown to participate in interactions that are typically perceived to involve large aromatic amino acids such as tryptophan and phenylalanine. Noncovalent interactions involving histidine have been shown to exist in the form of stacking between its imidazole ring and a number of DNA nucleobases.13
Histidine features in the “catalytic triad” of a number of biochemically important enzymes, such as serine and cysteine proteases, where it acts as a proton shuttle during the process of protein catabolism.14 The Manzetti mechanism15 suggests that matrix metalloproteinases, a set of well-characterised cancer therapeutic targets, attain catalysis through a pair of histidine residues that coordinate a Zn2+ ion. The penta-coordinate Zn2+ ion is induced to act as a reversible electron donor, and can hydrolyse the scissile peptide bond. Indeed, research within the field of biocatalysis has found evidence for histidine residues within tripeptide motifs co-ordinating even more exotic metal ions, such as Pt2+ and Au3+, and exhibiting chemotherapeutic properties.16
Five protonation states of histidine exist: His2+, His1+, His0, His1− and His2−, where the superscript denotes the formal charge state. In addition to these protonation states, the imidazole ring in His0 and His1− can exist in one of two tautomeric forms. This effect originates from the lone pairs of the nitrogen atoms contributing to π-delocalisation around the five-membered imidazole ring. The imidazole nitrogen atoms are labelled Nπ or Nτ, the former being the nitrogen one bond away from the β carbon in the alkyl sidechain, and the latter being the nitrogen two bonds away from β carbon,17 as shown in Fig. 1. For convenience, we also depict the major torsional degrees of freedom that are typically varied for conformational studies of histidine in Fig. 1; (φ,ψ) are the conventional Ramachandran dihedrals, while χ1 and χ2 are the side chain dihedrals. Tautomeric forms are denoted by specifying the protonated nitrogen, i.e. NπH or NτH. Using this nomenclature, we can uniquely label the seven microstates of histidine: His2+, His1+, His0[NπH], His0[NτH], His1−[NπH], His1−[NτH] and His2−. We use the nomenclature “microstate” throughout this work in reference to one of these seven forms of histidine.
 | ||
| Fig. 1 Zwitterionic histidine (His0[NτH]) where the imidazole nitrogen atoms have been labelled as indicated in the text. The two sidechain dihedral angles, χ1 and χ2, are also labelled. | ||
In this work, we present a number of developments that we have instituted and tested for the accurate computation of both Raman and ROA spectra. We have investigated only the His0 (i.e. both His0[NτH]and His0[NπH]) and His1+ charge states here, since these are the primary forms that histidine takes in the majority of biochemical systems at physiological pH. The issues of conformer selection, conformer solvation and conformer optimisation are each tackled independently, and their effects are demonstrated on both tautomeric systems and formally charged systems.
2. The problem of conformer generation
2.1 Solvation
The fact that biochemical systems are stabilised by solvent interactions makes their modelling problematic. Since the solvent plays an important role in dictating the energetics of a molecular system, it becomes imperative that spectroscopic predictions include some level of solvent modelling. It has been shown that simply omitting the solvent from spectroscopic calculations yields poor quality results that severely digress from experiment.18 Indeed, when dealing with charged species, such as zwitterionic amino acids, the molecules are energetically only stable if the solvent is included,19 and optimise to the neutral amine-carboxylic acid species in the absence of constraints.The two major models for solvation effects in ab initio calculations are implicit and explicit solvation. With the former,20 the solvent environment is modelled as a homogeneous dielectric medium, reducing the magnitude of electrostatic interactions relative to the system in vacuo. The Polarisable Continuum Model21 (PCM) and Conductor-like Screening Model22 (COSMO) have been effective in predicting molecular energies,23–25 but lack any atomic-level properties of the solvent, such as the solvent's ability to form hydrogen bonds with a solute. Implicit solvation methods have been found to offer minimal benefits in computing vibrational frequencies, and therefore vibrational spectra, relative to gas phase calculations.26
A number of explicit solvation schemes have been investigated. At the lowest end, one can include a small number of solvent molecules and treat the entire solute–solvent system quantum mechanically, perhaps embedded in an implicit solvation field. The number of explicit solvent molecules treated in this way is arbitrary, and their positioning around the solute can be problematic. Solvent molecules can be added in an ad hoc fashion around polar (or non-polar if the solvent is non-polar) groups, leading to significant improvement over gas phase spectra.27 However, a number of problems can also be attributed to this methodology, such as poor optimisation of the system geometry owing to its distance from a minimum on the potential energy surface.28
Another more popular method is the use of QM/MM, where the solvent is treated classically and the solute quantum mechanically. This has proven to be a very successful method for calculating spectra. For example, Cheeseman and coworkers29 have predicted the methyl-β-D-glucose ROA spectrum to an impressive level of accuracy, reproducing the vast majority of spectral features. More recently, this approach has been further validated on a number of other systems, such as glucuronic acid30 and β-D-xylose.31 However, one is still constrained in selecting a conservative number of solvent molecules to include in the calculation for it to remain tractable; simply including hundreds of solvent molecules in the QM/MM calculation is not routinely feasible.
2.2 Optimisation
Complications arise in the QM/MM method of modelling solvent during the geometrical optimisation of the system. For the normal modes of motion of the system to be correctly determined, the system is required to relax to an energetic minimum on the potential energy surface. Geometry optimisation is notoriously difficult for a system including even a small number of explicit solvent molecules;30,31 the inclusion of water molecules in these studies flattens the potential energy surface, making it difficult to find well-defined minima. Two methods to resolve this problem have therefore been proposed: OptAll and OptSolute. The OptAll scheme optimises the entire QM/MM system (with a less rigorous convergence threshold than is usually implemented), while the OptSolute method freezes all solvent molecules and optimises only the solute in the field of the static solvent. The latter method is naturally much quicker than the former, but was found to yield poorer, although still informative, quality spectra. Some trade-off between accuracy and computational tractability is to be expected, but without there being an accepted methodology for qualitatively comparing predicted spectra to experimental spectra, it is difficult to ascertain whether the improvement in spectral quality warrants the additional computational efforts.3. Technical details
3.1 Experimental setup
We have prepared samples of histidine at a pH of 7.8 and 4.2, both at a concentration of 0.26 M (equivalent to 40 mg mL−1). Spectra were collected over a period of 7 hours, using an incident wavelength of 532 nm, a laser power of 700 mW and a 1.47 s exposition time. All spectra have been normalised so that they can be directly compared with the computed spectra. The absolute amplitude is therefore irrelevant in our analysis.3.2 Molecular dynamics
The arrangement of solvent molecules is typically accomplished by use of molecular dynamics. The system is solvated and the resultant trajectory is parsed into a number of snapshot configurations. These configurations are subsequently used as the conformational ensemble for spectral calculations. Recent work32 has selected the snapshots entirely randomly, with very rough (qualitative) estimates used to maximise the conformational diversity of the ensemble. The snapshots are then energetically minimised, and those snapshots with a high Boltzmann weight form an ensemble that is considered representative of the dominant system conformations.We have conducted 100 ns molecular dynamics trajectories for His0[NτH], His0[NπH] and His1+, solvated in boxes comprising 469 water molecules, with a chloride ion added in the latter case to ensure the system remained electrically neutral. Throughout, we have used the GROMACS33 molecular dynamics package in conjunction with the OPLS-AA34 force field.
Energy minimisation of these systems was initially undertaken with the steepest descent method, until convergence of the total system energy was attained. Following energy minimisation, we have conducted two separate equilibration phases. The first was a 1 ns NVT equilibration, using the Berendsen thermostat to maintain a temperature of 300 K, whilst the second was a 1 ns NPT equilibration using the Parrinello–Rahman barostat to maintain both a temperature of 300 K and a pressure of 0.1 MPa (1 bar). The particle mesh Ewald methodology was used to treat long-range electrostatics. A cut-off distance of 10 Å was chosen for Coulombic and van der Waals interactions. Both stages of equilibration were verified as being properly equilibrated by checking the convergence of the temperature for the NVT equilibration and the density of the system for the NPT equilibration. Both showed convergence after roughly 100 ps, and so our equilibration was assumed to be sufficient.
Our final step involved a 100 ns production molecular dynamics run in the NPT ensemble at a temperature of 300 K and a pressure of 0.1 MPa. To this end, we have used the Berendsen thermostat coupled with the isotropic Parrinello–Rahman barostat. The dynamical timestep used for our simulations was 0.5 fs, with a snapshot geometry output every 5 ps, resulting in 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshot geometries. Coulombic and van der Waals interactions were treated as we have described in the preceding paragraph.
000 snapshot geometries. Coulombic and van der Waals interactions were treated as we have described in the preceding paragraph.
3.3 Filtering of similar geometries
For the following discussion, the 3 × N matrix X = [x1…xN]T, being the number of atoms in the molecule, is used to denote a molecular conformation, where xi is the Cartesian position vector of the ith atom.
being the number of atoms in the molecule, is used to denote a molecular conformation, where xi is the Cartesian position vector of the ith atom.
Perhaps the most ubiquitous form of geometrical comparison between two structures, X and Y, is the root mean square deviation (RMSD), which we denote 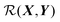 ,
,
 | (1) |
 is not invariant with respect to rigid transformations. For example, if X and Y possess the same internal geometry, but are rigidly translated relative to one another, then eqn (1) represents the two geometries as being dissimilar. The same result holds for the case of rigid rotations relative to one another. Of course, molecules in homogeneous environments are entirely equivalent after having undergone rigid translations, and so the RMSD in its current incarnation is of no value for our purposes.
is not invariant with respect to rigid transformations. For example, if X and Y possess the same internal geometry, but are rigidly translated relative to one another, then eqn (1) represents the two geometries as being dissimilar. The same result holds for the case of rigid rotations relative to one another. Of course, molecules in homogeneous environments are entirely equivalent after having undergone rigid translations, and so the RMSD in its current incarnation is of no value for our purposes.
We can render eqn (1) in a useful form by finding 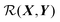 such that it is minimised with respect to all rigid rotations and translations, i.e. by minimising the function
such that it is minimised with respect to all rigid rotations and translations, i.e. by minimising the function
 | (2) |
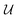 is an orthonormal matrix, i.e.
is an orthonormal matrix, i.e. , the identity matrix, and can therefore be interpreted as a matrix defining a rigid transformation.35 Taking the square root of
, the identity matrix, and can therefore be interpreted as a matrix defining a rigid transformation.35 Taking the square root of 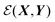 therefore corresponds to the minimised RMSD (mRMSD) between the two molecular conformations. A further step is required to ensure our definition of the mRMSD is robust: if the orthonormal transformation matrix
therefore corresponds to the minimised RMSD (mRMSD) between the two molecular conformations. A further step is required to ensure our definition of the mRMSD is robust: if the orthonormal transformation matrix  , does not constitute a right-handed system
, does not constitute a right-handed system  , then it represents an improper rotation, i.e. a transformation that can be represented by some combination of a rotation about an axis and subsequent reflection in a plane. Thus, we require computation of the determinant of
, then it represents an improper rotation, i.e. a transformation that can be represented by some combination of a rotation about an axis and subsequent reflection in a plane. Thus, we require computation of the determinant of  to ensure we deal only with proper rotations.
to ensure we deal only with proper rotations.
The minimisation of eqn (2) with respect to  can be undertaken in a number of ways. Historically, the orthonormality conditions of
can be undertaken in a number of ways. Historically, the orthonormality conditions of 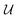 have been added to eqn (2) as Lagrange multipliers and formal solutions obtained, as given by Kabsch,36,37 after whom the algorithmic formalism for solution of eqn (2) is named. We proceed in deriving the form of
have been added to eqn (2) as Lagrange multipliers and formal solutions obtained, as given by Kabsch,36,37 after whom the algorithmic formalism for solution of eqn (2) is named. We proceed in deriving the form of  in a more physically intuitive way, elaborated upon in a number of more recent sources.38,39 For the sake of brevity, we simply present the computable expression for
in a more physically intuitive way, elaborated upon in a number of more recent sources.38,39 For the sake of brevity, we simply present the computable expression for  ,
,
 | (3) |
Our final consideration centres on whether  defines a proper or improper rotation, as we have previously alluded to. We can account for this by specifying that if
defines a proper or improper rotation, as we have previously alluded to. We can account for this by specifying that if  , then d = 1, otherwise d = −1, allowing us to give the final expression for
, then d = 1, otherwise d = −1, allowing us to give the final expression for 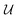 ,
,
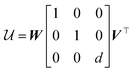 | (4) |
3.4 Ab initio spectrum calculation
All ab initio calculations were undertaken using the GAUSSIAN0941 software package, with the two-layer ONIOM method.42 Histidine was modelled in the high layer, and solvent was modelled in the low layer. The high layer was treated at the B3LYP/6-31G(d) level of theory,43 and the low layer with the AMBER99SB force field including TIP3P parameters for the water molecules. Electronic embedding was used, so that the low layer electrostatics were incorporated into the quantum mechanical Hamiltonian. The ab initio optimisations were performed with the Berny algorithm in the Cartesian basis, and no micro-iterations were used for electronic embedding.For calculation of the molecular optical activity tensors, we invoke the analytical two-step formalism, or the n + 1 algorithm,44 in which the harmonic frequency and ROA tensor calculations are separated into differing levels of theory. For calculation of the normal coordinates and harmonic frequencies, we have used the B3LYP/6-31G(d) level of theory, while for the frequency-dependent ROA tensors, we have used the B3LYP/rDPS level of theory.45 rDPS is a rarefied basis set that is based on the 3-21++G basis set with semi-diffuse p-functions on all hydrogen atoms.46 rDPS has been shown to provide a similar level of accuracy in the resulting spectra to much larger Dunning basis sets,45 such as aug-cc-pVDZ.
An excitation wavelength of 532 nm was used for calculation of the ROA tensors, in keeping with the conventional experimental setup. We then obtained scattered circular polarisation backscattered (SCP-180) ROA intensities. Individual conformer spectra were Boltzmann weighted, and those with a Boltzmann weight exceeding 0.5% were used to form the spectrum (using a Lorentzian bandwidth of 10 cm−1), for comparison with experimental spectra.
4. Conformational ensemble construction
Past work47 on computing the Raman and ROA spectra of zwitterionic histidine has implemented a simplistic conformational selection tool. Six major in vacuo conformational preferences for histidine were proposed to arise from the χ1,χ2 torsional degrees of freedom: trans-plus (χ2 = 180°, χ1 = 90°); trans-minus (χ2 = 180°, χ1 = −90°); gauche-plus–plus (χ2 = 60°, χ1 = 90°); gauche-plus–minus (χ2 = 60°, χ1 = −90°); gauche-minus–plus (χ2 = −60°, χ1 = 90°); and gauche-minus–minus (χ2 = −60°, χ1 = −90°). These conformers were solvated in an ad hoc manner (a number of water molecules were randomly added around the histidine in each computational model) and energetically minimised. However, the solvation of in vacuo energetic minima does not yield a physically realistic conformational ensemble. Intramolecular hydrogen bonds stabilise in vacuo structures, which are not as preferable when the solute is solvated. Under explicit solvation, interactions with solvent are more favourable than the intramolecular hydrogen bonds.48 In addition to this, zwitterionic amino acids are not stable in vacuo. This instability necessitates the introduction of non-physical constraints on energetic optimisation to maintain the zwitterionic form.For each system, we have utilised the Kabsch selection methodology outlined in Section 3.3. For each MD trajectory comprising 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshots, we have parsed the 20 snapshots whose solute geometries are the most mutually diverse by use of a greedy MaxMin heuristic. Solvent geometries were not included in the Kabsch filtering. We present a conformer analysis of the conformational ensemble obtained by this Kabsch “filtering” in Fig. 2.
000 snapshots, we have parsed the 20 snapshots whose solute geometries are the most mutually diverse by use of a greedy MaxMin heuristic. Solvent geometries were not included in the Kabsch filtering. We present a conformer analysis of the conformational ensemble obtained by this Kabsch “filtering” in Fig. 2.
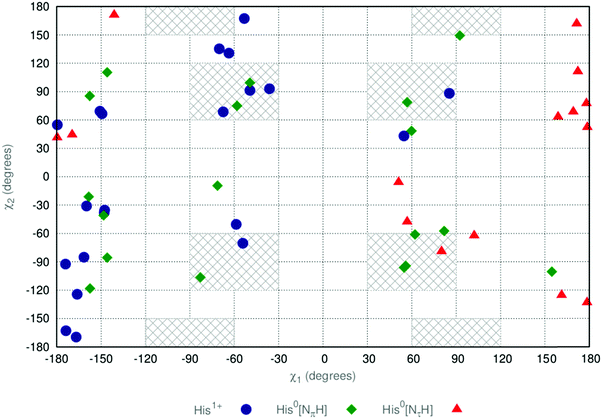 | ||
| Fig. 2 Sidechain dihedral values (χ1 and χ2) taken by conformers within the three ensembles obtained by a Kabsch filtering of the MD trajectories outlined in Section 3.2. His1+ (blue circles), His0[NπH] (green diamonds) and His0[NτH] (red triangles). Grey hatched regions correspond to those conformers used in ref. 47. | ||
We have highlighted in grey those regions of the (χ1,χ2) plot in Fig. 2 that correspond to the in vacuo minima employed by Deplazes and coworkers,47 ±30°. Concerning the His1+ conformers, the (χ2 = −60°, χ1 = 60°) region is not sampled at all. Analysis shows this fact to result from an unfavourable ammonium–imidazole NπH contact. Concerning the His0 conformers, when χ2 = 90°, a favourable ammonium–imidazole Nπ interaction stabilises the His0[NτH] microstate. The poor sampling of the χ1 = −60° region for the His0[NτH] microstate arises from an inability to form a stabilising carboxylate–imidazole NπH interaction. In contrast, the protonated NπH of the His0[NπH] and His1+ microstates allow for this stabilising interaction.
Importantly, we see the significant levels of sampling in the χ1 = ±180° regions for all ensembles. These conformations correspond to an extended imidazole group, where no intramolecular interactions with the zwitterionic groups are formed. In these regions, solvent molecules are able to favourably interact with both the zwitterionic groups and the imidazole, in keeping with the findings of ref. 48. We have therefore demonstrated the inadequacy of using in vacuo minima for the conformational sampling of solvated systems.
For the His0 spectra, we have combined both His0[NπH] and His0[NτH] microstate ensembles into a single ensemble. For our microsolvation studies, we have decided to use water clusters comprising 5, 10, 15 and 20 explicit water molecules. To this end, we have selected the closest [5,10,15,20] water molecules to the centre of mass of the zwitterionic histidine from each conformer.
5. Weighting and optimisation
The optimisation of solvated systems is notoriously difficult owing to the absence of well-defined minima on the PES. If the PES is significantly undulant, conventional minimisation algorithms struggle, as low order spatial derivatives do not suffice in describing the local topology of the potential energy surface.49 One is frequently reduced to sequentially optimising the system at a number of increasingly complex levels of theory to obtain convergence of the maximum atomic forces and displacements. Whilst tedious, it is also no guarantee of convergence, as we now outline.To circumvent having to compute (time-consuming) second order spatial derivatives of the energy at every step of the geometry optimisation, updating methods are typically invoked50,51 by commercially available quantum chemistry packages. Whilst one can in principle explicitly compute the second order spatial derivatives of the energy at each optimisation step, for the majority of systems this is not a feasible approach. As such, the Hessian is explicitly computed at the start of the geometry optimisation, and subsequently updated as a function of the displacement of the system from this initial geometry by use of first order derivative information. By approximating the Hessian at each step of the geometry optimisation, one can save a great deal of time. Indeed, such Hessian updating schemes have proven to be very accurate for a number of systems.52,53
However, we consider now the case where a complex system begins in a conformation that is far from the energetic minimum. Given that the potential energy surface is highly undulant, the Hessian updating scheme leads to increasingly poor approximations to the Hessian as the optimisation proceeds further from the initial geometry. As such, the geometry optimisation fails to converge. One is then required to adopt some intermediate approach, where the Hessian is explicitly calculated, updated for a number of time steps, followed by explicit recomputation. The frequency with which one performs the explicit recomputation of the Hessian is then a matter for striking a balance between efficiency and accuracy.
An alternative approach to optimising the entire system has been alluded to in Section 2.2. In the work of Zielinski et al.31 and Mutter et al.,30 two levels of optimisation were considered: OptAll and OptSolute. The former optimises the entire system, and the latter optimises only the solute in the field of the unoptimised solvent. Noting that, in these studies, the optimisations were performed on snapshots from MD trajectories, the system is initially far from the minimum energy conformation, rendering the optimisation all the more difficult. Hence, if one is able to “get away with” a simpler optimisation, the savings in computational time will be substantial.
The reasonable agreement of OptSolute with OptAll in the referenced works indicates that one does not necessarily require the entire system to be optimised to obtain informative spectra. Considering the solute–solvent system as a whole, the OptSolute methodology calculates the spectra of unoptimised systems; technically speaking, it is only a subsystem (in this case the solute) that is optimised. This then begs the question of the value of energetic minima for these calculations, and whether strict geometry optimisation is an unnecessary burden.
The OptSolute model is appealing owing to the reduced computational complexity of the resultant optimisation. However, its use raises three pertinent questions: (1) How should the individual conformer spectra be Boltzmann weighted?; (2) If the OptSolute scheme is valid, can we simplify the calculations further by adopting an even less rigorous optimisation criterion?; and (3) Are alternative subsystem optimisation schemes viable? We deal with, and elaborate upon, each of these questions in turn in the following sections. As our test case, we take microsolvated zwitterionic histidine with five explicit water molecules. The conformers have been taken from the snapshots obtained with the methodology outlined in Section 4.
5.1 Boltzmann weighting
If the solute is optimised in the field of the unoptimised solvent, we query whether it is appropriate to use the energy of the entire system for Boltzmann weighting the conformation? We make the (reasonable) assumption that the dominant spectral features arise from the solute, particularly in the higher wavenumber regions, where librational modes do not feature. Consider the effects of optimising the solute while freezing the solvent: the solute will adopt an energetically preferable conformation, while the solvent remains unoptimised. The Boltzmann weight of the solute–solvent system could be relatively low owing to a particularly unfavourable solvent conformation. However, if the solute is an a comparatively low energy conformation, the low Boltzmann weight is not a proper reflection of the contribution of the conformer's spectrum to the overall spectrum since the solute dictates the major features of the spectrum.In light of this argument, we propose two means for Boltzmann weighting the spectrum of a given conformer. The first takes the energy of the entire solute–solvent system (“solute–solvent-weighting”), while the second takes the energy of just the optimised solute, without the solvent (“solute-weighting”). The Boltzmann weights of the conformers from the two schemes are compared with one another in Table 1.
| Conformer number | Solute–solvent weight (%) | Solute weight (%) |
|---|---|---|
| 1 | 31.6 | 14.7 |
| 2 | 22.3 | 21.6 |
| 11 | 6.7 | 16.3 |
| 25 | 20.1 | 20.6 |
| 27 | 18.0 | 23.6 |
| 35 | 1.3 | 3.2 |
From Table 1, we see that for both Boltzmann weighting schemes, the same six conformers dominate the resultant spectrum, albeit in different proportions. The first conformer is dominant with solute–solvent-weighting, while the Boltzmann weight of the first conformer is roughly two times lower with solute-weighting. We can conclude that, in this case (and we have no reason to suspect that the result would not be general), both weighting schemes yield the same dominating conformers, but their contributions to the resulting spectrum differ rather significantly. To evaluate whether the resultant spectra are affected by the differing Boltzmann weights, we present the Raman and ROA spectra generated from the two schemes, in addition to the experimental spectra, in Fig. 3 and 4, respectively.
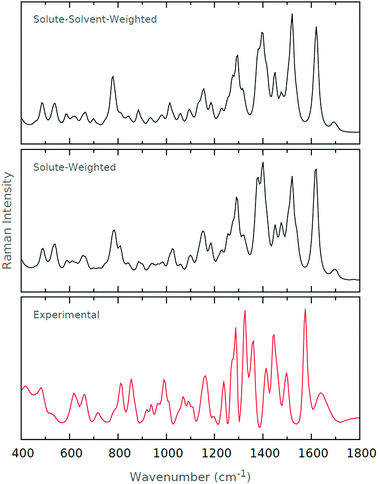 | ||
| Fig. 3 Raman spectra for the solute–solvent weighting and solute-weighting schemes. The experimental Raman spectrum is also shown. | ||
 | ||
| Fig. 4 ROA spectra for the solute–solvent weighting and solute-weighting schemes. The experimental ROA spectrum is also given. | ||
From the Raman spectra in Fig. 3, there appear to be no pronounced differences between the two weighting schemes. A number of subtle exceptions exist, but certainly none that render one spectrum superior to the other when compared with the experimental spectrum. From the ROA spectra in Fig. 4, we see that the two Boltzmann weighting schemes yield spectra that are again quite similar to the experimental spectrum. This similarity suggests that the Boltzmann weighting scheme does not massively impact on the spectra. However, there are a number of slight differences between the two. The 1350–1450 cm−1 region of the experimental spectrum is dominant, with a well-defined +ve/−ve/+ve profile. We see that the first positive region is recovered by both of our calculated spectra, but is arguably better modelled with the solute-weighting.
Indeed, it is interesting to note that this first peak is slightly blue-shifted relative to the experimental spectrum for the solute–solvent-weighting, whereas with the solute-weighting, this peak coincides quite well with the experimental spectrum. The subsequent −ve/+ve profile is present and well-recovered by both, but again the final positive peak is better recovered with the solute-weighting.
From the results we have given, we have concluded that the difference between the two different Boltzmann weighting schemes is small. In the absence of a definitive result, we have chosen to use the solute-weighting scheme owing to the small improvements we have alluded to in the 1350–1450 cm−1 region. We also believe that considering only solute energies makes intuitive sense in the context of the optimisation schemes, as we have discussed.
5.2 Level of optimisation
We now assess whether we can circumvent the need to perform stringent geometry optimisations on our system. We have used three levels of optimisation for the comparison: (i) no optimisation (conformers taken straight from the MD snapshots), (ii) the “Loose” (Maximum force ≤2.5 × 10−3 a.u.; Maximum displacement ≤1.0 × 10−2 Å), and (iii) “Regular” (Maximum force ≤4.5 × 10−4 a.u.; Maximum displacement ≤1.8 × 10−3 Å) optimisation schemes available in the GAUSSIAN09 package. The resultant spectra are presented in Fig. 5 and 6. A fourth level of optimisation, “Tight” (Maximum force ≤1.5 × 10−5 a.u.; Maximum displacement 6.0 × 10−5 Å), was also attempted, but the system proved difficult to converge, and so we have not pursued this level. | ||
| Fig. 5 Raman spectra for the unoptimised, loosely optimised and regularly optimised conformers. The experimental Raman spectrum is also given. | ||
 | ||
| Fig. 6 ROA spectra for the unoptimised, loosely optimised and regularly optimised conformers. The experimental ROA spectrum is also given. | ||
The Raman spectra in Fig. 5 obtained from the completely unoptimised conformers differ significantly from the other spectra formed from optimised conformers. This poor modelling is indicative of the fact that the MD snapshots are very far from energetic minima, and so are not representative of the conformational ensemble of the system. The ultimate arbiter is the comparison of the calculated spectrum with the experimental spectrum, and we see that agreement is poor between the unoptimised and experimental spectra. There appear to be no features of the experimental spectrum that are reproduced by the unoptimised spectrum.
Turning our attention to the optimised spectra, we see that the Raman spectra are very similar to one another, and reproduce a number of the features present in the experimental spectrum. The series of strong peaks in the 1200–1600 cm−1 region are largely accounted for in our computed spectra. However, we are unable to characterise one level of optimisation as superior to the other from the Raman spectra.
The ROA spectra given in Fig. 6 do, however, differ to some degree. Surprisingly, the spectral features in the 800–1000 cm−1 window appear to be poorly characterised by the regular optimisation spectrum, but are relatively strong in the loose optimisation spectrum. It could be that the amplitude of the peak at roughly 1100 cm−1 dwarfs these features in the regular optimisation. We note that this peak is not particularly strong in the experimental spectrum. Assessing the 1350–1450 cm−1 region, both the loose and regular optimisation schemes reproduce the +ve/−ve/+ve signal, with there being no notable difference between their qualities relative to the experimental spectrum. However, the signal appears to be red-shifted by roughly 50 cm−1 with the loose optimisation relative to both the regular optimisation and experimental spectra.
Based on these results, we have deemed the loose optimisation to be sufficient in reproducing the spectral features of the experimental spectrum. The regular optimisation offers little improvement in the calculated spectra relative to the loose optimisation. We do not consider the red-shifting of the loose optimisation relative to the experimental spectrum to be detrimental, particularly since the spectral features are still well-recovered. Considering the convergence level is roughly an order of magnitude more stringent for the regular optimisation, it seems to be an unnecessary additional effort to optimise the systems so thoroughly. Indeed, the loose optimisation requires roughly half the amount of time to compute relative to the regular optimisation for this system. Ensuring the system is at least somewhat close to an energetic minimum appears to be sufficient for computing spectra. We reiterate that if the system is far from an energetic minimum, as we understand the unoptimised MD snapshots to be, one obtains extremely poor computed spectra.
5.3 Alternative optimisation schemes
Given that the optimisation of a subsystem leads to informative spectra, the final point we wish to address is whether alternative subsystem optimisation schemes yield equally informative spectra. The OptAll scheme has been found to produce the highest quality spectra, and so this is the case we use as a benchmark. However, we can also formulate several alternative subsystem optimisation schemes:(a) OptSolute
The solute is optimised in the field of the unoptimised solvent. We have already alluded to this approach and its adoption in previous work, yielding spectra that are comparable to OptAll.
(b) OptSolvent
The converse approach to OptSolute, where the solvent is optimised in the field of the unoptimised solute. This approach is potentially all the more appealing, since the optimisation takes place in the low layer of the QM/MM, and is therefore faster.
(c) OptSolvent → OptSolute
A “two-step” subsystem optimisation scheme – the OptSolvent methodology is invoked, followed by OptSolute. By optimising the layers separately, we hope that we can recreate the optimisation resulting from OptAll.
(d) OptSolute → OptSolvent
The OptSolute methodology is invoked, followed by OptSolvent. We do not imagine this to differ from the previous approach, but is included for the sake of completeness.
(e) OptAll
The entire system is optimised simultaneously.
The first two methods, (a) and (b), are concerned with forsaking accuracy for a large decrease in computational cost. We expect these methods to yield spectra of poorer quality than OptAll, but to be far quicker to compute. Contrastingly, the last two methods, (c) and (d), look to replicate the quality of spectrum obtained by the OptAll scheme, while saving some level of computational time in the process. In the following, we will refer to each optimisation scheme by the letter it has been listed with in the above enumeration. For example, when referring to OptAll, we will use (e).
From the Raman spectra presented in Fig. 7, we immediately see that (b) performs particularly poorly. All three amide I–III regions (1650 cm−1, 1550 cm−1 and 1300 cm−1, respectively) are poorly represented, and the intensity of the low wavenumber regions is not in agreement with the experimental spectrum. However, the other four optimisation schemes yield spectra that are in good agreement with the experimental spectrum. The amide I–III regions are well-recovered, while the low wavenumber regions are modelled equally well. If we are to be fastidious, we may question the amide I regions of (a) and (d), where the signal does not possess the same relative intensity as that in the experimental spectrum. The best agreement with the experimental spectrum is arguably (c), which appears to recover the vast majority of spectral features featured in (e).
 | ||
| Fig. 7 Raman spectra for (a) OptSolute, (b) OptSolvent, (c) OptSolvent → OptSolute, (d) OptSolute → OptSolvent and (e) OptAll schemes. The experimental Raman spectrum is also given. | ||
Turning our attention to the ROA spectra of Fig. 8, we notice that the poor performance of (b) is continued, and virtually no experimental features are recovered. We also draw attention to the poor performance of (d) in the low wavenumber regions. In turn, this poor modelling of the low wavenumber regions obscures the finer details of the high wavenumber regions, and the spectrum as a whole deteriorates. Similarly, (a) appears to be a poor approximation to the experimental spectrum; the coarse details of the spectrum appear to be present, but the high wavenumber regions are poorly modelled. In contrast, (c) is in excellent agreement with both the spectra obtained through experiment and (e). With the exception of a few features in the low wavenumber regions, (c) and (e) are almost identical.
 | ||
| Fig. 8 ROA spectra for (a) OptSolute, (b) OptSolvent, (c) OptSolvent → OptSolute, (d) OptSolute → OptSolvent and (e) OptAll schemes. The experimental ROA spectrum is also given. | ||
Offering some explanation for the results we have obtained, the optimisation of the solute appears to be the key factor in guaranteeing the quality of computed spectra; the poor results from (a) and (c) presumably derive from the unoptimised state of the solute when the spectrum is calculated. To recreate the finer details of the spectrum, it also appears as if the solvent requires some level of optimisation, particularly with the ROA measurements. Hence, this is why (c) significantly outperforms (a). The Raman spectra seem to be robust, or mainly invariant, with regards to the level of solvent optimisation.
In conclusion, we feel that (c) and (e) offer the best recovery of experimental spectral features. However, we have found that the computational cost associated with (c) is reduced by more than fourfold on average relative to (e). Relative to the computational cost associated with (a), (c) is roughly 50% more expensive computationally. Therefore, it seems as if the OptSolvent → OptSolute or (c) methodology strikes an ideal balance between accuracy and computational time. We proceed with this methodology through the remainder of this work.
6. Microsolvation
We define microsolvation to be the explicit solvation of a system using a small number of water molecules, typically not extending beyond the second solvation shell of the solute. The major question we wish to answer is whether computed spectra from microsolvated systems are able to model experimental spectra, without having to resort to performing calculations on large explicitly solvated systems. If we can answer this query positively, then it facilitates the computation of solvated Raman and ROA spectra.6.1 Neutral histidine
For the Raman spectra in Fig. 9, we find that the amide I band at around 1600 cm−1 is well recovered by each of the microsolvated systems. Since the amide I band is largely indicative of peptide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching modes, it is initially surprising that its modelling appears to be independent of the level of microsolvation, where solvent interactions presumably damp the stretching mode. However, upon closer inspection of the microsolvated conformers used for the spectra, we find that the peptide C
O stretching modes, it is initially surprising that its modelling appears to be independent of the level of microsolvation, where solvent interactions presumably damp the stretching mode. However, upon closer inspection of the microsolvated conformers used for the spectra, we find that the peptide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is solvated in each conformer, rendering its modelling independent of the degree of microsolvation. Similarly, we recover the amide II triplet at ∼1450–1550 cm−1, albeit blue-shifted relative to the experimental spectrum. The triplet signature appears to be most profound with a solvation shell comprising 15 water molecules, where the central peak is dominant. This result is to be expected since a solvation shell of 15 water molecules appears to coincide with the number of water molecules comprising the first solvation shell for zwitterionic histidine. Since the amide II region is representative of peptide N–H bending and C–H stretching modes, we expect this region to be highly dependent on solvent interactions. It is, nevertheless, surprising that the quality of our computed spectra deteriorates with 20 water molecules.
O is solvated in each conformer, rendering its modelling independent of the degree of microsolvation. Similarly, we recover the amide II triplet at ∼1450–1550 cm−1, albeit blue-shifted relative to the experimental spectrum. The triplet signature appears to be most profound with a solvation shell comprising 15 water molecules, where the central peak is dominant. This result is to be expected since a solvation shell of 15 water molecules appears to coincide with the number of water molecules comprising the first solvation shell for zwitterionic histidine. Since the amide II region is representative of peptide N–H bending and C–H stretching modes, we expect this region to be highly dependent on solvent interactions. It is, nevertheless, surprising that the quality of our computed spectra deteriorates with 20 water molecules.
 | ||
| Fig. 9 Raman spectra for the various levels of microsolvation of His0. The experimental Raman spectrum is also shown for comparison. | ||
The amide III region is slightly less well-modelled by our microsolvated systems. In the experimental spectrum, we observe a well-defined quadruplet of peaks, spanning 1200–1350 cm−1. This region is dominated by C–N stretching and N–H bending modes, and we would expect this region to be as solvation-dependent as the other two regions we have discussed. We note that we do not manage to definitively recover the clear quadruplet seen in the experimental spectrum, although the profile does seem to become more enhanced as we increase the degree of microsolvation. Indeed, when 20 water molecules are included, we are able to discern four clear peaks in the amide III region.
Regarding the impact of the tautomeric forms of histidine, Ashikawa and Itoh54 have found that the breathing motions for His0[NπH] and His0[NτH] can be related to Raman peaks at 1304/1260 cm−1, respectively. In the same work, two additional marker regions characterising imidazole stretching modes between the tautomeric forms of histidine were proposed: 1568/1585 cm−1 and 1090/1105 cm−1. Later work by Toyama et al.55 has suggested an additional marker region at 1320/1354 cm−1. Unfortunately, the majority of these marker regions inhabit the strong amide regions of the Raman spectrum, making them difficult to discern. However, the 1090/1105 cm−1 region occupies a low intensity region of the Raman spectrum, and appears to be characterised in both our experimental and computed spectra, at each microsolvation level excluding the spectrum with 5 waters.
The experimental ROA spectrum is not quite as well-recovered as the microsolvated spectra, as depicted in Fig. 10. This is not to say that the ROA spectra are of poor quality, but simply suffer by comparison with the high quality of the Raman spectra. The dominant feature across both experimental and calculated spectra is the +ve/−ve/+ve signal at 1300–1500 cm−1, and is well-recovered at all levels of microsolvation. However, it is worth pointing out that the calculated spectra appear to be blue-shifted by ∼50 cm−1 relative to the experimental spectrum. This blue-shifting is somewhat surprising. Note that we have not undertaken abscissa-scaling by 0.96, as prescribed by Radom.56 Doing so would blue-shift the spectrum further, and so would result in the deterioration of our calculated spectra.
 | ||
| Fig. 10 ROA spectra for the various levels of microsolvation of His0. The experimental ROA spectrum is also shown for comparison. | ||
We note that as the level of microsolvation increases, the peak at 1050 cm−1 is amplified. A number of peaks exist in this region of the experimental spectrum, but none are as prominent as that in the microsolvated spectrum. Assessing the normal modes of motion around this region, we find that the majority are dominated by sidechain dihedral torsional degrees of freedom. This observation then suggests that the sidechain torsional degrees of freedom are more flexible in the microsolvated systems than in the experiment. Indeed, it is predominantly the zwitterionic groups and imidazole ring that form interactions with the solvent molecules in the microsolvated systems, and so it is to be expected that the alkyl sidechain be poorly solvated, and so not well recovered by the microsolvated spectra.
6.2 Cationic histidine
The literature regarding the calculation of Raman and ROA spectra of formally charged species is sparse. Indeed, the ab initio modelling of formally charged species is in itself difficult, since the basis sets require both diffuse functions and some description of polarisation, the former being of particular importance for anions. To assess the quality of Raman and ROA spectra of a formally charged species, we have selected cationic histidine. The fact that no tautomers exist for this species makes its modelling simpler.A formally charged species is presumed to undergo stronger interactions with solvent than the neutral species, and so we hypothesise that the degree of microsolvation will significantly influence the quality of the computed spectrum. Since the formal charge results from the protonation of the imidazole ring, we anticipate that the higher wavenumber regions will be poorly reproduced at the low levels of microsolvation since the explicit water molecules tend to primarily interact with the zwitterionic groups.
The computed Raman spectra of Fig. 11 are in relatively good agreement with the experimental Raman spectrum. The strong peaks at ∼1200 cm−1 and ∼1300 cm−1 become increasingly prominent as the degree of microsolvation increases. The peak at ∼1500 cm−1 is well-recovered by each of the microsolvated spectra. The resolution of the doublet of peaks at roughly 800 cm−1 is similarly improved as the degree of microsolvation increases. Interestingly, the general agreement with the experimental spectrum deteriorates when 10 explicit water molecules are used for microsolvation. However, those spectra including 5, 15 and 20 explicit water molecules are very similar.
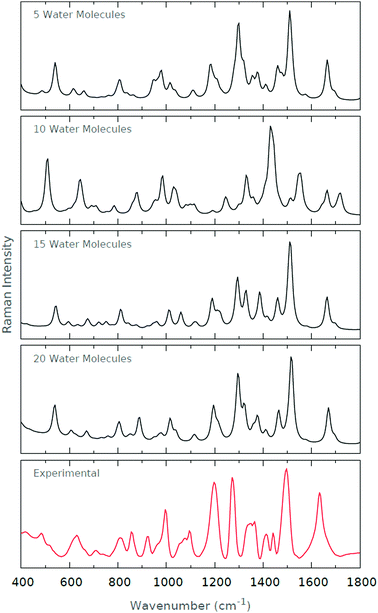 | ||
| Fig. 11 Raman spectra for the various levels of microsolvation of His1+. The experimental Raman spectrum is also shown for comparison. | ||
We offer a potential reason for the deterioration in spectrum quality when 10 explicit water molecules are included. When 5 explicit water molecules are included, the conformers are largely solvated around the backbone amide and carboxyl groups of the zwitterionic histidine. When 15 and 20 explicit water molecules are included, the conformers are completely solvated, i.e. both the backbone and sidechain groups of the zwitterionic histidine. However, when 10 explicit water molecules are included, only a couple of water molecules solvate the imidazole ring of the zwitterionic histidine. As such, we suggest that the partial solvation of the imidazole results in a biasing of certain vibrational frequencies originating from the imidazole–solvent interactions. The spectrum as a whole deteriorates since these imidazole–solvent frequencies then dominate the resultant spectrum. In summary, it is tempting to think of partial solvation as detrimental to the correct prediction of the vibrational spectra.
The computed ROA spectra in Fig. 12 are, however, not quite as successful in reproducing the major features of the experimental spectrum. The strong negative band at ∼1400 cm−1 is recovered in each of the computed spectra, and the positive doublet in the 1300–1350 cm−1 region appears to become clearer as the level of microsolvation increases.
 | ||
| Fig. 12 ROA spectra for the various levels of microsolvation of His1+. The experimental ROA spectrum is also shown for comparison. | ||
From previous, unpublished work on anionic adenosine triphosphate, we have found that the calculation of ROA spectra for formally charged species is rather difficult. One speculative reason for the poorer quality of the ROA spectra relative to the Raman spectra is the way one computes the intensity of spectral bands for the two spectroscopies. For Raman spectra, the intensity is given by the sum of the intensities of the right- and left-circularly polarised scattered light. For ROA spectra, the intensity is given by the difference in the intensities of the right- and left-circularly polarised scattered light. Therefore, ROA band intensities are more prone to error than the Raman band intensities. In other words, the ROA band intensities are smaller in magnitude than the Raman band intensities, and so the errors are amplified. It is this sensitivity to error that makes ROA a “gold-standard” spectroscopic technique, whereas Raman is somewhat more forgiving.
7. Conclusion
We have investigated and presented the results for a number of novel methodologies that can be used in the calculation of ab initio Raman and ROA spectra of solvated systems. We are suggestively vague in our use of the term “solvated systems”, since we see no reason why our methodology cannot be applied to systems outside of the domain of peptides, such as DNA bases.57,58 A novel conformational sampling methodology allows for the unambiguous extraction of a set of mutually diverse conformers from an MD trajectory of arbitrary length. We have shown that conformers do not require strict optimisation to obtain high quality spectra, and that a two-step subsystem optimisation (i.e. optimising the solvent while keeping the solute frozen, and subsequently optimising the solute while keeping the solvent frozen) yields spectra of the same quality as entire system optimisations. The microsolvation of both formally charged and neutral zwitterionic histidine species can yield calculated spectra that converge towards the experimental spectra.Acknowledgements
S. C. and M. G. L. thank the BBSRC for awarding DTP studentships and P. L. A. P. the EPSRC for the award of an Established Career Fellowship (EP/K005472). All authors are grateful to Professor P. Bouř for access to his ROA spectrometer for performing the experimental measurements.References
- L. D. Barron, J. Chem. Soc., Perkin Trans. 2, 1977, 1074 RSC.
- L. Barron and A. Buckingham, J. Am. Chem. Soc., 1979, 101, 1979 CrossRef CAS.
- L. D. Barron and J. Vrbancich, J. Chem. Soc., Chem. Commun., 1981, 771 RSC.
- O. V. Shishkin, A. Pelmenschikov, D. M. Hovorun and J. Leszczynski, Chem. Phys., 2000, 260, 317 CrossRef CAS.
- L. Hecht, A. L. Phillips and L. D. Barron, J. Raman Spectrosc., 1995, 26, 727 CrossRef CAS.
- L. Barron, L. Hecht, E. Blanch and A. Bell, Prog. Biophys. Biophys. Chem., 2000, 73, 1 CrossRef CAS.
- E. W. Blanch, L. Hecht and L. D. Barron, Methods, 2003, 29, 196 CrossRef CAS PubMed.
- A. Bell, L. Hecht and L. Barron, J. Am. Chem. Soc., 1998, 120, 5820 CrossRef CAS.
- Z. Shi, R. W. Woody and N. R. Kallenbach, Adv. Protein Chem., 2002, 62, 163 CrossRef CAS PubMed.
- E. W. Blanch, L. Hecht, C. D. Syme, V. Volpetti, G. P. Lomonossoff, K. Nielsen and L. D. Barron, J. Gen. Virol., 2002, 83, 2593 CrossRef CAS PubMed.
- L. Hecht, L. D. Barron, E. W. Blanch, A. F. Bell and L. A. Day, J. Raman Spectrosc., 1999, 30, 815 CrossRef CAS.
- M. J. Betts and R. B. Russell, Bioinf. Genet., 2003, 317, 289 Search PubMed.
- C. D. Churchill and S. D. Wetmore, J. Phys. Chem. B, 2009, 113, 16046 CrossRef CAS PubMed.
- P. Carter and J. A. Wells, Nature, 1988, 332, 564 CrossRef CAS PubMed.
- S. Manzetti, D. R. McCulloch, A. C. Herington and D. van der Spoel, J. Comput.-Aided Mol. Des., 2003, 17, 551 CrossRef CAS PubMed.
- S. Nobili, E. Mini, I. Landini, C. Gabbiani, A. Casini and L. Messori, Med. Res. Rev., 2010, 30, 550 CAS.
- P. Hudáky and A. Perczel, J. Phys. Chem. A, 2004, 108, 6195 CrossRef.
- K. J. Jalkanen, R. Nieminen, M. Knapp-Mohammady and S. Suhai, Int. J. Quantum Chem., 2003, 92, 239 CrossRef CAS.
- E. Tajkhorshid, K. Jalkanen and S. Suhai, J. Phys. Chem. B, 1998, 102, 5899 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161 CrossRef CAS PubMed.
- B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- O. h. O. Brovarets’ and D. M. Hovorun, J. Biomol. Struct. Dyn., 2015, 33, 28 Search PubMed.
- O. B. Ol’ha, R. O. Zhurakivsky and D. M. Hovorun, J. Mol. Model., 2013, 19, 4119 CrossRef PubMed.
- K. Jalkanen, I. Degtyarenko, R. Nieminen, X. Cao, L. Nafie, F. Zhu and L. Barron, Theor. Chem. Acc., 2008, 119, 191 CrossRef CAS.
- S. Luber and M. Reiher, J. Phys. Chem. A, 2009, 113, 8268 CrossRef CAS PubMed.
- K. H. Hopmann, K. Ruud, M. Pecul, A. Kudelski, M. Dračínský and P. Bour, J. Phys. Chem. B, 2011, 115, 4128 CrossRef CAS PubMed.
- J. R. Cheeseman, M. S. Shaik, P. L. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991 CrossRef CAS PubMed.
- S. T. Mutter, F. Zielinski, J. R. Cheeseman, C. Johannessen, P. L. Popelier and E. W. Blanch, Phys. Chem. Chem. Phys., 2015, 17, 6016 RSC.
- F. Zielinski, S. T. Mutter, C. Johannessen, E. W. Blanch and P. L. Popelier, Phys. Chem. Chem. Phys., 2015, 17, 21799 RSC.
- S. T. Mutter, F. Zielinski, P. L. Popelier and E. W. Blanch, Analyst, 2015, 140, 2944 RSC.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435 CrossRef CAS PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474 CrossRef CAS.
- G. B. Arfken, H. J. Weber and F. E. Harris, Mathematical methods for physicists: a comprehensive guide, Academic Press, 2011 Search PubMed.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922 CrossRef.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 827 CrossRef.
- E. A. Coutsias, C. Seok and K. A. Dill, J. Comput. Chem., 2004, 25, 1849 CrossRef CAS PubMed.
- S. Wallin, J. Farwer and U. Bastolla, Proteins: Struct., Funct., Bioinf., 2003, 50, 144 CrossRef CAS PubMed.
- J. B. Ghosh, Oper. Res. Lett., 1996, 19, 175 CrossRef.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, et al., Gaussian 09 (Revision E.01), Gaussian Inc., Wallingford, CT, 2009, p. 200 Search PubMed.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815 CrossRef CAS PubMed.
- I. Cukrowski and C. F. Matta, Chem. Phys. Lett., 2010, 499, 66 CrossRef CAS.
- K. Ruud and A. J. Thorvaldsen, Chirality, 2009, 21, E54 CrossRef CAS PubMed.
- J. R. Cheeseman and M. J. Frisch, J. Chem. Theory Comput., 2011, 7, 3323 CrossRef CAS PubMed.
- G. Zuber and W. Hug, J. Phys. Chem. A, 2004, 108, 2108 CrossRef CAS.
- E. Deplazes, W. Van Bronswijk, F. Zhu, L. Barron, S. Ma, L. Nafie and K. Jalkanen, Theor. Chem. Acc., 2008, 119, 155 CrossRef CAS.
- S. Ling, W. Yu, Z. Huang, Z. Lin, M. Harañczyk and M. Gutowski, J. Phys. Chem. A, 2006, 110, 12282 CrossRef CAS PubMed.
- A. B. Birkholz and H. B. Schlegel, Theor. Chem. Acc., 2016, 135, 1 CrossRef CAS.
- V. Bakken, J. M. Millam and H. B. Schlegel, J. Chem. Phys., 1999, 111, 8773 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49 CrossRef CAS.
- S. K. Lee, W. Li and H. B. Schlegel, Chem. Phys. Lett., 2012, 536, 14 CrossRef CAS.
- A. B. Birkholz and H. B. Schlegel, J. Comput. Chem., 2015, 36, 1157 CrossRef CAS PubMed.
- I. Ashikawa and K. Itoh, Biopolymers, 1979, 18, 1859 CrossRef CAS.
- A. Toyama, K. Ono, S. Hashimoto and H. Takeuchi, J. Phys. Chem. A, 2002, 106, 3403 CrossRef CAS.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502 CrossRef CAS.
- O. h. O. Brovarets, R. O. Zhurakivsky and D. M. Hovorun, J. Comput. Chem., 2014, 35, 451 CrossRef CAS PubMed.
- O. h. O. Brovarets and D. M. Hovorun, Phys. Chem. Chem. Phys., 2014, 16, 15886 RSC.
| This journal is © the Owner Societies 2016 |
