The reaction mechanism of polyalcohol dehydration in hot pressurized water

Abstract

The use of high-temperature liquid water (HTW) as a reaction medium is a very promising technology in the field of green chemistry. In order to fully exploit this technology, it is crucial to unravel the reaction mechanisms of the processes carried out in HTW. In this work, the reaction mechanism of 2,5-hexanediol dehydration in HTW has been studied by means of three different ab initio simulations: the string method, metadynamics and molecular dynamics in real time. It is found that the whole reaction involving protonation, bond exchange and deprotonation occurs in a single step without a stable intermediate. The hydrogen bonded network of the surrounding water has a vital role in assisting an efficient proton relay at the beginning and at the end of the reaction. It is confirmed that the reaction is energetically most favorable in the S_N2 pathway with an estimated barrier of 36 kcal mol⁻¹, which explains the high stereoselectivity and the reaction rate observed in experiment. The mechanistic insights provided by our study are relevant for a prominent class of reactions in the context of sustainable biomass processing, namely dehydration reactions of polyalcohol molecules.

---

1 Introduction

In the drive towards green chemical processes, the use of high-temperature water (i.e., subcritical liquid water above ∼200 °C) as a reaction medium in organic chemistry has recently attracted considerable attention.^1–4 Indeed, water offers many advantages over organic solvents because it is non-toxic, inexpensive, non-flammable and readily available.^2,5 Moreover, the solubility of small organic compounds in high-temperature liquid water (HTW) is largely enhanced with respect to the solubility in room-temperature water.² Hence, the use of HTW holds great promise in the design of cleaner, safer and environmentally benign chemical processes.

The reaction rates and product selectivities of the processes carried out in HTW can be very sensitive to temperature and water density or pressure,^1,2 which means that these process variables can be tuned to fully harness the special properties of HTW. It is clear that a detailed understanding of the mechanism and the role played by water in reactions is of paramount importance in order to find the optimum conditions for a given chemical process. In broader terms, this detailed understanding can also have relevant implications in the context of the origin of life^6,7 and in the context of energy and fuels.⁸ However, elucidation of the mechanism and the corresponding role of water can be a very complex task due to the multifaceted nature of water–substrate interaction, e.g. hydrogen bonding, polarity, acidity and basicity, hydrophobicity, etc. Furthermore the reaction mechanisms in HTW can be very different from the mechanisms operating in organic solvents or in room-temperature water.^9,10 It is well known that computational chemistry provides invaluable tools when it comes to unravelling reaction mechanisms. However, computational studies of organic reactions in HTW^9,10 are still very scarce compared with computational studies in aqueous media under ambient conditions.^11–15 Therefore, there is an urgent need to carry out in silico studies in order to better understand how reactions take place in aqueous media under extreme thermodynamic conditions. Here, we present a computational study aimed at unravelling the mechanism of the stereoselective transformation of 2,5-hexanediol (HDO) into dimethyltetrahydrofuran (DMTHF) by means of an intramolecular dehydration process in hot pressurized water.¹⁶

The development of green technologies for the processing of renewable biomass derivatives into valuable chemicals is essential for establishing a sustainable society.^17–21 In this context, dehydration of polyalcohol compounds constitutes one of the most important families of reactions.^22,23 Remarkable experiments conducted over the last years have demonstrated that these dehydration reactions can take place in CO₂-enriched HTW.^16,24–29 The addition of CO₂ to HTW leads to the fact that the pH of the aqueous medium lowers when this gas dissolves in water. It has been observed that an increase in the acidity of the aqueous medium can result in the acceleration of dehydration reactions since these transformations are acid-catalyzed processes. The use of CO₂ offers environmental advantages over the use of mineral acids. High-pressure CO₂/HTW technology is increasingly being used in acid-catalyzed reactions^4,30 and will most likely play a prime role in novel green methodologies of biomass processing.^20,31

One of the simplest dehydrations of polyalcohol compounds in HTW reported to date is the dehydration of HDO to DMTHF (see Fig. 1).^16,32 It is experimentally observed that this reaction is stereoselective in most aqueous solutions with strong acids such as HBr although exceptional cases exist such as sulfuric acid.³² The relevance of this reaction lies in the fact that it provided evidence that the CO₂/HTW technology can be employed to carry out stereoselective dehydration reactions. The experiments performed by Shirai and coworkers¹⁶ showed that the dehydration reaction of 2R,5R-HDO and 2S,5S-HDO in CO₂-enriched HTW furnishes the cis isomer of DMTHF with a selectivity of more than 85%. Here we employ different computational techniques, i.e. ab initio molecular dynamics simulations, metadynamics, determination of minimum energy paths by means of the string method, applied to different model systems, including microsolvation of an HDO molecule and full solvation of an HDO molecule in the condensed phase, with the aim of elucidating the mechanism of the dehydration reaction of HDO and providing a rationale to its stereoselectivity. Our simulations demonstrate that the lowest free energy pathway of the reaction corresponds to an S_N2 mechanism, by virtue of which the cleavage of the C–O bond takes place simultaneously with the formation of a new C–O bond. Prior to this bond exchange, one of the alcohol groups, which is the leaving group in the S_N2 reaction, gets protonated by means of a Grotthuss relay mechanism.^33,34 Yet the corresponding protonated HDO molecule is not a stable intermediate. Concerning the role of water, our simulations show that an increase in the number of water molecules in the first solvation shell of HDO results in an increase of the rate of the dehydration reaction. Overall, the details of the reaction mechanism at the atomistic level revealed by our simulations provide valuable insights not only for the specific reaction considered herein but also for the whole family of dehydration processes carried out in high-temperature liquid water.

Fig. 1 The dehydration reaction from 2R,5R-HDO to cis-2,5-DMTHF.

2 Method

This study has been done in three stages. At the first stage we calculated the minimum energy paths (MEPs) of the reaction for the microsolvated model which consists of an 2R,5R-HDO molecule and water molecules with an extra proton, i.e. HDO(H₂O)_xH⁺ (with x = 2, 4 and 6) under the free boundary conditions. To obtain the MEPs for the reactant and product minima chosen appropriately, we employ the string method^35,36 which is able to optimize the position of discrete images arranged along the path. This provides a rough estimate of the energy profile and the structural changes during the reaction. For comparison, the MEP calculation is done in the same way for the case where the proton is absent, i.e. HDO(H₂O)₆, to explore the possibility of the water-assisted pathway.^37–41

At the second stage we calculated the free energy landscape with respect to three collective variables (CV), d, ϕ and n, which are found to characterize the reaction in the first stage; d = r₂₈ − r₂₇ is the difference in bond distances between C₂–O₈ and C₂–O₇ atoms, ϕ is the dihedral angle with respect to the O₇–C₂–C₃–C₄ atoms, and n = n₇ is the hydrogen coordination number of the O₇ atom (see Fig. 2 and eqn (1) below for the definitions of atomic numbering and the coordination number). For this purpose, we used metadynamics simulations^42–44 of the microsolvated model mentioned above, as well as the aqueous solution of HDO where periodic boundary conditions are applied. In metadynamics the free energy basin is filled with a collection of history-dependent Gaussian hills accumulated where the system has sampled during the simulation. The free energy landscape obtained provides information on thermodynamic ensembles that belong to the reactant minimum and the transition states.

Fig. 2 Definition of structural variables: ϕ is the 7-2-3-4 dihedral angle (blue). d is the difference in 2–7 and 2–8 bond distances (green).

At the third stage we carried out molecular dynamics simulations of the aqueous solution running forwards and backwards starting from the structures near the transition state, which are taken from the second stage. This provides real time information of typical trajectories during the whole reaction process, albeit they were limited in number due to computational expense.

For the microsolvated model all the calculations were carried out using the PIMD code^45,46 combined with Turbomole.⁴⁷ For the electronic structure calculations, we employed the resolution-of-identity density functional theory (RIDFT)⁴⁸ with the PBE exchange correlation functional⁴⁹ using the SV(P) basis set.⁵⁰ We also employed the resolution-of-identity second-order Møller–Plesset perturbation theory (RIMP2)⁵¹ using the SV(P) basis set⁵⁰ in the MEP calculations. The MEPs described in terms of 120 discrete images from the HDO reactant to the DMTHF product were obtained using the string method. The three-dimensional metadynamics was carried out based on the Born–Oppenheimer scheme in the NVT ensemble with Nosé–Hoover chain thermostats^52–54 implemented in the PIMD code following the setup by Ensing et al.⁴³ The temperature was controlled at 523 K, with the time step of Δt = 0.25 fs. The size of Gaussian hills was gradually diminished as the reaction approached completion, and the final height (h) and the widths (w) were set to (h, w_d, w_ϕ, w_n) = (1.0 kcal mol⁻¹, 0.09 Å, 5.0°, 0.05). For a computational speedup, we used 12 walkers and we restricted the CV space to d < 1.85 Å and 132.5° < ϕ < 227.5°. The metadynamics simulations were run for 34 ps and 57 ps for the cases of x = 4 and x = 6, respectively, and on average a new hill was added every 15 fs for each walker.

For the aqueous solution, all the calculations were carried out using the CPMD code.⁵⁵ The system contained an HDO molecule, 70 water molecules and a proton in a cubic box with a fixed side length of 14.93 Å, which was estimated from a preliminary classical MD simulation in the NPT ensemble under the experimental conditions of 20 MPa and 523 K.¹⁶ A uniform background charge was added to maintain the charge neutrality of the system under the periodic boundary conditions. A similar setup was employed in previous ab initio MD simulations for systems with an excess proton, albeit the number of water molecules used therein (32,⁵⁶36⁹) were less than the present one (70). The main limitation arising from the system size is that the acidity (pH = 0.3) is set much lower than the experiment (pH = 4).¹⁶ The electronic structure calculations were done based on density functional theory with PBE exchange correlation functional⁴⁹ and Grimme’s D2 van der Waals correction⁵⁷ using the cut off at 25 Ryd in the plane wave (PW) basis functions. The core electrons were taken into account using Vanderbilt's ultrasoft pseudopotentials.⁵⁸ The fictitious mass of the orbitals was set to 400 a.u. The three-dimensional metadynamics was carried out based on the Car–Parrinello scheme⁵⁹ in the NVT ensemble using Nosé–Hoover chain thermostats,^52–54 where the temperature is controlled at 523 K, with the time step of Δt = 0.097 fs. The size of Gaussian hills was gradually diminished as the reaction approached completion, and the final height and the widths were set to (h, w_d, w_ϕ, w_n) = (0.3 kcal mol⁻¹, 0.005 Å, 0.3°, 0.005). For a computational speedup, we used 8 walkers, and we restricted the CV space to d < 2.5 Å. The metadynamics simulations were run for 100 ps, and on average a new hill was added every 44 fs. The two-dimensional metadynamics was also carried out in a similar manner with the collective variables d and ϕ being unrestricted in space. To obtain real-time trajectories, we ran molecular dynamics simulations based on the Car–Parrinello scheme⁵⁹ in the NVE ensemble with the initial velocity corresponding to 523 K, but without any temperature control during the simulation.

The coordination number is defined in two ways as the rational function,

andwhere the index j runs for all the hydrogen and carbon atoms, respectively, in eqn (1) and (2). The former was used in metadynamics simulations describing the number of O–H bonds, while the latter was used in the trajectory analysis of molecular dynamics simulations describing the sum of O–H and O–C bonds for a given oxygen atom i. The O–H and O–C bond length parameters were set to be d^OH_ij = 1.4 Å and d^OC_ij = 1.65 Å, respectively.

3 Results and discussion

3.1 Reaction path analysis

We begin by searching for probable reaction paths in the microsolvated model. After many trial and error static calculations, we learned the following things. Firstly, the HDO molecule has several stable conformations, either in the extended form or in the contracted form, as shown in Fig. 3. However, the conformation must be contracted at some point for the reaction to take place. Secondly, for a small microsolvated reactant, HDO(H₂O)_xH⁺, to be stable the extra proton must be hydrated by a sufficient amount of water molecules. In particular, the stable structures were found when the extra proton is absorbed into a water molecule as the hydronium ion, which is hydrogen bonded to three other water molecules, i.e. H₃O⁺(H₂O)₃. In fact as this structure is not available in the case of x = 2, its most stable form resulted in the protonated HDO molecule, failing to describe a stable state of proton in water. Thus at least x = 4 water molecules are required to properly describe the HDO molecule in a stable reactant state. This also implies that at least four water molecules are explicitly involved in the reaction process.

Fig. 3 Different conformations of the 2R,5R-HDO molecule: (a) the extended conformation (ϕ = 60°), (b) the extended conformation (ϕ = 300°), (c) the extended conformation (ϕ = 180°), (d) the contracted conformation with the internal hydrogen bond (ϕ = 300°), and (e) the contracted conformation without the internal hydrogen bond (ϕ = 180°).

Based on these observations, we next looked for reaction paths of the x = 4 and x = 6 microsolvated models that start from a configuration with the H₃O⁺(H₂O)₃ cluster included using the string method. Here we show the PBE results for the x = 6 case, as they were qualitatively similar to the PBE results for the x = 4 case (Fig. S1 in ESI†) and the RIMP2 results of the x = 6 case (Fig. S2 in ESI†). In Fig. 4, we show two types of minimum energy paths, Channels 1 and 2, that start from different conformations of HDO. In Channel 1, Structure I has an internal hydrogen bond with the dihedral angle being ϕ = 60° (cf.Fig. 3(c)), while in Channel 2 the hydrogen bond is broken with ϕ = 180° (cf.Fig. 3(d)). Investigating the process near Structure III in Fig. 4, the C₂–O₇ bond breaking and the C₂–O₈ bond forming are found to be stepwise and concerted, respectively, which is the signature of S_N1 and S_N2 mechanisms, respectively. Thus, let us refer to them hereafter as the S_N1- and S_N2-pathways.

Fig. 4 Structures along the minimum energy paths, Channels 1 and 2, obtained from the PBE/SV(P) calculations. Color codes: oxygen atoms in red, hydrogen atoms in white, carbon atoms in grey. As an exception, the oxygen atom bonded to an excess proton is marked in blue. The numbers I–V correspond to the positions in Fig. 5.

There are some aspects shared among S_N1 and S_N2 pathways. A proton is received before (Structure II) and released after (IV) the O–C bond breaking/forming, and thus the reactions take place via the proton-assisted mechanism, in accordance with the experimental suggestion.¹⁶ In the calculation it was found that this process performs efficiently by means of Grotthuss proton relay, showing that the hydrogen bond network between water molecules plays a significant role in the reaction. The reaction not only starts in (Structure I) but also ends in (V) in the H₃O⁺(H₂O)₃ cluster to recover the stable form of the hydrated proton.

The energy profile and the structure variables along the MEPs of the x = 6 microsolvated model are shown in Fig. 5. In Fig. 5(a) we can see that the energy profiles of both the S_N1- and S_N2-pathways are single peaked at their respective transition states (Structure III), corresponding to the O–C bond exchange configuration. This indicates that they are single step processes starting from the relevant HDO conformations. There is no stable intermediate before and after the O–C bond exchange, which is the main rate-determining step. However, a crucial difference is that the energy barrier of the S_N2-pathway, 40 kcal mol⁻¹, is much lower than that of the S_N1-pathway, 57 kcal mol⁻¹. This indicates that the S_N2-pathway is dominant, and therefore the reaction is stereoselective.

Fig. 5 The change along the minimum energy paths, Channels 1 (blue) and 2 (red), obtained from the PBE/SV(P) calculations. (a) The relative energy, and the structural variables (b) ϕ, (c) n₇ (solid line) and n₈ (dashed line), (d) r₂₇ (dashed line) and r₂₈ (solid line), and (e) d. The numbers I–V correspond to the ones in Fig. 4.

Although all the tendencies mentioned above are unchanged for the x = 4 microsolvated model, the energy barriers of the S_N1- and S_N2-pathways are found to be 58 and 41 kcal mol⁻¹, respectively, which are both slightly higher compared to the ones of the x = 6 microsolvated model. This implies that both reactions in the S_N1- and S_N2-pathways are accelerated in the presence of extra water molecules that are hydrogen bonded to HDO.

The change in O–C bond distances, r₂₈ and r₂₇, their difference d, the coordination number n, and the dihedral angle ϕ along the MEP are displayed in Fig. 5(b)–(e). This supports the proton assisted S_N1- and S_N2-mechanisms mentioned above. For instance, the sum of r₂₈ and r₂₇ values is found much larger in the S_N1-pathway (6.6 Å) than that of the S_N2-pathway (4.3 Å), since a short-lived carbocation is formed in the S_N1 reaction.

We also studied the water-assisted pathway of this reaction in the absence of a proton by carrying out the MEP calculation of the microcluster model HDO(H₂O)₆ (see Fig. S3 in ESI† for details). The energy barrier is found to be 57 kcal mol⁻¹, which is comparable with an earlier study of QM/MM calculation on the water-assisted pathway of 1,4-butanediol dehydration reaction in hot water, i.e. 53 and 62 kcal mol⁻¹, for different pathways in the absence of a proton.³⁸ However, the energy barrier is much larger than that of the HDO(H₂O)₆H⁺, 40 kcal mol⁻¹, in the presence of an excess proton, suggesting that the water-assisted pathway is not the dominant one in this case.

3.2 Free energy analysis

As mentioned above, the variables d, n, and ϕ are able to distinguish the reaction processes in terms of bond exchange, protonation, and S_N1/S_N2 characterization, respectively. Setting them to be the collective variables, three-dimensional metadynamics simulations of HDO aqueous solution were carried out at the temperature of 523 K (see Fig. S4 in ESI† for details). The free energy profiles were calculated from the basin of the HDO reactant to the transition state.

In Fig. 6, we display the free energy surface with respect to d, n and ϕ. Fig. 6(a) shows that the free energy minimum is located at about (n = 1, d > 1.5 Å) corresponding to the ensemble of structures in which the O₇H group is neutral and the C₂⋯O₈ distance is well separated, i.e. the original HDO molecule and a proton left in bulk water.

Fig. 6 Three-dimensional free energy surface of HDO aqueous solution with respect to d, ϕ and n₇, obtained from the PBE/PW metadynamics calculations. The views are in a direction (a) parallel to ϕ and (b) parallel to n₇.

Meanwhile the transition state can be identified when we detect an event of the O–C bond exchange crossing the d = 0 line. Such a transition state is found around (n = 2, d = 0), where the O₇ atom is bonded to two hydrogen atoms, forming an OH₂⁺ group. An important outcome is that the O–C bond exchange always occurs after protonation. The region of O–C bond exchange without protonation, (n = 1, d = 0), has never been visited because the free energy therein is too high. From the free energy profiles in Fig. 6(a), we also see that there is no minimum corresponding to the protonated HDO molecule, which is consistent with the finding of the previous MEP analysis. Therefore, protonation and O–C bond breaking are consecutive processes.

Note that by construction metadynamics always finds the reaction channel with the smallest free energy barrier. Analyzing the trajectory of all the walkers in metadynamics, it was found that the O₇H group is protonated by an extra proton in water. We were unable to detect either an OH⁻ intermediate in water or an O₈⁻ intermediate in HDO. Neither the unprotonated water molecules nor the OH group of the HDO molecule are the main source of protonation in this case. This finding is consistent with the result from the MEP calculations mentioned above that the water-assisted pathway is not a dominant one. Therefore we conclude that the proton is catalytic in this system, which must be relevant to the experimental fact that dehydration reactions in hot water can be accelerated by the acid environment, in particular under the subcritical conditions.

In Fig. 6(b), we show another side view of the free energy profile with respect to the variables ϕ and d. In this case, three minima are found at ϕ = 300°, 60° and 180° with d ≈ 2 Å. The minima at ϕ = 60°, 300° and ϕ = 180° correspond to the thermodynamic ensemble of structures where the HDO molecule is in a contracted conformation with and without the internal hydrogen bond, respectively. They are comparable with the structures shown in Fig. 3(d) and (e), respectively.

The transition state around (ϕ = 180°, d = 0 Å) is characteristic of the S_N2 reaction. Combining the results of Fig. 6(a) and (b), it can be concluded that the reaction only occurs when n = 2 and ϕ = 180° is realized at the same time. The S_N2 reaction always undergoes via the protonated state of HDO in the conformation without the internal hydrogen bond. The reaction proceeds neither for the unprotonated state in this conformation nor the protonated state in any other conformation.

The free energy profile of the x = 4 and x = 6 microsolvated models is shown in Fig. 7(a) and (b), respectively (also see Fig. S5 in the ESI† for another view of this free energy profile). In this case, the free energy has been obtained with a constraint of 132.5° < ϕ < 227.5° focusing on the important region for the S_N2 reaction. It could be seen that the free energy profile is qualitatively similar to the result of the aqueous solution, Fig. 6. In Table 1, we summarize the reaction barriers in the energy of MEP and in the free energy at 523 K, with respect to the x = 4 and x = 6 microsolvated models and aqueous solutions. In the x = 4 and x = 6 microsolvated models, the energy and free energy barriers of the S_N2 reaction obtained are similar in value. This supports the reliability of metadynamics and that the set of collective variables (d, ϕ, n) has been a reasonable choice. We can see that the barrier height is slightly decreased when the number of water molecules surrounding the HDO reactant is increased, which implies that the aqueous environment helps in accelerating the reaction. This is true not only for the S_N2-pathway but also for the S_N1 pathway. We can also see that the energy barrier is larger for the backward reaction, which is consistent with the fact that the backward reaction is not found in experiment.

Fig. 7 Three-dimensional free energy surface of (a) x = 4 and (b) x = 6 HDO microsolvated model with respect to d, ϕ and n₇, obtained from the PBE/SV(P) metadynamics calculations. The views are in a direction parallel to ϕ.

Table 1 The S_N2 activation energies and free energies in kcal mol⁻¹

System	Method	Forward		Backward
		ΔE	ΔA	ΔE
a The sum of contributions from the conformational change and reaction. b Ref. 16. c Estimation combined with transition state theory.
HDO(H2O)4H^+	PBE/def2-SV(P)	41	37	49
HDO(H2O)6H^+	PBE/def2-SV(P)	40	36	49
HDO(H2O)6H^+	MP2/def2-SV(P)	45		49
HDO(H2O)70H^+	PBE-D2/PW/USPP		36^a
HDO in H2CO3	Experiment^b		39^c

---

The free energy landscape shown in Fig. 6 has covered only the reactive region within the contracted HDO configuration (d < 2.5 Å). In order to study the free energy landscape of the region covering the conformational change, another metadynamics simulation of HDO aqueous solution was carried out in two dimensions, d and ϕ (with d > 1 Å).

The result is shown in Fig. 8. The free energy minima found at (d, ϕ) = (3.0 Å, 300°), (3.3 Å, 60°), and (3.5 Å, 180°) correspond to the structures shown in Fig. 3(a), (b) and (c), respectively. This indicates that the extended conformations of HDO are the most stable ones in aqueous solution. Compared with the extended conformation at (d, ϕ) = (3.5 Å, 180°), the contracted conformation with the internal hydrogen bond, (d, ϕ) = (1.9 Å, 60°) or (2.1 Å, 300°), is less stable by about 3 kcal mol⁻¹. Meanwhile, from Fig. 6 the free energy in the S_N2 transition state is 33 kcal mol⁻¹ more than that of the HDO reactant in the contracted conformation with the internal hydrogen bond. The sum of these free energy differences, 36 kcal mol⁻¹, is the final estimate of the S_N2 reaction barrier in the aqueous solution. This is in reasonable agreement with the experimental estimation of the free energy barrier, ΔA = 39 kcal mol⁻¹, which is obtained by combining the experimental rate constant (with the half life t_h ≈ 30 min at T = 523 K)¹⁶ and the transition state theory:

where h and k_B are Planck's constant and Boltzmann's constant, respectively.

Fig. 8 Two dimensional free energy surface of HDO aqueous solution with respect to ϕ and d, obtained from the PBE/PW metadynamics calculations. The focus is on the region of conformational changes of the HDO molecule.

3.3 Trajectory analysis

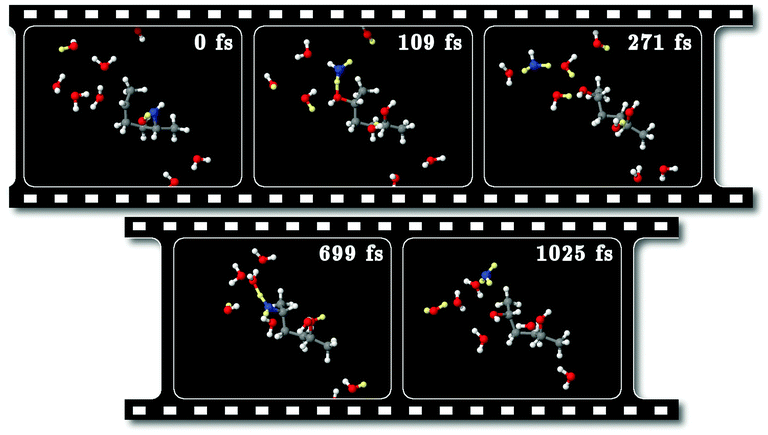
We studied the reaction process in real time by means of molecular dynamics simulations launched from the transition state region of the S_N2 reaction. The trajectories that led to either the reactant HDO or the product DMTHF correspond to the ones that have evolved backward and forward in time, due to time reversibility. The typical examples for such backward and forward trajectories are shown below. The results of other trajectories calculated (five backward and three forward) are shown in Fig. S6–S13 in the ESI.†

Fig. 10 and 12 are the snapshots and the structural variables N_x, r₂₇, r₂₈ and ϕ, respectively, along the backward trajectory. Fig. 11 and 9 show the respective results along a forward trajectory. Fig. 12 and 9 show the time evolution of the bond lengths and the dihedral angles, which start from the values of the transition state, r₂₇ ≈ r₂₈ ≈ 2.3 Å and ϕ ≈ 180°. The time evolutions near the transition state seem to resemble the changes along the S_N2 MEP shown in Fig. 5. The bondlengths quickly relax to the values of the reactant HDO (r₂₇ ≈ 1.4 Å, r₂₈ > 3 Å) and the product DMTHF (r₂₇ > 3 Å, r₂₈ ≈ 1.4 Å) in the backward and forward trajectories, respectively, within the sub-ps scale. This indicates that the bond exchange from C⋯O–C to C–O⋯C proceeds on this time scale.

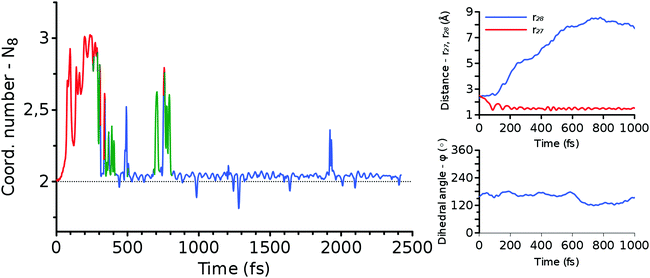Fig. 9 The change of structural variables N₈ (left panel), r₂₇ and r₂₈ (upper right panel), and ϕ (lower right panel) along the forward trajectory shown in Fig. 11. The color of N₈ indicates the position of an excess proton. It is red when O₈ is protonated, green when a water molecule hydrogen bonded to HDO is protonated, and blue otherwise.

Fig. 10 Snapshots of a backward trajectory of aqueous solution from the transition state to the reactant HDO obtained from the PBE/PW molecular dynamics calculations of aqueous solution. The water molecules are shown only for those close to HDO. Color codes: oxygen atoms in red, hydrogen atoms in white, carbon atoms in grey. As exceptions, the oxygen atom bonded to the excess proton is marked in blue, and the hydrogen atoms that are hydrogen bonded to other water molecules are marked in yellow.

Fig. 11 Snapshots of a forward trajectory of aqueous solution from the transition state to the product DMTHF obtained from the PBE/PW molecular dynamics calculations of aqueous solution. The water molecules are shown only for those close to DMTHF. Color codes: oxygen atoms in red, hydrogen atoms in white, carbon atoms in grey. As exceptions, the oxygen atom bonded to the excess proton is marked in blue, and the hydrogen atoms that are hydrogen bonded to other water molecules are marked in yellow.

Fig. 12 The change of structural variables N₇ (top panel), ϕ (middle panel), and r₂₇ and r₂₈ (bottom panel) along the backward trajectory shown in Fig. 10. The color of N₇ indicates the position of an excess proton. It is red when O₇ is protonated, green when a water molecule hydrogen bonded to HDO is protonated, and blue otherwise.

Meanwhile, the behavior of the coordination numbers, N₇ and N₈, is noticeably different from the one of the S_N2 MEPs, n₇ and n₈. In the real-time trajectories, we find a large amount of thermal vibration that allows the proton to jump back and forth between the HDO/DMTHF molecule and its neighboring water molecules, as can be seen in the snapshots of Fig. 10 and 11. This process can last for ps time scale until the proton is finally absorbed from/released into the bulk water via the proton relay. This occurs when the hydrogen bond network of water is transformed such that H₃O⁺ is surrounded by three other water molecules. In light of these trajectories and others shown in the ESI,† the timing of the creation of such a hydrogen bond network seems to be a statistical event.

4 Conclusions

In this paper the dehydration reaction of HDO in hot acidic water has been studied theoretically in three different analyses, i.e. MEP analysis by the string method, free energy analysis by metaydnamics simulations, and trajectory analysis by molecular dynamics simulations. The former two have been performed in the protonated microsolvated model, while the latter two have been performed in aqueous solution. All these computational results consistently indicate that the S_N2 pathway is more favorable than the S_N1 pathway, and thus supports the recent experimental result that this reaction proceeds with a high stereoselectivity in acidic water.¹⁶ The qualitative mechanism of the S_N2 pathway is schematically shown in Fig. 13, with an emphasis on how the water molecules are involved in the reaction. The free energy barrier for the S_N2 reaction is estimated to be 36 kcal mol⁻¹ in the aqueous solution, which is in reasonable agreement with a value converted from the experimental rate constant combined with the transition state theory, 39 kcal mol⁻¹.

Fig. 13 A qualitative reaction mechanism (S_N2).

The results obtained in these calculations do not contradict in any way to the reaction mechanism suggested in the experimental paper.¹⁶ However, our simulations have been able to add useful insights into the reaction mechanism with respect to the change in the energies and the structures step by step for each of the reaction processes. The reaction mechanism along with the respective time scales is summarized below.

1. The HDO molecule can fluctuate back and forth between different conformations in HTW. However, the extended conformation is more favorable than the contracted conformation from the viewpoint of free energy.

2. Few ps before of arriving at the transition state, the HDO molecule forms the contracted conformation.

3. At times less than a few ps before arriving at the transition state, one of the OH groups of HDO becomes protonated by the surrounding water via the Grotthuss relay mechanism.

4. At the same time as step 2 or 3, the HDO molecule must form the ϕ = 180° conformation.

5. A bond is exchanged between O–C and O⋯C at the same time in the S_N2 fashion, forming the ether ring. This occurs very quickly within a few tens of fs. This is the transition state of the whole reaction.

6. The bond angles are slightly shifted to adapt to the stable protonated DMTHF molecule.

7. The proton is picked up by water again in the Grotthuss relay, finalizing the reaction. It takes up to several ps for a proton to be released into bulk water after departing from the transition state.

The reaction proceeds in a single step. There is no stable intermediate throughout the reaction.

Finally it is important to comment on the role of water. On the quantitative basis, it is found that the energy barrier of the transition state is reduced as hydrogen bonded water molecules are increased, thus suggesting that water provides a field that accelerates the reaction. We provide a qualitative explanation on the role of water as an efficient solvent assisting the reaction.

The reaction proceeds only by way of the protonated HDO intermediate, capturing one proton at the early stage and releasing one proton at the last stage, wherein the proton must be stablized. Since the proton in the bulk can be stablized as a hydronium ion when it is hydrogen bonded to three water molecules, at least four water molecules are necessary to describe the whole reaction process.

As the proton is captured by the HDO reactant via the Grotthuss relay mechanism, the proper creation of a hydrogen bonded network is important. Once the HDO molecule is protonated it survives for a few ps although not being a stable intermediate. This is because for the protonated HDO molecule to lose the proton the hydrogen bond network must be rebuilt again. As the protonated HDO state lasts for more time, it provides more chance for an incoming energy to have the O–C bond elongated. If the system is in the contracted conformation, this immediately leads to the reaction. Once this happens, the extra proton is released into bulk water almost spontaneously without the need for energy, although it takes a few ps to form the hydrogen bond network.

The mechanistic insights offered by our work are not only relevant for the stereoselective dehydration reaction of HDO but also for the whole family of dehydration of polyalcohols in hot acidic water. We hope that our results will facilitate the design of more efficient and sustainable processes in HTW aimed at processing biomass derivatives.

Acknowledgements

This work was supported by Theoretical and Computational Chemistry Initiative (TCCI) and Computational Materials Science Initiative (CMSI) in the Strategic Programs for Innovative Research, MEXT, Japan. We thank for the priority use of the JAEA BX900 supercomputer in Center for Computational Science and E-systems at Tokai Research Establishment, JAEA. We are grateful to Dr A. Malins in JAEA for proofreading the manuscript of this paper. We also thank Prof. T. Sasaki at The University of Tokyo for useful discussions.

References

1. N. Akiya and P. E. Savage, Chem. Rev., 2002, 102, 2725–2750.
2. S. E. Hunter and P. E. Savage, Chem. Eng. Sci., 2004, 59, 4903–4909.
3. C.-J. Li, Chem. Rev., 2005, 105, 3095–3166.
4. M. A. Pigaleva, I. V. Elmanovich, Y. N. Kononevich, M. O. Gallyamov and A. M. Muzafarov, RSC Adv., 2015, 5, 103573.
5. M.-O. Simon and C.-J. Li, Chem. Soc. Rev., 2012, 41, 1415–1427.
6. C. Huber and G. Wächtershäuser, Science, 1997, 276, 245–247.
7. E. L. Shock, T. McCollom and M. D. Schulte, Origins Life Evol. Biospheres, 1995, 25, 141–159.
8. M. Siskin and A. R. Katritzky, Science, 1991, 254, 231–237.
9. N. N. Nair, E. Schreiner and D. Marx, J. Am. Chem. Soc., 2008, 130, 14148–14160.
10. E. Schreiner, N. N. Nair and D. Marx, J. Am. Chem. Soc., 2009, 131, 13668–13675.
11. O. Acevedo and K. Armacost, J. Am. Chem. Soc., 2010, 132, 1966–1975.
12. L. L. Thomas, J. Tirado-Rives and W. L. Jorgensen, J. Am. Chem. Soc., 2010, 132, 3097–3104.
13. M. Hatanaka and K. Morokuma, J. Am. Chem. Soc., 2013, 135, 13972–13979.
14. J. Zhang, Y. I. Yang, L. Yang and Y. Q. Gao, J. Phys. Chem. B, 2015, 119, 14505–14514.
15. J. Ribas-Arino, M. A. Carvajal, A. Chaumont and M. Masia, Chem. – Eur. J., 2012, 18, 15868–15874.
16. A. Yamaguchi, N. Hiyoshi, O. Sato and M. Shirai, ACS Catal., 2011, 1, 67–69.
17. A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick, J. P. Hallett, D. J. Leak and C. L. Liotta, Science, 2006, 311, 484–489.
18. A. Corma, S. Iborra and A. Velty, Chem. Rev., 2007, 107, 2411–2502.
19. X. Tong, Y. Ma and Y. Li, Appl. Catal., A, 2010, 385, 1–13.
20. R. A. Sheldon, Green Chem., 2014, 16, 950–963.
21. A. Farrán, C. Cai, M. Sandoval, Y. Xu, J. Liu, M. J. Hernáiz and R. J. Linhardt, Chem. Rev., 2015, 115, 6811–6853.
22. Y. Román-Leshkov, C. J. Barrett, Z. Y. Liu and J. A. Dumesic, Nature, 2007, 447, 982–985.
23. M. H. Haider, N. F. Dummer, D. W. Knight, R. L. Jenkins, M. Howard, J. Moulijn, S. H. Taylor and G. J. Hutchings, Nat. Chem., 2015, 7, 1028–1032.
24. S. E. Hunter and P. E. Savage, Ind. Eng. Chem. Res., 2003, 42, 290–294.
25. S. E. Hunter, C. E. Ehrenberger and P. E. Savage, J. Org. Chem., 2006, 71, 6229–6239.
26. A. Yamaguchi, N. Hiyoshi, O. Sato, K. K. Bando and M. Shirai, Green Chem., 2009, 11, 48–52.
27. A. Yamaguchi, N. Hiyoshi, O. Sato and M. Shirai, Green Chem., 2011, 13, 873–881.
28. A. Yamaguchi, N. Hiyoshi, O. Sato and M. Shirai, Catal. Today, 2012, 185, 302–305.
29. O. Sato, A. Yamaguchi and M. Shirai, Catal. Commun., 2015, 68, 6–10.
30. S. E. Hunter and P. E. Savage, AIChE J., 2008, 54, 516–528.
31. A. R. Morais, A. M. da Costa Lopes and R. Bogel-uukasik, Chem. Rev., 2014, 115, 3–27.
32. Á. Molnár, K. Felföldi and M. Bartók, Tetrahedron, 1981, 37, 2149–2151.
33. N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462.
34. D. Marx, ChemPhysChem, 2006, 7, 1848–1870.
35. E. Weinan, W. Ren and E. Vanden-Eijnden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301.
36. E. Weinan, W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103.
37. T. Arita, K. Nakahara, K. Nagami and O. Kajimoto, Tetrahedron Lett., 2003, 44, 1083–1086.
38. H. Takahashi, F. Miki, H. Ohno, R. Kishi, S. Ohta, S.-i. Furukawa and M. Nakano, J. Math. Chem., 2009, 46, 781–794.
39. H. Takahashi, H. Hashimoto and T. Nitta, J. Chem. Phys., 2003, 119, 7964–7971.
40. H. Takahashi, S. Hisaoka and T. Nitta, Chem. Phys. Lett., 2002, 363, 80–86.
41. Y. Nagai, N. Matubayasi and M. Nakahara, Bull. Chem. Soc. Jpn., 2004, 77, 691–697.
42. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
43. B. Ensing, A. Laio, M. Parrinello and M. L. Klein, J. Phys. Chem. B, 2005, 109, 6676–6687.
44. P. Raiteri, A. Laio, F. L. Gervasio, C. Micheletti and M. Parrinello, J. Phys. Chem. B, 2006, 110, 3533–3539.
45. M. Shiga, PIMD version 1.7, 2015.
46. S. Ruiz-Barragan, K. Ishimura and M. Shiga, Chem. Phys. Lett., 2016, 646, 130–135.
47. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
48. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
50. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
51. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
52. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
53. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
54. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
55. CPMD, Version 3.12.04, Copyright IBM Corp 1990-2016, Copyright MPI für Festkörperforschung Stuttgart 1997-2001; See also http://www.cpmd.org.
56. D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604.
57. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
58. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
59. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471.

---

Footnote

† Electronic supplementary information (ESI) available: Data of the MEP, metadynamics, and molecular dynamics calculations are provided. See DOI: 10.1039/c6cp05695d

---