Subtle solvation behaviour of a biofuel additive: the methanol complex with 2,5-dimethylfuran

Abstract

Methanol is shown to engage two nearly equivalent solvation sites in 2,5-dimethylfuran, the electron-rich π cloud and the electron-deficient oxygen site. The latter only wins by a slight margin, thanks to the methyl group undergoing secondary interactions with the ring. These secondary attractions reduce the hydrogen bond-induced OH frequency shift of the OH–O contact, whereas the π cloud allows for a combined action of both binding mechanisms in the OH–π arrangement. In total, the hydrophobic character of 2,5-dimethylfuran is well reflected in the weak pair interactions, as judged by the small solvation shifts. Methanol solvation of 2,3-benzofuran is revisited and shown to be more ambiguous than previously thought, involving competition between five- and six-ring π clouds and the oxygen site for the OH group. The six-ring π cloud is slightly preferred. FTIR spectroscopy in supersonic jets is in systematic agreement with dispersion-corrected harmonic B3LYP and also B2PLYP predictions for these competing furan docking sites. Deuteration of the OH group helps to identify the docking sites because of its attenuated zero-point energy weakening effect on localized hydrogen bonds. Extension to less methylated furans is proposed in the context of a future forecasting competition for the performance of quantum chemical methods for intermolecular interactions.

---

1 Introduction

The carbon skeleton of 2,5-dimethylfuran (DMFu) matches that of fructose, indicating that it may be an accessible biofuel additive.¹ In comparison with the established fuel additive ethanol, it is of similar volatility, but much less hygroscopic, a definite advantage in mixtures with hydrophobic hydrocarbons. Furthermore, it has a higher energy content. If the production costs for 2,5-dimethylfuran and related compounds can be further optimized^2,3 and the formation of polyaromatic hydrocarbons during combustion can be controlled,⁴ the physical properties of its mixtures deserve more attention. Among the relevant mixtures including this biofuel additive, methanol⁵ and higher alcohols⁶ stand out. The exploration of solvent complexes of 2,5-dimethylfuran promises to provide deeper insights into its hydrophobicity and we start here with an investigation of binary methanol (M) complexes, using linear FTIR spectroscopy in supersonic jets to derive reliable relative intensity ratios of different isomers. A recent investigation of the related 2,3-benzofuran (BFu) complexes with methanol⁷ using conformation-selective spectroscopy is revisited by FTIR spectroscopy, revealing some additional complexity and an unambiguous winner in the subtle energetic competition of the different solvation sites. Related work on ambiguous N-heterocycle docking by methanol includes imidazole,⁸ which is also relevant for ionic liquid solvation.⁹ Here, we focus on the considerably weaker hydrogen bonds in neutral complexes involving oxygen acceptor sites. The goal is thus to establish experimental docking preferences for alcohols to aromatic ethers.¹⁰

Previous investigations of this class of molecular complexes have revealed a wide spectrum of preferences (Fig. 1).^11–14 If the ether oxygen is not directly attached to the aromatic ring, one may safely expect that it is a more attractive binding site for the methanol molecule, with a concomitant pronounced bathochromic (red) shift of its OH oscillator. We are not aware of a study of such alcohol/ether complexes in the gas phase, but a comparison of alcohol complexes with alkyl ethers¹¹ and with benzene¹² is strongly suggestive of a stronger alcohol–ether interaction. If the oxygen is directly attached, such as in the model case of anisole,¹³ the competition between π and oxygen binding is much closer because of partial delocalization of an oxygen lone pair into the aromatic π cloud, but the oxygen site will usually still offer a slight energy advantage to an incoming alcohol, although standard quantum chemical calculations may not predict this correctly.¹⁴ If the phenyl oxygen is incorporated into a heteroaromatic ring structure like in 2,3-benzofuran, the delocalization of the oxygen lone pair intensifies and both π segments profit from this. Indeed, π- and O-docking were found to be more or less equivalent in a recent IR/UV study,⁷ both in theory and in experiment. One might argue that the distribution of the oxygen lone pair density over two rings dilutes the effect and the plain heterocycle furan might be a better case for a π preference. However, furan has not been studied by standard IR/UV techniques because of its ultrafast dynamics in the electronically excited states.¹⁵ The proposed biofuel 2,5-dimethylfuran should have an even higher π electron density due to the electron-pushing effect of the methyl groups, but part of this may be transferred back to the ring oxygen and therefore compensate the gain in π attractivity.

Fig. 1 R–OH solvation preferences for different classes of aromatic ethers represented by benzyl methyl ether, anisole, benzofuran and 2,5-dimethylfuran.

These qualitative reasonings need to be substantiated quantitatively and for such small model systems, this is indeed possible. On the theoretical side, it requires high quality dispersion corrected density functionals or highly correlated wavefunction methods.¹⁴ On the experimental side, dilute solution studies can offer an equilibrium distribution between the two docking sites, but they are distorted by thermal and solvent effects,¹⁶ largely masking any safe comparison to theory. Subtle differences between the competing hydrogen bonding sites therefore require a low temperature vacuum isolation technique and we propose jet-FTIR spectroscopy as a suitable method, which is not dependent on a long-lived electronically excited state. If the barrier between the two docking sites is high, supersonic jet expansion may freeze out a statistical distribution of docking isomers, but in the furan case, the two sites are so close together in space without any sterical obstacle in between, that one may safely assume that the barrier is low. As a consequence, conformational exchange between the two sites will only freeze out at a relatively low temperature on the order of 30–100 K. This low conformational freezing temperature allows us to detect energy differences between the two docking sites on a 1 kJ mol⁻¹ scale or even smaller based on the observed relative populations and their relaxation behaviour. This may appear unnecessarily ambitious, but one should remember that any systematic error in an isolated solute–solvent pair may amplify in the bulk solution by an order of magnitude. Therefore, only the most accurate first principles interaction energies are useful for many-body expansions and other fragmentation approaches to condensed phases.¹⁷

2 Methods

Highly dilute mixtures of DMFu (Acros Organics, 99%) and methanol (Roth, ≥99.9%) in helium (Linde, 4.6) are prepared by either guiding the helium flow through appropriately cooled separate liquid containers or preparing two-component mixtures with helium in pressurized gas containers, followed by pulsed admission of the two gas mixtures into a reservoir. From this reservoir, the ternary (sometimes quaternary, including traces of acetone as a relaxation promoter¹⁸) gas mixture is pre-expanded in a 145 ms pulse through six magnetic valves into a small chamber terminated by a 600 × 0.2 mm² slit. Through this slit, the gas expands more or less adiabatically into a 23 m³ vacuum chamber, before it interacts with the background gas. The latter is limited to a pressure of 0.8 mbar due to the size of the vacuum chamber despite the substantial gas flow. The expansion zone is probed along its long axis by the weakly focussed modulated beam of a Bruker 66v/S FTIR spectrometer and the feeble attenuation of this beam is detected by an InSb detector equipped with an optical filter transmitting the OH/CH/OD stretching range. A 2 cm⁻¹ interferometer scan is synchronized with the gas pulse, providing a full spectrum for each pulse. After a recovery period, during which the vacuum chamber continues to be evacuated by 2500 m³ h⁻¹ Roots pumps, background scans are recorded and the next gas pulse follows. This sequence is repeated 100–300 times and the individual spectra are co-added. Details are described elsewhere.¹⁹

On the computational side, a reliable method which is extensible to harmonic frequency calculations of benzofuran complexes is B3LYP-D3/aVTZ,^20–23 the popular hybrid functional augmented with Grimme's dispersion correction²⁴ and Becke–Johnson damping,²⁵ using an augmented triple zeta correlation-consistent basis set to minimize basis set superposition error. Anharmonic corrections to the zero-point energy difference are believed to be small for this kind of systems,¹⁴ likely smaller than residual harmonic errors. Residual thermal corrections to energy differences were neglected due to the generally low effective temperature in the jet, an experimental non-Boltzmann distribution among rotational and different vibrational degrees of freedom, the effective cancellation of contributions between most of the degrees of freedom of the interconverting isomers, and growing uncertainties in the harmonic treatment of the relevant very soft modes beyond the zero-point level. Electronic energies and equilibrium structures are checked by B2PLYP-D3/aVTZ optimization, i.e. adding a perturbative electron correlation treatment at the double-hybrid level.²⁶ If not stated otherwise, energy values are calculated with Turbomole 6.5²⁷ without inclusion of an Axilrod-Teller three-body dispersion contribution. The program package Gaussian09²⁸ is used for preoptimizations at B97D/TZVP level with manually chosen starting structures and calculations with the B2PLYP functional.

3 Results

3.1 DMFu

Previous quantum chemical calculations for the analogous methanol/anisole dimers suggest that the harmonic B3LYP-D3/aVTZ level should be adequate for exploratory quantum chemical calculations of methanol/2,5-dimethylfuran complexes.¹⁴ Three different conformers were found for the methanol/DMFu (MD) dimer. Two of them are oxygen-bound, whereas only one conformer (OH–π) realizes a π complex. Only a subtle energy difference of 0.4 kJ mol⁻¹ (see Table 1) is predicted to separate it from the global minimum oxygen-bound structure OH–O. Characteristically, this energy difference becomes twice as large (0.8 kJ mol⁻¹) when harmonic zero-point energy is neglected. OH–O interactions are more localized and therefore generate more intermolecular zero-point energy than OH–π interactions. Fig. 2 shows the structural difference between the two oxygen-bound conformers. OH–O has C_s symmetry and the methyl moiety is located above the π system. Its secondary interactions lead to a bent hydrogen bond with an OH–O angle of 155° and make sure that the interaction with oxygen is also more π-like, i.e. approaching the acceptor perpendicular to the furan plane. We avoid indicating this in the symbol, because the transition between σ and π character of the pair of lone pairs at the oxygen is continuous and π will be reserved for interactions to the aromatic carbon atoms in this study. With the methyl moiety pointing away from DMFu, OH–O′ lacks these interactions, involves a more σ-like interaction with the oxygen charge density and hence cannot compete in stability (1.6 kJ mol⁻¹). In the π-bound conformer, the methanol molecule is again positioned directly above DMFu, anchored not only by the hydrogen bond, but also by the CH interactions to the oxygen atom and C_α. The OH hydrogen bond is located over C_γ.

Table 1 Energies of methanol/ether complexes in kJ mol⁻¹ relative to the most stable conformer (bold face), excluding (E_e) and including (E₀) the harmonically approximated zero-point energy. Dashes mark conformers, which could not be optimized at the given computational level

Acceptor	Type^a	B3LYP-D3/aVTZ		B2PLYP-D3/aVTZ
		E e	E 0	E e	E 0
a See Fig. 2 and 5 (and Fig. S1 and S2 in the ESI) for the structures. b Value calculated using Gaussian 09. c Value calculated by Sasaki et al. at CCSD(T)/6-311++G(d,p) level, with the geometry and ZPE calculated at MP2/6-311++G(d,p) level.^7
2,5-Dimethylfuran	OH–π	0.8	0.4	0.8
	OH–O	0	0	0
	OH–O′	1.7	1.6	1.9
2-Methylfuran	OH–π	0.8	0.0	1.0	0.1
	OH–O	0	0	0	0
	OH–π′	1.4	0.5	1.6	0.7
	OH–O′	1.4	1.1	1.7	1.5
Furan	OH–π	0	0	0	0
	OH–O	0.3	0.8	0.0	0.5
	OH–O′	—	—	0.0	0.6
2,3-Benzofuran	OH–π6	0	0	0
	OH–O	1.1	2.2 (2.0^b, −0.1^c)	1.3
	OH–π5	1.4	1.6 (1.7^b)	1.6
	OH–π5′	—	—	2.1

---

Fig. 2 Structures of the most stable methanol/2,5-dimethylfuran dimers at B3LYP-D3/aVTZ level from two perspectives.

Relative electronic energies after geometry optimization with the double hybrid functional B2PLYP-D3/aVTZ do not differ much from the results at the B3LYP-D3/aVTZ level, only the OH–O′ conformer is further destabilized by 0.2 kJ mol⁻¹. Therefore the lower computational level appears justified at this stage.

The lighter analogues furan and 2-methylfuran offer fewer possibilities for secondary interactions to a methanol donor. The predicted preference for the oxygen-bound conformer first vanishes and then inverts upon removing one and two methyl groups (see Table 1). This emphasizes that the methylation of furan improves the π cloud attractivity even more at the oxygen end than at the carbon end of the heterocycle. Absolute dissociation energies of methanol are predicted to increase with α-methylation of the furan ring, roughly by 3 kJ mol⁻¹ per methyl group (see Table S1 in ESI†). In the following, we only test these predictions for DMFu, leaving the experimental solvent docking investigation of the other two furans for a future forecasting competition.

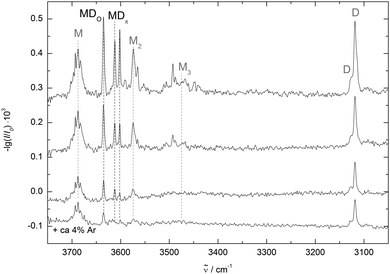
Fig. 3 shows three spectra of methanol/DMFu co-expansions in helium with decreasing concentration from top to bottom. DMFu has two distinct bands at 3118 cm⁻¹ and 3127 cm⁻¹ (D) corresponding to the antisymmetric and symmetric stretching fundamentals of the aromatic hydrogens, respectively. The shoulder at 3114 cm⁻¹ for the high concentration is possibly due to DMFu clusters. The methanol monomer (M) and dimer (M₂) bands enclose three bands of mixed clusters at 3635 cm⁻¹, 3612 cm⁻¹ and 3602 cm⁻¹. The less shifted ones behave similarly with dilution, while the latter decreases slightly relative to the others. This indicates a mixed trimer origin, most likely involving two DMFu units, although a metastable dimer contribution cannot be ruled out at this stage. A better relaxation of the clusters to the energetically preferred conformers can be achieved by the addition of argon. The corresponding spectrum is shown in the bottom trace of Fig. 3. Only the least red-shifted band marked MD_O persists, assigning it to the most stable conformer. A residual trace of the most shifted band supports its tentative mixed trimer assignment.

Fig. 3 Evolution of the binary complexes (MD) and the methanol dimer (M₂) with decreasing 2,5-dimethylfuran (D) and methanol (M) concentration from top to bottom. The band at 3602 cm⁻¹ shows the largest decrease and is therefore assigned at least partially to a trimer. The lowest trace shows the effect of adding 4% argon to the expansion and reveals the band marked MD_O as the most stable mixed dimer.

Comparing the measured wavenumbers to the quantum chemical results (bottom of Fig. 4 and Table 2) the bands at higher wavenumber can be assigned to the oxygen- and to the π-bound dimer, respectively. Note that the computed harmonic vibrational wavenumbers are scaled with a factor of 0.9634 to reproduce the experimental methanol monomer value of 3686 cm⁻¹. The oxygen-bound dimer wavenumber is predicted 10 cm⁻¹ and the π-bound dimer band 7 cm⁻¹ too low. This is typical for weak OH–O interactions (and even more pronounced in strong OH–O interactions like in methanol dimer, see Fig. 4). It is somewhat unexpected for OH–π contacts, where the shift tends to be underestimated in a monomer-scaled harmonic prediction.²⁹ However, this may not apply to heteroaromatic compounds like furans. The band with the largest shift coincides with the higher energy oxygen-bound conformer prediction, but this may be coincidental. A mixed trimer assignment is more likely because at the present level of calculation, scaled harmonic undistorted OH–O hydrogen bond shifts are systematically overestimated (by 22 cm⁻¹ in the related methanol/anisole¹⁴ and by 58 cm⁻¹ in the more strongly bound methanol/methanol dimer (Fig. 4)). On the other hand, adding a second dimethylfuran unit to one of the assigned mixed dimers could easily enhance their OH stretching downshift by the observed amount. In a superficial search for such a trimer the most stable conformer would correspond to a red shift overestimation of 20 cm⁻¹, which seems a more reasonable assignment than the OH–O′ dimer. Furthermore, the zero-point corrected OH–O′ to OH–O interconversion barrier is 0.1 kJ mol⁻¹ at B3LYP-D3/aVTZ level and thus far too low to stabilize the OH–O′ complex.

Fig. 4 MeO(H/D)/DMFu spectra in comparison to quantum chemical calculations at B3LYP-D3/aVTZ level. Wavenumbers are scaled to the methanol monomer and stretched by for MeOD (upper spectrum). The peak at 3612 cm⁻¹ decreases with deuteration relative to the 3635 cm⁻¹ peak. Therefore it is assigned to the π-bound conformer, in agreement with the theoretically predicted wavenumber sequence.

Table 2 Methanol OH stretching fundamental [small nu, Greek, tilde]_OH in cm⁻¹. Values are scaled to the experimental methanol monomer value of 3686 cm⁻¹ (multiplied by 0.9634 for B3LYP-D3 and by 0.9578 for B2PLYP-D3). Dashes mark conformers, which are not stable at the given computational level

Acceptor	Type	B3LYP-D3/aVTZ	B2PLYP-D3/aVTZ	[small nu, Greek, tilde] ^expOH
		[small nu, Greek, tilde] OH	[small nu, Greek, tilde] OH
2,5-Dimethylfuran	OH–π	3605		3612
	OH–O	3625		3635
	OH–O′	3600
2-Methylfuran	OH–π	3615	3616
	OH–O	3638	3640
	OH–π′	3621	3624
	OH–O′	3614	3618
Furan	OH–π	3631	3633
	OH–O	3642	3651
	OH–O′	—	3645
2,3-Benzofuran	OH–π6	3646		3636
	OH–O	3635		3645
	OH–π5	3640
	OH–π5′	—

---

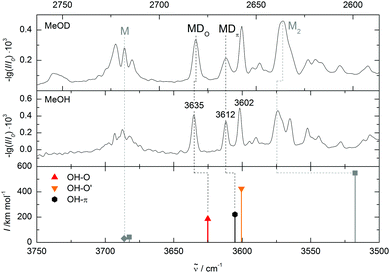
So far, the assignment of the oxygen- and π-bound complexes of methanol with DMFu rests on consistent theoretical predictions of their relative energy and vibrational wavenumber. Experimental support comes from methanol deuteration. This leaves the structure largely unaffected, but it reduces the zero-point motion in the hydrogen bond and therefore favours the conformer with larger zero-point energy destabilization. Typically, this is the more localized oxygen-bound conformer,¹⁴ and Table 1 confirms this rule from a computational perspective. Deuteration should therefore lead to a relatively more abundant oxygen-bound species in the experiment. The spectrum of the deuterated complex recorded under identical conditions is shown in Fig. 4 (upper trace). All three bands can still be observed, but the central band has lost in relative intensity and is thus confirmed as the π-bound structure.

The unusual predicted and observed sequence of OH–O and OH–π stretching bands, with oxygen coordination shifting even less than π coordination, remains to be discussed. It is due to distortion of the OH–O contact by the dispersion attraction of the methyl group to the furan ring. The OHO angle amounts to 155°, much less than in the OH–O′ complex (173°). In contrast to this competition between hydrogen bonding and methyl group dispersion, the two forces cooperate in the OH–π complex in attracting the methanol molecule to the ring plane. The overall energetics slightly favour the OH–O complex, but its hydrogen bond shift is thus inferior to that of the OH–π complex.

3.2 BFu

An inverted spectral sequence of OH–O and OH–π infrared signals has been observed before in the related dimer of methanol with 2,3-benzofuran (BFu) by Sasaki et al.⁷ and we have thus reinvestigated this more polyvalent system (Fig. 5).

Fig. 5 Structures of the most stable methanol/2,3-benzofuran dimers at B3LYP-D3/aVTZ level.

Two FTIR spectra with different relative concentrations are shown in Fig. 6. They are scaled to a similar absorbance of methanol. With two mixed dimer bands at 3645 cm⁻¹ and 3636 cm⁻¹ our experimental findings are in agreement with the band positions reported by Sasaki et al.⁷ Both bands of the mixed clusters can be assigned to dimers, as their relative intensity does not change much when drastically reducing the methanol concentration (middle trace) and both bands are still visible at this low concentration when no clusters beyond methanol dimer remain detectable. The conformational selectivity of the IR/UV technique⁷ has shown unambiguously that the two bands belong to different dimer conformations. An advantage of the FTIR approach is the availability of robust relative intensity information. The less shifted band is so much weaker that its underlying dimer must be less abundant than the dimer causing the more strongly shifted band. This indicates that the less shifted band belongs to the less stable dimer. When adding traces of acetone (bottom trace of Fig. 6) the weaker band decreases further to noise level. This may either be due to a better collisional cooling or due to solvent exchange mechanisms involving acetone as an intermediate binding partner.^18,30 Following the same considerations as for DMFu, methanol was deuterated to distinguish between oxygen and π coordination. The spectra are compared in Fig. 7. The further down-shifted band shows a relative absorbance decrease, assigning it to a π-bound conformer. This confirms the assignment by Sasaki et al. with the additional information from the FTIR spectra that the π coordination is energetically more favourable in this system.

Fig. 6 Spectra of methanol/benzofuran expansions in helium. The upper spectrum is obtained at high concentrations (see also Fig. 7). The middle one is obtained at high dilution, suppressing clusters beyond dimers. The lower spectrum includes traces of acetone, which suppresses the band at 3645 cm⁻¹. The methanol/acetone dimer band is marked with an asterisk. The spectra are scaled to similar methanol intensity.

Fig. 7 The spectra of methanol/benzofuran expansions in comparison to quantum chemical calculations at B3LYP-D3/aVTZ level. Wavenumbers are scaled to the methanol monomer. The monomer and dimer band of methanol are marked with M and M₂, respectively. The upper panel shows the spectrum of deuterated methanol with benzofuran, a spectrum with a lower benzofuran concentration is shown in gray. The peak at 3636 cm⁻¹ decreases with deuteration, therefore it is assigned to the π-bound conformer.

Applying the quantum chemical methods used successfully for DMFu, one finds an energy difference of 2.2 kJ mol⁻¹ (B3LYP-D3/aVTZ) between the OH–O and the OH–π conformer reported by Sasaki et al., which involves coordination of the benzene ring (see Table 1). The sign of the energy difference agrees with our experimental finding, that the OH–π conformer is more stable. However, we find a second OH–π conformer involving the furan ring, which has not been considered in the former work.⁷ Together with the other two conformers it is shown in Fig. 5, where we distinguish the two π structures by adding the size of the ring. OH–π5 is actually predicted 0.6 kJ mol⁻¹ lower in energy than OH–O after adding zero-point energy. Since there are only two bands in the experimental spectrum, different scenarios must be discussed: either there is accidental band overlap or one of the metastable structures relaxes to the most stable structure, whereas the other one is partially trapped. To explore the possibility of band overlap, it is of interest to compare with the theoretical predictions of the band positions (lowest trace in Fig. 7). The OH–π6 band at 3636 cm⁻¹ is predicted 10 cm⁻¹ too high (Table 2). This is qualitatively expected, when comparing to the related case of methanol/toluene,¹⁴ where the same level of computation predicts the OH–π6 conformation 14 cm⁻¹ too high, whereas in case of methanol/anisole the overestimation is accidentally 0 cm⁻¹. Using the def2-TZVP basis set the wavenumber for the latter is overestimated by 6 cm⁻¹.¹⁴ In contrast, for the observed 3645 cm⁻¹ band, the OH–π5 and OH–O signals should be predicted some 7 cm⁻¹ and 10 cm⁻¹ too low, if one may correlate with the DMFu case, which provides a similar local environment to the methanol (Table 2). The actual predictions are 5 cm⁻¹ and 10 cm⁻¹ too low, respectively. This leaves band overlap or any of the two metastable conformations as possible assignments of the minor experimental peak. In any case, the comparison to related systems explains why the spectral sequence is inverted between prediction and experiment. The deuteration experiment does not favour assignment of the minor peak to OH–π5, because the zero-point energy disadvantage relative to OH–π6 is too small (0.2 kJ mol⁻¹versus 1.1 kJ mol⁻¹ for OH–O) to explain the deuteration gain. The deuteration experiment also does not favour band overlap, because it is unlikely that the overlap persists upon deuteration. However, this cannot be ruled out with our non-selective method. The most likely explanation is a survival of OH–O besides the globally stable OH–π6 dimer for kinetic reasons. Fig. 8 outlines the transition states for each interconversion. These were obtained by the woelfling module of the Turbomole 7.0³¹ program followed by the QST3 method from Gaussian. When transforming the oxygen-bound conformer into the OH–π6 structure a secondary interaction to the ortho hydrogen needs to be broken while new CH–π interactions are formed, resulting in a barrier hight of 1.6 kJ mol⁻¹. This is not the case for the conversion of the OH–π5 arrangement. The secondary interactions being similar CH–π interactions, these can be transformed more easily due to the π cloud delocalization, leading to a barrier as low as 0.3 kJ mol⁻¹. Therefore, the most likely assignment is the original one by Sasaki et al. despite the discovery of a second metastable π coordination. In both experimental setups, OH–O is only observed due to kinetic trapping, which we overcome by acetone-catalysed relaxation.

Fig. 8 Transition states for the interconversion between the different conformers calculated at B3LYP-D3/aVTZ level relative to the OH–π6 conformer including zero-point energy. All energies are obtained with Gaussian 09, thus the slight discrepancy in energy difference between the conformers to Table 1.

4 Conclusions

The OH group of methanol prefers to coordinate a 2,5-dimethylfuran (DMFu) molecule at its oxygen site, but largely because the methyl group simultaneously solvates the aromatic ring. The competing π solvation by the OH group is only marginally less stable but shows a significantly larger bathochromic shift in the experimental infrared spectrum. The emerging picture is a rather freely roaming solvent molecule over the aromatic ring plane, which can be cryogenically trapped into two nearly isoenergetic but spectroscopically distinct binding sites. It is predicted at B3LYP-D3/aVTZ level that removal of one methyl group from DMFu brings the two binding sites into perfect balance, whereas removal of the second methyl group in furan gives the π coordination a distinct but still sub-kJ mol⁻¹ advantage. These very delicate theoretical predictions have to be confirmed or falsified by future experiments. At this stage we deliberately refrain from carrying out these measurements. We rather invite high level quantum chemistry predictions for this furan demethylation trend by theory groups. Once we have received two or more (by preference contradictory) predictions, we offer to carry out the experiments and to publish the results together with the participating theory groups in a kind of forecasting competition report.

For 2,3-benzofuran (BFu), we confirm the previous spectral assignments based on conformation-selective methods⁷ and we are able to show that six-ring π coordination is energetically preferred in this case, whereas oxygen coordination is only observed under kinetic trapping conditions and a newly postulated five-ring π coordination transforms smoothly into the six-ring location. Again, solvent roaming over the bicyclic aromatic compound can be controlled by the addition of relaxation agents.

The preferred docking sites for methanol on DMFu and BFu experimentally established in this work provide excellent tests for electronic structure calculations augmented by at least harmonic zero-point energy estimates. We are able to experimentally rank docking sites which are predicted to differ in energy by as little as 0.4 kJ mol⁻¹ and therefore to assess weak dispersion interactions on this energy scale in competition with classical hydrogen bonding. Furthermore, systematic comparison between related systems allows to discriminate and assign OH stretching band shifts separated by as little as 10 cm⁻¹.

By moving to longer chain alcohols as complexation partners, the binary complexes will start to model the interaction of DMFu with the main aliphatic fuel components. On the way, ethanol complexes could be studied to characterize the interaction between the present and proposed biofuel additives. Extension to mixed trimers including self-interaction of two DMFu units will also be feasible, as the jet-FTIR spectra indicate.

However, alcohols are not the only promising solvent partners for furans. It has been demonstrated before that the O vs. π preference of furan docking strongly depends on the chemical type of donor molecule.³² For acetylene, a He droplet experiment has provided evidence for both isomers³³ and the downshift of the asymmetric CH stretch was found to be slightly larger for π bonding, as also observed in the present methanol investigation. For indole, only the π-bound isomer was observed when docking to furan.³⁴ The same preference was found for metal ions exhibiting η⁵-, η²- and η¹-coordination to the carbon atoms opposite of the hetero atom.^35–37 Tungsten carbonyl complexes in solution were found to prefer the π face in 2,5-dimethylfuran, whereas the oxygen coordination is stable for furan and 2-methylfuran.³⁸ This is the opposite behaviour to the one observed here for methanol hydrogen bonding. All these findings support furans as promising hydrogen bond docking targets with a high sensitivity to donor and acceptor variations and a perspective of pronounced chemical control.

Acknowledgements

We thank Matthias Heger for valuable help and discussions. We greatly acknowledge financial support by the German Research Foundation (Su 121/5) in the context of the priority program SPP 1807 on dispersion interactions.

References

1. Y. Román-Leshkov, C. J. Barrett, Z. Y. Liu and J. A. Dumesic, Nature, 2007, 447, 982–985.
2. B. Saha and M. M. Abu-Omar, ChemSusChem, 2015, 8, 1133–1142.
3. M. Chidambaram and A. T. Bell, Green Chem., 2010, 12, 1253.
4. L.-S. Tran, B. Sirjean, P.-A. Glaude, K. Kohse-Höinghaus and F. Battin-Leclerc, Proc. Combust. Inst., 2015, 35, 1735–1743.
5. G. A. Olah, A. Goeppert and G. K. S. Prakash, Beyond oil and gas: the methanol economy, Wiley-VCH, Weinheim, 2006.
6. J. L. da Silva and M. Aznar, Fuel, 2014, 136, 316–325.
7. H. Sasaki, S. Daicho, Y. Yamada and Y. Nibu, J. Phys. Chem. A, 2013, 117, 3183–3189.
8. J. Zischang, J. J. Lee and M. A. Suhm, J. Chem. Phys., 2011, 135, 061102.
9. C. G. Hanke, N. A. Atamas and R. M. Lynden-Bell, Green Chem., 2002, 4, 107–111.
10. H. C. Gottschalk, J. Altnöder, M. Heger and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 1921–1924.
11. M. A. Suhm, in Advances in Chemical Physics, ed. S. A. Rice, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2009, vol. 142, pp. 1–57.
12. T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241.
13. B. Brutschy, Chem. Rev., 2000, 100, 3891–3920.
14. M. Heger, J. Altnöder, A. Poblotzki and M. A. Suhm, Phys. Chem. Chem. Phys., 2015, 17, 13045–13052.
15. T. Fuji, Y.-I. Suzuki, T. Horio, T. Suzuki, R. Mitrić, U. Werner and V. Bonačić-Koutecký, J. Chem. Phys., 2010, 133, 234303.
16. A. Allerhand and P. von R. Schleyer, J. Am. Chem. Soc., 1963, 85, 371–380.
17. K. U. Lao, K.-Y. Liu, R. M. Richard and J. M. Herbert, J. Chem. Phys., 2016, 144, 164105.
18. C. M. Lovejoy and D. J. Nesbitt, J. Chem. Phys., 1989, 90, 4671.
19. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
20. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
21. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
23. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
24. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
25. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
26. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
27. TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009.
29. J. Altnöder, S. Oswald and M. A. Suhm, J. Phys. Chem. A, 2014, 118, 3266–3279.
30. W. Y. Sohn, J. S. Kang, S. Y. Lee and H. Kang, Chem. Phys. Lett., 2013, 581, 36–41.
31. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
32. E. Sánchez-García and G. Jansen, J. Phys. Chem. A, 2012, 116, 5689–5697.
33. A. Metzelthin, O. Birer, E. Sánchez-García and M. Havenith, J. Chem. Phys., 2008, 129, 114307.
34. S. Kumar, V. Pande and A. Das, J. Phys. Chem. A, 2012, 116, 1368–1374.
35. R. L. Grimm, J. B. Mangrum and R. C. Dunbar, J. Phys. Chem. A, 2004, 108, 10897–10905.
36. P.-H. Su, F.-W. Lin and C.-S. Yeh, J. Phys. Chem. A, 2001, 105, 9643–9648.
37. P.-H. Su and C.-S. Yeh, Chem. Phys. Lett., 2000, 331, 420–424.
38. R. Krishnan, H. E. Gottlieb and R. H. Schultz, Angew. Chem., Int. Ed., 2003, 42, 2179–2181.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05413g

---