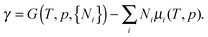Water adsorption and O-defect formation on Fe₂O₃(0001) surfaces

Abstract

The stability and reactivity of the hematite, Fe₂O₃(0001) surface are studied by density functional theory including an on-site Coulomb term (DFT+U). Even under oxygen rich conditions, the metal-terminated surface is shown to be stable. On this surface termination, the isolated water molecule forms a heterolytically dissociated structure with the OH⁻ group attached to a surface Fe³⁺ ion and the proton to a surface O²⁻ ion. Dissociative adsorption is strongly enhanced at oxygen vacancy sites. Here, the OH⁻ group fills the oxygen vacancy site. Dehydrogenation accompanied by defect healing is favoured compared to water desorption (178 kJ mol⁻¹ compared to 236 kJ mol⁻¹). The water adsorption energies (at 0 K) for the clean and defective surfaces are 100 kJ mol⁻¹ and 288 kJ mol⁻¹, respectively.

---

1 Introduction

Iron oxides are abundant minerals on earth¹ and play an important role in a variety of applications^2–4 ranging from geochemistry, weathering, corrosion science, biomedicine, magnetic devices to heterogeneous catalysis and photocatalysis. The surface chemistry of these oxides is dominated by interactions with water and solvated ions. Thus, a detailed understanding of the interaction between metal oxides and water, which determines oxide formation and dissolution, is indispensable. This study is devoted to one of the most common and stable iron oxide phases, hematite (α-Fe₂O₃), in particular to the adsorption of an isolated water molecule on the pristine and defective α-Fe₂O₃(0001) surfaces.

Hematite has the corundum crystal structure, with layers of distorted hexagonally close-packed oxygen ions separated by an iron double layer with Fe³⁺ occupying two-thirds of the octahedral sites with a – (Fe–O₃–Fe) – stacking sequence along the c axis.¹ Due to this layered structure different surface terminations are, in principle, possible (Fig. 1a–d). They fall into two classes: oxygen termination and iron termination.

Fig. 1 (left panel) Schematic representation (side view) of various surface terminations of the clean α-Fe₂O₃(0001) surface. Large red and small blue spheres represent oxygen and iron ions, respectively. (middle panel) Surface structure (top view) of the respective pristine terminations. All atoms lying below the topmost three layers are faded. (right panel) Surface structure of the considered defective terminations: (e) O_3−x–Fe–Fe–R, (f) Fe–O_3−x–Fe–R, (g) O_1−xFe–O₃–Fe–R, (h) OFe–O_3−x–Fe–R. All atoms lying below the topmost three layers are faded. Arrows point out at the defect sites.

The possible α-Fe₂O₃(0001) surface terminations have attracted a lot of attention both from experimentalists and theoreticians (see ref. 2, 5 and 6 and the references therein). Nevertheless, clear conclusions could not be reached so far. The reason might be that high oxygen pressures are necessary for the preparation of clean surfaces with well-defined structures and composition, which are hard to reconcile with experiments in ultrahigh vacuum environments. Furthermore, the use of photoemission spectroscopy and of scanning tunnelling microscopy is difficult because of the insulating character of hematite. Finally, experimental investigations of the surfaces of both bulk α-Fe₂O₃(0001) and epitaxially grown thin films showed significant variations in the relative stabilities of different surface terminations depending on the method of surface preparation.⁵

The computational results also disagree with each other.^7–11 Density functional theory (DFT) within the generalised gradient approximation (GGA) has shown that the Fe-terminated surface of hematite is preferred at low oxygen pressures and that O-terminated surfaces should occur at increasing oxygen chemical potentials (μ_O), leaving a small stability domain to ferryl-terminated surfaces.^7–9 Inclusion of a Hubbard-type on-site Coulomb repulsion (GGA+U approach) yields a ferryl-terminated surface at high μ_O and Fe-terminated surfaces at low potentials.^8,10 Within GGA+U, the O-terminated surface is out of the physically meaningful range of oxygen chemical potentials. To our best knowledge, more sophisticated computational approaches have not been employed when studying the stabilities of different hematite (0001) surface terminations.

DFT has also been used to study the adsorption of water on hematite surfaces.^9–13 In agreement with experiments^14,15 these studies show that upon water adsorption the hydroxylated terminations appear to be more stable than their dehydroxylated counterparts. However, the localised nature of the 3d states of iron in these studies was not always taken into account. Moreover, the reactivity of hematite surfaces with oxygen vacancy defects has been rarely addressed (see ref. 6 and the references therein).

Here, we examine the adsorption of an isolated water molecule on the pristine and defective α-Fe₂O₃(0001) surfaces, taking different terminations into account. Comparison will be made with α-Al₂O₃ as it shares the corundum structure with α-Fe₂O₃, but belongs to the non-reducible oxides.

2 Computational details

Spin-polarised DFT calculations based on plane-wave basis sets of 500 eV cutoff energy were performed with the Vienna ab initio simulation package (VASP).^16–18 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional¹⁹ was employed. The electron–ion interaction was described within the projector augmented wave (PAW) method²⁰ with Fe (3d, 4s), O (2s, 2p), and H (1s) states treated as valence states. The Brillouin-zone integration was performed on Γ-centred symmetry reduced Monkhorst–Pack meshes using a Gaussian smearing with σ = 0.05 eV, except for the calculation of total energies and densities of states (DOSs). For those calculations, the tetrahedron method with Blöchl corrections²¹ was employed. A 4 × 4 × 1 k-mesh was used in the case of ionic relaxations and 8 × 8 × 1 for single point calculations, respectively.

The DFT+U scheme^22,23 was adopted for the treatment of Fe 3d orbitals, with the parameter U_eff = U − J equal to 4 eV, which yields lattice constants a = 507 pm and c = 1387 pm, an Fe magnetic moment of 4.2μ_B, and a band gap of 2.1 eV for the bulk hematite, in good agreement with the most widely accepted experimental values, a = 504 pm and c = 1375 pm,²⁴ 4.6μ_B²⁵ and 2.1 eV,²⁶ respectively. We note that the band gap of bulk hematite is only 0.4 eV without the U correction, and it increases to 3.4 eV when a hybrid functional (here HSE06²⁷) is used. As suggested in ref. 28, the agreement with experiment can be significantly improved when using a reduced Fock exchange contributing in the HSE functional 12% instead of the standard HSE06 value of 25%. We found the HSE (12%) and PBE+U results to be almost identical to each other. For comparison reasons, selected calculations were performed using the original HSE06 functional.

The compensated polar (0001) hematite surfaces²⁹ were modelled by symmetric slabs. In total, four pristine Fe₂O₃(0001) terminations were considered (Fig. 1a–d). The used supercells contain 21, 23, 19, and 23 atomic layers in the case of Fe–O₃–Fe–R, Fe–Fe–O₃–R, O₃–Fe–Fe–R, and OFe–O₃–Fe–R, respectively, and a vacuum gap of approximately 2600 pm. For all these structures the ions of the 13 middle inner layers were fixed at their bulk positions during the structural optimisation procedure, whereas the positions (x, y, z-coordinates) of all other ions were fully relaxed until forces became smaller than 0.01 eV Å⁻¹. A (2 × 2) supercell in the lateral plane was adopted to allow a sufficient degree of surface reconstruction and non-integer composition ratios. The lattice constant in the lateral plane was set according to the optimised lattice constant of bulk hematite, a = 507 pm.

To quantify the structural stability, we define the surface free energy per unit cell γ at temperature T and pressure p as

Here, G(T, p, {N_i}) is the Gibbs free energy of the slab, and N_i with i = Fe, O are the numbers of iron and oxygen ions. The chemical potentials of Fe (μ_Fe) and O (μ_O) obey the constraint 2μ_Fe + 3μ_O = μ_Fe2O3, where μ_Fe2O3 is the chemical potential of one Fe₂O₃ formula unit in bulk hematite. Here G is replaced by the total energies from DFT+U calculations, neglecting contributions from configurational or vibrational entropies.³⁰ In this approximation μ_Fe2O3, is equal to the DFT+U total energy of bulk hematite per primitive unit cell. Thus, the surface energy per surface area reads
where A is the surface area, the factor 2 accounts for the presence of two identical surfaces in the structural slab model. The chemical potential μ_O can meaningfully vary only within a limited range. At lower limit, reduction of the oxide from Fe₂O₃ to magnetite (Fe₃O₄) will take place. At the upper limit, oxygen starts to condensate at the surface of hematite. These limiting values are given by

3μ_Fe2O3 − 2μ_Fe3O4 ≤ μ_O ≤ ½μ_O2.

The electrically neutral vacancies were created by removing an oxygen atom from the supercells of the same surface periodicity, i.e. (2 × 2). Thereby, the distance between repeated vacancies in the nearest-neighbour cells is larger than 1000 pm. The oxygen defect formation energy is defined as follows

ΔE_def(1/2O₂) = E(Fe_nO_m−1) + 1/2E(O₂) − E(Fe_nO_m)

where E(Fe_nO_m−1) and E(Fe_nO_m) are the energies of the hematite slab with and without oxygen vacancy, respectively, and E(O₂) is the energy of the gas phase oxygen molecule. Vacancies were formed at both sides of the slab.

To study the adsorption of a single H₂O molecule, a (2 × 2) surface cell of the size (101.4 × 101.4) pm was used with one water molecule added from one side of the slab. This corresponds to a quarter monolayer with respect to the surface iron ions. Adsorption energies were calculated as

ΔE_ads = E(H₂O/Fe_nO_m) − [E(Fe_nO_m) + E(H₂O)]

where E(Fe_nO_m) and E(H₂O) are the energies of the isolated hematite slab and water molecule, and E(H₂O/Fe_nO_m) is the energy of their interacting assembly. Dispersion interactions were considered adding a 1/r⁶ atom–atom term as parameterised by Grimme (“D2” parameterisation).³¹ In order to avoid truncation errors the Ewald summation for the dispersion term was performed.³²

The results for the Al₂O₃–H₂O interaction used for comparison were obtained with the same computational settings as for the Fe₂O₃–H₂O interaction. Our results for the water adsorption on the pristine Al₂O₃(0001) surface are in qualitative agreement with previously published data³³ obtained with a slightly different functional (Perdew and Wang 1991³⁴ augmented by the Grimme “D2” term).

3 Results and discussion

3.1 Surface stability

We consider four possible pristine terminations. Three of them are obtained by simple bulk cleavage above the oxygen layer (O₃–Fe–Fe–R, see Fig. 1a), above the Fe double layer (Fe–Fe–O₃–R, see Fig. 1b), and between the Fe layers (Fe–O₃–Fe–R, see Fig. 1c). One further possible termination, shown in Fig. 1d is a single-metal termination capped with O ions atop the metal ions to produce a layer of ferryl (Fe=O) species. As defects play an important role on oxide surfaces and can significantly influence the interaction of water with the surface,³⁵ oxygen surface vacancies (Fig. 1e–h) are also investigated.

Fig. 2 shows the Gibbs free energies per surface area for the studied surface terminations as functions of μ_O. The dashed black vertical lines bracket the allowed range of μ_O (for details, see Section 2). Fe–O₃–Fe–R is clearly the energetically most favourable surface termination. Another Fe-terminated surface, the Fe–Fe–O₃–R structure, was found to be energetically unfavourable over the whole range, except for extremely poor oxygen conditions where the termination is in thermodynamic equilibrium with the magnetite (Fe₃O₄) bulk phase. The O₃–Fe–Fe–R and OFe–O₃–Fe–R are stable only outside of the region of interest under extremely oxygen rich atmosphere. This is consistent with the previously published DFT results for the nondefective Fe₂O₃(0001) surface.⁸

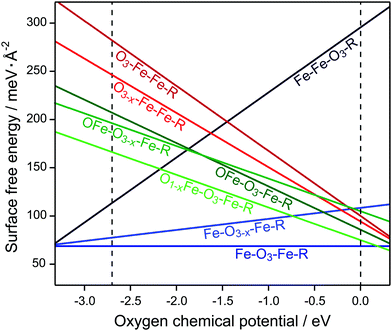Fig. 2 Surface energies of different Fe₂O₃(0001) surface terminations. The dashed vertical lines indicate the allowed range of oxygen chemical potential, μ_O (see text for details).

The overall stability of the Fe–O₃–Fe–R structure may have a very simple explanation as it is the only structure without a notable surface dipole. Furthermore, on structure optimisation the surface Fe ions significantly relax inward, accompanied by charge redistribution in the surface layer. In our calculations, the lowest empty surface state, which has predominantly Fe 3d_z² character, is 1.57 eV above the Fermi level (Fig. 3a).

Fig. 3 Total and site-projected density of states for (a) Fe–O₃–Fe–R and (b) Fe–O_3−x–Fe–R. Fe_S/Fe_S−1/Fe_S−2 denote surface/subsurface/subsubsurface Fe sites. In (b) zoom around E_F is shown as an inset. (c) Top view of the relaxed Fe–O₃–Fe–R structure. Large red and small blue spheres represent oxygen and metal ions, respectively. (d and e) Top views of the relaxed Fe–O_3−x–Fe–R and Al–O_3−x–Al–R structures, respectively, with the corresponding electron densities for a surface oxygen vacancy superimposed.

The O₃–Fe–Fe–R termination has the largest dipole at the surface. This surface termination has a very unfavourable free energy, which decreases fast with increasing μ_O. The O-terminated surface can become more stable, however, upon creation of oxygen vacancies (see Fig. 2). Thus, the O_3−x–Fe–Fe–R and OFe–O₃–Fe–R structures have consistently lower free energies than O₃–Fe–Fe–R for the whole range of μ_O. Creating vacancies in the OFe–O₃–Fe–R surface layer further stabilises this termination, whereas O-vacancies in the subsurface layers of OFe–O₃–Fe–R and Fe–O₃–Fe–R destabilise the respective surfaces. Still, the latter structure is the most stable among all studied defective surfaces, except for high μ_O values.

The defect formation energies show a similar pattern (Table 1): while removing oxygen yields an energy gain in the case of O_3−x–Fe–Fe–R and O_1−x–Fe–O₃–Fe–R, the defective Fe–O_3−x–Fe–R and OFe–O_3−x–Fe–R structures are less stable than the parent terminations. Hybrid functionals yield qualitatively similar results for the relative surface stabilities compared to DFT+U, see ESI† (Fig. S1) for surface free energies obtained with different computational approaches.

Table 1 Oxygen defect formation energies, ΔE_def, and surface free energies, γ (for T = 1100 K, p = 10⁻⁶ mbar), obtained for different Fe₂O₃(0001) surface terminations with PBE+U (available HSE06 results are shown in parentheses)

Structure	ΔEdef(1/2O2)/kJ mol^−1	γ/kJ mol^−1 nm^−2
a 354 kJ mol^−1 if dispersion is taken into account.
Fe–O3−x–Fe–R	337^a (292)	801
O3−x–Fe–Fe–R	−51	2119
OFe–O3−x–Fe–R	166	1738
O1−x–Fe–O3–Fe–R	−91 (−100)	1449

---

Comparison with experiment is not an easy task as different preparation methods can lead to different results and, sometimes, even to different phases being formed. Some studies indicate the coexistence of Fe₂O₃(0001) and FeO(111) phases, see, e.g.ref. 36. Recently, it was shown that the so-called biphase termination of α-Fe₂O₃ is related to a thin overlayer of Fe₃O₄.³⁷ It was proposed that the effect of the metal substrate, often used for preparation of epitaxial thin films, cannot be ignored even in the case of rather thick (10–50 nm) iron oxide layers.^37,38 When growing α-Fe₂O₃ as films on Pt(111), the coexistence of two different domains (a single-metal termination and a ferryl termination) was observed at intermediate pressures, while higher and lower pressures led to one or the other of these domains becoming dominant.³⁹ Contrary to the observations made when growing α-Fe₂O₃ films on metal surfaces, the clean α-Fe₂O₃(0001) surface grown epitaxially (≈35 nm thick) on α-Al₂O₃(0001) is single-Fe-terminated and, in this case, the surface structure of α-Fe₂O₃(0001) is similar to that of α-Al₂O₃(0001) (1 × 1).⁴⁰ There was no evidence for a stable O-terminated surface in this X-ray photoelectron diffraction experiments. The same conclusions were reached when studying the surface of a bulk α-Fe₂O₃(0001) crystal by STM² and LEED.³⁸ Our slabs of around 20 atomic layers model the Fe₂O₃ single crystal surface or a bulk-like thick film. Thus, comparison of the presented results with those of ref. 2, 38 and 40 is adequate and good agreement between calculations and experiment is achieved.

A further possibility to compare our results with experiment provides simulation of STM images (for details, see ESI,† Fig. S3). In agreement with the site-projected density of states calculated for the pristine Fe₂O₃(0001) (see Fig. 3a), one observes imaging of the oxygen sublattice for the bias voltage of −2.5 V (occupied states) and the uppermost Fe sublattice for the bias voltage of +2.5 V (unoccupied states). This is in agreement with the available experimental results for the surface of a bulk α-Fe₂O₃(0001) crystal.²

The results we obtain for α-Fe₂O₃(0001) are in qualitative agreement with the data available for the isomorphic α-Al₂O₃ surface.⁷ The common features are: (i) the single-metal termination is energetically most favourable; (ii) creating O-vacancies in the subsurface layer destabilises the respective surface; (iii) among the O-terminated surfaces, those containing less oxygen ions at the surface are more stable. In the case of (0001) surfaces of hematite and corundum there is only one dominating low energy surface termination in the allowed μ_O range: the single-metal termination. Therefore, from now on, we will focus on this particular surface termination, i.e. Fe–O₃–Fe–R, as well as on the corresponding defective structure, namely Fe–O_3−x–Fe–R.

3.2 Oxygen vacancies

Removal of an oxygen atom reduces the coordination number of the three neighbouring iron ions, leading to strong modification of the local lattice structure. The Fe_S–Fe_S−1–Fe_S−2 triangle (for notations, see Fig. 3c) shrinks and the Fe_S–Fe_S−1 and Fe_S–Fe_S−2 distances become smaller (ca. 5%), whereas the Fe_S−1–Fe_S−2 distance stays almost unchanged. Simultaneously, Fe_S moves inwards, whereas Fe_S−2 and Fe_S−3 are moving out of the surface. Overall, all three metal ions are moving closer to the centre of the triangle, i.e. the former position of O. Similar changes have been observed when comparing Al–O₃–Al–R and Al–O_3−x–Al–R.⁴¹

As result of the O-vacancy (V_O) formation,

[2Fe³⁺,O²⁻] → [2Fe²⁺,V_O] + ½O₂,

two electrons of O²⁻ are left behind and occupy the easily available Fe 3d states on neighbouring Fe_S−1 and Fe_S−2 ions (Fig. 3d).³⁵ (With HSE06 the same conclusion is reached). In the calculated DOS of Fe–O₃–Fe–R a well localised defect state appears in the energy gap just below E_F (Fig. 3b). The DOS of the defective corundum (0001) surface can be found in ref. 41.

In Al₂O₃, the excess electrons localise in the vacancy,

[2Al³⁺,O²⁻] → [2Al³⁺,2e⁻] + ½O₂,

and are stabilised by electrostatic effects only⁴¹ (see also Fig. 3e). The resulting ΔE_def(1/2O₂) for Al₂O₃ is as large as 550 kJ mol⁻¹, much larger than for the reducible Fe₂O₃(0001) oxide (337 kJ mol⁻¹, Table 1).

3.3 Adsorption of an isolated water molecule

3.3.1 Pristine surface. On adsorption of single water molecule attaches with its oxygen atom to an Fe surface ion (Fe–O_H2O distance 217 pm). This molecular adsorption structure, called “M”, is shown in Fig. 4a. The surface iron ion is pulled out of the surface by 24 pm and the water molecule is tilted towards one of the nearest neighbouring oxygen ions with respect to the surface plane allowing the formation of a hydrogen bond with a neighboured surface oxygen ion (H⋯O distance 174 pm). This result differs from the outcome of ref. 12, where a configuration with the water molecule parallel to the surface plane was shown to be energetically more favourable than tilted or perpendicular configurations. Our tests show that the result strongly depends on the force threshold for ionic relaxation (for further details, see ESI,† Fig. S2). Moreover, in the ref. 12 the PBE-GGA functional is used without an U term for the Fe 3d-states whereas we use PBE+U.

Fig. 4 (a–c) Top and side views of the adsorption structures of one water molecule on the pristine single-Fe terminated Fe₂O₃(0001) surface. Large red and small blue spheres represent oxygen and metal ions, respectively. In the top views, all atoms lying below the topmost four layers are faded. The water molecule is shown with orange (larger) and white (smaller) spheres, for O and H respectively. The calculated adsorption energy (kJ mol⁻¹, dispersion included) is given below each individual side-view plot. For comparison the values for the respective structures of the H₂O/Al₂O₃(0001) system are given in parenthesis. The side-view cuts are made perpendicular to the surface through the dashed line as shown in the respective top view.

The tilted structure we find for of a single adsorbed water molecule on Fe₂O₃ is different from the parallel configuration found to be most stable on Al₂O₃(0001).³³

In addition to M, two different dissociated structures, called “D1” and “D2”, were investigated, with an OH⁻ group at the surface Fe ion and a proton either at a neighbouring (Fig. 4b) or a distant surface oxygen ion (Fig. 4c), respectively. Due to the strong interaction between the surface Fe ion and the hydroxyl group, the Fe–O distance is shorter (184 and 185 pm in D1 and D2, respectively) than in M (216 pm). The strong interaction causes also an outward relaxation of a surface cation by 26 pm and 16 pm for D1 and D2, respectively. On protonation, the surface O²⁻ ion is pulled out of the surface by ca. 20 pm and the neighbouring iron ions are pushed away from their positions in the pristine surface.

Fig. 4 shows the same relative stabilities of the three adsorption structures for hematite and corundum (D1 > M > D2), although the binding is much stronger for the corundum surface. This is due to smaller ionic radius for Al³⁺ (54 pm) compared to Fe³⁺ (65 pm).⁴² Compared to PBE+U+D2, HSE06+D2 gives very similar results for the adsorption energy (−100 kJ mol⁻¹, −117 kJ mol⁻¹, and −82 kJ mol⁻¹ for M, D1, and D2, respectively).

3.3.2 Defective surface. Fig. 5 shows the optimised adsorption structures of water on the defective Fe₂O₃(0001) surface. The surface defect binds the H₂O molecule more strongly. Similarly to the adsorption on the pristine surface, the water oxygen atom is attached to the surface Fe ion (M-d in Fig. 5, with an O_H2O–Fe distance of 203 pm) and the surface Fe ion is pulled out of the surface by ca. 15 pm. The water molecule is shifted towards the oxygen vacancy and the hydrogen bond is formed between one of the hydrogen atoms and the neighbouring surface oxygen ions. This bond is apparently stronger than in the case of M, which is reflected by the shorter H⋯O bond distance (147 pm).

Fig. 5 (a–d) Top views of the studied adsorption structures of one water molecule on the defective single-Fe terminated Fe₂O₃(0001) surface. Large red and small blue spheres represent O²⁻ and Fe³⁺ ions, respectively. The water molecule is shown with orange (larger) and white (smaller) spheres, for O and H, respectively. Fe²⁺ ions are shown in black. Arrows point to the defect site. All ions lying below the topmost four layers are faded. For the M-d (a) and D1-d (b) structures side views are given to the right of the corresponding top views. The cut is made perpendicular to the surface through the dashed line. The calculated adsorption energy (kJ mol⁻¹, dispersion included) is given below each individual structure. For comparison, the respective results for the H₂O/Al₂O₃(0001) system are given in parenthesis.

There are two very stable structures, D1-d and D2-d in which water is dissociated into OH⁻ and H⁺, with OH⁻ is filling the oxygen vacancy. The two defect electrons remain localised in Fe-3d states. The proton can be attached to two different oxygen sites. In the D1-d structure the two surface OH groups formed coordinate to the same iron surface ion, whereas in the D2-d structure they are further apart. The former structure is more stable with a binding energy of −236 kJ mol⁻¹ instead of −211 kJ mol⁻¹.

In the D3-d adsorption structure, a hydride (H⁻) ion is occupying the oxygen vacancy position. Formally, it is created when the proton in the vacancy position picks up the two electrons left behind on vacancy formation:

[2Fe²⁺,V_O] + H⁺ → [2Fe³⁺,H⁻]

The latter process is not favourable and, therefore, the D3-d structure is much less stable than the D1-d and D2-d structures.

For Al₂O₃, the relative stabilities of the two different types of structures are reversed. On defect formation, the two electrons left behind fill the vacancy position because there are no d-states available to accommodate the electrons,

[2Al³⁺,O²⁻] → [2Al³⁺,2e⁻] + ½O₂.

The energy released on reaction of the proton with the two electrons in the vacancy site explains the large adsorption energy (−288 kJ mol⁻¹, see Fig. 5d) at the defect site, but in Al₂O₃ the defect is much more difficult to create.

In the D1-d and D2-d structures, the surface iron ion relaxes back closer to the surface plane. In the D3-d structure (as in D1) the OH group is bended slightly towards the vacancy, which is now occupied by the hydride ion. From the energetic point of view this structure is significantly less favourable than the other three structures.

Contrary to Fe₂O₃, for Al₂O₃ both molecular and dissociative adsorption is energetically less favourable at surface defects than at the pristine surface, except when the hydride ion occupies the vacancy site.

Fig. 6 shows different states of water adsorption on the pristine and defective Fe₂O₃(0001) surfaces obtained with PBE+U+D2. The presence of water reduces the defect formation energy and enhances the reducibility. The O-defect formation energy is lowered from 354 kJ mol⁻¹ for the dry surface to 222 kJ mol⁻¹ for the surface with an adsorbed water molecule. In Al₂O₃, the O-defect formation energy is reduced by approximately the same value, 550 kJ mol⁻¹ and 427 kJ mol⁻¹ for the surfaces without and with an adsorbed water molecule, respectively. Dehydrogenation of the hydrated defective surfaces heals the defect. It requires 178 kJ mol⁻¹ and 33 kJ mol⁻¹ for hematite and corundum, respectively, significantly less than water desorption (236 and 288 kJ mol⁻¹, respectively, see Fig. 6).

Fig. 6 Energy diagram (kJ mol⁻¹) for the adsorption of H₂O on the pristine and defective Fe₂O₃ (black) and Al₂O₃ (blue) (0001) surfaces.

3.3.3 Comparison with other iron-oxide materials. For comparison with available studies of other iron oxides with Fe³⁺ surface ions we present in this section our PBE+U results without dispersion correction. We obtained qualitatively similar results with and without dispersion correction.

When comparing the interaction of a water molecule with the three-fold coordinated Fe³⁺ ions in hematite (α-Fe₂O₃(0001)) and magnetite (Fe₃O₄(111)),^43,44 the four-fold coordinated Fe³⁺ ions in goethite (α-FeOOH(101)),⁴⁵ akaganeite (β-FeOOH(100)),⁴⁵ and lepidocrocite (γ-FeOOH(010))⁴⁵ as well as the five-fold coordinated Fe³⁺ ion in magnetite (Fe₃O₄(100))^46,47 (Table 2), the interaction strength decreases with increasing coordination number of the surface iron ion. Dissociated structures are stable only when both iron cations and oxygen anions occur on an oxide surface.

Table 2 Adsorption energies and the equilibrium distances between Fe-ion of the substrate and O of water as obtained for different iron-oxide materials with PBE+U (available PBE+U+D₂ results are shown in parentheses)

Substrate	Coordination number of FeS	Adsorption mode	ΔEads/kJ mol^−1	d Fe–O/pm
a See Fig. 4.
α-Fe2O3(0001)	3	Molecular	−83 (−95)^a	216 (217)
α-Fe2O3(0001)	3	Dissociative	−100 (−104)^a	184 (184)
Fe3O4(111)^43,44	3	Dissociative	−140 (−167)	191
α-FeOOH(101)^45	4	Molecular	−9	236
β-FeOOH(100)^45	4	Molecular	−37	236
γ-FeOOH(010)^45	4	Molecular	3	239
Fe3O4(100)^47	5	Molecular	−38	222
Fe3O4(100)^47	5	Dissociative	−73	184

---

Molecular water binds more strongly on the three-fold coordinated Fe³⁺ ions on the hematite (0001) surface than on the five-fold coordinated Fe³⁺ ions on the magnetite (100) surface which is also reflected in shorter Fe–O_H2O distances (216 pm compared to 222 pm). In both cases, water extends a hydrogen bond to a neighboured surface oxygen ion (note: the presently accepted model of Fe₃O₄(100)⁴⁸ deviates from that utilised in ref. 46 and 47. Still it contains both five-fold coordinated Fe³⁺ and O²⁻ in the surface layer).

Furthermore, for both oxides dissociative adsorption is more favourable than molecular adsorption. However, for magnetite the adsorption energy is not sensitive to the position of the proton on the surface (−70 kJ mol⁻¹ for H⁺ attached to a neighbouring oxygen ion and −73 kJ mol⁻¹ for H⁺ on the more distant surface oxygen ion).^46,47 For hematite the relative positions of the hydroxyl group and the proton are of crucial importance (−100 kJ mol⁻¹ for the nearest oxygen ion vs. −62 kJ mol⁻¹ for the more distant oxygen ion, without dispersion term). Dissociation of a single water molecule was also found when considering the Fe₃O₄(111) surface terminated by octahedrally coordinated iron ions.^43,44

Similarly to hematite, the adsorption on the defective magnetite surface is strongly favourable over adsorption on the pristine one.^46,47 Here quantitative comparison is complicated by the more complex structure of magnetite. The formation energy for an oxygen vacancy varies between 241 and 337 kJ mol^−1 46,47 depending on the presence of tetrahedrally coordinated Fe ions in its neighbourhood. Nevertheless, the general (qualitative) behaviour of the defective Fe₃O₄(100) and Fe₂O₃(0001) is very similar. In both cases, electrons localise on two subsurface iron ions,⁴⁶ dissociative adsorption on the defective surface is favoured over the molecular one, and the OH group, formed on heterolytic dissociation, fills the oxygen vacancy.

4 Conclusion

Relative stabilities of the pristine and defective α-Fe₂O₃ surfaces were studied by density functional theory within the PBE+U(+D2) approach. Even under oxygen rich conditions the metal-terminated surface was shown to be stable. This is in agreement with experiments on single crystals.^2,38,40 On this surface termination isolated water molecules form an dissociated structure with an OH group attached to a surface iron ion and a protonated surface oxygen ion. The isostructural α-Al₂O₃(0001) (corundum) shows a similar behaviour unless the oxygen vacancy is created. The nature of oxygen vacancies is different in reducible (here: α-Fe₂O₃) and non-reducible (here: α-Al₂O₃) oxides.³⁵ In the case of hematite, dissociative adsorption is strongly promoted at the surface defect sites. Here, the electrons left behind on vacancy formation are accommodated into low-lying empty 3d states of the Fe ions. On dissociative water adsorption, the OH⁻ fills the vacancy position. In contrast, in corundum, the vacancy site is filled with two electrons that repel OH⁻. Here, the proton resulting from dissociated water forms a hydride ion (H⁻).

For both Fe₂O₃ and Al₂O₃ the O vacancy formation energy becomes lower if an adsorbed water molecule is present. On increasing the temperature, water would not desorb from the defect site, but rather dehydrogenation accompanied by defect healing will occur.

Among different iron oxides with Fe³⁺ surface ions the strength of the interaction with water molecules depends on the coordination number of the Fe³⁺ ions as well as on the composition of the surface, i.e. the coexistence of oxygen and iron ions in the topmost layer. The adsorption behaviour of water on the Fe₂O₃(0001) and Fe₃O₄(100) surfaces is similar.

Acknowledgements

We thank the German Research Foundation (DFG) for financial support within the Collaborative Research Centre (SFB) 1109 and the North-German Supercomputing Alliance (HLRN) for providing computer time.

References

1. R. M. Cornell and U. Schwertmann, The Iron Oxides, Wiley, Weinheim, 2003.
2. G. E. Brown, V. E. Henrich, W. H. Casey, D. L. Clark, C. Eggleston, A. Felmy, D. W. Goodman, M. Grätzel, G. Maciel, M. I. McCarthy, K. H. Nealson, D. A. Sverjensky, M. F. Toney and J. M. Zachara, Chem. Rev., 1999, 99, 77–174.
3. A. Kay, I. Cesar and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 15714–15721.
4. H. Kuhlenbeck, S. Shaikhutdinov and H.-J. Freund, Chem. Rev., 2013, 113, 3986–4034.
5. D. P. Woodruff, Chem. Rev., 2013, 113, 3863–3886.
6. G. S. Parkinson, Surf. Sci. Rep., 2016, 71, 272–365.
7. X. G. Wang, A. Chaka and M. Scheffler, Phys. Rev. Lett., 2000, 84, 3650–3653.
8. A. Rohrbach, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125426.
9. T. Trainor, A. Chaka, P. Eng, M. Newville, G. Waychunas, J. Catalano and G. Brown, Surf. Sci., 2004, 573, 204.
10. S. Souvi, M. Badawi, J. Paul, S. Cristol and L. Cantrel, Surf. Sci., 2013, 610, 7.
11. M.-T. Nguyen, N. Seriani and R. Gebauer, J. Chem. Phys., 2013, 138, 194709.
12. S. Yin, X. Ma and D. E. Ellis, Surf. Sci., 2007, 601, 2426–2437.
13. S. Yin and D. E. Ellis, Surf. Sci., 2008, 602, 2047–2054.
14. P. Liu, T. Kendelewicz, G. Brown, Jr., E. Nelson and S. Chambers, Surf. Sci., 1998, 417, 53.
15. S. Yamamoto, T. Kendelewicz, J. Newberg, G. Ketteler, D. Starr, E. Mysak, K. Andersson, H. Ogasawara, H. Bluhm, M. Salmeron, G. Brown and A. Nilsson, J. Phys. Chem., 2010, 114, 2256.
16. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
17. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257.
18. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
19. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
20. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
21. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
22. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
23. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
24. L. W. Finger and R. M. Hazen, J. Appl. Phys., 1980, 51, 5362.
25. J. M. D. Coey and G. A. Sawatzky, J. Phys. Chem., 1971, 4, 2386–2407.
26. S. Mochizuki, Phys. Status Solidi A, 1977, 41, 591–594.
27. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
28. Z. D. Pozun and G. Henkelman, J. Chem. Phys., 2011, 134, 224706.
29. P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984.
30. K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406.
31. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
32. T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097.
33. J. Wirth and P. Saalfrank, J. Phys. Chem. C, 2012, 116, 26829–26840.
34. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12947.
35. M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219–270.
36. R. J. Lad and V. E. Henrich, Surf. Sci., 1988, 193, 81–93.
37. C. H. Lanier, A. N. Chiaramonti, L. D. Marks and K. R. Poeppelmeier, Surf. Sci., 2009, 603, 2574–2579.
38. M. Lübbe and W. Moritz, J. Phys.: Condens. Matter, 2009, 21, 134010.
39. X. G. Wang, W. Weiss, S. K. Shaikhutdinov and M. Ritter, Phys. Rev. Lett., 1998, 81, 1038–1041.
40. S. Thevuthasan, Y. J. Kim, S. I. Yi, S. A. Chambers and J. Morais, Surf. Sci., 1999, 425, 276–286.
41. J. Carrasco, J. R. B. Gomes and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064116.
42. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
43. P. Dementyev, K.-H. Dostert, F. Ivars-Barceló, C. P. O Brien, F. Mirabella, S. Schauermann, X. Li, J. Paier, J. Sauer and H.-J. Freund, Angew. Chem., Int. Ed., 2015, 54, 13942–13946.
44. X. Li and J. Paier, J. Phys. Chem. C, 2016, 120, 1056–1065.
45. K. Otte, W. W. Schmahl and R. Pentcheva, Surf. Sci., 2012, 606, 1623–1632.
46. N. Mulakaluri, R. Pentcheva, M. Wieland and W. Moritz, Phys. Rev. Lett., 2009, 103, 176102.
47. N. Mulakaluri, R. Pentcheva and M. Scheffler, J. Phys. Chem. C, 2010, 114, 11148–11156.
48. R. Bliem, E. McDermott, P. Ferstl, M. Setvin, O. Gamba, J. Pavelec, M. A. Schneider, M. Schmid, U. Diebold, P. Blaha, L. Hammer and G. S. Parkinson, Science, 2014, 346, 1215–1218.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05313k

---