Predicting molecular self-assembly at surfaces: a statistical thermodynamics and modeling approach†
Received
28th July 2016
, Accepted 21st October 2016
First published on 21st October 2016
Abstract
Molecular self-assembly at surfaces and interfaces is a prominent example of self-organization of matter with outstanding technological applications. The ability to predict the equilibrium structure of a self-assembled monolayer (SAM) is of fundamental importance and would boost the development of bottom-up strategies in a number of fields. Here, we present a self-consistent theory for a first-principles interpretation of 2D self-assembly based on modeling and statistical thermodynamics. Our development extends the treatment from finite-size to infinite supramolecular objects and delineates a general framework in which previous approaches can be recovered as particular cases. By proving the existence of a chemical potential per unit cell, we derive an expression for the surface free energy of the SAM (γ), which provides access to the thermodynamic stability of the monolayer in the limit of the ideal gas approximation and the model of energetics in use. Further manipulations of this result provide another expression of γ, which makes the concentration dependence as well as the temperature dependence of 2D self-assembly explicit. In the limit of the approximations above, this second result was used to analyze competitive equilibria at surfaces and rationalize the concentration- and temperature-dependent polymorphism in 2D. Finally, the theory predicts that there exists a critical aggregation concentration (Ccac) of monomers above which 2D self-assembly can be viewed as a “precipitation” in a solubility equilibrium. Numerical analysis of thirteen model SAMs on graphene shows that the value of Ccac sets an absolute scale of 2D self-assembly propensity, which is useful to compare chemically distinct and apparently unrelated self-assembly reactions.
Introduction
Molecular self-assembly is one of the most significant phenomena at the nanoscale.1 It is so, not only because it is the basis of life,2 but also because it provides the path of lowest energy consumption to the fabrication of nano-objects with controlled morphologies and properties.3 Among its multiple facets,4 molecular self-assembly at surfaces (Fig. 1) stands out as a prominent example for technological applications. Achieving control over the forces that steer 2D self-assembly by chemical functionalization of the building blocks is key to boost the development of bottom-up approaches in fields as diverse as the nanofabrication of electronic circuits,5 organic electronics,6 sensing,7,8 catalysis,9 energy storage10 and conversion,11,12 and the large-scale production of graphene.13,14
 |
| | Fig. 1 Schematic representation of molecular self-assembly at surfaces. In (a) the free monomers in solution are in equilibrium with finite-size objects physisorbed at the solid–liquid interface. In (b) the monomers are in equilibrium with an extended periodic 2D architecture. | |
Despite the fact that rational design of molecules for biological and pharmaceutical applications is well established, only a few are attempts to formally refine the predictions of self-assembly in materials science.4 In particular, there exists no general framework to assess the thermodynamic stability of the self-assembled monolayer (SAM), predict its polymorphism as a function of temperature,15 solvent,16 or concentration of monomers,17 and/or rationalize competitive self-assembly at surfaces and interfaces.18,19 One major obstacle in this endeavor is that the thermodynamic equilibrium structure of the SAM is the result of a subtle interplay between the energy gained upon molecular adsorption and association and the entropy lost upon surface confinement, whose accurate evaluation is computationally challenging. The numerical evaluation of the (thermodynamic) stability of a given 2D architecture would provide means to access whether the observed SAM is formed under kinetic or thermodynamic control,20,21 which is difficult to access experimentally.
To fill this gap, several theoretical approaches based on modeling and statistical mechanics have been proposed. Following the pioneering work of Reuter and Scheffler on the chemisorption of gases on metal surfaces,22 one prominent class of methods aims at assessing the thermodynamic stability of the SAM through evaluation of its surface free energy, i.e. the reversible work per unit of area to cover a surface by molecular self-assembly. Provided that the chemical potential of the SAM can be accurately accessed from the electronic energy of a model architecture with periodic boundaries,22 this approach quantifies the thermodynamic stability of the monolayer as a function of the chemical potential of the monomers. Unfortunately, the validity of these predictions is mostly limited to chemisorption in a vacuum, where the SAM and the substrate are fully commensurate and the entropy stabilization of the monolayer is insignificant. Nonetheless, the same approach was used to model the 2D self-assembly of a bisterpyridine derivative physisorbed at the liquid–graphite interface, where the SAM and the substrate were not commensurate.23 Despite the fact that the results provided a (qualitative) interpretation of the concentration-dependent 2D polymorphism, the numerical evaluation of the surface free energy of the SAM imposed the use of more approximate force-field calculations and the neglect of the vibrational contribution. In addition, no link was provided between the surface free energy and the actual solute concentration, which is the experimental quantity under control.
A conceptually different approach follows from the early work of Shakhnovich and Whitesides on the quantification of the entropy change in multi-particle self-assembly.24 In this approach, the entropic cost of association is estimated using a simple statistical mechanical model, which provides analytical expressions for the absolute entropy of both the self-assembled and the monomeric states. Following up this work, Lackinger and coworkers developed an original thermodynamic model to quantify both the energy gain and the entropy cost of self-assembly from first principles.20,25 Under the assumptions that the vibrational contribution to the free energy of self-assembly is negligible and that the translational and rotational entropies of the SAM are zero, the thermodynamic stability of a given architecture is quantified by measuring the reversible work (per unit of area) for transferring one monomer from the solution to the monolayer. Although effective, the per molecule and per unit of area approach of Lackinger is not entirely justified and provides no solution to the conceptual problem of dealing with an infinite-sized supramolecular object, whose molecularity is not defined.
To rationalize the equilibrium between distinct polymorphs formed by an alkoxylated dehydrobenzoannulene (DBA) derivative as a function of the concentration of monomers in solution, Lei et al.26 developed a distinct thermodynamic model considering that the interconversion between the dense (linear) and porous (honeycomb) architecture per unit of area must involve the desorption of monomers, which are released in the supernatant solution. Based on this idea, a correlation between the equilibrium constant and the degree of surface coverage of the two polymorphs was established, which provides experimental access to the difference in their thermodynamic stability under the experimental conditions. Extensions of this model to account for both domain-size effects,27 and the entropy associated with solvent coadsorption15 were reported later on. A characteristic result of these approaches is the formulation of a critical concentration to switch between two polymorphs, which is related to the entropy gain going from the dense to the porous SAM.27
In the following, we present a self-consistent framework for the theoretical interpretation of a 2D self-assembly based on modeling and statistical thermodynamics. By introducing the concept of chemical potential per unit cell, we derive a useful expression for the surface free energy of the SAM, which can be numerically evaluated in the limit of the ideal gas and the rigid rotor, harmonic oscillator approximations. This result provides an interpretation of the 2D polymorphism evidenced by scanning probe techniques and allows one to quantify the critical aggregation concentration in 2D self-assembly. In the limit of the approximations introduced, this approach sets the ground for a first principles interpretation of molecular self-assembly at surfaces and interfaces.
Theory
Finite-size 2D self-assembly
Let us consider the spontaneous association (or self-assembly) of freely diffusing molecules in solution into a finite-size supramolecular object at the solid–liquid interface; see Fig. 1a. If we restrict ourselves to monocomponent systems at chemical equilibrium, this process is described bywhere A is the monomeric species, B is the 2D self-assembled architecture, and α is the molecularity of the reaction. Under chemical equilibrium conditions, the chemical potential of the product equalizes that of the reactant (multiplied by their stoichiometric coefficients) such that for eqn (1)By expressing all chemical potentials as a function of their concentration in solution| |  | (3) |
where T is the temperature, C⊖ is the standard concentration, and  is the standard chemical potential of the i-th component, eqn (2) leads to the definition of the equilibrium constant K for the self-assembly reaction
is the standard chemical potential of the i-th component, eqn (2) leads to the definition of the equilibrium constant K for the self-assembly reaction| |  | (4) |
which provides a constraint on the equilibrium concentration of the reactants and products at a given temperature. In the limit of idealized solution behavior, i.e. the particle independence ansatz, and at a constant temperature T and volume V, the chemical potential can be expressed as| |  | (5) |
with qi and Ni being the molecular partition function and the number of molecules of the i-th component, respectively.28 Introducing the rigid rotor, harmonic oscillator (RRHO) approximation and the Born–Oppenheimer hypothesis, the partition function of a freely diffusing monomer in a vacuum can be written in closed form, which provides an approximated expression for the chemical potential of the monomers| |  | (6) |
where n is the number of atoms, m is the molecular mass, IX, IY, IZ are the principal moments of inertia, σ is the symmetry number, νj is the vibrational frequencies, and De is the electronic energy at the ground state. Similarly, the chemical potential of a finite-sized supramolecular object physisorbed on a surface is| |  | (7) |
where the volume V has turned into a surface area S, IZ is the principal moment of inertia of the supramolecule about the axis perpendicular to the surface, the number of vibrational modes has increased to 3n − 3 as one translational and two rotational degrees of freedom are effectively converted into internal vibrations upon 2D confinement, and De includes the interaction with the surface. In the limit of the approximations above, eqn (6) and (7) provide numerical access to the standard chemical potential difference for a finite-sized 2D self-assembly.
Unit-cell chemical potential
The approach presented above is generalized here to self-assembly into infinite, defect-free supramolecular architectures at the solid–liquid interface, which can still be described by eqn (1). In this case and due to the non-finite nature of B, a major concern arises from the molecularity of the reaction, α, which is not defined. Exploiting the periodicity of the SAM, this problem is tackled by expressing the chemical potential of B as a function of the free energy per unit cell, which, as we shall see, is a thermodynamic observable in the limit of infinite 2D architectures. Also, since the number of molecules per unit cell (nuc) is architecture-dependent, it is useful to consider the unit-cell free energy per molecule| |  | (8) |
Hereafter the superscript ′ is used to indicate a quantity that is normalized by nuc; note that for a given architecture of ncells unit cells, the relation nuc·ncells = α holds. By deconvoluting the chemical potential of B into translational, rotational, vibrational and electronic contributions, the unit-cell free energy per molecule is analyzed with α going to infinity. Because the translational contribution grows logarithmically with the mass of the supramolecule (eqn (7)), which is a linear function of α as mB = αmA, its contribution to the unit-cell chemical potential varies as ln(α)/α and goes to zero with increasing α. Thus,| |  | (9) |
A similar conclusion can be drawn for the rotational contribution, which increases logarithmically with the square root of IZ (eqn (7)). In fact, approximating the 2D supramolecule with a solid disk of radius rB, its moment of inertia is IZ = mBrB2 = mBAB/π with mB and AB its mass and surface area. Since the surface area can be expressed as AB = αAA with AA the surface area per monomer, the moment of inertia can be approximated as IZ = α2mAAA/π, which grows quadratically with α. If so, the rotational contribution to the unit-cell chemical potential varies as ln(α)/α, which goes to zero with increasing α| |  | (10) |
More involved is the evaluation of the vibrational contribution. As mentioned above, the internal dynamics of a freely diffusing molecule (or supramolecule) in 2D is described by 3n − 3 vibrational modes, where n is the number of atoms in the supramolecule. Assuming that the internal vibrations of the monomer do not change upon self-assembly, i.e. the rigid-body ansatz, for each monomer addition, two translational and one rotational degrees of freedom are effectively converted into three internal vibrations of the architecture and| |  | (11) |
where m is the number of atoms in the monomer and indexes i and j run over the internal and external vibrations of the monomer in the mean field of the SAM; the latter corresponding to rigid-body oscillations and rocking. Clearly, eqn (11) shows that the vibrational contribution to the unit-cell free energy does not vanish with increasing α. Rather, it converges to a finite value that depends on the chemical nature of the monomers and the architecture. Thus,| |  | (12) |
Finally, using a classical force field representation of interactions, which is pairwise additive, the electronic energy of B is EB = ncellsEuc = αEuc′, such that| | 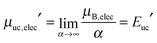 | (13) |
which is independent of α. Moreover, since the energy per unit cell includes contributions from the interaction with the substrate (ads), the interaction between monomers in the monolayer (sam) and the strain energy upon surface confinement (strain), Euc′ can be further decomposed as| | | Euc′ = Eads′ + Esam′ + Estrain′ | (14) |
where Estrain′ is evaluated as the difference in energy between the molecular configuration physisorbed in the mean field of the SAM and the one optimized in isolation. Taken together, the results of eqn (9)–(13) show that the chemical potential per unit cell is| | | μuc′ = Euc′ + μuc,vib′ | (15) |
which has a finite value that is independent of α. Importantly, eqn (15) can be numerically evaluated using an explicit molecular model of the SAM and the substrate.14,29,30 In the limit of sufficiently large supramolecular architectures (α → +∞), eqn (8) yieldswhich shows that the chemical potential of the SAM is a linear function of the chemical potential of one unit cell. Because the translational contribution to the unit-cell free energy vanishes with increasing α (eqn (9)), the chemical potential of an infinite-size 2D architecture is volume- and thus concentration-independent, which implies  . As a result, the assumption that the chemical potential of the SAM is a function of surface coverage26 appears unjustified, at least in the limit of large and crystalline supramolecular architectures.
. As a result, the assumption that the chemical potential of the SAM is a function of surface coverage26 appears unjustified, at least in the limit of large and crystalline supramolecular architectures.
Surface free energy of the SAM
The result of eqn (16) enables one to express the chemical potential difference upon self-assembly as a linear function of α. In fact, introducing the result of eqn (16) into eqn (2) yieldswhich shows that the chemical potential change is proportional to the reversible work of transferring one freely diffusing monomer in solution to the SAM. Although this does not solve the problem of the molecularity for an infinite-sized self-assembly, it has important consequences. In fact, since α is related to the surface area A covered by the SAM14 by| | 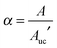 | (18) |
where Auc′ is the area of the unit cell per molecule inside the cell, eqn (17) can be usefully recast in| |  | (19) |
which is now independent of α. This fundamental result yields a numerically accessible expression for the surface free energy of the SAM (γ), which provides access to the thermodynamic stability of 2D self-assembly. Importantly, the use of γ addresses the molecularity issue by expressing the free energy of self-assembly per unit of surface area covered by the SAM. Finally, in the limit of idealized solution behavior and the RRHO approximation, the result of eqn (19) can be separated into energetic (γE) and entropic (γS) contributions as| |  | (20) |
| |  | (21) |
which provide fundamental insights on the key factors affecting the stability of the SAM; see the ESI† for the derivation of eqn (20) and (21).
Since the chemical potential of the unit cell is concentration independent  , introducing the result of eqn (3) into eqn (19) yields a second expression for γ
, introducing the result of eqn (3) into eqn (19) yields a second expression for γ
| |  | (22) |
which makes its dependence on both the concentration of monomers and the density of surface packing (
i.e. the inverse of the unit-cell area) explicit. Finally, when chemical equilibrium between the molecules adsorbed on the surface and those dissolved in the supernatant solution is established,
γ = 0 and
eqn (22) yields
| |  | (23) |
which defines the critical concentration of monomers above which the self-assembled state is preferred. Interestingly,
eqn (23) shows that the critical aggregation concentration is temperature dependent. Assuming that the energetic (
γE) and entropic (
γS) contributions to the standard surface free energy do not vary with temperature,
eqn (22) yields
| |  | (24) |
which expresses the temperature dependence of
γ; note that

as the energetic contribution is volume-independent. Similarly to the critical aggregation concentration,
eqn (24) can be used to define a critical aggregation temperature
| | 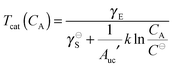 | (25) |
above which 2D self-assembly is disfavored.
Computational methods
The numerical evaluation of the surface free energy was carried out using fully atomistic models of the monomer and the SAM. Due to the large number of atoms involved (up to 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) geometry optimization was based on the classical General Amber Force Field (GAFF),31 which was shown to accurately reproduce the binding energy of small molecules on graphite.32 Although higher levels of theory, e.g. semiempirical quantum mechanics (SQM) or density functional theory (DFT), would be desirable, their use is hindered by the too intense computational effort for non-commensurate physisorbed monolayers.23 The evaluation of γ is based on the calculation of three quantities: the chemical potential of the monomer (μA), the chemical potential of the unit cell of the SAM (μuc′), and the area of the unit cell (Auc′).
000) geometry optimization was based on the classical General Amber Force Field (GAFF),31 which was shown to accurately reproduce the binding energy of small molecules on graphite.32 Although higher levels of theory, e.g. semiempirical quantum mechanics (SQM) or density functional theory (DFT), would be desirable, their use is hindered by the too intense computational effort for non-commensurate physisorbed monolayers.23 The evaluation of γ is based on the calculation of three quantities: the chemical potential of the monomer (μA), the chemical potential of the unit cell of the SAM (μuc′), and the area of the unit cell (Auc′).
First, the chemical potential of the monomeric state (μA) was determined solving eqn (6) on a fully optimized geometry of one monomer in a vacuum. For this purpose, the vibrational frequencies were obtained by normal mode analysis, while the electronic energy De was set as the zero of the energy scale. Because the result of eqn (6) is concentration dependent, i.e. it depends on volume V and the number of molecules N, the value of μA was calculated at the standard concentration of C⊖ = 1 M and then evaluated at any other concentration viaeqn (3). All chemical potentials have been computed at the temperature of 300 K.
The chemical potential of the SAM (μuc′) was obtained from the numerical evaluation of eqn (8) using the “method of the supramolecules”. This implies modeling a series of increasingly larger finite-size architectures, whose chemical potentials in a vacuum can be determined using eqn (7), and solving eqn (8) numerically in the limit of α going to infinity. For each value of α, an atomistic model of the SAM was generated based on high resolution STM images and energy-minimized on top of a graphene layer to resolve steric clashes; see the ESI† for details. Vibrational frequencies were obtained using a reduced basis normal mode analysis,33 where the atomic coordinates of the substrate are kept fixed and the normal modes determined in the mean field of the immobilized substrate. For the evaluation of the electronic contribution (Euc′), we found that eqn (13) converges very slowly with the size of the supramolecule due to border effects, i.e. the large number of molecules sitting at the periphery of the model SAM. Interestingly, a considerably more efficient approach to Euc′ is provided by averaging the result of eqn (14) over the inner (non-peripheral) cells of the 2D architecture. As the internal energy of the monolayer (Esam) can be decomposed into the energy of interaction between the molecules inside the unit cell (Eintra) and energy of interaction with the surrounding cells (Einter)
| | | Esam = Eintra + ½Einter | (26) |
with the factor of 1/2 introduced to avoid double-counting,
34Euc′ can be straightforwardly obtained from a single geometry optimization of a large model SAM followed by a series of single-point energy evaluations using
e.g. the block facility in CHARMM
35 to switch on only the required interactions. Finally, the area of the unit cell (
Auc′) was obtained by averaging over the inner cells of the geometry-optimized 2D architecture.
As a last note, since the chemical potentials of the SAM and monomers were evaluated in the limit of the ideal gas approximation, the calculated surface free energies are systematically affected by the absence of solvent, which leads to a non-realistic overestimation of the chemical potential of the monomer. As we shall see, the introduction of solvent corrections based on an approximated implicit solvent model (see the ESI†) demonstrates the impact of the solvent on the thermodynamics of 2D self-assembly. More quantitative determinations of the surface free energy of the SAM including solvent effects will be reported elsewhere.
Results
Chemical potential of the unit cell
The first theoretical result we want to prove is the existence of a chemical potential per unit cell in 2D self-assembly. This goal implies showing the existence of the limit in eqn (8) or equivalently that the translational, rotational, vibrational, and electronic contributions converge to finite values in the limit of infinite crystalline architectures.
For illustration, we have analyzed the self-assembly of trimesic acid (TMA, see Fig. 2A) on graphite in the characteristic chickenwire architecture (CHK).16 As shown in Fig. 2B, this SAM is characterized by a hexagonal unit cell, which contains two TMA molecules paired by double hydrogen-bonding interactions. These molecules, in turn, interact with the surrounding molecules by forming eight additional hydrogen bonds, which are equally shared among the four neighboring molecules. Both the directionality and the strength of the intermolecular interactions make this SAM an ideal system to study 2D self-assembly.
 |
| | Fig. 2 (A) Chemical structure of trimesic acid (TMA, benzene-1,3,5-tricarboxylic). (B) Unit cell of TMA self-assembly in the chickenwire architecture. (C) Model supramolecular structures used to evaluate the chemical potential of the unit cell in the chickenwire architecture with α equal to 8, 18, 32, 72, 128, and 200 molecules. (D) Translational, rotational, vibrational and electronic contributions per monomer to the chemical potential of the SAM with increasing α. | |
Using the “method of the supramolecules” (see Computational methods), larger and larger architectures were modeled to evaluate the chemical potential per unit cell of the SAM; see Fig. 2C. Various contributions to μuc′ are shown in Fig. 2D with increasing α. As predicted theoretically (see Theory), the translational and rotational contributions rapidly go to zero. The convergence of the vibrational contribution is somewhat slower but its variation with α has a total amplitude that is less than 1 kcal mol−1. Concerning the electronic contribution, two trends are shown in Fig. 2D, which correspond to eqn (13) (red) and eqn (14) (blue), respectively. As discussed above, the evaluation of eqn (13) is suboptimal and converges very slowly with increasing α. In sharp contrast, the result of eqn (14) averaged over the inner unit cells of the 2D architecture (blue points) converges rapidly, although it does so to a significantly lower value. Interestingly, by fitting the red points in Fig. 2D with 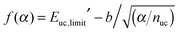 , the value of the unit-cell energy in the limit of infinite architectures is equivalent to that provided by eqn (14); see the ESI† for a derivation of f(α).
, the value of the unit-cell energy in the limit of infinite architectures is equivalent to that provided by eqn (14); see the ESI† for a derivation of f(α).
Based on these results, the energy per unit cell of the chickenwire architecture is −53.5 kcal mol−1. By decomposing this energy in adsorption (Eads′ = −25.7 kcal mol−1), association (Esam′ = −29.1 kcal mol−1) and strain (Estrain′ = 1.3 kcal mol−1) as done in eqn (14), one finds that adsorption and recognition in the SAM introduce similar contributions, whereas the molecular strain is negligible. Perhaps surprisingly, this indicates that although TMA is a relatively small molecule exposing strongly interacting recognition groups, the contribution from physisorption is of the same magnitude as the stabilization arising from H-bonding. Finally, including the vibrational contribution (μuc,vib′ = 81.2 kcal mol−1), eqn (15) yields a μuc′ value of 27.7 kcal mol−1.
To demonstrate the generality of this approach, the convergence of eqn (8) was explored in thirteen chemically diverse SAMs on graphite. The choice of the substrate was just a matter of convenience as both the theoretical results and the computational methodologies are general and valid for any architecture physisorbed on a periodic substrate. The investigated SAMs include: (1) strongly interacting benzenecarboxylic acids, such as isophthalic acid (ISA),36 terephthalic acid (TRA),36 and trimesic acid (TMA);16,37 (2) two bases, N9-ethyl guanine (GUA)38 and melamine (MEL),39 whose self-assembly is steered by multiple hydrogen bonds; (3) a series of linear alkanes with a chain length of twelve that are substituted at one terminus with one carboxylic group (A12),14 one hydroxyl group (B12),40 one chlorine group (L12),41 or nothing (C12);40–42 and (4) two large poly-aromatic hydrocarbons, coronene (COR)30,43 and perchlorocoronene (CLC).30 An illustration of the modeled SAMs, which span a wide range of molecular size, density of packing and energy of interaction is given in Fig. 3. In all cases, the translational and rotational contributions to μuc′ go to zero with increasing α, whereas the vibrational and electronic contributions converge to finite values; see the ESI.† These results demonstrate that in the limit of sufficiently large 2D architectures the chemical potential per unit cell is a thermodynamic observable, which exists independently of the chemical nature and strength of molecular recognition in the SAM.
 |
| | Fig. 3 Modeled self-assembled monolayers and their chemical structures. | |
We note in passing that whereas the vibrational contribution to the chemical potential per unit cell is significant, its contribution to the chemical potential difference is often very small; compare μvib′ with Δμvib′ in Table S3 (ESI†). Nonetheless, analysis of the vibrational entropy contribution to γ for the thirteen SAMs in Fig. 3 suggests that molecular vibrations must be taken into account in two limiting cases: when the SAM is formed by rigid and weakly interacting molecules (e.g. coronene, COR) where the “external” vibrational entropy gain may significantly favor the self-assembled state, or when the SAM is formed by flexible and strongly interacting molecules (e.g. dodecanoic acid, A12) where the “internal” vibrational entropy loss may introduce a non-negligible unfavorable contribution. More details are given in the ESI.†
Concentration-dependent self-assembly
The existence of a chemical potential per unit cell (eqn (15)) provides straightforward access to the thermodynamic stability of the SAM through the evaluation of its surface free energy (eqn (19)). In fact, since γ is proportional to ΔμAB, 2D self-assembly will occur if and only if γ is lower than zero. In addition, since γ is architecture-dependent through both the strength of molecular recognition in the monolayer (Esam′) and the density of packing (Auc′), its numerical evaluation allows one to compare the relative stability of different SAMs, which is useful to explore competitive equilibria at surfaces29,30 and rationalize the concentration-dependent 2D polymorphism.25,26,44
To illustrate this aspect, we analyzed the concentration dependence of trimesic acid (TMA) self-assembly, which was shown by the STM to form three distinct monolayers: (1) the porous hexagonal or chickenwire (CHK) architecture; (2) the slightly more dense flower (FLW); and (3) the densely-packed superflower (SFW); see Fig. 3. In all cases, 2D self-assembly is mediated by strong recognition events based on multiple H-bonding interactions, which promote the formation of linear dimers forming the essential unit of CHK or trigonal trimers that are found both in FLW and SFW. Remarkably, it was shown by the STM under ultra-high vacuum conditions that TMA self-assembly is strongly dependent on the degree of surface coverage, with the porous CHK observed at low coverage, whereas the denser FLW and SFW stabilized at progressively increased coverage.37 To explore the concentration-dependent polymorphism of TMA self-assembly, the three SAMs in Fig. 3 were modeled and their γ determined using eqn (19) at 1 M concentration of monomers. Due to the apparent inability of the GAFF force field to reproduce the dimerization energy of TMA in a vacuum relative to MP2 calculations, both the energy and the chemical potential of the unit cell per architecture were corrected a posteriori based on ab initio calculations with smaller molecular fragments (see the ESI†). The results in Table 1 show that the energetics favor CHK versus FLW and SFW by 1 and 3 kcal mol−1, respectively, due to the stronger interaction per molecule associated with the formation of the linear recognition events. As the monomeric state of the three self-assembly reactions is the same, this trend is also reflected by the standard chemical potential difference per molecule, Δμ⊖′, which favors CHK (Table 1). However, when the density of packing is considered (eqn (19)), the SFW architecture corresponds to the lowest γ and is correctly predicted as the thermodynamic product. This result indicates that at a high concentration of monomers the higher density of packing of SFW, which allows one to dispose more monomers on a given surface area, provides the largest energy gain on self-assembly, despite the fact that this architecture involves weaker recognition events. The situation is different at a lower concentration of monomers, where the formation of more porous architectures such as FLW, which involve less monomers per unit of area, is favored by a lower entropy cost of surface confinement. Indeed, at a monomer concentration of 10−20 M the calculations predict that the FLW architecture is more stable by 0.5 and 0.9 kcal mol−1 nm−2 relative to CHK and SFW, respectively (Table 1). Analogously, at a monomer concentration of 10−25 M the porous CHK is predicted as the stable state. Taken together, these results support the idea that the concentration-dependent 2D polymorphism arises from an energy/entropy compensation, which favors porous architectures at low concentrations of monomers and densely-packed monolayers under saturating conditions.
Table 1 Stability of the three experimental (CHK, FLW, and SFW) and one hypothetical (STR) assemblies of TMA. The first three columns contain the unit cell area, unit cell energy and the difference in chemical potential per molecule, respectively. In the last three columns the value of the surface free energy is reported at three different monomer concentrations
| |
A
uc′ [Å2] |
E
uc′ [kcal mol−1] |
Δμ⊖′ (1 M) [kcal mol−1] |
γ [kcal mol−1 nm−2] |
| 1 M |
10−20 M |
10−25 M |
| CHK |
121.1 |
−53.5 |
−36.3 |
−30.0 |
−7.5 |
−1.8 |
| FLW |
98.2 |
−52.4 |
−35.1 |
−35.7 |
−8.0 |
−1.0 |
| SFW |
76.6 |
−50.1 |
−32.7 |
−42.7 |
−7.1 |
1.8 |
| STR |
117.0 |
−45.2 |
−29.3 |
−25.0 |
−1.7 |
4.1 |
The entropy/enthalpy compensation above is quantitatively expressed by eqn (22), which shows that γ is a linear function of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CA with a negative slope proportional to the density of packing (1/Auc′). This implies that the thermodynamic stability of the SAM (relative to the disassembled state) increases with the concentration of monomers in the supernatant solution but also that densely-packed architectures are intrinsically more sensitive to changes in the monomer concentration. Thus, eqn (22) is useful to compare the stability of different SAMs as a function of concentration and predict the domains of dominance of various morphs. The results for TMA self-assembly at 300 K in a vacuum are shown in Fig. 4. They indicate that at a high concentration of monomers SFW corresponds to the lowest γ. However, because γSFW grows steeper than γFLW, there exists a critical concentration (10−17.9 M) below which the less dense FLW is thermodynamically favored. Similarly, the existence of a second critical concentration corresponding to the phase transition to the porous CHK is predicted at even lower concentrations (10−21.9 M). Finally, at extremely low concentrations (10−26.5 M), there exists a third critical concentration below which the entropically stabilized monomeric state dominates and 2D self-assembly does not occur. Since the 2D switching concentrations predicted for TMA are unphysically low, a correction based on a solvent-accessible surface area was introduced to account for solvent effects (see the ESI†). Interestingly, the inclusion of an approximated solvation free energy contribution up-shifts all critical concentrations by about ten orders of magnitude, yielding qualitatively more reasonable results; see the upper x axis (in blue) in Fig. 4. Finally, by imposing chemical equilibrium between any two observed architectures B and C (i.e. γB = γC) eqn (22) yields
CA with a negative slope proportional to the density of packing (1/Auc′). This implies that the thermodynamic stability of the SAM (relative to the disassembled state) increases with the concentration of monomers in the supernatant solution but also that densely-packed architectures are intrinsically more sensitive to changes in the monomer concentration. Thus, eqn (22) is useful to compare the stability of different SAMs as a function of concentration and predict the domains of dominance of various morphs. The results for TMA self-assembly at 300 K in a vacuum are shown in Fig. 4. They indicate that at a high concentration of monomers SFW corresponds to the lowest γ. However, because γSFW grows steeper than γFLW, there exists a critical concentration (10−17.9 M) below which the less dense FLW is thermodynamically favored. Similarly, the existence of a second critical concentration corresponding to the phase transition to the porous CHK is predicted at even lower concentrations (10−21.9 M). Finally, at extremely low concentrations (10−26.5 M), there exists a third critical concentration below which the entropically stabilized monomeric state dominates and 2D self-assembly does not occur. Since the 2D switching concentrations predicted for TMA are unphysically low, a correction based on a solvent-accessible surface area was introduced to account for solvent effects (see the ESI†). Interestingly, the inclusion of an approximated solvation free energy contribution up-shifts all critical concentrations by about ten orders of magnitude, yielding qualitatively more reasonable results; see the upper x axis (in blue) in Fig. 4. Finally, by imposing chemical equilibrium between any two observed architectures B and C (i.e. γB = γC) eqn (22) yields
| |  | (27) |
which provides the value of the switching concentration between any two B and C architectures as a function of their unit-cell areas and their standard surface free energy. Strikingly, this expression is essentially the same as the one of Bellec
et al.,
27 which was obtained following a completely different approach (see the ESI
† for details).
 |
| | Fig. 4 Surface free energy of the SAM versus monomer concentration for trimesic acid (TMA) self-assembly in the three experimentally observed architectures, i.e. chickenwire (CHK), flower (FLW), and superflower (SFW), plus the hypothetical stripe (STR). The concentration dependence of TMA self-assembly is striking. The calculations indicate that at low monomer concentrations the disassembled state A is favored. By increasing the concentration of monomers, the CHK, FLW, and SFW architectures are predicted to form in this order. In sharp contrast, the value of γ for the STR monolayer is higher than the others at any monomer concentration, indicating that this architecture will not be observed at equilibrium. The x axis at the bottom (black) refers to monomer concentrations in a vacuum, whereas the values on the top (blue) include corrections to account for solvent effects (see the ESI†). | |
Temperature-dependent self-assembly
The result of eqn (24) shows that the surface free energy of the SAM not only depends on the concentration of monomers, but also on the temperature of the system. To explore the temperature dependence of TMA self-assembly, the stability of the three SAMs above was analyzed as a function of temperature at a monomer concentration of 10−9 M using eqn (24). The results in Fig. 5A show that the stability of the SAM decreases with increasing temperature due to the entropic stabilization of the monomeric phase. Similar to the concentration dependence, three switching temperatures exist at 278 K, 364 K, and 317 K, which set the domains of dominance of various SAMs in the temperature space. Interestingly, under the assumption that both the energy and entropy contributions to γ are temperature independent, the switching temperature between any two B and C architectures can be calculated at a given concentration of monomers (CA) from only the knowledge of γE and  and the surface packing of the two SAMs as
and the surface packing of the two SAMs as| |  | (28) |
Finally, combining eqn (25) for the most porous SAM (CHK) with eqn (28) for the concentration dependence of the CHK/FLW and FLW/SFW switching temperatures, a temperature/concentration phase diagram for TMA self-assembly was obtained; see Fig. 5B. The diagram shows that the most dense architecture (SFW) is favored at high concentrations and low temperatures, whereas the monomeric state is most stable at low concentrations and high temperatures. More porous architectures are predicted to appear at intermediate conditions. Interestingly, we predict that for a monomer concentration that is close to the experimental conditions (∼10−9 M) the three architectures may be observed by temperature modulation in a rather narrow range (about 90 K).
 |
| | Fig. 5 (A) Temperature dependence of the surface free energy of the SAMs formed by trimesic acid (TMA) at a monomer concentration of 10−9 M. The densest architecture (i.e. SFW) is most favored at low temperatures. (B) Temperature–concentration phase diagram for the 2D self-assembly of TMA. | |
Competitive equilibria at surfaces
In addition to 2D polymorphism, eqn (22) can be effectively used to rationalize competitive self-assembly equilibria at surfaces. To illustrate this aspect, the 2D self-assembly of coronene (COR) and perchlorocoronene (CLC) were compared. As discussed elsewhere,30 a perchloro functionalization of coronene was found to enhance the 2D self-assembly propensity both energetically and entropically. Using eqn (22), a phase diagram for the competitive self-assembly of these two molecules on graphite can be built by comparing the surface free energy of the corresponding SAMs as a function of the concentration of COR (x axis) versus CLC (y axis) in solution; see Fig. 6. Using the condition γCOR = γCLC to define the phase boundary, which is a straight line in a log–log plot, the domains of dominance of coronene (γCOR < γCLC) versus perchlorocoronene (γCLC < γCOR) self-assembly can be identified. In addition, Fig. 6 shows that at very low concentrations of monomers, neither γCOR nor γCLC is negative and no SAM is formed. Interestingly, the results in Fig. 6 indicate that despite the fact that perchlorocoronene self-assembly is preferred at equal concentrations of coronene and perchlorocoronene in solution, coronene self-assembly can be observed by changing the relative concentrations in solution. Consistently, several examples of deterministic control over the SAM by modulation of the relative concentrations in mixtures have been reported in the literature.18,19
 |
| | Fig. 6 Phase diagram for the competitive 2D self-assembly in coronene/perchlorocoronene mixtures. The solid black lines indicate the critical aggregation concentrations of coronene and perchlorocoronene self-assembly, below which no SAM may form. The red line indicates γCOR = γCLC, which corresponds to equal probability to observe one or the other SAM. Below the red line, the thermodynamic product is the SAM formed by coronene (blue zone). Above the red line, it is the SAM formed by perchlorocoronene (green zone). The dashed line indicates equal concentrations of coronene versus perchlorocoronene in the supernatant solution. | |
Critical aggregation concentration
The last theoretical result we want to discuss is the existence of a critical aggregation concentration (Ccac) in self-assembly at surfaces and interfaces. As shown by eqn (23), the theory predicts that at chemical equilibrium there exists a critical concentration of monomers above which self-assembly occurs. Because Auc′γ⊖ in eqn (23) is equal to Δμ⊖′, which corresponds to the reversible work for transferring one monomer from the solution to the 2D architecture, the theory predicts that such a critical aggregation concentration: (1) is architecture-dependent through the strength of the interactions in the SAM (Esam′ in eqn (14)); (2) it is substrate-dependent through the strength of physisorption (Eads′ in eqn (14)); (3) it depends on the chemical nature of the solvent, whose interaction with the monomers modulates the value of  ; and (4) it is surface-packing independent. Interestingly, since the lower the Ccac, the higher the thermodynamic stability of the SAM relative to the monomeric state under standard conditions, Ccac sets an absolute scale of 2D self-assembly propensity, which can be used to compare chemically distinct and apparently unrelated events.
; and (4) it is surface-packing independent. Interestingly, since the lower the Ccac, the higher the thermodynamic stability of the SAM relative to the monomeric state under standard conditions, Ccac sets an absolute scale of 2D self-assembly propensity, which can be used to compare chemically distinct and apparently unrelated events.
To illustrate this aspect, the critical aggregation concentration was predicted for the thirteen 2D architectures in Fig. 3. To this aim, the value of Ccac was calculated using eqn (23) by modeling the SAM on a single-layer graphene and evaluating Δμ⊖′ based on GAFF force-field calculations in a vacuum. The results in Fig. 7 show that the predicted Ccac spans twenty orders of magnitude. Although the absolute values have little physical meaning, which is due to the absence of the solvent in the calculations, the ranking indicates that the architectures corresponding to the lowest Ccac are those formed by perchlorocoronene (CLC) and trimesic acid (TMA), which share little chemical homology. In fact, while the former is a large polyaromatic hydrocarbon with highly polarizable groups which significantly enhance its physisorption on graphite,30 the latter is a small planar compound that steers the formation of a 2D SAM by strong H-bonding interactions in the monolayer. Analogously, coronene (COR) and N9-ethyl guanine (GUA) are predicted to have similar Ccac values despite being chemically diverse. Thus, these results indicate that similar 2D self-assembly propensities can be achieved by orthogonal chemical strategies.
 |
| | Fig. 7 Critical aggregation concentrations (CAC) for the thirteen SAMs in Fig. 3. For TMA, both the hydrogen-bond corrected (red) and uncorrected (blue) values of the CAC are given (see the ESI†). | |
An interesting comparison is provided by dodecane (C12) and derivatives obtained by chemical functionalization at one terminus via carboxy-(A12), alcohol-(B12), or chlorine-(L12) substitutions. Because these molecules produce compact architectures with comparable unit-cell areas, this analysis illustrates how the thermodynamic stability of the SAM may be modulated by chemical design. As shown in Fig. 7, the introduction of an alcohol or a chlorine group lowers the Ccac value by two orders of magnitude relative to dodecane (C12), whereas chemical functionalization by carboxylic acid substitution does so by five orders of magnitude. Also, the results indicate that chlorine substitution (L12), which enhances surface adsorption relative to C12, versus alcohol functionalization (B12), which strengthens molecular recognition in the SAM by H-bonding, produce similar effects. Taken together and consistent with a recent report by us,30 these results suggest that chemical tailoring of the molecular components is a potentially useful strategy to modulate molecular self-assembly at surfaces and interfaces.
Towards supramolecular engineering
To fully understand the polymorphism observed in competitive equilibria at surfaces in interfaces, it is crucially important to rationalize why alternative and energetically possible supramolecular arrangements are actually not observed. For this purpose, a previously unreported SAM by TMA was used as a model by arranging monomers in a stripe-like (STR) fashion; see Fig. 4. In this architecture, TMA is involved in two linear recognition events along the stripe and one weaker dipolar interaction across the stripes, which effectively corresponds to an out-of-register version of CHK. As shown in Table 1, this model SAM is energetically favorable and slightly more dense than CHK. Analysis of γ in Fig. 4 shows that unlike CHK, FLW and SFW, there exists no concentration of monomers for which γSTR is lowest. Thus, despite the intrinsic energetic stability, there is no thermodynamic reason to observe STR at chemical equilibrium. This interesting observation raises the fundamental question on the requirements for a given architecture to be observed in a concentration dependent STM experiment, i.e. where the concentration of monomers is progressively increased and self-assembly is imaged at the solid–liquid interface.25,26,44 The results shown in Fig. 4 are quite instructive in this respect. In fact, since the slope of γ is proportional to the density of packing (1/Auc′), they explain why the most dense SFW architecture is observed at high concentrations of monomers. In addition, because the strength of the per-molecule interactions in the SAM dictates the value of the critical aggregation concentration, i.e. the intercept on the x axis, they indicate that the emergence of more porous SAMs (i.e. CHK or FLW) can be observed under diluted conditions only when self-assembly involves the formation of stronger recognition events, e.g. the substitution of trigonal (weak) with linear (strong) hydrogen bonds in TMA self-assembly. Finally, Fig. 4 suggests that supramolecular patterns like STR, which are characterized by weaker interactions per molecule and intermediate densities of packing cannot be observed. Based on these observations, we conclude that 2D polymorphism can be predicted by comparing both the energetics and the density of packing of different model architectures. By ranking the SAMs according to their standard chemical potential difference (Δμ⊖′) in ascending order, the sequence of 2D phases can be predicted by searching for less energetically favorable but denser architectures until the most packed one is found. Interestingly, this also implies that the densest architecture will always be observed at high concentrations of monomers and independently of its energetics, provided that this concentration is lower than the monomer solubility in a given solvent. By contrast, porous architectures characterized by weakly interacting building blocks will hardly be imaged at surfaces.
Discussion
Molecular self-assembly at surfaces and interfaces is a prominent example of self-organization of matter with outstanding technological applications. Achieving control over the equilibrium structure of a self-assembled monolayer (SAM) from first principles is key to the development of bottom-up strategies in a number of fields. Following up the seminal work of Reuter and Scheffler,22 we have generalized their theoretical approach and presented a self-consistent framework based on modeling and statistical mechanics for a first-principles interpretation of 2D self-assembly. In the limit of the ideal gas approximation and the accuracy of the model of energetics in use (here molecular mechanics), our approach provides straightforward access to the thermodynamic stability of the SAM, and opens to a quantitative interpretation of the concentration and temperature dependence of 2D self-assembly, competitive equilibria at surfaces and interfaces, and 2D polymorphism. The theoretical results emerging from this development are summarized below along with a discussion of their significance.
First, we have demonstrated the existence of a chemical potential per unit cell of the SAM in the limit of infinite and defect-free architectures. This fundamental result, which is usually taken for granted,20,23,26 shows that the chemical potential per unit cell (and not per molecule) is a thermodynamic observable that is dominated by the strength of molecular adsorption and recognition but that also includes a sizable vibrational contribution, which is usually neglected.20,23,24 The existence of a chemical potential per unit cell provides a simple expression for the surface free energy of the SAM (eqn (19)), which gives numerical access to its thermodynamic stability in the limit of the ideal gas and the rigid rotor, harmonic oscillator approximations. Remarkably, eqn (19) has already been used by us to rationalize the chain-length dependence of the graphite-exfoliation yield in the presence of fatty acids,14 provide an interpretation of competitive self-assembly of three diarylethene photoisomers on graphite,29 and design an improved graphite/graphene surface binder by the perchloro substitution of coronene.30 Interestingly, this expression of γ provides a theoretical foundation to the per molecule, per unit of area approach of Lackinger and coworkers.20,25 Moreover, since the vibrational contribution to the chemical potentials of SAM and monomers are of the same order of magnitude, it justifies the common assumption that the vibrational contribution to the free energy of self-assembly can be safely ignored;20,23 we note however that when the SAM is formed by rigid and weakly-interacting molecules (e.g. coronene) or flexible and strongly-interacting molecules (e.g. dodecanoic acid) the vibrational entropy contribution may be significant (i.e. between 10% and 20%). Finally, in the limit of the introduced approximations, our expression of γ can be straightforwardly separated in energy and entropy contributions, which provide fundamental insight into the key factors controlling the stability of the SAM. In this context, our derivation provides correct expressions for both energy and entropy contributions including e.g. the internal energy of the translations, rotations and vibrations, which was missing in previous work.20 And, the newly introduced decomposition of the unit-cell energy (eqn (14)) provides a general strategy for its numerical evaluation, which is valid even when the molecules within the unit cell are energetically not equivalent.
Simple manipulations of eqn (19) yielded a second important result, which makes the concentration dependence of the surface free energy of the SAM explicit (eqn (22)). In the limit of the model of the energetics, this second result enabled us to study the competition between different SAMs formed by the same building blocks and rationalize the 2D polymorphism evidenced by scanning probe techniques upon varying the initial concentration of monomers. Our analysis of trimesic acid self-assembly (Fig. 4) illustrates that the evaluation of γ per architecture is useful to predict the domains of dominance of various polymorphs, quantify critical concentrations corresponding to 2D phase transitions, and rationalize why alternative and theoretically possible SAMs are not observed experimentally. The fundamental result of eqn (22) shows that the thermodynamic stability of the SAM is strongly dependent on the density of surface packing, i.e. the number of molecules per unit of area, indicating that the higher the density, the stronger the sensitivity of the SAM to the concentration of monomers in solution. This result supports the idea that 2D polymorphism is the manifestation of an enthalpy/entropy compensation, which favors (energy-stabilized) densely-packed architectures at high concentrations of monomers and (entropically-stabilized) porous architectures under diluted conditions.15,26 Importantly, our analysis makes it clear that despite the fact that the densest SAM will always be observed at high monomer concentrations (provided that this concentration is physical and lower than the monomer solubility) a more porous architecture may form under diluted conditions if and only if its energetics per molecule are more favorable than in the denser SAM; i.e. if the former involves stronger recognition events then the latter. Thus, by ranking a series of theoretically possible SAMs formed by the same building block based on the energy gain per molecule on self-assembly, the sequence of 2D morphs in a concentration-dependent STM experiment can be predicted starting from the energetically most favorable architecture and searching for increasingly denser supramolecular arrangements.
Finally, the theory predicts that at chemical equilibrium there exists a critical concentration of monomers (Ccac) above which 2D self-assembly is spontaneous. The expression of Ccac derived here is architecture-, substrate-, and solvent-dependent. Since the lower the critical concentration, the higher the thermodynamic stability of the SAM relative to the monomeric state will be, the value of Ccac sets an absolute scale of 2D self-assembly propensity, which may be used to compare chemically distinct and apparently unrelated events. Intriguingly, the existence of a critical aggregation concentration indicates that 2D self-assembly can be regarded as a “precipitation” in a solubility equilibrium, which does not stop until such a critical concentration of monomer is attained in solution. If so, we predict that if the volume of the supernatant solution is small enough, the critical concentration would be reached before the entire surface is covered and 2D self-assembly would stop at submonolayer coverage. Providing experimental evidence of a concentration-dependent degree of surface coverage, e.g. by STM imaging,25,26,44 would prove the existence of a Ccac in 2D self-assembly. More generally, the actual values of Ccac and/or the 2D switching concentrations in polymorphic self-assembly, which are both computationally and experimentally accessible, may open up to more quantitative interpretations of self-assembly beyond imaging. In this context, experimental determinations of these critical concentrations at a given temperature will provide stringent benchmarks for available thermodynamic models and guide the development of future theoretical and modeling approaches.
A straightforward extension of the theory above provided equations to explore the temperature dependence of molecular self-assembly at surfaces and interfaces. Assuming that both the energy and entropy contributions to the surface free energy of the SAM are temperature independent, eqn (22) provides an expression of γ which makes both the concentration and temperature dependence explicit (eqn (24)). Interestingly, this result indicates that for a given concentration of monomers there exist a critical aggregation temperature (Tcat) above which self-assembly is disfavored and one or more 2D switching temperatures in the case of polymorphic self-assembly. Similar to the critical concentration, experimental determinations of the critical temperature may provide additional benchmarks for the theoretical models. By combining the concentration dependence of Tcat (eqn (25)) with that of the 2D switching temperatures (eqn (28)) a temperature–concentration phase diagram for TMA self-assembly at the solid–liquid interface was derived. Beside the fundamental relevance of this result, which allows one to rationalize both the concentration and temperature-dependence of the surface-induced 2D polymorphism, this analysis suggests that 2D self-assembly is significantly more sensitive to changes in temperature than monomer concentration. Thus, the modulation of temperature15,20 rather than concentration26 appears as a most promising approach to explore structural phase transitions at the solid–liquid interface.
A major shortcoming of the approach presented here is the lack of appropriate treatment of the solvent, which results in non-physical values of the critical aggregation concentrations in 2D self-assembly. To account for solvation effects on 2D self-assembly, a pioneering attempt is the one of Lackinger and coworkers, which provided experimental access to the full enthalpic driving force using a modified Born–Haber cycle.45 In the same spirit, approximated corrections have been introduced computationally based on implicit solvent models46 or molecular dynamics simulations with an explicit treatment of the solvent.45 In this work, the inclusion of corrections based on a solvent-accessible surface area model to account for the desolvation of both monomers and the substrate (see the ESI†) was shown to have dramatic effects on the numerical results, up-shifting the critical concentrations for TMA self-assembly by about ten orders of magnitude. These and previous16 results, which demonstrated the influence of the excluded volume25 and solvent coadsorption on the formation of 2D porous networks,20 strongly support a pivotal role of the solvent on the thermodynamics of 2D self-assembly. Further work in this direction is urgently needed.
Another limitation concerns the treatment of the conformational entropy change, which has been evaluated only in the harmonic limit. To account for anharmonicity, which can be significant for flexible molecules particularly in the monomeric phase, computationally more intensive approaches based on molecular dynamics, e.g. the confinement free-energy method,47,48 could be used. More generally, the development of quantitative models to predict 2D self-assembly beyond the ideal gas and the rigid rotor, harmonic-oscillator approximations is an important step forward, which is left for the future.
In conclusion, we have presented a self-consistent framework for the theoretical interpretation of molecular self-assembly at surfaces and interfaces based on modeling and statistical thermodynamics. In the limit of the approximations introduced, this approach provides numerical access to the thermodynamic stability of the SAM from first principles, which is expected to aid the design of bottom-up approaches in a number of technological applications.
Acknowledgements
Prof. Paolo Samorí and Dr Thomas Hermans are gratefully acknowledged for a critical reading of the manuscript. This work was granted access to the HPC resources of [CCRT/CINES/IDRIS] under the allocation 2015-[076644] made by GENCI (Grand Equipement National de Calcul Intensif). S. C. received support from IdeX (grant no. 16141). Financial support from the International Center for Frontier Research in Chemistry (icFRC) and the Agence Nationale de la Recherche (ANR) through the LabEx project Chemistry of Complex Systems (ANR-10-LABX-0026 CSC) is gratefully acknowledged. We are grateful to Joel Montalvo-Acosta for the solvation free energy calculations.
References
- G. M. Whitesides and B. Grzybowski, Self-assembly at all scales, Science, 2002, 295(5564), 2418–2421 CrossRef CAS PubMed.
- D. J. Kushner, Self-assembly of biological structures, Bacteriol. Rev., 1969, 33(2), 302 CAS.
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Challenges and opportunities for structural DNA nanotechnology, Nat. Nanotechnol., 2011, 6(12), 763–772 CrossRef CAS PubMed.
- C.-A. Palma, M. Cecchini and P. Samorì, Predicting self-assembly: from empirism to determinism, Chem. Soc. Rev., 2012, 41(10), 3713–3730 RSC.
- J. Puigmartí-Luis, A. Minoia, H. Uji-i, C. Rovira, J. Cornil, S. De Feyter, R. Lazzaroni and D. B. Amabilino, Noncovalent control for bottom-up assembly of functional supramolecular wires, J. Am. Chem. Soc., 2006, 128(39), 12602–12603 CrossRef PubMed.
- R. M. Westervelt, Graphene nanoelectronics, Science, 2008, 320(5874), 324–325 CrossRef CAS PubMed.
- Q. H. Wang and M. C. Hersam, Room-temperature molecular-resolution characterization of self-assembled organic monolayers on epitaxial graphene, Nat. Chem., 2009, 1(3), 206–211 CrossRef CAS PubMed.
- T. Zhang, Z. Cheng, Y. Wang, Z. Li, C. Wang, Y. Li and Y. Fang, Self-assembled 1-octadecanethiol monolayers on graphene for mercury detection, Nano Lett., 2010, 10(11), 4738–4741 CrossRef CAS PubMed.
- G. M. Scheuermann, L. Rumi, P. Steurer, W. Bannwarth and R. Mülhaupt, Palladium nanoparticles on graphite oxide and its functionalized graphene derivatives as highly active catalysts for the Suzuki–Miyaura coupling reaction, J. Am. Chem. Soc., 2009, 131(23), 8262–8270 CrossRef CAS PubMed.
- M. Pumera, Graphene-based nanomaterials for energy storage, Energy Environ. Sci., 2011, 4(3), 668–674 CAS.
- P. V. Kamat, Graphene-based nanoassemblies for energy conversion, J. Phys. Chem. Lett., 2011, 2(3), 242–251 CrossRef CAS.
- V. Ferri, M. Elbing, G. Pace, M. D. Dickey, M. Zharnikov, P. Samorì, M. Mayor and M. A. Rampi, Light-powered electrical switch based on cargo-lifting azobenzene monolayers, Angew. Chem., 2008, 120(18), 3455–3457 CrossRef.
- A. Ciesielski, S. Haar, M. El Gemayel, H. Yang, J. Clough, G. Melinte, M. Gobbi, E. Orgiu, M. V. Nardi, G. Ligorio, V. Palermo, N. Koch, O. Ersen, C. Casiraghi and P. Samorì, Harnessing the liquid-phase exfoliation of graphene using aliphatic compounds: A supramolecular approach, Angew. Chem., 2014, 126(39), 10523–10529 CrossRef.
- S. Haar, A. Ciesielski, J. Clough, H. Yang, R. Mazzaro, F. Richard, S. Conti, N. Merstorf, M. Cecchini, V. Morandi, C. Casiraghi and P. Samorì, A supramolecular strategy to leverage the liquid-phase exfoliation of graphene in presence of surfactants: unraveling the role of the length of fatty acids, Small, 2015, 11, 1691–1702 CrossRef CAS PubMed.
- M. O. Blunt, J. Adisoejoso, K. Tahara, K. Katayama, M. Van der Auweraer, Y. Tobe and S. De Feyter, Temperature-induced structural phase transitions in a two-dimensional self-assembled network, J. Am. Chem. Soc., 2013, 135(32), 12068–12075 CrossRef CAS PubMed.
- M. Lackinger, S. Griessl, W. M. Heckl, M. Hietschold and G. W. Flynn, Self-assembly of trimesic acid at the liquid–solid interface a study of solvent-induced polymorphism, Langmuir, 2005, 21(11), 4984–4988 CrossRef CAS PubMed.
- A. Ciesielski, P. J. Szabelski, W. Rżysko, A. Cadeddu, T. R. Cook, P. J. Stang and P. Samorì, Concentration-dependent supramolecular engineering of hydrogen-bonded nanostructures at surfaces: predicting self-assembly in 2D, J. Am. Chem. Soc., 2013, 135(18), 6942–6950 CrossRef CAS PubMed.
- L. Kampschulte, T. L. Werblowsky, R. S. K. Kishore, M. Schmittel, W. M. Heckl and M. Lackinger, Thermodynamical equilibrium of binary supramolecular networks at the liquid–solid interface, J. Am. Chem. Soc., 2008, 130(26), 8502–8507 CrossRef CAS PubMed.
- A. Ciesielski, M. El Garah, S. Haar, P. Kovaříček, J.-M. Lehn and P. Samorì, Dynamic covalent chemistry of bisimines at the solid/liquid interface monitored by scanning tunnelling microscopy, Nat. Chem., 2014, 6(11), 1017–1023 CrossRef CAS PubMed.
- R. Gutzler, T. Sirtl, J. F. Dienstmaier, K. Mahata, W. M. Heckl, M. Schmittel and M. Lackinger, Reversible phase transitions in self-assembled monolayers at the liquid–solid interface: temperature-controlled opening and closing of nanopores, J. Am. Chem. Soc., 2010, 132(14), 5084–5090 CrossRef CAS PubMed.
- U. Mazur and K. W. Hiips, Kinetic and thermodynamic processes of organic species at the solution-solid interface: The view through an STM, Chem. Commun., 2015, 51, 4737–4749 RSC.
- K. Reuter and M. Scheffler, Composition, structure, and stability of RuO2(110) as a function of oxygen pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65(3), 035406 CrossRef.
- C. Meier, M. Roos, D. Künzel, A. Breitruck, H. E. Hoster, K. Landfester, A. Gross, R. J. Behm and U. Ziener, Concentration and coverage dependent adlayer structures: from two-dimensional networks to rotation in a bearing, J. Phys. Chem. C, 2010, 114(2), 1268–1277 CAS.
- M. Mammen, E. I. Shakhnovich, J. M. Deutch and G. M. Whitesides, Estimating the entropic cost of self-assembly of multiparticle hydrogen-bonded aggregates based on the cyanuric acid – melamine lattice, J. Org. Chem., 1998, 63(12), 3821–3830 CrossRef CAS.
- J. F. Dienstmaier, K. Mahata, H. Walch, W. M. Heckl, M. Schmittel and M. Lackinger, On the scalability of supramolecular networks: High packing density vs. optimized hydrogen bonds in tricarboxylic acid monolayers, Langmuir, 2010, 26(13), 10708–10716 CrossRef CAS PubMed.
- S. Lei, K. Tahara, F. C. De Schryver, M. Van der Auweraer, Y. Tobe and S. De Feyter, One building block, two different supramolecular surface-confined patterns: Concentration in control at the solid–liquid interface, Angew. Chem., 2008, 120(16), 3006–3010 CrossRef.
- A. Bellec, C. Arrigoni, G. Schull, L. Douillard, C. Fiorini-Debuisschert, F. Mathevet, D. Kreher, A.-J. Attias and F. Charra, Solution-growth kinetics and thermodynamics of nanoporous self-assembled molecular monolayers, J. Chem. Phys., 2011, 134(12), 124702 CrossRef PubMed.
-
D. A. McQuarrie, Statistical Mechanics, University Science Books, 2000 Search PubMed.
- S. Bonacchi, M. El Garah, A. Ciesielski, M. Herder, S. Conti, M. Cecchini, S. Hecht and P. Samorì, Surface-induced selection during in situ photoswitching at the solid/liquid interface, Angew. Chem., Int. Ed., 2015, 54, 4865–4869 CrossRef CAS PubMed.
- S. Conti, M. G. del Rosso, A. Ciesielski, J. Weippert, A. Böttcher, Y. Shin, G. Melinte, O. Ersen, C. Casiraghi, X. Feng, K. Müllen, M. M. Kappes, P. Samorì and M. Cecchini, Perchlorination of coronene enhances its propensity to self-assembly on graphene, ChemPhysChem, 2016, 17, 352–357 CrossRef CAS PubMed.
- J. Wang, R.
M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS PubMed.
- S. Conti and M. Cecchini, Accurate and efficient calculation of the desorption energy of small molecules from graphene, J. Phys. Chem. C, 2015, 119(4), 1867–1879 CAS.
- B. R. Brooks, D. Janežič and M. Karplus, Harmonic analysis of large systems. I. Methodology, J. Comput. Chem., 1995, 16(12), 1522–1542 CrossRef CAS.
- A. Warshel and S. Lifson, Consistent force field calculations. II. Crystal structures, sublimation energies, molecular and lattice vibrations, molecular conformations, and enthalpies of alkanes, J. Chem. Phys., 1970, 53(2), 582–594 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, CHARMM: the biomolecular simulation program, J. Comput. Chem., 2009, 30(10), 1545–1614 CrossRef CAS PubMed.
- M. Lackinger, S. Griessl, T. Markert, F. Jamitzky and W. M. Heckl, Self-assembly of benzene-dicarboxylic acid isomers at the liquid solid interface: steric aspects of hydrogen bonding, J. Phys. Chem. B, 2004, 108(36), 13652–13655 CrossRef CAS.
- Y. Ye, S. Wei, Y. Wang, X. Shao, X. Xu, F. Cheng, L. Jianlong and K. Wu, A unified model: self-assembly of trimesic acid on gold, J. Phys. Chem. C, 2007, 111, 10138–10141 CAS.
- A. Ciesielski, R. Perone, S. Pieraccini, G. P. Spada and P. Samorì, Nanopatterning the surface with ordered supramolecular architectures of N9-alkylated guanines: STM reveals, Chem. Commun., 2010, 46(25), 4493–4495 RSC.
- A. Ciesielski, S. Haar, G. Paragi, Z. Kupihár, Z. Kele, S. Masiero, C. F. Guerra, F. M. Bickelhaupt, G. P. Spada, L. Kovács and P. Samorì, Supramolecular H-bonded porous networks at surfaces: exploiting primary and secondary interactions in a bi-component melamine–xanthine system, Phys. Chem. Chem. Phys., 2013, 15(30), 12442–12446 RSC.
- C. L. Claypool, F. Faglioni, W. A. Goddard, H. B. Gray, N. S. Lewis and R. A. Marcus, Source of image contrast in STM images of functionalized alkanes on graphite: a systematic functional group approach, J. Phys. Chem. B, 1997, 101(31), 5978–5995 CrossRef CAS.
- Q. Chen, H.-J. Yan, C.-J. Yan, G.-B. Pan, L.-J. Wan, G.-Y. Wen and D.-Q. Zhang, STM investigation of the dependence of alkane and alkane (C18H38, C19H40) derivatives self-assembly on molecular chemical structure on HOPG surface, Surf. Sci., 2008, 602(6), 1256–1266 CrossRef CAS.
- L. C. Giancarlo and G. W. Flynn, Raising flags: applications of chemical marker groups to study self-assembly, chirality, and orientation of interfacial films by scanning tunneling microscopy, Acc. Chem. Res., 2000, 33(7), 491–501 CrossRef CAS PubMed.
- J. Thrower, E. E. Friis, A. L. Skov, L. Nilsson, M. Andersen, L. Ferrighi, B. Jørgensen, S. Baouche, R. Balog and B. Hammer, Interaction between coronene and graphite form temperature-programmed desorption and DFT-vdW calculations: importance of entropic effects and insights into graphite interlayer binding, J. Phys. Chem. C, 2013, 117(26), 13520–13529 CAS.
- X. Shen, X. Wei, P. Tan, Y. Yu, B. Yang, Z. Gong, H. Zhang, H. Lin, Y. Li, Q. Li, Y. Xie and L. Chi, Concentration-controlled reversible phase transitions in self-assembled monolayers on HOPG surfaces, Small, 2015, 11(19), 2284–2290 CrossRef CAS PubMed.
- W. Song, N. Martsinovich, W. M. Heckl and M. Lackinger, Born–Haber cycle for the monolayer self-assembly at the liquid–solid interface: assessing the enthalpic driving force, J. Am. Chem. Soc., 2013, 135, 14854–14862 CrossRef CAS PubMed.
- J. R. Reimers, D. Panduwinata, J. Visser, Y. Chin, C. Tang, L. Goerigk, M. J. Ford, M. Sintic, T. Sum, M. J. J. Coenen, B. L. M. Hendriksen, J. A. A. W. Elemans, N. S. Hush and M. J. Crossley, A priori calculations of the free energy of formation from solution of polymorphic self-assembled monolayers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(45), E6101–E6110 CrossRef CAS PubMed.
- M. Cecchini, S. V. Krivov, M. Spichty and M. Karplus, Calculation of free-energy differences by confinement simulations. Application to peptide conformers, J. Phys. Chem. B, 2009, 113, 9728–9740 CrossRef CAS PubMed.
- J. Esque and M. Cecchini, Accurate calculation of conformational free energy differences in explicit water: the confinement-solvation free energy approach, J. Phys. Chem. B, 2015, 119, 5194–5270 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05249e |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Marco
Cecchini
and
Marco
Cecchini
 *
*

 is the standard chemical potential of the i-th component, eqn (2) leads to the definition of the equilibrium constant K for the self-assembly reaction
is the standard chemical potential of the i-th component, eqn (2) leads to the definition of the equilibrium constant K for the self-assembly reaction








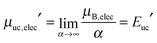
 . As a result, the assumption that the chemical potential of the SAM is a function of surface coverage26 appears unjustified, at least in the limit of large and crystalline supramolecular architectures.
. As a result, the assumption that the chemical potential of the SAM is a function of surface coverage26 appears unjustified, at least in the limit of large and crystalline supramolecular architectures.
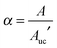



 , introducing the result of eqn (3) into eqn (19) yields a second expression for γ
, introducing the result of eqn (3) into eqn (19) yields a second expression for γ


 as the energetic contribution is volume-independent. Similarly to the critical aggregation concentration, eqn (24) can be used to define a critical aggregation temperature
as the energetic contribution is volume-independent. Similarly to the critical aggregation concentration, eqn (24) can be used to define a critical aggregation temperature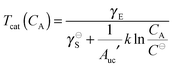
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) geometry optimization was based on the classical General Amber Force Field (GAFF),31 which was shown to accurately reproduce the binding energy of small molecules on graphite.32 Although higher levels of theory, e.g. semiempirical quantum mechanics (SQM) or density functional theory (DFT), would be desirable, their use is hindered by the too intense computational effort for non-commensurate physisorbed monolayers.23 The evaluation of γ is based on the calculation of three quantities: the chemical potential of the monomer (μA), the chemical potential of the unit cell of the SAM (μuc′), and the area of the unit cell (Auc′).
000) geometry optimization was based on the classical General Amber Force Field (GAFF),31 which was shown to accurately reproduce the binding energy of small molecules on graphite.32 Although higher levels of theory, e.g. semiempirical quantum mechanics (SQM) or density functional theory (DFT), would be desirable, their use is hindered by the too intense computational effort for non-commensurate physisorbed monolayers.23 The evaluation of γ is based on the calculation of three quantities: the chemical potential of the monomer (μA), the chemical potential of the unit cell of the SAM (μuc′), and the area of the unit cell (Auc′).
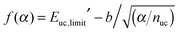 , the value of the unit-cell energy in the limit of infinite architectures is equivalent to that provided by eqn (14); see the ESI† for a derivation of f(α).
, the value of the unit-cell energy in the limit of infinite architectures is equivalent to that provided by eqn (14); see the ESI† for a derivation of f(α).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CA with a negative slope proportional to the density of packing (1/Auc′). This implies that the thermodynamic stability of the SAM (relative to the disassembled state) increases with the concentration of monomers in the supernatant solution but also that densely-packed architectures are intrinsically more sensitive to changes in the monomer concentration. Thus, eqn (22) is useful to compare the stability of different SAMs as a function of concentration and predict the domains of dominance of various morphs. The results for TMA self-assembly at 300 K in a vacuum are shown in Fig. 4. They indicate that at a high concentration of monomers SFW corresponds to the lowest γ. However, because γSFW grows steeper than γFLW, there exists a critical concentration (10−17.9 M) below which the less dense FLW is thermodynamically favored. Similarly, the existence of a second critical concentration corresponding to the phase transition to the porous CHK is predicted at even lower concentrations (10−21.9 M). Finally, at extremely low concentrations (10−26.5 M), there exists a third critical concentration below which the entropically stabilized monomeric state dominates and 2D self-assembly does not occur. Since the 2D switching concentrations predicted for TMA are unphysically low, a correction based on a solvent-accessible surface area was introduced to account for solvent effects (see the ESI†). Interestingly, the inclusion of an approximated solvation free energy contribution up-shifts all critical concentrations by about ten orders of magnitude, yielding qualitatively more reasonable results; see the upper x axis (in blue) in Fig. 4. Finally, by imposing chemical equilibrium between any two observed architectures B and C (i.e. γB = γC) eqn (22) yields
CA with a negative slope proportional to the density of packing (1/Auc′). This implies that the thermodynamic stability of the SAM (relative to the disassembled state) increases with the concentration of monomers in the supernatant solution but also that densely-packed architectures are intrinsically more sensitive to changes in the monomer concentration. Thus, eqn (22) is useful to compare the stability of different SAMs as a function of concentration and predict the domains of dominance of various morphs. The results for TMA self-assembly at 300 K in a vacuum are shown in Fig. 4. They indicate that at a high concentration of monomers SFW corresponds to the lowest γ. However, because γSFW grows steeper than γFLW, there exists a critical concentration (10−17.9 M) below which the less dense FLW is thermodynamically favored. Similarly, the existence of a second critical concentration corresponding to the phase transition to the porous CHK is predicted at even lower concentrations (10−21.9 M). Finally, at extremely low concentrations (10−26.5 M), there exists a third critical concentration below which the entropically stabilized monomeric state dominates and 2D self-assembly does not occur. Since the 2D switching concentrations predicted for TMA are unphysically low, a correction based on a solvent-accessible surface area was introduced to account for solvent effects (see the ESI†). Interestingly, the inclusion of an approximated solvation free energy contribution up-shifts all critical concentrations by about ten orders of magnitude, yielding qualitatively more reasonable results; see the upper x axis (in blue) in Fig. 4. Finally, by imposing chemical equilibrium between any two observed architectures B and C (i.e. γB = γC) eqn (22) yields

 and the surface packing of the two SAMs as
and the surface packing of the two SAMs as
 ; and (4) it is surface-packing independent. Interestingly, since the lower the Ccac, the higher the thermodynamic stability of the SAM relative to the monomeric state under standard conditions, Ccac sets an absolute scale of 2D self-assembly propensity, which can be used to compare chemically distinct and apparently unrelated events.
; and (4) it is surface-packing independent. Interestingly, since the lower the Ccac, the higher the thermodynamic stability of the SAM relative to the monomeric state under standard conditions, Ccac sets an absolute scale of 2D self-assembly propensity, which can be used to compare chemically distinct and apparently unrelated events.






